Structural adaptation of microvessel diameters in response to metabolic stimuli: where are the oxygen sensors?

Abstract

Maintenance of functional vascular networks requires structural adaptation of vessel diameters in response to hemodynamic and metabolic conditions. The mechanisms by which diameters respond to the metabolic state are not known, but may involve the release of vasoactive substances in response to low oxygen by tissue (“tissue signaling”, e.g., CO₂, adenosine), by vessel walls (“wall signaling”, e.g., prostaglandins, adenosine), and/or by red blood cells (RBCs) (“RBC signaling”, e.g., ATP and nitric oxide). Here, the goal was to test the potential of each of these locations of oxygen-dependent signaling to control steady-state vascular diameters and tissue oxygenation. A previously developed theoretical model of structural diameter adaptation based on experimental data on microvascular network morphology and hemodynamics was used. Resulting network characteristics were analyzed with regard to tissue oxygenation (Oxdef; percentage of tissue volume with Po₂ < 1 Torr) and the difference between estimated blood flow velocities and corresponding experimental data [velocity error (V_err); root mean square deviation of estimated vs. measured velocity]. Wall signaling led to Oxdef < 1% and to the closest hemodynamic similarity (V_err: 0.60). Tissue signaling also resulted in a low oxygen deficit, but a higher V_err (0.73) and systematic diameter deviations. RBC signaling led to widespread hypoxia (Oxdef: 4.7%), unrealistic velocity distributions (V_err: 0.81), and shrinkage of small vessels. The results suggest that wall signaling plays a central role in structural control of vessel diameters in microvascular networks of given angioarchitecture. Tissue-derived and RBC-derived signaling of oxygen levels may be more relevant for the regulation of angiogenesis and/or smooth muscle tone.

structural adaptation in response to both hemodynamic and metabolic conditions is necessary for the maintenance of functionally adequate vessel networks (59, 70). If it is assumed that vessel diameters respond only to hemodynamic stimuli, i.e., wall shear stress and intravascular pressure, theoretical arguments show that complex microvascular networks degrade to single arteriovenous shunts (36, 32, 55). Therefore, responses to metabolic signals are needed to generate and preserve multiple parallel flow pathways, which are essential for meeting the metabolic needs of the tissue because of the limited diffusion distance of metabolites, especially oxygen. As a crucial requirement for cell energy metabolism that is contained only in small quantities in tissue, oxygen is of particular importance as a metabolic signal for the adjustment of vessel diameters.

The goal of the present work is to examine the potential ability of several mechanisms of oxygen responsiveness to provide adequate structural control of microvessel diameters. Relatively little direct experimental evidence is available on metabolic control of structural diameter adaptation. Therefore, one may start from considering oxygen response mechanisms involved in the acute control of blood flow, by variation of smooth muscle tone in arterioles and small arteries. These mechanisms may also be involved in structural adaptation, since sustained changes in tone have been shown to lead to corresponding changes of structural vessel diameter (3, 44). However, it should be noted that structural diameter adaptation does not necessarily require preceding changes in smooth muscle tone. As an example, vascular meshes generated by vasculogenesis during embryonic development do not possess proper smooth muscle layers and thus smooth muscle tone. Nevertheless, they remodel to give well-organized microvascular networks exhibiting systematic vessel diameter variation along arteriovenous flow pathways. Similarly, adult capillaries are subject to structural diameter adjustment (23, 41).

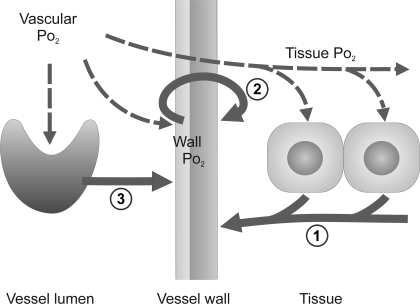
A number of physiological models have been proposed for the mechanism by which vascular diameters respond to local oxygen levels via changes in smooth muscle tone. These models generally assume that vasoactive substances are released at a rate that increases with decreasing local oxygen availability. Three main potential sources for such vasoactive substances have been identified: the parenchymal tissue, the red blood cells (RBCs), and the vessel wall (Fig. 1), as discussed in detail below.

Fig. 1.

Schematic drawing of metabolic signaling mechanisms identified in vivo. Vascular oxygen level affects hemoglobin saturation in red blood cells (RBC) and diffuses to vessel wall and tissue cells (dashed arrows). Resulting local oxygen levels evoke release of metabolic signaling substances from these structures (solid arrows), which, on reaching the vessel wall, cause diameter changes. The corresponding signaling modes investigated in this study are “tissue signaling” (1), “wall signaling” (2), and “RBC signaling” (3).

Several substances are known to be released by tissue cells in an oxygen-dependent manner, evoking vasodilation after diffusion to nearby vessel segments. Among these substances are adenosine, a degradation product of adenosine triphosphate (ATP), that accumulates when oxygen supply and demand are mismatched (6), and carbon dioxide that is produced in proportion to the rate of oxygen consumption and probably acts on vascular smooth muscle cells via a decrease in local pH (8).

Based on findings of oxygen-dependent release of various vasodilators, RBCs have also been suggested to be involved in vascular tone regulation. RBCs were shown to deliver ATP from intracellular pools in association with offloading of oxygen from the hemoglobin (5, 20, 21, 28, 29). Hypoxia was also shown to cause the release of nitric oxide (NO) from RBC hemoglobin via induction of allosteric transition from the relaxed to the tense state (40, 48, 64). A further mechanism involves the deoxyhemoglobin-mediated reduction of nitrite to NO (12, 24, 46).

As a third possibility, the vessel wall itself may generate vasoactive substances in response to changes in local oxygen tension. Various potent vasodilators are produced by endothelial cells in direct response to low Po₂, including NO, prostaglandins, “endothelium-derived hyperpolarizing factor”, and adenosine (9, 14, 19, 31, 43, 45, 50). Alternatively, low oxygen levels may lead to changes in smooth muscle cell function, causing muscle relaxation (for review, see Ref. 65).

The experimental evidence cited above shows the implication of these three different modes of metabolic signaling, referred to in the following as “tissue signaling,” “wall signaling,” and “RBC signaling” for the regulation of vascular tone. Here, we analyze the capability of each of these metabolic signaling modes to control the structural adaptation of vessel diameters in microvascular networks in response to local oxygen levels. A previously developed mathematical model of structural diameter adaptation in terminal vascular beds (55) is used. Such mathematical simulations have the advantage of allowing explicit control of the biological mechanisms represented in the model.

In the model used here, structural adaptation of vessel diameters in microvascular networks with given topologies is simulated by considering the responses of each segment to local hemodynamic and metabolic stimuli, including the contribution of information transfer along the vessel wall. All vessel segments (arterioles, capillaries, and venules) are treated equivalently with respect to their remodeling responses to adaptive stimuli. The model is based on experimental data of complete microvascular networks from the rat mesentery. In the experimental setup used, no significant spontaneous smooth muscle tone was detected in the microvessels analyzed. Thus the measured vessel diameters represent the eventual result of structural vascular adaptation to hemodynamic and metabolic conditions. Correspondingly, only steady-state conditions resulting from long-term vessel diameter adjustment to a maintained metabolic and hemodynamic state are considered.

In the present study, the three metabolic signaling modes (tissue signaling, wall signaling, and RBC signaling) are tested separately. For each mode, simulation results are then compared with experimental data to determine which mode is most consistent with observations and, therefore, most likely to represent an actual mechanism for structural diameter adaptation in vivo.

MATERIAL AND METHODS

Experimental data.

After approval by the University and State authorities for animal welfare, all surgical and experimental procedures were carried out in accordance with the German Animal Protection Act. Microvascular networks in fat-free and lymph vessel-free portions of the mesenteries of two male Wistar rats (∼300 g body wt) from the animal facilities of the Charité Berlin were observed by intravital video microscopy in a scanning procedure lasting ∼20 min, as described previously (54). Heart rate, arterial pressure, anesthetic level, and fluid balance were monitored. In the experimental setup used, no significant spontaneous smooth muscle tone was detected in the microvessels analyzed. The vasodilator papaverine (10⁻⁴ M) was continuously applied to prevent possible development of vascular tone during the scanning procedure. Vessels in the thin mesenteric membrane, as studied here, are known to exhibit only low smooth muscle tone compared with other terminal vascular beds, e.g., in skeletal muscle. The existence of a finite vessel tone before the experiment with the organ still in situ cannot be excluded. However, since there is no indication for any significant tone in situ, the observed (structural) diameters and flow velocities are assumed to constitute the best obtainable data set representing the result of long-term adjustment of vessel diameters to hemodynamic and metabolic conditions.

Diameter, length, hematocrit, and blood flow velocity were measured offline in all segments between branch points using a digital image analysis system. Velocity measurements are based on the principle of spatial correlation analysis, which allows reliable measurements of velocities up to ∼40 mm/s (51, 52). Perfusion rates of all boundary segments were calculated from measured vessel diameters and blood flow velocities. Results are presented for a microvascular network containing 576 vessel segments. The network was supplied with oxygenated blood by a main feeding arteriole (diameter 28 μm, blood flow 410 nl/min) and drained by a main venule (diameter 59 μm), as primary boundaries, and included secondary boundaries: 30 inputs and 4 outputs, with vessel diameters of 10 and 12 μm (median), and blood flow of 3 and 8 nl/min (median), respectively. For comparison, a second mesenteric network with 389 vessel segments was examined.

Reconstruction and discretization.

Arrangement of vessels in the tissue was reconstructed from video recordings offline using network reconstruction software developed in house. Network data were generated by interactively tracing vessel segments as polygonal curves from numerous fields of view that were video recorded during intravital microscopy. The resulting database describes the topological (vessel connection) and the morphological (segmental length, diameter, and location) network structure and was completed with measured vessel parameters (e.g., hematocrit, blood flow velocity).

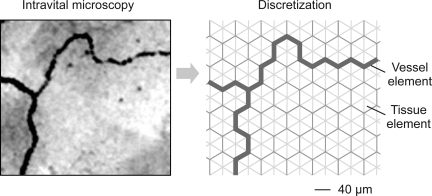
For simulation of diffusive exchange, a discretization approach was used. All vessel segments of the almost planar microvascular network were mapped onto a regular hexagonal (“honeycomb”) grid (Fig. 2). Hexagonal grids were chosen because three grid lines meet at any junction point, corresponding to segments in vascular bifurcations, at a uniform angle of 120° between grid lines. Each vessel segment linking two adjacent bifurcations was converted into a connected series of vessel elements corresponding to the edges of the hexagonal grid. The (three-dimensional) crossing of two segments cannot be directly projected to a two-dimensional grid. Therefore, crossings were represented using the two nodes adjacent to the crossing, with the segments involved crossing in the course of the connecting hexagonal edge between these nodes. On this hexagonal edge, two vessel elements were generated in the model, one for each vessel segment of the crossing, sharing localization in the tissue. The main network studied contained 18 vessel crossings.

Fig. 2.

Approach for definition of vessel elements (grid lines) and tissue elements (triangles) from videomicroscopic recordings by discretization. Locations and connections of vessels visible on videorecordings (left) are used to map the microvascular network to a dense hexagonal grid, with any hexagon being composed of six triangles (right).

A hexagonal edge length of 40 μm, equivalent to about one-tenth of average segment length measured in vivo, was chosen as a compromise between precision of vascular network representation and computational load in simulations. Discretization of curved vessel segments to a series of straight elements usually leads to a summed length of elements that deviates from the measured segment length. To correct for this, a factor was determined for each segment by dividing the measured segment length by the summed length of its vessel elements obtained by discretization. The length of all hexagonal edges of the segment is then multiplied by this factor. The resulting adjusted hexagonal edge length is used for the calculation of diffusive exchange area.

The area of each hexagon was divided into six equilateral triangles, defining tissue elements. Tissue elements were assigned a thickness of 20 μm, according to literature data for the rat mesentery (4). Each tissue element has three neighboring tissue elements (elements with one common edge) and, possibly, one neighboring vessel element (on the hexagonal edge). Each vessel element has neighboring tissue elements at opposing sides.

Discretization of the main mesenteric network, which contains 576 vessel segments, resulted in 4,740 vessel elements and 31,379 tissue elements. Network and tissue parameters were visualized using in-house computer software based on the graphic libraries of OpenGL for graphical presentation of vessel networks and tissue elements.

Model simulation.

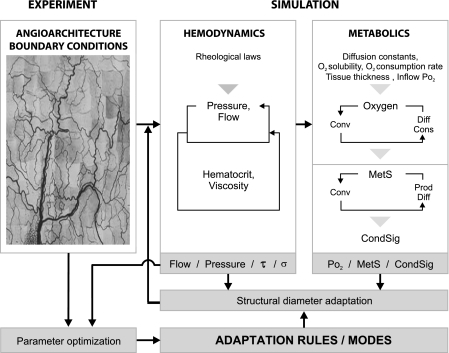
The overall approach used in the theoretical simulations has been described previously (55, 59) and is summarized in Fig. 3. The input to the model consists of experimental data on microvascular network structure and conditions in boundary segments. Based on these data, vascular network hemodynamic parameters are calculated, which serve as the input for the determination of oxygen distribution in vascular network and tissue. Local oxygen content is assumed to stimulate the production of a metabolic signal substance, according to the different modes tested (see below). Starting from experimentally measured diameters for all segments, hemodynamic and metabolic stimuli evoke vessel diameter adjustment in each vessel segment, according to the assumed set of adaptation rules (see below, Adaptation model). The quantitative impact of individual stimuli on segment diameter change is determined by parameters in the adaptation rules, which were optimized via comparison of simulated to experimental blood flow velocities. Physiological constants used in this model are given in Table 1. Adjustment of vessel diameters in the mesenteric vascular network in response to the local oxygenation was simulated, assuming one of the three modes: tissue signaling, wall signaling, or RBC signaling.

Fig. 3.

Simulation of structural diameter adaptation. Experimental data on network structure and rheological laws are used to simulate blood flow, transmural pressure, hematocrit, and viscosity for each vessel segment. Oxygen distribution in the vascular network and the tissue is estimated via an iterative loop, alternately calculating oxygen convection (Conv) in the network and oxygen diffusion (Diff) and consumption (Cons) in the tissue. The adaptation model is shown with shaded background. A metabolic signaling substance (MetS) is produced (Prod), dependent on the calculated local oxygen level, according to the selected mode (tissue signaling, wall signaling, RBC signaling) and undergoes diffusion and convection. Vascular concentration of MetS leads to the generation of a signal that is conducted upstream (CondSig) along flow pathways. Stimuli derived from hemodynamic conditions (flow, pressure, wall shear stress τ, and wall stress σ) and metabolic conditions determine diameter adaptation for each vessel segment, according to an assumed set of adaptation rules. Comparison of simulated with experimental network data is performed to optimize parameters used in the adaptation.

Table 1.

Standard values of model parameters for oxygen transport and consumption

Description	Parameter	Value	Unit	Reference No.
Blood parameters
Oxygen binding capacity of RBC	CRBC	0.52	ml O2/ml	10
Po2 at half-maximal hemoglobin saturation	Po2 50	38	Torr	30
Hill equation exponent	n	3		30
Solubility of oxygen in RBC	αRBC	3.38×10−5	cm3 O2·cm−3·Torr−1	1
Solubility of oxygen in plasma	αpl	3×10−5	cm3 O2·cm−3·Torr−1	33
Krogh diffusion coefficient in plasma	Kpl	8.3×10−10	cm3 O2·cm−1·s−1·Torr−1	33
Tissue parameters
Oxygen diffusion coefficient	Dt	1.04×10−5	cm2/s	69
Solubility of oxygen	αt	3×10−5	cm3 O2·cm−3·Torr−1	69
Krogh diffusion coefficient	Kt = Dt ·αt	3.12×10−10	cm3 O2·cm−1·s−1·Torr−1
Oxygen demand	M0	0.01	cm3 O2·cm−3·min−1	27, 66
Po2 at half-maximal oxygen consumption	P0	1	Torr	13, 62
Thickness of the mesentery		20	μm	4

RBC, red blood cells.

Network hemodynamics.

Input data for the calculation of vascular network hemodynamics comprise morphological data (diameter and length) for each segment and data on network topology (segment connection matrix). Boundary conditions comprise flow or pressure for all segments entering or leaving the network, as well as the discharge hematocrit in all inflow segments. Details of the hemodynamic model (Fig. 3, top middle panel) have been described earlier (61). The flow resistance of each vessel segment is estimated, taking into account the experimentally determined variation of apparent viscosity of blood with vessel diameter and hematocrit, Fahraeus-Lindqvist effect (61), and the phase separation of RBCs and plasma in diverging bifurcations (60). Blood flow for each segment is determined by alternately calculating rheological parameters (segment hematocrit, viscosity) and hemodynamic parameters (segment blood flow, nodal pressure) until stable values are achieved. Values of wall shear stress in each segment are calculated from the pressure, diameter, and length values.

Oxygen distribution.

The input to the determination of oxygen distribution consists of topological data (tissue and vessel element arrangement) and morphological data (tissue element edge length and height, vessel element diameter and length), and of vessel network convective transport characteristics (blood flow and discharge hematocrit for each segment). Steady-state oxygen distribution in the vascular network and the surrounding tissue is determined by iteratively calculating oxygen convection in the vascular network, oxygen diffusion and oxygen consumption by the tissue (Fig. 3, top part of top right panel), until convergence is achieved (average change of tissue Po₂ < 10⁻³ Torr). The model obeys mass conservation, and the difference between total oxygen inflow and outflow equals the summed oxygen consumption by the tissue, assuming zero diffusive flux at the outer boundaries of the tissue region considered.

A finite difference model of oxygen transport was developed using the vessel elements (subscript “ves”) and tissue elements (subscript “tis”) generated as described above. Each element is characterized by a single Po₂. In the model, a linear Po₂ gradient between centers of neighboring elements is assumed. This gradient is estimated as ΔPo₂/Δs, where Δs is the distance between these centers. Temporal discretization to time intervals Δt was performed using an explicit single-step procedure in which new parameter values are derived from values at the previous step.

The convective oxygen flux (J_O2^conv) of a vessel element is determined, considering both hemoglobin-bound oxygen and oxygen dissolved in RBCs and plasma, according to

$$J_{{\mathrm{O}}_2}^{\text{conv}}=\mathrm{Q}{\mathrm{c}}_{\text{ves}}$$ (1)

$${\mathrm{c}}_{\text{ves}}={\mathrm{H}}_{\mathrm{D}}{\mathrm{C}}_{\text{RBC}}\mathrm{S}{\mathrm{o}}_2(\mathrm{P}{\mathrm{o}}_{2\text{ves}})+{\mathrm{H}}_{\mathrm{D}}{\alpha }_{\mathrm{R}\mathrm{B}\mathrm{C}}\mathrm{P}{\mathrm{o}}_{2\text{ves}}+(1-{\mathrm{H}}_{\mathrm{D}}){\alpha }_{\text{pl}}\mathrm{P}{\mathrm{o}}_{2\text{ves}}$$ (2)

and Q is blood flow, c_ves is oxygen volume concentration of the blood, H_D is discharge hematocrit; C_RBC is oxygen-carrying capacity of erythrocytes, Po_2ves is Po₂ of the vessel element, and α_RBC and α_pl are oxygen solubility in RBCs and plasma, respectively. Differences between plasma and intraerythrocyte Po₂ are neglected (25). Erythrocyte oxygen saturation (So₂) as a function of Po₂, So₂ (Po_2ves), is determined according to the Hill equation, So₂ (Po_2ves) = Po_{2 ves}ⁿ/(Po_{2 ves}ⁿ+ Po_{2 50}ⁿ), assuming values typical for rat blood for the Hill coefficient (n) and the half-saturation oxygen pressure (Po_{2 50}) (Table 1).

Oxygen diffusion is assumed between tissue elements and between tissue elements and all types of vessels (arterioles, capillaries, venules). Within the tissue, oxygen consumption, diffusivity, and solubility are assumed to be uniform. Oxygen diffusion rate (J_O2^diff) is described according to Fick's law of diffusion by

$$J_{{\mathrm{O}}_2}^{\text{diff}}=-KA\frac{\Delta \mathrm{P}{\mathrm{o}}_2}{\Delta \mathrm{s}}$$ (3)

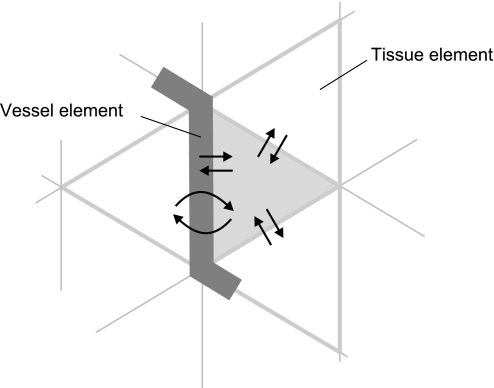
where K is the Krogh diffusion coefficient of tissue or blood plasma, i.e., the product of oxygen solubility and oxygen diffusion coefficient. For diffusion between two tissue elements, the area for diffusive exchange (A) corresponds to hexagonal edge length, multiplied by the thickness of the tissue, reduced by the vessel element diameter in the presence of a vessel element. For diffusion between a tissue and a vessel element, width and height of the diffusion area are the adjusted length of the vessel element and one-half of the vessel element perimeter, respectively. If the diameter of the vessel element exceeded the assumed thickness of the tissue of 20 μm, the thickness of adjacent tissue elements was increased to equal the vessel diameter (4). For each diffusion time step and each element, diffusive oxygen exchange rate J_O2^diff with all neighboring elements is calculated (Fig. 4).

Fig. 4.

Simulation of oxygen diffusion in the finite difference model of oxygen transport. Any finite element is assumed to exchange oxygen by diffusion with all neighboring elements, resulting in a net oxygen loss or gain for each element. For a selected tissue element (shaded triangle), simulated exchange processes with its neighboring vessel and tissue elements are indicated by arrows.

Rate of total diffusive oxygen loss (J_{O2 tot}^diff) for tissue and vessel elements is determined from all individual exchange processes with neighboring elements according to

$$J_{{\mathrm{O}}_2\text{tot}}^{\text{diff}}=K{\displaystyle \sum _{i}Ai}\frac{\mathrm{P}{\mathrm{o}}_2-\mathrm{P}{\mathrm{o}}_{2i}}{\Delta Si}$$ (4)

where i enumerates all neighboring vessel and tissue elements of the element under consideration, Po₂ is the Po₂ of this element. For neighboring element i, Po_2i is the Po₂, A_i is the area for diffusive exchange with the element under consideration, and Δs_i is the distance of its center to the center of the element under consideration.

The oxygen consumption rate (M) of the tissue is assumed to depend on Po₂, according to Michaelis-Menten kinetics with

$$\mathrm{M}(\mathrm{P}{\mathrm{o}}_{2\text{tis}})={\mathrm{M}}_0\frac{\mathrm{P}{\mathrm{o}}_{2\text{tis}}}{{\mathrm{P}}_0+\mathrm{P}{\mathrm{o}}_{2\text{tis}}}$$ (5)

where M₀ is oxygen demand, i.e., consumption when oxygen supply is not limiting, Po_2tis is the Po₂ of the tissue element, and P₀ is the Po₂ at which oxygen consumption equals 50% of demand (Table 1). Experimental data on the oxygen demand in the rat mesentery differ significantly. Reported values include, e.g., 60 nl O₂·cm⁻³·s⁻¹ (∼0.004 cm³ O₂·cm⁻³·min⁻¹) (27) and 2.4 × 10⁻⁴ ml O₂·cm⁻³·s⁻¹ (∼0.014 cm³ O₂·cm⁻³·min⁻¹) (66). In the model, M₀ was set to 0.01 cm³ O₂·cm⁻³·min⁻¹ as a compromise between such experimental data. Based on literature data on intra- and extravascular Po₂ values (16, 17, 68) and corresponding to studies by Pittman and coworkers (49, 67), the vessel wall was considered as part of the tissue.

In each step (k) of the iterative scheme, oxygen volume concentration (c) and Po₂ in tissue and vessel elements of the preceding time step (k − 1) are used to calculate oxygen diffusion, consumption, and convection, resulting in updated values of c and Po₂. First, for all finite elements (vessel elements, tissue elements), the oxygen diffusion exchange with all directly neighboring elements is calculated using Po₂ values of the previous time step for all elements, and the rate of total diffusive oxygen loss, J_{O2 tot}^{diff (k)}, is determined according to Eq. 4.

Next, oxygen content (Vo₂) and oxygen volume concentration in each element are updated. In tissue elements, Vo₂ of the actual time step is determined by subtracting (adding) the total diffusive oxygen loss (gain) and the amount of oxygen consumed per time interval from Vo₂ of the previous time step according to

$$\mathrm{V}{\mathrm{o}}_{2\text{tis}}^{(k)}=\mathrm{V}{\mathrm{o}}_{2\text{tis}}^{(k-1)}-[{\mathrm{J}}_{{\mathrm{O}}_{2^{\text{tot},\text{tis}}}}^{\text{diff}(k)}+\mathrm{M}(\mathrm{P}{\mathrm{o}}_{2\text{tis}}^{(k)}){\mathrm{V}}_{\text{tis}}]\Delta t$$ (6)

where V_tis is the volume of the tissue element. Vo₂ is used to calculate the oxygen volume concentration according to c_tis^(k) = Vo_{2 tis}^(k)/V_tis.

In vessel elements, updating Vo₂ content combines the consideration of diffusive oxygen loss to the tissue and of convective oxygen transport through the network. Starting with the known oxygen inflow in input boundaries, J_{O2 in,ves}^conv of all vessel elements is updated along flow pathways using the oxygen outflow (J_{O2 out,ves}^conv) their respective feeding vessel elements. J_{O2 out,ves}^conv is calculated from the flow rate and the oxygen volume concentration of the outflowing blood (c_out,ves). Vo_2,ves^(k) is then determined on the basis of oxygen mass balance in the vessel, considering the intravascular V̇o₂ and oxygen transport by convection and diffusion as

$$\mathrm{V}{\mathrm{o}}_{2,\text{ves}}^{(k)}={\mathrm{V}}_{\text{ves}}\frac{{\mathrm{c}}_{\text{in},\text{ves}}^{(k)}+{\mathrm{c}}_{\text{out},\text{ves}}^{(k)}}{2}=\mathrm{V}{\mathrm{o}}_{2,\text{ves}}^{(k-1)}+(J{\mathrm{o}}_{2\text{in},\text{ves}}^{\text{conv}(k)}-J{\mathrm{o}}_{2\text{out},\text{ves}}^{\text{conv}(k)}-J{\mathrm{o}}_{2\text{tot},\text{ves}}^{\text{diff}(k)})\Delta t$$ (7)

where V_ves is the volume of the element and c_ves^(k) = (c_in,ves + c_out,ves^(k))/ 2 is the mean oxygen volume concentration in the vessel element. The mean oxygen volume concentration in the vessel element is determined by c_ves^(k) = [c_in,ves^(k)+ c_out,ves^(k)]/2 and is used to calculate the new Vo₂ according to Vo_{2 ves}^(k) = c_ves^(k) V_ves.

Finally, Po₂ is updated in each element using c^(k). In tissue elements, Po_2tis is calculated according to Po_{2 tis}^(k) = α_tc _tis^(k), where α_t is the solubility of oxygen in the tissue. In vessel elements, Po_2ves and So₂ are determined by an iterative solution of Eq. 2. Calculations are repeated until the average change of tissue Po₂ between two consecutive time steps is smaller than the set criterion (average change of Po_2tis < 10⁻³ Torr).

For validation of the O₂ transport model simulation, a theoretical test system was created. The test system consisted of one vessel segment and a large, adjacent tissue region, which was completely avascular to avoid interactions with other segments. The simulated Po₂ profile along a line perpendicular to the vessel wall meets theoretical expectations of an exponential oxygen decline within the tissue and lies within the brackets of different in vivo findings for the rat mesentery using the phosphorescence quenching method (27, 66). An alternative approach to validate the present model is the analysis of overall oxygen extraction in the vascular network. For the network studied, the model predicts an arteriovenous Po₂ decline of 8.4–19.5 Torr in dependence on the Po₂ assumed for the main arteriole of 70–95 Torr. This corresponds to experimental findings in the rat mesentery of 12.8 Torr (26).

Adaptation model.

The adaptation model (Fig. 3, bottom, gray background) is based on the hypothesis that the steady-state vessel diameter of each vessel segment is determined by responses to several stimuli derived from local hemodynamic and metabolic conditions/signals. A logarithmic relationship between signal and evoked adaptive stimulus was assumed in accordance with the Weber-Fechner law. Diameter changes triggered by these stimuli are assumed to be governed by the same rules in all segments of the network. The diameter adaptation process is inherently unbounded, and the final (steady-state) diameter of a given vessel is only determined by the adaptive stimuli, derived from the surrounding conditions, and the assumed adaptation rules.

For each vessel segment, the sum of hemodynamic and metabolic stimuli gives the net adaptive stimulus S_tot, which determines the change (ΔD) of the vessel diameter (D) per time step (Δt) according to

$$\frac{\Delta D}{\Delta t}={\mathrm{S}}_{\text{tot}}•D$$ (8)

with

$${\mathrm{S}}_{\text{tot}}=k_{\mathrm{h}}({\mathrm{S}}_{\tau }+k_{\mathrm{p}}{\mathrm{S}}_{\mathrm{p}})+k_{\mathrm{m}}({\mathrm{S}}_{\mathrm{m}}+k_{\mathrm{c}}{\mathrm{S}}_{\mathrm{c}})-k_{\mathrm{s}}$$ (9)

Hemodynamic stimuli (S_τ, S_p) are derived from local wall shear stress (τ) and transmural pressure (p), respectively. Metabolic stimuli (S_m, S_c) correspond to the local concentration of a metabolic signal substance at the vessel wall and to a conducted signal, respectively (see below). The constants k_h and k_m determine the impact of overall hemodynamic and of metabolic stimuli for diameter adjustment, respectively. Because the net adaptive stimulus S_tot is zero in the equilibrium state, only the relative strength of hemodynamic and metabolic stimuli is relevant, and k_h was set to 1. Thus the relative impact of metabolic stimuli compared with hemodynamic stimuli is determined by k_m. The constant k_p is used to weigh the relative impact of pressure effects to shear stress effects. The constant k_c relates the effects of conducted stimuli to the effects of stimuli derived from local metabolite concentration.

The parameter k_s was introduced into the model to balance the effect of adaptive stimuli for vessel diameter adjustment derived from wall shear stress and the metabolic situation, which are assumed to evoke diameter increase (see below). Thus k_s can be interpreted mathematically as a construct to allow the achievement of equilibrium. On the other hand, k_s can be interpreted biologically to represent a “shrinking tendency” of vessels in the absence of positive growth stimuli. This is in accordance with results in experimental studies, showing atrophy or degradation in the absence of positive trophic stimuli, e.g., in unloaded or denervated muscles, and in cell cultures if no growth/survival factors are added to the culture medium.

Vessel diameter adaptation is simulated as an iterative process, alternately updating surrounding conditions (hemodynamic, metabolic) and vessel diameters. Since no information on dynamics of adaptive response of vessel diameters is included in the present approach, the time step duration Δt is an arbitrary parameter.

Increased wall shear stress is assumed to lead to an increase in vessel diameter, and the signal from wall shear stress was calculated as S_τ = log [(τ + τ_o)/ε], where τ_o [τ_o = 0.103 dyn/cm² (56)] is a small constant included to ensure that S_τ remains bounded for very low shear stress values. The dimensional constants ε (numerical value of 1) here and in the following equations are introduced to ensure correct dimensions.

The stimulus caused by transmural pressure is assumed to decrease vessel diameter and is calculated as S_p = −log [τ_e(p)/ε], assuming that the transmural pressure (p) controls the set point of the vascular feedback control to shear stress τ_e(p). According to experimental data, this set point level τ_e(p) increases sigmoidally with p as τ_e(p) = [100 − 86 exp(−5,000 {log [log (p/ε)]}^5.4)]ε (58).

The metabolic signals are assumed to correspond to the local Po₂ or So₂. According to the aim of the present study, three metabolic signaling modes were implemented, with rules for release of the metabolic signaling substance exhibiting the same general structure. The signal substance is assumed to be released at a rate J_m (measured in arbitrary units), depending on the following: 1) the oxygen-dependent hypothetical vasoactive metabolic signal substance is generated if Po₂ (So₂) in the respective oxygen-sensing structure falls below a reference level (Po_2ref, So_2ref), assuming a linear increase of production rate with decreasing V̇o₂. The oxygen-dependent signal is set to zero, in case the present value exceeds the reference value; 2) the size of the substance-releasing structure; and 3) a scaling constant β_X introduced to guarantee that, under “baseline” conditions, i.e., assuming experimental segment diameters, the total amount of metabolite released per time is the same for all tested modes. Metabolite release resulting from tissue signaling was arbitrarily chosen as a reference, setting the respective scaling constant, β_T, to 1. The scaling constants for wall signaling, β_W, and RBC signaling, β_RBC, were adjusted accordingly.

In tissue signaling, signal substance is released from each tissue element according to

$$J_{\mathrm{m}}=(1-\frac{\mathrm{P}{\mathrm{o}}_{2\text{tis}}}{\mathrm{P}{\mathrm{o}}_{2\text{ref}}}){\mathrm{V}}_{\text{tis}}{\beta }_{\mathrm{T}}$$ (10)

where the size of the substance-releasing structure is represented by the volume of the tissue element (V_tis).

In wall signaling, substance release was assumed to occur in proportion to segment length (L), with substance flux added to the blood calculated as

$$J_{\mathrm{m}}=(1-\frac{\mathrm{P}{\mathrm{o}}_{2\text{seg}}}{\mathrm{P}{\mathrm{o}}_{2\text{ref}}})L{\beta }_{\mathrm{W}}$$ (11)

with β_W = 1.38. For a given Po₂, the evoked relative diameter change (ΔD/D) was assumed to be identical in vessels of equal length and flow rate, which requires the generation of identical metabolic stimuli (S_m) in these vessels. As S_m is assumed to depend on the metabolite concentration in the flowing blood (see below, Eq. 14), respective metabolite release rates from the vessel wall have also to be identical, although these vessels may exhibit differing inner surface areas due to unequal diameters. Consequently, metabolite release was assumed to be independent of vessel diameters.

In RBC signaling, corresponding to experimental findings on ATP release from erythrocytes (39), signal substance is released in response to the local value of So₂ and in proportion to the local (tube) hematocrit (H_T) according to

$$J_{\mathrm{m}}=(1-\frac{\mathrm{S}{\mathrm{o}}_{2\text{seg}}}{\mathrm{S}{\mathrm{o}}_{2\text{ref}}}){\mathrm{V}}_{\text{seg}}{\mathrm{H}}_{\mathrm{T}}{\beta }_{\text{RBC}}$$ (12)

(β_RBC = 0.03), where So_2seg and So_2ref are So₂ for the average Po₂ of the segment and for the reference oxygen partial pressure, respectively; V_seg is the intravascular volume.

In tissue signaling, the metabolic signal substance reaches wall and lumen of vessel segments only after diffusion. A diffusion coefficient of D_met = 4 × 10⁻⁶ cm²/s, as determined for nucleotides (18, 35), was used. In contrast, the metabolic signaling substance is delivered into the flowing blood directly in wall signaling and RBC signaling. The metabolic signal substance entering the segment lumen locally in each vessel segment (J_m,seg) is added to the amount of metabolic signal substance convected from upstream regions (J_m,seg^up), resulting in substance flux at the downstream end of the segment (J_m,seg^down), according to

$$J_{\mathrm{m},\text{seg}}^{\text{down}}=J_{\mathrm{m},\text{seg}}^{\text{up}}+J_{\mathrm{m},\text{seg}}$$ (13)

At vascular branch points, the metabolic signal substance is distributed in proportion to blood flow. No decay of the signal substance was assumed. Metabolic signal substance transport is determined according to the same approach as is used for oxygen, described above.

The local concentration of metabolic signal substance in the blood (c_m) is used to calculate the metabolic stimulus (S_m) according to

$${\mathrm{S}}_{\mathrm{m}}=\log (1+\frac{{\mathrm{c}}_{\mathrm{m}}}{\epsilon })$$ (14)

If the signal substance is transported exclusively by intravascular convection, c_m corresponds to the mean substance concentration in the vessel segment (c_m,seg). Intravascular concentration is determined according to c_m,seg = J_m,seg/(Q˙ + Q˙_ref), where Q˙ is segment blood flow. Q˙_ref is a small constant included to keep concentration values bounded for very low segment blood flow. In case of additional diffusive transport across the tissue, c_m is determined from both the segment concentration and the average concentration in all tissue elements directly adjacent to the segment (c_m,tis), according to c_m = (c_m,seg + c_m,tis)/2.

In accordance with experimental and theoretical findings, showing the importance of information transfer along flow pathways for coordinating diameter adjustment in vascular networks (63) and for preventing arteriovenous shunts (56), metabolic information is assumed to be conducted upstream along vessel walls throughout the entire network (11), in addition to the downstream convection. A local conducted signal (J_c, dimensionless) is generated in each vessel in proportion to the local metabolic stimulus and to segment length according to

$$J_{\mathrm{c}}={\mathrm{S}}_{\mathrm{m}}L\epsilon$$ (15)

J_c is added to the conducted signal reaching the segment from downstream parts of the vessel network (J_c^down). At converging bifurcations, the signal is equally distributed to the (upstream) feeding segments, independent of their blood flow, in diverging bifurcations signals of the (downstream) daughter segments sum up. The conducted signal declines along vessel segments with exponential length constant L_c, leading to a conducted signal on the upstream end of the segment (J_c^up), according to

$$J_{\mathrm{c}}^{\text{up}}=J_c^{\text{down}}\exp (-\frac{L}{L_c})+J_c\exp (-\frac{L}{2L_c})$$ (16)

assuming that the metabolic signal entering the segment from downstream segments decays over the total segment length, whereas the metabolic signal added locally decays over a one-half segment length only. The conducted stimulus (S_c) for diameter adaptation based on the midsegment conducted signal is defined as

$${\mathrm{S}}_{\mathrm{c}}=\frac{J_{\mathrm{c}}}{J_{\mathrm{c}}+J_{\text{ref}}}$$ (17)

where J_ref is a reference conducted signal.

Experimentally recorded microvascular networks exhibit secondary input and output boundaries, in addition to the main feeding and draining vessels. For secondary boundaries, values must be assigned for So₂ and flux of metabolic signal substance (inputs) and conducted signals (outputs). To minimize possible artifactual effects of these assigned values on simulation results, the respective values were estimated relative to calculated values of pressure and flow for main feeding and draining segments.

For all simulation runs, the following boundary conditions were set as close as possible to the in vivo state while testing different adaptation characteristics: Po₂ in the main feeding arteriole (value: 95 Torr, estimated); discharge hematocrit in input boundary segments (values: individually measured for each segment); transmural pressure in the main draining venule [value: 13.8 Torr, according to measurements (61)]; and flow rates in all other segments entering or leaving the network (values: calculated from measured flow velocities and vessel diameters). Alternatively, it would have been feasible to assign pressure values (instead of flow rates) to all boundary segments. However, flow rates were chosen, with the exception of the main venule, because they could be based on actual experimental values.

Diameter adaptation was simulated until convergence was achieved (segment average diameter change < 10⁻⁵ μm). Usually ∼2,000 adaptation runs corresponding to 10- to 20-min calculation time on a conventional personal computer (2.5 GHz) were needed.

Variation of model parameters.

For each metabolic signaling mode, the combination of adaptation parameters leading to vascular network structures with highest similarity to in vivo structures was determined. The most sensitive indicator for functional similarity is given by the blood flow velocity error (V_err), indicating the difference between blood flow velocities observed in vivo and those resulting from simulated adaptation. V_err is calculated as root mean square relative deviation (RMS) of predicted from measured vessel segment blood flow velocities. Velocity differences are especially sensitive, since even small changes of diameters elicit large changes in flow velocity. In addition, the relative measurement errors of velocities are smaller than those of vessel diameters (59).

The deviation of velocities predicted by the flow model for experimentally measured diameters (without simulated adaptation) from corresponding measured velocities resulted in a V_err of 0.61 (RMS) with a SE of the mean of about ±0.01 (57). The value of 0.61 is close to the achievable minimum, given the experimental and theoretical constraints (61). Increases of the V_err above this reference are used to evaluate hemodynamic similarity to the in vivo situation reached by different metabolic signaling modes, corresponding to findings of earlier related studies (61, 57). Such increases proved to react sensitively and consistently to modifications of adaptation modes or parameters (55). The robustness of the V_err depends on the size of the network analyzed and is thus supported here by the relatively high number of vessel segments studied (576 segments).

In the present study, a downhill simplex procedure (47) for the optimization of the model parameters (k_m, k_c, k_p, k_s, Po_2ref, Q˙_ref, J_ref, L_c) (59) was used to minimize V_err for each metabolic signaling mode. The total vascular volume results from the simulated adaptation process. For the network state at minimal V_err, tissue oxygen deficit was determined as the percentage of tissue elements exhibiting a Po₂ < 1 Torr. In addition, diameter error (Dia_err) and hematocrit error were calculated as RMS deviation of predicted from measured vessel diameter or vessel hematocrit, respectively.

In addition, a systematic variation of the two most relevant parameters of the simulated adaptation, the relative strength of metabolic vs. hemodynamic stimuli (k_m) and the effective strength of conducted signaling of the metabolic information (k_c^eff = k_m k_c), was used to investigate overall effects of individual metabolic signaling modes on functional network properties. The constant k_p was not included in the scans because of the low impact on the respective results (55). The model constant k_m was varied from 0.1 to 2.0 in steps of 0.1, and k_c^eff was varied from 0.0 to 3.0 in steps of 0.125. For each combination of k_m and k_c^eff in the two-dimensional scans, the V_err, the tissue oxygen deficit, the pressure difference between the feeding arteriole and the draining venule, and the mean capillary pressure were determined. During the scans, k_s was used to fix the total intravascular volume of the network to the experimentally determined value to counteract changes in the effective strength of stimuli derived from a given situation accompanying the variation of k_m and k_c^eff.

RESULTS

Detailed results are given for the network with 576 vessel segments and an oxygen level in the main feeding arteriole of 95 Torr. Similar results were obtained for this network, assuming a feeding Po₂ of 70 Torr (26), and for the second mesenterial network with 389 vessel segments (data not shown).

For each metabolic signaling mode, the network characteristics at minimal V_err and the corresponding optimized model parameters (k_m, k_c, k_p, k_s, Po_2ref, Q˙_ref, J_ref) are shown in Table 2. Optimizations robustly yielded values for L_c substantially higher than the maximal flow path length through the network (∼9 mm). Therefore, L_c was set to infinity in the model for all metabolic signaling modes, corresponding to an unattenuated spread of the conducted signal. Such a nondecaying propagation of signals along the vessel wall was also found experimentally (22).

Table 2.

Characteristic network parameters obtained by model simulations of hemodynamics and oxygen distribution using experimental diameters and diameters after simulated adaptation with different metabolic signaling modes

	Experimental Diameters	Simulated Diameter Adaptation
		Tissue Signaling	Wall Signaling	RBC Signaling
Network characteristics
Verr	0.61	0.73	0.60	0.81
Diaerr	0	0.50	0.38	0.68
Hcerr	0.51	0.65	0.58	0.92
OxDef, %	0.7	0.2	0.2	4.7
Vol, nl	44	43	42	35
Optimized adaptation parameters
km		1.30	0.80	0.64
kc		1.52	1.60	2.17
kp		0.90	0.35	0.65
ks		3.24	2.51	1.89
Pref, mmHg		115	95	92
Q˙ref, nl/min		0.007	0.012	0.012
Jref		4,822	4,925	5,537

See text for definitions of acronyms. For simulated adaptation, optimized values of adaptation parameters are given.

The lowest value of V_err, 0.60, was achieved, assuming wall signaling. Other signaling modes (tissue signaling, RBC signaling) resulted in significantly higher V_err values. The largest value, obtained for RBC signaling, indicates unrealistic network structures and function. Dia_err and hematocrit error also exhibited minimal values, assuming wall signaling. The oxygen deficit was <1% in wall signaling and tissue signaling, while RBC signaling resulted in an oxygen deficit of 4.7%.

For experimental diameters, the estimated oxygen deficit was 0.7%, whereas it is reasonable to assume that, in vivo, no oxygen deficit is present. Various causes may underlie this discrepancy, including simplifying assumptions made in the model (e.g., with respect to the assumed oxygen diffusivity, tissue thickness, homogeneity of oxygen consumption, and absence of oxygen exchange with the surrounding peritoneal fluid). However, due to their effect on flow resistance, measurement errors in vessel diameters may play a dominant role. Accordingly, simulated adaptation, which eliminates possible measurement errors in vessel diameters, led to lower oxygen deficits for wall signaling and tissue signaling.

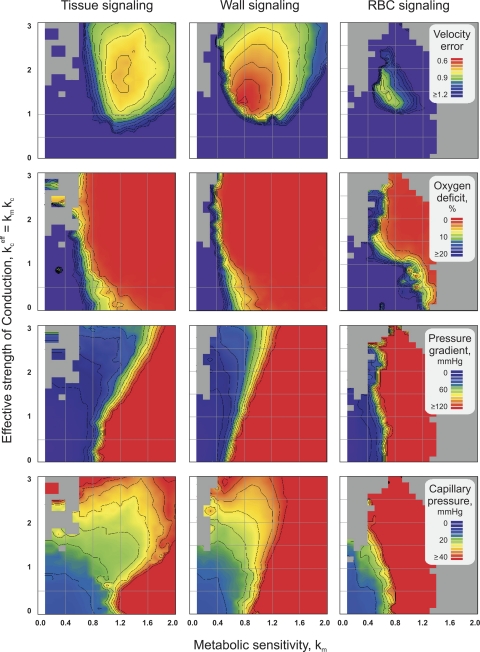
Functional network properties resulting from systematic variation of the metabolic sensitivity (k_m) and strength of conductive transfer of metabolic information upstream (k_c^eff = k_m k_c) are shown in Fig. 5. Lower values of V_err and oxygen deficit of the tissue (rows 1 and 2) indicate higher consistency with data obtained for the in vivo network. For the bulk pressure drop across the network and for the mean capillary pressure (rows 3 and 4), closest to consistency with experimental data is achieved within defined pressure ranges (50–90 and 23–27 Torr, respectively).

Fig. 5.

Effects of varying the relative impact of metabolic stimuli compared with hemodynamic stimuli (k_m) and the effective strength of reactions to metabolic signals conducted upstream (k_c^eff) on network properties. In all plots, light gray regions correspond to numeric instabilities in the calculation of hemodynamics. Row 1: matching between simulated and experimental blood flow velocities in the network (velocity error V_err). Row 2: tissue oxygen deficit (percentage of tissue area with Po₂ < 1 Torr). Row 3: bulk pressure drop across vascular network. Row 4: mean capillary pressure.

The V_err (Fig. 5, first row) reaches a single minimum in each mode, with values given in Table 2. However, individual minimal values of V_err markedly differ for the different signaling modes, with the lowest V_err reached by wall signaling. For all modes, tissue oxygen deficit (Fig. 5, second row) occurs if k_m values are lower than a critical level. The pressure difference between the feeding arteriole and the draining venule (Fig. 5, third row) and the mean capillary pressure (Fig. 5, fourth row) both rise with increasing k_m in all three metabolic signaling modes.

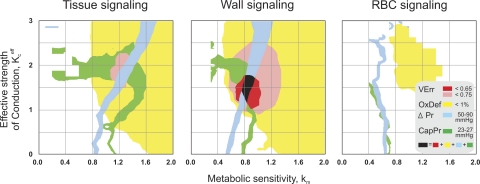
For the comparison of the different metabolic signaling modes tested, it is relevant to identify parameter domains in which all critical functional network properties exhibit realistic values compared with experimental data (Fig. 6). For all modes, tissue oxygen deficit is absent over wide ranges of model constants, whereas physiological values for the pressure difference between the feeding arteriole and the draining venule and the capillary pressure are obtained only for narrow bands of model parameter combinations. In tissue signaling and wall signaling, parameter combinations exist that yield a coincidence of the lowest respective V_err, minimal oxygen deficit, and physiological pressure values. However, regions of low V_err are larger, and the minimal V_err is markedly lower in wall signaling than in tissue signaling. In RBC signaling, no overlap of ranges for model parameter combinations leading to adequate tissue oxygenation and pressure distributions is observed. Also, low levels of V_err are not obtained for any parameter combination.

Fig. 6.

Synopsis of combinations of k_m and k_c^eff leading to low V_err, absence of oxygen deficit (OxDef), and realistic values for the pressure drop across vascular network (ΔPr) and mean capillary pressure (CapPr). Assuming both tissue signaling and wall signaling, network structures at minimal V_err coincide with physiological values of all other parameters (OxDef, ΔPr, CapPr). However, minimal V_err is markedly lower for wall signaling (<0.65) than for tissue signaling (0.65 < V_err < 0.75). In RBC signaling, minimal V_err exceeds 0.75, and model constant combinations leading to physiological oxygen and pressure distributions do not overlap.

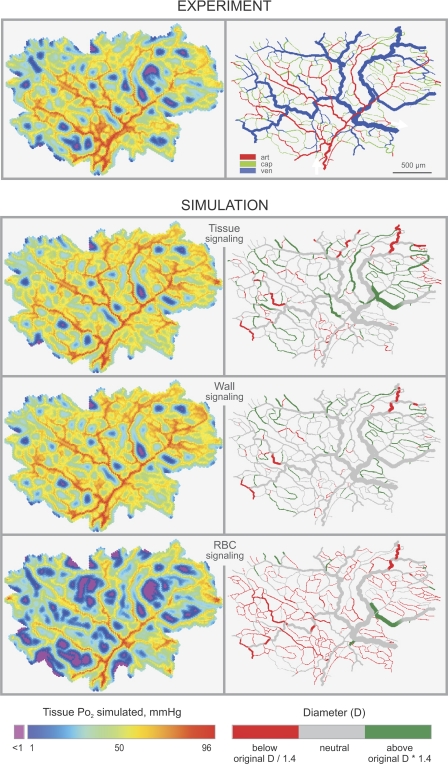
Figure 7 shows distributions of tissue oxygen levels and deviations between predicted and observed diameters for the three metabolic signaling modes, analyzed at the respective minimal levels of V_err. Both tissue signaling and wall signaling led to oxygen distributions within the tissue, similar to those estimated for in vivo network structures. However, tissue signaling caused unrealistic diameter increase in some feeding arterioles and shrinkage of some large venules. In the case of wall signaling, significant diameter deviations were fewest and exhibited a seemingly random distribution. The most pronounced diameter deviations were seen as a result of RBC signaling with excessive shrinking of small vessels.

Fig. 7.

Predicted tissue oxygen levels (left) and vessel diameters (right) in a mesenteric microvascular network. Experiment, results with measured diameters; vessels color-coded for segment type derived from adjacent bifurcations (diverging, converging). art, Arteriole; cap, capillary; ven, venule. White arrows indicate flow direction in the feeding arteriole and the draining venule. Simulation, results for three assumed signaling modes. Vessels are color-coded for deviation of predicted from measured diameters. Tissue signaling gives good tissue oxygenation, but some distal arterioles are unrealistically large, and some venules are too small. Wall signaling gives good tissue oxygenation and no systematic diameter deviations. RBC signaling results in large undersupplied tissue regions and shrinking of small vessels.

DISCUSSION

In the present study, the ability of different modes of metabolic signaling in response to the local oxygenation to achieve adequate oxygen supply to the tissue and realistic vascular network hemodynamics by long-term structural adjustment of vessel diameters in microvascular networks was studied. Of the three modes of metabolic signaling considered (Fig. 1), wall signaling gives functionally most adequate results with low oxygen deficit in the tissue, in combination with a high similarity to measured data, as evidenced by low blood flow velocity deviations (V_err). Tissue signaling also provides realistic oxygen distributions, but leads to a somewhat higher systematic deviation of flow velocities and vessel diameters from those measured in vivo. RBC signaling results in poor oxygen supply and diameter distributions, which strongly differ from experimental data.

This study is based on experimental data from the rat mesentery (60). The mesentery has a relatively low metabolic demand (27, 66), some of which might be met by diffusion from the surrounding peritoneal fluid. Two extreme cases can be considered. 1) The surrounding peritoneal fluid is well stirred, leading to a homogenous Po₂ at all parts of the mesenteric surface. The mesenteric membrane would thus be homogenously supplied with oxygen. Microvascular networks in the mesentery would not be needed for oxygen supply. 2) The peritoneal fluid is unstirred. Because the peritoneal fluid exhibits low oxygen solubility, each tissue region would control the Po₂ of the adjacent peritoneal fluid, necessitating a microvasculature for adequate oxygen supply.

In the mesenteries studied, networks exhibited relatively homogenous distributions of microvessels, supporting assumption 2. Also, measured network morphologies and flows resulted in adequate oxygen supply to the tissue, when oxygen consumption typical for connective tissue was assumed. This suggests that vessel diameters observed in vivo represent the result of the adjustment to the metabolic demand of the surrounding mesenterial tissue (58). In the oxygen transport model used here, the mesentery was consequently assumed to be supplied with oxygen only by its vasculature. A limited additional supply with oxygen by the peritoneal fluid would tend to homogenize oxygenation, but would not change the conclusions of the present study. The conclusions of the present study regarding metabolic control of structural adaptation reflect general principles of the mechanisms considered, as discussed below, which should not depend critically on the specific angioarchitecture and design of a given microvascular bed or on the exact level of metabolic demand.

For a given oxygenation, the amount of metabolic signaling substance released depends on characteristics of the signaling structures. In RBC signaling, the metabolic substance is delivered in proportion to the number of RBCs in the vessel, which is determined by vessel volume and hematocrit. Thus the mismatch between oxygen supply and demand, assuming RBC signaling, can be explained as follows. Microvessels in underperfused tissue regions are characterized by low RBC flux and/or content. The amount of signaling substance released in a given vessel of the underperfused region at a given RBC So₂ may, therefore, also be low, evoking a weak metabolic stimulus, allowing further decrease in vascular diameter and blood flow, in a positive feedback mechanism. This cannot be overcome by the fact that the pronounced decrease in So₂ in underperfused tissue regions naturally increases the amount of metabolic signaling substance released by each RBC (39). Consequently, both vessel volume and hematocrit may further decline, corresponding to a further reduction of the number of signaling RBCs, again leading to a diameter decline.

In additional simulations, phase separation effects (53, 54) were eliminated, leading to a homogenous hematocrit throughout the network. The absence of a decrease in V_err (V_err = 0.81) indicates that resulting amounts of metabolic signal substance released were still insufficient to guarantee adequate capillary diameters.

These considerations are supported by supplementary simulations (data not shown) on RBC signaling, assuming release of the metabolic signal substance proportional to the decline of hemoglobin So₂ between entrance and exit of a segment, according to studies on the liberation of NO from S-nitrosohemoglobin by RBCs (40). In this case, the metabolite is released from each RBC in a finite amount during the arteriovenous oxygen desaturation cycle of hemoglobin. Thus the amount of signaling substance depends not only on hematocrit, but additionally on blood volume flow, which are both reduced in underperfused tissue regions. Accordingly, simulated adaptation with this type of RBC metabolite release led to even stronger hypoxia and even higher deviations from experimentally determined network characteristics.

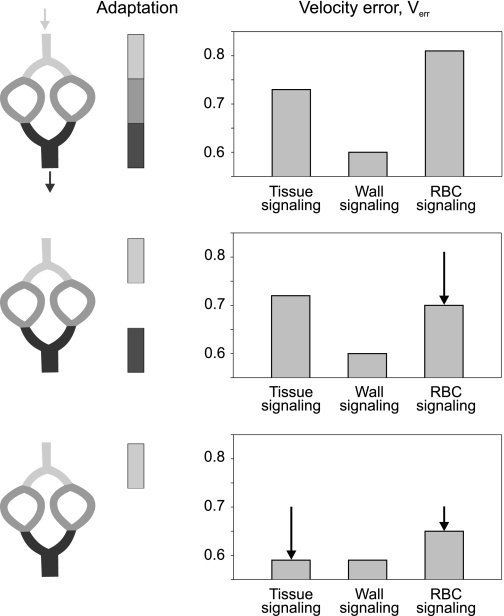
Although RBC signaling seems inadequate for structural control of blood flow distribution in microvascular networks, this mechanism may well play a role in adjusting total network blood flow to acute changes in tissue metabolic demand (2). Provided that the distribution of structural vessel diameters is adjusted by other metabolic signaling modes, the So₂ in collecting venules reflects the overall match of oxygen supply to demand in the network. In case of relative underperfusion, a large RBC population experiences low So₂, leading to a strong RBC-derived metabolic signal in draining venules. This signal could be transferred to feeding arterioles by upstream conduction along the vessel wall (11) and/or diffusion of a metabolic signaling substance (34), especially for parallel arteriole-venule arrangements, evoking arteriolar diameter increase and augmenting total network blood flow. A role for RBC signaling in the control of arteriolar vessel diameters is supported by findings of additional calculations, in which adaptation was allowed only in arterioles and venules or only in arterioles, respectively, and adaptation parameters were optimized as described before (see Fig. 8). When only arterioles were allowed to adjust their diameters, V_err for RBC signaling was markedly reduced (Fig. 8, bottom). However, the reference value of V_err determined for experimentally measured diameters (V_err = 0.61) was not reached.

Fig. 8.

Effects of applying simulated diameter adaptation to all segment types (top row), only to arterioles and venules (middle row), and only to arterioles (bottom row) on minimal V_err. Arrows (diagrams, right) correspond to the difference of V_err from values in the row above. For wall signaling, low levels of V_err are obtained, irrespective of the extent of simulated adaptation. For tissue signaling, V_err is reduced to low levels, if venular diameters are not adapted. In RBC signaling, V_err is markedly reduced, if adaptation is restricted to arterioles.

The described feedback problems do not occur for wall signaling or tissue signaling. In these modes, the number of cells generating the signaling substance is independent of local hemodynamics. Tissue cells might seem to be the most probable origin of metabolic signals for vascular diameter adaptation, since the primary task of microvascular networks is the adequate supply of the tissue with substrates. Surprisingly, the present study suggests that wall signaling is better suited to control vessel diameters than tissue signaling. Both tissue signaling and wall signaling are capable of preventing oxygen deficit in tissue, but wall signaling leads to a lower V_err and Dia_err.

This apparent paradox may be explained by considering the factors influencing oxygen levels at the oxygen sensor in both signaling modes. The oxygenation of tissue cells is determined both by their distance to the nearest vessels (diffusion-limited transport) and by the perfusion rate in these vessels (flow-limited transport). The perfusion rate, in turn, depends on vascular diameter. The diffusion distance can be modified only by changes in vessel density regulated by angiogenesis or vessel pruning. Consequently, control of vascular diameters by metabolic signals derived from the tissue cannot guarantee adequate tissue oxygenation, if vessel density is too low. In this situation, tissue cells would continue to produce increased levels of the metabolic signaling substance, despite excessive increase of vessel lumen in the respective regions, compromising the feedback between the metabolic signal production and tissue hypoxia. In Fig. 7, this is reflected by the increased number of arterioles, with diameters enlarged relative to the experimental measurements.

In contrast to tissue hypoxia, hypoxia of the vessel wall occurs only when perfusion is insufficient relative to oxygen extraction. This can be addressed by increased vessel diameter, leading to reduced resistance and increased flow rate. Thus a signal derived from the vessel wall is better suited for controlling vascular diameters. Signals delivered by tissue cells, on the other hand, would be better suited to regulate vessel density by inducing angiogenesis (or pruning). In the present study, no hypoxia was observed in the rat mesenteries serving as a reference when oxygen demand typical for connective tissue was assumed in the oxygen transport model. Thus there were probably no strong angiogenetic signals present.

The difference between tissue signaling and wall signaling with respect to the achieved degree of similarity to real network characteristics (V_err, Dia_err) seems to be small. However, this difference is robust and reproducible and is maintained for a number of modifications of the adaptation scheme including the following: 1) not allowing capillaries to adjust their diameters (tissue signaling: V_err = 0.72, wall signaling: V_err = 0.61; Fig. 8, middle); 2) keeping the discharge hematocrit constant at a value of 0.4 throughout the network by abolishing phase separation (tissue signaling: V_err = 0.73, wall signaling: V_err = 0.60); and 3) using a different network angioarchitecture, i.e., the second, smaller mesenterial network (tissue signaling: Dia_err = 0.40, wall signaling: Dia_err = 0.28; flow velocities were not measured for this network).

For tissue signaling, a reduction of V_err to the reference value (V_err = 0.61, which corresponds to the values obtained from wall signaling); however, was observed when venular diameters were fixed, in addition to fixing capillary diameters (Fig. 8, bottom). Therefore, the signals generated in this mode seem to be inadequate to regulate venular adaptation. A possible explanation may be that the caliber of venules should relate more to the oxygen extraction in the drained capillary bed in contrast to the oxygenation of the tissue in which they are embedded (which is influenced by oxygen exchange with neighboring vessels).

In the modeling approach used, only one metabolic signaling mode was assumed to be active at a time. By this means, consequences of the signaling mode under consideration for network properties are revealed more clearly, and the ability of each mode to play a leading role can be evaluated. However, different metabolic signaling modes may cooperate in vivo. Corresponding experimental data are difficult to obtain because of methodological difficulties in guaranteeing stable conditions and also in blocking all but one metabolic signaling mode over periods of time needed for structural adaptation.

Both in vitro and in vivo approaches have been used experimentally. Isolated vessels perfused with RBC-free solutions with different Po₂ exhibited an oxygen reactivity that depended on the integrity of the endothelial cell layer (9, 14, 31, 38, 45, 50), suggesting wall signaling to have an important impact on vessel diameter adaptation. It was also shown that, in isolated rat cerebral arterioles (passive maximum diameter 76.4 ± 4.5 μm), low extraluminal oxygen tension resulted in vasodilation, only if the vessels were perfused with RBCs (15), suggesting the importance of RBC signaling. In an extended in vitro approach, larger septal artery segments from rat hearts, with and without a layer of surrounding cardiac tissue, were used (42). In this setup, hypoxic relaxation was augmented by the presence of parenchyma, indicating tissue signaling to play a role in tone regulation upon impaired oxygen supply.

Experiments directly addressing the relative impact of tissue and vessel-derived, oxygen-dependent signals in diameter adaptation in vivo are rare. In acute experiments in the hamster cheek pouch, Jackson and colleagues (7, 37, 38) used a technique that allows arterioles to be separated from the surrounding parenchyma. In these studies, global changes in superfusate Po₂ evoked significant, reproducible changes in arteriolar tone and diameter (37). However, this was not the case for local Po₂ changes at the vessel wall, produced by microapplication of fluid to the vessel surface or by cannulation and perfusion of the arteriole. In addition, observed vascular diameter changes were not influenced by the presence of RBCs in the vessel lumen (7, 37). Jackson (37) hypothesized that oxygen sensors are located either in the parenchyma adjacent to the vessel segment studied or in vessels downstream. The latter alternative would require conduction of signals derived from the local metabolic situation upstream along vessel walls.

Thus experimental findings on the localization of the oxygen sensor for acute diameter adaptation are still not congruent. For structural adaptation, corresponding experimental data are not even available. Also, the molecular mechanisms of oxygen sensing in terminal vascular beds are not well understood. Identification of mechanisms for oxygen sensing by vessel walls, under conditions in which Po₂ is relatively high and metabolism is not limited by oxygen availability, is an important unresolved question.

In conclusion, the present study indicates that vessel wall signaling is centrally involved in the long-term, steady-state adjustment of vessel diameters in microvascular networks in response to metabolic signals. Tissue signaling, which seems to be of minor importance for this type of diameter adaptation, may have a crucial role in stimulating the generation of new vessels by sprouting angiogenesis in hypoxic tissue regions. RBC signaling, although incapable of guaranteeing adequate structural diameter adaptation within the network, may play a supporting role for the adjustment of network total blood flow to metabolic demand, via changes in vessel tone.

GRANTS

This study was supported by Deutsche Forschungsgemeinschaft Grant FOR 341/TP1 and by National Heart, Lung, and Blood Institute Grant HL034555.

DISCLOSURES

No conflicts of interest are declared by the author(s).