A tetrahedral entropy for water

Abstract

We introduce the space-dependent correlation function C _Q(r) and time-dependent autocorrelation function C _Q(t) of the local tetrahedral order parameter Q ≡ Q(r,t). By using computer simulations of 512 waterlike particles interacting through the transferable interaction potential with five points (TIP5 potential), we investigate C _Q(r) in a broad region of the phase diagram. We find that at low temperatures C _Q(t) exhibits a two-step time-dependent decay similar to the self-intermediate scattering function and that the corresponding correlation time τ_Q displays a dynamic cross-over from non-Arrhenius behavior for T > T _W to Arrhenius behavior for T < T _W, where T _W denotes the Widom temperature where the correlation length has a maximum as T is decreased along a constant-pressure path. We define a tetrahedral entropy S _Q associated with the local tetrahedral order of water molecules and find that it produces a major contribution to the specific heat maximum at the Widom line. Finally, we show that τ_Q can be extracted from S _Q by using an analog of the Adam–Gibbs relation.

It has long been appreciated that the local structure around a molecule of liquid water arising from the vertices formed by four nearest neighbors is approximately tetrahedral at ambient pressure and that the degree of tetrahedrality increases when water is cooled (1–5). An important advance occurred in the past 10 years when computer simulations allowed the quantification of the degree of tetrahedrality (6–10) by assigning to each molecule a local tetrahedral order parameter Q (11–16). At high temperatures, the probability distribution P(Q,T) is bimodal, with one peak corresponding to a high degree of tetrahedrality and the other to a less tetrahedral environment (Fig. 1). Upon decreasing temperature, the peak associated with a high degree of tetrahedrality grows, suggesting that the local structure of water becomes much more tetrahedral at lower temperatures (13, 14, 17).

Fig. 1.

Dependence on Q of the probability density function P(Q,T) for nine values of T. At high T, P(Q,T) is bimodal with peaks at high and low values of Q. The magnitude of the high Q value peak grows as it shifts toward the larger values of Q upon decreasing temperature whereas the magnitude of the low Q value peak decreases and, at sufficiently low temperatures, P(Q,T) becomes unimodal. Analogous plots are shown for TIP4P and TIP5P models, respectively, in refs. 13 and 17. Error bars are shown in green.

Introduction

Water has been hypothesized to belong to the class of polymorphic liquids, phase separating—at sufficiently low temperatures and high pressures—into two distinct liquid phases: a high density liquid (HDL) with smaller Q and a low density liquid (LDL) with larger Q (18). The coexistence line separating these two phases may terminate at a liquid–liquid (LL) critical point, above which (in the LL supercritical region) appears a line of correlation length maximum in the pressure–temperature plane. The locus of maximum correlation length in the one-phase region is called the Widom line T _W ≡ T _W(P) (19), near which different response functions, such as isobaric specific heat C _P and isothermal compressibility K _T, display maxima. Recent neutron-scattering experiments (20) and computer simulations (19) show that the dynamics of water gradually cross over from being non-Arrhenius for T > T _W to Arrhenius for T < T _W.

Although dynamic heterogeneities have received considerable attention (21, 22), static heterogeneities have attracted less interest. In this paper, we ask how the tetrahedral order and its spatiotemporal correlations change upon crossing the Widom line. To this end, we introduce three quantities of physical interest: (i) the space-dependent correlation function C _Q(r), (ii) the time-dependent autocorrelation function C _Q(t), and (iii) the tetrahedral entropy S _Q. These functions can also be usefully applied to study other locally tetrahedral liquids, such as silicon (23–25), silica (26), and phosphorus (27).

Model

We perform molecular dynamics (MD) simulations of N = 512 water-like molecules interacting via the transferable interaction potential with five points (TIP5 potential), (28), which exhibits a LL critical point at T _C ≈ 217 K and P _C ≈ 340 MPa (29, 30). We carry out simulations in the NPT ensemble at atmospheric pressure (P = 1 atm) for temperatures ranging from 320 K down to 230 K.

Results

Space- and Time-Dependent Correlations of the Tetrahedral Order Parameter.

To quantify the local degree of tetrahedrality, we calculate the local tetrahedral order parameter (13)

where ψ_ikj is the angle formed by the molecule k and its nearest neighbors i and j. The average value 〈Q〉 ≡(1/N) ∑_k Q _k increases with decreasing T and saturates at lower T, whereas |d〈Q〉/dT| has a maximum at the Widom line T _W ≈ 250 K (31–33).

To characterize the space-dependent correlations of the local order parameter, we find all the pairs of molecules i and j whose oxygens are separated by distances belonging to the interval [r −Δr/2,r + Δr/2]. The number of such pairs is

where r _ij is the distance between the oxygens of molecules i and j. The sum is taken over all molecules in the system and

For Δr ← 0, δ(r _ij − r, Δr) ← δ(r _ij − r)Δr where δ(r _ij − r) is the Dirac δ-function. N(r, Δr) can be approximated as

where N is the total number of molecules in the system, g _OO(r) is the oxygen–oxygen-pair correlation function, and ρ is the number density.

Next, we find the local order parameters Q _k and Q _l for all such pairs of molecules and compute their mean,

their variance,

and covariance,

Finally, we introduce the space-dependent correlation function of the local tetrahedrality Q,

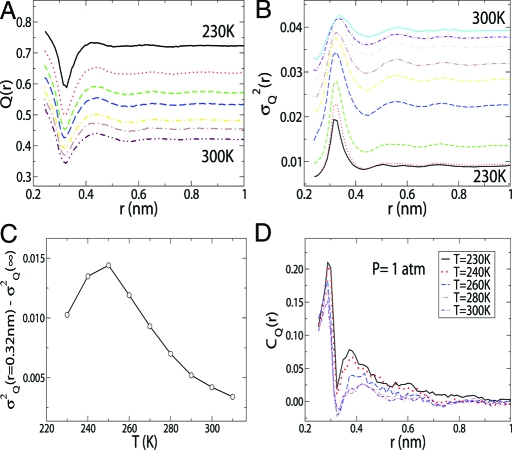
In Figs. 2 A and 2 B, we show Q(r) and σ_Q ²(r) for different temperatures and atmospheric pressures. The behavior of Q(r) and its variance σ_Q ²(r) as a function of the distance r has a clear physical meaning. For molecules separated by 0.32 nm, Q(r) has a deep minimum characterizing the distortion of the first tetrahedral coordination shell of the four nearest neighbors by the intrusion of a “fifth neighbor” (34). Conversely, the quantity σ_Q ²(r = 0.32 nm) −σ_Q ²(∞) for such molecules dramatically increases upon decreasing temperature (see Fig. 2 C), and has a maximum at T ≈ 246 K, which is approximately equal to the ambient pressure value of T _W (≈ 250 K for the TIP5P model) reported in refs. 19 and 31–33. A measure qualitatively similar to Q(r) has been studied in case of solvation structure of water around carbohydrate molecules (35). In Fig. 2 D, we show C _Q(r) for different temperatures for P = 1 atm. C _Q(r) has positive maxima at positions of the first and second peaks in the oxygen–oxygen pair correlation function. Water molecules separated by r ≈ 0.32 nm exhibit weak anticorrelation in local tetrahedral order at high temperatures, which changes to positive correlation upon decreasing the temperature below T _W.

Fig. 2.

Average tetrahedral order parameter, its variance and spatial correlations as functions of separation between water molecules for different temperatures. (A and B) The average order parameter Q(r) (A) and its variance, σ_Q ²(r) (B), as a function of the distance r. (C) Temperature dependence of σ_Q ² (r = 0.32nm) −σ_Q ²(∞) shows a maximum at the Widom temperature, suggesting that the local fluctuations in Q at the fifth-neighbor distance increase upon decreasing temperature and have a maximum at the Widom line. (D) Spatial correlation function C _Q(r) of the tetrahedral order parameter Q (Eq. 1) at various temperatures for pressure P = 1 atm. C _Q(r) has positive peaks at the positions of the nearest-neighbor peaks in oxygen–oxygen pair correlation function g _OO(r) at high T. Although the position of the first maximum of C _Q(r) remains fixed for all the temperatures, the position of the second maximum moves slightly to the smaller r as the temperature decreases. A negative minimum at the fifth-neighbor distance r ≈ 0.32 nm for high T implies that the local tetrahedral order parameters of a central molecule and its fifth neighbor are anticorrelated at T > 250 K. Interestingly, the anticorrelation at r = 0.32 nm changes to positive correlation below the T _W ≈ 250 K.

To study the time development of the local tetrahedral order parameter, we introduce the time-dependent autocorrelation function

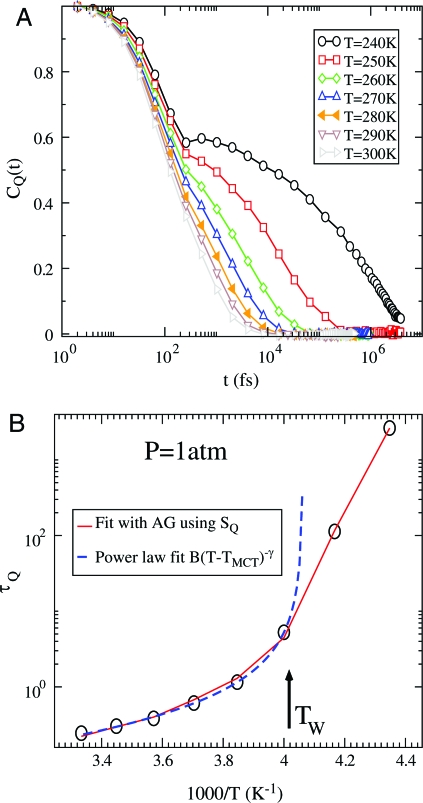
where Q _i(t) is the tetrahedral order parameter of each molecule in the system and 〈Q _i〉 is the ensemble average. In Fig. 3 A we show C _Q(t) for different temperatures. The decay of C _Q(t) is reminiscent of the decay of the self-intermediate scattering function. The long-time behavior of C _Q(t) is exponential at high T but at low T can be fit with a stretched exponential exp[−(t/τ)^β], where 0 < β < 1 (36).

Fig. 3.

Temperature dependence of time autocorrelation function of local tetrahedral order parameter and relaxation times. (A) Autocorrelation function C _Q(t) of tetrahedral order parameter Q at various temperatures. C _Q(t) is exponential at high temperatures but displays a visible two-step decay at low temperatures. (B) Correlation time τ_Q extracted from C _Q(t) (circles). The solid line is the fit using the Adam–Gibbs relation (Eq. 13) between the tetrahedral entropy S _Q(T), and the tetrahedral relaxation time τ_Q. The dotted lines in B show the power-law fit B(T − T _MCT)^−γ with the fitting parameters B = 25.39, T _MCT = 246.18, and γ = 1.17. The behavior of τ_Q deviates from the power-law fit for the temperatures below the Widom-line temperature (indicated by a vertical arrow) T _W where a cross-over to Arrhenius behavior at lower temperature occurs.

For simplicity, we define the correlation time τ_Q as the time required for C _Q(t) to decay by a factor e. Fig. 3 B shows the values of τ_Q as function of 1/T on an Arrhenius plot. The behavior of τ_Q is non-Arrehenius at high temperatures and can be fit by a power law B(T − T _MCT)^−γ where B = 25.39, the mode coupling temperature (37) T _MCT ≈ 246.186, and γ = 1.17722 are the fitting parameters. At low T, τ_Q deviates from the power-law fit and becomes Arrhenius. This cross-over in relaxation of local tetrahedral order occurs near T _W, similar to the cross-over found in density relaxation (19, 20, 38).

Tetrahedral Entropy and Tetrahedral Specific Heat.

Because Q measures the local tetrahedral order, it must contribute to the entropy of the system. We next derive an expression for this “tetrahedral entropy” S(Q ₁,Q ₂,…,Q _N), which we define to be the logarithm of the number of states corresponding to the interval between (Q ₁,Q ₂,….,Q _N) and (Q ₁ + ΔQ ₁,Q ₂ +Δ Q ₂,…,Q _N + ΔQ _N) in the hypercubic space formed by Qs. According to Eq. 1, $\frac{8}{3}$(1 − Q _k) = const defines a surface of a six-dimensional hypersphere of radius $\sqrt{\frac{8}{3}(1-Q_k)}$ in the space defined by the cosines of the six tetrahedral angles ψ_ikj of Eq. 1. Hence we assume that the number of states between Q _k and Q _k + ΔQ _k of molecule k scales as (1 − Q _k)^3/2ΔQ _k because the number of independent dimensions is 5. We further assume that the order parameters of each molecule are independent, an assumption justified by the small value of C _Q(r) (see Fig. 2 C). Thus we can define the number of states Ω(Q ₁,Q ₂,….,Q _N) in the interval between (Q ₁,Q ₂,….Q _N) and (Q ₁ + ΔQ ₁,Q ₂ + ΔQ ₂,…,Q _N + ΔQ _N) as the product

where Ω₀ = const. Hence the tetrahedral entropy of the entire system is given by

where k _B is the Boltzmann constant and $S_0=k_B[\ln {\Omega }_0+\frac{3}{2}\ln \left(\frac{8}{3}\right)]$. If P(Q,T) is the distribution of Q at a given temperature T, then the tetrahedral entropy S _Q(T) per particle at temperature T can be written as

In Fig. 4 A, we show that S _Q(T) − S ₀ decreases with decreasing temperature as expected.

Fig. 4.

Temperature dependence of tetrahedral entropy S _Q(T) (A), defined in Eq. 11, (the red solid line is a guide to the eye) and tetrahedral specific heat C _P ^Q = T(∂S _Q/∂T)_P (B), which has a maximum around the same temperature, T ≈ 250 ± 10 K ≈ T _W, where the total specific heat C _P ^Total has a maximum. Moreover, the difference ΔC _P of the two specific heats is a constant within the error bars for all the temperatures, hence suggesting that C _P ^Q is responsible for the Widom-line transformations.

We further define a measure of “tetrahedral specific heat” as C _P ^Q ≡ T(∂S _Q(T)/∂T)_P. Fig. 4 B shows the temperature dependence of C _P ^Q and total specific heat C _P ^Total for P = 1 atm. C _P ^Q shows a maximum at T ≈ 250 ± 10 K ≈ T _W, where the total specific heat C _P ^Total also has a maximum (19, 31, 32, 33), suggesting that the fluctuations in tetrahedral order reach a maximum at T _W(P). Moreover, comparing the tetrahedral specific heat in Fig. 4 B with the total specific heat, we find that the C _P ^Q is a major contribution to the C _P ^Total and, particularly, the difference ΔC _P of the two specific heats remains a constant within the error bar for all temperatures studied, hence suggesting that C _P ^Q is responsible for the Widom-line transformations.

To relate the tetrahedral entropy S _Q(T) to the tetrahedral relaxation time τ_Q(T) associated with the local tetrahedral ordering, we propose the following generalization of the Adam–Gibbs relation between the translational relaxation time and configurational entropy (39, 40),

where τ_Q(0) is the tetrahedral relaxation time at very large T, and A is a parameter playing the role of activation energy. Accordingly, we calculate τ_Q(T) (Fig. 3 B) from S _Q(T) by using Eq. 13 with three free parameters: A, τ(0), and S ₀. We find that S ₀ ≈ 4.21k _B. The values of τ_Q(T) calculated by using Eq. 13 are within error bars of the values of τ_Q(T) calculated from the autocorrelation function (see Fig. 3 B).

Fig. 3B is an Arrhenius plot of τ_Q, calculated from Eq. 13 . The temperature dependence of τ_Q is different at low and high temperatures, changing from non-Arrhenius (a T-dependent slope on the Arrhenius plot), which can be fit by a power law at high temperatures, to Arrhenius (a constant slope) at low temperatures (20, 19, 31–33).

Relation of Tetrahedral Entropy to Translational Order Parameter and Translational Entropy.

In this section, we investigate the relation of S _Q with (i) the translational order parameter t* (41) defined as

and (ii) the translational entropy S ² (42, 43) obtained from the two-point translational correlations, which is defined as

where ρ is density and g(r) is the oxygen–oxygen radial distribution function.

The excess entropy S ² describes the contribution of two-point correlations to the total entropy of the system. It has been found that S ² agrees very well with the total entropy in different systems including some models of water (43, 44).

In Fig. 5 A, we show S _Q as a function of average tetrahedral order parameter Q̄ for different temperatures and atmospheric pressure. S _Q varies approximately as log(1 − Q̄) for the range of temperature studied. To justify this dependence of S _Q on Q̄, we expand Eq. 12,

where F is a function of moments of the fluctuations (Q − Q̄). Hence, if we ignore F compared with the first term, then S _Q ∼ log(1 − Q̄). In Fig. 5 A, we plot the above function (dashed line), assuming a constant F = −0.40 for all temperatures studied (230 – 320 K) and find that it agrees well with the values of S _Q computed by using Eq. 12 at low T but deviates slightly at high T.

Fig. 5.

Relation of tetrahedral entropy to tetrahedral order parameter and contribution of two-point translational correlations to entropy S ² for temperatures T = 230,240,245,250,260,270,280,290,300,320 K. (A) Test of the relation of Eq. 16 for the relation between the tetrahedral entropy S _Q and the tetrahedral order parameter Q̄, assuming F = −0.40 independent of temperature. (B) S _Q as a function of t* shows that S _Q decreases linearly with t*. The dashed line is a linear fit through the data. (C) Fig. 5 A and B are consistent with the possibility that the average translational order parameter t* varies as log(1 − Q̄). (D) Dependence of S _Q on S _ex. S _Q changes linearly with S ² at low temperatures, but the linearity begins to break down for T > T _W ≈ 250 K.

Furthermore, Fig. 5 B shows that S _Q varies linearly with t*. Combining the results of Figs. 5 A and B, we form Fig. 5 C, which demonstrates s simple relation between tetrahedral and translational oder parameters. We next find that, at low T, S _Q changes linearly with S ²; however it is nonlinear for high T. Note that a simple nonlinear relation between Q and t* was found for the SPC/E model of water in the structurally anomalous region (13). Moreover, Fig. 5 D shows that the temperature where this change in behavior occurs roughly coincides with the temperature of the Widom line T _W.

Discussion and Summary

In summary, we have studied the space and time correlations of local tetrahedral order Q, presumably related to local tetrahedral heterogeneities. We find that the space-dependent correlation of the the local tetrahedral order is anticorrelated for the molecules separated by 3.2 Å at high temperatures. This negative correlation changes to positive correlation upon decreasing T below the Widom temperature T _W(P). Further, we define a measure of the tetrahedral entropy S _Q and find that the specific heat associated with the tetrahedral ordering is responsible for the Widom-line transformations. Finally, we find that S _Q well describes tetrahedral relaxation using the Adam–Gibbs relation. Moreover, we find a simple approximate relation between tetrahedral and translational order parameters Q̄ and t*. On the completion of this work, we were made aware by a referee that Lazardis and Karplus have studied the orientational entropy calculated from the two-point angular correlation function (45). Although they find that the orientational entropy of water has a major contribution to the total entropy, a contribution of orientational fluctuations to the total specific heat was not studied. The tetrahedral entropy S(Q) defined in this paper captures the two-point orientational correlations but is much easier to compute in contrast to the computation of orientational entropy from the two-point angular correlation function and hence offers a rather simpler way to investigate the entropy associated with local structures.