Abstract
The action potential, once triggered in ventricular or atrial myocytes, automatically proceeds on its time course or is generated spontaneously in sinoatrial node pacemaker cells. It is induced by complex interactions among such cellular components as ion channels, transporters, intracellular ion concentrations, and signaling molecules. We have developed what is, to our knowledge, a new method using a mathematical model to quantify the contribution of each cellular component to the automatic time courses of the action potential. In this method, an equilibrium value, which the membrane potential is approaching at a given moment, is calculated along the time course of the membrane potential. The calculation itself is based on the time-varying conductance and the reversal potentials of individual ion channels and electrogenic ion transporters. Since the equilibrium potential moves in advance of the membrane potential change, we refer to it as the lead potential, VL. The contribution of an individual current was successfully quantified by comparing dVL/dt before and after fixing the time-dependent change of a component of interest, such as the variations in the open probability of a channel or the turnover rate of an ion transporter. In addition to the action potential, the lead-potential analysis should also be applicable in all types of membrane excitation in many different kinds of cells.
Introduction
The membrane potential (Vm) of excitable cells shows active changes, such as generation of action potentials or spontaneous oscillations, which are automatically generated by complex interactions among multiple cellular components including ion channels, transporters, ion concentrations, signaling molecules, or even by Vm itself. Electrophysiological studies have been conducted to elucidate the ionic mechanisms underlying these active Vm changes. A central problem in cardiac physiology has been to determine which cellular component is responsible for slow diastolic depolarization in sinoatrial (SA) node cells and for repolarization of the long-lasting ventricular action potential.
The contribution of each cellular component is difficult to measure with conventional experimental approaches that simply record changes in Vm or current size by modifying a component of interest. The difficulty arises because modification of a specific channel or transporter alters the activity of other channels or transporters secondarily via changes of Vm or ion concentrations. Therefore, only a qualitative inference can be drawn from the multiple layers of sequential events induced by modifying a given component. To overcome the experimental limitations, simulation studies have been attempted using mathematical models based on experimental findings. These models allow examination of modal shifts in the system behavior by modifying parameters of cellular components (1–4), stability of the system (3,4), and/or sensitivity of related parameters (5,6). However, it is difficult to estimate the contribution of each component quantitatively from these analyses because of the complexity underlying cardiac membrane excitation.
In this article, we propose what we believe to be a new analytic method, which we refer to as lead-potential analysis, to quantify the contribution of each cellular component to automatic changes in Vm. Our method could be used, for example, to determine the slow diastolic depolarization in the SA node or the long-plateau repolarization of the ventricular action potential. Using this method, a theoretical equilibrium potential (lead potential, VL) is calculated while leaving the time course of Vm intact. The contribution of a given component is evaluated from modification of dVL/dt induced by eliminating the time-dependency of the component.
The theoretical background is presented, and then the method is applied to SA node cells and ventricular myocytes as representative cardiac cell models.
Methods
Definition of the lead potential (VL)
We will derive an equilibrium value of Vm, which Vm tends to approach at a given time of observation (tob). We aim at expressing the membrane as a minimum linear electrical circuit in Fig. 1 B.
Figure 1.
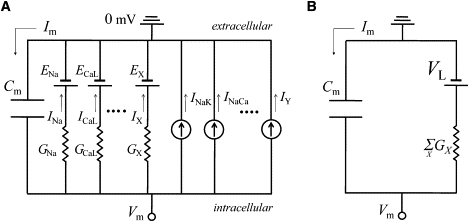
Equivalent electrical circuit of the cell membrane. (A) An equivalent circuit for the membrane electrical behavior expressed by Eq. 5. Cm, membrane capacitance; EX, reversal potential for a channel X; IY, current through transporter Y; Im, total membrane current. (B) A reduced circuit equivalent to Eq. 7.
The temporal change of Vm is described with a fundamental equation in the absence of any extra current and spatial variation of Vm within a single cell,
| (1) |
where Cm is the whole cell membrane capacitance, and Im is the sum of membrane currents through all ion channels and electrogenic transporters in a single cell. In most mathematical models, a current of channel X (IX) is described by Ohm's law,
| (2) |
or the Goldman-Hodgkin-Katz (GHK) current equation with a constant field approximation,
| (3) |
where gmax and pmax (which are defined as constants) are the maximum conductance and permeability, respectively. [S] is the concentration of ion S, and F, R, T, and zs are the usual thermodynamic parameters. The value p(o) is the open probability of a channel, which is determined by Vm- and/or ligand-dependent gating, pore-blocking, or unspecified mechanisms underlying the rectifying properties of ion channels. Erev is a reversal potential for the channel in Eq. 2, and f(Vm) represents the nonlinear part of the GHK equation in Eq. 3.
The following arguments are made at the moment of observation (t = tob). Since the electric elements are assumed to be linear, f(Vm) is expressed as
| (4) |
where E is the value of intersection of the tangential line with the voltage axis. Then, all the channel currents can be expressed in the common form of GX × (Vm − EX), where
in Eq. 2, and
in Eq. 3.
Thus, Eq. 1 is described as
| (5) |
where X and Y are labels for a channel current and an ion transporter current, respectively. Equation 5 is equivalent to a linear electrical circuit shown in Fig. 1 A. An individual channel is expressed with one battery (EX) and one conductance (GX), and each transporter is represented by a current source (IY). Cm is assumed to be constant. Equation 5 can be rearranged as
| (6) |
Then, Eq. 6 is described as
| (7) |
where
| (8) |
| (9) |
Then, if we consider Vm as a free variable, Eq. 7 corresponds to Fig. 1 B. Therefore, Vm tends to approach an equilibrium value, VL, with a time constant τ at each time point. Fig. 2 shows the temporal changes of VL and Vm during an action potential in the SA node cell model (7) and ventricular myocyte model (8) obtained by calculating Eq. 8 at every moment. As VL leads changes of Vm in advance, we refer to it as the lead potential. Note that VL crosses Vm only when dVm/dt = 0.
Figure 2.
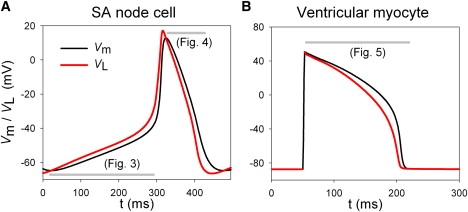
Time-dependent changes of VL (red) and Vm (black) in the SA node cell model (A) and ventricular myocyte model (B). The period for current injection was excluded from calculation of VL in panel B (50–52 ms). The gray bars indicate the time spans analyzed in Figs. 3–5.
Estimation of contributions of ion channels and transporters to the automaticity of Vm
According to Fig. 1 B and Eq. 7, the automatic change of Vm is driven by the time-dependent change in VL, and τ represents the passive property of the membrane. Therefore, the membrane automaticity can be expressed in terms of dVL/dt with complete exclusion of τ:
| (10) |
Here, we will calculate the extent to which a component of interest affects dVL/dt. Toward this end, we determine dVL_Fix/dt after eliminating the time-dependent change of the component of interest (i.e., , , or ), leaving all the other components intact. We refer to this process of eliminating the time-dependent change as fixing. For example, when we fix Gi, we set in Eq. 10:
| (11) |
The relative contribution, rc, is defined as
| (12) |
and rc satisfies the equation
| (13) |
An rc of positive sign means that a component is operating to incline dVL/dt in the same direction as the control dVL/dt. On the other hand, an rc of negative sign means that a component interferes with the change of VL by inclining dVL/dt in the opposite direction. If a component is entirely responsible for dVL/dt, dVL_Fix/dt is 0 and rc equals 1.
Application to cell models
In this study, the temporal changes of rc were calculated for p(o), f′(Vm), EX, and IY. We confirmed that Eq. 13 was satisfied with a precision of 10−4, that is, the sum of rc became 1 at every moment (not shown). For physiological interest, we showed rc obtained by fixing p(o) for ion channels, or IY for transporters in Figs. 3–5. For the rest of the components, the time average of rc was given in Table 1. The sum of rc for EX (Erev in Eq. 2 and E in Eq. 4) and rc for f′(Vm) (in Eq. 4) were presented for individual ion species; K+, Na+, Ca2+, and Cl− fluxes through all channels. These correspond to contributions of rectification in the GHK equations and shift of the reversal potentials due to the change of ion concentrations.
Figure 3.
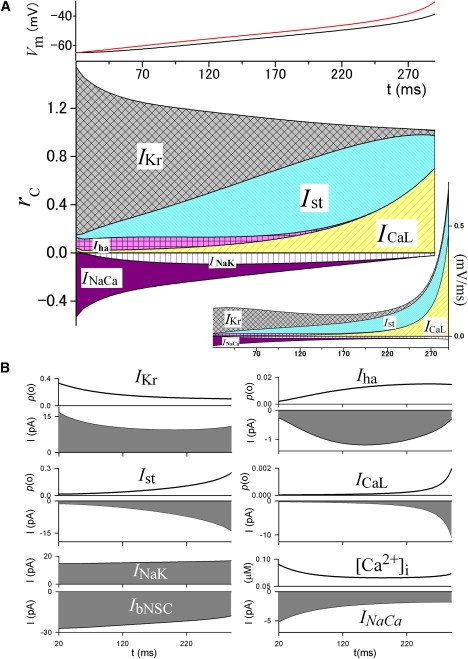
Time profile of rc during slow diastolic depolarization in the SA node model. (A) (Top) Time-dependent changes of VL (red) and Vm (black). These are the same curves as those shown in Fig. 2A. (Bottom) Time-dependent changes of rc of the major current components calculated by Eq. 12. (Inset, right bottom) The numerators in Eq. 12 for the corresponding currents. (B) Changes of p(o) or amplitude of the corresponding currents, and [Ca2+]i. It should be noted that the numerical calculation of rc has poor precision when dVL/dt approaches 0 because rc is normalized with dVL/dt (the denominator in Eq. 12). Therefore, we excluded the ranges in which dVL/dt is close to zero from the analyses (also done in Figs. 4 and 5).
Figure 4.
Time profile of rc during repolarization of the SA node action potential. (A) (Top) Time-dependent changes of VL (red) and Vm (black). These are the same curves as those shown in Fig. 2A. (Bottom) Time-dependent changes of rc of the major membrane currents. (B) Changes of p(o) or amplitude of the corresponding currents, and [Ca2+]i.
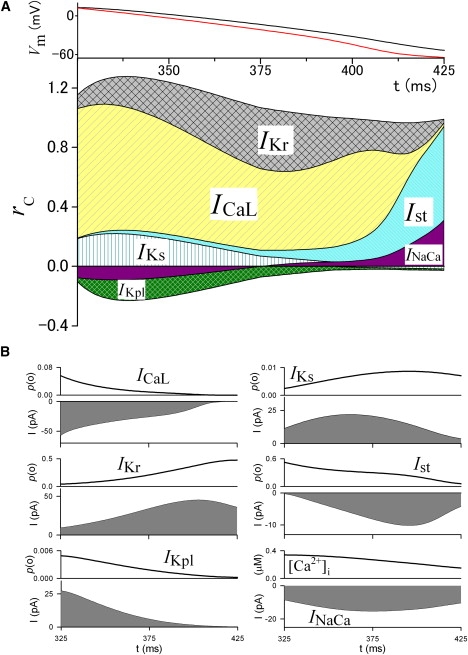
Figure 5.
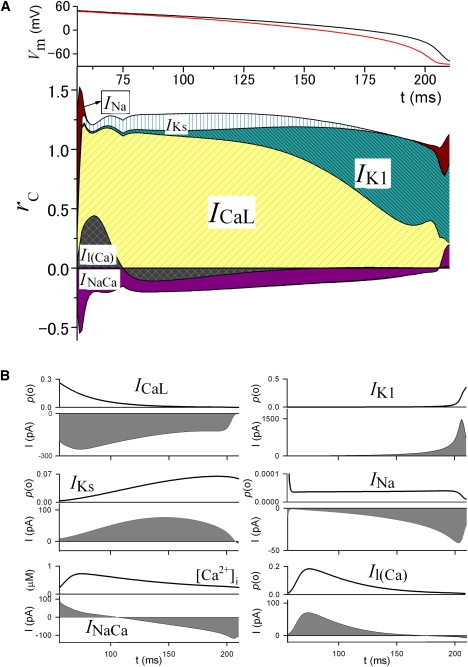
The time profile of rc during repolarization of the ventricular action potential. (A) (Top) Time-dependent changes of VL (red) and Vm (black). These are the same curves as those shown in Fig. 2B. (Bottom) Time-dependent changes of rc of the major membrane currents. (B) Changes of p(o) or amplitude of the corresponding currents, and [Ca2+]i.
Table 1.
Average rc of cellular components
| Components | SA node depolarization | SA node repolarization | Ventricular repolarization |
|---|---|---|---|
| p(o) of ion channels | |||
| INa | 0.0009 | 0.0001 | 0.0124 |
| ICaL | 0.1615 | 0.5798 | 0.8729 |
| ICaT | 0.0082 | 0.0008 | −0.0003 |
| Ist | 0.3746 | 0.1261 | — |
| Iha | 0.0520 | −0.0038 | — |
| IK1 | 0.0106 | 0.0011 | 0.2419 |
| IKr | 0.5925 | 0.2673 | 0.0261 |
| IKs | 0.0186 | 0.0868 | 0.0814 |
| Ito | — | — | −0.0045 |
| IKpl | −0.0124 | −0.0684 | −0.0012 |
| Il(Ca) | −0.0047 | 0.0143 | 0.0073 |
| IKATP | ∼0∗ | ∼0∗ | ∼0∗ |
| IKACh | 0.0058 | 0.0151 | — |
| IVRCC | — | — | -0.0008 |
| ICFTR | — | — | 0 |
| Turnover rate of transporters | |||
| INaCa | −0.1519 | 0.0087 | −0.1264 |
| INaK | −0.0603 | −0.0170 | −0.0009 |
| IPMCA | 0.0040 | ∼0 | −0.0012 |
| EXand f′(Vm) | |||
| K+ flux | −0.0050 | 0.0313 | 0.0103 |
| Na+ flux | 0.0053 | −0.0137 | −0.0059 |
| Ca+ flux | 0.0004 | −0.0286 | −0.1122 |
| Cl− flux | ∼0∗ | ∼0∗ | 0.0011 |
| Sum | 1 | 1 | 1 |
The rc for p(o) of nongating currents, IbNSC, IClb, or ICab, is zero. Abbreviations for currents: INa, Na+ current; ICaL, L-type Ca2+ current; ICaT, T-type Ca2+ current; Ist, sustained inward current; Iha, hyperpolarization-activated cation current; IK1, inward rectifier K+ current; IKr, delayed rectifier K+ current, rapid component; IKs, delayed rectifier K+ current, slow component; Ito, transient outward current; IKpl, voltage-dependent K+ current (plateau current); Il(Ca), Ca2+-activated background cation current; IKATP, ATP-sensitive K+ current; IKACh, Acetylcholine-activated K+ current; IVRCC, volume-regulated Cl− channel current; INaCa, Na+/Ca2+ exchange current; INaK, Na+/K+ pump current; IPMCA, plasma membrane Ca2+-ATPase current; IbNSC, background nonselective cation current; IClb, background Cl− current; ICab, background Ca2+ current; ICFTR, cystic fibrosis transmembrane conductance regulator (CFTR) Cl− channel current.
rc < 10−4.
The value dVL/dt in Eq. 12 is calculated numerically with a time step 0.005 ms. Numerical integration of differential equations of the model was conducted by Euler method with a time step 0.005 ms. When using smaller time steps than 0.005 ms, the results, for practical purposes, remained the same.
Results
As a case study, rc defined by Eq. 12 was evaluated in various phases of the action potential in the SA node and ventricular cell models. The value Im includes the following ion channels and ion transporters in the SA node cell model (7),
| (14) |
and in the ventricular myocyte model (8),
| (15) |
The definitions of the abbreviations are presented in the legend of Table 1. To facilitate understanding of the results below, the sign of rc is summarized in Table 2. For example, if an inward current is carried through a channel and the p(o) of the channel increases, this increases dVL/dt, and makes rc positive in the depolarization phase (dVL/dt >0) or negative in the repolarization phase (dVL/dt<0).
Table 2.
Polarity of rc
| Action potential phase | Direction of current | Channel |
Transporter |
||
|---|---|---|---|---|---|
| dp(o)/dt > 0 | dp(o)/dt < 0 | dIY/dt > 0 | dIY/dt < 0 | ||
| dVL/dt > 0 (depolarization) | Inward | + | − | − | + |
| Outward | − | + | |||
| dVL/dt < 0 (repolarization) | Inward | − | + | + | − |
| Outward | + | − | |||
Slow diastolic depolarization in SA node cells
Fig. 3 A shows rc for the major currents obtained by fixing p(o) of ion channels, or by fixing the turnover rate of transporters during diastolic depolarization in the SA node cell model. Fig. 3 B shows the time-dependent variations of p(o) and the current amplitude. The magnitude of dVL/dt remained nearly constant at ∼0.09 mV/ms during the initial 200 ms after the maximum diastolic potential, and increased exponentially thereafter, as shown in Fig. 3 A and the inset in this figure. At the beginning of depolarization, dVL/dt is largely determined by the deactivation of the outward IKr (i.e., the decrease in p(o) of IKr). As rc of IKr decreases, it is substituted by those of the inward currents, Ist and ICaL, via depolarization-dependent activation. The rc of Ist reached a peak of ∼0.63 and then decreased after 220 ms, which is simply biased by the much larger increase in rc of ICaL (inset in Fig. 3). Although ICaL is the main current in the upstroke of the action potential, a tiny increase of p(o) (<0.002) before upstroke also plays a significant role in leading the diastolic depolarization. Inward Iha also plays a positive role at the early stage with an rc of ∼0.1. This is relatively small because the increase of p(o) saturates at ∼250 ms and the amplitude of Iha is small. The lead-potential analysis clearly separates the role of IbNSC from that of Vm-gated currents. It has been reported that IbNSC, the largest inward current of ∼−25 pA, plays a role in diastolic depolarization by driving Vm toward its reversal potential of ∼0 mV (9). However, the rc of IbNSC is zero because IbNSC is a nongated channel current (i.e., p(o) = 1), exclusive of trivial contributions of EX or f′(Vm). Inward INaCa has a negative rc, because the amplitude of INaCa gradually decreases during the diastolic depolarization period. This decrease of INaCa is attributable to a decrease of [Ca2+]i in the first two-thirds of the depolarization phase after the peak reached in the previous action potential and a continuous increase in Vm. INaK also has a negative rc because the outward INaK increases with depolarizing Vm.
Repolarization of the SA node action potential
Surprisingly, inward ICaL has a larger rc in driving repolarization than any of the other outward currents (Fig. 4). This effect is attributable to a continuous decrease in p(o) through Ca2+-dependent inactivation during the action potential and also through removal of the voltage-dependent activation in the final rapid repolarization. The p(o) of the outward IKr continuously increases via fast recovery from inactivation and thereby its rc is positive throughout the duration of the action potential. IKs initially has a positive rc comparable to that of IKr, and then its rc gradually decreases because the increase of p(o) becomes slower. Ist plays the largest role near the end of repolarization because its activation gate has a dynamic range that is more negative than those for ICaL and IKr. The monotonic decrease in the p(o) of IKpl via Vm-dependent rectification interferes with repolarization with rc ∼−0.1. INaCa also hampers repolarization in the initial half of the repolarization phase with a negative rc but accelerates repolarization in the latter half because the amplitude of the inward INaCa initially increases and then decreases.
Repolarization in ventricular myocytes
As in the SA node cells, ICaL is the major current that determines the plateau potential shape with the largest rc by its time-dependent decrease of the p(o) in the repolarization of the ventricular action potential (Fig. 5). The value rc of IK1 gradually substitutes that of ICaL in the latter half of the plateau, since the p(o) of the outward IK1 progressively increases due to release from the Mg2+ block. Another outward current, IKs, is responsible for the repolarization during an initial 130 ms (for the repolarization near plateau potential) with rc of ∼0.15 due to the increase of the p(o). The rapid decrease in the p(o) of INa via inactivation immediately after the upstroke of the action potential plays a major role in phase 1 repolarization. Additionally, the final decrease of the p(o) via deactivation of INa in phase 3 repolarization is responsible for its positive rc. Although INa provides an inward current that progressively increases up to −40 pA, its rc is invisibly small during the plateau because the p(o) hardly changes, and acts like a background current. The rc of the outward Il(Ca) is determined by the time course of the intracellular Ca2+ transient, as shown in Fig. 5 B. The initial rapid increase in [Ca2+]i increases the p(o) of Il(Ca), resulting in a relatively large rc during the initial 20 ms followed by a negative rc due to the decay of [Ca2+]i. The amplitude of INaCa steadily decreases from outward to inward along the decay time course of [Ca2+]i, and thereby INaCa has a negative rc during the plateau, except in the last rapid repolarizing phase. These currents with a negative rc work to hamper the repolarization. The rest of the currents, such as IbNSC, IVRCC, INaK, and IKr, which are not shown in Fig. 5, make minor or no contributions.
Discussion
Major ion channels and electrogenic ion transporters have been identified by both the biochemical and electrophysiological studies of cardiac membrane excitation. The roles of these functional components in generating the spontaneous SA node action potential or autonomic repolarization of ventricular action potentials have been discussed qualitatively based on the dynamic characteristics of the individual current components. The lead-potential analysis developed in our study allows quantification of the relative contribution to the automatic changes in Vm by defining the new concepts of VL (Eq. 8) and rc (Eq. 12). This is the first method, to our knowledge, to enable estimation of the negative, as well as the positive, contributions along the time course of Vm. In addition, the contribution of the p(o) of each ion channel can be considered separately from those of rectification in the GHK equation and the change of ion concentrations (rc of EX and f′(Vm) in Table 1). In the case studies in the SA node and ventricular cell models, the rc value of EX and f′(Vm) was much smaller than that of the p(o) of ion channels. Thus, the selection of an Ohmic (Eq. 2) or a GHK equation (Eq. 3) for describing ion flux may not be critical for considering the rc in mathematical cell models.
Comparison with other methods of analyzing membrane excitation
A variety of methods have been applied to analyze the mechanisms underlying membrane excitation in mathematical cell models. In this section, lead-potential analysis is compared with previous methods. The most common approaches are inhibition methods, in which a selected ionic current is excluded or decreased in amplitude and consequent changes in membrane excitation are analyzed (10,11). This method is simple, but interpretation of the results is complicated and often somewhat equivocal, because not only the selected current but also other currents are secondarily affected by modification of the action potential or ion concentrations. Furthermore, the nonlinear behavior of the system prevents quantitative estimation of the contribution of each current. Sensitivity analysis can overcome these difficulties by measuring modifications induced by an infinitesimal change of a parameter of interest (i.e., a partial derivative) (5,6). We regard lead-potential analysis as a type of sensitivity analysis because Eq. 12 can be rewritten using the partial derivative of VL with respect to a fixed component (x; p(o), EX, f′(Vm), and IY):
| (16) |
Compared to sensitivity analysis, rc can be directly interpreted as contribution to automaticity, because the partial derivative of VL is weighted by , the actual change of x at a given moment. is merely multiplied for normalization.
Bifurcation analysis is also commonly used to analyze the relationships between functional components and membrane excitability. This approach surveys equilibrium points in parameter space (bifurcation diagram) and determines critical values at which bifurcations occur. Bifurcation analyses have been successfully applied to systems with macroscopic modal changes in the Vm dynamics, such as extinction of spontaneous pacemaking in the SA node cell (3), induction of reentrant arrhythmias or ectopic beats in cardiac muscles (2), abnormal initiation of spontaneous oscillatory firing in ventricular myocytes (4), and repetitive trains of action potentials in muscle fiber (1). Thus, bifurcation analysis is useful for examination of behavioral responses on the level of the entire system with respect to time-independent parameters such as maximum conductance of a channel. Bifurcation analysis qualitatively interprets the results based on topological changes in bifurcation diagrams and, as simplification is required to make the problems manageable, the conclusions from bifurcation diagrams are valid under a specific condition only. On the other hand, lead-potential analysis can be used to clarify the ionic mechanisms in a selected phase of membrane excitation, and provides quantitative measures of the contributions of time-dependent variables of individual ion channels or transporters to the automatic movement of Vm. Furthermore, in its application, simplification is not required for a complicated electrophysiological cell model. Since these two methods integrate information in different respects, we consider that they are complementary for obtaining a comprehensive understanding of the ionic mechanisms underlying membrane excitation.
Comparison with the previous lead-potential method
Lead-potential analysis was first introduced by Sarai et al. (12) to evaluate the contribution of individual current components to slow diastolic depolarization in the SA node model. The new method differs from the previous method in two ways: the equation for VL and the method of estimating the contribution of ion channels and transporters. First, VL in the earlier work was defined by the equation
| (17) |
where GK, GNa, and GCa are the whole cell conductances for the net currents Inet,K, Inet,Na, and Inet,Ca, respectively, after excluding INaK, which is generated by the active transporter. Na+ and Ca2+ components of INaCa were included in Inet,Na and Inet,Ca, respectively, as INaCa is driven passively by the electrochemical driving force. Neglecting the fact that several currents were described with the nonlinear GHK equation, the whole cell conductances were approximated by the following Ohmic equations:
| (18) |
| (19) |
| (20) |
Fig. 6 A compares the old VL calculated with Eq. 17 (blue curve) with the new VL calculated with Eq. 8 (red curve) in the guinea-pig SA node model (7) after adding the passive IClb and the active IPMCA to Eq. 17. The two curves differ because the rectification given by the GHK equation was neglected in the previous study, thereby the old VL cannot be used for quantitative estimation of the contributions of individual ion channels and transporters. Indeed, the two curves become identical in a model in which all the channel currents are described with Ohmic equations.
Figure 6.
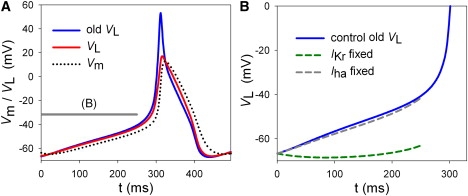
Comparison of VL determined by Eq. 8 (red solid) with the old VL determined by Eq. 17 (blue solid). (A) Both VL values meet with Vm (black dotted) at dVm/dt = 0. The curves for the present VL and Vm are the same as those shown in Fig. 2. The gray bars indicate the time spans analyzed in panel B. (B) Modified time courses of VL after fixing of IKr (green dashed) or Iha (gray dashed). The VL (blue) curve is the same as the blue curve in panel A.
In contrast to continuous estimation of dVL/dt by fixing a component at every moment in the new method, the time-dependent change was fixed throughout the slow diastolic depolarization in the previous lead-potential analysis. In Fig. 6 B, the value of p(o) for IKr or Iha determined at the maximum diastolic potential was used for the next 250 ms to observe the modification of VL. Comparison of the modified time course of VL with the control suggested that deactivation of IKr plays the major role in driving slow diastolic depolarization. However, this conclusion is still qualitative. In contrast, the new lead-potential analysis provides temporal profiles of the contributions and successfully shows the ionic mechanisms of slow diastolic depolarization when taken together with the profile of p(o) and the current size (Figs. 3 B, 4 B, and 5 B).
Limitations and applications of lead-potential analysis
Equation 8 for VL in Methods includes the assumption that an ion transporter acts like a current source. It should be noted that this assumption might cause an error in the calculation of the lead potential because any responses of transporter currents to changes in electrochemical driving force are ignored. An alternative description might be a linear equation with Vm for its ion driving force, like a channel current. For example, when INaK is expressed by a steady-state equation as in many cellular models (10,13), the conductance of the NaK pump, GNaK, might be calculated as
| (21) |
where ENaK, the reversal potential of INaK, is given as
| (22) |
ENa and EK are the Nernst equilibrium potential and ΔGMgATP is the free energy change by hydrolysis of ATP. In this case, GNaK is included in the total conductance of a cell as for channels, and Eq. 8 should also be modified with Eq. 21. However, GNaK is hard to define with Eq. 21 when INaK is generated by multiple states-transitions, as in the Kyoto model. GNaK is closely linked to INaK because the transport of ions necessarily causes the rearrangement of the state distribution. Therefore, transporter currents generated by states-transitions cannot be expressed with a battery and a conductance like a channel current. Thus, we treated a transporter current as a current source for simplicity in this study.
The selection of components to fix in the lead-potential analysis is dependent on the questions in a study, and the minimum constraint is that Eq. 13 should be satisfied for all the fixed components. For example, ICaL is usually described by Vm-gated activation, inactivation, and Ca2+-dependent inactivation. In addition, ICaL is known to be affected by [ATP]i. The model equation of ICaL can be expressed as
| (23) |
where
| (24) |
| (25) |
and f(Vm) is the nonlinear part of the GHK equation as in Eq. 3. In this case, rc may be calculated for individual terms, d, f, fCa, and [ATP]i, instead of p(o). However, Vm or [Ca2+]i inside of i, j, or k in Eq. 24 should not be fixed instead of d, f, and fCa, which are determined by state transitions.
Several types of models have been published for cardiac membrane excitation. However, it is difficult to assess the different models by comparing simulation results with corresponding experimental findings, such as the action potential shape, voltage-clamp recordings of the whole cell as well as individual current components, or the responses of the model to various kinds of perturbations. The comparison becomes even more difficult when different models show similar behavior but with distinct mechanisms. Lead-potential analysis may provide additional clues to assess the relevance of models by analyzing the underlying mechanisms in individual cell models.
In this study, we introduced a new analytic method to quantify the contributions of the cellular components to automaticity of Vm, with application of the method to cardiac membrane excitation. Since Eqs. 1–12 include no assumption specific for cardiac membrane excitation, the new method of lead-potential analysis may be generally applied to different cell types to clarify the ionic mechanisms underlying automatic membrane potential changes.
Acknowledgments
This work was supported by Ritsumeikan-Global Innovation Research Organization at Ritsumeikan University and the Biomedical Cluster Kansai project of the Ministry of Education, Culture, Sports, Science, and Technology of Japan.
References
- 1.Cannon S.C., Brown R.H., Corey D.P. Theoretical reconstruction of myotonia and paralysis caused by incomplete inactivation of sodium channels. Biophys. J. 1993;65:270–288. doi: 10.1016/S0006-3495(93)81045-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chay T.R., Lee Y.S. Studies on re-entrant arrhythmias and ectopic beats in excitable tissues by bifurcation analyses. J. Theor. Biol. 1992;155:137–171. doi: 10.1016/s0022-5193(05)80593-4. [DOI] [PubMed] [Google Scholar]
- 3.Kurata Y., Hisatome I., Imanishi S., Shibamoto T. Roles of L-type Ca2+ and delayed-rectifier K+ currents in sinoatrial node pacemaking: insights from stability and bifurcation analyses of a mathematical model. Am. J. Physiol. Heart Circ. Physiol. 2003;285:H2804–H2819. doi: 10.1152/ajpheart.01050.2002. [DOI] [PubMed] [Google Scholar]
- 4.Kurata Y., Hisatome I., Matsuda H., Shibamoto T. Dynamical mechanisms of pacemaker generation in IK1-downregulated human ventricular myocytes: insights from bifurcation analyses of a mathematical model. Biophys. J. 2005;89:2865–2887. doi: 10.1529/biophysj.105.060830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kim T.H., Shin S.Y., Choo S.M., Cho K.H. Dynamical analysis of the calcium signaling pathway in cardiac myocytes based on logarithmic sensitivity analysis. Biotechnol. J. 2008;3:639–647. doi: 10.1002/biot.200700247. [DOI] [PubMed] [Google Scholar]
- 6.Weaver C.M., Wearne S.L. Neuronal firing sensitivity to morphologic and active membrane parameters. PLOS Comput. Biol. 2008;4:e11. doi: 10.1371/journal.pcbi.0040011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Himeno Y., Sarai N., Matsuoka S., Noma A. Ionic mechanisms underlying the positive chronotropy induced by β1-adrenergic stimulation in guinea pig sinoatrial node cells: a simulation study. J. Physiol. Sci. 2008;58:53–65. doi: 10.2170/physiolsci.RP015207. [DOI] [PubMed] [Google Scholar]
- 8.Takeuchi A., Tatsumi S., Sarai N., Terashima K., Matsuoka S. Ionic mechanisms of cardiac cell swelling induced by blocking Na+/K+ pump as revealed by experiments and simulation. J. Gen. Physiol. 2006;128:495–507. doi: 10.1085/jgp.200609646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dokos S., Celler B., Lovell N. Ion currents underlying sinoatrial node pacemaker activity: a new single cell mathematical model. J. Theor. Biol. 1996;181:245–272. doi: 10.1006/jtbi.1996.0129. [DOI] [PubMed] [Google Scholar]
- 10.Demir S.S., Clark J.W., Murphey C.R., Giles W.R. A mathematical model of a rabbit sinoatrial node cell. Am. J. Physiol. 1994;266:C832–C852. doi: 10.1152/ajpcell.1994.266.3.C832. [DOI] [PubMed] [Google Scholar]
- 11.Zhang H., Holden A.V., Kodama I., Honjo H., Lei M. Mathematical models of action potentials in the periphery and center of the rabbit sinoatrial node. Am. J. Physiol. Heart Circ. Physiol. 2000;279:H397–H421. doi: 10.1152/ajpheart.2000.279.1.H397. [DOI] [PubMed] [Google Scholar]
- 12.Sarai N., Matsuoka S., Kuratomi S., Ono K., Noma A. Role of individual ionic current systems in the SA node hypothesized by a model study. Jpn. J. Physiol. 2003;53:125–134. doi: 10.2170/jjphysiol.53.125. [DOI] [PubMed] [Google Scholar]
- 13.Rice J.J., Jafri M.S., Winslow R.L. Modeling short-term interval-force relations in cardiac muscle. Am. J. Physiol. Heart Circ. Physiol. 2000;278:H913–H931. doi: 10.1152/ajpheart.2000.278.3.H913. [DOI] [PubMed] [Google Scholar]


