Abstract
Time series data provided by single-molecule Förster resonance energy transfer (smFRET) experiments offer the opportunity to infer not only model parameters describing molecular complexes, e.g., rate constants, but also information about the model itself, e.g., the number of conformational states. Resolving whether such states exist or how many of them exist requires a careful approach to the problem of model selection, here meaning discrimination among models with differing numbers of states. The most straightforward approach to model selection generalizes the common idea of maximum likelihood—selecting the most likely parameter values—to maximum evidence: selecting the most likely model. In either case, such an inference presents a tremendous computational challenge, which we here address by exploiting an approximation technique termed variational Bayesian expectation maximization. We demonstrate how this technique can be applied to temporal data such as smFRET time series; show superior statistical consistency relative to the maximum likelihood approach; compare its performance on smFRET data generated from experiments on the ribosome; and illustrate how model selection in such probabilistic or generative modeling can facilitate analysis of closely related temporal data currently prevalent in biophysics. Source code used in this analysis, including a graphical user interface, is available open source via http://vbFRET.sourceforge.net.
Introduction
Single-molecule biology has triumphed at creating well-defined experiments to analyze the workings of biological materials, molecules, and enzymatic complexes. As the molecular machinery studied becomes more complex, so too do the biological questions asked and, necessarily, the statistical tools needed to answer these questions from the resulting experimental data. In a number of recent experiments, researchers have attempted to infer mechanical parameters (e.g., the typical step size of a motor protein), probabilistic parameters (e.g., the probability per turn that a topoisomerase releases from its DNA substrate), or kinetic parameters (e.g., the folding/unfolding rates of a ribozyme) via statistical inference (1–9). Often the question of interest is not only one of selecting model parameters but also selecting the model, including from among models that differ in the number of parameters to be inferred from experimental data. The most straightforward approach to model selection generalizes the common idea of maximum likelihood (ML)—selecting the most likely parameter values—to maximum evidence (ME): selecting the most likely model.
In this article, we focus on model selection in a specific example of such a biological challenge: revealing the number of enzymatic conformational states in single-molecule Förster resonance energy transfer (smFRET) data. FRET (10–13) refers to the transfer of energy from a donor fluorophore (which has been excited by short-wavelength light) to an acceptor fluorophore (which then emits light of a longer wavelength) with efficiency that decreases as the distance between the fluorophores increases. The distance dependence of the energy transfer efficiency implies that the quantification of the light emitted at both wavelengths from a fluorophore pair may be used as a proxy for the actual distance (typically ∼1–10 nm) between these fluorophores. Often a scalar summary statistic (e.g., the “FRET ratio” IA/(IA + ID) of the acceptor intensity to the sum of the acceptor and donor intensities) is analyzed as a function of time, yielding time series data that are determined by the geometric relationship between the two fluorophores in a nontrivial way. When the donor and acceptor are biochemically attached to a single molecular complex, one may reasonably interpret such a time series as deriving from the underlying conformational dynamics of the complex.
If the complex of interest transitions from one locally stable conformation to another, the experiment is well modeled by a hidden Markov model (HMM) (14), a probabilistic model in which an observed time series (here, the FRET ratio) is conditionally dependent on a hidden, or unobserved, discrete state variable (here, the molecular conformation). HMMs have long been used in ion channel experiments in which the observed dynamic variable is voltage, and the hidden variable represents whether the channel is open or closed (15,16). More recently, Talaga proposed adapting such modeling for FRET data (17), and Ha and co-workers developed HMM software designed for FRET analysis (18). Such existing software for biophysical time series analysis implement ML on individual traces and require users either to guess the number of states present in the data, or to overfit the data intentionally by asserting an excess number of states. Resulting errors commonly are then corrected via heuristics particular to each software package. It would be advantageous to avoid the subjectivity (as well as extra effort) on the part of the experimentalist that is necessary in introducing thresholds or other parameterized penalties for complex models, as well as to derive principled approaches likely to generalize to new experimental contexts and data types. To that end, our aim here is to implement ME directly, avoiding overfitting even within the analysis of each individual trace, rather than as a postprocessing correction.
This article begins by describing the general problem of using probabilistic or generative models for experimental data (generically denoted y), in which one specifies the probability of the data given a set of parameters of biophysical interest (denoted ) and possibly some hidden value of the state variable of interest (denoted z). We then present one particular framework, variational Bayesian expectation maximization (VBEM), for estimating these parameters and at the same time finding the optimal number of values for the hidden-state variable z. (In this article, bold print is used for variables which are extensive in the number of observations.) We next validate the approach on synthetic data generated by an HMM, with parameters chosen to simulate data comparable to experimental smFRET data of interest. Having validated the technique, we apply it to experimental smFRET data and interpret our results. We close by highlighting advantages of the approach, suggesting related biophysical time-series data that might be amenable to such analysis, and outlining promising avenues for future extension and developments of our analysis.
Parameter and Model Selection
Since the techniques we present here are natural generalizations of those that form the common introduction to statistical techniques in a broad variety of natural sciences, we first remind the reader of a few key ideas in inference necessary before narrowing to the description of smFRET data, briefly discussing ML methods for parameter inference and ME methods for model selection. Note that since the ML-ME discussion does not rely on whether or not the model features hidden variables, for the sake of simplicity we first describe the inference in the context of models without hidden variables.
Maximum likelihood inference
The context in which most natural scientists encounter statistical inference is that of ML; in this problem setting, the model is specified by an expression for the likelihood, —i.e., the probability of the vector of data y given some unknown vector of parameters of interest, . (Although this is not often stated explicitly, this is the framework underlying minimization of χ2 or sums of squared errors; cf. Section S1 in the Supporting Material for more details.) In this context, the ML estimate of the parameter is
| (1) |
ML methods are useful for inferring parameter settings under a fixed model (or model complexity), e.g., a particular parameterized form with a fixed number of parameters. However, when one would like to compare competing models (in addition to estimating parameter settings), ML methods are generally inappropriate, as they tend to “overfit”, because likelihood always increases with greater model complexity.
This problem is conceptually illustrated in the case of inference from FRET data as follows: if a particular system has a known number of conformational states, say K = 2, one can estimate the parameters (the transition rates between states and relative occupation of states per unit time) by maximizing the likelihood, which gives a formal measure of the “goodness of fit” of the model to the data. Consider, however, an overly complex model for the same observed data with K = 3 conformational states, which one might do if the number of states is itself unknown. The resulting parameter estimates will have a higher likelihood or “better” fit to the data under the maximum likelihood criterion, as the additional parameters have provided more degrees of freedom with which to fit the data. The difficulty here is that maximizing the likelihood fails to accurately quantify the desired notion of a “good fit” which should agree with past observations, generalize to future ones, and model the underlying dynamics of the system. Indeed, consider the pathological limit in which the number of states, K, is set equal to the number of FRET time points observed. The model will exactly match the observed FRET trace, but will generalize poorly to future observations. It will have failed to model the data at all, and nothing will have been learned about the true nature of the system; the parameter settings will simply be a restatement of observations.
The difficulty in the above example is that one is permitted both to select the model complexity (the number of parameters in the above example) and to estimate single “best” parameter settings, which results in overfitting. Although there are several suggested solutions to this problem (reviewed in Bishop (19) and MacKay (20)), we present here a Bayesian solution for modeling FRET data that is both theoretically principled and practically effective (see Maximum evidence inference, below). In this approach, one extends the concepts pertaining to maximum likelihood to that of maximum marginal likelihood, or evidence, which results in an alternative quantitative measure of “goodness of fit” that explicitly penalizes overfitting and enables one to perform model selection. The key conceptual insight behind this approach is that one is prohibited from selecting single “best” parameter settings for models considered, and rather maintains probability distributions over all parameter settings.
Maximum evidence inference
The ML framework generalizes readily to the problem of choosing among different models, not only models of different algebraic forms, but also nested models in which one model is a parametric limit of another, e.g., models with hidden variables or variables in polynomial regression. (A two-state model is a special case of a three-state model with an empty state; a second-order polynomial is a special case of a third-order polynomial with one coefficient set to 0.) In this case, we introduce an index K over possible models, e.g., the order of the polynomial to be fit or, here, the number of conformational states, and hope to find the value of K∗ that maximizes the probability of the data, given the model, p(y|K):
| (2) |
The quantity p(y|K) is referred to as the marginal likelihood, or evidence, as unknown parameters are marginalized (or summed out) over all possible settings. The second expression in Eq. 2 follows readily from the rules of probability provided we are willing to model the parameters themselves (in addition to the data) as random variables. That is, we must be willing to prescribe a distribution from which the parameters are drawn, given one choice of the model. Since this term is independent of the data y, it is sometimes referred to as the “prior”; the treatment of parameters as random variables is one of the distinguishing features of Bayesian statistics. (In fact, maximizing the evidence is the principle behind the oft-used Bayesian information criterion (BIC) (34), an asymptotic approximation valid under a restricted set of circumstances, explored more thoroughly in Section S2 of the Supporting Material.) In this form, we may interpret the marginal likelihood, p(y|K), as an averaged version of the likelihood over all possible parameter values, where the prior weights each such value. Unlike the likelihood, the evidence is largest for the model of correct complexity and decreases for models that are either too simple or too complex, without the need for any additional penalty terms. There are several explanations for why evidence can be used for model selection (19). Perhaps the most intuitive is to think of the evidence as the probability that the observed data was generated using the given model (which we are allowed to do, since ME is a form of generative modeling). Overly simplistic models cannot generate the observed data and, therefore, have low evidence scores (e.g., it is improbable that a two-FRET-state model would generate data with three distinct FRET states). Overly complex models can describe the observed data, but they can generate so many different data sets that the specific observed data set becomes improbable (e.g., it is improbable that a 100-FRET-state model would generate data that only has three distinct FRET states (especially when one considers that the evidence is an average taken over all possible parameter values)).
In addition to performing model selection, we would like to make inferences about model parameters, described by the probability distribution over parameter settings given the observed data, , termed the posterior distribution. Bayes' rule equates the posterior with the product of the likelihood and the prior, normalized by the evidence:
| (3) |
Although ME, above, does not give us access to the posterior directly, as we show below, VBEM gives not only an approximation to the evidence but also an approximation to the posterior.
Variational approximate inference
Although in principle calculation of the evidence and posterior completely specifies the ME approach to model selection, in practice, exact computation of the evidence is often both analytically and numerically intractable. One broad and intractable class is that arising from models in which observed data are conditionally dependent on an unknown or hidden state to be inferred; these hidden variables must be marginalized over (summed over) in calculating the evidence in Eq. 2. (For the smFRET data considered here, these hidden variables represent the unobservable conformational states.) As a result, calculation of the evidence now involves a discrete sum over all states, z, in addition to the integrals over parameter values, :
| (4) |
This significantly complicates the tasks of model selection and posterior inference. Computing the terms in Eqs. 2 and 3 requires calculation of the evidence, direct evaluation of which requires a sum over all K settings for each of T extensive variables z (where T is the length of the time series). Such a sum is intractable even for K = 2 and modest values of T, e.g., on the order of 25. Although there exists various methods, such as Monte Carlo techniques, for numerically approximating such sums, we appeal here to variational methods for a scalable, robust, and empirically accurate method for approximate Bayesian inference. (For a discussion regarding practical aspects of implementing Monte Carlo techniques, including burn-in, convergence rates, and scaling, cf. Neal (21).)
To motivate the variational method, we note that we wish not only to select the model by determining K∗ but also to find the posterior probability distribution for the parameters, given the data, i.e., . This is done by finding the distribution that best approximates , i.e.,
| (5) |
where DKL is the usual Kullback-Leibler divergence, which quantifies the dissimilarity between two probability distributions. A simple identity (derived in Section S3 of the Supporting Material) relates this quantity to the evidence, p(y|K):
| (6) |
where is an analytically tractable functional (owing to a simple choice of the approximating distribution ). The inequality in Eq. 6 results from the property DKL ≥ 0, with equality if and only if . Mathematically, Eq. 6 illustrates that minimizing the functional simultaneously maximizes a lower bound on the evidence and minimizes the dissimilarity between the test distribution, q, and the parameter posterior distribution.
Qualitatively, the best test distribution gives not only the best estimate of the evidence but also the best estimate of the posterior distribution of the parameters themselves. In going from Eq. 4 to Eq. 6, we have replaced the problem of an intractable summation with that of bound optimization. As is commonly the case in bound optimizations, the closeness of this bound to the true evidence cannot be calculated. The validity of the approximation must be tested on synthetic data (as described in Numerical Experiments).
Calculation of F is made tractable by choosing an approximating distribution, q, with conditional independence among variables that are coupled in the model given by p; for this reason, the resulting technique generalizes mean-field theory of statistical mechanics (20). Just as in mean-field theory, the variational method is defined by iterative update equations; here, the update equations result from setting the derivative of F with respect to each of the factors in the approximating distribution q to 0. This procedure for calculating evidence is known as VBEM, and can be thought of as a special case of the more general expectation maximization algorithm (EM). (We refer the reader to Bishop (19) for a more pedagogical discussion of EM and VBEM.) Since F is convex in each of these factors, the algorithm provably converges to a local (though not necessarily global) optimum, and multiple restarts are typically employed. Note that this is true for EM procedures more generally, including as employed to maximize likelihood in models with hidden variables (e.g., HMMs). In ML inference, practitioners on occasion use the converged result, based on one judiciously chosen initial condition, rather than the optimum over restarts; this heuristic often prevents pathological solutions (cf. Bishop (19), Chapter 9).
Statistical Inference and FRET
Hidden Markov modeling
The HMM (14), illustrated in Fig. S9 of the Supporting Material, models the dynamics of an observed time series, y (here, the observed FRET ratio) as conditionally dependent on a hidden process, z (here, the unknown conformational state of the molecular complex). At each time t, the conformational state, zt, can take on any one of K possible values, conditionally dependent only on its value at the previous time via the transition probability matrix p(zt|zt−1) (i.e., z is a Markov process); the observed data depend only on the current-time hidden state via the emission probability p(yt|zt). According to the convention of the field, we model all transition probabilities as multinomial distributions and all emission probabilities as Gaussian distributions (18,22), ignoring for the moment the complication of modeling a variable distributed on the interval (0, 1) with a distribution of support (−∞, ∞).
For smFRET time series with observed data (y1,…,yT) = y and corresponding hidden-state conformations (z1,…,zT) = z, the joint probability of the observed and hidden data is
| (7) |
where comprises four types of parameters: a K-element vector, , where the kth component, πk, holds the probability of starting in the kth state; a K × K transition matrix, A, where aij is the probability of transitioning from the ith hidden state to the jth hidden state (i.e., aij = p(zt = j|zt−1 = i)); and two K-element vectors, and , where μk and λk are the mean and precision of the Gaussian distribution of the kth state.
As in Eq. 4, the evidence follows directly from multiplying the likelihood by priors and marginalizing:
| (8) |
The and each row of p(A|K) are modeled as Dirichlet distributions; each pair of μk and λk are modeled jointly as a Gaussian-gamma distribution. These distributions are the standard choice of priors for multinomial and Gaussian distributions (19). If we also assume that factorizes into , this HMM can be solved via VBEM (cf. Ji et al. (23)). Algebraic expressions for these distributions can be found in the Supporting Material (Section S6.1). Their parameter settings and the effect of their parameter settings on data inference can be found in Sections S6.2 and S6.3, respectively, of the Supporting Material. We found that for the experiments considered here, and the range of prior parameters tested, there is little discernible effect of the prior parameter settings on the data inference.
The variational approximation to the above evidence utilizes the dynamic program termed the forward-backward algorithm (14), which requires O(K2T) computations, rendering the computation feasible. (In comparison, direct summation over all terms requires O(KT) operations.) We emphasize that although individual steps in the ME calculation are slightly more expensive than their ML counterparts, the scaling with the number of states and observations is identical. As discussed in Variational Approximate Inference, above, in addition to calculating the evidence, the variational solution yields a distribution approximating the probability of the parameters given the data. Idealized traces can be calculated by taking the most probable parameters from these distributions and calculating the most probable hidden-state trajectory using the Viterbi algorithm (24).
Rates from states
HMMs are used to infer the number of conformational states present in the molecular complex, as well as the transition rates between states. Here, we follow the convention of the field by fitting every trace individually (since the number and mean values of smFRET states often vary from trace to trace). Unavoidably, then, an ambiguity is introduced in comparing FRET state labels across multiple traces, since “state 2” may refer to the high variant of a low state in one trace and to the low variant of a high state in a separate trace. To overcome this ambiguity, rates are not inferred directly from , but rather from the idealized traces, , where
| (9) |
and are, for ME, the parameters specifying the optimal parameter distribution, , or, for ML, the most likely parameters, . The number of states in the data set can then be determined by combining the idealized traces and plotting a 1D FRET histogram or transition density plot (TDP). Inference facilitates the calculation of transition rates by, for example, dwell-time analysis, TDP analysis, or by dividing the sum of the dwell times by the total number of transitions (18,25). In this work, we determine the number of states in an individual trace using ME. To overcome the ambiguity of labels when combining traces, we follow the convention of the field and use 1D FRET histograms and/or TDPs to infer the number of states in experimental data sets and calculate rates using dwell-time analysis (Section S5.3 in the Supporting Material).
Numerical Experiments
We created a software package to implement VBEM for FRET data called vbFRET. This software was written in MATLAB (The MathWorks, Natick, MA) and is available open source, including a point and click GUI. All ME data inference was performed using vbFRET. All ML data inference was performed using HaMMy (18), although we note that any analysis based on ML should perform similarly (see Section S5.1 in the Supporting Material for practicalities regarding implementing ML). Parameter settings used for both programs, methods for creating computer-generated synthetic data, and methods for calculating rate constants for experimental data can be found in Section S5 in the Supporting Material. According to the convention of the field, in subsequent sections, the dimensionless FRET ratio is quoted in dimensionless “units” of FRET.
Example: maximum likelihood versus maximum evidence
To illustrate the differences between ML and ME, consider the synthetic trace shown in Fig. 1, generated with three noisy states (K0 = 3) centered at μz = (0.41, 0.61, 0.81) FRET. This trace was analyzed by both ME and MLwith K = 1 (underfit), K = 3 (correctly fit), and K = 5 (overfit) (Fig. 1 A). In the cases where only one or three states are allowed, ME and ML perform similarly. However, when five states are allowed, ML overfits the data, whereas ME leaves two states unpopulated and correctly infers three states, illustrated clearly via the idealized trace.
Figure 1.
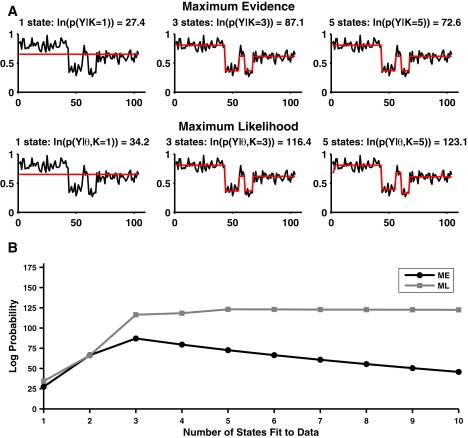
A single (synthetic) FRET trace analyzed by ME and ML. The trace contains three hidden states. (A) (Upper) Idealized traces inferred by ME when K = 1, K = 3, and K = 5, as well as the corresponding log(evidence) for the inference. The data are underresolved when K = 1, but for both K = 3 and K = 5, the correct number of states is populated. (Lower) Idealized traces inferred by ML when K = 1, K = 3, and K = 5, as well as the corresponding log(likelihood). Inferences when K = 1 and K = 3 are the same as for ME, but the data are overfit when K = 5. (B) The log (evidence) from ME (black) and log likelihood from ML (gray) for 1 ≤ K ≤ 10. The evidence is correctly maximized for K = 3, but the likelihood increases monotonically.
Moreover, whereas the likelihood of the overfitting model is larger than that of the correct model, the evidence is largest when only three states are allowed (; however, p(y|K) peaks at K = K0 = 3). The ability to use the evidence for model selection is further illustrated in Fig. 1 B, in which the data seen in Fig. 1 A are analyzed using both ME and ML with 1 ≤ K ≤ 10. The evidence is greatest when K = 3; however, the likelihood increases monotonically as more states are allowed, ultimately leveling off after five or six states are allowed.
Statistical validation
ME can be statistically validated by generating synthetic data, for which the true trajectory of the hidden state, z0, is known, and quantifying performance relative to ML. We performed such numerical experiments, generating several thousand synthetic traces, and quantified accuracy as a function of signal/noise ratio via four probabilities: 1), accuracy in the number of states, : the probability in any trace of inferring the correct number of states (where |z0| is the number of states in the model generating the data and is the number of populated states in the idealized trace); 2), accuracy in states, : the probability in any trace at any time of inferring the correct state; 3), sensitivity to true transitions: the probability in any trace at any time that the inferred trace, , exhibits a transition, given that z0 does; and 4), specificity of inferred transitions: the probability in any trace at any time that the inferred trace, z0, does not exhibit a transition, given that the true trace does not. We note, encouragingly, that for the ME inference, always equaled K∗ as defined in Eq. 2.
We identify each inferred state with the true state that is closest in terms of their means, provided the difference in means is <0.1 FRET. Inferred states for which no true state is within 0.1 FRET are considered inaccurate. Note that we do not demand that one and only one inferred state be identified with the true state. This effective smoothing corrects overfitting errors in which one true state has been inaccurately described by two nearby states (consistent with the convention of the field for analyzing experimental data).
For all synthetic traces, K0 = 3 with means centered at μz = (0.25, 0.5, 0.75) FRET. Traces were made increasingly noisy by increasing the standard deviation, σ, of each state. Ten different noise levels, ranging from σ ≈ 0.02 to σ ≈ 0.15, were used. Given the FRET states' mean separation and transition rates, and the lengths of the traces, this noise range varies from unrealistically noiseless to unrealistically noisy. Trace length, T, varied from 50 ≤ T ≤ 500 time steps, drawn randomly from a uniform distribution. One time step corresponds to one time-binned unit of an experimental trace, which is typically 25–100 ms for most CCD-camera-based experiments. Fast-transitioning (mean lifetime of 4 time steps between transitions) and slow-transitioning (mean lifetime of 15 time steps between transitions) traces were created and analyzed separately. Transitions were equally likely from all hidden states to all hidden states. For each of the 10 noise levels and two transition speeds, 100 traces were generated (2000 traces in total). Traces for which K0 = 2 (Fig. S7) and K0 = 4 (Fig. S8) were created and analyzed as well. The results were qualitatively similar and can be found in Section S7 of the Supporting Material.
As expected, both programs performed better on low noise traces than on high noise traces. ME correctly determined the number of FRET states more often than did ML in all cases except for the noisiest fast-transitioning trace set (Fig. 2, upper left). Of the 2000 traces analyzed here using ME and ML, ME overfit one and underfit 232, and ML overfit 767 and underfit 391. In short, ME essentially eliminated overfitting of the individual traces, whereas ML overfit 38% of individual traces. More than 95% (all but nine) of ME underfitting errors occurred on traces with FRET state noise >0.09, whereas ML underfitting was much more evenly distributed (at least 30 traces at every noise level were underfit by ML). The underfitting of noisy traces by ME may be a result of the intrinsic resolvability of the data, rather than a shortcoming of the inference algorithm; as the noise of two adjacent states becomes much larger than the spacing between them, the two states become indistinguishable from a single noisy state (in the limit, there is no difference between a one-state and a two-state system if the states are infinitely noisy). The causes of the underfitting errors by ML are less easily explained, but such errors suggest that the ML algorithm has not converged to a global optimum in likelihood (for reasons explained in Section S5.2 in the Supporting Material).
Figure 2.
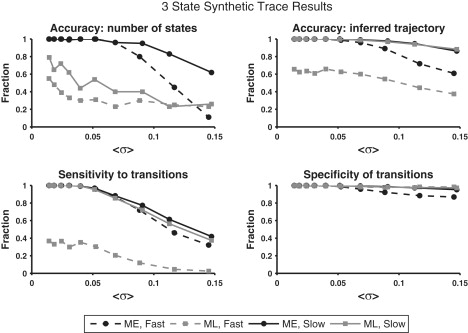
Comparison of ME and ML as a function of increasing hidden-state noise. Fast-transitioning (hidden-state mean lifetime of four time steps) and slow-transitioning (hidden-state mean lifetime of 15 time steps) traces were created and analyzed separately. Each data point represents the average value taken over 100 traces. (Upper left) : the probability in any trace of inferring the correct number of states. (Upper right) : the probability in any trace at any time that a transition is inferred given that a transition actually occurred. (Lower left) Sensitivity to true transitions: the fraction of time the correct FRET state was inferred during FRET trajectories. (Lower right) Specificity of inferred transitions: the probability in any trace at any time that no transition is inferred given that no transition actually occurred. Error bars on all plots were omitted for clarity and because the data plotted represent mean success rates for Bernoulli processes (and, therefore, determine the variances of the data as well).
In analyzing the slow-transitioning traces, the methods performed roughly equally on Probabilities 2–4 (always within ∼5% of each other). For the fast-transitioning traces, however, ME was much better at inferring the true trajectory of traces (by a factor of 1.5–1.6 for all noise levels) and showed superior sensitivity (by a factor of 2.7–12.5) to transitions at all noise levels. The two methods showed the same specificity to transitions until a noise level of σ > 0.8, beyond which ML showed better specificity (by a factor of 1.06–1.13). Inspection of the individual traces showed that all three of these results were due to ML missing many of the transitions in the data.
These results on synthetic data suggest that when the number of states in the system is unknown, ME clearly performs better at identifying FRET states. For inference of idealized trajectories, ME is at least as accurate as ML for slow-transitioning traces and more accurate for fast-transitioning traces. The performance of ME on fast-transitioning traces is particularly encouraging, since detection of a transient biophysical state is often an important objective of smFRET experiments, as discussed below.
Results
Having validated inference with vbFRET, we compared ME and ML inference on experimental smFRET data, focusing our attention on the number of states and the transition rates. The data we used for this analysis report on the conformational dynamics of the ribosome, the universally conserved ribonucleoprotein enzyme responsible for protein synthesis, or translation, in all organisms. One of the most dynamic features of translation is the precisely directed mRNA and tRNA movements that occur during the translocation step of translation elongation. Structural, biochemical, and smFRET data overwhelmingly support the view that during this process, ribosomal domain rearrangements are involved in directing tRNA movements (3,6,25–31). One such ribosomal domain is the L1 stalk, which undergoes conformational changes between open and closed conformations that correlate with tRNA movements between so-called classical and hybrid ribosome-bound configurations (Fig. S10 A) (6,31–33).
Using fluorescently labeled tRNAs and ribosomes, we recently developed smFRET probes between tRNAs (smFRETtRNA–tRNA) (27), ribosomal proteins L1 and L9 (smFRETL1–L9) (6), and ribosomal protein L1 and tRNA (smFRETL1–tRNA) (32). Collectively, these data demonstrate that upon peptide bond formation, tRNAs within pretranslocation (PRE) ribosomal complexes undergo thermally driven fluctuations between classical and hybrid configurations (smFRETtRNA–tRNA) that are coupled to transitions of the L1 stalk between open and closed conformations (smFRETL1–L9). The net result of these dynamics is the transient formation of a direct L1 stalk-tRNA contact that persists until the tRNA and the L1 stalk stochastically fluctuate back to their classical and open conformations, respectively (smFRETL1–tRNA). This intermolecular L1-stalk-tRNA-contact is stabilized by binding of elongation factor G (EF-G) to PRE and maintained during EF-G-catalyzed translocation (6,32).
Here we compare the rates of L1-stalk closing (kclose) and opening (kopen) obtained from ME and ML analysis of smFRETL1–L9 PRE complex analogs (PMN) under various conditions (which have the same number of FRET states by both inference methods) with the number of states inferred for smFRETL1–tRNA PMN complexes by ME and ML. (FRET complexes shown in Fig. S10 B.) These data were chosen for their diversity of smFRET ratios. The smFRETL1–L9 ratio fluctuates between FRET states centered at 0.34 and 0.56 (i.e., a separation of 0.22 FRET), whereas the smFRETL1–tRNA ratio fluctuates between FRET states centered at 0.09 and 0.59 FRET (i.e., a separation of 0.50 FRET). In addition, smFRETL1–L9 data were recorded under conditions that favor either fast-transitioning (PMNfMet+EFG) or slow-transitioning (PMNfMet and PMNPhe) complexes (complex compositions listed in Table 1).
Table 1.
Comparison of smFRETL1–L9 transition rates inferred by ME and ML
| Data set∗ | Method | kclosed (sec-1) | kopen (sec-1) |
|---|---|---|---|
| PMNPhe† | ME | 0.66 ± 0.05 | 1.0 ± 0.2 |
| ML | 0.65 ± 0.06 | 1.0 ± 0.3 | |
| PMNfMet‡ | ME | 0.53 ± 0.08 | 1.7 ± 0.3 |
| ML | 0.52 ± 0.06 | 1.8 ± 0.3 | |
| PMNfMet+EFG | ME | 3.1 ± 0.6 | 1.3 ± 0.2 |
| (1 μM)§ | ML | 2.1 ± 0.4 | 1.0 ± 0.2 |
| PMNfMet+EFG | ME | 2.6 ± 0.6 | 1.5 ± 0.1 |
| (0.5 μM)§ | ML | 2.0 ± 0.3 | 1.0 ± 0.1 |
Rates reported here are the mean ± SD from three or four independent data sets. Rates were not corrected for photobleaching of the fluorophores.
PMNPhe was prepared by adding the antibiotic puromycin to a posttranslocation complex carrying deacylated-tRNAfMet at the E site and fMet-Phe-tRNAPhe at the P site, and thus contains a deacylated-tRNAPhe at the P site.
PMNfMet was prepared by adding the antibiotic puromycin to an initiation complex carrying fMet-tRNAfMet at the P site, and thus contains a deacylated-tRNAfMet at the P site.
1.0 μM and 0.5 μM EF-G in the presence of 1 mM GDPNP (a nonhydrolyzable GTP analog) were added to PMNfMet, respectively.
First, we compared the smFRETL1–L9 data obtained from PMNfMet, PMNPhe, and PMNfMet+EFG. As expected from previous studies (32), 1D histograms of idealized FRET values from both inference methods showed two FRET states centered at 0.34 and 0.56 FRET (and one additional state due to photobleaching, for a total of three states). When individual traces were examined for overfitting, however, ML inferred four or five states in 20.1 ± 3.7% of traces in each data set, whereas ME inferred four or five states in only 0.9 ± 0.5% of traces. Consequently, more postprocessing was necessary to extract transition rates from idealized traces inferred by ML.
Our results (Table 1) demonstrate that there is very good overall agreement between the values of kclose and kopen calculated by ME and ML. For the relatively slow-transitioning PMNfMet and PMNPhe data, the values of kclose and kopen obtained from ME and ML are indistinguishable. For the relatively fast-transitioning PMNfMet+EFG data, however, the obtained values of kclose and kopen differ slightly between ME and ML. Since the true transition rates of the experimental smFRETL1–L9 data can never be known, it is impossible to assess the accuracy of the rate constants obtained from ME or ML in the same way as with the analysis of synthetic data. Although we cannot say which set of kclose and kopen values are most accurate for this fast-transitioning data set, our synthetic results would predict a larger difference between rate constants calculated by ME and ML for faster-transitioning data and suggest that the values of kclose and kopen calculated with ME have higher accuracy (Fig. 2).
Consistent with previous reports (6), ML infers two FRET states centered at flow ≡ 0.09 and fhigh ≡ 0.59 FRET (plus one photobleached state) for all smFRETL1–tRNA data sets. Conflicting with these results, however, ME infers three FRET states (plus a photobleached state) for these data sets. Two of these FRET states are centered at flow and fhigh, as in the ML case, whereas the third “putative” state is centered at fmid ≡ 0.35 FRET, coincidentally at the mean between flow and fhigh. Indeed, TDPs constructed from the idealized trajectories generated by ME or ML analysis of the PMNfMet+EFG smFRETL1–tRNA data set show the appearance of a new, highly populated state at fmid in the ME-derived TDP that is virtually absent in the ML-derived TDP (Fig. S11). Consistent with the TDPs, ∼46% of transitions in the ME-analyzed smFRETL1–tRNA trajectories are either to or from the new fmid state (Fig. 3 B). This fmid state is extremely short-lived; ∼75% of the data assigned to fmid consist of a single observation, i.e., with a duration at or below the CCD integration time (here, 50 ms) (Fig. 3 C). A representative ME-analyzed smFRETL1–tRNA trace is shown in Fig. 3 A.
Figure 3.
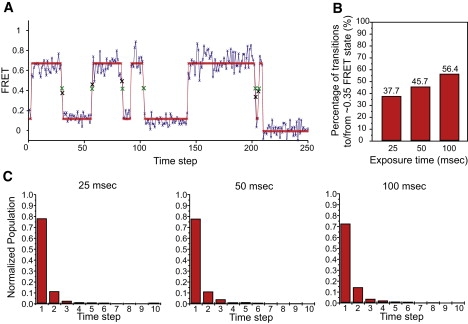
Analysis of the smFRETL1–tRNAfmid state. (A) A representative smFRETL1–tRNA trace idealized by ME, taken from the 50-ms exposure time data set. Both the observed data (blue) and idealized path (red) are shown. Individual data points, real and idealized, are shown as Xs. To emphasize the data at or near fmid, the Xs are enlarged and the observed and idealized data are shown in black and green, respectively. (B) Bar graph of the percentages of transitions to or from the fmid state under 25 ms, 50 ms, and 100 ms CCD integration time. (C) Normalized population histograms of dwell time spent at the fmid state under 25 ms, 50 ms, and 100 ms CCD integration time.
There are at least two possible explanations for this putative new state. The first is that fmid originates from a very short-lived (i.e., lifetime ≤50 ms), bona fide, previously unidentified intermediate conformation of the PMN complex. The second is that fmid data are artifactual, resulting from the binning of the continuous-time FRET signal during CCD collection. Each time-binned data point represents the average intensity of thousands or more photons. If a transition occurs 25 ms into a 50-ms time step, half the photons will come from the flow state and half from the fhigh state, resulting in a datum at approximately their mean. This type of CCD blurring artifact would be lost in the noise of closely spaced FRET states, but would become more noticeable as the FRET separation between states increases.
To distinguish between these two possibilities, we recorded PMNfMet+EFG smFRETL1–tRNA data at half and double the integration times (i.e., 25 ms and 100 ms). If the fmid state is a true conformational intermediate, then 1), the percentage of transitions exhibiting at least one data point at or near fmid should increase as the integration time decreases; and 2), the number of consecutive data points defining the dwell time spent at or near fmid should increase as the integration time decreases. Conversely, if the fmid state arises from a time-averaging artifact, then 1), the percentage of transitions containing at least one data point at or near fmid should increase as the integration time increases, because longer integration times increase the probability that a transition will occur during the integration time; and 2), the number of consecutive data points defining the dwell time spent at or near the fmid state should be independent of the integration time, because transitions occurring within the integration time will always be averaged to generate a single data point.
Consistent with the view that the fmid state arises from time averaging over the integration time, Fig. 3 B demonstrates that the percentage of transitions containing at least one data point at or near fmid increases as the integration time increases. This manifests as an increase in the density of transitions starting or ending at fmid as the integration time decreases for the ME-derived TDPs in Fig. S11. These data are further supported by the results presented in Fig. 3 C, demonstrating that the number of consecutive data points defining the dwell time of the fmid state is remarkably insensitive to the integration time. We conclude that the fmid state identified by ME is composed primarily of a time-averaging artifact that we refer to as “camera blurring”, and we call the ME-inferred fmid state the “blur state”. Although ML infers four or five states in 35% of the traces (compared to only 25% for ME), for some reason, ML significantly suppresses, but does not completely eliminate, detection of this blur state in the individual smFRET trajectories. At present, we cannot determine whether this is a result of the ML method itself (i.e., overfitting noise in one part of the trace may cause it to miss a state in another) or due to the specific implementation of ML in the software we used (Section S5.1 in the Supporting Material). In retrospect, the presence of blur states should not be surprising, since they follow trivially from the time averaging that results from averaging over the CCD integration time. In Section S8 of the Supporting Material, we propose a method for correcting these blur artifacts.
The observation that ML analysis does not detect a blur state that is readily identified by ME analysis is in line with our results on synthetic data, in which ME consistently outperforms ML with regard to detecting the true number of states in the data, particularly in fast-transitioning data, and strongly suggests that ME will generally capture short-lived intermediate FRET states that ML will tend to overlook. Although this feature of ML might be desirable in terms of suppressing blur states such as the one we have identified in the smFRETL1–tRNA data set, it is undesirable in terms of detecting bona fide intermediate FRET states that may exist in a particular data set.
Conclusions
These synthetic and experimental analyses confirm that ME can be used for model selection (identification of the number of smFRET states) at the level of individual traces, improving accuracy and avoiding overfitting. In addition, ME inference solved by VBEM provides q∗, an estimate of the true parameter and idealized trace posterior, making possible the analysis of kinetic parameters, again at the level of individual traces. As a tool for inferring idealized traces, ME produces traces that are visually similar to those of ML; in the case of synthetic data generated to emulate experimental data, ME performs with comparable or superior accuracy. The idealized trajectories inferred by ME required substantially less postprocessing, however, since ME usually inferred the correct number of states to the data and, consequently, did not require states with similar idealized values within the same trace to be combined in a postprocessing step. The superior trajectory inference, accuracy, and sensitivity to transitions of ME on fast-transitioning synthetic traces suggests that the differences in transition rates calculated for fast-transitioning experimental data is a result of superior fitting by ME as well.
In some experimental data, ME detected a very short-lived blur state, which comparison of experiments at different sampling rates suggests is the result of a camera time-averaging artifact. Once detected by ME, the presence of this intermediate state is easily confirmed by visual inspection, yet it was not identified by ML inference. Although not biologically relevant in this instance, this result suggests that ME inference is able to uncover real biological intermediates in smFRET data that would be missed by ML.
We conclude by emphasizing that this method of data inference is in no way specific to smFRET. The use of ME and VBEM could improve inference for other forms of biological time series where the number of molecular conformations is unknown. Some examples include motor protein trajectories with an unknown number of chemomechanical cycles (i.e., steps), DNA/enzyme binding studies with an unknown number of binding sites, and molecular dynamics simulations in which important residues exhibit an unknown number of rotamers.
All code used in this analysis, as well as a point-and-click GUI interface, is available open source via http://vbFRET.sourceforge.net.
Supporting Material
Eight sections, 11 figures, and two tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01513-6.
Supporting Material
Acknowledgments
It is a pleasure to acknowledge helpful conversations with Taekjip Ha and Vijay Pande, Harold Kim and Eric Greene for their comments on the manuscript, mathematical collaboration with Alexandro D. Ramirez, and Subhasree Das for managing the Gonzalez laboratory.
This work was supported by a grant to C.H.W. from the National Institutes of Health (5PN2EY016586-03) and grants to R.L.G. from the Burroughs Wellcome Fund (CABS 1004856), the National Science Foundation (MCB 0644262), and the National Institutes of Health's National Institute of General Medical Sciences (1RO1GM084288-01). C.H.W. also acknowledges the generous support of Mr. Ennio Ranaboldo.
Footnotes
Jake M. Hofman's present address is Yahoo! Research, 111 West 40th St., New York, NY 10018.
References
- 1.Koster D., Wiggins C., Dekker N. Multiple events on single molecules: Unbiased estimation in single-molecule biophysics. Proc. Natl. Acad. Sci. USA. 2006;103:1750–1755. doi: 10.1073/pnas.0510509103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Moffitt J.R., Chemla Y.R., Aathavan K., Grimes S., Jardine P.J. Intersubunit coordination in a homomeric ring ATPase. Nature. 2009;457:446–450. doi: 10.1038/nature07637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Munro J.B., Altman R.B., O'Connor N., Blanchard S.C. Identification of two distinct hybrid state intermediates on the ribosome. Mol. Cell. 2007;25:505–517. doi: 10.1016/j.molcel.2007.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhuang X.W., Bartley L.E., Babcock H.P., Russell R., Ha T.J. A single-molecule study of RNA catalysis and folding. Science. 2000;288:2048–2051. doi: 10.1126/science.288.5473.2048. [DOI] [PubMed] [Google Scholar]
- 5.Zhuang X.W., Kim H., Pereira M.J.B., Babcock H.P., Walter N.G. Correlating structural dynamics and function in single ribozyme molecules. Science. 2002;296:1473–1476. doi: 10.1126/science.1069013. [DOI] [PubMed] [Google Scholar]
- 6.Fei J., Kosuri P., MacDougall D.D., Gonzalez R.L. Coupling of ribosomal L1 stalk and tRNA dynamics during translation elongation. Mol. Cell. 2008;30:348–359. doi: 10.1016/j.molcel.2008.03.012. [DOI] [PubMed] [Google Scholar]
- 7.Yildiz A., Tomishige M., Vale R.D., Selvin P.R. Kinesin walks hand-over-hand. Science. 2004;303:676–678. doi: 10.1126/science.1093753. [DOI] [PubMed] [Google Scholar]
- 8.Wiita A.P., Perez-Jimenez R., Walther K.A., Grater F., Berne B.J. Probing the chemistry of thioredoxin catalysis with force. Nature. 2007;450:124–127. doi: 10.1038/nature06231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Myong S., Rasnik I., Joo C., Lohman T.M., Ha T. Repetitive shuttling of a motor protein on DNA. Nature. 2005;437:1321–1325. doi: 10.1038/nature04049. [DOI] [PubMed] [Google Scholar]
- 10.Jares-Erijman E.A., Jovin T.M. FRET imaging. Nat. Biotechnol. 2003;21:1387–1395. doi: 10.1038/nbt896. [DOI] [PubMed] [Google Scholar]
- 11.Joo C., Balci H., Ishitsuka Y., Buranachai C., Ha T. Advances in single-molecule fluorescence methods for molecular biology. Annu. Rev. Biochem. 2008;77:51–76. doi: 10.1146/annurev.biochem.77.070606.101543. [DOI] [PubMed] [Google Scholar]
- 12.Roy R., Hohng S., Ha T. A practical guide to single-molecule FRET. Nat. Methods. 2008;5:507–516. doi: 10.1038/nmeth.1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schuler B., Eaton W.A. Protein folding studied by single-molecule FRET. Curr. Opin. Struct. Biol. 2008;18:16–26. doi: 10.1016/j.sbi.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rabiner L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE. 1989;77:257–286. [Google Scholar]
- 15.Qin F., Auerbach A., Sachs F. Maximum likelihood estimation of aggregated Markov processes. Proc. R. Soc. Lond. B. Biol. Sci. 1997;264:375–383. doi: 10.1098/rspb.1997.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Qin F., Auerbach A., Sachs F. A direct optimization approach to hidden Markov modeling for single channel kinetics. Biophys. J. 2000;79:1915–1927. doi: 10.1016/S0006-3495(00)76441-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Andrec M., Levy R.M., Talaga D.S. Direct determination of kinetic rates from single-molecule photon arrival trajectories using hidden Markov models. J. Phys. Chem. A. 2003;107:7454–7464. doi: 10.1021/jp035514+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.McKinney S.A., Joo C., Ha T. Analysis of single-molecule FRET trajectories using hidden Markov modeling. Biophys. J. 2006;91:1941–1951. doi: 10.1529/biophysj.106.082487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bishop C.M. Springer; New York: 2006. Pattern Recognition and Machine Learning. [Google Scholar]
- 20.MacKay D.J. Cambridge University Press; Cambridge, United Kingdom: 2003. Information Theory, Inference, and Learning Algorithms. [Google Scholar]
- 21.Neal, R. 1993. Probabilistic Inference Using Markov Chain Monte Carlo Methods. Technical Report CRG-TR-93–1, Department of Computer Science, University of Toronto.
- 22.Dahan M., Deniz A.A., Ha T.J., Chemla D.S., Schultz P.G. Ratiometric measurement and identification of single diffusing molecules. Chem. Phys. 1999;247:85–106. [Google Scholar]
- 23.Ji S., Krishnapuram B., Carin L. Variational Bayes for continuous hidden Markov models and its application to active learning. IEEE Trans. Pattern Anal. Mach. Intell. 2006;28:522–532. doi: 10.1109/TPAMI.2006.85. [DOI] [PubMed] [Google Scholar]
- 24.Viterbi A.J. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans. Inform. Theory. 1967;13:260–269. [Google Scholar]
- 25.Cornish P.V., Ermolenko D.N., Noller H.F., Ha T. Spontaneous intersubunit rotation in single ribosomes. Mol. Cell. 2008;30:578–588. doi: 10.1016/j.molcel.2008.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Moazed D., Noller H.F. Intermediate states in the movement of transfer RNA in the ribosome. Nature. 1989;342:142–148. doi: 10.1038/342142a0. [DOI] [PubMed] [Google Scholar]
- 27.Blanchard S.C., Kim H.D., Gonzalez R.L., Puglisi J.D., Chu S. tRNA dynamics on the ribosome during translation. Proc Natl. Acad. Sci, USA. 2004;101:12893–12898. doi: 10.1073/pnas.0403884101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kim H.D., Puglisi J.D., Chu S. Fluctuations of transfer RNAs between classical and hybrid states. Biophys. J. 2007;93:3575–3582. doi: 10.1529/biophysj.107.109884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Agirrezabala X., Lei J., Brunelle J.L., Ortiz-Meoz R.F., Green R. Visualization of the hybrid state of tRNA binding promoted by spontaneous ratcheting of the ribosome. Mol. Cell. 2008;32:190–197. doi: 10.1016/j.molcel.2008.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Julian P., Konevega A.L., Scheres S.H., Lazaro M., Gil D. Structure of ratcheted ribosomes with tRNAs in hybrid states. Proc. Natl. Acad. Sci. USA. 2008;105:16924–16927. doi: 10.1073/pnas.0809587105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cornish P.V., Ermolenko D.N., Staple D.W., Hoang L., Hickerson R.P. Following movement of the L1 stalk between three functional states in single ribosomes. Proc. Natl. Acad. Sci. USA. 2009;106:2571–2576. doi: 10.1073/pnas.0813180106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fei J., Bronson J.E., Hofman J.M., Srinivas R.L., Wiggins C.H. Allosteric collaboration between elongation factor G and the ribosomal L1 stalk direct tRNA movements during translation. Proc. Natl. Acad. Sci. USA. 2009 doi: 10.1073/pnas.0908077106. (published ahead of print, doi: 10.1073/pnas.0908077106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sternberg S.H., Fei J., Prywes N., McGrath K.A., Gonzalez R.L. Translation factors direct intrinsic ribosome dynamics during termination and ribosome recycling. Nat. Struct. Mol. Biol. 2009;16:861–868. doi: 10.1038/nsmb.1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Schwarz G. Estimating the dimension of a model. Ann. Stat. 1978;6:461–464. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


