Frequency-dependent disynaptic inhibition in the pyramidal network: a ubiquitous pathway in the developing rat neocortex

Abstract

The general structure of the mammalian neocortex is remarkably similar across different cortical areas. Despite certain cytoarchitectural specializations and deviations from the general blueprint, the principal organization of the neocortex is relatively uniform. It is not known, however, to what extent stereotypic synaptic pathways resemble each other between cortical areas, and how far they might reflect possible functional uniformity or specialization. Here, we show that frequency-dependent disynaptic inhibition (FDDI) is a generic circuit motif that is present in all neocortical areas we investigated (primary somatosensory, auditory and motor cortex, secondary visual cortex and medial prefrontal cortex of the developing rat). We did find, however, area-specific differences in occurrence and kinetics of FDDI and the short-term dynamics of monosynaptic connections between pyramidal cells (PCs). Connectivity between PCs, both monosynaptic and via FDDI, is higher in primary cortices. The long-term effectiveness of FDDI is likely to be limited by an activity-dependent attenuation of the PC–interneuron synaptic transmission. Our results suggest that the basic construction of neocortical synaptic pathways follows principles that are independent of modality or hierarchical order within the neocortex.

Introduction

The mammalian neocortex consists of dozens of functional areas that are engaged in a variety of different tasks, ranging from the integration of primary sensory information to memory storage and high-level cognitive processing. Given this wide range of functions, its general design is relatively homogeneous between different cortical areas. In its standard form, the mammalian neocortex is a continuous six-layered structure, and shows, depending on the specific area, a more or less pronounced modular organization termed the cortical column. The ratio between excitatory (spiny stellate and pyramidal) neurons and inhibitory (local circuit) neurons is relatively constant (∼80 to 20%) (Braitenberg & Schüz, 1998), and the distribution of many though not all visualizable molecular markers is relatively homogeneous (Dong, 2007). Neuron types are layer-specific rather than area-specific, and as a consequence cortical areas have been mainly defined according to their interconnections with other cortical or subcortical regions. Another aspect that distinguishes cortical areas quantitatively is the thickness of the individual layers and correspondingly the cell density per layer and column (DeFelipe et al. 2002), and the neocortical cytoarchitectural specializations have also been used to classify different areas for over 100 years (Brodmann, 1909).

Much less is known about the area-specific physiology and dynamics of specific synaptic pathways, and to what extent they might reflect or define the function of a cortical area. Thick-tufted layer 5 pyramidal cells (PCs) are one of the principle output neurons of the cortex and are among the cortical cell types that are investigated in greatest detail (Markram et al. 1997; Spruston, 2008). They are interconnected with glutamatergic synapses that are mainly formed on basal and oblique dendrites and display depressing short-term dynamics in juvenile rodents. Recently, the direct recruitment of inhibitory synaptic potentials from intermediate interneurons induced by PC activity has received special attention (Kapfer et al. 2007; Ren et al. 2007; Silberberg & Markram, 2007; Molnár et al. 2008). Frequency-dependent disynaptic inhibition (FDDI) has been shown to be an important dynamic and activity-dependent synaptic pathway in layer 5 and layer 2/3 of the primary somatosensory cortex (Kapfer et al. 2007; Silberberg & Markram, 2007). High frequency spiking (∼70 Hz) in a single PC can lead, via a strongly facilitating synapse, to suprathreshold activity in specific nearby interneurons, e.g. the Martinotti cell. These cells in turn project back to the pyramidal cell population and preferentially inhibit the apical and tufted dendrites (Silberberg & Markram, 2007).

In the present study we investigate five different cortical areas in juvenile rats by comparing their monosynaptic excitatory (direct EPSPs) and FDDI connectivity between large layer 5 pyramidal cells. We show that FDDI is a generic inhibitory pathway existing in all investigated cortical areas, with a prevalence which is more than double that of monosynaptic excitatory connections and with kinetics that exhibit area-specific differences. FDDI has a lateral extent comparable to monosynaptic excitatory connectivity, and also drops in amplitude in a similar way. FDDI becomes weaker or disappears after repetitive high frequency stimulation, with the fatigue of the PC–interneuron synapse as one possible reason.

Methods

Slice preparation

Experiments were carried out according to the Swiss national and institutional guidelines and comply with The Journal's policies and regulations (Drummond, 2009). Fourteen- to 18-day-old, non-anaesthetized Wistar rats were quickly decapitated and their brains carefully removed and placed in iced artificial cerebrospinal fluid (ACSF). Slices (300 μm) were cut on an HR2 vibratome (Sigmann Elektronik, Heidelberg, Germany). Parasagittal slices, approximately 1.7–2.2 mm lateral to the midline, were cut to access primary somatosensory cortex (SSC, above the anterior extremity of the hippocampus ± 1 mm), primary motor cortex (MC, 2–4 mm anterior to the hippocampus), or secondary visual cortex (VC2, 3–5 mm posterior) (Fig. 1A) (Sherwood & Timiras, 1970; Paxinos & Watson, 1998). Slices of primary auditory cortex (AC, approximately 2 mm dorsal to the rhinal fissure) and also VC2 (∼4 mm lateral to the midline) were obtained by coronal slices, rostrocaudally positioned where the corpus callosum (CC) joins the two hemispheres and the hippocampus completely ‘encloses’ subcortical structures (around bregma – 4.8 mm). Slices of medial prefrontal cortex (mPFC) were coronally cut, rostrocaudally positioned where the CC was already visible but not yet joined (around bregma + 2.5 mm). Slices were incubated at 37°C for 30–60 min and then left at room temperature until recording. Cells were visualized by infrared differential interference contrast videomicroscopy utilizing either a C2400-03 camera (Hamamatsu, Hamamatsu City, Japan) mounted on an upright Axioscope FS microscope (Zeiss, Oberkochen, Germany), or a VX55 camera (Till Photonics, Gräfeling, Germany) mounted on an upright BX51WI microscope (Olympus, Tokyo, Japan). Thick-tufted layer 5 PCs were selected according to their large soma size (15–25 μm) and their apparent large trunk of the apical dendrite. Care was taken to use only ‘parallel’ slices, i.e. slices that had a cutting plane parallel to the course of the apical dendrites and the primary axonal trunk. This ensured sufficient preservation of both the PCs’ axonal and dendritic arborizations.

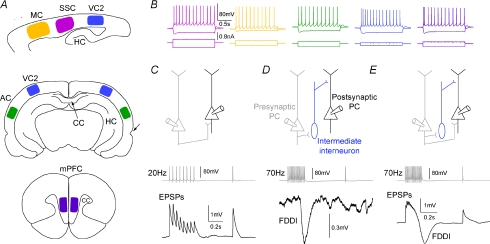
Figure 1. Cortical areas and stimulation protocols.

A, cortical areas that have been investigated. Top, parasagittal slice with primary motor cortex (yellow, MC), primary somatosensory cortex (pink, SSC), and secondary visual cortex (blue, VC2). Hippocampus abbreviated as HC. Middle, coronal slice with VC2 and primary auditory cortex (green, AC). Intact corpus callosum (CC) and rhinal fissure are indicated by arrows. Bottom, coronal slice with medial prefrontal cortex (purple, mPFC). B, firing pattern and hyperpolarizing voltage response to de- and hyperpolarizing step currents. All cells were continuous or burst-regular spiking. C, two pyramidal cells (PCs), directly interconnected. The presynaptic cell was stimulated with an 8 spike–20 Hz train plus recovery test pulse 0.5 s later in order to determine EPSP kinetics and short-term dynamics. D, two PCs interconnected via a single (or multiple) interneuron(s). High frequency stimulation in the presynaptic PC (15 spikes, 70 Hz) elicits suprathreshold activity in a nearby interneuron, which in turn gives rise to FDDI in a neighbouring PC. E, two PCs connected with both monosynaptic EPSPs and FDDI.

Chemicals and solutions

Slices were continuously superfused with ACSF containing (in mm) 125 NaCl, 25 NaHCO₃, 2.5 KCl, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂, and 25 d-glucose, bubbled with 95% O₂–5% CO₂. The intracellular pipette solution contained (in mm) 110 potassium gluconate, 10 KCl, 4 ATP-Mg, 10 phosphocreatine, 0.3 GTP, 10 N-2-hydroxyethylpiperazine-N′-2-ethanesulfonic acid (Hepes), and 13 biocytin, adjusted to pH 7.3–7.4 with 5 m KOH. Osmolarity was adjusted to 290–300 mosmol l⁻¹ with d-mannitol (25–35 mm). The membrane potential values given were not corrected for the liquid junction potential, which was approximately −14 mV. Chemicals were from Sigma Aldrich (Steinheim, Germany) or Merck (Darmstadt, Germany). The endocannabinoid receptor antagonist AM251 was from Tocris (Ellisville, MO, USA).

Electrophysiological recordings

Multiple somatic whole cell recordings (2–12 cells simultaneously) were performed with Axopatch 200B or Multiclamp 700B amplifiers (Molecular Devices, Union City, CA, USA) in the current clamp mode at 34 ± 1°C bath temperature. Data acquisition was performed via an ITC-18 or ITC-1600 board (Instrutech Co., Port Washington, NY, USA), connected to a PC or Macintosh running a custom-written routine under IGOR Pro (Wavemetrics, Portland, OR, USA). Sampling rates were 5–10 kHz, and the voltage signal was filtered with a 2 kHz Bessel filter. Patch pipettes were pulled with a Flaming/Brown micropipette puller P-97 (Sutter Instruments Co., Novato, CA, USA) and had an initial resistance of 3–8 MΩ.

Stimulation protocols

Monosynaptic, direct excitatory connections were identified by stimulation of a presynaptic cell with a 20 Hz train of eight strong and brief current pulses (1–3.5 nA, 2–4 ms), followed by a so-called recovery test response 0.5 s after the end of the train, all precisely and reliably eliciting action potentials (APs). Disynaptic connections (FDDI) were characterized by the same protocol but at a higher frequency (70 Hz) and 15 APs. Occasionally, postsynaptic PCs were slightly depolarized from a potential of ∼−62 mV to −58 to −60 mV to increase the driving force for inhibitory connections. This resulted in slightly larger amplitudes, but was usually not necessary to detect FDDI. It has been previously shown that FDDI is based on a GABA_A conductance (Silberberg & Markram, 2007). Although the intracellular and extracellular chloride concentrations amount to a reversal potential of ∼−68.6 mV, we observed hyperpolarizing somatic currents. This was probably due to the location of the interneuron–PC synapses at distant locations of the apical dendrite, which has been reported to have a more depolarized membrane potential (Stuart & Spruston, 1998; Berger et al. 2001).

Data analysis

Connectivity ratios, both for monosynaptic excitatory and FDDI, were calculated as the ratio between observed versus tested connections between a pair of cells. A pair of cells could therefore maximally have two connections (both directions), a triplet could have six connections, and a cluster of n neurons could potentially have n(n− 1) connections. The error bars of the connectivity ratios express, based on the binomial distribution, the standard error of the mean (s.e.m.) estimate according to s.e.m.= (P(1 −P)/(n− 1))^1/2, with P being the observed (estimated) connectivity ratio (probability of connection) and n the number of tested connections (Zar, 1999). For analysis of the kinetics of FDDI and monosynaptic excitation (EPSPs), the membrane potential baseline V_bl was calculated as the average membrane potential V_m 1–99 ms prior to stimulation onset (see Figs 4C and 5C). Both FDDI and EPSPs were detected visually based on the mean response of 10–50 repetitions, corresponding roughly to a crossing of V_bl plus 3–7 times the standard deviation of V_bl. Due to noise, extraction of kinetic parameters for events equal to or smaller than 0.1–0.15 mV was barely possible and those results were then not included in the analysis. They were, however, taken into account for estimation of the connectivity ratios. Some experiments in the SSC were also used in a different context for a study on summation properties of disynaptic connections (unpublished observations), and not all SSC connections were used for the kinetic analysis of EPSPs and FDDIs (260 out of 667 monosynaptic excitatory and 679 out of 1383 FDDI connections). FDDI ‘contaminated’ with monosynaptic excitatory connections were also excluded from the kinetic analysis. FDDI amplitude was extracted as the difference between the minimal voltage V_peak 0.06–0.4 s after stimulation onset t_stim and V_bl. The slope of the rising phase of FDDI was calculated linearly between 20 and 80% of the amplitude. The intersection of this line and the baseline was taken as the response onset time t_onset. The slope of the decaying phase and FDDI offset were calculated accordingly. FDDI symmetry, describing the position of the V_peak relative to onset and offset, was calculated as (t_peak−t_onset)/(t_onset−t_offset). The overshoot was the maximal voltage reached within 0.2 s after t_peak, relative to V_bl. EPSP amplitude was extracted as the difference between the maximal voltage V_peak 3–18 ms after stimulation onset and V_bl (Fig. 5C). Stimulation onset t_stim was defined as the time of the peak of the presynaptic AP. For the 2nd to 8th EPSPs, V_bl was calculated from 1 to 2 ms prior to t_stim. The EPSP rising phase was calculated between 20 and 80% of the amplitude, τ_rise was a single exponential fit between 0 and 100%. Time to peak was the difference between t_peak and t_stim. Paired pulse ratio (PPR) was defined as the ratio between second and first EPSP amplitude. All analysis on synaptic kinetics was performed with IGOR Pro. Synaptic short-term dynamics were fitted with a phenomenological model (Markram et al. 1998), giving estimates for release probability: utilization (U), absolute synaptic efficacy (A_se), recovery from depression (D), and synaptic facilitation (F). Statistical analysis and model fitting were performed with MATLAB using the Kruskal–Wallis test followed by Dunn's method for multiple comparisons with a significance level of α= 0.01 or 0.05 (Zar, 1999). Distance-dependent connectivity ratios were fitted with a Gaussian with the standard deviation σ as the only free parameter since it gave better results than an exponential fit (FDDI, Gaussian fit with σ= 290 μm, χ²_Gauss= 0.53, as compared with single exponential fit with λ= 221 μm, χ²_exp= 0.76; EPSPs, Gaussian fit with σ= 265 μm, χ²_Gauss= 0.58, as compared with single exponential fit with λ= 211 μm, χ²_exp= 0.60). Distance-dependent amplitudes were fitted with single exponentials.

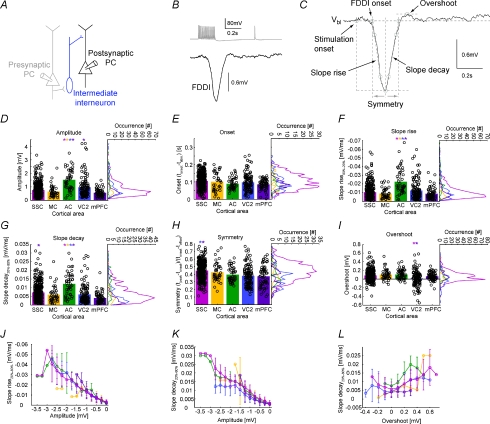
Figure 4. Area-specific kinetics of FDDI.

A, a presynaptic PC (grey), connecting to an interneuron (blue), in turn innervating a postsynaptic PC (black). B, stimulation of the presynaptic PC leading to FDDI in the postsynaptic PC. C, parameters extracted from the disynaptic inhibitory response. D–I, amplitude, onset time (t_onset–t_stim), slopes of the rising and decaying phases, symmetry (t_peak−t_onset)/(t_onset−t_offset) and overshoot of the FDDI response. Colour code corresponds to areas depicted in Fig. 1. Bar graphs show the mean, black circles individual data points (scattered for better illustration). Vertical histograms contain 31 equally spaced bins. See Methods for a detailed description of the parameter extraction. Error bars denote standard deviation. Only highly significant differences (P < 0.01), colour coded (in one direction for a pair) are marked with an asterisk (Kruskal–Wallis test followed by Dunn's method for multiple comparisons, see Table 1). J, slope rise time as a function of FDDI amplitude. K, slope decay time as a function of FDDI amplitude. L, slope decay time as a function of overshoot. For J–L, abscissa was divided into 15 (J and K), or 12 (L) equally spaced bins. Colour coding for the different areas as in the histograms.

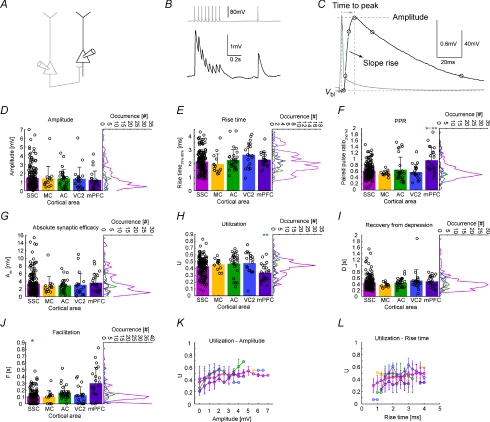
Figure 5. Area-specific kinetics of EPSPs and short term dynamics of EPSP trains.

A, a presynaptic PC (grey) connecting to a postsynaptic PC (black). B, stimulation of the presynaptic PC leading to EPSPs in the postsynaptic PC. C, parameters extracted from the monosynaptic excitatory response. D and E, amplitude and 20–80% rise time of the first EPSP in the train. F, paired pulse ratio of 2nd over 1st EPSP amplitude. G–J, parameters extracted from a fit to a model of synaptic dynamics: bar graphs show the mean, black circles individual data points (scattered for better illustration). Vertical histograms contain 31 equally spaced bins. See Methods for a detailed description of the parameter extraction. Error bars denote standard deviation. Only highly significant differences (P < 0.01), colour coded (in one direction for a pair) are marked with an asterisk (Kruskal–Wallis test followed by Dunn's method for multiple comparisons, see Table 2). K–L, utilization as a function of amplitude and rise time. Abscissa was divided into 15 (K) or 17 (L) equally spaced bins. Colour coding for the different areas as in the histograms.

Results

We recorded from 1584 PCs (SSC, 1193; MC, 40; AC, 56; VC2, 170; mPFC, 125) in 367 slices of 163 rats aged between 14 and 18 days (mean 15 days). Two to 12 thick-tufted/large layer 5 PCs were patched simultaneously, with one cell stimulated and the other remaining cells passively recorded in order to observe possible synaptic connections. In some cases step currents (1.5 s, ∼−300 to 500 pA) were injected to characterize the intrinsic properties of the cells (Figure 1B). All cells were continuous or sometimes burst-regular spiking, and showed a typical sag in response to a hyperpolarizing step current. Two different protocols were applied to investigate synaptic connectivity between PCs (exemplified in Fig. 1). A 20 Hz train revealed short-term dynamics and kinetics of the excitatory connection between two directly connected PCs (Fig. 1C). FDDI, mediated via an intermediate interneuron such as the Martinotti cell, was triggered and analysed with a 70 Hz train of 15 APs (Fig. 1D). Biphasic responses were seen when both pathways were present and stimulation frequency was sufficiently high (Fig. 1E). These cases were not analysed any further in the current study, although they were still included in the FDDI connectivity count.

FDDI is a generic sub-circuit of the neocortex

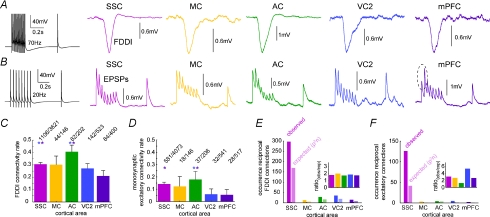
FDDI was present between large layer 5 PCs in all investigated cortical areas (Fig. 2A; SSC, MC, AC, VC2 and mPFC). The dynamics of excitatory connections between PCs were always dominated by synaptic depression, with the exception of responses in the mPFC that had a facilitatory component as well (Fig. 2B). The connectivity rate (ratio between observed connections and tested connections) of disynaptic inhibition ranged between 21% (mPFC) and 40.6% (AC), and was always more than double the monosynaptic excitatory connectivity ratio in each area, which ranged between 5.4 and 18% (Fig. 2C and D). Interestingly, several monosynaptic excitatory connectivity ratios were significantly higher in primary areas such as SSC and AC than in VC2 or mPFC (two-sided χ² test of a contingency table followed by Tukey-type multiple comparison testing for proportions (Zar, 1999); P < 0.01 for SSC–mPFC, SSC–VC2, AC–mPFC, AC–VC2). There were also highly significant differences between some areas for FDDI connections (P < 0.01 for SSC–mPFC, AC–mPFC, and AC–VC2; P < 0.05 for AC–SSC). We did not find significant differences between MC and any other cortical area, which is possibly due to the relatively small sampling size in MC. Reciprocal connections, that is, cell A projecting to cell B and vice versa, are displayed in Fig. 1E and F. Given the observed connectivity rates for single connections one can estimate how many reciprocal connections one expects to find assuming random network statistics (expected). For example, monosynaptic excitatory reciprocal connections between PCs have been reported to be more frequent than expected in SSC and VC (Markram et al. 1997; Song et al. 2005; but see Lefort et al. 2009). The actual observed reciprocal FDDI connectivity rates were 1.68–1.96 times higher than expected. For excitatory connections, the discrepancy in connectivity rates between observed and expected and also between the different areas was higher (ranging from 1.2 in AC to 5.28 in VC), possibly also due to a smaller sampling size.

Figure 2. Connectivity ratios of FDDI and EPSPs in different cortical areas.

A, high frequency stimulation (70 Hz) of a PC and examples of responses in a postsynaptic PC in SSC, MC, AC, VC2 and mPFC. B, 20 Hz stimulation of a PC and examples of responses in a postsynaptic PC in the same cortial areas as in A. C, FDDI connectivity rate between PCs in the investigated cortical areas. Highly significant differences were found between some areas (P_SSC−AC= 0.0027, P_SSC−mPFC= 7.24 × 10⁻⁵, P_AC−VC2= 4.44 × 10⁻⁴, P_AC−mPFC= 3.78 × 10⁻⁷, two-sided χ² test). D, monosynaptic excitatory connectivity between PCs in the investigated cortical areas. Significant differences were found between primary (SSC, MC, AC) and non-primary (VC2, mPFC) cortices (P_SSC−VC2= 7.6 × 10⁻⁸, P_SSC−mPFC= 2.3 × 10⁻⁸, P_MC−VC2= 0.0081, P_MC−mPFC= 0.0037, P_AC−VC2= 3.74 × 10⁻⁷, P_AC−mPFC= 1.02 × 10⁻⁷, two-sided χ² test). E, occurrence of reciprocal FDDI connections between PCs in the investigated cortical areas. Expectancy was calculated as P²n. Inset shows the ratio between observed and expected occurrences. F, occurrence of reciprocal monosynaptic excitatory connections between PCs in the investigated cortical areas. Colour code as in Fig. 1. Error bars in C and D denote s.e.m.

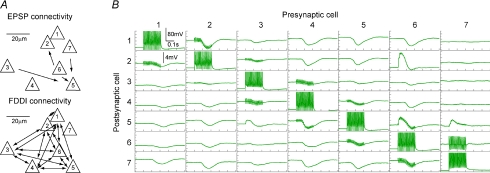
The remarkably high connectivity rates in the auditory cortex are illustrated in Fig. 3. The example shows a seven-cell cluster that featured 4 monosynaptic excitatory and 30 disynaptic inhibitory connections (Fig. 3A). Thus, in this particular cluster, the connectivity ratios were 4/42 = 9.5% and 30/42 = 71.4%, respectively. Interestingly, the FDDI connectivity between cells 1–6 is complete, that is, each cell is connected to each other (Fig. 3A and B). Cell 7 was not involved in this inhibitory circuit with the stimulation protocol used. As can be seen in the connectivity matrix, FDDI responses varied considerably in amplitude and kinetics, and these parameters are illustrated in Fig. 4 and summarized in Table 1 for the different investigated areas. Fifteen APs at 70 Hz were elicited in a presynaptic PC, and the FDDI response was recorded in the postsynaptic cell (Fig. 4A and B). Note that the exact number of interneurons mediating this response is not known. Six different parameters have been extracted from this compound inhibitory potential (Fig. 4C; see also Methods). FDDI in the auditory cortex seems to stand out. Here, we find the largest average amplitudes (−1.52 ± 0.79 mV), and the fastest rise and decay slopes (−0.02 ± 0.02 mV ms⁻¹ and 0.01 ± 0.01 mV ms⁻¹, Fig. 4D, F and G), rendering the response properties of auditory PCs most transient. A possible explanation for large amplitudes could be a more negative chloride reversal potential in PCs of the auditory cortex compared with other areas. We therefore determined the reversal potential of FDDI in auditory cortex by current clamping the postsynaptic PC to various hyperpolarized potentials while stimulating a FDDI-mediating PC. We found an average reversal potential in AC of −76.04 ± 7.72 mV (n= 5), which is remarkably similar to values obtained in the SSC by Silberberg and colleagues using the same intra- and extracellular solutions (−78.9 ± 10.3 mV, n= 55; Silberberg & Markram, 2007). Thus, it is unlikely that a larger chemical gradient of chloride ions is responsible for large FDDI amplitudes in AC.

Figure 3. Seven-cell cluster example in AC.

A, relative somatic positions of seven simultaneously patched cells and their connectivity in the AC. Cell 5 received monosynaptic excitatory input from cells 3, 6 and 7, and cell 2 received input from cell 6. Cells 1–6 were all interconnected with FDDI. B, matrix of the membrane potentials of all seven cells in response to high frequency stimulation. Postsynaptic voltage response to a presynaptic stimulation (on the diagonal) is shown in the corresponding row. Electrodes (cells) next to the stimulated electrode (on the secondary diagonals in the matrix) show stimulation artifacts in the voltage trace.

Table 1.

Kinetics of FDDI

	SSC (n= 363)	MC (n= 41)	AC (n= 46)	VC2 (n= 119)	mPFC (n= 67)	KW test, Dunn P < 0.01	KW test, Dunn P < 0.05
Amplitude (mV)	−0.718 ± 0.488	−0.651 ± 0.427	−1.518 ± 0.787	−0.971 ± 0.796	−0.558 ± 0.271	3–1,2,4,5	3–1,2,4,5
						4–5	4–5
Onset (s)	0.107 ± 0.043	0.193 ± 0.062	0.190 ± 0.032	0.195 ± 0.053	0.185 ± 0.030		1–5
Slope rise (mV ms−1)	−0.010 ± 0.008	−0.009 ± 0.006	−0.023 ± 0.015	−0.012 ± 0.011	−0.009 ± 0.006	3–1,2,4,5	3–1,2,4,5
Slope decay (mV ms−1)	0.007 ± 0.005	0.006 ± 0.005	0.012 ± 0.007	0.006 ± 0.006	0.004 ± 0.003	3–1,2,4,5	3–1,2,4,5
						1–5	1–4,5
Symmetry	0.448 ± 0.114	0.426 ± 0.124	0.396 ± 0.098	0.379 ± 0.133	0.374 ± 0.137	1–4,5	1–3,4,5
Overshoot (mV)	0.083 ± 0.116	0.101 ± 0.122	0.107 ± 0.107	0.017 ± 0.179	0.066 ± 0.088	4–1,3	4–1,2,3

Kinetic parameters of FDDI for SSC, MC, AC, VC2 and mPFC as displayed in Fig. 4 (means ±s.d.). Statistically significant differences between individual areas, tested with Kruskal–Wallis (with α < 0.01 and α < 0.05 significance level) followed by Dunn's method for multiple comparisons, are shown in the two rightmost columns.

The onset (Fig. 4E) was remarkably homogeneous between all areas, indicating that the excitability of the intermediate interneurons by PCs is likely to be relatively similar. Alternatively, excitability and the kinetics of the participating synaptic pathways could vary between the different areas while being tuned to match a certain onset timing. The symmetry of FDDI represents the relative position of the peak response with regard to its onset and offset. A perfectly symmetrical response would have a symmetry value of 0.5. But a typical postsynaptic potential (PSP), for example, has a much faster rise time constant than decay time constant, and therefore its response peak is very close to the beginning of the PSP, giving symmetry values of close to 0. On the contrary, FDDI is in general in all areas far more symmetric, yielding values between 0.37 ± 0.14 (mPFC) and 0.45 ± 0.11 (SSC), with the SSC significantly different from VC2 and mPFC. These high values can be explained by the abundance of the cationic H-current (I_h) in the apical and tufted dendrites in PCs, leading to a fast depolarization, milliseconds after stimulus onset (Silberberg & Markram, 2007). The same current is also responsible for the overshoot, a depolarization following the hyperpolarizing FDDI signal. It does not occur in every connection, and especially in VC2 it seems to be frequently lacking (0.02 ± 0.18 mV), showing highly significant differences from SSC and mPFC (0.08 ± 0.12 mV and 0.07 ± 0.09 mV).

FDDI with large amplitudes had fast rise and decay times in all investigated cortical areas (Fig. 4J and K). The mean correlation coefficients were −0.82 ± 0.06 and 0.73 ± 0.15, respectively. Therefore, the multiple differences found between AC and other cortices might reflect a single specialization of this circuitry in AC, e.g. larger unitary IPSPs produced by the interneuron–PC synapse. We also find a dependence between decay time and overshoot (Fig. 4L, correlation coefficient 0.40 ± 0.20). Decay time and overshoot depend on I_h (Silberberg & Markram, 2007), so the expression of this current should have a similar impact on both of them.

Similar kinetics but different short-term dynamics of EPSPs between PCs

The properties of monosynaptic excitatory connections between PCs were elucidated using 8 APs–20 Hz stimulation trains (Fig. 5A and B). Four kinetic parameters of the first EPSP were extracted (Fig. 5C). Amplitude, 20–80% rise time, and time to peak do not show a strong area specificity (Fig. 5D and E, Table 2). Only the single exponential fit to the rising phase, τ_rise, shows significant differences (mPFC vs. SSC and MC, VC2 vs. MC, Table 2). In contrast, short-term dynamics show some more diversity between the areas, especially regarding connections in the mPFC. The paired pulse ratio (PPR) between the second and the first EPSP is significantly higher (P < 0.01) in mPFC (0.97 ± 0.41) compared to all other areas (SSC, 0.62 ± 0.23; AC, 0.66 ± 0.41; MC, 0.55 ± 0.08; and VC2, 0.58 ± 0.24; Figs 2B and 5F, Table 2). The increased PPR in mPFC is caused by a reduced release probability, reflected in the low utilization (U) value of the model fit of synaptic dynamics (mPFC, 0.34 ± 0.13) compared to most other areas (P < 0.01 with AC, 0.47 ± 0.16, and VC2, 0.48 ± 0.16; P < 0.05 with SSC, 0.43 ± 0.13, Fig. 5H). Further, the facilitation time constant F is significantly higher in mPFC (mPFC, 0.301 ± 0.230 s) compared with other areas (P < 0.01, with SSC, 0.110 ± 0.086 s; P < 0.05, with MC, 0.102 ± 0.089 s, and VC2, 0.125 ± 0.125 s, Fig. 5J). F is also different between SSC and AC (P < 0.05, 0.110 ± 0.086 s and 0.165 ± 0.097 s, respectively). Recovery from depression (Fig. 5I) and absolute synaptic efficacy (Fig. 5G) show no significant differences between the areas. Thus, the synaptic dynamics of direct connections in the mPFC seem to be most dissimilar due to their low initial release probability. We find some dependencies between kinetics and short-term dynamics parameters as illustrated by Fig. 5K and L. Large-amplitude synapses also had a high utilization parameter (Fig. 5K), which is reflected in a positive correlation coefficient in all areas (0.38 ± 0.16; for SSC, 0.29). This indicates that large-amplitude synaptic connections are not only strong per se, but they also have a high release probability (which is equivalent to the utilization parameter in the synaptic dynamics model). We also find a correlation between 20–80% rise time and utilization (Fig. 5L, correlation coefficient 0.16 ± 0.17, for SSC, 0.33) which was unexpected.

Table 2.

Kinetics and short-term dynamics of monosynaptic EPSPs

	SSC (n= 171)	MC (n= 14)	AC (n= 29)	VC2 (n= 20)	mPFC (n= 22)	KW test, Dunn, P < 0.01	KW test, Dunn, P < 0.05
Amplitude (mV)	1.460 ± 1.291	1.399 ± 1.373	1.397 ± 1.011	1.346 ± 1.352	1.223 ± 1.028
Rise time (ms)	2.122 ± 0.751	1.952 ± 0.743	2.249 ± 0.757	2.628 ± 0.882	2.262 ± 0.521
τrise (ms)	2.377 ± 0.860	1.932 ± 0.526	2.675 ± 0.988	3.034 ± 0.972	3.163 ± 0.856	2–4,5	2–4,5
						1–5	1–4,5
Time to peak (ms)	8.072 ± 2.286	7.993 ± 3.126	8.288 ± 1.965	8.930 ± 2.807	8.309 ± 2.022
PPR	0.623 ± 0.228	0.545 ± 0.082	0.659 ± 0.411	0.583 ± 0.243	0.970 ± 0.407	5–1,2,3,4	5–1,2,3,4
Ase (mV)	3.340 ± 2.857	2.818 ± 2.428	2.865 ± 1.687	3.064 ± 2.932	3.624 ± 2.352
U	0.431 ± 0.126	0.460 ± 0.075	0.470 ± 0.157	0.479 ± 0.155	0.337 ± 0.126	5–3,4	5–1,3,4
D (s)	0.452 ± 0.217	0.374 ± 0.072	0.446 ± 0.140	0.518 ± 0.353	0.491 ± 0.178
F (s)	0.110 ± 0.086	0.102 ± 0.089	0.165 ± 0.097	0.125 ± 0.125	0.301 ± 0.230	5–1	5–1,2,4
							1–3

Kinetic parameters of direct EPSPs for SSC, MC, AC, VC2 and mPFC as displayed in Fig. 5 (means ±s.d.). Statistically significant differences between individual areas, tested with Kruskal–Wallis (with α < 0.01 and α < 0.05 significance level) followed by Dunn's method for multiple comparisons, are shown in the two rightmost columns. PPR, paired pulse ratio. A_se, absolute synaptic efficacy; U, utilization; D, recovery from depression; F, synaptic facilitation (see methods).

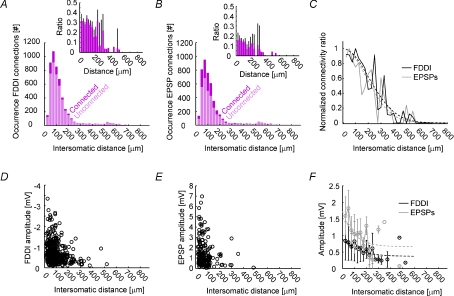
Distance-dependent drop of connectivity

The SSC connectivity data presented so far include only cell pairs that are of equal or less than 150 μm intersomatic distance. In order to investigate the spatial extent of FDDI and monosynaptic excitatory connectivity, we recorded from laterally spread PCs in SSC and investigated the distance dependence of synaptic parameters. Figure 6A and B show the distance-dependent occurrence of FDDI and monosynaptic excitatory connections, respectively. As can be seen in the insets, the connectivity rates are relatively stable for the first 100–150 μm (binning was 25 μm), and then drop towards zero. In Fig. 6C, FDDI and monosynaptic excitatory connectivity rates are normalized in order to better compare their relative extent. Both graphs were reasonably fitted with Gaussians and show a very similar course (σ_FDDI= 290 μm, σ_EPSPs= 265 μm). FDDI and monosynaptic excitation were found between cells with an intersomatic distance of up to 526.7 μm. We also tested several kinetic parameters for their distance dependence. The only striking effect we could observe was for FDDI and EPSP amplitudes (Fig. 6D and E). Using a binning of 25 μm, we could fit the distance dependence with single exponentials (λ_FDDI= 97 μm, y(∞)_FDDI= 0.66 mV, λ_EPSPs= 126 μm, y(∞)_EPSPs= 0.37 mV).

Figure 6. Distance-dependent drop of connectivity.

A, occurrence of FDDI connections as a function of the intersomatic distance of two PCs. Light pink shows the number of unconnected pairs, dark pink the number of connected pairs. Inset shows the ratio of connected over unconnected pairs. Binning was in 25 μm steps. B, occurrence of monosynaptic connections as a function of the intersomatic distance of two PCs. Labelling and binning as in A. C, normalized connectivity ratio as a function of the intersomatic distance of two PCs (black, FDDI; grey, EPSPs). Dashed lines are Gaussian fits (FDDI, λ= 290 μm; EPSPs, λ= 265 μm). Binning as in A. D, FDDI amplitude as a function of intersomatic distance. E, EPSP amplitudes as a function of intersomatic distance. F, FDDI and EPSP amplitudes as a function of intersomatic distance, binned in 25 mm steps. Dashed lines are exponential fits (FDDI, black, λ= 97 μm; EPSPs, grey, λ= 126 μm). Error bars denote s.e.m. (A and B) or standard deviation (F).

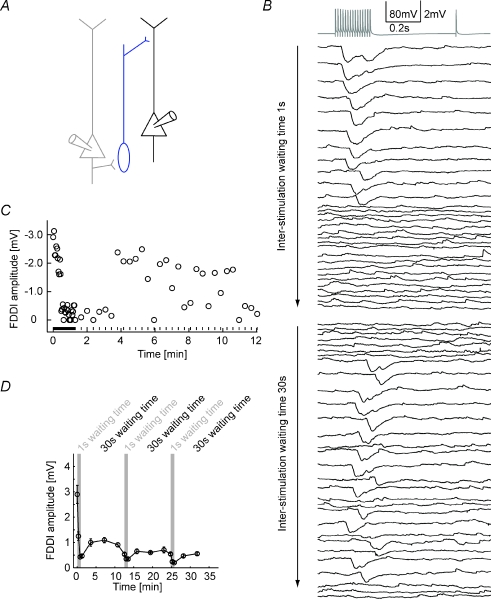
Fatigue of the PC–interneuron synapse

Screening the connectivity pattern within a multi-cell cluster requires multiple repetitive stimulation of all cells in order to obtain sufficiently good and noise-free average responses (see Methods). Long waiting periods of tens of seconds were interleaved with repetitive stimulation of a given cell. FDDI was especially prone to disappear when the waiting times were too short, and reappeared when inter-stimulation intervals (ISIs) were long enough, as shown in Fig. 7. The presynaptic cell of a pair of PCs connected via a non-patched intermediate interneuron (Fig. 7A) was stimulated with 70 Hz (15 APs) (Fig. 7B). The first 30 repetitions were interrupted with very short ISIs of 1 s, leading to a disappearance of FDDI after the 11th stimulation. Repetitions of 30–60 were interleaved with 30 s ISIs, and FDDI reappeared after 8 stimulations (Fig. 7B and C). In this specific example, the inhibitory response did not seem to regain the reliability that it used to have, expressed in FDDI failures in multiple repetitions with 30 s ISIs. Figure 7D summarizes the data of seven cases with three alternating short and long ISI periods. With this protocol, FDDI does recover from 1 s ISIs, but never reaches the initial amplitudes. The reason might be that even 30 s ISIs are not long enough to enable full recovery of the participating biophysical processes.

Figure 7. Stability of FDDI after repetitive stimulation.

A, a PC (grey) connecting via an interneuron (blue) to a postsynaptic PC (black). B, high frequency stimulation of the presynaptic PC (grey) with the individual responses of the postsynaptic PC (black). The first 30 repetitions were applied with only 1 s waiting time between each stimulus application, the last 30 repetitions were done with 30 s waiting time. C, FDDI amplitude as a function of time and inter-stimulation interval (waiting time). Circles denote the amplitude, lines at the bottom of the graph the time of stimulation. D, FDDI amplitude as a function of time, with a binning of 10 repetitions. Grey background illustrates the epochs of ‘fast’ stimulation with small inter-stimulation intervals (1 s waiting time). Error bars denote s.e.m.

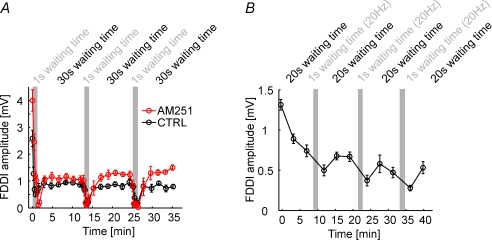
What is causing this strong activity-dependent effectiveness of FDDI? As seen in the traces in Fig. 7B, FDDI seems to be present or not present, and disappears ad hoc, without a pronounced gradual decline. Thus, neurotransmitter pool depletion in the interneuron–PC synapse is an unlikely reason for FDDI vanishing, since this would be expected to happen in a more gradual way. The (possibly only) FDDI-mediating interneuron is the Martinotti cell (Silberberg & Markram, 2007), which is likely to be part of the low threshold spiking (LTS) neuron population. LTS neurons have been shown to hyperpolarize upon repetitive suprathreshold stimulation, and this hyperpolarization has been shown to be dependent on an intracellular signalling pathway via endocannabinoid receptors (Bacci et al. 2004). The disappearance of FDDI could therefore be attributed to a somatic hyperpolarization of the interneurons, making discharge, which is essential for FDDI signalling, less likely. We blocked this endocannabinoid pathway by applying 10 μm AM251, but this did not prevent FDDI from disappearing during 1 s ISI stimulation, though the recovery of the amplitude is slightly improved (n= 3, Fig. 8A). Thus, spiking-induced hyperpolarization of interneurons is also probably not the main reason for FDDI disappearance. Finally, we replaced the 70 Hz–1 s ISI stimulation protocol with a 20 Hz–0.3 s ISI stimulation (Fig. 8B). With this protocol the number of presynaptic APs stays the same, but we do not elicit any spikes in the intermediate interneuron since the frequency is not high enough. Thereby, we isolate spiking-dependent effects in the interneuron from effects in the PC–interneuron synapse. And indeed, we always find a decrease in FDDI amplitude after the 20 Hz stimulation phases (n= 6), indicating that FDDI disappearance might be due to an activity-dependent weakening of the PC–interneuron synapse. This reversible weakening might cause a delay of recovery from short-term depression, or, as described earlier, synaptic fatigue as it is reversible and inducible with relatively low frequencies (Abrahamsson et al. 2005).

Figure 8. The PC–interneuron synapse limits FDDI stability.

A, FDDI amplitude as a function of time and inter-stimulation interval in control conditions (black) and in the presence of the endocannabinoid receptor antagonist AM251 (10 μm, red). B, FDDI amplitude as a function of time and inter-stimulation interval, with ‘fast’ stimulation (small waiting time) of 20 instead of 70 Hz. Stimulation of 20 Hz does not usually trigger suprathreshold activity in the interneuron, therefore allowing the isolation of synaptic- from spike-evoked effects. Error bars denote s.e.m.

Discussion

The current study reveals properties of disynaptic inhibitory and monosynaptic excitatory connections in five different cortical areas. We characterized the kinetics of both signalling pathways and synaptic short-term dynamics of excitatory connections. We thereby show that cortical areas of different modalities resemble one another in terms of the existence of FDDI, but show differences in connectivity rates and some kinetic parameters. In addition, we show the distance dependence of connectivity rates and synaptic parameters, and the activity-dependent drop of FDDI connections in the SSC.

FDDI as a functionally relevant generic neocortical sub-circuit motif

FDDI has been recently described between layer 5 and between layer 2/3 PCs of the primary somatosensory cortex of rats (Kapfer et al. 2007; Silberberg & Markram, 2007). It is mediated via somatostatin-positive interneurons, i.e. the Martinotti cell and perhaps other interneurons that receive strongly facilitating input from PCs. In the above studies as well as the present one long and high frequency trains, which are not very likely to happen during sparse neocortical activity in vivo, were used to observe the inhibitory response. The number of APs as well as the train frequency necessary to trigger FDDI is, however, greatly reduced by synchronous activation of a few PCs (unpublished observations). In vivo studies showed the occurrence of high frequency bursts in layers 5 and 2/3 (de Kock & Sakmann, 2008), therefore the necessary conditions for FDDI signalling appear to exist under physiological conditions. Another recent study found evidence for modulation of dendritic Ca²⁺ spikes by deep-layer interneurons, both in vitro and in vivo (Murayama et al. 2009).

We show that FDDI exists in all investigated areas, thus suggesting that frequency-dependent feed-forward and feedback projections are a fundamental microcircuit motif in the cortex.

Area-specific specializations

Regarding monosynaptic excitatory connections between PCs, the mPFC has previously been shown to feature specialized synaptic properties in ferrets (Wang et al. 2006). Subpopulations of PCs seem to interconnect with more facilitating synapses, and also display morphological heterogeneities, namely an early branching of the apical dendrite. Intrinsic response properties of mPFC PCs have been reported to show wide-range sensitivity to input fluctuations (Arsiero et al. 2007), and together with the observed synaptic facilitation their relevance for persistent working memory has been stressed. Although not the focus of our study, we did not observe morphological differences such as a very early branching apical dendrite in mPFC PCs. We did find, however, compared to the other cortical areas, significantly elevated paired pulse ratios and a reduced initial release probability.

Disynaptic inhibition was most frequent, and was strongest and fastest in the auditory cortex. This might reflect the nature of auditory processing, requiring a high temporal precision for the encoding of fast events. It should be considered, however, that our analysis of FDDI kinetics is based on average responses, and that two synapses are involved in the synaptic response. A large jitter in the spike timing of the intermediate interneuron can lead to widely distributed IPSP onsets in the postsynaptic PC, which is expressed in slow rising and decay times in the average response. Therefore, a fast average FDDI response could also reflect precise triggering of interneuron spiking. Another aspect that should be considered when comparing different (primary) cortical areas in juvenile rats is the onset time of functioning of the sense concerned. In rats, the eyes open at around postnatal day P14 (authors’ observations), whereas the hearing onset is around P12 (Uziel et al. 1981), and somatosensory sensing is even earlier. Therefore, the maturation of neurons and synaptic circuits, especially the formation of experience-dependent processes, may substantially vary depending on the specific area, which would result in different synaptic properties at a given, young age. Even during adolescence, biophysical properties of central synapses do substantially change. Synaptic connections in the primary somatosensory cortex, for example, undergo a developmental switch from dominating depressing to facilitating responses between P14 to young adulthood (Reyes & Sakmann, 1999; Williams, 2005). It remains to be tested whether PC–PC connections in the mPFC are just advanced in their maturation and not functionally different because of different purposes. Therefore, it would be essential to investigate whether synaptic differences between cortical areas become stronger in more mature animals.

An aspect that is very likely to have caused some variability to our data is the diversity of the pyramidal cell population. We chose the largest PCs for recording, which might be a relatively homogeneous under infra-red videomicroscopy identifiable cell population in the primary SSC (thick-tufted PCs; Le Béet al. 2007), but more diverse in frontal cortex regions (Morishima & Kawaguchi, 2006). It has recently been shown that cortical sub-networks in layer 5 and also in layer 6 exist, with preferred connectivity between pyramidal cells targeting the same (subcortical) regions (Mercer et al. 2005; Morishima & Kawaguchi, 2006, Le Béet al. 2007, Brown & Hestrin, 2009). Therefore, some measured connectivity rates may underestimate connectivity within subnetworks, since PCs from different populations tend to be less connected to each other. Whether a heterogeneous population of PCs is also the reason for the relatively low connectivity rates in ‘higher’ cortical areas like VC2 and mPFC remains to be elucidated. It should be considered, however, that the slice preparations of the investigated cortical areas required different cutting planes, which might have differentially lowered the observed connectivity rates. We therefore took care to only choose slices with a cutting plane parallel to the apical dendrite and principal axonal branch, which usually preserves the cells’ arborizations best.

The overrepresented reciprocity that we and also several previous studies in layers 2/3 and 5 observed (Markram et al. 1997; Sjöström et al. 2001; Holmgren et al. 2003; Song et al. 2005) might stem from relatively separated, non-identified subnetworks with high intrinsic connectivity. One recent thorough study in the mouse barrel cortex, however, did not observe an overrepresentation of reciprocity in any of the six investigated layers (Lefort et al. 2009). They distinguished layer 5A and B and found connectivity ratios of 19.1% and 7.2% between PCs, respectively. These are between our and previously found estimates that are based on connectivity rates between somato-dendritically defined cells (Markram et al. 1997; Sjöström et al. 2001; Song et al. 2005). One possible explanation for Lefort's different reciprocity could be the separate treatment of layer 5A and B, the extraordinary specialization of the barrel cortex, or general differences between mouse and rat neocortex. More research is necessary for finding out more about non-randon distributions in different cortical areas and animals.

Lateral extent of connectivity

Most paired recording studies that mention the intersomatic distance between the recorded cells did not find a very prominent drop of connectivity ratio for the first tens of micrometres distance, either between layer 2/3 or layer 5 PCs in somatosensory or visual cortex (Holmgren et al. 2003; Song et al. 2005). This is in agreement with our data: both FDDI and EPSP connectivity were relatively stable for the first 100–150 μm. The connectivity started to drop thereafter, and was best fitted with Gaussians with a standard deviation of 265–290 μm. It needs to be considered that any connectivity rates obtained from acute slices suffer from bias in the estimates due to cut dendrites and axon along the slicing plane. This bias can be reduced if the recorded cells are located as deep as possible in the slice but will always be a source of error in slice experiments. Moreover, this uncertainty might be larger for large intersomatic distances. Likewise, amplitude drops of EPSP might be explained by a higher likelihood of cut synaptic contacts for distant cells. Some of the synaptic contacts between Martinotti cells and PCs are located at the dendritic tuft, electrotonically remote from the soma. It may be that due to the dendritic spread of PCs and the axonal spread of Martinotti cells in layer 1, FDDI also occurs at larger distances, but is mediated only by those distal synapses that might escape detection by somatic recordings.

Activity dependence of FDDI signalling

We found FDDI to be a very sensitive pathway that would disappear rapidly upon fast high frequency repetitive stimulation if the inter-stimulation intervals were too short. This decay can probably be attributed to a loss of strength of the PC–interneuron synapse, since this decay was also present for lower, 20 Hz stimulation frequency that did not elicit spikes in the interneuron. Repetitive suprathreshold activity in LTS cells is known to lead to slow self-inhibition, mediated by the endocannabinoid 2-arachidonoylglycerol (Bacci et al. 2004; Marinelli et al. 2008). We did not find evidence for an involvement of this pathway since the endocannabinoid receptor antagonist AM251 could not prevent FDDI decline. The investigated PC–interneuron pathway, which might be exclusively composed of the PC–Martinotti cell synapse, has a strongly facilitating response for short (∼8–15 spikes) train protocols (Silberberg & Markram, 2007). It remains to be determined whether this synapse becomes fatigued after repetitive high-frequency stimulation. If so, this pathway might be relatively inactive during epileptiform activity in diseased brain tissue, though it might be able to prevent the onset of seizures.

In this study we have shown that FDDI between layer 5 pyramidal neurons, which has been previously described in the SSC (Silberberg & Markram, 2007), is a common and robust microcircuit feature across the entire rat neocortex, including granular, agranular, sensory and motor regions. In all tested areas, the occurrence of FDDI was higher than that of monosynaptic excitation between PCs, yet the prevalence as well as kinetic properties varied between areas. We also quantified the lateral spatial extent of FDDI (and monosynaptic connections), as well as its use-dependent fatigue. These findings add to our knowledge about the diverse role of inhibitory interneurons in the neocortical microcircuitry and provide a quantitative description of spatial and temporal properties of a specific inhibitory sub-circuit. Further experimental and theoretical studies are still required in order to understand the role of FDDI in the intact brain and at different cortical states.

Glossary

Abbreviations

AC

auditory cortex

AP

action potential

FDDI

frequency-dependent disynaptic inhibition

MC

motor cortex

mPFC

medial prefrontal cortex

PC

pyramidal cell

SSC

somatosensory cortex

VC2

secondary visual cortex

Author contributions

T.K.B., G.S., and H.M. designed the experiments, T.K.B. and R.P. performed the experiments, T.K.B. analysed the data. T.K.B. and G.S. wrote the manuscript. All authors discussed the results and commented on the manuscript.