Sparse Coding of Birdsong and Receptive Field Structure in Songbirds

Abstract

Auditory neurons can be characterized by a spectro-temporal receptive field, the kernel of a linear filter model describing the neuronal response to a stimulus. With a view to better understanding the tuning properties of these cells, the receptive fields of neurons in the zebra finch auditory fore-brain are compared to a set of artificial kernels generated under the assumption of sparseness; that is, the assumption that in the sensory pathway only a small number of neurons need be highly active at any time. The sparse kernels are calculated by finding a sparse basis for a corpus of zebra-finch songs. This calculation is complicated by the highly-structured nature of the songs and requires regularization. The sparse kernels and the receptive fields, though differing in some respects, display several significant similarities, which are described by computing quantative properties such as the seperability index and Q-factor. By comparison, an identical calculation performed on human speech recordings yields a set of kernels which exhibit widely different tuning. These findings imply that Field L neurons are specifically adapted to sparsely encode birdsong and supports the idea that sparsification may be an important element of early sensory processing.

1 Introduction

It has long been established that the firing rate behaviour of many cells in the primary visual and auditory areas can be predicted by a linear filter model. Any discussion of this prediction must be undertaken with several caveats: the accuracy of the prediction is modest (Machens et al. 2004; Eggermont et al. 1983; Theunissen et al. 2000; Sen et al. 2001) and there are numerous non-linear effects which make the calculation of the kernel dependent on the corpus of stimuli (Margoliash 1983; Theunissen et al. 2001; Theunissen and Doupe 1998; deCharms et al. 1998). Furthermore, the model predicts only the spike rate and provides no information about spike timing. Nonetheless, these linear models do associate a particular kernel to a given cell and it is obviously interesting to ask what determines the selection of these kernels.

This question is perhaps unusually well-specified in the case of song birds. Since song birds are adept at distinguishing between different con-specific songs, these songs can be considered an important class of natural sounds. Ideally, sensory processing is studied using stimuli whose statistics reflect those of the natural environment (deCharms et al. 1998). A guiding principle in neural coding is that sensory systems should efficiently encode such stimuli, and in fact, there is already evidence from the study of the visual system, that the linear kernels of visual neurons are related to a sparse code for natural images (Vincent et al. 2005; Olshausen and Field 1996; Vinje and Gallant 2000). Furthermore, modelling of auditory systems (Lewicki 2002) has shown that the tuning properties of cochlear hair cells are well predicted by a sparse code for natural sound waveforms. The aim of this paper is to extend these ideas to the avian auditory system. The methods used are similar to those employed in these previous studies, however, additional difficulties arise because birdsong does not well-sample the entire frequency-time domain.

The male zebra finch sings; along with a variety of simple calls, such as warning cries, the male bird has a single, identifying song, which develops under the tutelage of an adult male. The female finch does not sing, however, both the male and female birds are able to distinguish songs. Songs usually begin with a series of introductory notes, followed by two or three repetitions of the motif: a series of complex frequency stacks known as syllables, separated by pauses. Syllables are typically about 50ms long, with songs lasting about two seconds. Although perhaps discordant to the human ear, zebra finch songs have a very rich and complex structure. Importantly, the zebra finch auditory system is believed to be highly tuned to detect and recognise this song structure (Margoliash 1983; deCharms et al. 1998; Theunissen et al. 2000).

Just as the behaviour of V1 cells in visual cortex is decribed by a linear model which convolves the stimulus image with a receptive field (Jones and Palmer 1987), the stimulus-response properties of auditory neurons are often described in terms of a linear filter model (Aertsen and Johannesma 1981; Theunissen et al. 2001). The spectro-temporal receptive field (STRF) is a linear kernel relating the spectrogram of the stimulus to the firing rate response of the neuron. While linear in the spectrogram, the STRF model is non-linear in the stimulus due to a non-linear transformation in the calculation of the spectrogram. This static non-linearity is thought to mimic the behaviour of cochlear hair cells at the earliest stage of auditory processing. Such a linear mapping from spectrogram to response is rather naive and, not surprisingly, gives an incomplete description of neuronal behaviour (Machens et al. 2004; Eggermont et al. 1983; Theunissen et al. 2000; Sen et al. 2001). Nonetheless, the model does provide a good approximation for some cells, and a description of how information is processed and encoded in the primary auditory areas should account for this linear behaviour.

As described in several previous studies, (Theunissen et al. 2001; Machens et al. 2004; Sen et al. 2001), it is possible to calculate STRFs for auditory neurons from electrophysiological recordings. In particular, the STRFs of Field L neurons in the zebra finch auditory forebrain have been calculated and parameterised by a number of quantitative measures such as the location and width of the time and frequency peaks. These STRFs are also characterised by a number of distinctive spectral and temporal features such as narrowband selection and on-off switching. We investigate whether these properties of simple neurons can arise naturally from a sparse coding strategy for natural sounds. Specifically, we consider optimal strategies for the encoding of an ensemble of 20 zebra finch songs and generate a set of optimal kernels which sparsely encode this ensemble using an Olshausen-Field type algorithm (Olshausen and Field 1996). This learning algorithm has been succesfully used to calculate sparse bases for natural images. Here, we adapt it for use with highly correlated, ill-conditioned data, and apply it to the birdsong spectrograms.

2 Spectrotemporal Receptive Fields

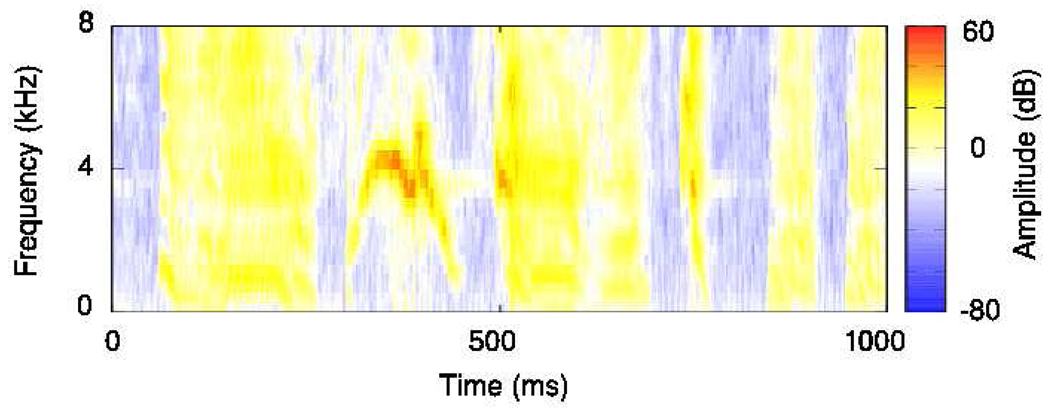
As described in (Theunissen and Doupe 1998), we consider a spectrographic representation of the songs, where the spectrogram represents the log amplitude of the stimulus in frequency and time, obtained from a time-windowed Fourier transform of the song waveform. Here, spectrograms are represented by a combination of n_f = 32 narrowband signals, {s_f(t)}, with centre frequencies between 250 and 8000Hz (Fig. 1).

Figure 1.

A sample spectrogram of one of our zebra finch song recordings. Amplitude is shown on a colour scale from blue (lowest) to red (highest) The temporal resolution of the spectrogram is 1ms, and the spectral resolution is 250Hz

According to the linear filter model, an approximate firing rate is calculated by convolving the spectrogram with a kernel h_f(s):

$$\tilde{r}(t)={\displaystyle \sum _{f=1}^{n_f}\int s_f(t-s)h_f(s)ds}$$ (1)

In practice, this integral is taken over a biologically relevant interval, on the order of 100ms, effectively restricting the support of h_f(s). The linear kernel is chosen so that the predicted firing rate r͂(t) gives the best possible approximation to r(t), the instantaneous firing rate response of the neuron to the stimulus at time t. The firing rate r(t) is estimated from the poststimulus time histogram of the neuron, averaged over several presentations of the stimulus and smoothed with a Hanning window (Blackman and Tukey 1959).

The prediction error is usually defined by the L² measure

$$\epsilon =\sqrt{\int {(r-\tilde{r})}^{2}dt}$$ (2)

and the kernel h_f(s) chosen so as to minimize ε. Although the formula for ε has the appearance of an integral, time is, in practice, discretized into δ_t =1ms bins and the convolution is rewritten in matrix form with time indices τ and σ corresponding to t = τδ_t for time and s = σδ_t, corresponding to the temporal support of the STRF. Hence temporal arguements are replaced by indices

$$\begin{array}{cccc}{R}_{\tau }=r(\tau {\delta }_t),& {\tilde{R}}_{\tau }=\tilde{r}(\tau {\delta }_t),& S_{\tau f}=s_f(\tau {\delta }_t),& H_{f\sigma }=h_f(\sigma {\delta }_t)\end{array}$$ (3)

and the STRF model equation, (1), is now

$${\tilde{R}}_{\tau }={\displaystyle \sum _{f=1}^{n_f}{\displaystyle \sum _{\sigma =1}^{n_s}{S}_{\tau -\sigma ,f}{H}_{f\sigma }}}$$ (4)

where σ = 1 … n_s where T = n_sδ_t is the temporal width of the STRF. The error is now given by

$${\epsilon }^2={\displaystyle \sum _{\tau =1}^{n_t}{(R_t-{\tilde{R}}_t)}^2{\displaystyle \sum _{\tau =1}^{n_t}{(R_{\tau }-{\displaystyle \sum _{\sigma ,f}{S}_{\tau -\sigma ,f}{H}_{f\sigma }})}^2}}$$ (5)

where L = n_tδ_t is the length of the experiment, one second here.

Differentiating with respect to H_fσ gives the usual least squares fit solution

$${\displaystyle \sum _{\tau ,\rho ,g}{S}_{\tau -\sigma ,f}{S}_{\tau -\rho ,g}{H}_{g\rho }={\displaystyle \sum _{\tau }{R}_{\tau }{S}_{\tau -\sigma ,f}}}$$ (6)

It is possible to use the discrete Fourier transform to solve this equation by deconvolution (Theunissen et al. 2001; Sen et al. 2001); however, here, for simplicity, it will be solved by noting that this is just a matrix equation disguised by the large number of different indices. To make this clear the indices σ and f are vectorized so that I = (f −1)n_s + σ and J = (g − 1)n_s + ρ and hence S_τI = S_τ−σ,f and, for example, H_J = H_gρ. Now, the equation becomes

$${\displaystyle \sum _{J=1}^{n_f{n}_s}{(S^{T}S)}_{IJ}{H}_J=C_I}$$ (7)

where C_I = Σ_τR_τS_τ−σ,f and, for clarity, the shorthand

$${(S^{T}S)}_{IJ}={\displaystyle \sum _{\tau }{S}_{\tau I}{S}_{\tau J}}$$ (8)

has been used for the square matrix. Now, H_J, and therefore the STRF, is recovered by inverting S^TS.

In practice, however, this precise solution does not give the best STRF estimate, and the STRF calculated in this way will, in fact, give a poor prediction of the response to novel stimuli not used in the calculation. This is a consequence of overfitting to the training data.

As discussed above, to realistically characterise neural responses, we must use stimuli which provoke a strong response in the neurons of interest (deCharms et al. 1998; Theunissen et al. 2000; Theunissen and Doupe 1998). In fact, the existence of an easily specified ensemble of natural stimuli is a key advantage of using song birds in studies of the auditory system. However, there is a disadvantage: natural sounds such as birdsong have a high degree of temporal and spectral auto-correlation, and so the majority of the information in the stimulus is contained in a relatively small number of significant dimensions. As a result, there exist dimensions within the stimulus space along which the variance is extremely low and in which noise becomes significant. Since the least squares solution gives equal weighting to all dimensions in the stimulus, this results in the STRF being fitted to the noise in these dimensions. In other words, the stimulus autocorrelation matrix S^TS is generally ill-conditioned. This problem must be overcome by a process of regularisation.

In these calculations, the autocorrelation matrix S^TS has a number of very small eigenvalues, corresponding to low variance dimensions. These become very large on inversion, and have the effect of amplifying noise in the experimental data. As in (Theunissen et al. 2000; Sen et al. 2001) a regularized solution is obtained by removing the contributions of these low eigenvalue directions, and thus projecting the song data down onto a subspace of significant dimensions. Hence, if

$${(S^{T}S)}_{IJ}={\displaystyle \sum _{\alpha }{\lambda }_{\alpha }{E}_{\alpha I}{E}_{\alpha J}}$$ (9)

is the spectral decomposition of S^TS over its eigenvalues λ_α and eigenvectors E_α then the regularization is achieved by taking the Moore-Penrose pseudoinverse (Penrose 1955)

$${(S^{T}S)}_{IJ}^{+}(\epsilon )={\displaystyle \sum _{\alpha :{\lambda }_{\alpha }>\epsilon }\frac{1}{{\lambda }_{\alpha }}{E}_{\alpha I}{E}_{\alpha J}.}$$ (10)

The tolerance value, ε, is chosen so as to give the most accurate prediction of the response to novel stimuli. This is achieved by means of cross-validation. A subset of the data, known as the validation set, is put aside and the kernels are calculated using the remainder of the data, known as the training set. The kernels are then used to predict the response to the validation data. The tolerance value is chosen as that which miniminses the prediction error for the validation set.

3 Sparse Coding

According to the sparse coding hypothesis for sensory systems, only a small subset of the neurons in a sensory pathway need be strongly active while accurately encoding a given stimulus (Olshausen and Field 2004, 1996; Field 1994; Atick 1992). From an information theoretic point of view, an ideal sparse coding regime is one in which the neuronal firing rates are statistically independent (Atick 1992; Lewicki 2002; Olshausen and Field 1996) and individual cells favour either low or high activity. Here, neurons are identified with kernels or STRFs, so each neuron corresponds to one direction in a stimulus space. In this section, we calculate an optimal set of linear kernels which sparsely encode zebra finch song.

Using the same vectorized notation as in the previous section, S_τI can be thought of as a patch of the stimulus spectrogram with the same temporal width as the STRFs, ending at the time t = τδ_t. The spectrogram patch is decomposed at fixed time τ over a basis B_nI where n is a component index. Hence, let

$${\tilde{S}}_{\tau I}={\displaystyle \sum _n{A}_{\tau n}{B}_{nI}}$$ (11)

where A is the matrix of components. Assuming that the basis B is invertible, it is possible to choose the component matrix A so that S͂_τI = S͂_τI by setting

$$A_{\tau n}={\displaystyle \sum _I{S}_{\tau I}{(B^{-1})}_{In}.}$$ (12)

Where each row of B is a basis vector associated with the neuron n. In this way, the n^th column of the inverse basis B⁻¹ is equivalent to the STRF, H_I, of the neuron n and A_τn is equivalent to the firing rate of that neuron at time t = τδ_t. However, in an efficient coding regime, we must also require that the firing rates be sparse. This is achieved by placing a constraint on A and allowing a trade off between the sparseness of the representation and the accuracy of the stimulus reconstruction S͂. Furthermore, as with the STRFs, it will be neccessary to regularize the calculation.

Following the method of Olshausen and Field (Olshausen and Field 1996) we seek to minimise an energy function, E(A, B; μ) for the sample at each time τ:

$$E={\displaystyle \sum _I{(S_{\tau I}-{\tilde{S}}_{\tau I})}^2-\mu }{\displaystyle \sum _{n}C(A_{\tau n})}$$ (13)

where the first term represents the reconstruction error in the representation, and where C(·) is some sub-linear cost function which penalises redundancy in the coding for a given sample. A typical choice (Olshausen and Field 1996) which is used here, is

$$C(A_{\tau n})=-[\text{log}(1+A_{\tau n}{A}_{\tau n})],$$ (14)

which favours representations having fewer non-zero coefficients, since ${\displaystyle {\sum }_i{\text{log}}_i(1+x_i^2)\ge \text{log}(1+{\displaystyle {\sum }_i{x}_i^2)}}$ for all x_i. μ is a positive constant which determines the relative importance of sparseness and reconstruction accuracy.

To find the minimum a two-step iterative method is used: E(A, B; μ) is first minimised with respect to the components A_τn by conjugate gradient descent, averaged over many samples. The basis functions are then updated by

$$\text{Δ}{B}_{nI}=\eta {\langle A_{\tau n}(S_{\tau I}-{\tilde{S}}_{\tau I})\rangle }_{\tau }$$ (15)

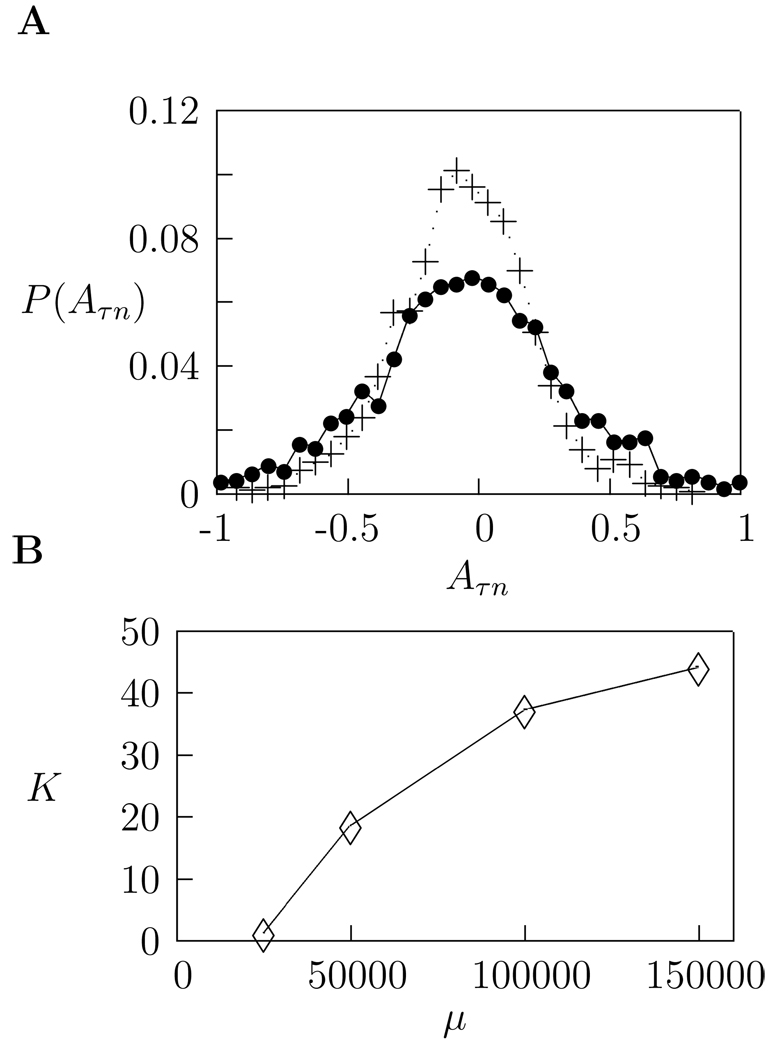
where η > 0 is the learning rate. Beginning with a random basis set, this algorithm converges after several thousand iterations to a matrix B of optimal basis functions which allow an accurate sparse encoding of the stimulus. Figure 2 shows the increase in the sparseness of the system after learning. The optimal kernels are now given by B⁻¹. Hence, B must be required to be invertible and well conditioned.

Figure 2.

A Distribution of weights for learned basis functions (dotted line) compared to those for a random basis (solid line) averaged over all filters. The large peak and heavy tail of the distribution for learned basis functions is characteristic of a sparse response. B: The kurtosis, K, of the distribution of weights for learned basis functions increases as a function of the sparseness parameter.

Difficulties arise in this calculation due to the highly correlated nature of the data used. Such difficulties are dealt with in many studies (Olshausen and Field 1996; Bell and Sejnowski 1997) by a process of whitening, or sphering the data. However, in this case, in order to allow for the inversion of our basis, and the direct comparison of our sparse kernels with auditory STRFs, we proceed by means of dimensionality reduction, as used in the calculation of STRFs. As we have described in Section 2 above, the regularized STRF is calculated by removing the contributions due to low variance dimensions in the stimulus, and projecting the songs onto a sub-space of high-variance dimensions. Hence, if, as above

$${(S^{T}S)}_{IJ}={\displaystyle \sum _{\alpha }{\lambda }_{\alpha }{E}_{\alpha I}{E}_{\alpha J}}$$ (16)

and anything with an I index can be decomposed over the eigenbasis

$$\begin{array}{lll}{S}_{\tau I}\hfill & =\hfill & {\displaystyle \sum _{\alpha }{s}_{\tau \alpha }{E}_{\alpha I}}\hfill \\ {\tilde{S}}_{\tau I}\hfill & =\hfill & {\displaystyle \sum _{\alpha }{\tilde{s}}_{\tau \alpha }{E}_{\alpha I}}\hfill \\ B_{nI}\hfill & =\hfill & {\displaystyle \sum _{\alpha }{b}_{n\alpha }{E}_{\alpha I}.}\hfill \end{array}$$ (17)

Substituting these into the energy function, and using ∑_I E_αIE_βI = δ_αβ,

$$E={\displaystyle \sum _{\alpha }{(s_{\tau \alpha }-{\tilde{s}}_{\tau \alpha })}^2-\mu {\displaystyle \sum _{n}C(A_{\tau n}).}}$$ (18)

To project the problem onto the significant stimulus dimensions, we need only restrict the range of α. We write 𝒜(ε) for the set of α such that λ_α > ε, where ε is a cut-off value seperating the high-variance dimensions of the songs - the ones that will be preserved - from the noise. The energy function now becomes

$$E(\epsilon )={\displaystyle \sum _{\alpha \in 𝒜(\epsilon )}{(s_{\tau \alpha }-{\tilde{s}}_{\tau \alpha })}^2}-\mu {\displaystyle \sum _{n}C(A_{\tau n})}$$ (19)

and we minimize over b_nα rather than B_nI. B_nI can be reconstructed as

$$B_{nI}={\displaystyle \sum _{\alpha \in 𝒜(\epsilon )}{b}_{n\alpha }{E}_{\alpha I}}.$$ (20)

To obtain a set of optimal kernels, B must now be inverted. If a complete representation is chosen, where the number of basis elements N is the same as the number of dimensions in the stimulus; N = |𝒜(ε)| then the matrix b is square and

$$B_{In}^{-1}={\displaystyle \sum _{\alpha \in 𝒜(\epsilon )}{E}_{\alpha I}{b}_{\alpha n}^{-1}}.$$ (21)

Alternatively, an overcomplete representation can be considered where N > |𝒜(ε)|, in which case b⁻¹ must be replaced by the Moore-Penrose pseudoin-verse, b⁺ (ε).

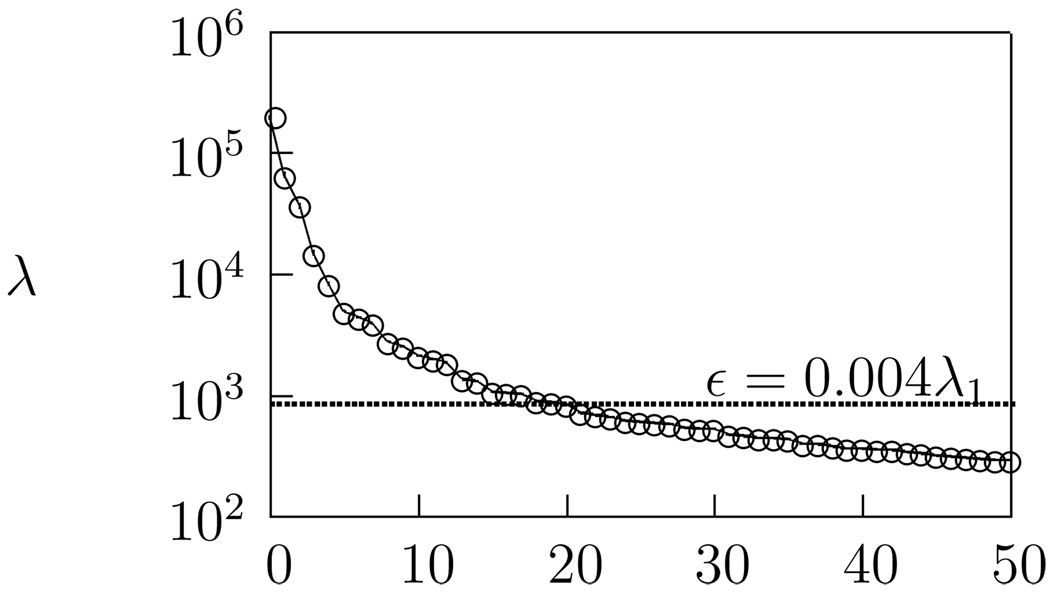
The eigenvalue cut-off, ε, is often expressed in terms of the tolerance factor ε/λ₁, where λ₁ is the largest eigenvalue. In STRF calculations the optimal tolerance factor is determined through cross validation. Here, we have used a tolerance value of 0.004. This is within the range of tolerance values used in the calculation of actual Field L STRFs (Theunissen et al. 2000; Sen et al. 2001) and gives 20 dimensions: |𝒜(ε)| = 20, (see Fig. 3). This value is sufficient to remove noise while still allowing an accurate reconstruction of the stimulus, with more than 90% of stimulus variance explained.

Figure 3.

𝒜(ε) is the set of α such that λ_α > ε. Here ε = 0.004λ₁. The contributions due to low-eigenvalue dimensions are ignored.

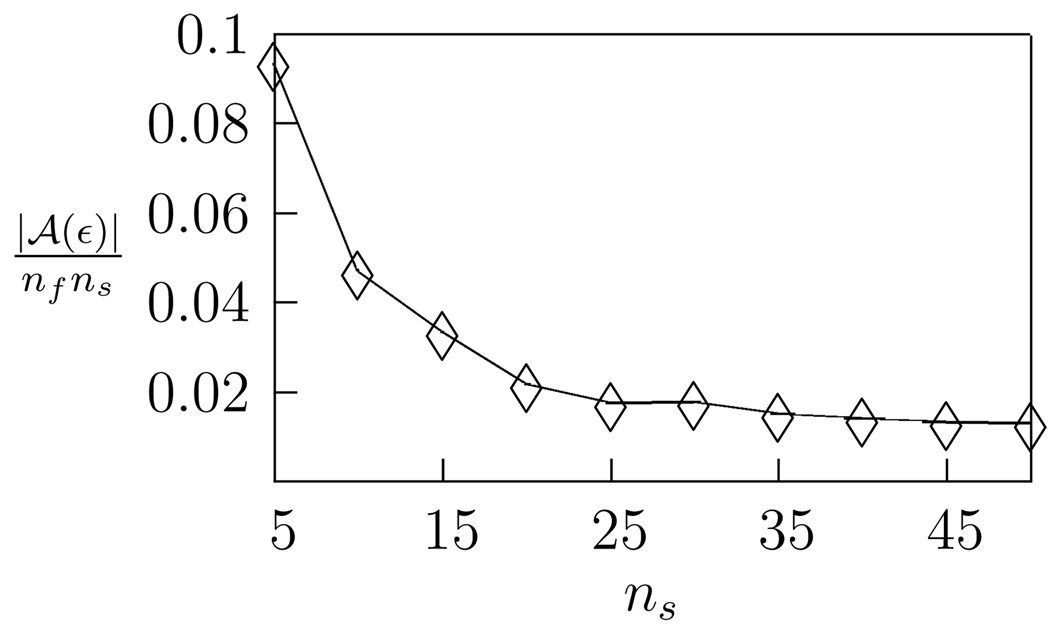
It should also be noted that |𝒜(ε)| is dependent on the length of the samples chosen, since longer samples will display a higher degree of temporal auto-correlation, and hence will have a higher proportion of noisy, low-eigenvalue dimensions. Figure 4 shows the proportion of dimensions above threshold as a function of sample length.

Figure 4.

Proportion of dimensions above tolerance as a function of sample width (ε = 0.004). Longer samples contain a higher degree of temporal correlation, and so have proportionally fewer high variance dimensions. Here |𝒜(ε)| is the number of significant dimensions, and n_fn_s is the total number of dimensions in the stimulus space.

4 Results

We apply these methods to an ensemble of 20 zebra finch song spectrograms, each of one to two seconds duration. For suitable choices of ε and μ, we obtain a set of optimal kernels sharing many of the observed characteristics of STRFs in the zebra finch auditory forebrain.

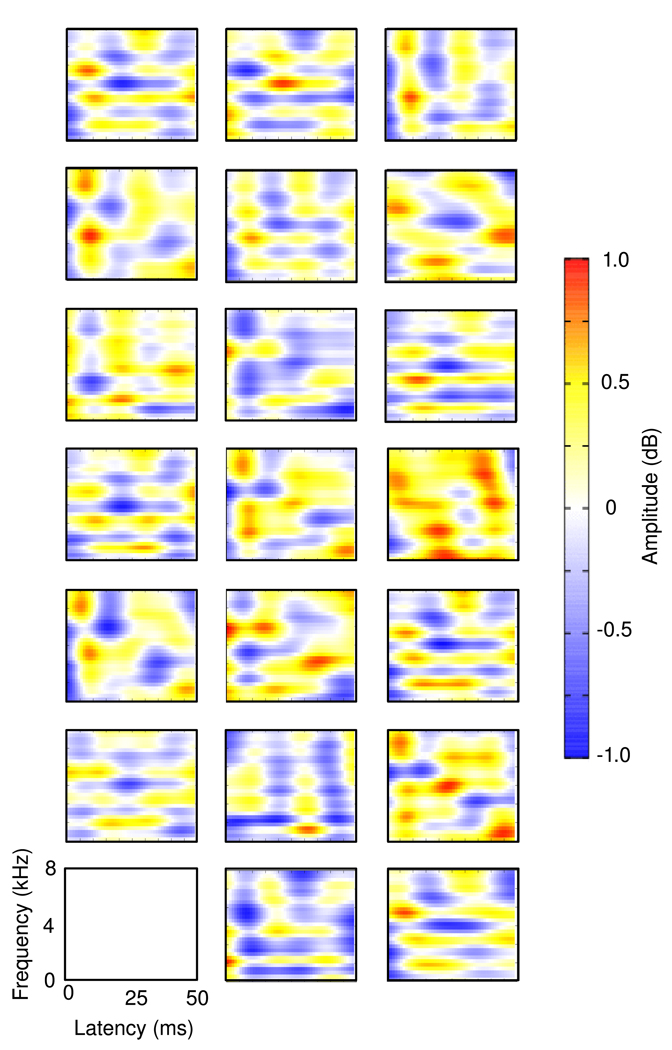
Figure 5 shows the set of optimal kernels of length 50ms calculated for N = |𝒜(ε)| = 20. We observe a number of similarities with actual neuronal STRFs for Field L neurons. There are excitatory and inhibitory peaks on similar scales to those found in Field L STRFs, with both excitatory and in-hibitory regions having similar amplitude, and kernels are localized in space and time, though possibly not as markedly localized as some STRFs of experimentally observed cells. Many of the sparse kernels show sensitivity to complex features such as frequency stacks, which are a common feature of zebra finch song. These kernels are qualitatively similar to many found in Field L of the zebra finch forebrain, though it should be noted that the multiple peaks obseved in these kernels are not common to the majority of Field L STRFs. Importantly, though these kernels display some differences from Field L STRFs, it appears that those similarities which are observed increase with sparsification of the system, and are not observed in non-sparse filters.

Figure 5.

Set of 20 learned optimal filters calculated using a complete representation with μ = 150, 000 and tolerance value 0.004. Amplitude is shown on a colour scale from blue (lowest) to red (highest).

Furthermore, we can quantitatively characterise the sparse kernels using a number of spatial parameters, and compare these values to those obtained from auditory STRFs. Parameters commonly used to characterise STRFs include the width of the largest peak in both time and frequency directions, W_t and W_f; the peak frequency, F_peak; the time to the largest peak T_peak; the quality factor, Q; the best modulation frequency, BMF and the spectral-time separability, SI.

These values, as calculated from the sparse kernels, agree well with those found in several studies of the avian auditory forebrain (Zaretsky and Konishi 1976; Muller and Leppelsack 1985; Heil and Scheich 1991; Theunissen et al. 2000) (See Table 1). The observed range of peak frequencies, F_peak closely matches that found in Field L STRFs, as do the seperability index, SI, and quality factor, Q.

Table 1.

The range of STRF parameter values obtained from each of the three sets of calculated kernels, compared to those for Field L STRFs as given in Theunissen et al. 2000, (F_peak) and for subregion L3 STRFs as given in Sen et al. 2001, (Q, SI, BMF). Mean values are shown in parentheses. Note: T_peak is also given in Sen et al. 2001. However, we cannot compare this value to T_peak obtained from predicted kernels as the predicted values do not incorporate latencies determined by the auditory pathway.

Parameter	Field L	Sparse	Non-Sparse	Voice
Fpeak (Hz)	375–5125	750–5250	250–7750	250–3750
Q	0.4–7.8 (2.5)	1.4–4.8 (2.9)	0.3–3.9 (1.4)	0.3–3.0 (0.93)
SI	0.49–0.83 (0.66)	0.43–0.84 (0.59)	0.38–0.67 (0.5)	0.41–0.75 (0.52)
BM F (Hz)	5–30 (15)	0–40 (8)	0–20 (10)	0–40 (10)
Wf (Hz)	n/a	850–2200 (1100)	700–2750 (1700)	250–3750 (1300)
Wt (ms)	n/a	10–20 (14.2)	11–37 (21.4)	3–9 (6.6)

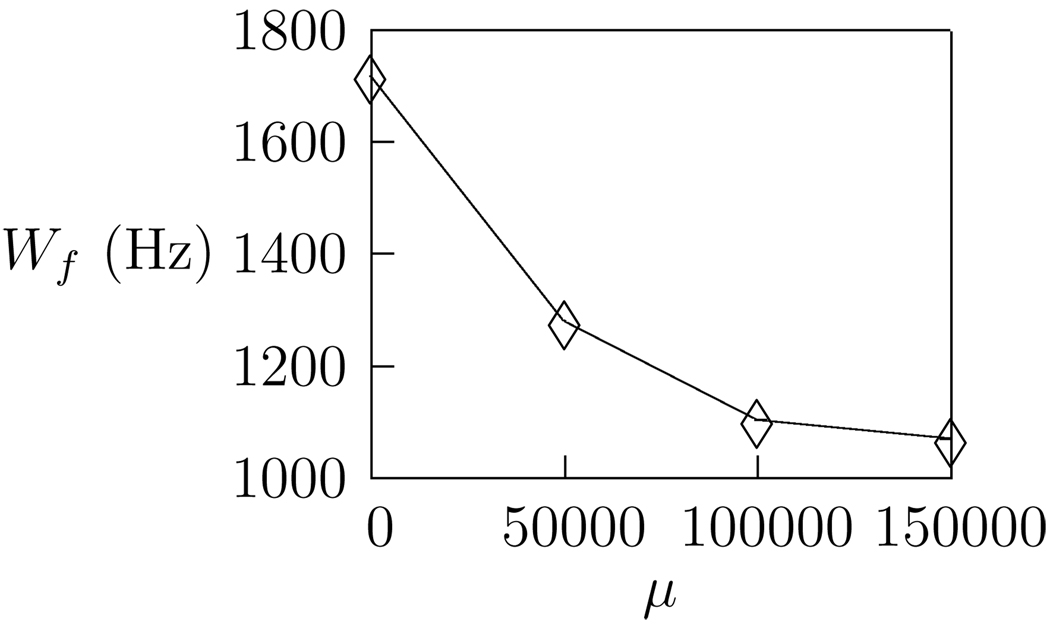
The sparse kernels exhibit fine spectral tuning with localized peaks of average width W_f =1.1 kHz, and temporal tuning with W_t typically in the range of 10 – 20ms (mean value 14.2ms). The kernels show little variation in peak widths, and W_f appears largely independent of peak frequency. Interestingly, W_f is seen to decrease as a function of the sparseness parameter, μ, as shown in Figure 6 suggersting that localized kernels arise as a result of sparsification.

Figure 6.

Average spectral peak width, W_f as a function of sparseness parameter. Sharp spectral tuning arises from increased sparseness in the system.

The sharpness of the spectral tuning is measured by the quality factor, Q, defined as the ratio of the peak frequency to the width: Q = F_peak/W_f. Values of Q are in the range 1 – 5 (mean value 2.9), matching the findings of Theunissen et al. (2000).

The best modulation frequency, BMF, is a measure of the AM frequency to which a neuron is best tuned, and is obtained from the Power Spectral Density of the linear kernel. The BMFs of individual sparse kernels were in the range 0 – 40Hz, with 90% of sites having BMF ≤ 20Hz (resolution 20Hz), indicating a strong preference for low frequency amplitude modulations, as seen in auditory STRFs (Sen et al. 2001). The overall BMF of the set of optimal kernels was obtained by concatenating peak timeslices of all the sparse kernels. This gives an overall BMF value of 8Hz (resolution 1Hz).

Spectral-temporal seperability is measured by the SI value, obtained from the Singular Value Decomposition (SVD) of the STRF (Sen et al. 2001). It is

$$SI=\frac{{\rho }_1^{\prime }}{{\displaystyle {\sum }_{i=1}^{n-1}{\rho }_i^{\prime }}}$$ (22)

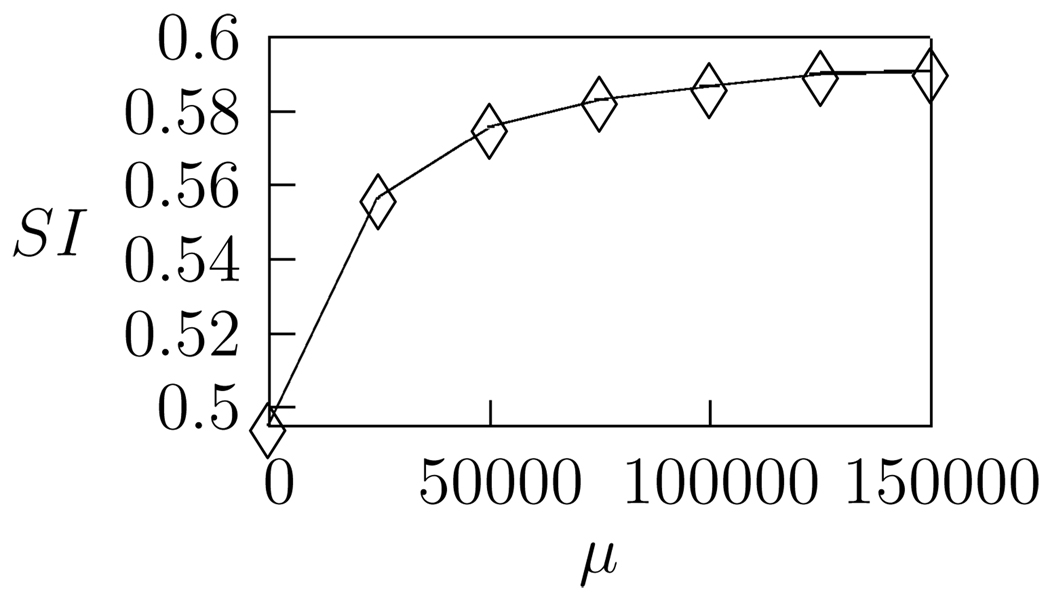
where ${\rho }_i^{\prime }={\rho }_i-{\rho }_n$, and ρ_i is the i^th singular value. As in Sen et al. (2001), we choose n = 4 since the majority of features in the sparse kernels are accurately reconstructed from the first three singular values. As is the case with actual Field L neuronal STRFs, kernels are obtained with a wide variation in separability, ranging from relatively complex inseparable kernels to simpler, roughly separable kernels. Values of SI are in the range 0.43 – 0.84, with a mean value of 0.59 for the kernels shown in Figure 5. In general, we observe that the average separability of the sparse kernels increases as a function of the sparseness parameter, μ, (Fig. 7) indicating that separability arises as a consequence of sparse coding.

Figure 7.

The average separability of the 20 sparse kernels increases with the sparseness parameter μ.

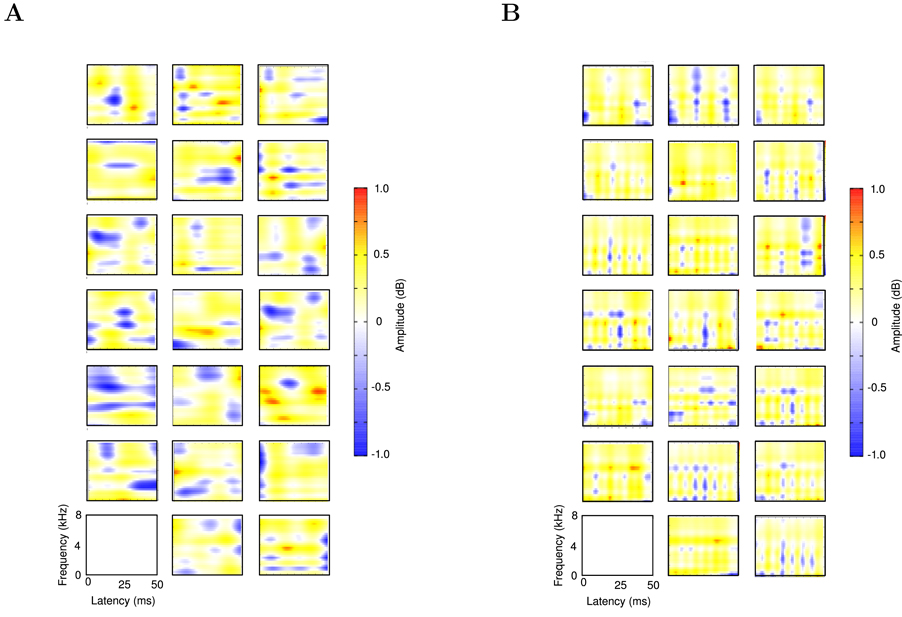
For comparison, we also calculated a set of non-sparse kernels by setting μ = 0 (Fig. 8). These kernels exhibit significantly broader tuning than our sparse kernels and more closely resemble PCA kernels than auditory STRFs. Peak frequencies, F_peak are not restricted to low frequencies, occuring over the range (250 – 7750Hz), while peaks are broader in both time and frequency directions, with mean values W_f = 1.7kHz, W_t = 20ms and Q = 1.4. In addition, in order to rule out ensemble effects, the calculation of the sparse basis was repeated using new song recordings not used in the initial calculation. The inclusion of this new song data was found to have no significant effect on the results. Furthermore, we applied our algorithm to an ensemble of low noise human voice recordings and calculate the corresponding sparse kernels. As with the non-sparse filters mentioned above, these filters differ significantly in their tuning from those calculated for birdsong and from Field L STRFs. This disimilarity further supports the hypothesis that the tuning of Field L neurons is specifically adapted to encode con-specific song. To better illustrate this, we calculate the standard deviation of the distributions of SI and Q for each of our three filter sets, and use this to quantify the deviation of the Field L filter mean from the mean of each of these sets. As can be seen, the deviation for our sparse filters is significantly smaller than for our two control filter sets. However, we currently lack a suitable statistical model by which to further analyise the significance of our prediction.

Figure 8.

A set of non-sparse filters for our ensemble of birdsong. B: Sparse filters calculated for an ensemble of human voice recordings. These recordings were made using a Pearl CC 30 microphone in a semi-anechoic chamber, at a sampling rate of 44,100Hz. The text used was Jonothan Swift’s A Modest Proposal. This text is in the public domain. Both the text and the original WAV files can be found at http://www.maths.tcd.ie/~mnl.

Table 1 below summarises the tuning properties of each of the filter sets. Table 2 shows the deviation of the field L mean values for Q and SI from the mean of each calculated filter set.

Table 2.

The deviations, ΔQ and ΔSI of field L mean parameter values from predicted mean values for our three filter sets. In each case, σ is the standard deviation in the given parameter for the corresponding filter set.

Parameter	Sparse	Non-Sparse	Voice
ΔQ	0.4 = 0.3σ, σ = 1.3	1.1 = 1.1σ, σ=1	1.57 = 1.4σ, σ = 1.1
ΔSI	0.07 = 0.6σ, σ = 0.11	0.16 = 2.3σ, σ = 0.07	0.14 = 1.2σ, σ = 0.12

5 Discussion

The modified Olshausen-Field type algorithm described above identifies a sparse structure of dimension |𝒜(ε)| within the song spectrograms. We generated a system of STRF-like linear kernels which accurately and efficiently encode this structure. The similarity between these kernels and neuronal STRFs from the zebra finch suggests that the zebra finch auditory pathway is well adapted to encode this structure. In particular, the fine spectral tuning and localized peaks characteristic of many Field L STRFs are seen to arise in the sparse kernels as a consequence of sparsification. Similarly, greater separability is seen to arise from increased sparsification of the system. By comparison, both the set of non-sparse kernels and the sparse kernels calculated for human speech differ significantly in their tuning parameters from zebra finch auditory STRFs. This supports our hypothesis that the tuning is specifically optimised to encode conspecific song.

The main result here is the comparison of the sparse kernels with experimentally measured STRFs. In order to make this comparison, it is necessary to regularize the calculation. There are three reasons for this. Firstly, the biologically relevant timescale appears to be quite long, at about 50ms: as shown in Figure 4, longer samples possess a lower proportion of significant dimensions. Secondly, the corpus of stimuli we consider is limited to bird songs. It would be tempting to add other natural sounds to sample other stimulus dimensions, however, since sensory neurons are non-linear (Margoliash 1983; deCharms et al. 1998; Theunissen et al. 2000), the sparse kernels would be less relevant to the electrophysiological experiments which were performed using clean songs in an acoustically isolated environment (Sen et al. 2001). Finally, the sparse kernels are computed by inverting the sparse basis, potentially allowing noise to dominate the result.

Efficient or sparse coding certainly seems to be one of the primary goals of early visual processing (Bell and Sejnowski 1997; Olshausen and Field 1996; Vincent et al. 2005) and there is reason to believe that the same is true for auditory systems. Lewicki (2002) for example, considered a sparse basis for an ensemble of natural sound waveforms composed of animal vocalizations and environmental noises. Interestingly, for a specific mixture of sounds he found that this sparse basis has similar tuning properties to the fibres of the auditory nerve. Since the focus is on an earlier stage of sound processing, far shorter, 8ms, samples are used and the basis is not inverted; for this reason regularization is not required and so this calculation differs from ours, though the conclusion is very much in the same spirit. Furthermore, Smith and Lewicki (2006) have shown that such sparse codes yield extremely efficient representations of acoustic signals.

In the specific case of birdsong, the idea that the receptive fields are adapted to song is supported by (Woolley et al. 2005), where there is a comparison between the tuning properties of cells and the statistical structure of the songs themselves. Recent modelling of avian auditory areas (Blatter and Hahnloser 2008) also suggests that sparse coding in Field L could play a role in higher level avian auditory processes such as song selection.

The results presented here suggest that there does in fact exist such a sparse coding in Field L, and imply the existence of a sparsifying interaction between Field L cells. However, the nature of this interaction is unknown. It seems unlikely that a direct gradient descent of the type described here could be implemented in a realistic neural network. Instead, sparsification is assumed to come about as a result of a locally inhibitory interaction between cells. An interesting avenue for further research would be to model this interaction in a biophysically realistic manner.