Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2009 Oct 28;105(1):71–77. doi: 10.1093/aob/mcp262

Size-dependent leaf area ratio in plant twigs: implication for leaf size optimization

Dongmei Yang 1, Karl J Niklas 2, Shuang Xiang 1, Shucun Sun 1,3,*
PMCID: PMC2794065  PMID: 19864268

Abstract

Background and Aims

Although many hypotheses have been proposed to explain variation in leaf size, the mechanism underlying the variation remains not fully understood. To help understand leaf size variation, the cost/benefit of twig size was analysed, since, according to Corner's rule, twig size is positively correlated with the size of appendages the twig bears.

Methods

An extensive survey of twig functional traits, including twig (current-year shoots including one stem and few leaves) and leaf size (individual leaf area and mass), was conducted for 234 species from four broadleaved forests. The scaling relationship between twig mass and leaf area was determined using standardized major axis regression and phylogenetic independent comparative analyses.

Key Results

Leaf area was found to scale positively and allometrically with both stem and twig mass (stem mass plus leaf mass) with slopes significantly smaller than 1·0, independent of life form and habitat type. Thus, the leaf area ratio (the ratio of total leaf area to stem or twig mass) decreases with increasing twig size. Moreover, the leaf area ratio correlated negatively with individual leaf mass. The results of phylogenetic independent comparativeanalyses were consistent with the correlations. Based on the above results, a simple model for twig size optimization was constructed, from which it is postulated that large leaf size–twig size may be favoured when leaf photosynthetic capacity is high and/or when leaf life span and/or stem longevity are long. The model's predictions are consistent with leaf size variation among habitats, in which leaf size tends to be small in poor habitats with a low primary productivity. The model also explains large variations in leaf size within habitats for which leaf longevity and stem longevity serve as important determinants.

Conclusions

The diminishing returns in the scaling of total leaf area with twig size can be explained in terms of a very simple model on twig size optimization.

Key words: Allometry, leaf size, twig size, leaf area ratio, scaling relationship, broadleaved species

INTRODUCTION

Leaf size-twig size is one of the leading dimensions of variation in plant functional traits (Westoby et al., 2002). It has been long recognized that twig size is positively correlated with the size of attached appendages. Known as Corner's rule (Corner, 1949), this correlation has been widely demonstrated both for interspecific and intraspecific comparisons (White 1983a, b; Brouat et al., 1998; Preston and Ackerly, 2003; Westoby and Wright, 2003; Sun et al., 2006; Normand et al., 2008). The cost/benefit analysis of twig size can be helpful in understanding the evolution of leaf, fruit, seed and inflorescence size.

Within twigs (i.e. terminal branches or current-year shoots), at least two functional components can be identified: the photosynthetic organs (leaves), and the supporting and transporting structures (stems). Leaves function to intercept light and are responsible for carbon gain, while stems function to directly or indirectly mechanically support leaves and to provide water and nutrients. Previous studies have revealed that species with thick twigs have a greater ratio of total leaf area to stem cross-sectional area (Preston and Ackerly, 2003; Westoby and Wright, 2003; Sun et al., 2006) and a larger leaf mass fraction (the ratio of leaf mass to twig mass that includes leaf mass and stem mass) compared with those with thin twigs (Pickup et al., 2005; Wright et al., 2007). However, these findings cannot serve to characterize the cost versus benefit of leaf versus twig size in terms of carbohydrates. The ability of a twig to intercept light is proportional to the total leaf area supported by the twig, but not to leaf mass, and the investment in twigs should be more directly proportional to twig mass than to stem cross-sectional area. Thus, the form of the scaling relationship between total leaf area and twig mass should be quantified to determine the size-dependent leaf deployment efficiency of twigs (Yang et al., 2009).

Relative growth rate is predicted by the West, Brown and Enquist model to decrease with body size, which has been demonstrated both interspecifically and intraspecifically (Niklas and Enquist, 2002). Consistent with the model's prediction, individual leaf area and total leaf surface area increase at a slower pace than individual leaf mass and whole plant mass, respectively, while leaf nutrient and free water content per unit leaf mass decrease with increasing leaf size (Milla and Reich, 2007; Niklas et al., 2007). These diminishing returns may be a fundamental attribute of all photoautotrophs (Enquist and Niklas, 2002; Niklas and Enquist, 2002; Niklas et al., 2007). At the twig level, the scaling relationships between leaf size and twig size have been extensively explored (Sun et al., 2006; Xiang et al., 2009; Yang et al., 2009) both between leaf lamina and petiole size (Li et al., 2008) and between leaf size and number (Yang et al., 2008), which have collectively demonstrated that large-twigged species do not have an advantage in leaf deployment efficiency (e.g. total leaf area per twig mass) over their counterparts. Based on a much more comprehensive survey on twig functional traits, this study reports on the ‘diminishing returns’ in the scaling of total leaf area, which a twig supports, with twig size (leaf mass plus stem mass). Leaf area and mass, and twig mass for 234 woody angiosperms from four subtropical evergreen forests were measured, and the form of the scaling relationship between total leaf area and twig mass was determined. Based on the results, a simple conceptual model for twig size optimization (emphasizing a cost/benefit analysis) was constructed and tested to predict the variation of leaf size–twig size between and within habitats.

MATERIALS AND METHODS

Site description

The dataset contains measurements on woody plants from four sites in Sichuan province, south-west China, which include Emei Mountain, Luoji Mountain, Pingwu Mountain and Gongga Mountain. These mountains are located between latitudes 27° and 33°N, longitudes 101° and 105°E, in the subtropical evergreen forest region of south-west China (Investigation Group for Sichuan Vegetation, 1980; Liu, 1985; Tang and Ohsawa, 1999). The climate of the region is of continental monsoon type. Mean annual precipitation is between 1000 and 2000 mm, of which >70 % occurs in the summer season between June and September. The mean annual temperature ranges between 6·0 and 13·1 °C, with the maximum in July and the minimum in January. The climate conditions for each forest site are compiled in Table 1.

Table 1.

General description of the study sites

Site Forest type Latitude, longitude Altitude (m) MAP (mm) MAT (ºC) Soil type
Emei 1 EBF 29°33′–29°34′N, 103°22′–103°26′E 1100 1930 13·1 Montane yellow soil
Emei 2 EBF 29°33′–29°34′N, 103°22′–103°26′E 1500 1940 11·2 Montane yellow soil
Luoji EBF 27°43′N, 102°19′E 2300–2500 1000 9·5 Montane yellow brown soil
Pingwu EBF 32°09′–32°12′N, 104°16′–104°20′E 1300–1800 1187 11·0 Montane yellow soil
Gongga EBF 29°32′–29°37′N, 101°58′–102°04′E 1800–2400 1500–1700 10·0 Montane brown soil and montane dark brown soil
Gongga MF 29°32′–29°37′N, 101°58′–102°04′E 2400–2800 1500–1700 6·0 Montane brown soil and montane dark brown soil
Open in a new tab

EBF, Evergreen broadleaved forest; MF, mixed forest; MAP, mean annual precipitation; MAT, mean annual temperature; Emei 1, low altitude of Emei Mountain; Emei 2, high altitude of Emei Mountain.

Twig sampling

In this study, ‘twigs’ are defined as terminal (current year), unbranched shoots, i.e. the structure from the terminal apical meristem to the first proximal side-branch; each twig consists of a terminal set of internodes and the leaves borne by them. We sampled 161 evergreen species (Emei low altitude, 37; Emei high altitude, 38; Luoji, 39; Pingwu, 54; Gongga, 32) and 73 deciduous species (Gongga low altitude, 54; Gongga high altitude, 32). The total number of species sampled was 234, belonging to 96 genera from 44 families (see Supplementary data, available online), with evergreens represented by 39 species and deciduous plants represented by 13 species in common among the sites. Some of the data collected from Gongga and Emei Mts have been published (Li et al., 2008; Yang et al., 2008; Xiang et al., 2009).

Twigs were sampled from June to August 2006, when leaf expansion and shoot growth were completed. For each of the study species, three to five individuals were randomly selected away from track edges, and three to five random branches with tips at the outer surface of plant's crown were chosen for each individual, so as to minimize the variation in twig functional traits. For large trees, a 4-m-high aluminium ladder and a 4-m-long lopper were used to reach sun-exposed branches. The sampling scheme was the same as in Sun et al. (2006) and Li et al. (2008). The twigs that did not bear fruits and flowers were dried to constant mass at 70 °C for 48 h and weighed; total leaf area on each twig was measured by scanning all leaves before drying and then digitizing the scanned images. The following parameters were derived from the measurements: leaf number per twig, total leaf area, total leaf mass and stem mass. Average area and mass of individual leaves were calculated by dividing total leaf area and mass with leaf number. Twig mass was the sum of total leaf mass and stem mass. Leaf mass and stem mass were used to represent total leaf mass and total stem mass, respectively, unless specified otherwise.

Data analysis

Data for all twig traits were all log10 transformed to fit a normal distribution. For interspecific comparisons, each trait was averaged arithmetically per individual and then per species; species averages were also log10 transformed for additional analysis. A hierarchical ANOVA on the measured variables for deciduous species from the evergreen broadleaved forest of Gongga Mountain was conducted as a representative regional sampling because the species number at this site was the largest among plant species groups. Variance between species was found to be consistently the largest component, and variance between individuals was always greater than that between twigs on the same individual (Table 2).

Table 2.

Hierarchical variance components for the functional traits of the deciduous species at evergreen broadleaved forest of Gongga Mountain (ANOVA type I sums of squares, converted to percentages at each level)

Component Species Individuals within species Twigs within individuals
Twig mass 62·4 24·4 13·2
Stem mass 59·3 24·3 16·4
Total leaf area 60·9 25·5 13·6
Total leaf mass 62·2 24·2 13·6
Open in a new tab

All data were log transformed prior to analysis. The residual variance is assumed to be the variance between twigs.

The relationships among paired traits (Table 3) were determined by standardized major axis regression because there is a possibility of measurement error in both x and y variables and allometric slopes were of particular interest. Slopes were calculated using standardized major axis regression (Warton et al., 2006); slope heterogeneity was tested using the methods of Warton and Weber (2002). The allometric equation parameters were computed using (S)MATR Version 2·0 (Falster et al., 2006; http://www.bio.mq.edu.au/ecology/SMATR/).

Table 3.

Standardized Major Axis regression slopes, intercepts after common slopes and 95 % confidence intervals (CIs) for log–log regression relationships between leaf size and twig mass for different species groups and different sites

y–x Site Forest type Life form n r2 P Slope CIs Intercept
TLA–TM Emei 1 EBF EB 37 0·923 <0·001 0·839 0·763–0·923 1·586
Emei 2 EBF EB 38 0·918 <0·001 0·823 0·747–0·907 1·523
Luoji EBF EB 39 0·821 <0·001 0·823 0·715–0·947 1·413
Pingwu EBF EB 54 0·787 <0·001 0·848 0·746–0·963 1·522
Gongga EBF EB 32 0·883 <0·001 0·842 0·742–0·957 1·537
Gongga EBF DB 54 0·873 <0·001 0·809 0·732–0·893 1·699
Gongga MF DB 32 0·880 <0·001 0·847 0·745–0·963 1·658
TLM–TM Emei 1 EBF EB 37 0·992 <0·001 0·997 0·967–1·028 –0·093
Emei 2 EBF EB 38 0·995 <0·001 1·017 0·992–1·042 –0·089
Luoji EBF EB 39 0·986 <0·001 1·026 0·987–1·067 –0·087
Pingwu EBF EB 54 0·983 <0·001 1·003 0·967–1·039 –0·100
Gongga EBF EB 32 0·994 <0·001 1·000 0·972–1·029 –0·085
Gongga EBF DB 54 0·992 <0·001 1·006 0·981–1·031 –0·094
Gongga MF DB 32 0·995 <0·001 0·994 0·969–1·020 –0·083
TLA–SM Emei 1 EBF EB 37 0·795 <0·001 0·779 0·667–0·909 2·332
Emei 2 EBF EB 38 0·867 <0·001 0·809 0·715–0·915 2·404
Luoji EBF EB 39 0·479 <0·001 0·751 0·592–0·953 2·252
Pingwu EBF EB 54 0·433 <0·001 0·758 0·615–0·933 2·326
Gongga EBF EB 32 0·746 <0·001 0·780 0·647–0·940 2·392
Gongga EBF DB 54 0·680 <0·001 0·727 0·622–0·851 2·510
Gongga MF DB 32 0·770 <0·001 0·753 0·630–0·900 2·498
TLM–SM Emei 1 EBF EB 37 0·799 <0·001 0·926 0·795–1·080 0·911
Emei 2 EBF EB 38 0·834 <0·001 0·999 0·871–1·145 0·904
Luoji EBF EB 39 0·595 <0·001 0·937 0·759–1·157 0·941
Pingwu EBF EB 54 0·653 <0·001 0·896 0·761–1·055 0·889
Gongga EBF EB 32 0·794 <0·001 0·926 0·783–1·096 0·963
Gongga EBF DB 54 0·718 <0·001 0·904 0·781–1·048 0·901
Gongga MF DB 32 0·841 <0·001 0·884 0·762–1·025 0·946
ILM–ILA Emei 1 EBF EB 37 0·914 <0·001 1·180 1·061–1·311 –1·808
Emei 2 EBF EB 38 0·919 <0·001 1·349 1·225–1·485 –1·742
Luoji EBF EB 39 0·893 <0·001 1·165 1·045–1·299 –1·587
Pingwu EBF EB 54 0·808 <0·001 1·122 0·993–1·267 –1·734
Gongga EBF EB 32 0·857 <0·001 1·120 0·973–1·289 –1·743
Gongga EBF DB 54 0·855 <0·001 1·180 1·061–1·311 –1·953
Gongga MF DB 32 0·844 <0·001 1·095 0·945–1·268 –1·898
TLM–TLA Emei 1 EBF EB 37 0·914 <0·001 1·189 1·075–1·315 –2·012
Emei 2 EBF EB 38 0·904 <0·001 1·235 1·113–1·371 –1·932
Luoji EBF EB 39 0·836 <0·001 1·248 1·091–1·428 –1·798
Pingwu EBF EB 54 0·825 <0·001 1·183 1·053–1·329 –1·942
Gongga EBF EB 32 0·876 <0·001 1·187 1·042–1·353 –1·945
Gongga EBF DB 54 0·868 <0·001 1·244 1·124–1·376 –2·150
Gongga MF DB 32 0·879 <0·001 1·174 1·031–1·336 –2·089
Open in a new tab

EBF, Evergreen broadleaved forest; MF, mixed forest; EB, evergreen broadleaved species; DB, deciduous broadleaved species; TM, twig mass; TLA, total leaf area; TLM, total leaf mass; ILA, individual leaf area; ILM, individual leaf mass; SM, stem mass.

Because observed leaf size variation among species may be biased to some degree by species-selection, phyletic affects can have a significant effect on the relationships between leaf size and other traits. In order to remove the effect of phylogeny, phylogenetically independent comparative protocols were also used to analyse the trait–pair relationships (Table 4). The phylogenetic tree was constructed following Phylomatic, version 4·01 (http://www.Phylodiversity.Net/phylocom/; Webb et al., 2008). The branch length on the tree does not indicate the time of evolutionary divergence that arises from speciation between species or taxa. The calculation for the trait–pair relationships across correlated evolutionary divergences was performed using COMPARE, version 4.6b (http://compare.bio.indiana.edu/) following the method of Martins (2004). Only the tree was constructed and phylogenetic independent comparative analyses conducted for the deciduous species in the Gongga evergreen forest as a representative since the species number was the largest among the study sites. Regression of evolutionary divergence data was conducted using standard model I techniques.

Table 4.

The result of phylogenetically independent comparative analysis for the relationships between trait pairs for the deciduous woody species (n = 54) of a subtropical forest on Gongga Mountain

y–x r2 P a b
TLA–TM 0·870 <0·001 0·757 0·008
TLA–SM 0·710 <0·001 0·598 −0·001
TLM–TM 0·992 <0·001 0·990 0·000
TLM–SM 0·767 <0·001 0·762 −0·012
ILM–ILA 0·837 <0·001 1·053 −0·007
LAR–ILM 0·206 0·001 −0·185 0·002
Open in a new tab

The simple regression equation of y = ax + b was used; regression coefficients (a) and the y-intercepts (a) are provided.

TLA, Total leaf area; TM, twig mass; SM, stem mass; TLM, total leaf mass; ILA, individual leaf area; ILM, individual leaf mass; LAR, leaf area ratio.

RESULTS

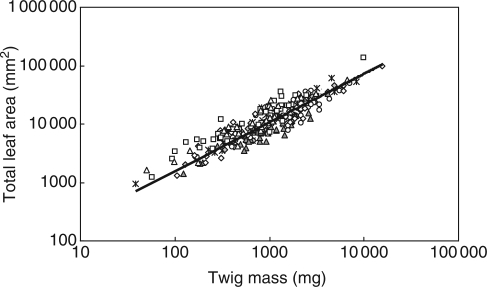
Total leaf area scaled positively with twig mass at each site and for each plant species group (Table 3). The best-fit common regression slope was 0·831 (95 % CI = 0·797, 0·866; Fig. 1), which was significantly smaller than 1·0. This allometric relationship was conserved across habitats and functional species groups (Table 3). Total leaf area also scaled positively and allometrically with stem mass across habitats and species groups (Table 3), with a common slope of 0·771 (95 % CI = 0·724, 0·821). Slope heterogeneity was not detected among species groups. Total leaf mass and stem mass accounted for about 80 % and 20 % of twig mass, respectively. Total leaf mass scaled positively with twig mass across habitats and species groups (Table 3), with a common slope of 1·005 (95 % CI = 0·994, 1·016). Total leaf mass was positively correlated with stem mass across habitats and species groups, with a common slope of 0·949 (95 % CI = 0·898, 1·005; Table 3). With few exceptions, total leaf mass scaled positively and allometrically with total leaf area (Table 3), with a common scaling slope of 1·197 (95 % CI = 1·144, 1·251), which was significantly greater than 1·0 (P < 0·001).

Fig. 1.

Fig. 1

Open in a new tab

The scaling relationships between total leaf area and twig mass across the species from different study sites. The line shows the standardized major axis regression curve. Symbols: circles, the Pingwu Mt. species; diamonds, the evergreen species of Gongga Mt. evergreen forest; squares, the deciduous species of Gongga Mt. evergreen forest; triangles, the deciduous species of Gongga Mt. mixed forest; asterisks, the low altitude species of Emei Mt.; closed diamonds, the high altitude species of Emei Mt.; closed triangles, the Luoji Mt. species.

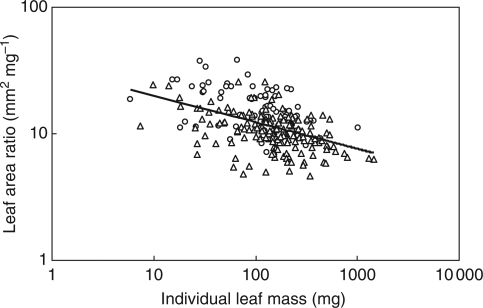
The relationships between total leaf area and twig mass, between total leaf area and stem mass and between total leaf mass and twig mass were strong when expressed as correlated evolutionary divergences for deciduous species of the Gongga evergreen forest (Table 4). The correlations between total leaf mass and stem mass, between individual leaf mass and individual leaf area were also significant across correlated evolutionary divergences for species (Table 4). In addition, across all species, leaf area ratio (the ratio of total leaf area to twig mass) was significantly and negatively correlated with individual leaf mass (r = −0·47, P < 0·001; Fig. 2). This relationship was conserved across evolutionary divergences (Table 4). The ratio of total leaf area to stem mass was negatively correlated with individual leaf area (r = −0·32, P < 0·001). However, the correlation between leaf area ratio and individual leaf area was not significant.

Fig. 2.

Fig. 2

Open in a new tab

The cross-species relationship between leaf area ratio (the ratio of total leaf area to twig mass) and individual leaf mass for all the species from different study sites. Symbols: circles, the deciduous species; triangles, the evergreen species.

DISCUSSION

It has been shown that the increase in total leaf area fails to keep pace with increasing twig size in both life forms and in all the study sites, both across species and across correlated evolutionary divergences. This ‘diminishing returns’ suggests that the leaf area ratio decreases with increasing twig mass, which has important implications for the optimization of leaf versus twig size.

Diminishing returns in the scaling of light interception with twig mass

Diminishing returns in the scaling of total leaf area with twig mass is predictable based on theoretical grounds. For example, according to the ‘pipe model’ theory (Shinozaki et al., 1964; Niklas, 1992), the total leaf area supported by a twig should be proportional to the cross-sectional area of conducting tissues of the twig. However, in addition to supplying leaves with water and nutrients, twigs also provide mechanical support for static loads and the drag forces exerted on leaves by wind (Niklas, 1999; Sun et al., 2006), both of which require additional biomass investments. Thus, the relationship between total leaf area and twig size is expected to be allometric (with a slope <1·0) rather than isometric (with a slope = 1·0).

There is also a proximate mechanism that can explain the size-dependent leaf area ratio. As noted, the present study indicates that total leaf mass scales isometrically with twig mass, which is consistent with previous studies showing that leaf mass scales isometrically with respect to stem diameter and mass annually (Niklas and Enquist, 2002; Niklas and Cobb, 2006; Sun et al., 2006). In the current study, the scaling exponent for the relationship between total leaf mass and stem mass is slightly but not significantly smaller than 1·0, indicating that the increase in total leaf mass associated with a twig is generally proportional to the increase in stem mass (Table 3). Because twig mass is the sum of leaf mass and stem mass and total leaf mass accounts for a large proportion of twig mass, the isometric scaling relationship between total leaf mass and twig mass is predictable. On the other hand, it was found that total leaf mass scales allometrically with total leaf area (Table 3). This is consistent with several recent studies since total leaf area and individual leaf area are positively correlated in plant twigs (Westoby and Wright, 2003; Sun et al., 2006; Milla and Reich; 2007). Niklas et al. (2007) have also shown that the cost of light interception increases with leaf size based on large datasets. In summary, leaf area ratio should and does decrease with increasing twig size due to the isometric leaf mass versus stem mass relationship and the allometric relationship of leaf mass versus leaf area.

The leaf area ratio is an important component affecting the relative growth rate of plants (e.g. Poorter and Remkes, 1990; Meerts and Garnier, 1996.). In whole plants, it is highly correlated with relative growth rates, which can be attributed to its positive correlation with specific leaf area and with the leaf mass fraction (Poorter and Remkes, 1990). If these correlations are conserved across twigs, the size-dependency of the leaf area ratio indicates that large twigs tend to have smaller relative growth rates, which is consistent with several recent studies reporting diminishing returns in the scaling of leaf area versus mass (Milla and Reich, 2007; Niklas et al., 2007) and allometric relationships between the investments in lamina area and lamina support tissues (Niinemets et al., 2006, 2007a, b; Li et al., 2008), all of which accord with the prediction that relative growth rates should decrease with increasing plant size as predicted by the West, Brown and Enquist model.

The diminishing returns reported here may have important implications for leaf size optimization. According to Corner's rule, the twig size-dependency of leaf deployment efficiency may be translated into a leaf size-dependent leaf area ratio, since leaf size and twig size are positively correlated. In this study, individual leaf area was positively correlated with total leaf area (r = 0·851, P < 0·001) and individual leaf mass was positively correlated with total leaf mass (r = 0·898, P < 0·001). Moreover, analysis of the pooled dataset shows that leaf area ratio decreases with increasing individual leaf mass (Fig. 2 and Table 4), but not with individual leaf area. In passing, we speculate that the inconsistency in the relationships among leaf area ratio with respect to leaf area and leaf mass may be due to large variations in specific leaf area resulting from phenotypic plasticity and functional adaptation to local environmental conditions.

Implications of the cost/benefit model for leaf size–twig size optimization

Based on the results obtained in the present study, it is possible to build a simple model on twig size optimization. For a typical twig lacking seeds and inflorescences, the construction cost for any given year is positively correlated with the leaf mass plus stem mass, but negatively correlated with leaf longevity and stem longevity, because increased longevity extends the functional time and thus decreases the cost per year. The benefit of a twig is usually proportional to total leaf area, and is positively correlated with area-based photosynthetic rate and leaf life span, provided that self-shading is not extensive. Although longevity may differ among leaves and stems even on the same twig, the cost (C) and the benefit (B) of a twig can be crudely estimated with the equations.

graphic file with name mcp262eqn1.jpg 1
graphic file with name mcp262eqn2.jpg 2

where TLA = total leaf area, Pharea = area-based net photosynthesis rate, SM = stem mass, LL = leaf longevity, SL = stem longevity and TLM = total leaf mass. To make interspecific comparisons possible, B and C are estimated for a 1-year period. If LL and SL are <1 year, LL = 1·0 and SL = 1·0 in eqn (1). Detailed processes such as changes in leaf photosynthetic capacity during leaf expansion were not taken into account, and average values for Pharea, LL and SL were used in these equations.

Because TLM scales isomterically with respect to SM and twig mass (Table 3), SM should scale isometrically with twig mass. Therefore, the carbon gain per unit cost is given by eqn (3).

graphic file with name mcp262eqn3.jpg 3

where α = TLM/TM and β = SM/TM, i.e. leaf mass ratio and stem mass ratio, and TM is twig mass. Because TLA/TM decreases with increasing TM (i.e. the slope of the relationship of TLA versus TM is <1·0), it is expected that small twigs (or small leaves according to Corner's rule) will be favoured over larger ones to maximize B/C provided that all other parameters such as leaf photosynthetic capacity and longevity are constant, and that large twigs or large leaves tend to occur when Pharea is high and/or LL and/or SL are large.

The predictions of this extremely simple model are generally consistent with leaf size or twig size variation among habitats and within habitats. First, according to the model and assuming all other parameters are constant, leaf size–twig size should vary with the product of area-based net photosynthesis rates and leaf longevity (i.e. Pharea × LL), which yields the total carbon gain per unit leaf area during a single year. Noting that Pharea × LL should be closely related to resource availability in a habitat, total leaf carbon gain per year should increase from resource-poor to resource-rich habitats. It can be expected therefore that leaf size or twig size will increase more in resource-rich/high productivity areas than in less-productive habitats, and also that large leaves (and seeds) are more likely to occur in favourable sites as predicted by Corner's rule. Put differently, although large twigs have a lower efficiency in terms of deploying leaf area compared with their smaller counterparts, large twigs can be advantageous in resource-rich habitats, where they might obtain benefits greater than their cost.

These predictions are also consistent with the results reported by many previous studies. Indeed, a large body of literature has demonstrated that leaf size tends to decline with increasing elevation (Givnish, 1984; McDonald et al., 2003), decreasing mean annual temperature and rainfall (Givnish, 1984; Wolfe, 1995; McDonald et al., 2003), and lower soil fertility (Ashton and Hall, 1992; McDonald et al., 2003). Similarly, in a global comparison, average seed size tends to increase toward the tropics (Moles and Westoby, 2003; Moles et al., 2007).

Furthermore, our simple model suggests that even within the same habitat (where total carbon gain per year is comparatively constant), changes in leaf and stem longevity can have dramatic effects on the balance between cost and benefit and subsequently on leaf size–twig size optimization. For example, in poor habitats, annual total carbon gain is low, but leaf and stem longevity may increase, thereby decreasing the annual construction cost of leaves and stems. If so, plants growing in poor habitats can have large leaves by decreasing twig construction costs per year to maximize the benefit to cost ratio as illustrated by some subalpine Rododendron species, which have larger leaves compared with deciduous species occupying the same site (e.g. Betula and Populus; see Shen et al., 2004). Likewise, in the case of shade-tolerant species such as Fatsia japonica, leaves tend to be long-lived and are borne on stems that can live as long as the individual plant. In contrast, in resource-rich habitats, if leaf and stem longevity are reduced, construction costs increase, which according to the present model would require a reduction in leaf size to maximize the benefit to cost ratio, e.g. Taxodium distichum and Metasequoia glyptostroboides shed their current-year shoots before winter (Zhen and Fu, 1978) as do some temperate forest Ulmus and Betula spp. (Shen et al., 2004).

Clearly consistency between the predictions of the model and trends reported here and by other workers does not guarantee that it is comprehensive. Indeed, there is room for considerable theoretical improvement. This caveat is particularly important in light of the covariance among leaf and stem longevity and area-based net photosynthesis rates (i.e. Pharea) among species, which makes it extremely difficult to predict leaf size variation from the any single species. For example, leaf longevity and Pharea are often negatively correlated (Wright et al., 2004) such that increases in leaf longevity may not necessarily be associated with increases in leaf size (see Ackerly and Reich, 1999). In addition, the costs of reproduction have not been incorporated into the present model even though flowering and fruiting can incur large energetic and mechanical costs (Kawamura and Takeda, 2006). In passing, however, it is worth noting that across a broad spectrum of angiosperms, the mass of reproductive structures is reported to scale as the 1·8 power of stem diameter (Niklas, 1993), which suggests that the mechanical cost of reproduction is not as large as the hydraulic cost. In addition, the diminishing returns in the scale of leaf area ratio to twig size may be compensated by the advantages in leaf arrangement (Niklas, 1988; King and MainDonald, 1999; Valladares et al., 2002) and height growth (e.g. Ackerly, 1999). Far more complicated models than the one presented here are required therefore to provide detailed and accurate predictions at the level of individual species or different functional species groups (e.g. Parkhurst and Loucks, 1972; Taylor, 1975; Givnish and Vermeij, 1976; Givnish, 1987).

Nevertheless, the cost/benefit analysis of twig size provided by the present model improves our understanding of leaf size optimization and evolution by drawing attention to the importance of leaf and stem longevity, which should be studied more extensively as an important functional trait in plants in relation to plant functional types, habitats and other functional traits.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org/ and lists the trait means for the 234 temperate broadleaved species examined.

Supplementary Material

[Supplementary Data]
mcp262_index.html (683B, html)

ACKNOWLEDGEMENTS

We thank Xianming Gao, Xiaocheng Yan, Guoyong Li, Xinwei Wu, Dongmei, Jin, Yan Li, Yanan Li, Yin Zhou, Shuo Wang, Qin Shi and Gang Pang for field assistance and Jianxin Sun for helpful comments on the early version of this manuscript. We also thank the staff of Maoxian Ecological Station of CERN and the biological station at Mts Emei and Gongga for permitting this study to be conducted. This study was financially supported by National Science Foundation of China (30670333), the Chinese Academy of Sciences (KZCX2-XB2-02) and Special Research Program for Public-welfare Forestry (200804001).

LITERATURE CITED

  1. Ackerly DD. Self-shading, carbon gain and leaf dynamics: a test of alternative optimality models. Oecologia. 1999;119:300–310. doi: 10.1007/s004420050790. [DOI] [PubMed] [Google Scholar]
  2. Ackerly DD, Reich PB. Convergence and correlations among leaf size and function in seed plants: a comparative test using independent contrasts. American Journal of Botany. 1999;86:1272–1281. [PubMed] [Google Scholar]
  3. Ashton PS, Hall P. Comparisons of structure among mixed dipterocarp forests of north-western Borneo. Journal of Ecology. 1992;80:459–481. [Google Scholar]
  4. Brouat C, Gibernau M, Amsellem L, McKey D. Corner's rules revisited: ontogenetic and interspecific patterns in leaf–stem allometry. New Phytologist. 1998;139:459–470. [Google Scholar]
  5. Corner EJH. The durian theory or the origin of the modern tree. Annals of Botany. 1949;13:367–414. [Google Scholar]
  6. Enquist BJ, Niklas KJ. Global allocation rules for patterns of biomass partitioning in seed plants. Science. 2002;295:1517–1520. doi: 10.1126/science.1066360. [DOI] [PubMed] [Google Scholar]
  7. Falster DS, Warton DI, Wright IJ. User's guide to SMATR: Standardised Major Axis Tests & Routines Version 2·0. 2006. Copyright 2006. http://www.bio.mq.edu.au/ecology/SMATR/11. March 2006.
  8. Givnish TJ. Leaf and canopy adaptations in tropical forests. In: Medina E, Mooney HA, Vázquez-Yánes C, editors. Physiological ecology of plants of the wet tropics. Boston: Dr W. Junk Publishers; 1984. pp. 51–84. [Google Scholar]
  9. Givnish TJ. Comparative studies of leaf form: assessing the relative roles of selective pressures and phylogenetic constraints. New Phytologist. 1987;106(Suppl.):131–160. [Google Scholar]
  10. Givnish TJ, Vermeij GJ. Sizes and shapes of liane leaves. American Naturalist. 1976;100:743–778. [Google Scholar]
  11. Investigation Group for Sichuan Vegetation. Sichuan vegetation. Chengdu: Sichuan People's Publishing House; 1980. [in Chinese] [Google Scholar]
  12. Kawamura K, Takeda H. Costs and probability of flowering at the shoot level in relation to variability in shoot size within the crown of Vaccinium hirtum (Ericaceae) New Phytologist. 2006;171:69–80. doi: 10.1111/j.1469-8137.2006.01737.x. [DOI] [PubMed] [Google Scholar]
  13. King DA, MainDonald J. Tree architecture in relation to leaf dimensions and tree stature in temperate and tropical rain forests. Journal of Ecology. 1999;87:1012–1024. [Google Scholar]
  14. Li GY, Yang DM, Sun SC. Allometric relationships between lamina area, lamina mass, and petiole mass of 93 temperate woody species vary with leaf habit, leaf form, and altitude. Functional Ecology. 2008;22:557–564. [Google Scholar]
  15. Liu ZG. Vegetation of Gongga Mountain. Chengdu: Sichuan Science and Technology Press; 1985. [in Chinese] [Google Scholar]
  16. McDonald PG, Fonseca CR, Overton JM, Westoby M. Leaf-size divergence along rainfall and soil-nutrient gradients: is the method of size reduction common among clades? Functional Ecology. 2003;17:50–57. [Google Scholar]
  17. Martins EP. 2004. COMPARE, version 4.6b. Computer programs for the statistical analysis of comparative data. http://compare.bio.indiana.edu/ 20 May 2008.
  18. Meerts P, Garnier E. Variation in relative growth rate and its components in the annual Polygonum aviculare in relation to habitat disturbance and seed size. Oecologia. 1996;108:438–445. doi: 10.1007/BF00333719. [DOI] [PubMed] [Google Scholar]
  19. Milla R, Reich PB. The scaling of leaf area and mass: the cost of light interception increases with leaf size. Proceedings of the Royal Society B – Biological Sciences. 2007;274:2109–2114. doi: 10.1098/rspb.2007.0417. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Moles AT, Westoby M. Latitude, seed predation and seed mass. Journal of Biogeography. 2003;30:105–128. [Google Scholar]
  21. Moles AT, Ackerly DD, Tweddle JC, et al. Global patterns in seed size. Global Ecology and Biogeography. 2007;16:109–116. [Google Scholar]
  22. Niinemets Ü, Portsmuth A, Tobias M. Leaf size modifies support biomass distribution among stems, petioles and mid-ribs in temperate plants. New Phytologist. 2006;171:91–104. doi: 10.1111/j.1469-8137.2006.01741.x. [DOI] [PubMed] [Google Scholar]
  23. Niinemets Ü, Portsmuth A, Tena D, Tobias M, Matesanz S, Valladares F. Do we underestimate the importance of leaf size in plant economics? Disproportional scaling of support costs within the spectrum of leaf physiognomy. Annals of Botany. 2007a;100:283–303. doi: 10.1093/aob/mcm107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Niinemets Ü, Portsmuth A, Tobias M. Leaf shape and venation pattern alter the support investments within leaf lamina in temperate species: a neglected source of leaf physiological differentiation? Functional Ecology. 2007b;21:28–40. [Google Scholar]
  25. Niklas KJ. Plant biomechanics: an engineering approach to plant form and function. Chicago, IL: University of Chicago Press; 1992. [Google Scholar]
  26. Niklas KJ. The role of phyllotactic pattern as a ‘Developmental Constraint’ on the interception of light by leaf surfaces. Evolution. 1988;42:1–16. doi: 10.1111/j.1558-5646.1988.tb04103.x. [DOI] [PubMed] [Google Scholar]
  27. Niklas KJ. The allometry of plant reproductive biomass and stem diameter. American Journal of Botany. 1993;80:461–467. [Google Scholar]
  28. Niklas KJ. Research review: a mechanical perspective on foliage leaf form and function. New Phytologists. 1999;143:19–31. [Google Scholar]
  29. Niklas KJ, Cobb ED. Biomass partitioning and leaf N,P-stoichiometry: comparisons between tree and herbaceous current-year shoots. Plant, Cell and Environment. 2006;29:2030–2042. doi: 10.1111/j.1365-3040.2006.01578.x. [DOI] [PubMed] [Google Scholar]
  30. Niklas KJ, Enquist BJ. Canonical rules for plant organ biomass partitioning and growth allocation. American Journal of Botany. 2002;89:812–819. doi: 10.3732/ajb.89.5.812. [DOI] [PubMed] [Google Scholar]
  31. Niklas KJ, Cobb ED, Niinemets Ü, et al. ‘Diminishing returns’ in the scaling of functional leaf traits across and within species groups. Proceedings of the National Academy of Sciences of the USA. 2007;104:8891–8896. doi: 10.1073/pnas.0701135104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Normand F, Bissery C, Damour G, Lauri PE. Hydraulic and mechanical stem properties affect leaf-stem allometry in mango cultivars. New Phytologist. 2008;178:590–602. doi: 10.1111/j.1469-8137.2008.02380.x. [DOI] [PubMed] [Google Scholar]
  33. Parkhurst DF, Loucks OL. Optimal leaf size in relation to environment. Journal of Ecology. 1972;60:505–537. [Google Scholar]
  34. Pickup M, Westoby M, Basten A. Dry mass cost of deploying leaf area in relation to leaf size. Functional Ecology. 2005;19:88–97. [Google Scholar]
  35. Poorter H, Remkes C. Leaf area ratio and net assimilation rate of 24 wild species differing in relative growth rate. Oecologia. 1990;83:553–559. doi: 10.1007/BF00317209. [DOI] [PubMed] [Google Scholar]
  36. Preston KA, Ackerly DD. Hydraulic architecture and the evolution of shoot allometry in contrasting climates. American Journal of Botany. 2003;90:1502–1512. doi: 10.3732/ajb.90.10.1502. [DOI] [PubMed] [Google Scholar]
  37. Shen ZH, Liu ZL, Wu J. Altitudinal pattern of flora on the eastern slope of Mt. Gongga. Biodiversity Science. 2004;12:89–98. [in Chinese] [Google Scholar]
  38. Shinozaki K, Yoda K, Hozumi K, Kira T. A quantitative analysis of plant form – the pipe model theory. I. Basic analysis. Japanese Journal of Ecology. 1964;14:97–105. [Google Scholar]
  39. Sun SC, Jin DM, Shi PL. The leaf size–twig size spectrum of temperate woody species along an altitudinal gradient: an invariant allometric scaling relationship. Annals of Botany. 2006;97:97–107. doi: 10.1093/aob/mcj004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tang CQ, Ohsawa M. Altitudinal distribution of evergreen broad-leaved trees and their leaf-size pattern on a humid subtropical mountain, Mt. Emei, Sichuan, China. Plant Ecology. 1999;145:221–233. [Google Scholar]
  41. Taylor SE. Optimal leaf form. In: Gates DM, Schmerl RB, editors. Perspectives in biophysical ecology. Berlin: Springer Verlag; 1975. pp. 73–86. [Google Scholar]
  42. Valladares F, Skillman JB, Pearcy RW. Convergence in light capture efficiencies among tropical forest shade tolerant plants with contrasting crown architectures: a case of morphological compensation. American Journal of Botany. 2002;89:1275–1284. doi: 10.3732/ajb.89.8.1275. [DOI] [PubMed] [Google Scholar]
  43. Warton DI, Weber NC. Common slope tests for bivariate errors-in-variables models. Biometrical Journal. 2002;44:161–174. [Google Scholar]
  44. Warton DI, Wright IJ, Falster DS, Westoby M. Bivariate line-fitting methods for allometry. Biological Reviews. 2006;81:259–291. doi: 10.1017/S1464793106007007. [DOI] [PubMed] [Google Scholar]
  45. Webb CO, Ackerly DD, Kembel SW. Phylocom: software for the analysis of phylogenetic community structure and trait evolution. Bioinformatics. 2008;24:2098–2100. doi: 10.1093/bioinformatics/btn358. [DOI] [PubMed] [Google Scholar]
  46. Westoby M, Wright IJ. The leaf size–twig size spectrum and its relationship to other important spectra of variation among species. Oecologia. 2003;135:621–628. doi: 10.1007/s00442-003-1231-6. [DOI] [PubMed] [Google Scholar]
  47. Westoby M, Falster DS, Moles AT, Vesk PA, Wright IJ. Plant ecology strategies: some leading dimensions of variation between species. Annual Review of Ecology and Systematics. 2002;33:125–159. [Google Scholar]
  48. White PS. Evidence that temperate east North American evergreen woody plants follow Corner's rules. New Phytologist. 1983a;95:139–145. [Google Scholar]
  49. White PS. Corner's rules in eastern deciduous trees: allometry and its implications for the adaptive architecture of trees. Bulletin of the Torrey Botanical Club. 1983b;110:203–212. [Google Scholar]
  50. Wolfe JA. Paleoclimatic estimates from tertiary leaf assemblages. Annual Review of Earth and Planetary Sciences. 1995;23:119–142. [Google Scholar]
  51. Wright IJ, Reich PB, Westoby M, et al. The worldwide leaf economics spectrum. Nature. 2004;428:821–827. doi: 10.1038/nature02403. [DOI] [PubMed] [Google Scholar]
  52. Wright IJ, Ackerly DD, Bongers F, et al. Relationships among ecologically important dimensions of plant trait variation in seven neotropical forests. Annals of Botany. 2007;99:1003–1015. doi: 10.1093/aob/mcl066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Xiang S, Wu N, Sun S. Within-twig biomass allocation in subtropical evergreen broad-leaved species along an altitudinal gradient: allometric scaling analysis. Trees: Structure and Function. 2009;23:637–647. [Google Scholar]
  54. Yang DM, Li GY, Sun SC. The generality of leaf size versus number tradeoff in temperate woody species. Annals of Botany. 2008;102:623–629. doi: 10.1093/aob/mcn135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Yang DM, Li GY, Sun SC. The effects of leaf habit, leaf form and habitat type on leaf/stem relationship in temperate woody species. Journal of Vegetation Science. 2009;20:359–366. [Google Scholar]
  56. Zhen WZ, Fu LG. Flora of China. Vol. 7. Beijing, China: Science Press; 1978. [in Chinese] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
mcp262_index.html (683B, html)
mcp262_1.pdf (85.8KB, pdf)

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES