DIFFEOMORPHIC SURFACE FLOWS: A NOVEL METHOD OF SURFACE EVOLUTION

Abstract

We describe a new class of surface flows, diffeomorphic surface flows, induced by restricting diffeomorphic flows of the ambient Euclidean space to a surface. Different from classical surface PDE flows such as mean curvature flow, diffeomorphic surface flows are solutions of integro-differential equations in a group of diffeomorphisms. They have the potential advantage of being both topology-invariant and singularity free, which can be useful in computational anatomy and computer graphics. We first derive the Euler–Lagrange equation of the elastic energy for general diffeomorphic surface flows, which can be regarded as a smoothed version of the corresponding classical surface flows. Then we focus on diffeomorphic mean curvature flow. We prove the short-time existence and uniqueness of the flow, and study the long-time existence of the flow for surfaces of revolution. We present numerical experiments on synthetic and cortical surfaces from neuroimaging studies in schizophrenia and auditory disorders. Finally we discuss unresolved issues and potential applications.

1. Introduction

Surface evolution is both an important tool and an intriguing focus of mathematical research in geometric analysis, e.g., [5], and geometric PDEs, e.g., [37]. It also has been extensively applied in image processing, e.g., [3], and computer vision and interface modeling, e.g., [38]. In this paper, we develop and study a novel method of surface evolution under the action of the diffeomorphisms of the ambient Euclidean space.

We are interested in flows that can minimize surface area or mean curvature of a surface without inducing changes in topology or creating singularities. Therefore, it is natural to consider surface flows that are described by diffeomorphisms of the ambient Euclidean space. Motivated by the general framework of deformable template theory [17], we study transformations acting on objects, rather than the objects themselves. More specifically, we analyze flows on a group of diffeomorphisms of Euclidean space, rather than studying flows on the surfaces themselves. The foundations of this general framework have been rigorously established and have enabled comparisons to be made between deformable objects; see [11, 32] and the references therein. The theory has been successfully applied to image matching problems in which landmarks [24], curves [14], or surface patches [41] evolve under diffeomorphisms of Euclidean space. Here we use this framework in a variational setting, in an approach that is reminiscent of shape optimization methods [10].

In this paper, we transform variational formulations of classical surface flows (that minimize geometrical properties such as area, elastic energy, or total curvature) into optimization problems on a group of diffeomorphisms. This approach leads to solving the corresponding Euler–Lagrange equations as evolutions in the group that induce, via the group action, stable evolutions of surfaces. We call such flows diffeomorphic surface flows.

In the last decade, there have been studies on geometric flows such as the celebrated mean curvature flow, e.g., [12] and references therein, surface diffusion flow, e.g., [13], and the Willmore flow, e.g., [27, 26]. The equations for these surface flows are second or fourth order parabolic PDEs which require sophisticated numerical methods, e.g., [9]. Moreover, these flows can change surface topology and introduce singularities, e.g., [12, 29, 30].

We show that diffeomorphic surface flows can be regarded as smooth versions of the corresponding classical surface flows. They flow to minimize the energy while preserving surface topology and do not break down due to finite-time singularities since they are induced from the evolution of diffeomorphisms. Moreover, these flows are solutions of integro-differential equations on the diffeomorphism group, which are somewhat easier to discretize than the PDEs that govern the classical surface flows.

A major motivation for this work came from a desire to smooth triangulated cortical surfaces that are generated by marching cubes or tetrahedra isosurface algorithms [28, 18] based on a threshold derived from the segmentation of volumetric images of the brain, e.g., [35, 36]. In addition, topological defects generated by isosurface algorithms can be corrected by multiscale and morphological operations, e.g., [20, 21]. The end result is a triangulated surface that may contain several anomalous protrusions which may distort the true curvature of the surface and thus confound the interpretation of possible biological processes in disease such as neuronal migration of tissues, e.g., [1, 4]. Smoothing flows could be used to minimize these distortions. However, it is important that the topological properties of the surfaces be preserved to reflect the inherent biology at the scale of the voxel resolution of 0.5mm³ or 1mm³ and to not generate additional artifacts.

Algorithms for smoothing “noisy” surfaces have been the focus of intense efforts in the computer vision field, e.g., [23, 45]. Unfortunately little effort has been made to apply these sophisticated algorithms to cortical surfaces without losing accuracy and simplification. Among the earliest such algorithms, Joshi et al. [25] used the approach of Hamann [19] for generating local quadratic approximations to a discrete surface in order to locally smooth triangulated meshes and thus curvature. More sophisticated algorithms have since been developed. Among the most recent such methods are PDE algorithms based on the powerful level set method, e.g., [39, 43, 7], which, however, may lead to topological changes or singularities that may confound biological inference.

In this paper, we will present some encouraging preliminary results in which cortical surfaces are smoothed using diffeomorphic surface flows. In future work we will further develop the method and apply it in statistical analysis of cortical surfaces.

The organization of the paper is as follows. In section 2 we describe the mathematical background on flows of diffeomorphisms, classical surface energies, and the variational formulation for the surface flow. In section 2.3 we derive the Euler–Lagrange equations for diffeomorphic surface flows for a general elastic energy before focusing our attention on diffeomorphic mean curvature flow. In section 3 we prove the short-time existence of the solution of the diffeomorphic mean curvature flow equation and discuss the long-time existence for surfaces of revolution. In section 4 we describe a numerical implementation of the method, and in section 5 we present the results of our numerical simulations. Finally, unresolved issues and future directions are discussed in section 6.

2. Mathematical background

2.1. Flows of diffeomorphisms

The set of diffeomorphisms, φ, of ℝ³ forms a group under the operation of composition of mappings. Following the theory of flows of diffeomorphisms [11, 40], we introduce a Hilbert space V of smooth vector fields on ℝ³, which is assumed to be continuously included in ${\chi }_0^1({ℝ}^3)$, the set of all C¹ vector fields that converge to zero (with their first derivatives) at infinity, equipped with the supremum norm. Any time-dependent vector field, ν_t : ℝ → V, generates a trajectory, φ_t, in the group of diffeomorphisms by

$$\frac{\partial {\phi }_t}{\partial t}\circ {\phi }_t^{-1}={\nu }_t,$$ (2.1)

with initial condition φ₀ = Id. We let 𝒢 denote the group generated by all solutions φ_t of (2.1) with ν_s ∈ V for all s ≤ t and max_s≤t∥ν_s∥_V < ∞. (The fact that this set forms a group is proved, for example, in [40].) We shall also use the notation 𝒢_V to make explicit the dependence of this group on the Hilbert space V.

We want to implement gradient descent algorithms in the group of diffeomorphisms, which is an issue often referred to as shape optimization [10]. A basic notion in this context is the one of shape differential. Given a scalar function F defined on 𝒢_V and an element φ ∈; 𝒢_V, the shape differential of F at φ, denoted ∂F(φ), is (if it exists) the linear form on V (∂F(φ) ∈ V*) defined by

$$\partial F(\phi ).\upsilon =\frac{d}{d\epsilon }F((\text{id}+\epsilon \upsilon )\circ \phi ).$$

Assume that, for each φ, a dot product 〈.〉_φ is defined on V*. The gradient of F at φ with respect to this dot product, denoted ∇F(φ), is then defined by the following identity: for all m ∈ V*,

$${\langle \partial F(\phi ),m\rangle }_{\phi }=m.\nabla F(\phi ).$$

The associated gradient descent algorithm is the flow defined by

$$\frac{d\phi }{dt}=-\nabla F(\phi )\circ \phi .$$ (2.2)

By the chain rule, we can write

$$\frac{d}{dt}F(\phi )=\frac{d}{d\epsilon }F((\text{id}-\epsilon \nabla F(\phi ))\circ \phi )=-\parallel \partial F(\phi ){\parallel }_{\phi }^2,$$ (2.3)

which shows that the algorithm does indeed minimize F. If ∇F(φ) is a smooth vector field over a time interval [0, T], then φ in (2.2) is the flow associated to an ODE and therefore a diffeomorphism.

We denote by K the duality operator between V* and V, defined by m.υ = 〈Km, υ〉_V for m ∈ V* and υ ∈ V. The assumption that V is continuously included in ${\chi }_0^1({ℝ}^3)$ implies that K is a kernel operator, making V a reproducing kernel Hilbert space [2, 42]. Indeed, for a ∈ ℝ³, the linear form m = a ⊗ δ_x defined by m.υ = a^Tυ(x) is continuous on V, so that K (a ⊗ x) ∈ V is well defined and obviously linear in a. This defines a mapping (also denoted K) from ℝ³ × ℝ³ to GL₃(ℝ) by

$$K(x,y)a=K(a\otimes {\delta }_x)(y).$$ (2.4)

A key point here is that V can be specified by the definition of its kernel. In our case, K will be chosen as a scalar Gaussian kernel (or more precisely by a Gaussian kernel multiplied by the identity matrix). The corresponding Hilbert space (at scale σ) is defined by

$$V_{\sigma }=\left\{\upsilon =K^{1/2}u={\displaystyle {\int }_{{ℝ}^3}{e}^{-\frac{2\parallel x-y{\parallel }^2}{{\sigma }^2}}u(y)dy,u\in L^2(}{ℝ}^3)\right\},$$ (2.5)

where the inner product on V_σ is defined by 〈K^1/2u, K^1/2u′〉V = 〈u,u′〉_L². The associated kernel is K = (K^1/2)², which is proportional to exp(−∥x − y∥²/(2σ²)).

The dual dot product on V* comes straightforwardly from the fact that K is a duality operator, yielding

$${\langle m,\tilde{m}\rangle }_{V^{*}}=m.(K\tilde{m}).$$

The φ-dependent dot product 〈. , .〉_φ used in this paper will be weighted versions of this dual product, taking the form

$${\langle m,\tilde{m}\rangle }_{\phi }={\langle {\rho }_{\phi }m,{\rho }_{\phi }\tilde{m}\rangle }_{V^{*}}=m.({\rho }_{\phi }K({\rho }_{\phi }\tilde{m})),$$

where ρ_φ is a nonnegative scalar function and (ρ_φm).υ := m(ρ_φυ). The associated gradient descent algorithm becomes

$$\frac{d\phi }{dt}=-({\rho }_{\phi }K({\rho }_{\phi }\partial F(\phi )))\circ \phi .$$ (2.6)

We now describe how this is implemented, with a suitable choice for ρ_φ, for surface evolution.

2.2. Surface energy

We consider the general surface energy functional [34, 22]

$$E(\sum )={\displaystyle {\int }_{\sum }(\alpha +\beta H^2-\gamma G)d\sigma ,\text{\hspace{1em}\hspace{1em}where\hspace{1em}}\alpha \ge 0,\beta \ge \gamma \ge 0,}$$ (2.7)

where H and G are the mean and Gauss curvature of Σ, respectively. This elastic energy functional is a linear combination of three basic energy functionals:

• area: U(Σ) = ∫_Σ dσ,

• Willmore energy: U (Σ) = ∫_Σ 4H² dσ, and

• total curvature: $U(\Sigma )={\displaystyle {\int }_{\Sigma }(4H^2-2G)d\sigma ={\displaystyle {\int }_{\Sigma }(k_1^2+k_2^2)d\sigma }}$, where k₁, k₂ are principal curvatures.

These energy functionals can be locally minimized using the classical surface flows known as mean curvature (area-minimizing), Willmore, and total curvature flow, respectively.

We generate diffeomorphic surface flows as follows. If Σ₀ is the initial surface, we can define F(φ) = E(φ(Σ₀)). We then let Σ_t= φ_t(Σ₀), where φ_t is given by (2.6).

2.3. Euler–Lagrange equation

In this section, we derive the gradient flow equation for the diffeomorphic surface flow minimizing the elastic energy. From section 2.2, we first compute the variation of the energy. The following lemma is due to Nitsche [34]. For simplicity, we suppose that all surfaces are oriented and closed. Let the surface be Σ(p) and its variation be Σ_ε(p) = Σ(p) + εν (p).

LEMMA 2.1 (variation of elastic energy)

For surface elastic energy, E(Σ) = ∫_Σ (α + βH² − γG)dσ, the energy variation is

$$\frac{\partial }{\partial \epsilon }E{({\sum }_{\epsilon })}_{{|}_{\epsilon =0}}={\displaystyle {\int }_{\sum }\alpha {\nu }^{\perp }H-\beta {\nu }^{\perp }({\mathrm{\Delta }}_{\sum }H+2H(H^2-G))d\sigma ,}$$ (2.8)

where ν^⊥ = 〈ν, N〉 is the normal component of the vector field ν, Δ_Σ is the intrinsic Laplace operator, and N is the surface normal.

A proof may be found in Willmore [44, pp. 279–282].

Remark 1

For a closed surface, the term with γ is absent since by the Gauss– Bonnet theorem, the integral of the Gauss curvature is a constant.

This lemma directly provides the expression of the shape derivative of F at φ, since, for Σ = φ(Σ₀), ((id + ευ) ∘ φ) (Σ₀) = Σ + ευ(Σ), yielding

$$\partial F(\phi ).\nu ={\displaystyle {\int }_{\sum }\alpha {\nu }^{\perp }H-\beta {\nu }^{\perp }({\mathrm{\Delta }}_{\sum }H+2H(H^2-G))d\sigma .}$$

Now, from (2.6), we obtain the diffeomorphic evolution equations, in which we assume that ρ_φ depends on φ only via the deformed surface Σ, hence employing the notation ρ_φ = ρ_Σ and Σ_t = φ_t ∘ Σ₀:

$$\begin{array}{l}\frac{\partial {\phi }_t(y)}{\partial t}=-{\rho }_{{\Sigma }_t}({\phi }_t(y))\hfill \\ ·{\displaystyle {\int }_{q\in {\Sigma }_t}(\alpha H-\beta ({\mathrm{\Delta }}_{{\Sigma }_t}H+2H(H^2-G)))K({\phi }_t(y),q){\rho }_{{\Sigma }_t}(q)N(q)d{\sigma }_t(q).}\hfill \end{array}$$ (2.9)

We define ρ_Σ as an area normalization factor as follows. Define, for a surface Σ, the local area function

$$a_{\Sigma }(p)={\displaystyle {\int }_{q\in \Sigma }K(p,q)d\sigma .}$$ (2.10)

We then set

$${\rho }_{\Sigma }(p)=a_{\Sigma }{(p)}^{-1/2}.$$ (2.11)

Choosing this normalization ensures that the right-hand sides in the diffeomorphic flows have the same dimensions as the corresponding classical flows (e.g., 1/length for the mean curvature flow). Doing so, the large-scale behavior (relative to the width of the kernel) is expected to be similar for both flows.

Although all quantities introduced so far are defined on the whole space, we are primarily interested in the evolution of the surface Σ_t = φ_t ∘ Σ₀. Hence, for the area and Willmore energy functionals, the equations that govern the flow of each point p = φ_t(y) on the closed surface Σ_t are given by the following integro-differential equations:

• diffeomorphic mean curvature flow (α = 1 and β = 0):

  $$\frac{\partial p}{\partial t}=-a_{{\Sigma }_t}^{-1/2}(p){\displaystyle {\int }_{q\in {\Sigma }_t}K(p,q)H(q)a_{{\Sigma }_t}^{-1/2}(q)N(q)d{\sigma }_t,}$$ (2.12)
• diffeomorphic Willmore flow (α = 0 and β = 1):

  $$\begin{array}{l}\frac{\partial p}{\partial t}=a_{{\Sigma }_t}^{-1/2}(p)\hfill \\ ·{\displaystyle {\int }_{q\in {\Sigma }_t}K(p,q)({\mathrm{\Delta }}_{{\Sigma }_t}H(q)+2H(q)(H^2(q)-G(q)))a_{{\Sigma }_t}^{-1/2}(q)N(q)d{\sigma }_t.}\hfill \end{array}$$ (2.13)

We will use these formulae in the numerical implementation in section 4. Notice that they are similar to the corresponding equations for the classical mean curvature and Willmore flows. The diffeomorphic surface flows have the same energy minimizing property as their classical counterparts, but since they are diffeomorphisms, they preserve the topology of the surface. In the next section, we focus only on diffeomorphic mean curvature flow.

3. Diffeomorphic mean curvature flow

From now on, we use the Gaussian kernel function

$$K(p,q)=e^{-\frac{\parallel p-q{\parallel }^2}{2{\sigma }^2}}.$$ (3.1)

Here σ is the kernel size, which corresponds (up to a change in the normalization factor) to the reproducing kernel of V_σ given by (2.5).

The flow equation is therefore given by

$$\frac{\partial {\phi }_t(y)}{\partial t}=-a_{{\Sigma }_t}({\phi }_t{(y))}^{-1/2}{\displaystyle {\int }_{q\in {\Sigma }_t}{e}^{-\frac{\parallel {\phi }_t(y)-q{\parallel }^2}{2{\sigma }^2}}H(q)a_{{\Sigma }_t}{(q)}^{-1/2}N(q)d{\sigma }_t,}$$ (3.2)

with the initial condition φ₀ = id. As indicated by (2.3), this is an area-minimizing flow for the surface Σ_t, with the explicit formula

$$\frac{d\left|{\Sigma }_t\right|}{dt}=-{\displaystyle {\int }_{{\Sigma }_t^2}{e}^{-\frac{\parallel p-q{\parallel }^2}{2{\sigma }^2}}{\left(\frac{H(p)N(p)}{\sqrt{a_{{\Sigma }_t}(p)}}\right)}^T\left(\frac{H(q)N(q)}{\sqrt{a_{{\Sigma }_t}(q)}}\right)d{\sigma }_t(p)d{\sigma }_t(q).}$$

3.1. Short-time existence of solution

The classical flows are local flows and by PDE theory, there are short-time solutions for smooth initial data. Because of the integro-differential form of diffeomorphic surface flows, short-time existence follows from standard ODE arguments on Banach spaces.

THEOREM 1 (short-time existence and uniqueness)

For any initial compact smooth surface, there exists a unique solution for the flow equation (3.2) in a small time interval [0, t₀].

Proof

Consider the space A = ℝ³ × GL₃(ℝ) × Bil(ℝ³, ℝ³), where the last factor is the set of bilinear functions from ℝ³ × ℝ³ to ℝ³. A generic element of A will be denoted Q = (ε, F, S), and we will consider the Banach space B of continuous functions Q(·) : ℝ³ → A, with the supremum norm

$$\parallel Q\parallel =\parallel \epsilon {\parallel }_{\infty }+\parallel F{\parallel }_{\infty }+\parallel S{\parallel }_{\infty }.$$ (3.3)

Here ε(y) is a C² vector field that converges to zero (with its first and second derivatives) at infinity, and F(y) and S(y) are first and second derivatives of ε(y).

Letting φ(y) = y + ε(y), we first embed (3.2) in an ODE on B. We rewrite the right-hand side of (3.2) using integrals over Σ₀. Covering Σ₀ with local charts f : U → Σ₀, we have that Σ_t(y) = φ_t ∘ f (y). Suppose that {f_u, f_u, N₀} is an orthonormal basis at the point y. Then, using N(t, φ(y)) = dφ^−T N₀/∥dφ^−T N₀∥ [6] and the expression for the mean curvature in coordinates (omitting the subscript t), we have

$$\begin{array}{ll}H(t,\phi )=\hfill & \frac{1}{\parallel d\phi f_u\times d\phi f_{\upsilon }{\parallel }^2\parallel d{\phi }^{-T}{N}_0{\parallel }^2}(\langle d{\phi }^{-1}{d}^2\phi (f_u,f_u)+f_{uu},N_0\rangle \parallel d\phi f_{\upsilon }{\parallel }^2\hfill \\ \hfill & +\langle d{\phi }^{-1}{d}^2\phi (f_{\upsilon },f_{\upsilon })+f_{\upsilon \upsilon },N_0\rangle \parallel d\phi f_u{\parallel }^2\hfill \\ \hfill & -2\langle d{\phi }^{-1}{d}^2\phi (f_u,f_{\upsilon })+f_{u\upsilon },N_0\rangle \langle d\phi f_u,d\phi f_{\upsilon }\rangle ).\hfill \end{array}$$

Defining the quadratic forms on TΣ = dφTΣ₀,

$$A_{\phi }(g,h)=\langle d{\phi }^{-1}{d}^2\phi (d{\phi }^{-1}g,d{\phi }^{-1}h),N_0\rangle$$ (3.4)

and

$$I{I}_{\phi }(g,h)=-\langle d{\phi }^{-1}g,d{N}_{0}d{\phi }^{-1}h\rangle ,$$ (3.5)

and using the fact that ∥dφf_u × dφf_υ∥ = |det Dφ| ∥dφ^−T N₀∥, we can rewrite

$$H(t,\phi )=\frac{\text{trace}(A_{\phi })+\text{trace}(I{I}_{\phi })}{|\det D\phi {|}^2\parallel d{\phi }^{-T}{N}_0{\parallel }^4}.$$ (3.6)

So, the evolution equation can be written as

$$\begin{array}{l}\frac{\partial {\phi }_t(y)}{\partial t}=-a_{\Sigma }{({\phi }_t(y))}^{-1/2}\hfill \\ ·{\displaystyle {\int }_{{\Sigma }_0}{e}^{-\frac{\parallel {\phi }_t(x)-{\phi }_t(y){\parallel }^2}{2{\sigma }^2}}\frac{\text{trace}(A_{{\phi }_t})+\text{trace}(I{I}_{{\phi }_t})}{|\det D{\phi }_t|\parallel d{\phi }_t^{-T}{N}_0{\parallel }^4}{a}_{\Sigma }{({\phi }_t(x))}^{-1/2}d{\phi }_t^{-T}{N}_0(x)d{\sigma }_0,}\hfill \end{array}$$ (3.7)

with

$$a_{\Sigma }(\phi (y))={\displaystyle {\int }_{{\Sigma }_0}{e}^{-\frac{\parallel \phi (x)-\phi (y){\parallel }^2}{2{\sigma }^2}}|\det D\phi |\parallel d{\phi }^{-T}{N}_0\parallel d{\sigma }_0(x).}$$

Introducing dφ = Id + dε = Id + F and d²φ = d²ε = S, (3.7) takes the form

$$\frac{d\epsilon }{dt}=J_0(\epsilon ,F,S).$$ (3.8)

The time evolution of F is obtained by computing the differential of this equation with respect to the space variable. Since in (3.7), the variable y appears only in evaluations of φ (not its derivatives), it is clear that the evolution of F will also take the form dF/dt = J₁ (ε, F, S). Since the same argument can be made for S, we obtain the fact that (ε, F, S) follows an ODE in B of the form

$$\frac{d\epsilon }{dt}=J_0(\epsilon ,F,S),\frac{dF}{dt}=J_1(\epsilon ,F,S),\frac{dS}{dt}=J_2(\epsilon ,F,S).$$ (3.9)

It is clear now that J₀, J₁, J₂ are integrals of rational functions of ε, F, S which are well defined in a neighborhood of (ε, F, S) = (0, 0, 0). This ensures short-term existence of solutions of the system in B.

It remains to show that, if (ε, F, S) is a solution of this system, the first component, ε, is in fact a solution of (3.8) with initial condition ε₀ = 0. For this it suffices to prove that ε is twice differentiable, with its first and second differentials given by F and S. This follows from standard arguments for ODEs, and we omit the details here. Finally, it is easy to see that we have a unique solution φ(y) = y + ε(y) for the original flow equation (3.2).

Remark 2

The result in Theorem 1 also holds for the more general diffeomorphic surface evolution

$$\begin{array}{ll}\frac{\partial {\phi }_t(y)}{\partial t}=\hfill & a_{{\Sigma }_t}^{-1/2}({\phi }_t(y))\hfill \\ \hfill & ·{\displaystyle {\int }_{q\in {\Sigma }_t}K({\phi }_t(y),q)f(q,N(q),dN(q),d^{2}N(q),\mathrm{...},d^{m}N(q))a_{{\Sigma }_t}^{-1/2}(q)d{\sigma }_t,}\hfill \end{array}$$

where f has continuous derivatives for each variable, Σ₀ is a smooth surface, m is an integer, and N is the surface normal. The proof follows along the same general lines as the proof we gave above. We rewrite the integral as an integral on the original surface and the function f as a function G(φ, dφ, d²φ, … , d^m+1φ). Then the equations of the derivatives of dφ, d²φ, … , d^m+1φ involve only the derivatives of the kernel and G.

We can show that the solution φ is in fact a diffeomorphism by standard arguments using Gronwall’s lemma [46, Chap. 10].

THEOREM 2 (diffeomorphism)

If φt is the solution of the flow equation (3.2) on the interval [0, T], then φ_t is a diffeomorphism for all t ∈ [0, T].

We have the following important consequence.

COROLLARY 1 (topology invariance and singularity free)

The solution of the flow equation (3.2) at each time t gives a smooth surface with the same topology as the initial surface as long as the solution exists.

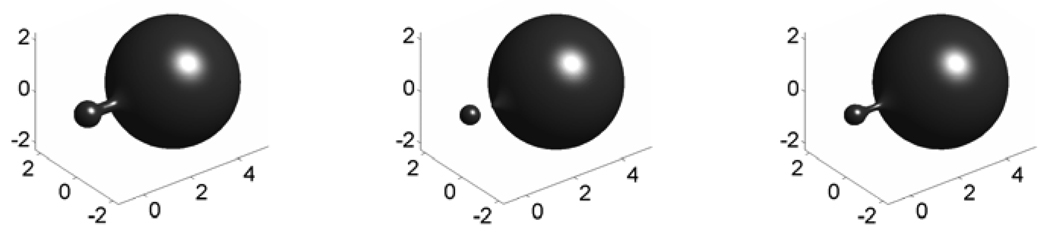
We are obviously interested in the long-time existence of the flow. Numerical evidence and analysis for simple surfaces so far suggest that the flow has a longtime solution. However, the interactions between remote parts of a surface make the long-time behavior difficult to analyze (see, for example, Figure 1). Analyzing the proof of Theorem 1, we see that being able to extend a solution beyond a given time t < t₀ depends only on the regularity of the surface at time t. More precisely, a standard lower-bound of how far a current solution of an ODE in a Banach space can be extended beyond t is directly related to the Lipschitz constant of the ODE. In our proof, the Lipschitz properties of the system rely on the surface only via upper-bounds on the second derivative of the normal in (3.6) and via lower-bounds on the local area a_Σ. So solutions of (3.9) can be extended in time as long as the surface does not develop singularities.

FIG. 1.

Interaction of three nearby spheres during the diffeomorphic mean curvature flow. The initial radius of all spheres is 0.5, and the minimum distance among them is 0.1. The kernel size is σ = 0.3, and the stopping time is T = 1.

A consequence of this analysis is that, if we can exhibit an evolution starting at some Σ₀ on some interval [0, T] on which the total curvature of the evolving surface remains bounded from above and the local area remains bounded from below, then this evolution is the only solution of (3.2) starting at Σ₀.¹ This property will be used in the next section when we provide simplified equations for surfaces of revolution.

3.2. Surfaces of revolution

In this subsection we analyze the diffeomorphic mean curvature flow for a surface of revolution, Σ. Because of the uniqueness of solutions, the solution of (3.2) must preserve rotational symmetry. Consequently, it suffices to evolve the profile curve of Σ. Therefore, here we derive an equation for the evolution of the profile curve for the diffeomorphic mean curvature flow equation (3.2). It is much more computationally efficient to solve the equation for the profile curve than it is to solve the full flow equation (3.2) for a triangulated surface.

We parameterize a surface of revolution by

$$\mathrm{x}(u,\upsilon )=(\alpha (u)\cos \upsilon ,\alpha (u)\sin \upsilon ,\beta (u)).$$ (3.10)

Here u ∈ [−1, 1], υ ∈ [0, 2π], and the profile curve γ(u) = (α(u), β(u)) satisfies suitable conditions. For a closed curve, we need α > 0, while for an open curve, we require that α ≥ 0 with α = 0 only at the end points, and also β′ = 0 at the end points. Here and below α′, β′ denote the derivatives of the functions α, β. The orientation of the curve is taken to be counterclockwise.

We now derive the induced flow equation for the profile curve. First, we have

$$N=\frac{(-\beta \prime \text{cos}\upsilon ,-\beta \prime \text{sin}\upsilon ,\alpha \prime )}{\sqrt{{(\alpha \prime )}^2+{(\beta \prime )}^2}},$$ (3.11)

$$d\sigma =\alpha \sqrt{{(\alpha \prime )}^2+{(\beta \prime )}^2}dud\upsilon ,2H=\frac{\beta \prime }{\alpha \sqrt{{(\alpha \prime )}^2+{(\beta \prime )}^2}}+\kappa ,$$ (3.12)

where κ is the curvature of the profile curve and the normal vector N is outward pointing.

Using these expressions, we can characterize the evolution of the profile curve x(u, 0) = (α(u), 0, β(u)) as follows:

$$\begin{array}{l}\frac{\partial \alpha (u)}{\partial t}=-a{(u)}^{-1/2}\hfill \\ ·{\displaystyle {\int }_{-1}^1{e}^{-\frac{1}{2{\sigma }^2}({(\alpha (u)-\alpha (u_t))}^2+{(\beta (u)-\beta (u_t))}^2)}{g}_1(\alpha (u)\alpha (u_t))H(u_t)\alpha (u_t)\beta \prime (u_t)a{(u_t)}^{-1/2}d{u}_t,}\hfill \\ \frac{\partial \beta (u)}{\partial t}=a{(u)}^{-1/2}\hfill \\ ·{\displaystyle {\int }_{-1}^1{e}^{-\frac{1}{2{\sigma }^2}({(\alpha (u)-\alpha (u_t))}^2+{(\beta (u)-\beta (u_t))}^2)}{g}_0(\alpha (u)\alpha (u_t))H(u_t)\alpha (u_t)\alpha \prime (u_t)a{(u_t)}^{-1/2}d{u}_t,}\hfill \\ a(u)={\displaystyle {\int }_{-1}^1{e}^{-\frac{1}{2{\sigma }^2}({(\alpha (u)-\alpha (u_t))}^2+{(\beta (u)-\beta (u_t))}^2)}{g}_0(\alpha (u)\alpha (u_t))\alpha (u_t)\sqrt{\alpha \prime {(u_t)}^2+\beta \prime {(u_t)}^2}d{u}_t,}\hfill \end{array}$$ (3.13)

where

$$g_1(x)={\displaystyle {\int }_0^{2\pi }{e}^x(\text{cos}(\upsilon )-1)/{\sigma }^2\text{cos}(\upsilon )d\upsilon ,g_0(x)={\displaystyle {\int }_0^{2\pi }{e}^{x(\text{cos})(\upsilon )-1)/{\sigma }^2}d\upsilon .}}$$

For a discrete profile curve consisting of finite line segments, (3.13) is a system of ODEs which has a short-time solution and can be solved numerically using MATLAB. In section 5 we use this system of ODEs to study the long-time behavior of the solution for surfaces of revolution.

For the classical mean curvature flow of a surface of revolution the only possible singularities are on the axis of revolution [12]. We conjecture that for a closed profile curve if the curvature is bounded, then α > 0 for all time. In fact, numerical results suggest that an even stronger result is true.

CONJECTURE 1 (long-time solution for surfaces of revolution)

There exists a unique solution for the flow equation (3.13) for all t ≥ 0.

3.3. Sphere evolution

When the surface is the sphere, we have an explicit solution for the diffeomorphic mean curvature flow equation.

PROPOSITION 1 (sphere evolution)

If the initial surface Σ₀ is a sphere of radius R₀, then the solution of the diffeomorphic mean curvature flow (3.2) exists for all time, and at each time t the surface Σ_t is a sphere of radius R_t, where R_t satisfies the equation

$$\frac{d{R}_t}{dt}=-\frac{(R_t^2+{\sigma }^2)e^{-2R_t^2/{\sigma }^2}+R_t^2-{\sigma }^2}{R_t^3(1-e^{-2R_t^2/{\sigma }^2})}.$$ (3.14)

Proof

By symmetry and from the uniqueness of solutions, the evolving surface remains a sphere at all times. Equation (3.14) is a direct application of the general formulae with α(u_t) = R_tcos(πu_t/2), β(u_t) = R_tsin(πu_t/2) at u₀ = 1. For example,

$$\begin{array}{ll}{a}_{{\sum }_t}(1)\hfill & =2\pi {\displaystyle {\int }_{-1}^1{e}^{-\frac{R_t^2}{{\sigma }^2}(1-\text{sin}\frac{\pi u_t}{2}}{R}_t^2\frac{\pi }{2}\text{cos}\frac{\pi u_t}{2}d{u}_t}\hfill \\ \hfill & =2\pi R_t^2{e}^{-\frac{R_t^2}{{\sigma }^2}}{\displaystyle {\int }_{-1}^1{e}^{\frac{R_t^{2}z}{{\sigma }^2}}}dz\hfill \\ \hfill & =2\pi {\sigma }^2(1-e^{-\frac{2R_t^2}{{\sigma }^2}}).\hfill \end{array}$$

Similar computations can be done for the other integral, leading to (3.14). One can check that the function f(r),

$$r\mapsto -\frac{(r^2+{\sigma }^2)e^{-2r^2/{\sigma }^2}+r^2-{\sigma }^2}{r^3(1-e^{-2r^2/{\sigma }^2})},$$

is well defined and differentiable over ℝ (including 0), vanishes at 0, and is negative for r > 0. This implies that solutions starting at R₀ > 0 decrease without reaching 0, and can be extended to infinite time.

A Taylor expansion of the equation at R_t = 0 yields dR_t/dt ≃ −(2/3σ²)R_t at t = 0, yielding an exponential decay of the radius.

By a similar argument, we can show that the following proposition holds.

PROPOSITION 2 (cylinder evolution)

The evolution of a circular (infinite) cylinder exists and is unique for all t ≥ 0.

We leave the proof to the reader. In this case, the first order expansion for the evolution of the radius is dR_t/dt ≃ −(1/2σ²)R_t, yielding here also an exponential decay, at a rate slower than for the sphere.

Recall that for the classical mean curvature flow, a sphere vanishes into a point and the circular cylinder into the y axis at finite time [12]. However, the diffeomorphic mean curvature flow preserves surface topology for all times.

In the left panel of Figure 2 we compare the classical mean curvature flow for a sphere to the diffeomorphic mean curvature flow for a range of kernel sizes, σ. Notice that for the mean curvature flow the surface collapses to a point at time t = 0.5, whereas for all kernel sizes the solution of the diffeomorphic mean curvature flow exists for all times. Moreover, from the evolution equation (3.14), it is not hard to prove that for the unit sphere, as the kernel size converges to zero, the solution of the diffeomorphic mean curvature flow converges to that of the mean curvature flow over the interval 0 ≤ t ≤ 0.5. This suggests the following conjecture.

FIG. 2.

Diffeomorphic mean curvature flow of a sphere. Left: Flows with different kernel sizes, σ (dotted curves). The classical mean curvature flow is indicated by the solid curve with stars. Right: Validation of the numerical algorithm in section 4 (circles) by comparison with the analytical solution from Theorem 1 (dashed curves) with σ = 0.5. The classical mean curvature flow is indicated by the solid curve.

CONJECTURE 2 (mean curvature flow limit)

Suppose, for an initial compact smooth surface, that the mean curvature flow exists for all times t ∈ [0, T]. Then for any time T₁ < T, on the time interval [0, T₁] the diffeomorphic mean curvature flow converges uniformly to the mean curvature flow as the kernel size goes to zero.

4. Numerical implementation

In this section we give the details of the numerical implementation of diffeomorphic surface flows via the Runge–Kutta method. We focus on two aspects: the estimation of geometric quantities such as the normal and curvature on discrete surfaces, and the ODE solver for diffeomorphic surface flows.

4.1. Discrete differential geometry of surfaces

Surfaces are discretized as triangulated meshes. Consequently, to numerically solve the diffeomorphic surface flow equations, we need to define discrete geometry quantities that approximate the normal and curvature functions on a smooth surface. Several such discretization methods have been described in the literature but none is universally used [19, 15, 31, 8]. We will use the discrete differential operators method of Meyer et al. [31], which is easy to implement and suitable for our examples.

Given a triangulated mesh with vertices υ_i and faces f_j, the vertex one-ring R₁(i) of a vertex υ_i is the set of all adjacent vertices, and the face one-ring F₁(i) of υ_i is the set of all faces containing υ_i. We determine the geometry at each vertex from the vertex one-ring of that vertex. If none of the triangles in F₁(i) is obtuse, we define the area A(υ_i) at the vertex υ_i to be the Voronoi area of that vertex:

$$A_{\text{Voronoi}}=\frac{1}{8}{\displaystyle \sum _{j\in R_1(i)}(\text{cot}{\alpha }_{ij}+\text{cot}{\beta }_{ij})\parallel {\upsilon }_i-{\upsilon }_j\parallel ,}$$ (4.1)

where α_ij and β_ij are the two angles opposite the edge υ_iυ_j in the two triangles sharing that edge. However, if some of the triangles in F₁(i) are obtuse, we define the area A(υ_i) to be the mixed area A_mixed described in [31].

Then the mean curvature normal vector $\overline{HN}$ at υ_i is given by

$$\overline{HN}({\upsilon }_i)=\frac{1}{4A({\upsilon }_i)}{\displaystyle \sum _{j\in R_1(i)}(\text{cot}{\alpha }_{ij}+\text{cot}{\beta }_{ij})({\upsilon }_i-{\upsilon }_j).}$$ (4.2)

We can also obtain the normal, mean curvature, and Gauss curvature formulae [31], which are not used in this paper.

4.2. ODE solution

We evolve a triangulated surface via its vertices; i.e., the surface vertices are used to discretize the flow equation (3.2). The resulting ODE system is solved numerically using a Runge–Kutta method.

The algorithm is as follows.

ALGORITHM 1. ODE solver for diffeomorphic surface flow.
1:	Initialize the flow time T and kernel size σ
2:	Initialize surface with υi and Fj
3:	Generate the one-ring neighborhood structure R1(i) and F1(i) for each vertex
4:	while t < T do
5:	Compute the geometry of the surface $\overline{H{N}_i}=\overline{HN}({\upsilon }_i)$ and Ai= Amixed(υi)
6:	Compute the Gaussian kernel weights Kij = K (υi, υj)
7:	Compute the local area weights loci= (∑j=allKijAj)−0.5
8:	Compute the flow speed term ui = −loci ∑j=all Kij locj ${\overline{HN}}_j{A}_j$
9:	Obtain the new vertices from a Runge–Kutta solver υi = RK (υi, ui)
10:	end while
11:	Output the surface

Remark 3

We did not attempt to determine an automatic stopping condition. We simply stopped after time T.

Remark 4

It is possible to use implicit ODE solvers.

Remark 5

In step 8, for each i it is possible to sum only over those indices j for which the Gaussian kernel K_ij exceeds a small threshold. Alternatively, for large kernel size one could use the fast Gauss transform [16].

Remark 6

For mean curvature flows of surfaces of revolution, we used a public-domain MATLAB toolbox for level set methods [33]. For mean curvature flows of triangulated meshes we used Algorithm 1 but with $u_i=-{\overline{HN}}_i$.

5. Results

We used MATLAB to implement the algorithm on a Pentium IV 3.2 GHz machine with 2 GB of RAM. In general for a synthetic surface with 7200 faces and 3600 vertices, one loop takes about 10 seconds. However, for cortical surface applications we used a C++ implementation that takes about 1 second per loop for a surface with 5000 vertices.

Sphere

In the right panel of Figure 2 we show the diffeomorphic mean curvature flow of a sphere for a kernel size of σ = 0.3 computed using Algorithm 1 (circles) and using the ODE (3.14) for the radius of the sphere (dashed curve). The agreement between the two methods is excellent. For comparison, we show the result for the classical mean curvature flow with a solid curve. For the algorithm, we generated an initial sphere with 642 vertices and 1280 faces using recursive subdivision of a cube. The solution of the ODE (3.14) was obtained using the MATLAB function ode45. As shown in Figure 1, three disconnected spheres can influence one another. It would be very interesting but difficult to analyze the long-time behavior of such interactions.

Circular torus

The circular torus was generated by rotating a circle about the y axis. The triangulated mesh had 3600 vertices and 7200 faces. We chose a “fat” torus with inner radius 0.2 and outer radius 1.2, as shown in Figure 3. In the right panel of Figure 3 we examined the solutions of the diffeomorphic mean curvature flow, obtained both by solving the surface of revolution flow equation (3.13) using the MATLAB function ode45 and by flowing the triangulated surface using Algorithm 1 indicated by dashed curves and plus symbols. The initial surface is represented by the two largest circles. The close agreement between the two sets of curves provides a mutual validation of both algorithms. For the surface flow we obtain the profile curves from the discrete surface by projecting the evolving base curves onto the plane.

FIG. 3.

Flow of a fat torus. Left: The fat torus with mean curvature indicated by the grayscale. Right: Comparison between the profile curves obtained using the ODE solution of (3.13) for surfaces of revolution and those obtained using the numerical algorithm in section 4.2, respectively, indicated by dashed curves and plus symbols. The initial profile curve is shown with the two largest solid circles. Here T = 0.5, and σ = 0.3.

Figure 4 provides a comparison between diffeomorphic flow with small σ (left) and classical mean curvature flow (right). For the latter, the profile curve reaches the y axis, changes topology, and eventually becomes a sphere. On the other hand, for the diffeomorphic mean curvature flow, part of the curve very closely approaches the y axis but slows down as time increases to infinity and does not actually reach the y axis. In fact, the profile curve flows towards a semicircular shape. This experiment also illustrates the scale-dependent aspect for diffeomorphic flows. In Figures 3 (right) and 4 (left), diffeomorphic flows starting from the same surfaces have very different evolutions. The large value of σ in the first figure prevents the torus from collapsing on itself as it does in the second case, which is much closer to mean curvature evolution.

FIG. 4.

Comparison of flows for the fat torus. Left: Diffeomorphic mean curvature flow with σ = 0.1 and T = 0.25 obtained using the ODE algorithm for surfaces of revolution. Right: Classical mean curvature flow with T = 0.2.

Dumbbell

Figure 5 and Figure 6 show results for a dumbbell generated by a curve with neck shape y = x²+c and c = 0.3. In the right-hand panel of Figure 6 we see that for the classical mean curvature flow, the thin neck breaks down and the dumbbell becomes two spheres. However, the diffeomorphic mean curvature flow does not break down even though, as we see in the right-hand panel of Figure 5, it flows towards two spheres connected by a very thin tube. One likely explanation for this shape is that the cylindrical part flows faster than the spherical part where the width of the neck is smaller than the kernel size.

FIG. 5.

The flow of a dumbbell. Left: The dumbbell with mean curvature coloring. Right: The diffeomorphic mean curvature flow with σ = 0.3 and T = 1.

FIG. 6.

Comparison of flows for the dumbbell in Figure 5. Left: Diffeomorphic mean curvature flow with σ = 0.1 and T = 0.25. Right: Mean curvature flow with T = 0.25.

Dumbbell with asymmetric ends

To illustrate typical problems encountered in real applications, we constructed a dumbbell shape with asymmetric ends. Figure 7 shows promising results. For classical mean curvature flow, the smaller end vanished quickly unlike in the diffeomorphic mean curvature flow.

FIG. 7.

Comparison of flows for a dumbbell with asymmetric ends. Left: The dumbbell with asymmetric ends. Middle: Mean curvature flow for T = 0.025. Right: Diffeomorphic mean curvature flow with kernel size σ = 0.1 and T = 0.025.

Cortical surfaces

Figure 8 illustrates the application of diffeomorphic and classical mean curvature flows to a superior temporal gyrus cortical surface [35]. The voxel resolution of the image volume from which this surface was generated was 1 mm³. For the diffeomorphic flows we used a kernel size of σ = 0.3. For surfaces with boundary, we simply flow the boundary vertex along with the closest interior vertex. The top row indicates the smoothing effect of both flows. Magnified views of a crest region of the surface indicate that mean curvature flow results in singular folds unlike diffeomorphic flows. Furthermore, the left-hand panel of Figure 9 shows that Hausdorff distances between the original surface and the final surfaces are within one voxel. The smoothing effect of the flows is also reflected in the mean curvature histograms in the right-hand panel of Figure 9.

FIG. 8.

The top row shows STG cortical surfaces at T = 0 (left), T = 1 with mean curvature flow (middle), and T = 1 with diffeomorphic mean curvature flow using σ = 0.3 (right). Mean curvature is indicated by the vertical color bar. The bottom row shows the corresponding magnified view of the crest on the STG which is a subset of the region within the black borders indicated in the top row. The irregular color pattern in the magnified view of the mean curvature flow indicates that singularities occurred during the evolution with triangles crossing over.

FIG. 9.

Left: Cumulative density function profiles of the oriented distances between the original surface and final surfaces. Right: Mean curvature histograms of the original and final surfaces at T = 1.

6. Discussion

In this study, we proposed diffeomorphic surface flows as an alternative to classical mean curvature and Willmore flows. We obtained the flow equation for the elastic energy of a closed surface and proved the short-time existence and uniqueness of the flow. Then we examined the diffeomorphic mean curvature flow both by analyzing the case of a surface of revolution and by numerical experiments on arbitrary discrete surfaces. Our conjecture is that the solution continues to be well behaved for long times while preserving some of the characteristics of classical mean curvature flows (such as smoothing and decreasing area).

Furthermore, in computational anatomy applications, diffeomorphic surface flows can be used to evolve submanifolds of the brain such as planum temporale, superior temporal gyrus (STG), and cingulate cortical surfaces in neuroimaging studies of schizophrenia and auditory disorders. They can also be used for smoothing where the speed is controlled by changing the kernel size without changing the topology.

Diffeomorphic flows, while they clearly avoid topological changes, cannot, however, be considered as smoothing flows. Since they generate a diffeomorphic evolution, they cannot make a surface smoother (in terms of the number of derivatives) than it was initially. In particular, they cannot deal with surfaces corrupted by white noise. They can, however, have some smoothing effect, in the sense that they reduce the curvature of the surfaces on which they operate. There is an important scale factor in this regard, related to the scale of the kernel. Bumps larger than the kernel size will in general be removed in a way similar to classical flows, whereas small bumps are likely to survive after long time intervals. The choice of the kernel size therefore needs to be adapted to the roughness of the surface.

Several open problems remain. Among the numerical issues, there is a need to improve the discretization methods, especially in the case of the Willmore flow for which the computation of higher derivatives is a potential source of instability.

We have already mentioned the issue of long-term existence of the flow. As discussed in this paper, this requires controlling the smoothness of the surface during the evolution, which is made difficult by nonlocal interactions. The limit behavior of the evolution as the kernel size tends to zero is another open problem. It seems reasonable to expect that it should somewhat resemble the classical flows, but the nature of the convergence (and proof) needs to be investigated.

Another interesting issue, related to long-term evolution, is to characterize the limit shapes of the shrinking surfaces for the diffeomorphic mean curvature flow. Our experiments seem to indicate that such limit shapes exist and are not restricted to spheres.

It would be interesting also, for theoretical and practical purposes, to consider numerical schemes in which the kernel size is allowed to evolve with time, starting with a rigid evolution and progressively decreasing spatial smoothing to get closer to the mean curvature flow. The question here is to define sufficient conditions for such an annealed scheme that ensure a diffeomorphic evolution while providing a smoothing effect similar to that of the standard mean curvature flow.

While these topics provide interesting sources of future work, diffeomorphic surface flows already represent a promising family of surface evolutions. Initial experiments in this paper demonstrate several important features, regarding, in particular, the absence of topological change, that make them appropriate for a large range of practical situations.