Molecular dynamics simulations and coupled nucleotide substitution experiments indicate the nature of A·A base pairing and a putative structure of the coralyne-induced homo-adenine duplex

Abstract

Coralyne is an alkaloid drug that binds homo-adenine DNA (and RNA) oligonucleotides more tightly than it does Watson–Crick DNA. Hud’s laboratory has shown that poly(dA) in the presence of coralyne forms an anti-parallel duplex, however attempts to determine the structure by NMR spectroscopy and X-ray crystallography have been unsuccessful. Assuming adenine–adenine hydrogen bonding between the two poly(dA) strands, we constructed 40 hypothetical homo-(dA) anti-parallel duplexes and docked coralyne into the six most favorable duplex structures. The two most stable structures had trans glycosidic bonds, but distinct pairing geometries, i.e. either Watson–Crick Hoogsteen (transWH) or Watson–Crick Watson–Crick (transWW) with stability of transWH > transWW. To narrow down the possibilities, 7-deaza adenine base substitutions (dA→7) were engineered into homo-(dA) sequences. These substitutions significantly reduced the thermal stability of the coralyne-induced homo-(dA) structure. These experiments strongly suggest the involvement of N7 in the coralyne-induced A·A base pairs. Moreover, due to the differential effect on melting as a function of the location of the dA→7 mutations, these results are consistent with the N1–N7 base pairing of the transWH pairs. Together, the simulation and base substitution experiments predict that the coralyne-induced homo-(dA) duplex structure adopts the transWH geometry.

INTRODUCTION

DNA intercalators are typically planar molecules that bind between adjacent base pairs in nucleic acid structures. By binding to DNA, intercalators have been shown to alter or inhibit DNA synthesis, translation, and protein expression (1,2). These properties are likely associated with their potential mutagenicity (3). The distinct binding properties of intercalators can also be harnessed to create novel molecular assemblies (4), as diagnostic probes (5) and as DNA directed therapeutics (6–11). Hence, there is considerable interest in understanding the nature of nucleic acid structural transitions associated with intercalation.

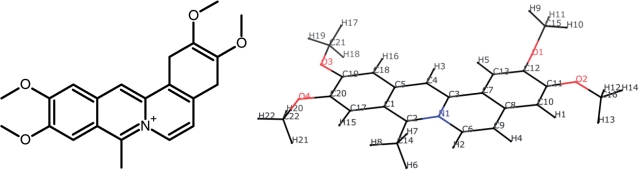
Coralyne (Figure 1) is an anti-leukemic agent whose anti-cancer activity is likely related to its ability to intercalate DNA (12,13). Coralyne also stabilizes DNA in the topoisomerase complex and inhibits the activity of this enzyme (14). To better understand the mechanisms of action of coralyne and ultimately how to design better intercalators targeting DNA, structural studies are clearly necessary. However, no structure has been determined for coralyne bound to DNA. In this research, we specifically focused on interactions of coralyne with homo-(dA) and tried to assess possible structures of coralyne-bound homo-(dA) duplexes.

Figure 1.

The molecular structure of coralyne (left) and its structure after ab initio geometry optimization (right) at the HF/6-31G* level. Atom names used in this work are shown on the right (where the first letter denotes the atomic symbol) with oxygen colored red and nitrogen blue. Supplementary Table S1 provides further details on the structure and the coralyne force field used in the simulations.

Coralyne interaction with DNA is somewhat unique compared to other DNA binding molecules since it binds tightly to homo-(dA) sequences, as well as double-stranded DNA, DNA triplexes and homo-(rA) duplexes (15–22). The Hud lab previously demonstrated the selective binding of coralyne to homo-(dA) oligonucleotides and polymers (16,23,24). The coralyne-bound homo-(dA) duplex exhibits a single and cooperative melting transition around 50°C which implies that the structure is a single component. They also proved that coralyne binds to the homo-(dA) self-structures at a maximum molar ratio of one coralyne per four adenine bases (23). Coralyne binding promotes the formation of anti-parallel homo-(dA) duplexes with a helical structure that is compatible with flanking Watson–Crick B-form helices (16,23,24). As the coralyne-stabilized homo-(dA) duplex is not stable below pH 5.0, this structure is distinct from the poly(rA) parallel-stranded duplex formed at low pH (25). Not only is the strong affinity towards homo-(dA) oligonucleotides unusual, the binding constant for the association of coralyne and homo-(dA) is 1.05 × 10⁵ M⁻¹, which is almost eight times greater than the binding constant between coralyne and calf thymus DNA (1.25 × 10⁴ M⁻¹) (15).

The structure of the homo-(dA) duplex with coralyne has not been determined, but this is not due to a lack of effort. Specifically, the Hud laboratory has made several attempts to determine the structure (Persil, Plavec and Hud, unpublished data). In one set of experiments, NMR spectroscopy was used to study the binding of coralyne to duplexes formed with d(A)₈–d(A)₈ mismatches between flanking Watson–Crick duplexes. This system was previously used to confirm the strand number and the strand orientation (anti-parallel) of the coralyne-induced homo-(dA) structure using CD spectroscopy (16). However, coralyne was found to be in exchange with this DNA duplex on the intermediate NMR time scale. As a consequence, most DNA aromatic and coralyne ¹H resonances were too broad to allow structural determination (16). NMR spectra collected during the titration of coralyne into a sample of this duplex suggested that coralyne moves between multiple sites within the homo-(dA) mismatches, as the movement and broadening of DNA resonances could not be fit by a model in which a single site (out of four putative binding sites) was preferentially loaded first by coralyne. This apparent movement between sites with increasing coralyne concentration also exasperated an attempt to localize binding sites based upon measuring changes in chemical shifts, an approach that is fruitful if only a small number of resonances exhibit significant line broadening during small molecule titration (11). In an attempt to circumvent these problems, additional duplexes were constructed where the homo-(dA) regions within the same flanking Watson–Crick duplex were reduced to (dA)₄ and (dA)₂, thereby limiting the possible coralyne sites within A·A base pairs to two and one, respectively. Similar difficulties with resonance line broadening again frustrated attempts to determine a solution-state structure. Attempts to crystallize DNA oligonucleotides with A·A mismatches in the presence of coralyne have also proven unsuccessful.

As an alternative to NMR and crystallography, biomolecular simulation and modeling methods were applied in an attempt to narrow down the possibilities and to better understand the interaction of coralyne with homo-(dA) duplexes. This differs from standard approaches to nucleic acid structure prediction based on secondary structure predictions where fragments (26–28), coarse-graining (29,30), or user manipulations (31–33) are used to build up 3D models (34). Instead, as DNA duplex structure is straightforward to build, we built and modeled multiple plausible base-paired B-DNA duplex geometries. Restrained and unrestrained molecular dynamics (MD) simulation with implicit and explicit solvent attempted to sample the free-energy surfaces around the model geometries. Although this approach was tractable due to the constraints imposed by the anti-parallel geometry of the coralyne-induced homo-(dA) duplex and access to large-scale computational resources, this brute-force modeling required more than three years of work, was rather tedious, and the results are not easily amenable to full validation. Although the proposed model is plausible and fits the known experimental and simulation data, it is clear that the methods cannot yet be considered fully predictive or routine.

COMPUTATIONAL APPROACH

Modeling the base pairings between adenine-bases

Based on previous experimental results suggesting that the coralyne-bound homo-(dA) duplex within the context of flanking B-DNA duplexes is only stable when the strands are anti-parallel (16), similarity to B-DNA was assumed. Based on the clean melting profile, it was also assumed that the adenine bases would very likely have 1:1 base pairing between the two strands. Nevertheless, there are still many ways for two adenine bases to base pair. To further narrow the possibilities, base pairings involving the protonation of one or both adenine bases were ignored since the coralyne-induced homo-(dA) self-structure does not form below pH 5.0 (16). Moreover, as irregular hydrogen bonds (H-bonds)—specifically bifuricated, water-inserted, or C-H involving H-bonds—are rare in DNA duplexes, these were also excluded. These assumptions drastically reduced the number of possible base pairs to investigate (Supplementary Figure S1).

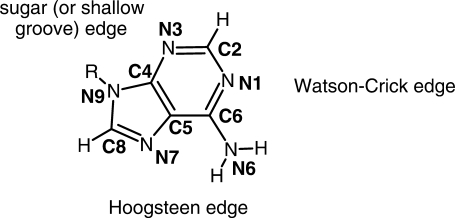
According to base pairing rules (35,36) expanded by Leontis and Westhof (37,38) four factors need to be considered in the construction of base pairs: base-sugar conformation, glycosidic bond orientation, interacting edges, and local strand orientation. Base-sugar conformation is mainly determined by the dihedral angle of the glycosidic torsion χ (O1′-C1′-N9-C8), where the bases adopt either the syn or anti conformation with respect to the sugar of the nucleotide. The glycosidic bonds that connect the bases to the sugar and backbone can either be oriented on the same side (cis) or the opposite side (trans) with respect to plane of base-pairs. The three interacting edges are classified Watson–Crick (W), Hoogsteen (H) or shallow groove (S) edges (Figure 2). Local strand orientations simply fall into either parallel or anti-parallel.

Figure 2.

The 2D structure of an adenine base with its heavy atom names depicting the base edges.

All possible H-bonding pairs between the four nitrogen acceptors (N1, N3, N7 and N9) and the remaining nitrogen (N6) were considered. After omitting base pairs with steric clash with the backbone, only 11 possible donor-acceptor combinations remain (Supplementary Figure S1). At least six (transWW, transWH, transHH, cisWW, transHS and cisHS) out of the 11 bp have been observed in natural RNAs (39–42). For anti-parallel duplexes, if the two bases can overlap after rotating around the base on the plane of the base-pair, the base-sugar conformations should be either anti–syn or syn–anti. If they cannot, they should be either anti–anti or syn–syn. All the plausible combinations of H-bonds, base-sugar, and glycosidic bond orientations are listed in Table 1 and are shown in Figure 3. For convenience, a specific base-pair will be referred to by its base-sugar conformation and its (abbreviated) interacting edges. For example, cisWH indicates that the backbones are on the same side, or cis, of the base pair plane and the interacting edges of the base pairs are one Watson–Crick edge and one Hoogsteen edge.

Table 1.

The complete set of adenine base pairs between two adenine bases and their conformational properties

Base-sugar conformation	Glycosidic bond orientation	Interacting edges	Number of H-bonds	Symmetry of the H-Bond(s)
Anti–Anti or Syn–Syn	Cis	W/W	1	No
Anti–Anti or Syn–Syn	Cis	H/H	1	No
Anti–Anti or Syn–Syn	Cis	W/S	1	No
Anti–Anti or Syn–Syn	Trans	W/H	2	No
Anti–Anti or Syn–Syn	Trans	H/S	1	No
Anti–Syn or Syn–Anti	Cis	W/H (type a)	1	No
Anti–Syn or Syn–Anti	Cis	W/H (type b)	1	No
Anti–Syn or Syn–Anti	Trans	W/W	2	Yes
Anti–Syn or Syn–Anti	Trans	H/H	2	Yes
Anti–Syn or Syn–Anti	Trans	W/S	1	No
Anti–Syn or Syn–Anti	Cis	H/S	1	No

The classifications define the orientation of the glycosidic bonds (cis or trans), the interacting edges [Watson–Crick (W), Hoogsteen (H) or shallow groove (S) and the base-sugar conformation which is dependent on the local strand orientation (anti–syn, syn–anti, anti–anti, or syn–syn)].

Figure 3.

The repetitive units composed of four adenine bases in homo-(dA) duplexes. The arrows between base pairs indicate the ‘symmetry’ property of the H-bonds. Single arrows are non-symmetric H-bonds and double arrows are symmetric H-bonds, respectively. (The directions of the arrows are arbitrary.) ‘A’ indicates an anti base-sugar conformation and ‘S’ indicates a syn base-sugar conformation. The nomenclature chosen to denote each homo-(dA) duplex contains multiple pieces of information about the structure. The information is separated by hyphens, the first part denotes the type of the base pair, and the second and the third parts denote whether the base pairs are alternating and whether the base pairs are reversed, respectively. ^aBase-sugar conformation, ^bSymmetricity of the H-bond(s), ^cAlternating H-bond, ^dAlternating base-sugar conformation, ^eDuplexes belonging to the category.

Modeling the structures of homo-(dA) duplexes

As a compromise between the computational load and the size of the model, 12-mer homo-(dA) strands were modeled; this is consistent with the previous experimental work that suggests that the length of the homo-(dA) sequence should be at least eight bases (and preferably longer) to induce the characteristic complex (16). In building the homo-(dA) duplex models, choices had to be made regarding assignment of the 11 possible types of the base pairings (Supplementary Figure S1) to the individual 12 bp in the homo-(dA) duplex. Clearly, building 11¹² different combinations of base pairings is not feasible. As coralyne binds the homo-(dA) duplexes at a ratio of one coralyne per four bases, maximally, this supports limiting models to repeats of regular structure at the base pair or base pair step level. Further simplification involved the assumption that only a single type of A·A base pairing would occur within a given structure. A rationalization for this is that adjacent base pairs tend to maximize their overlap. At the base pair step level, it is also possible that the homo-(dA) duplex could have either alternating or non-alternating base pairs while still retaining the regular base pair step structure. The alternation is caused by the lack of symmetry from either non-symmetric H-bonds or non-symmetric base-sugar conformations. This leads to two different orientations for the base pairs. In a homo-(dA) duplex with alternating base pairs, the two base pairs alternate the direction of the hydrogen bonding. For cisWH (both type a and b), transWS and cisHS, there is one additional complication when building the structures. These pairing structures have non-symmetric H-bonds and also their base-sugar conformations are not symmetric. Therefore, the base pairs can have four combinations because both the base-sugar conformation and the H-bond can be alternating. To distinguish these, two of the four are denoted as ‘reversed’ (or -rev, see Figure 3) with respect to the other. Reversed pairs refer to the pairs with shorter distances between their backbones. We will also refer to the syn–syn base pairs as ‘reversed’ with respect to the anti–anti base pairs for cisWW, cisHH, cisWS, TransWH and transHS. Based on all restrictions described, 40 different structures of the homo-(dA) duplex were built and modeled (Figure 3).

METHODS

Computational methods

All of the models depicted in Figure 3 were built close to idealized B-DNA geometries in the absence of coralyne as described in detail in the Supplementary Data. Simulations were then performed on all of the models using the AMBER8-10 program suites (43,44) with the ff99 and ff99-bsc0 force fields (45,46). As none of these duplexes has been observed experimentally in the absence of coralyne, restraints enforcing H-bonds between the two strands were applied. The models were simulated in implicit solvent with a generalized Born treatment in molecular dynamics (MD) simulation on the nanosecond time scale and their solvation free energies were compared using MM-PBSA (47,48). On the basis of this initial investigation, a subset of ‘stable’ homo-(dA) duplexes were selected for further modeling. In each of these models, coralyne molecules were incorporated either binding in the minor groove or as intercalators between base pairs. With intercalation, many different orientations were investigated. These models were evaluated in another round of MD simulations in implicit solvent. Analysis of MM-PBSA energetics, hydrogen bond occupancy and other properties further pruned the set of models to investigate. This divide-and-conquer approach, removing models that behaved poorly, continued with the addition of more coralyne molecules binding in analogy with the successful binding modes. At this point the remaining models were solvated in TIP3P water (49) and MD was performed. H-bond occupancies, relative orientation of the inserted coralyne molecules, and the free energies calculated by the MM-PBSA method were utilized as approximate metrics to estimate relative stability of the models. Complete details outlining the procedure are supplied in the Supplementary Data.

Experimental materials and methods

Coralyne chloride was purchased from Sigma and the concentrations of stock solutions in H₂O were determined spectrophotometrically by using ε₄₂₀ = 14 500 M⁻¹cm⁻¹. The unmodified oligonucleotides were purchased from Integrated DNA Technologies (IDT). Modified oligonucleotides were synthesized on an Expedite 8909 DNA synthesizer. 7-Deaza-dA-CE Phosphoramidite was purchased from Glen Research and used as received. All of the oligonucleotides were purified by HPLC, desalted and characterized by mass spectroscopy. Concentrations of the stock solutions were calculated by the using the following extinction coefficients for the unmodified oligonucleotides: (i) 5′-d(GAC CCG CAA AAA AAA CCT CGC C)-3′, ε₂₆₀ = 212 100 M⁻¹ cm^−1; (ii) 5′-d(GGC GAG GAA AAA AAA GCG GGT C)-3′, ε₂₆₀ = 231 900 M⁻¹ cm⁻¹. All the samples were 60 µM in adenine base (only the adenines in the middle counted) and 15 µM coralyne. The samples were prepared in 20 mM NaCl and 1× BPE (1 mM Na₂EDTA, 6 mM Na₂HPO₄ and 2 mM NaH₂PO₄) at pH 7.

CD spectra were acquired on a JASCO J-810 CD spectropolarimeter equipped with a Peltier temperature control unit. Spectra were acquired using a 5-mm strain-free rectangular cell. CD melting profiles were acquired as full spectra from 5 to 95°C in 1°C steps, at 1°C/min. Melting curves were obtained by fitting each spectrum to a two-state model of a linear superposition of the 5°C and 95°C spectra.

RESULTS AND DISCUSSION

Modeling the coralyne-free homo-(dA) duplexes with restraints in implicit solvent

Before attempting to model the structure of coralyne-induced homo-(dA) duplexes, we built the 40 anti-parallel homo-(dA) duplex structures depicted in Figure 3 (in the absence of coralyne) and investigated their structural stability. Based on the results of short MD simulations (with applied H-bonding restraints), we pruned the set of possible duplex structures for further investigation. Many of the 40 initial models were highly unstable in restrained MD simulation. Six of the duplex models maintained high H-Bond occupancies and planar base pairs and these were chosen for further study, specifically: cisWH(a), cisWH(b)-alt, transHH, transWH, trnasWS and transWW. Further details on the selection process are described in the Supplementary Data. We note that since homo-(dA) duplexes in the absence of coralyne have not been observed experimentally, our implied assumption that the relative stabilities of the duplexes should mirror those of the coralyne complex is the most weakly supported assumption of the initial modeling efforts. However, as the number of plausible models is so large, particularly with the inclusion of coralyne, it was necessary to reduce our investigation to a tractable set. At the end of this section, further discussion is provided that probes the validity of this initial assumption.

Homo-(dA) duplex-coralyne complexes in implicit solvent

One coralyne was inserted into each of the six chosen homo-(dA) duplex model structures. The final snapshot from the previous 1 ns MD simulations of the homo-(dA) duplexes were taken and coralyne molecules were placed in the center of the duplexes (surrounded by residues 6, 7, 18 and 19). Both groove binding and intercalating model structures were built separately. For the intercalative models, the coralyne molecules were placed into multiple orientations rotating the coralyne along the stacking plane from 0° to 360° at 45° intervals; as many of the different coralyne orientations converged to approximately two to three common angles, 45° intervals was deemed sufficient. Flipped coralyne models were also built. For each model, MD was performed for 3 ns with full base pair restraints. This was deemed necessary to stabilize the coralyne free parts of the helix. To evaluate the models, the binding free energies of the coralyne and the homo-(dA) duplexes were calculated using the MM-PBSA method (Table 2 and Supplementary Table S5). The binding free energy, ΔG, is given by G_com − G_rec − G_lig, where the free energies are calculated using the partial structures [com: homo-(dA) and coralyne complex, rec: homo-(dA) duplex, lig: coralyne] of each snapshot and averaged over the whole interval. The entropic contributions were not calculated. However, as the entropic contributions among the same duplexes are nearly identical, their exclusion does not affect the ranking of the binding energies as long as they are compared within the same duplex. The calculations suggest that the groove binding models were not as favorable as the intercalation models. The ΔG_binding for the groove binding models was never more favorable than −15 kcal/mol (see Supplementary Table S5 for details), whereas the intercalation models ranged from −20 to −30 kcal/mol (Table 2 and Supplementary Table S6). Assuming rotational/translational entropic losses in the range of ∼12–15 kcal/mol upon binding (50), this clearly disfavors minor groove binding and places the intercalation binding free energies closer to the range of experiment. Based on this, the groove binding models were excluded from further analyses. Subsequently, the restraints on the base pairs adjacent to the coralyne (between residue 6 and 19 and between residue 7 and 18) were removed for the intercalation models and another 3 ns of MD simulations were carried out and the total 6 ns MD simulations were analyzed. To describe the models, a notation was devised. This notation specifies the type of homo-(dA) duplex structure, the number of coralyne molecules, and the initial coralyne angles, all separated by hyphens. The coralyne angle is an index indicating the relative orientation of the coralyne molecule to the neighboring base pairs (see the Supplementary Data for the definition). Addition of ‘-f ’ denotes a flipped coralyne whereas omission means the coralyne is not flipped. For example, transWH-c1-180d-f denotes the base pair type (transWH), the number of coralyne molecules (1), the initial degree of the coralyne angle (180°), and that the coralyne was flipped.

Table 2.

Calculated binding free energies (ΔG) and hydrogen bond occupancies of selected intercalation binding models

Complex	H-bond occupancy (%)		ΔG (kcal/mol)		Coralyne angle (°)
	Res 6–19	Res 7–18	Avg	Dev	Avg	Dev
cisWH(a)-c1-270d	42.3	63.8	− 25.33	3.42	216.78	6.73
cisWH(b)-alt-c1-45d	75.5	82.0	− 28.01	2.75	10.03	5.05
transHH-c1-0d	56.8	58.9	− 26.15	3.47	22.25	7.03
transHH-c1-225d	58.3	59.6	− 25.46	3.66	219.93	15.55
transWH-c1-45d	59.0	66.8	− 26.53	3.72	29.78	17.06
transWH-c1-180d	61.2	59.8	− 32.48	3.12	193.57	5.81
transWH-c1-270d-f	53.9	59.7	− 27.39	3.77	184.24	13.07
transWS-c1-45d-f	45.4	57.9	− 25.02	4.28	336.51	7.25
transWW-c1-0d	63.8	62.9	− 28.73	2.95	344.21	3.85
transWW-c1-135d-f	57.3	64.3	− 31.06	2.73	148.89	4.93
transWW-c1-315d-f	61.1	64.4	− 29.68	2.74	325.29	4.09

Only the polar and non-polar contributions of the free energies were calculated. The free energies of the complex [homo-(dA) duplex and coralyne], receptor [homo-(dA) duplex] and ligand (coralyne) were calculated using the partial structures extracted from the same snapshots. ΔG was averaged over the final 1 ns period. The naming convention of the complexes is explained in the text. The occupancies of the H-bonds were calculated separately for the two base pairs (between residue 6 and 19 and between residue 7 and 18).

Not all of the structures investigated were stable in MD simulation. Specifically, the coralyne in the cisWH(a)-c1-315d-f, transHH-c1-315d and transWH-c1-135d-f model structures exited the intercalation pocket during the initial 1 ns of MD. The origin of this instability was not investigated deeply and could result from poor initial model building and/or instability of the bound model with that particular type of duplex; the removal of these duplex structures at this stage is a limitation in the present work. The remainder of the complexes did not show obvious irregularities. To evaluate the various model structures of the homo-(dA) duplex-coralyne complex, the following properties were measured: the average occupancy of the H-bonds, the coralyne binding free energy, and the coralyne angle. The results over the last 1 ns of the MD simulations are shown in Table 2 and Supplementary Table S6. Some of the structures maintained an average H-bond occupancy of over 50% even after removing the restraints on the base pairs neighboring the coralyne, but some did not. In an attempt to avoid pruning too many models, structures with > 40% average H-bond occupancy for both base pairs (above and below the coralyne) were selected for further study. During the MD simulation, the coralyne molecules reoriented (generally to ∼0 or ∼180°) to maximize overlap; this implies that specific base pairs prefer their specific coralyne angles.

To prune further, structures with the lowest coralyne binding energy were chosen from the set of structures with an average H-bond occupancy over 40%. The selected complexes are shown in Table 2 with the full data reported in Supplementary Table S6. When selecting the models, the restraint energy was neglected; this is justified since the restraints were applied to maintain the helix geometry in the absence of coralyne, they were generally comparable, and also since the low energy selection was typically performed within a given helix type.

Homo-(dA)-coralyne complexes in explicit solvent

To more accurately investigate the structures of the complexes, four additional coralyne molecules, consistent with the experimental stoichiometry of one coralyne per four bases (23), were inserted into the models listed in Table 2 and the structures were solvated in TIP3P water. To avoid violating the neighbor exclusion principle (51), four coralynes were placed at every other intercalation pocket, specifically those formed by (residue 2, 3, 23 and 22), (residue 4, 5, 21 and 20), (residue 8, 9, 17 and 16) and (residue 10, 11, 15 and 14). The average coralyne angles in Table 2 were imposed on the newly inserted coralynes. With a full set of base pair restraints, MD simulation was performed for 3 ns after the initial minimization and equilibration. Afterwards, restraints on all the base pairs neighboring the coralynes were removed—only the terminal restraints remained—and followed by an additional 3 ns of MD. Finally, additional MD simulations of 6 ns duration were continued without restraints for a total of 12 ns of MD simulations on each model structure.

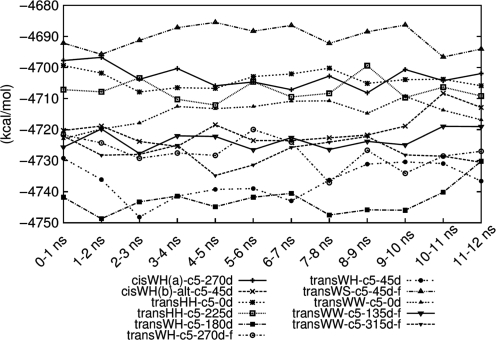
The free energies of the complexes were calculated using the MM-PBSA method (Figure 4). The absolute free energy value itself means little because the reference (or zero of the) free energy of the MM-PBSA method is strongly dependent on the force field employed. However, the relative free energy is useful for approximately ranking the relative stability of the complexes. Moreover, it is useful for computing the binding free energies of the reaction,

Figure 4.

The absolute free energies [E_MM + G_polar + G_non-polar − T(S_trans + S_rot + S_vib)] of the 5-coralyne-homo-(dA)-duplex’s complexes calculated by MM-PBSA. Although the standard deviations are large and range from 20 to 25 kcal/mol (unlike the standard errors which decrease as more configurations are averaged), the averages are robust. In general, the complexes located lower in the plot are more stable in water than those that are located higher.

5 coralyne + 2 single-stranded homo-(dA) → 5-coralyne-homo-(dA)-duplex complex

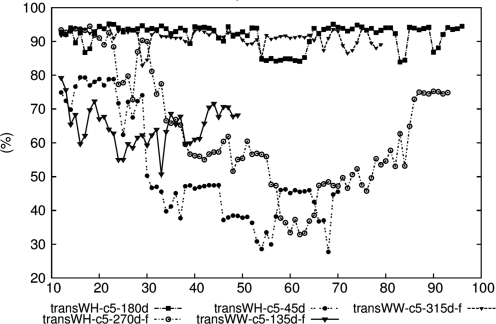
which are estimated via ΔG_binding = G_complex − 5G_coralyne – 2G_{single-stranded homo-(dA)}. Assuming the 5G_coralyne and 2G_{single-stranded homo-(dA)} values are identical for each of different models, i.e. independent of the complex, we can assume that ΔG_binding = G_complex + c where c is a constant. Therefore, the difference of the free energies of any two complexes (ΔG_complex) is same as the difference of the binding energies of any two reactions (ΔΔG_binding). However, this does not allow us to determine the sign of ΔG_binding. We discuss the absolute value of ΔG_binding in the Supplementary Data. Generally, the free energies of the complexes did not fluctuate significantly regardless of whether the restraints were applied during the MD simulations or not. The complexes could be ranked according to their estimated free energies. The transWH-c5-180d and transWH-c5-45d-f structures were the most stable among the complexes. The transWW-c5-315d-f, transWH-c5-270d-f, and transWW-c5-135d-f structures followed next. The duplexes with single H-bonded base pairs (cisWH(a) and transWS) generally bound coralyne less strongly than other duplexes.

The coralyne angles were also measured to determine if each coralyne molecule was oriented in the same manner. The results are described in the Supplementary Data. Briefly, unstable coralyne angles were only observed at the terminal coralynes. As instability at the terminal could suggest gradual destruction of the duplex, longer MD simulation was subsequently applied.

The average occupancy of the H-bond between the bases adjacent to the coralyne molecules tended to decrease as time elapsed (Supplementary Figure S8). The pronounced drops after 3 ns, for all conformations, were caused by the removal of restraints. Base pairs with a single H-bond (cisWH(a)-c5-270d and transWS-c5-45d-f) did not maintain the high occupancy compared to the others. Generally the energetically more stable structures in MM-PBSA analysis had higher H-bond occupancy. However, with each of the complexes the average occupancy of the hydrogen bond did not appear to reach a plateau, suggesting that longer simulations are required.

In the initial MM-PBSA analysis, the free energies span a range of ∼50 kcal/mol. Because of this wide range, it was assumed that choosing the five model structures with the lowest energies would not risk elimination of the most stable structure. As a result, we chose transWH-c5-180d, transWH-270d-f, transWH-45d, transWW-c5-135d-f and transWW-315d-f and carried out longer MD simulations (without the restraints on the base pairs). The selected model structures had narrow ranges of the coralyne angles and had high average H-bond occupancies, which implies that structural stability accompanies the energetic stability. Along with the extension of the MD simulation, the ff99-bsc0 modifications were tested for comparison as well. ff99-bsc0 is a refined force field of ff99 which represents more realistic population of α/γ backbone torsions of homo-nucleotides (46). The MD simulations were extended up to at least 40 ns.

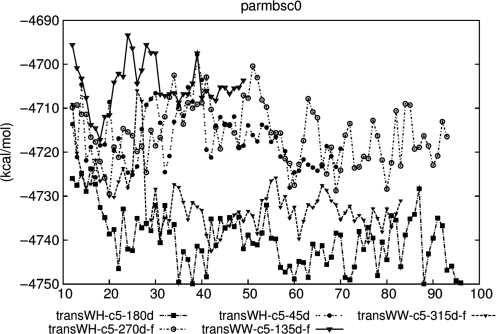
The order of the free energy values for the selected model structures showed little variance in the extended MD period when ff99 is continuously applied (Supplementary Figure S9). However, the apparent downward shift of the free energy of transWW-c5-315d-f was observed with the ff99-bsc0 force field after 28 ns (Figure 5) and this shift in energy is large relative to the 50 kcal/mol cutoff which is a potential limitation. At the same time, transWH-c5-45d became energetically less stable than transWW-c5-315d-f. Interestingly, a separation of values for transWH-c5-180d and transWW-c5-315d-f from the rest of the group was observed with ff99-bsc0. As well as the change in order, there were differences in the absolute value of the free energies between the two force fields. Basically ff99-bsc0 modifies the backbone torsions slightly but its Hamiltonian does not differ very much from ff99’s. Therefore, large conformational changes are presumed to contribute mainly to the shift of the absolute values, which also implies that there were abnormal transitions of α/γ torsions in the ff99 simulations. Coralyne angles were also measured and good angle distributions corresponded to favorable free energies (Supplementary Data). In summary, longer MD simulations in explicit solvent with both force fields consistently ranked the transWH geometries as the most favorable, followed by the transWW geometries.

Figure 5.

The free energies of the selected model structures during the extended MD period. The units of the x-axis are nanoseconds of MD simulation with the ff99-bsc0 force field.

The average occupancies of the H-bonds were analyzed and the results are illustrated in Figure 6 and Supplementary Figure S10. The transWH-c5-180d and transWW-c5-315d-f models maintained high occupancy most of the time with both force fields, whereas transWH-c5-270d-f showed discrepancies between the two force fields. The occupancy of the structure was relatively high in ff99 while it was low and fluctuated with ff99-bsc0. The occupancy should be compared to the control homo-(dA) duplex which does not have intercalated coralyne, as the homo-(dA) duplexes become unstable without coralyne (Supplementary Figure S11).

Figure 6.

The average occupancies of the H-bonds of selected model structures during the extended MD period. The H-bond occupancy (%) is on the y-axis and the time in nanoseconds is on the x-axis. The data is with the ff99-bsc0 force field.

Summarizing the three analyses, only the transWH-c5-180d and transWW-c5-315d-f model structures show high energetic stability, consistently aligned coralynes and high H-bond occupancy. For these model structures, the results were consistent between the two force fields. The major difference between ff99 and ff99-bsc0 comes from the results of transWH-c5-270d-f. In ff99, transWH-c5-270d-f showed moderate stability, but ff99-bsc0 did not show this stability. This implies that the structure was potentially over-stabilized by the α/γ artifact of ff99. Absolute free energies of the structures violating neighbor exclusion principle (i.e. with seven coralyne molecules) as well as structures with five coralyne molecules were also estimated (Supplementary Data). Although these estimations were not very successful, interpretations regarding the relative stabilities of the structures are still valid.

Base substitution experiments

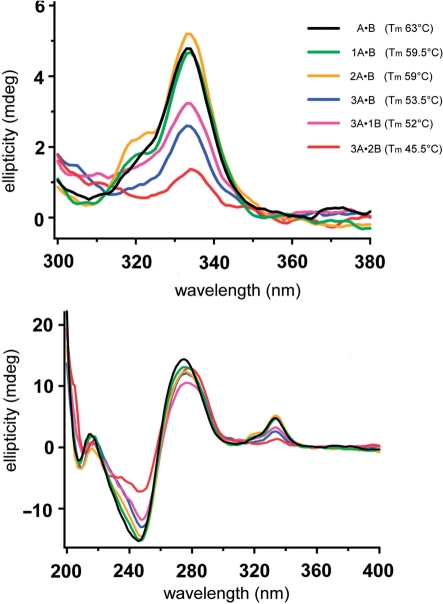
To partially test the reliability of the predictions from simulation, we turned to base substitution experiments. As the N6 nitrogen of adenine is the only hydrogen bond donor, it is involved in every known A·A base pairing structure, and therefore believed essential to the coralyne-induced duplex. Therefore, to test for putative base pairings, it makes sense to mutate away one or more of the hydrogen acceptors, specifically N1, N3 or N7 (Figure 2). The most obvious first target is removal of the N7 atom of adenine as this is involved in only two mono-hydrogen bonded base interactions [cisHH and cisWH(a); Supplementary Figure S1B and S1F] and two out of three of the di-hydrogen bonded base interactions including those with one N7 (N1 and N7) or two N7 interactions (transWH and transHH; Supplementary Figure S1D and S1I). Moreover, it is involved in only one of the putative low energy structures found in simulation (transWH), unlike N1 which is involved in both and N3 which is involved in neither. To test the importance of the N7 hydrogen bond acceptor in the coralyne-induced home-(dA) duplex, 7-deaza-adenine (dA→7) substitutions were made at different places in the homo-(dA) sequence and their effect on the binding of coralyne and duplex thermal stability were assessed using the previously developed coralyne-homo-(dA) duplex with eight adenine–adenine mismatches embedded in seven Watson–Crick base pairs at both ends (16). The duplex sequence is provided in Table 3 as (A·B). Within this parent system, deoxyadenosine residues at specific positions were replaced with 7-deaza-deoxyadenosine residues (dA→7), and the stability of these duplexes was investigated in the absence and presence of coralyne. The complete list of melting temperatures is given in Table 3 for the parent and all substituted duplexes. In the absence of coralyne, the Tm of all duplexes investigated was the same within experimental error (±1.5°C), even with up to six dA→7 substitutions. In contrast, there is a clear Tm decrease for the modified duplexes in the presence of coralyne. For example, the Tm of the duplex decreased from 63°C, for the parent A·B duplex, to 59.5°C for 1A·B and 53.5°C for 3A·B, duplexes with only one and four dA→7 substitutions, respectively. Further destabilization, with a reduction in Tm to 45.5°C, was observed upon the incorporation of additional 7-deaza-deoxyadenosine residues across from each other in the two strands of a duplex (e.g. 3A·2B).

Table 3.

Melting temperatures of DNA duplexes in the presence and the absence of coralyne (Supplementary Figure S18)

Name	Sequence	Tm (°C) w/o coralyne	Tm (°C) with coralyne
(A·B)	5′-_______AAAAAAAA_______-3′	34.5	63.0
	3′-_______AAAAAAAA_______-5′
	One substitution
(1A·B)	5′-_______AAAA7AAA_______-3′	34.5	59.5
	3′-_______AAAAAAAA_______-5′
(A·1B)	5′-_______AAAAAAAA_______-3′	33.5	59.0
	3′-_______AAAA7AAA_______-5′
	Two substitutions
(2A·B)	5′-_______AA7A7AAA_______-3′	33.5	59.0
	3′-_______AAAAAAAA_______-5′
(A·2B)	5′-_______AAAAAAAA_______-3′	32.5	59.5
	3′-_______AA7A7AAA_______-5′
(A·3B)	5′-_______AAAAAAAA_______-3′	33.5	58.0
	3′-_______AAA7A7AA_______-5′
(A·4B)	5′-_______AAAAAAAA_______-3′	34.5	58.5
	3′-_______AAA77AAA_______-5′
(1A·1B)	5′-_______AAAA7AAA_______-3′	33.5	59.0
	3′-_______AAAA7AAA_______-5′
	Three substitutions
(1A·2B)	5′-_______AAAA7AAA_______-3′	33.0	55.0
	3′-_______AA7A7AAA_______-5′
(1A·3B)	5′-_______AAAA7AAA_______-3′	33.0	53.0
	3′-_______AAA7A7AA_______-5′
(1A·4B)	5′-_______AAAA7AAA_______-3′	34.5	51.5
	3′-_______AAA77AAA_______-5′
(2A·1B)	5′-_______AA7A7AAA_______-3′	33.0	53.5
	3′-_______AAAA7AAA_______-5′
	Four substitutions
(2A·2B)	5′-_______AA7A7AAA_______-3′	34.0	50.0
	3′-_______AA7A7AAA_______-5′
(2A·3B)	5′-_______AA7A7AAA_______-3′	34.0	50.0
	3′-_______AAA7A7AA_______-5′
(2A·4B)	5′-_______AA7A7AAA_______-3′	34.0	50.5
	3′-_______AAA77AAA_______-5′
(3A·B)	5′-_______AA7777AA_______-3′	34.5	53.5
	3′-_______AAAAAAAA_______-5′
	Five substitutions
(3A·1B)	5′-_______AA7777AA_______-3′	34.0	52.0
	3′-_______AAAA7AAA_______-5′
(3A·2B)	5′-_______AA7777AA_______-3′	34.0	45.5
	3′-_______AA7A7AAA_______-5′
(3A·3B)	5′-_______AA7777AA_______-3′	35.5	48.0
	3′-_______AAA7A7AA_______-5′
(3A·4B)	5′-_______AA7777AA_______-3′	34.5	48.0
	3′-_______AAA77AAA_______-5′

7 = 7-deaza-deoxyadenosine. All sequences have the same flanking Watson–Crick base-paired regions. For example, (A·B) is the duplex formed by oligos A and B:

A = 5′-GACCCGCAAAAAAAACCTCGCC-3′; B = 3′-CTGGGCGAAAAAAAAGGAGCGG-5′

The results show clear destabilization of the homo-(dA) self structure only when coralyne is present. This strongly suggests the important role of the N7 atom in the coralyne-induced homo-(dA) structure and implies base pairing involving N7, specifically either the cisHH, cisWH(a), transHH or transWH base pairings. As the modeling suggests that transWH is significantly energetically favored over the other plausible models involving N7 base pairing, the combined base substitution and simulation experiments predict that the coralyne-induced homo-(dA) duplex structure adopts transWH base pairings. The molecular dynamics also suggest that although the coralynes are tightly bound and relatively immobile on the MD simulation time scale, the self-structure is highly flexible with a large twist variation and a largely extended structure. This twisting mobility may partially explain the difficulties in determining the structure experimentally.

In the absence of coralyne, changes were observed in the CD spectra of the A·B duplexes with dA→7 substitutions (Figure S19). The substitution of only 1 nt (e.g. A·B versus A·1B) resulted in only minor spectral changes. However, increasing the number of substitutions resulted in additional spectral changes. Specifically, the CD band intensities at 220 and 247 nm decreased in intensity, while the CD band around 280 nm was shifted to shorter wavelength. In the presence of the coralyne, CD spectral changes also correlate with the increasing number of adenine substitutions. Most importantly, the intensity of the induced CD bands between 300 and 360 nm, which report coralyne binding to homo-(dA) duplexes (16,23,24), decreased with the incorporation of multiple dA→7 substitutions (Figure 7). This result is fully consistent with a reduced affinity of coralyne to the modified duplexes with increasing number of substitutions, which would be expected if the dA→7 substitution destabilizes the particular A·A base pairing structure that is recognized by coralyne.

Figure 7.

CD spectra of selected (A–B) duplexes in the presence of coralyne at 5°C. Shown are the region of the CD spectra that reports coralyne binding to poly-(dA) (top panel) and the full spectra of the same samples (bottom panel).

The reduction in the coralyne-induced stability of A·A mismatches in duplexes containing dA→7 substitutions strongly suggests the participation of adenine N7 in the A·A base pairing of the coralyne-bound structure. If N7 is involved in A·A base pairing, then one can eliminate the A·A pairing structures S1A, S1C, S1E, S1G, S1H, S1J and S1K. The remaining possibilities are the symmetric Hoogsteen–Hoogsteen pair (N7/N7, Supplementary Figure S1I), in which N7 is the only H-bond acceptor; the asymmetric Watson–Crick-Hoogsteen pair (N1/N7, Supplementary Figure S1D), where both N1 and N7 are involved in base pairing H-bonds; and two of the single H-bonded base pairs [cisHH and cisWH(a)].

Of the remaining possible base pairs, we propose that the asymmetric N1/N7 base pairing can also explain the variation in Tm of the dA→7 substituted duplexes. As demonstrated in Table 3, the decrease in duplex thermal stability is not strictly proportional to the number of modifications, but also depends on the relative positions of multiple modifications. For example, both (1A·B) and (2A·B) duplexes have the same Tm of 59°C, even though these two sequences have one and two dA→7 substitutions, respectively. Again, the Tm of (1A·2B), (1A·3B), (1A·4B) and (2A·1B) vary between 51.5°C and 55°C, even though they all have three substitutions. This analogy can also be extended to duplexes in the series with four or more substitutions. As discussed above, an asymmetric base pairing structure (such as N1/N7), can exist in two base orientations with respect to the overall duplex. In the first scenario, adenines can align on one strand while all using their Watson–Crick face for pairing while on the other strand the bases use only their Hoogsteen face. In the second scenario, the bases alternate along the same strand, using the Watson–Crick face or Hoogsteen face. Given this orientational flexibility, it is possible that some dA→7 substitutions do not exhibit as great a Tm change as others because the N1/N7 A·A base pairs are able to compensate for the removal of one N7 H-bond acceptor by converting between the two orientations. This proposed dA→7 ‘compensation rearrangement’ is not possible with a symmetric base pair, such as the N7/N7 Hoogsteen-Hoogsteen pair. Thus, if the N7/N7 base pair were the base pair adopted by homo-adenine duplexes upon coralyne binding, one would expect to see a more linear response in the decrease in Tm with the number of dA→7 substitutions. In principle, the single H-bonded base pairs of cisHH and cisWH(a) also remain possibilities. However, such a pairing would likely be less stable than a base pair with two H-bonds and free energetic analysis strong disfavors cisWH(a) with coralyne (Figure 4).

There is one caveat that should be considered regarding the strength of the conclusions that can be drawn between the thermal denaturation studies and the expected base pairing within the coralyne-induced homo-adenine duplex. Gold and co-workers have recently shown that substitution of guanine by 7-deaza-guanine in duplex DNA locally reduces the stability of Watson–Crick base pairs (52). These investigators have proposed that reduced hydration, cation binding and stacking interactions at sites of 7-deaza-guanine substitutions could be the origin of the reduced stability. It is therefore possible that at least some of the decreased stability of the duplexes containing dA→7 substitutions could be due to reduced stacking interactions between the 7-deaza-adenine and coralyne.

Structure of the coralyne-induced homo-d(A) duplex transWH model

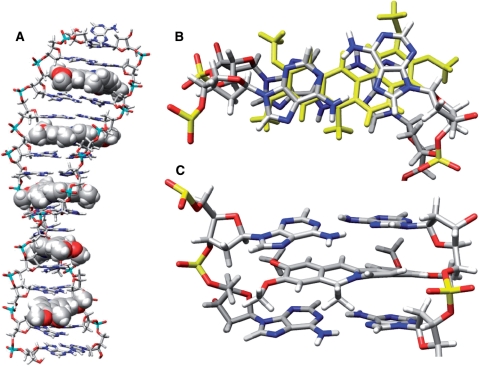
Figure 8 shows the putative structure of the transWH model structure and information on the torsion angles and distributions is provided in the Supplementary Data. Models of the transWW geometry are shown in the Supplementary Data (Supplementary Figure S15). A notable feature of both models is the distinct under-twist compared to canonical DNA. For the structure shown in Figure 8, the helical repeat is around 13–14 bp steps compared to ∼10 bp steps for canonical B-DNA. Both structures also have a significantly wider minor groove. One likely stabilizing feature of both geometries is the accommodating buckle of the A·A base pairs that follows the kink in the coralyne at the nitrogen due to the nearby methyl group. Distinct hydration patterns are also evident in the grooves and with the backbones. In the ‘minor’ groove, each AA base pair is hydrated by approximately three to five distinct hydration sites (Supplementary Figure S17) located at N3, between the pairs, and at N1 with peripheral groove hydration at the backbones (O4′ and O5′) and cones of hydration around the phosphates. Less distinct or high occupancy hydration is at the coralyne in the minor groove, except for bridging water between the hydration sites at the center of the base pairs. Clear hydration is also evident in the major groove but to a lesser extent. High occupancy water binding sites appear near the adenine bases with water bridges through the coralyne-binding site.

Figure 8.

Graphical illustrations of representative structures of the transWH geometry from cluster analysis. All of the molecular graphics represent representative configurations from dominant clusters sampled over the course of MD simulation on the transWH-c5-180d model structure. The clustering was performed over the MD trajectory from ∼12–96 ns with ptraj either over the entire molecule or over the four base-coralyne binding unit as described in the Supplementary Data. (A) The entire coralyne-induced homo-(dA) duplex with the DNA shown as a stick figure and the coralyne as solid spheres. Note that the structure is rather extended and under-twisted as compared to canonical B-DNA. (B) View of the stacking with coralyne (yellow) for the minimal binding unit. (C) A close up view of the minimal binding unit. The kink in the coralyne structure at the nitrogen imparted by the nearby methyl leads to a distinct and slight buckle in the W–H base pairs.

TransWH have anti base-sugar conformations for both pairing adenines, but their hydrogen bonds are not symmetric across the duplex. Based on the modeling results presented here, we propose that the interacting edges of homo-(dA) duplex should be Hoogsteen edge for one strand and Watson–Crick edge for the other strand or possibly mixed, however not uniformly mixed (i.e. alternating H/W with W/H). In our initial modeling studies of the free homo-(dA) duplex, we tried uniformly alternating Hoogsteen–Watson–Crick on Watson–Crick–Hoogsteen and found this geometry unfavorable. The tendency to have repeats of Hoogsteen–Watson–Crick down the duplex (where the Hoogsteen face could be on either strand) may partially explain why it was not possible to determine the 3D structure of the duplex. As the DNA oligomers (Table 3) have different sequences for the flanking Watson–Crick stems, and since the pairing between adenine bases is not symmetric, at least two structures (each differing by which strand adopts the Hoogsteen pairing) could result. As the effect of the flanking sequences is likely minimal, the free energies of these structures should be similar. As a result, the structures may populate almost equally and this could broaden or complicate NMR peak assignments. Regarding the issue of the non-symmetric homo-(dA) duplexes, there is another caveat for our final 3D structures. Homo-(dA) duplexes with alternating base pairs were mostly discarded as shown in Supplementary Tables S3-S4 except cisWH(b)-alt. TransWH-alt was also removed from the initial screening of homo-(dA) duplex. This was actually expected because the frequent alternation of the base pairs possibly loads more tension on the backbone structures and destabilizes the whole duplex structure. However, it is possible that the transWH duplex may have occasional reversion in a long duplex, especially as the experiments suggest the coralyne sites are dynamic and insensitive to some of the d(A→7) mutations. Moreover, as the base-sugar conformations of transWH pairs are anti for the both bases, switching from the H/W pair to the W/H pair is relatively easy compared to reversions involving glycosidic bond rotation in the structures (as shown in Supplementary Figure S1D, G and H). In any case, the frequency of reversion both in time and space aspects requires further investigation.

Validation of the simulation results

As simulation can model virtually anything and since the underlying models have not been extensively validated and assessed with respect to their ability to reliably rank putative models of unusual DNA structures, further evidence beyond the base substitution experiments will be required to validate the choice of the transWH model. However, we note that some validation of the underlying AMBER force field models comes from their ability to properly model hydrogen bonding energetics, stacking and geometries compared to high level QM calculations (53–55), even for non-Watson–Crick base pairing (56). Moreover, with the AMBER force fields, a wide array of nucleic acid systems have been reliably modeled (57,58), including unusual nucleic acid structures such as G-quadruplex DNA (50,59), zipper DNA (60), minor groove binders bound to DNA (61), and RNA structures full of mismatches (62). The simulation protocols are able to properly model dynamics (63), solvation (64) and relative energetics (48,65). Despite these successes, there are known problems with the AMBER force field approach, including salt crystallization below the saturation limit (66,67) and anomalous population of DNA backbone conformational substates (46). Moreover, the simplified brute-force yet tractable approach used here, starting first with homo-(dA) duplex models in the absence of coralyne before gradually modeling in coralyne structures is not perfect, as homo-(dA) duplex structures in the absence of coralyne have not been observed experimentally. Nevertheless, the observed trends indirectly support the suggestion that the transWH structure is most stable. Clearly H-bonds are important since, as shown in Figure 4, all the single H-bond structures were less stable than their double H-bond structure counterparts. Also, since all the double H-bond structures survived the initial screen, we effectively sampled a full landscape of the double H-bond structures interacting with coralyne. Of the low energy structures, only transWH involves N7 H-bonds. The importance of the N7 of the adenine base limits base pairing models to cisHH, transWH, cisWH(a), and transHH. Among these, only the interactions of coralyne with cisHH duplexes were not modeled; however, the observation that natural cisHH structures have not been found indirectly suggests low stability of this base pairing arrangement. The close approach of the sugars and narrow backbones in cisHH compared to transWH likely destabilizes the former and make it less compatible with flanking B-DNA.

CONCLUSION

In conclusion, we have attempted to model the characteristic structure of the coralyne-induced homo-(dA) duplex using molecular dynamics simulations with both explicit and implicit solvent. In order to predict a structure, a hierarchical approach was applied building tentative coralyne-free duplexes, followed by single coralyne-bound and multiple coralyne bound structures, pairing down the list of proposed structures at each stage. Proposed structures included models with all possible A·A base pairing types. The energetic and structural stability among each model was assessed allowing an effective ranking of each model. After the number of putative models was reduced, extended MD simulation was performed in explicit solvent with both the ff99 and ff99-bsc0 force fields in AMBER. The most favorable structure in terms of energetics, structural stability and hydrogen bonding was the transWH geometry. To further validate the simulation results, 7-deaza-adenine base substitutions were experimentally engineered into a previously studied coralyne-induced homo-d(A) duplex structure surrounded by flanking B-DNA. The results clearly indicate the importance of the adenine N7 atom as base substitutions lead to a substantial lowering of the melting temperature. Moreover, the results with differential localization of the base substitutions are consistent with the one hydrogen bond pairing seen with the transWH base pairing. Together, biomolecular simulation and experiment suggest a putative structure for the coralyne-induced homo-d(A) duplex structure that has eluded spectroscopic and crystallographic investigation to date; however the full validity of this structure remains to be determined and the elaborate brute-force protocol applied is not without limitations and clearly not yet ready for bulk prediction.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science Foundation [CHE0404677 (to N.V.H.)]; National Aeronautics and Space Administration Exobiology Program [NNG04GJ32G (to N.V.H.)]; National Institutes of Health 1S10RR17214 [R01-GM081411 (to T.E.C.)]. Funding for open access charge: National Institutes of Health grant funds to T.E.C.

Conflict of interest statement. None declared.