Abstract
Background
Although spontaneous use of the more-affected arm and hand after stroke is an important determinant of participation and quality of life, a number of patients exhibit decreases in use following rehabilitative therapy. A previous neurocomputational model predicted that if the dose of therapy is sufficient to bring performance above a certain threshold, training can be stopped.
Objective
The aim of this study was to test the hypothesis that there exists a threshold for function of the paretic arm and hand after therapy. If function is above this threshold, spontaneous use will increase in the months following therapy. In contrast, if function is below this threshold, spontaneous use will decrease.
Methods
New computer simulations are presented showing that changes in arm use following therapy depend on a performance threshold. This prediction was tested by reanalyzing the data from the Extremity Constraint-Induced Therapy Evaluation (EXCITE) trial, a phase III randomized controlled trial in which participants received constraint-induced movement therapy for 2 weeks and were tested both 1 week and 1 year after therapy.
Results
The results demonstrate that arm and hand function measured immediately after therapy predicts, on average, the long-term change of arm use. Above a functional threshold, use improves. Below this threshold, use decreases.
Limitations
The reanalysis of the EXCITE trial data provides a “group” threshold above which a majority of patients, but not all, improve spontaneously. A goal of future research is to provide the means to assess when patients reach their individual threshold.
Conclusion
Understanding of the causal and nonlinear relationship between limb function and daily use is important for the future development of cost-effective interventions and prevention of “rehabilitation in vain.”
Stroke is the leading cause of disability in the United States, and about 65% of survivors of stroke experience long-term upper-extremity functional limitations. In more than half of patients with severe paresis after stroke, recovery of upper-extremity function is achieved solely by use of the less-affected limb.1 Improving use of the more-affected arm is important, however, because difficulty in using this arm in daily tasks has been associated with both reduced participation and quality of life.2,3
There now is evidence that intensive, task-specific practice, in which patients actively engage in repeated attempts to produce motor behaviors beyond their present capabilities, is effective for improving upper-extremity function and use after stroke.4–9 Constraint-induced movement therapy (CIMT) in particular, which involves intense, functionally oriented task practice of the more-affected upper limb along with restraint of the less-impaired limb for 90% of waking hours, was shown in the Extremity Constraint-Induced Therapy Evaluation (EXCITE) phase III randomized controlled trial to largely improve limb function and arm use compared with usual and customary care.7,9 Several weeks of challenging rehabilitative training with the upper limb contralateral to the lesion reverses, at least partially, the loss of cortical representation due to stroke through recruitment of adjacent brain areas.10–12 Such reorganization may last several years after the initial injury13 and has been linked to change in performance.14
Long-term change in arm and hand use in the months following therapy, however, is variable among patients. In some patients, use continues to improve in the months following therapy.9,15,16 Earlier, we proposed that the repeated attempts to use the affected arm in daily activities can promote motor learning that improves performance and function15; this improvement in function, in theory, could further increase arm use. However, for other patients, improvements can be short-lasting. For a number of patients in the EXCITE trial, for instance (see Results section), and presumably for a larger number of patients who receive usual and customary care, a decrease in use of the affected arm appears in the year following therapy. If this decrease is large, rehabilitation is in vain. Accordingly, understanding the conditions that lead to sustained gains in arm use following an intense bolus of therapy is important.
To achieve a unimanual task, such as drinking from a glass, a patient recovering from stroke can be conceptualized as a decision maker who chooses to use either the more-affected limb or less-affected limb (the decisions here need not be made consciously). The choice of limb use will presumably depend on many factors, including lesion characteristics, impairment and functional levels, motor training, previously rewarding or punishing experience after stroke, and motivation.
In a recent computational model,17 we modeled bilateral reaching movements in patients recovering from stroke to explore the interactions between the adaptive decision process of limb use and limb performance. Here, “arm performance” is defined as the directional error of the movement toward the selected target and is the equivalent of “arm and hand function” in patients. Therapy is a simulation of CIMT: the simulated patient is forced to use the affected arm. When no therapy is given, the patient is free to choose 1 of the 2 arms to reach a target appearing on a circle centered on (overlapping) initial hand locations. Our neural model contains 2 independent motor cortices, each controlling the contralateral arm, with one being affected by stroke.* Before each movement, one motor cortex is selected by an adaptive decision-making system, tentatively located in cortico-striatal networks.
In our model, neural reorganization in the motor cortex was modeled with a neural learning rule that aims to achieve 2 goals concurrently. The first goal is to reorganize the neural code to increase arm performance via error-based learning (also called “supervised learning”). The second goal is to maximize neural resources for particular desired movement directions to minimize movement variability via Hebbian learning (a model of long-term potentiation, which also is called “unsupervised learning” because there is no teacher).
Furthermore, in the model, the decision to use one limb or the other is made by comparing the “action value” of each limb in the adaptive decision-making system. The values for each arm are updated based on reward prediction errors (this type of learning also is called “reinforcement learning”). If performance-based rewards are greater than expected, the arm will be chosen more often for this particular movement. If not, the arm will be chosen less often.
Simulation results showed that after small doses of therapy, the model exhibited a simple form of learned non-use, as use increased with therapy but decreased again to low levels after therapy (for a more complete account of learned non-use, see Wolf18). With large doses of therapy, use increased after therapy. With a specific intermediate dose of therapy, there is no change in use after therapy. That is, there is a threshold for rehabilitation. This threshold is an emergent property of the learning dynamics and exists only when the 3 types of learning—error-driven, Hebbian-like, and reward-based—are implemented.17 The model further showed that, similar to experimental observations, sufficient CIMT in the model reversed the cortical representation loss, principally because of the synergistic effect of supervised learning and unsupervised learning, which was “adaptive.” No rehabilitation, or too little rehabilitation, increased this loss, principally because of reorganization due to unsupervised learning, which was “maladaptive” (see Han et al17 for further details and results).
The present article directly tests the hypothesis that there is a threshold level for function of the paretic arm and hand after therapy. If function is above this threshold, spontaneous use will increase in the months following therapy. In contrast, if function is below this threshold, spontaneous use will decrease or deteriorate in the months following therapy, and compensatory use of the nonparetic hand will further develop. We first present new computer simulations of the model to directly show the emergence of the hypothesized performance threshold that determines average long-term limb use in simulated patients. We then tested our prediction of a threshold with a reanalysis of clinical data from the EXCITE clinical trial.7
Method
Computer Simulation Methods
The objective of these computer simulations is to test the hypothesis that there is a threshold level for function of the paretic arm and hand after therapy in simulations that mimic the conditions of the EXCITE trial. Our model, although necessarily highly simplified, contains key ingredients that make it applicable to the participants in the EXCITE trial. First, as described above, our model is a model of stroke recovery that contains up-to-date knowledge about plastic processes underlying stroke recovery. Second, therapy in the model has been modeled loosely after CIMT. That is, during therapy, the simulated patient is constrained to use the affected arm. Third, in the model, lesion sizes can easily be varied to capture the diversity of patients with stroke in the EXCITE trial. Finally, the model makes predictions of long-term changes in arm use as a function of performance just after therapy, and the EXCITE data precisely capture such variables in these time frames. In our previous work,17 “identical” simulated patients (same lesion size and location) received various doses of therapy. In the present study, in contrast, we simulated patients with various lesion locations and sizes, and all simulated patients received the same dose of therapy.
Specifically, we simulated 125 patients with locations of the lesion center randomly chosen within the affected motor cortex. The lesion sizes were empirically determined within a range of 16% to 43% of the affected motor cortex sizes, because such lesion sizes lead to effects that are neither too mild (to need therapy) nor too severe (to benefit from therapy). All patients received the same dose of 400 forced-use trials of therapy (corresponding to the 2 weeks of CIMT that was the standard dose in EXCITE). Then, for each simulated patient, we measured use of the affected arm just after therapy (corresponding to the 1-week posttest in the EXCITE trial) and in a delayed follow-up test, given after 3,000 free-choice trials following therapy (corresponding to the 1-year posttest in the EXCITE trial). All other simulation parameters are shown in Han et al.17
We developed sigmoid models of spontaneous arm use as a function of the error both immediately after therapy and 3,000 trials after therapy. For this purpose, we fitted the equivalent linear models to the data: Y=a ERROR + b, where Y=log (USE/(100%−USE)), USE is the average spontaneous arm use either just after therapy or 3,000 trials after therapy, and ERROR is the average of directional error (in degrees) just after therapy. USE and ERROR are computed from the average of 100 trials over the affected range. The parameter a is the sigmoid slope, the parameter b is a free parameter, and log is the natural logarithm. We report the P value obtained from these linear regression models with transformed Y values. We compared linear fits and sigmoid fits with root mean square error (RMSE) in spontaneous arm use.
Reanalysis of Clinical Data From the EXCITE Trial
The objective of this reanalysis of the data from the EXCITE clinical trial7 was to test the prediction, derived from our simulations, of a performance threshold, on average, in patients poststroke.
We performed a retrospective analysis of data from the 169 patients enrolled in the EXCITE trial who did not withdraw from the trial.7 Briefly, in the EXCITE trial, subjects were randomly assigned to either an immediate CIMT group or a delayed CIMT group. The immediate CIMT group received 2 weeks of therapy after inclusion in the study (Pre1); the delayed CIMT group received no immediate therapy but did receive 2 weeks of therapy after a 1-year delay (Pre2). Subjects were tested with the Wolf Motor Function Test (WMFT) and the Motor Activity Log (MAL) at Pre1, at 1 week after the immediate CIMT group received therapy (Post1), at Pre2, and at 1 week after the delayed CIMT group received therapy (Post2). All subjects were tested again at 24 months after inclusion in the study (MT24).7,19 In the current analysis, we compared arm use 1 week after therapy with arm use a year later, so time of therapy was not a factor in this analysis. We thus combined all data in the EXCITE trial at these points and studied arm function and use in the posttest just following therapy (Post1 for the immediate CIMT group and Post2 for the delayed CIMT group) and arm function and use in the delayed 1-year posttest (Pre2 for the immediate CIMT group and MT24 for the delayed CIMT group).
Briefly, the WMFT measures performance time (up to 120 seconds) needed for patients with stroke to perform 15 laboratory-based arm function tasks requiring use of the more-affected upper extremity.20–22 The WMFT also contains a shoulder strength (force-generating capacity) task and a grip strength task. Additionally, the quality of motor function during the timed tasks is assessed by independent raters using the 6-point Functional Activity Scale (FAS). The WMFT has good reliability and validity and has been shown not to suffer from a learning effect.22 In our analyses, as in Wolf et al,21 the natural logarithm of the WMFT time score was used to normalize the distribution. In the MAL, patients (or their caregivers) rate how well (on the Quality of Movement [QOM] scale) and how much (on the Amount of Use [AOU] scale) the paretic arm is used spontaneously to accomplish 30 activities of daily living outside of the laboratory.23,24 Each item on the MAL has an 11-point scale, with scores ranging from 0 (no use) to 5 (normal) in increments of 0.5. Validity and reliability of the MAL scores have been established.24 In our analyses, we present average MAL AOU scale scores.
Our neural computational model predicts that if performance is above threshold after therapy, use will increase between 1 week after and 1 year after therapy (positive change). If performance is below threshold, use will decrease (negative change). The model thus predicts a positive correlation between performance and change in use after therapy. To test this prediction, we performed 2 correlation analyses. The first correlation analysis was performed to determine the relationship between the difference in average MAL AOU scale scores from 1 week posttherapy to 1 year posttherapy and the logarithm of the WMFT time score. The second correlation analysis was performed to determine the relationship between the difference in average MAL AOU scale scores from 1 week posttherapy to 1 year posttherapy and the WMFT FAS scores. We then verified this theoretically driven prediction with a data-driven (hypothesis-free) analysis using a stepwise linear regression (see Appendix for details). In this analysis, a large number of variable predictors initially were entered in the linear model that predicts long-term changes in MAL AOU scale scores. If a measure of function 1 week after therapy is a significant predictor of long-term changes in use, this stepwise linear regression would give further support to the threshold hypothesis.
In view of the predictions of our simulations on the sigmoidal shapes of the relationship between performance 1 week after therapy and use both 1 week after therapy and after a delay of 1 year and because the MAL AOU scale is bounded between 0 and 5, we developed sigmoid models of the average MAL AOU scale scores as a function of the WMFT FAS scores both immediately (1 week) after therapy and 1 year after therapy. For this purpose, we fitted the equivalent linear models to the data: Y=a FAS + b, where Y=−log (5/MAL − 1), MAL is the MAL AOU scale score taken either in the 1-week posttest or the 1-year posttest, FAS is the WMFT FAS score, the parameter a is the sigmoid slope, the parameter b is a free parameter, and log is the natural logarithm. We report the P value obtained from these linear regression models with transformed Y values. We compared linear fits and sigmoid fits with the RMSE in MAL scores, where a smaller RMSE indicates a better fit.
In this analysis with sigmoidal models, we included only patients with WMFT and MAL data available at both time points (although all subjects included in our analysis completed the trial, a number of data points were missing at either the 1-week posttest or the 1-year posttest). Furthermore, to obtain convergence of the sigmoidal fit, we removed 2 subjects with perfect MAL AOU scores (scores of 5 at 1 week after therapy; no participants had scores of 5 at 1 year following therapy). We thus analyzed data from 132 subjects. We also compared sigmoidal models and linear models after removal of outliers, defined as individuals with residuals (observed-predicted values) greater than 2 standard deviations of the residuals.
We compared the sigmoid models at 1 week posttherapy and at 1 year posttherapy by computing and comparing the confidence intervals (CIs) at 95% and 90% of the slope parameter of the sigmoid regression models. We predicted that for those subjects whose performance was above threshold after therapy, use would increase from 1 week posttherapy to 1 year posttherapy. Contrarily, we predicted that for those subjects whose performance was below threshold, use would decrease. Assuming that sigmoid models are a good fit to the use data at 1 week posttherapy and at 1 year posttherapy, this prediction can be tested by the change in slope of the sigmoids from 1 week posttherapy to 1 year posttherapy. The slope should be greater at 1 year posttherapy than at 1 week posttherapy. Finally, the performance threshold was obtained at the crossing of the sigmoids at 1 week posttherapy and at 1 year posttherapy. The prediction is that the 2 curves will cross because the slope is greater at 1 year posttherapy than at 1 week posttherapy. Above this crossing point, use will be greater at 1 year posttherapy than at 1 week posttherapy, on average. Below this crossing point, use will be smaller at 1 year posttherapy than at 1 week posttherapy, on average. Thus, this crossing represents an average threshold. We set the significance level at P=.05.
Results
Computer Simulation
To test the hypothesis that spontaneous use will increase in the months following therapy if arm performance after therapy is above a threshold, we first investigated arm use at 0 trials and at 3,000 trials following therapy as a function of performance just after therapy. For simulated patients above threshold, spontaneous arm use should increase, on average, from 0 to 3,000 trials. For patients below threshold, the spontaneous arm use should decrease, on average, from 0 to 3,000 trials.
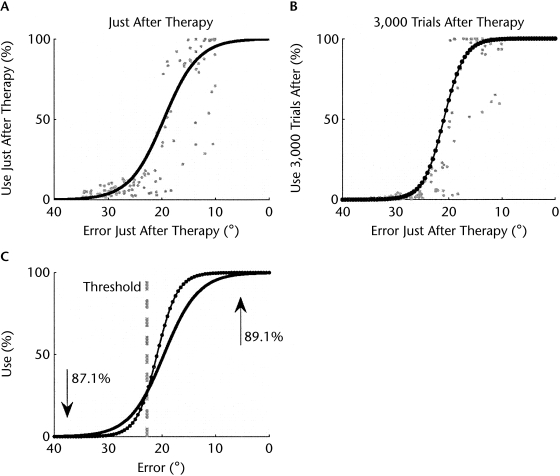
In the model, performance is measured as angular error between the target direction and the actual arm movement direction. Spontaneous arm use is measured as percentage of use of the affected arm to the targets in the range of movement directions most affected by the lesion (in the model, the lesions affect some ranges more than others; see Han et al17 for details). Figure 1A shows that for most simulated patients with high performance after therapy, spontaneous arm use was high and saturated to maximum use (100% in the model). Conversely, for simulated patients with low performance, use saturated near zero. Because of these ceiling and floor effects, arm use after therapy was fit better by a sigmoidal function of performance (RMSE=17.08, P<.0001) than by a linear function of performance (RMSE=18.74, P<.0001). Figure 1B shows that arm use in the follow-up test at 3,000 trials after therapy also was fit better by a sigmoidal function (RMSE=18.98, P<.0001) than by a linear function (RMSE=19.36, P<.0001). Finally, the slope of the sigmoid model in the long-term follow-up test was steeper than that just after therapy (slope just after therapy=0.31; slope 1 year after therapy=0.52).
Figure 1.
Simulated data of use of the affected arm (A) just after therapy and (B) 3,000 trials after therapy as a function of performance (reach directional error in the model) just after therapy for 125 simulated subjects with different lesion sizes and locations. (C) Comparison of the sigmoidal fit of use just after therapy and 3,000 trials after therapy. The intersection of the 2 curves gives the threshold in arm performance above which use increases and below which use decreases. The upward arrow indicates that 89.1% of the simulated subjects above threshold showed increased arm use after therapy. The downward arrow indicates that 87.1% of the simulated subjects below threshold showed decreased arm use after therapy. Note that we reversed the x axis, to compare with the data of Figure 2.
The intersection of the 2 curves gives an average (or “group”) threshold in arm performance, corresponding to a reaching error of 22.8 degrees. Above this threshold, the arm use of most simulated patients (89.1%) improved spontaneously following therapy; below this threshold, the arm use of most simulated patients (87.1%) worsened following therapy.
These simulation results make 3 testable predictions. First, the relationship between use after therapy and function after therapy is sigmoidal, and this is true if spontaneous use is measured just after therapy or in a delayed follow-up test. Second, the sigmoid is steeper in the follow-up test than just after therapy. Third, the intersection of the sigmoid for use just after therapy with the sigmoid for use in the long-term follow-up test (Fig. 1C) gives an average threshold in performance above which use improves spontaneously following therapy and below which use worsens. We next tested these predictions with a reanalysis of clinical data from the EXCITE trial.
Clinical Data Analysis
The correlation analysis between the difference in average MAL AOU scores from just after therapy to 1 year posttherapy and the logarithm of the WMFT time score shows that function (WMFT score) was positively correlated with change in use (MAL AOU scale score) (Pearson correlation r=−.172, P=.046, n=135). A similar correlation analysis shows that the WMFT FAS score correlated better with long-term changes in use (r=.22, P<.010, n=134).
Among a large number of variables included as potential predictors of change in MAL AOU scores after therapy in the stepwise regression analysis, only 2 variables were included in the final model (P<.0005, R2=.123, n=133): the WMFT FAS score posttherapy (P<.0001, standardized coefficient=0.42) and the “weight to box” task with the more-affected arm (a strength task part of the WMFT) measured upon enrollment (P<.005, standardized coefficient=−0.34) (see the Appendix for details).
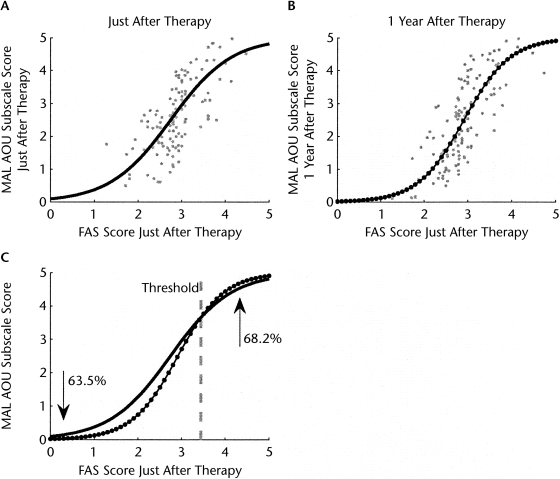
The sigmoid models of the average MAL AOU scale scores as a function of the WMFT FAS scores showed a good fit to the data both immediately (1 week) after therapy (RMSE=0.83, P<.0001) and 1 year after therapy (RMSE=0.86, P<.0001). The mean slope of the sigmoid model was larger at 1 year after therapy (mean slope=1.71, standard error [SE] of slope=0.14, 95% CI=1.43–1.99, and 90% CI=1.47–1.94) than at 1 week after therapy (mean slope=1.31, SE=0.13, 95% CI=1.05–1.58, and 90% CI=1.09–1.53). The corresponding linear models fit the data with similar RMSE values (RMSE=0.83, P<.0001 and RMSE=0.87, P<.0001) for the 1-week and 1-year models, respectively.
The strength of the relationships between MAL AOU scale scores and WMFT FAS scores at 1 week and 1 year after therapy increased after removal of outliers. Based on our criterion for outlier removal, 4 subjects were removed in the 1-week model, 5 subjects were removed in the 1-year model, and 3 subjects were outliers for both the 1-week and 1-year models; thus, n=128 for the 1-week model and n=127 for the 1-year model). Compared with the sigmoid models without outlier removal, these models with outlier removal (Figs. 2A and B) showed improved fit to the data (1 week after therapy: RMSE=0.76, P<.0001; 1 year after therapy: RMSE=0.79, P<.0001) and smaller CIs of the slopes both 1 week after and 1 year after therapy (1 week after therapy: mean slope=1.44, SE of slope=0.13, 95% CI=1.19–1.68, 90% CI=1.23–1.64; 1 year after therapy: mean slope=1.91, SE=0.14, 95% CI=1.63–2.18, 90% CI=1.67–2.14). Finally, the sigmoid models with outlier removal fit the 1-week and 1-year data better than the linear models with outlier removal (1 week after therapy: n=130, RMSE=0.78, P<.0001; 1 year after therapy: n=129, RMSE=0.83, P<.0001).
Figure 2.
Use of the more-affected arm, as recorded by the Motor Activity Log Amount of Use (MAL AOU) subscale: (A) 1 week after therapy and (B) 1 year after therapy as a function of arm and hand function (Functional Ability Scale [FAS]) 1 week after therapy for subjects of the EXCITE trial. (C) Comparison of the sigmoidal fit of use 1 week after therapy and 1 year after therapy. The intersection of the 2 curves gives the functional threshold (FAS score=3.44) above which uses increases and below which use decreases. The upward arrow indicates that 68.2% of subjects above threshold showed increased arm use after therapy. The downward arrow indicates that 63.5% of subjects below threshold showed decreased arm use after therapy.
Thus, the slope of the sigmoidal model 1 year after therapy was greater than the slope of the sigmoidal at 1 week after therapy, although there was a very small overlap of the 95% CIs (by 0.05) but no overlap of the 90% CIs. The results were qualitatively similar without outlier removal, but the 95% CIs for the sigmoid slopes overlapped somewhat (by 0.15); however, there was less overlap of the 90% CIs (by 0.06). The steeper slope of the sigmoid at 1 year posttherapy compared to 1 week posttherapy is well illustrated in Figure 2C, in which we plotted the 2 sigmoids (models without outliers).
The intersection of the 2 sigmoids with mean slopes gives the average threshold in function, given by WMFT FAS score=3.44. Among 22 subjects with function above this threshold, 15 (68.2%) showed an increase in use in the year following therapy (model without outliers). Conversely, among 104 subjects with function below this threshold, only 38 (36.5%) showed an increase in use in the year following therapy (Fig. 2C). Thus, as predicted by the computational model, when function 1 week after therapy was above this average threshold, subjects on average showed improvements in use in the year following therapy, and when function 1 week after therapy was below this average threshold, subjects on average experienced a worsening of use in the year following therapy.
Discussion
To better understand the interactions between arm function and use after therapy, we have presented new simulations with conditions that mimic those of the EXCITE trial. These simulations made 3 new predictions, all of which were confirmed in a reanalysis of arm use and function data from the EXCITE trial.
First, the relationship between use after therapy and performance is better fit by a sigmoidal model than a linear regression model, and this sigmoidal relationship is true whether use is measured 1 week after therapy or in a follow-up test. The differences, however, between the linear fits and sigmoidal fits are not very large (as shown by the relatively small differences in RMSE between linear and sigmoidal models at 1 week after therapy and at 1 year after therapy in the outlier removal conditions). Thus, this sigmoidal relationship needs to be verified with other clinical databases. A sigmoidal relationship can result for 2 possible, nonexclusive reasons. The first possible reason is simply that the MAL AOU scale does not adequately measure arm use when use is high or low. The second possible reason is an actual nonlinear relationship between function and use in patients, at least on average. A floor effect would suggest that when function is low, the arm is not used at all. A ceiling effect would suggest that when function is high but less than maximal, the arm is used as if the patient did not have a stroke.
Second, the sigmoid is steeper in the 1-year follow-up test than 1 week after therapy. This indicates that, for the average patient in EXCITE trial, if function is high 1 week after therapy, use improves. Conversely, and again on average, if function is low 1 week after therapy, use worsens.
Third, the intersection of the sigmoid for use 1 week after therapy with the sigmoid for use in the 1-year follow-up test gives an average (or group) threshold in function of WMFT FAS score=3.44. An FAS score of 3 is given if the affected arm performance does not require assistance from the other arm but is limited by synergistic movements, or is performed slowly or with effort. An FAS score of 4 is given if the affected arm performance is close to normal (ascertained by performance of the less-affected limb and with premorbid dominance considered) but slightly slower and may lack precision, fine coordination, or fluidity. If function is above the threshold 1 week after therapy, use of the more-affected arm in the year following therapy improves, on average. On the contrary, if function is below this threshold, use is not sustained, on average. Thus, functional abilities just after therapy predict change in use in the long-term following therapy, and, on average, a functional threshold can be determined.
In the stepwise regression analysis of the EXCITE trial data, only a measure of arm and hand function (the WMFT FAS) and shoulder strength 1 week after therapy predicted change in use. Furthermore, shoulder strength was negatively correlated with a future change in use, although this correlation was only moderate (−.34). How can this result be interpreted? One possibility is that patients with greater shoulder strength may be better able to compensate with the proximal arm for the lower-functioning distal upper extremity. Because of these compensatory movements, use of the hand is not reinforced and decreases. Another, nonexclusive possibility is that increase in arm strength correlates with a shrinkage of neural areas encoding the distal representation and an increase in neural areas encoding the proximal representation; this would explain the negative correlation. In any case, because stepwise regression is an exploratory tool, these results and predictions warrant further investigation by studies that combine brain imaging or neural recording and behavioral data analysis. Furthermore, we note that we have defined shoulder strength as performance of the “weight to box” task of the WMFT. This task does not directly measure shoulder strength, and thus the correlation might be different if strength is tested with the actual shoulder strength test.
Limitations and Future Work
A practical clinical implication of the present work is the determination of a stopping criterion to determine the dose of therapy for each patient. The intersection of the sigmoid curves in our reanalysis of the EXCITE trial data gives a “group” threshold, above which most patients improve spontaneously.
A goal of our future research, therefore, is to provide the means to assess when an individual reaches his or her personal threshold so that therapy may be stopped without adverse effect. More research is needed, however, before we are able to provide robust threshold values for individual patients and before such a stopping rule can be implemented in the clinic, for the following reason. Notably, the predictive capability of our simple sigmoidal models is rather low: only 68.2% of subjects above the threshold showed improvement in use; conversely, 36.5% of subjects below the threshold showed improvement in use. Such low predictive values arise because our sigmoidal models are simple averaged models that do not consider individual lesion size, location, or any other patient characteristics, such as motivation, handedness, and so on, besides function 1 week after therapy.
To be able to determine functional thresholds for individual patients, we are currently extending this work in 2 aspects. First, we are developing individualized predictive models that can be used for individualized determination of threshold and dose. We previously argued from a theoretical viewpoint,17 and confirmed to some extent here with clinical data, that stroke recovery is a time-varying process (arm use changes in the year following therapy) that is nonlinear (arm use can increase or decrease in the year following therapy, depending on arm function after therapy). We currently are developing time-varying and nonlinear models of recovery that will use neurological data such as stroke lesion location and volume as regressors. Second, both the WMFT FAS and the MAL AOU scale are lengthy tests that are impractical to use in the clinic. To address this, we are developing a novel, easy-to-administer, reliable, and valid measure of arm use that is based on actual arm choices in a bilateral arm reaching task.25
Based on predictions from these novel models and tools, we expect to determine the functional threshold with high confidence for individual patients and, as a result, to determine the patient-specific dose of therapy that will bring function above this threshold. Such an understanding of nonlinear relationships between limb function and use is important for the future development of cost-effective interventions and the prevention of “rehabilitation in vain.”
Supplementary Material
Appendix.
Stepwise Regression
To confirm our theoretical prediction, we used a stepwise regression to determine, in a purely data-driven way, what variables potentially predicted changes in Motor Activity Log Amount of Use (MAL AOU) scale scores after therapy. We used the combined procedures for inclusion and exclusion of variables in SPSS version 14.a The criteria for variable inclusion and exclusion were: probability of F to enter ≤0.050, probability of F to remove ≥0.10. We found that among a large number of variables (see below) initially considered to predict changes in MAL AOU subscale scores after therapy, only 2 variables were included in the final regression model (regression model with 2 regressors: P<.0005, R2=0.123, n=133). The first variable to be included was the Wolf Motor Function Test Functional Activity Scale (WMFT FAS) score posttherapy (P<.0001, standardized coefficient=0.42). The second variable to be included was the “weight to box” task with the more-affected arm (a strength task part of the WMFT) measured upon enrollment in the study (P<.005, standardized coefficient=−0.336). The following variables, measured upon enrollment, just before therapy, and 1 week after therapy, were not included in the final model by the stepwise regression algorithm:
Upon enrollment: age, marital status, sex, affected side, concordance (did the stroke affect the dominant hand?), functional level (high or low), hand domain of the Stroke Impact Scale (SIS), Fugl-Meyer (FM) motor score, FM proprioception score, total FM score, MAL AOU and Quality of Movement (QOM) subscale scores, time score of the WMFT, and grip strength of the more-affected arm.
Before therapy: hand function domain of the SIS, natural logarithm of time score of the WMFT, FM motor score.
1 week after therapy: natural logarithm of time score of the WMFT, FM motor score (SIS data not available after therapy; see Wolf et al7 and Winstein et al19 for details).
Dr Schweighofer, C.E. Han, Dr Wolf, and Dr Winstein provided concept/idea/research design and data analysis. Dr Schweighofer, Dr Wolf, Dr Arbib, and Dr Winstein provided writing. C.E. Han, Dr Wolf, and Dr Winstein provided data collection. Dr Winstein provided project management. Dr Wolf provided fund procurement, participants, and facilities/equipment. Dr Wolf and Dr Winstein provided institutional liaisons. Dr Wolf, Dr Arbib, and Dr Winstein provided consultation (including review of manuscript before submission).
The authors thank Dr Jean Zhang, Dr Paul Thompson, and Dr Phill Miller for providing the EXCITE trial data and Dr James Gordon for helpful discussions.
The model was presented at the 37th Annual Meeting of the Society for Neuroscience Annual; November 3–7, 2007; San Diego, California.
This work was funded, in part, by National Institutes of Health/National Institute of Neurological Disorders and Stroke grant P20 RR020700-01 and R01 HD 37606.
Note that our model does not account for the approximately 20% of uncrossed fibers from the corticospinal tract.
SPSS Inc, 233 S Wacker Dr, Chicago, IL 60606.
References
- 1.Nakayama H, Jorgensen HS, Raaschou HO, Olsen TS. Compensation in recovery of upper extremity function after stroke: the Copenhagen Stroke Study. Arch Phys Med Rehabil 1994;75:852–857 [DOI] [PubMed] [Google Scholar]
- 2.Duncan PW, Wallace D, Lai SM, et al. The Stroke Impact Scale version 2.0: evaluation of reliability, validity, and sensitivity to change. Stroke 1999;30:2131–2140 [DOI] [PubMed] [Google Scholar]
- 3.Mayo NE, Wood-Dauphinée S, Cote R, et al. Activity, participation, and quality of life 6 months poststroke. Arch Phys Med Rehabil 2002;83:1035–1042 [DOI] [PubMed] [Google Scholar]
- 4.Butefisch C, Hummelsheim H, Denzler P, Mauritz KH. Repetitive training of isolated movements improves the outcome of motor rehabilitation of the centrally paretic hand. J Neurol Sci 1995;130:59–68 [DOI] [PubMed] [Google Scholar]
- 5.Kwakkel G, Wagenaar RC, Twisk JW, et al. Intensity of leg and arm training after primary middle-cerebral artery stroke: a randomized trial. Lancet 1999;354:191–196 [DOI] [PubMed] [Google Scholar]
- 6.Wolf SL, Blanton S, Baer H, et al. Repetitive Task practice: a critical review of constraint induced therapy in stroke. Neurologist 2002;8:325–338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wolf SL, Winstein CJ, Miller JP, et al. Effect of constraint-induced movement therapy on upper extremity function 3 to 9 months after stroke: the EXCITE randomized clinical trial. JAMA 2006;296:2095–2104 [DOI] [PubMed] [Google Scholar]
- 8.Winstein CJ, Wolf SL. Task-oriented training to promote upper extremity recovery. In: Stein J, Macko R, Winstein CJ, Zorowitz R. eds. Stroke Recovery and Rehabilitation New York, NY: Demos Medical; ;2008:267–290 [Google Scholar]
- 9.Wolf SL, Winstein CJ, Miller JP, et al. Retention of upper limb function in stroke survivors who have received constraint-induced movement therapy: the EXCITE randomised trial. Lancet Neurol 2008;7:33–40 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nudo RJ, Wise BM, SiFuentes F, Milliken GW. Neural substrates for the effects of rehabilitative training on motor recovery after ischemic infarct. Science 1996;272:1791–1794 [DOI] [PubMed] [Google Scholar]
- 11.Kleim JA, Barbay S, Nudo RJ. Functional reorganization of the rat motor cortex following motor skill learning. J Neurophysiol 2998;80:3321–3325 [DOI] [PubMed] [Google Scholar]
- 12.Liepert J, Bauder H, Wolfgang HR, et al. Treatment-induced cortical reorganization after stroke in humans. Stroke 2000;31:1210–1216 [DOI] [PubMed] [Google Scholar]
- 13.Taub E, Uswatte G, Morris DM. Improved motor recovery after stroke and massive cortical reorganization following constraint-induced movement therapy. Phys Med Rehabil Clin N Am 2003;14:S77–S91, ix [DOI] [PubMed] [Google Scholar]
- 14.Conner JM, Culberson A, Packowski C, et al. Lesions of the basal forebrain cholinergic system impair task acquisition and abolish cortical plasticity associated with motor skill learning. Neuron 2003;38:819–829 [DOI] [PubMed] [Google Scholar]
- 15.Winstein CJ, Rose DK, Tan SM, et al. A randomized controlled comparison of upper-extremity rehabilitation strategies in acute stroke: a pilot study of immediate and long-term outcomes. Arch Phys Med Rehabil 2004;85:620–628 [DOI] [PubMed] [Google Scholar]
- 16.Fujiwara T, Kasashima Y, Osada M, et al. Motor improvement and corticospinal modulation induced by hybrid assistive neuromuscular dynamic stimulation (HANDS) therapy in patients with chronic stroke. Clin Neurophysiol 2008;119:e82–e82 [DOI] [PubMed] [Google Scholar]
- 17.Han CE, Arbib MA, Schweighofer N. Stroke rehabilitation reaches a threshold. PLoS Computat Biol 2008;4:e1000133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wolf SL. Revisiting constraint-induced movement therapy: are we too smitten with the mitten? Is all nonuse “learned”? and other quandaries. Phys Ther 2007;87:1212–1223 [DOI] [PubMed] [Google Scholar]
- 19.Winstein CJ, Miller JP, Blanton S, et al. Methods for a multisite randomized trial to investigate the effect of constraint-induced movement therapy in improving upper extremity function among adults recovering from a cerebrovascular stroke. Neurorehabil Neural Repair 2003;17:137–152 [DOI] [PubMed] [Google Scholar]
- 20.Wolf SL, Lecraw DE, Barton LA, Jann BB. Forced use of hemiplegic upper extremities to reverse the effect of learned nonuse among chronic stroke and head-injured patients. Exp Neurol 1989;104:104–132 [DOI] [PubMed] [Google Scholar]
- 21.Wolf SL, Catlin PA, Ellis M, et al. Assessing the Wolf Motor Function Test as an outcome measure for research in patients after stroke. Stroke 2001;32:1635–1639 [DOI] [PubMed] [Google Scholar]
- 22.Wolf SL, Thompson PA, Morris DM, et al. The EXCITE trial: attributes of the Wolf Motor Function Test in patients with subacute stroke. Neurorehabil Neural Repair 2005;19:194–205 [DOI] [PubMed] [Google Scholar]
- 23.Uswatte G, Taub E, Morris D, et al. Reliability and validity of the upper-extremity Motor Activity Log-14 for measuring real-world arm use. Stroke 2005;36:2493–2496 [DOI] [PubMed] [Google Scholar]
- 24.Uswatte G, Taub E, Morris D, et al. The Motor Activity Log-28: assessing daily use of the hemiparetic arm after stroke. Neurology 2006;67:1189–1194 [DOI] [PubMed] [Google Scholar]
- 25.Chen SY, Han CE, Parikh N, et al. BART: a novel laboratory-based instrument to quantify preferred limb use in patients after stroke. Presented at: 38th Annual Meeting of the Society for Neuroscience;November 15–19, 2008;Washington, DC [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.