SHOULDER DEMANDS IN MANUAL WHEELCHAIR USERS ACROSS A SPECTRUM OF ACTIVITIES

Abstract

Objective

Investigate shoulder joint kinetics over a range of daily activity and mobility tasks associated with manual wheelchair propulsion to characterize demands placed on the shoulder during the daily activity of manual wheelchair users.

Design

Case series.

Subjects

Twelve individuals who were experienced manual wheelchair users.

Methods

Upper extremity kinematics and handrim wheelchair kinetics were measured over level propulsion, ramp propulsion, start and stop over level terrain, and a weight relief maneuver. Shoulder intersegmental forces and moments were calculated from inverse dynamics for all conditions.

Results

Weight relief resulted in significantly higher forces and ramp propulsion resulted in significantly higher moments than the other conditions. Surprisingly, the start condition resulted in large intersegmental moments about the shoulder equivalent with that of the ramp propulsion, while the demand imparted by the stop condition was shown to be equivalent to level propulsion across all forces and moments.

Conclusions

This study provides characterization of daily living and mobility activities associated with manual wheelchair propulsion not previously reported and identifies activities that result in higher shoulder kinetics when compared to standard level propulsion.

INTRODUCTION

The incidence of upper extremity (UE) pain in manual wheelchair users is remarkably high [Bayley et al, 1987; Curtis et al, 1999; Gellman et al, 1988; Pentland and Twomey, 1994; Sie et al, 1992; Wylie and Chakera, 1988], and is hypothesized to be a consequence of the repetitive nature and significant stresses associated with daily wheelchair use [Janssen et al, 1994; Subbarao et al, 1995]. The shoulder joint is the most common site of upper extremity pain in manual wheelchair users, with the reported incidence of pain ranging from 32%–78% [Boninger et al, 2001; McCasland et al, 2006; Salisbury et al, 2006]. Surveys indicate that shoulder pain occurs during many activities of daily life, but is most intense during activities of daily living including wheelchair propulsion up an incline, transfers, and other weight-bearing tasks [Curtis et al, 1999; Curtis et al, 1995; McCasland et al, 2006].

Despite the many studies analyzing the kinematics of manual wheelchair propulsion [Bednarczyk and Sanderson, 1994; Cooper et al, 1999; Davis et al, 1998; Finley et al, 2005; Gagnon et al, 2008; Nawoczenski et al, 2003; Rao et al, 1996; Riek et al, 2008; Rudins et al, 1997; Sanderson and Sommer, 1985; Van Drongelen et al, 2005], no causative link has been found between wheelchair propulsion and UE injury. Accordingly, investigators examined UE joint kinetics (forces and moments) in this population to explore the connection between mechanical loads during wheelchair propulsion and UE pathology. Intersegmental forces and moments are calculated values determined in response to external loading from an inverse dynamics model using rigid-body equilibrium equations. These model-estimated kinetic values are not directly measured and do not represent joint surface loading, but rather represent forces and moments between modeled rigid body segments. Although joint kinetics offer only partial insight into joint demands during an activity, they have been shown to provide a valuable, non-invasive characterization of demands associated with wheelchair propulsion. Recently, Mercer et al. [2006] reported asymptomatic manual wheelchair users who demonstrated larger shoulder joint forces and moments during level wheelchair propulsion were more likely to exhibit signs of shoulder pathology on MRI examination than those experiencing smaller kinetics. The results of this study indicate the value of joint kinetics as a metric in investigating mechanisms underlying the development of UE pain among manual wheelchair users.

In order to better understand the full range of kinetic demands on the shoulder in this population, activities beyond standard level propulsion require investigation. Previous studies have reported the shoulder joint kinetics during the push and/or recovery phases of level propulsion [Boninger et al, 1999; Boninger et al, 1997; Collinger et al, 2008; Koontz et al, 2002; Koontz et al, 2007; Kulig et al, 1998; Mercer et al, 2006; Robertson et al, 1996; Sabick et al, 2004; Van Drongelen et al, 2005; Veeger et al, 2002]. Many of these studies were performed on an ergometer for power and/or speed control. Fewer have investigated shoulder joint forces and moments during demanding conditions such as up an incline [Cerquiglini et al, 1981; Kulig et al, 1998; Sabick et al, 2004; Van Drongelen et al, 2005] or during a weight relief maneuver [Van Drongelen et al, 2005]. Koontz et al. [Koontz et al, 2005] reported on handrim kinetics during start-up propulsion, but we are not aware of any studies that have reported on shoulder kinetics during other phases of propulsion including start-up or stopping. A full description of all phases of propulsion is needed for a thorough understanding. The purpose of this study was to investigate shoulder joint kinetics over a range of daily activity and mobility tasks associated with manual wheelchair propulsion. Shoulder intersegmental forces and moments were calculated for level propulsion (level), ramp propulsion (ramp), start and stop on level terrain, and a weight relief maneuver (weight relief).

It is critical to the understanding of UE pathology in manual wheelchair users to fully investigate the activities that may be associated with injury. We hypothesize that the more difficult propulsion tasks such as ramp and start propulsion will result in higher shoulder moments when compared to level propulsion. Further, we hypothesize that the weight relief maneuver will result in higher shoulder forces when compared to the other conditions tested.

METHODS

Subjects

Twelve experienced manual wheelchair users without any current upper extremity injury were recruited for study participation (Table 1). Eleven participants were manual wheelchair users secondary to spinal cord injury; one secondary to spina bifida. All participants were between 29 and 56 years old (Average age of 43 ± 6.4 years) and had a minimum of one year of experience as a manual wheelchair user (Average 18 ± 9.0 years of experience, range of 1–29 years). Prior to testing all subjects underwent a physical examination by a licensed physical therapist for evaluation of UE strength, pain, and joint stability. Individuals were excluded from study participation if they reported having any upper extremity pain or injury within the past 6 months, or their occupation involved repetitive overhead activities. Additional study exclusion criteria included findings of incomplete/painful upper extremity range of motion or muscle weakness as determined by the physical examination. The study protocol was approved by the Mayo Clinic Institutional Review Board and informed consent was obtained from all research participants before initiating test procedures.

Table 1.

Subject Demographics

Subject	Gender	Age (years)	Height (cm)	Weight (kg)	Arm Dominance	Physical Disability	SCI Level	Years as Wheelchair User
1	M	45	178	79	R	SCI	T11	24
2	F	42	163	61	L	SCI	T12	14
3	M	44	183	86	R	SCI	T10	11
4	M	42	175	67	R	SCI	L1	16
5	M	45	180	61	R	SCI	T10	18
6	M	45	170	80	L	SCI	T4	22
7	M	56	170	82	R	SCI	T12	22
8	M	46	180	94	R	SCI	T5	29
9	M	29	152	61	R	SB	NA	29
10	M	42	175	75	R	SCI	T10	5
11	M	35	185	136	R	SCI	L1	1
12	M	45	183	114	R	SCI	T10	26

Abbreviations:

M=Male

F=Female

R=Right

L=Left

SCI=Spinal Cord Injury

SB=Spina Bifida

Instrumentation and Data Collection

SmartWheel devices (Three Rivers Holdings, Mesa, AZ) were fitted bilaterally to the subject’s wheelchair prior to testing (Fig. 1). The SmartWheel is a commercially available, wireless, force-and torque-sensing device used to measure three-dimensional forces (F_x, F_y, F_z) and moments (M_x, M_y, M_z) at the pushrim during propulsion and functional task [Cooper et al, 1997]. The precision (0.2 N) and resolution (2 N) of the SmartWheel rims have been documented [Cooper et al, 1997]. Application of the SmartWheel did not alter individual wheelchair settings. Subjects were allowed a self-determined amount of time to acclimate to the SmartWheels. The pushrim kinetics were collected at 240 Hz and low-pass filtered at 30 Hz with an eighth-order, zero-lag digital Butterworth filter [Cooper et al, 2002].

Figure 1.

Instrumented Smartwheel on subject’s wheelchair frame.

Kinematic data were recorded at 240 Hz using a 10 camera Real-time Eagle Motion Analysis system (Motion Analysis Corp., Santa Rosa, CA). Reflective markers were placed on 15 anatomical landmarks on the subject’s trunk and right upper extremity to define joint centers and segment lengths (Table 2). Additionally, three markers were placed on each SmartWheel for constructing a local wheel coordinate system. Marker position data were digitally filtered using a fourth-order, zero-phase, low-pass Butterworth filter with a 6-Hz cutoff frequency. Before dynamic data collection, a static, neutral position was collected for development of the local anatomical coordinate system.

Table 2.

Segment and Coordinate System (CS) Definitions

SEGMENT	MARKERS	CS ORIGIN	CS Sign Convention
Trunk	Sternum Xiphoid C7 T10	Geometric Center between Xiphoid and T10	Anterior (+X), posterior (−X) Medial (+Y), lateral (−Y) Superior (+Z), inferior (−Z)
Upperarm	Acromion process Medial epicondyle Lateral epicondyle	Shoulder center Defined by regression equation by de Leva47.
Forearm	Medial epicondyle Lateral epicondyle Radial styloid Ulnar styloid	Geometric center between epicondyle markers
Hand	Radial styloid Ulnar styloid 2nd MCP 5th MCP	Geometric center between radial and ulnar markers

Five dynamic conditions were evaluated in the following order: push phase of level propulsion, push phase of ramp propulsion up a 1:12 incline, push phase of start, negative acceleration phase of stop, and during a weight relief maneuver. The level and ramp propulsion conditions were performed over a distance of 10 m. In performing the start condition, subjects began from rest and were instructed to begin propelling at the onset of data collection. For the stop condition, the subjects began propelling over a 10 m distance and when they approached a designated line, they were instructed to bring their chair to a complete rest as they would when approaching a closed door. For the weight relief, subjects began at rest, then lifted the weight of their body with their hands on the handrim, held the position for 3 seconds, and returned to initial rest position. All conditions were performed at a self-selected speed. Five trials were performed for each condition, and subjects were allowed to rest between trials as needed. The kinematic and kinetic data for each trial were used as inputs to an inverse dynamics model.

Data Analysis

A three-dimensional model of the right upper extremity was developed using Visual3D (C-Motion Inc., Germantown, MD). The model consisted of four rigid body segments: trunk, right upper arm, right forearm, and right hand. Local anatomic coordinate systems, following the right hand rule, were defined for each segment based on the UE marker set (Table 2) Euler angles were used to describe the joint kinematics of the distal segment relative to the proximal segment following the ISB recommended rotation sequences for the wrist, elbow, and shoulder joints [Wu et al, 2005].

The shoulder intersegmental forces and moments at the wrist, elbow, and shoulder were determined using a recursive inverse dynamic procedure implemented in Visual3D [Hof, 1992; Kaufman et al, 1995]. In the recursive approach, the proximal joint reaction force in the global coordinate system is determined using an iterative algorithm that allows for the application of any external force to the segment as follows:

$${\mathbf{F}}_{\mathit{proximal}}=\sum _{i-1}^n{m}_i({\mathbf{a}}_i+\mathbf{g})+\sum _{j-1}^q{\mathbf{F}}_q+{\mathbf{F}}_{\mathit{distal}}$$

where

m_i = mass of segment i

a_i = linear acceleration of segment i

n = number of distal segments connected in chain

q = nu mber of external forces

F_q = applied external forces

The proximal moment due to the inertial forces and applied moments at the joint is determined as follows:

$$M_{\mathit{proximal}}=\sum _{i-1}^n({\mathbf{C}}_i+{\mathbf{R}}_i\times {\mathbf{A}}_i)+\sum _{j-1}^q({\mathbf{P}}_j\times {\mathbf{F}}_q)+\sum _{k-1}^p{\tau }_k+M_{\mathit{distal}}$$

where

C_i = inertial torque in the global coordinate system

R_i = distance from center of gravity of each distal segment to proximal joint

A_i = m_i(a_i+g)

P_j = vector from the application of external force to proximal joint

p = number of external moment couples

τ_k = applied external moment couples

Segment mass and center of gravity (relative to subject height and weight) were based on existing anthropometric data [Dempster, 1955], as was the moment of inertia for each segment [McConville et al, 1980]. The assumed point of hand contact for the external SmartWheel pushrim forces and moments was the second metacarpalphalangeal joint [Robertson et al, 1996]. The external forces and moments from the SmartWheel were transformed from the wheel reference frame into the global coordinate system before being applied to the second metacarpalphalangeal joint. The resulting shoulder intersegmental forces were expressed in the humerus coordinate system, distal segment to the shoulder joint. The humerus coordinate system was centered at the shoulder center [de Leva, 1996]. The force direction definitions were as follows: anterior (+) and posterior (−) of the x axis, medial (+) and lateral (−) of the y axis, and superior (+) and inferior (−) of the z axis. Shoulder intersegmental moments, about the shoulder joint center, were expressed in a non-orthogonal joint coordinate system (JCS) in accordance with the ISB recommendations for kinematics [Wu et al, 2005]. The JCS representation expresses the kinematics and moments in terms of the plane of elevation (POE), elevation, and axial rotation [Collinger et al, 2008]. The moment direction definitions were as follows: POE flexion (+) and POE extension (−) moments about the trunk z axis, elevation abduction (+) and elevation adduction (−) moments about the humerus x axis, and internal (+) and external (−) rotation moments about the humerus z axis. To simplify the data representation and discussion, moments about the trunk z axis will be referred to as either as a flexion or extension moment, and those about the humerus x axis will be referred to as either an abduction or adduction moment.

The shoulder intersegmental forces and moments were calculated for all trials of all conditions. The first and last trials for all conditions were disregarded. For the remaining three trials, a starting and ending event was defined for each condition to extract the data of interest. For conditions involving forward propulsion (level, ramp, and start), one push phase was chosen from the remaining trials. The start and end of the push phase were defined based on the detection of an applied propulsion moment to the handrim and the removal of that applied moment [Kwarciak et al, 2007]. For the stop condition, the starting event occurred when a negative propulsion moment was applied on the handrim and ended with the wheelchair returning to rest. The starting event of the weight relief maneuver occurred at detection of an applied inferior force on the handrim, and the ending event occurred when the handrim force returned to zero (subjects returned to rest and removed their hands from the rim). The data chosen from each of the three remaining trials were normalized to 101 points and averaged to obtain a mean cycle for each subject and each condition. Peak shoulder forces and moments during the mean task cycle in each direction were identified for each subject using an algorithm implemented in MATLAB (Mathworks Inc., Natick, MA). Forces were normalized to subject body weight and moments were normalized to body weight and height to reduce the variability in the data due to these factors and allow for comparing between studies. The peak kinetic values were averaged to represent the mean peak forces and moments at the shoulder.

Statistical Analysis

The variables of interest were the peak shoulder intersegmental forces and moments during the wheelchair activities and propulsion tasks: level, ramp, start, stop, and weight relief. A one-way ANOVA with five repeated measures (level, ramp, start, stop, and weight relief) was performed for each variable of interest (α =.05). Separate analyses were performed for each axis direction. When significant main effects were observed, post hoc Tukey pairwise comparisons (α = .05) were performed to compare the means of each kinetic direction between each condition. The Tukey test was chosen for its conservative analysis and control over Type 1 errors. All statistical analyses were performed in SAS (SAS Institute, Cary, NC).

RESULTS

There was a significant main effect of condition for the shoulder intersegmental forces in four of the six force directions: anterior (p=.001), posterior (p<.001), medial (p=.003), and superior (p<.001) (Fig. 2). There were no observed shoulder inferior forces during any of the conditions, so the direction was removed from the analysis. Post-hoc analysis indicated that in the ramp condition the anterior force was significantly higher than level, weight relief, start, and stop; and the posterior force of the ramp and weight relief conditions were significantly higher than level, start, and stop (Fig. 2). Additionally, the weight relief medial force was significantly higher than level, start, and stop, but not different from ramp (Fig. 2). The weight relief superior force was significantly higher than level, ramp, start, and stop (Fig. 2). The level, start, and stop conditions were statistically equivalent for all force directions. There was no main effect of condition for the shoulder lateral force (p=0.334) (Fig. 2).

Figure 2.

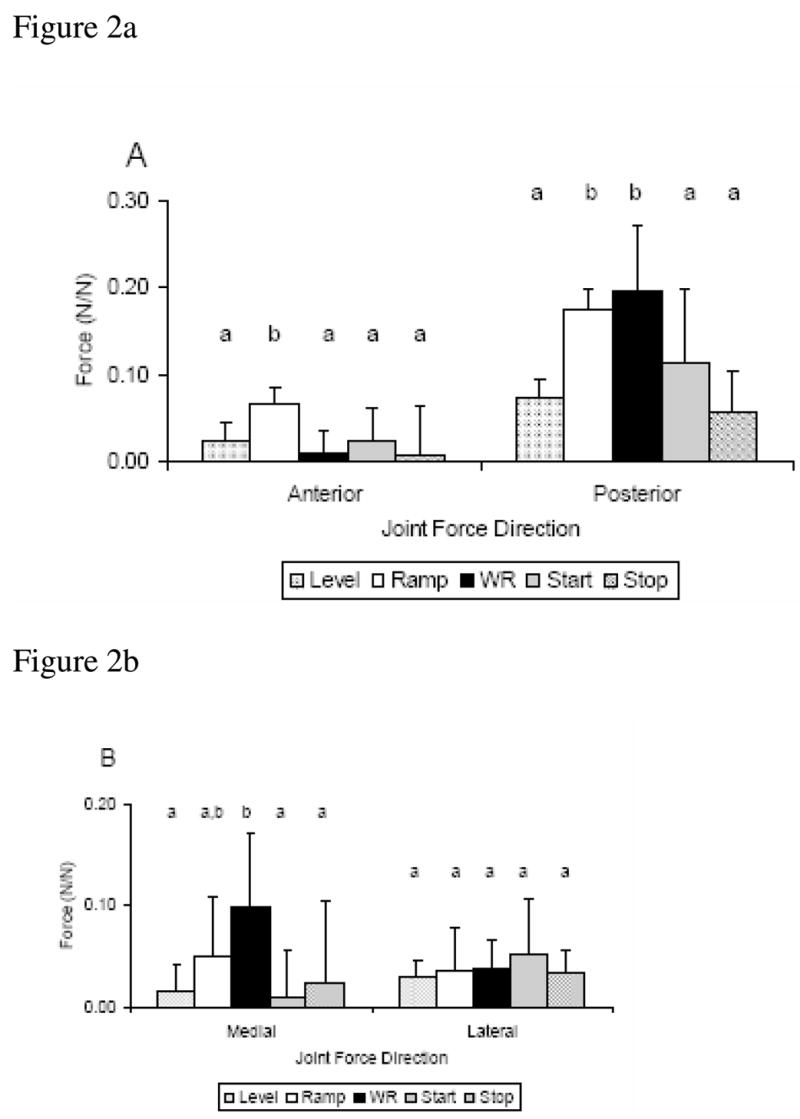
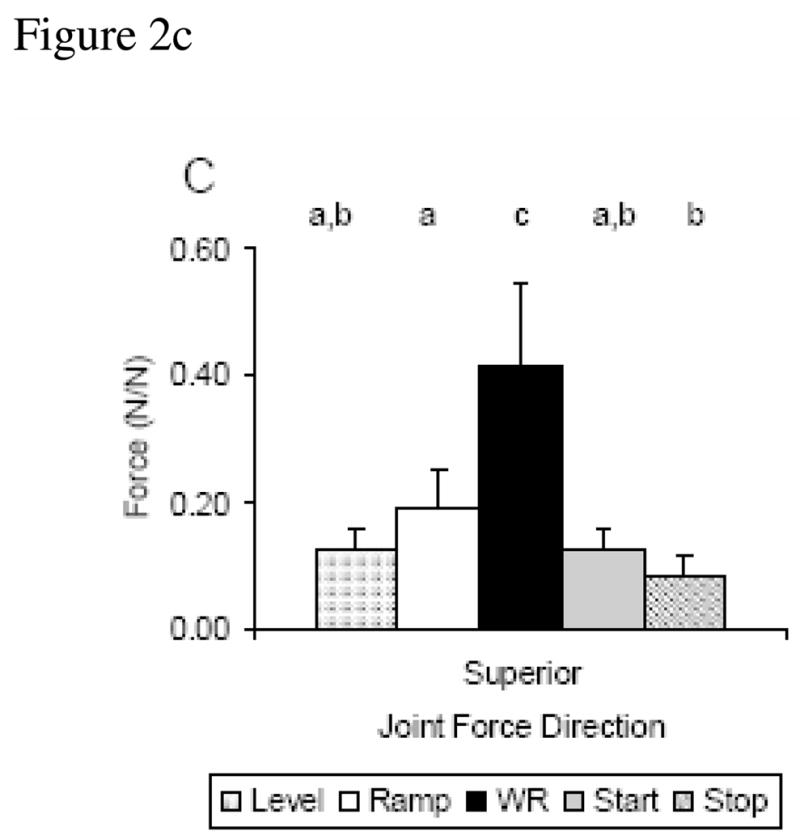
(A–C). Mean and standard deviation across condition for peak forces in each direction, (A) Anterior/Posterior, (B) Medial/Lateral, (C) Superior. Statistically significant different conditions (p≤0.05) are identified by lower case letters.

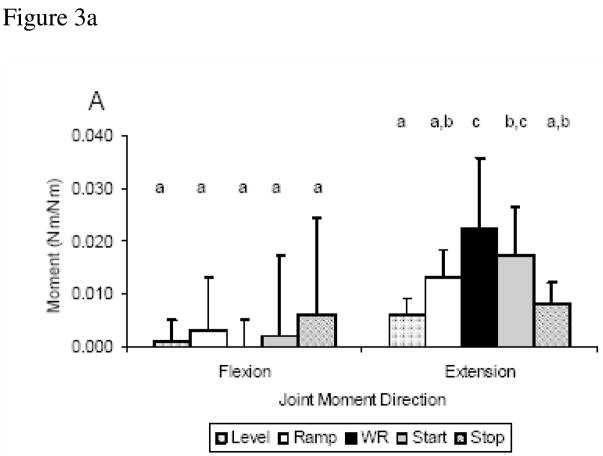
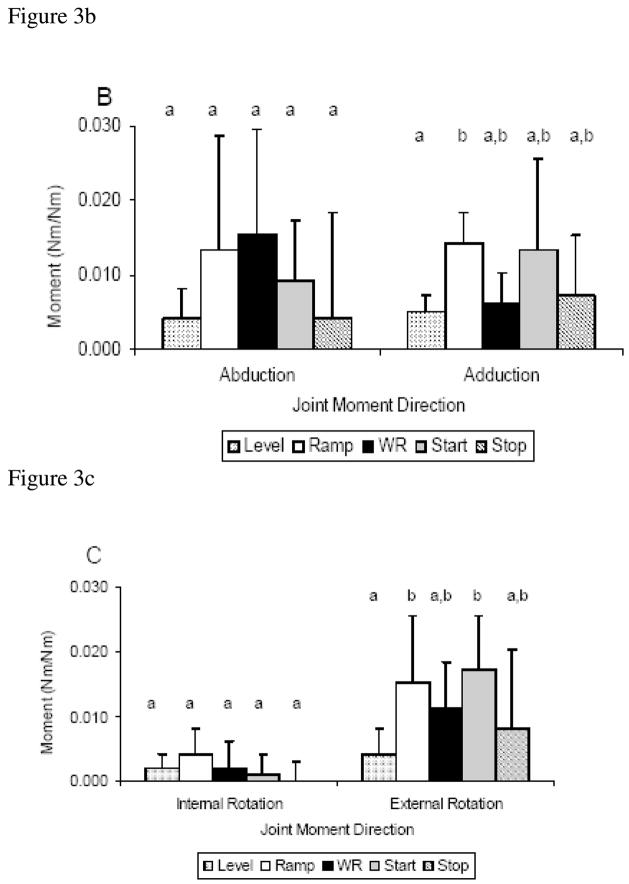
Analysis of the shoulder intersegmental moments revealed a significant main effect of condition for three of the six moment directions: extension (p<.001), adduction (p=.009), and external rotation (p=.004) moments (Fig. 3). Post-hoc analysis indicated the extension moment for weight relief was equivalent to that of start but significantly greater than the level, ramp, and stop (Fig. 3). Additionally, the adduction moment for ramp was significantly higher than the level condition, and the external rotation moment of ramp and start were significantly greater than in the level condition (Fig. 3). There was no main effect of condition for the flexion (p=0.742), abduction (p=0.092), or internal rotation moments (p=0.102) (Fig. 3).

Figure 3.

(A–C). Mean and standard deviation across condition for peak moments in each direction, (A) Flexion/Extension, (B) Abduction/Adduction, (C) Internal/External Rotation. Statistically significant different conditions (p≤0.05) are identified by lower case letters.

DISCUSSION

The results of this study indicate that the joint intersegmental forces and moments at the shoulder vary significantly across daily activity and mobility tasks associated with manual wheelchair propulsion. Consistent with our hypotheses, the weight relief condition resulted in significantly higher shoulder forces than the level, start, and stop conditions. The ramp condition followed the weight relief condition in magnitude in many of the force directions. While these results are not surprising, the six directional force values for all five conditions have not been previously reported. Also consistent with our hypotheses, the shoulder moments during ramp and start conditions were higher than level propulsion for the majority of the reported moments. The shoulder moments of the ramp and start conditions were shown here to be unexpectedly equivalent. This is the first investigation to highlight the large kinetics experienced at the shoulder during the starting of propulsion. The inclusion of start and stop conditions in this study completes a full investigation of peak kinetics during all intervals of level propulsion [Hurd et al, 2008].

While joint intersegmental forces and moments cannot be directly linked to pain or injury etiology, several specific shoulder moment and force magnitudes have been correlated with signs of shoulder pathology from MRI. Large superior forces during propulsion have been associated with an increased prevalence of shoulder pathology on MRI scans [Mercer et al, 2006]. The weight relief condition in this study resulted in a peak superior force (0.42±0.13 N/N) greater than two times the magnitude of ramp propulsion (0.19±0.06 N/N) and three times the magnitude of level propulsion (0.12±0.04 N/N). This data, based on our model estimates, shows the potential of weight relief and ramp to be very high loading activities when compared to level propulsion and may over time contribute to pathology in the shoulder. High extension moments and abduction moments are loads that have also been correlated with signs of shoulder pathology [Mercer et al, 2006]. Ramp propulsion, weight relief and the start condition all exhibited higher extension and abduction moments when compared to level. It is consistent across our data that the weight relief, ramp and start conditions exhibit the highest shoulder intersegmental forces and moments and place the largest estimated load on the shoulder.

The level of injury risk of an activity is not only dependent on the load the activity produces at a joint, but also on the frequency with which the activity is performed. If high load activities such as weight relief, ramp propulsion, and start-up propulsion are performed once during a day, they may not have a negative impact on the joint. Unfortunately, the high load activities in this study do have a frequency that causes concern. The U.S. Department of Health and Human Services recommends performing weight relieving movements every 15 minutes to prevent pressure ulcers for those able to shift their own body weight [1992]. The high frequency in combination with the high forces positions the weight relief maneuver as an activity that places the shoulder under a high risk of pain or injury. Starting propulsion and ramp propulsion are also common components to independent mobility. Starting from rest occurs numerous times during a day, and inclines of varying degrees are frequent outdoors and within indoor settings. The high load activities are also performed without a recovery period, with other high load activities or level propulsion commonly to follow [Van Drongelen et al, 2005]. For people who use manual wheelchairs, a large percentage of the day, every day, is spent participating in high demand activities, placing every user at a high risk for pain and injury.

It is challenging to compare joint kinetics across studies because of investigator specific marker sets and biomechanical models. The forces reported in this study for level, ramp and weight relief were of a similar relative magnitude as values previously reported in the literature [Collinger et al, 2008; Koontz et al, 2002; Kulig et al, 1998; Sabick et al, 2004; Van Drongelen et al, 2005]. The kinetics in this study were normalized to body weight (forces) and body weight and height (moments) comparable to normalization methods implemented during lower extremity analysis. This has not been the trend in upper extremity wheelchair research; therefore, direct comparisons of force and moment magnitudes were not possible. The ISB has recommended the nonorthogonal JCS for kinematic description [Wu et al, 2005], and because of its anatomical significance, the JCS has been recommended for lower extremity moment representation for clinical interpretation [Schache and Baker, 2007]. In agreement with the rationale put forth by Schache and Baker [2007], we have chosen to represent the shoulder moments in the JCS. The direct comparison of moments across studies, except for the axial rotation moment, is therefore, not legitimate. The axial rotations from this study compare favorably to those reported by Sabick et al. [2004] where the ratio of the external to internal moment ratio was 3.7 and the same ratio from the current study was 3.8.

This study had limitations. First, the clinical interpretation made from model-estimated intersegmental forces and moments calculated from inverse dynamics is limited. The forces do not represent joint surface loading (joint contact force), and the joint moment is only an estimate of the net activity of all muscle groups crossing a particular joint. As it is unfeasible to measure invivo joint contact forces without an invasive procedure, more complex musculoskeletal modeling and optimization techniques are required to estimate the contact forces and individual muscle contributions to the joint moment. With muscle optimization algorithms and their estimated joint contact forces, it is possible to identify activities and strategies that place manual wheelchair users at risk for injuries such as impingement and anterior sublaxation. Second, there was a small sample number. The recent multi-site study by Collinger et al. [2008] highlights the need for more collaborative work to achieve data that can be widely applied between studies and individuals [van der Woude et al, 2001]. Third, the shoulder is represented as a thoracohumeral pseudo-joint where the proximal segment is the thorax. The proximal segment of the anatomical glenohumeral joint is the scapula. A scapula tracking device is necessary to accurately represent the glenohumeral kinematics and kinetics, and although the model used in this study incorporated ISB recommended rotation sequences and the Euler sequence order for the JCS, the marker set and subsequent segment coordinate systems do not completely follow the recommendations. This will not allow for a complete comparison between published data. Finally, this study presented only on shoulder kinetics. UE injury during wheelchair propulsion and activities of daily living occurs commonly at the elbow and wrist joints as well as at the shoulder. Elbow and wrist kinetics are necessary for a thorough discussion on UE injury and injury prevention.

CONCLUSIONS

In conclusion, this study offers insight to shoulder demands across a spectrum of activities. High forces during weight relief and large moments during ramp propulsion were expected. Surprisingly, the start condition resulted in large moments about the shoulder equivalent with that of the ramp propulsion, while the estimated demand imparted by the stop condition was shown to be equivalent to level propulsion across all forces and moments. This study provides characterization of daily living and mobility activities associated with manual wheelchair propulsion not previously reported and identifies activities that result in higher shoulder intersegmental kinetics when compared to standard level propulsion.

Biographies

Kai-Nan An, Ph.D., has a joint appointment as consultant in the Department of Orthopedic Surgery and in the Department of Physiology and Biophysics at Mayo Clinic, Rochester, MN. He holds the academic rank of Professor of Bioengineering, Mayo Medical School, and is recognized with the distinction of a named professorship, the John and Posy Krehbiel Professorship of Orthopedics. An author of more than 600 peer-reviewed publications, Dr. An's interests in research include biomechanics, biomaterials, orthopedics and rehabilitation.

Dr. Hurd is a post-doctoral research fellow in the Motion Analysis Laboratory, Department of Orthopaedics at the Mayo Clinic in Rochester, MN. She received her undergraduate degree (physical therapy) from the University of Missouri-Columbia, and both master and doctoral degrees (biomechanics and movement science) from the University of Delaware. Dr. Hurd is a physical therapy board certified sports specialist. Her research emphasis is neuromuscular contributions to joint stability, and clinically she specializes in sports injuries to the shoulder, knee, and elbow.

Kenton R. Kaufman, Ph.D., P.E. Kenton Kaufman is the Director of the Biomechanics Laboratory, Professor of Bioengineering, and Consultant in the Departments of Orthopedic Surgery, Physiology and Biomedical Engineering at the Mayo Clinic. He is a registered professional engineer. He received his Ph.D. degree in biomechanical engineering from North Dakota State University in 1988. Dr. Kaufman’s research focuses on the biomechanics of human movement. He currently holds several grants from NIH, with projects aimed at improving the mobility of disabled individuals. He has published over 100 scientific papers, 35 book chapters, and holds 6 patents. He was elected as a Fellow in the American Institute for Medical and Biological Engineering in 2002.

Melissa M.B. Morrow is a doctoral student in the Mayo Graduate School at Mayo Clinic. She received her B.S.E. in Biomedical Engineering at Tulane University in 2003. Her doctoral research is focused on the modeling of shoulder biomechanics during wheelchair propulsion.