Reaction Pathway and Free Energy Barrier for Reactivation of Dimethylphosphoryl-inhibited Human Acetylcholinesterase

Abstract

The dephosphorylation/reactivation mechanism and the corresponding free energy profile of dimethylphosphoryl-inhibited conjugate of human acetylcholinesterase (AChE) has been studied by performing first-principles quantum mechanical/molecular mechanical free energy (QM/MM-FE) calculations. Based on the QM/MM-FE results, for the favorable reaction pathway, the entire dephosphorylation/reactivation process consists of three reaction steps, including the nucleophilic water attack on the P atom, the spatial reorganization of the dimethylphosphoryl group, and the dissociation between the dimethylphosphoryl group and Ser203 of AChE. The overall free energy barrier for the entire dephosphorylation/reactivation reaction is found to be the free energy change from the initial reactant to the transition state associated with the spatial reorganization step, and the calculated overall free energy barrier (20.1 to 23.5 kcal/mol) is reasonably close to the experimentally-derived activation free energy of 22.3 kcal/mol. In addition, key amino acid residues and their specific roles in the reaction process have been identified.

Introduction

Organophosphorus (OP) compounds, such as paraoxon, methamidophos, sarin, soman, VX, and tabun, are highly neurotoxic due to their irreversible inhibition of acetylcholinesterase (AChE), an essential enzyme for metabolizing neurotransmitter acetylcholine (ACh). Due to the neurotoxicity associated with the irreversible inhibition of AChE, OP compounds have been used in modern agriculture as insecticides (e.g. paraoxon) and in military as chemical warfare nerve agents (e.g. sarin, soman, VX, and tabun). The acute toxicity of over-exposure to such OP compounds is well known. Exposure to OP compounds may result in serious damage to the nervous system.^1-3 However, in spite of the efforts in trying to reduce the toxic effects from OP insecticides, the broad distribution of OP compounds still causes several hundred thousands of intoxications each year, of which some are fatal.^4-9 In addition, the OP nerve agents continue to be a threat to the society due to their possible use during military conflicts or in terrorist acts.^10-12

The chemical reaction of an OP compound with AChE consists of two major stages. The first stage is phosphorylation of AChE, leading to a phosphorylated enzyme in which the P atom of the OP compound covalently bonds to the hydroxyl oxygen of the catalytic serine residue (Ser203) of AChE. The second stage is either an aging process in which another ester group of the OP compound leaves the P atom or a dephosphorylation process in which the hydroxyl oxygen of Ser203 leaves the P atom. The first stage, i.e. the phosphorylation, is generally much faster, leading to a quick inhibition of the enzyme. As a result, the second stage, i.e. the aging or dephosphorylation, is generally known as a rate-determining step of the reaction. Whereas the aging process produces an aged enzyme which no longer can be reactivated, the dephosphorylation process returns the enzyme to its original active form. So, the dephosphorylation is also known as the reactivation of the enzyme. The phosphorylation and dephosphorylation/reactivation constitute the entire hydrolysis process.

For most OP compounds, the dephosphorylation process is slower than the aging process. This causes the second stage mainly to undergo the aging process, making AChE irreversibly inactive. Moreover, for some OP compounds that are very toxic, such as sarin and DFP (diisopropylfluorophosphate), the dephosphorylation process is too slow to be observed while the aging process happens at an observable reaction rate.¹³ Thus, it is necessary to reduce or remove the toxicity of the OP compounds by increasing the dephosphorylation reaction rate through site-directed mutagenesis. However, the detailed mechanism of dephosphorylation of AChE-OP conjugates still remains unclear and some crucial mechanistic issues including the nature of the transition state have not yet been addressed. The goal of the present study is to understand the fundamental reaction mechanism of the dephosphorylation of human AChE (AChE)-OP conjugate.

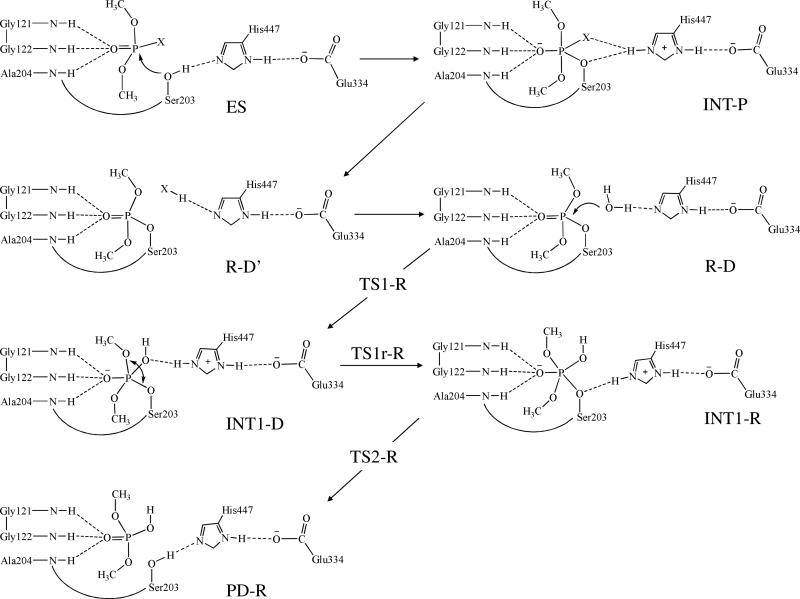
Although the detailed mechanism of dephosphorylation of AChE-OP conjugates remains unclear in literature, various techniques including X-ray crystallography,¹⁴ site-directed mutagenesis,¹⁵ and molecular modeling¹⁶ have been used to explore some valuable insights into the reaction mechanism. All of the reported studies indicate that OP compounds mainly interact with the catalytic triad (consisting of Ser203, His447, and Glu334) and oxyanion hole (consisting of Gly121, Gly122, and Ala204) in the active site of AChE. Based on the available mechanistic insights and in light of the detailed mechanistic insights obtained from our recent computational studies on AChE- and butyrylcholinesterase (BChE)-catalyzed hydrolysis of carboxylic esters (e.g. ACh, butyrylcholine, (+)-cocaine, and (−)-cocaine),^17-24 we can reasonably assume that the catalytic residues for AChE-catalyzed hydrolysis of an OP compound should be the same as those for BChE-catalyzed hydrolysis of cocaine. Based on this assumption, our initial computational exploration of the possible AChE-OP reaction pathways in the present study led us to propose a more hypothesis of the detailed reaction mechanism for AChE-catalyzed hydrolysis of an OP compound (Scheme 1 using paraoxon-methyl as a typical example).

Scheme 1.

Starting from this mechanistic hypothesis, in the present study, we have carried out first-principles quantum mechanical/molecular mechanical-free energy (QM/MM-FE) calculations^25-28 to test the hypothesis and uncover the detailed reaction pathway for the dephosphorylation reaction of AChE-OP conjugate. In the QM/MM-FE calculations, first-principles QM/MM reaction coordinate calculations were followed by free energy perturbation (FEP) calculations on the protein environment in order to more reasonably account for the dynamic effects of protein environment on the free energy barriers for an enzymatic reaction. Our QM/MM simulations are based on the pseudobond first-principles QM/MM approach,^25,26,28,29 which has been demonstrated to be powerful in simulating a variety of enzymes,^27,30-40 and some theoretical predictions^30,32 were subsequently confirmed by experimental studies.^41-43 Very recently, this pseudobond first-principles QM/MM approach has been successfully employed to redesign a more efficient cocaine hydrolase, whose catalytic efficiency has been improved by 2000-fold in comparison with the wild-type enzyme.¹⁸

In our current study, paraoxon-methyl was chosen as a typical representative of the OP inhibitors of AChE, as the experimental kinetic data were well-established for this reaction system. The computational results clearly reveal the detailed reaction pathway and the corresponding free energy profile for the dephosphorylation reaction process. The computational results also demonstrate the specific roles of some key residues involved in the reaction process.

Methods

Structure Preparation

The starting model of enzyme-substrate complex was constructed on the basis of the X-ray crystal structure of human AChE complexed with fasciculin-II (PDB code 1B41).⁴⁴ The ligand fasciculin-II was removed from the X-ray crystal structure and the missing loops of the protein were built by SWISS homology server.⁴⁵ The dimethylphosphoryl structure was built by referring the orientation of diethylphosphoryl moiety in the crystal structure of mouse AChE-DFP conjugate (PDB code 2JGI).⁴⁶ The missing hydrogen atoms were added using the LEaP module of AMBER8 program.⁴⁷ All the crystal water molecules were kept and appropriate sodium ions were added to neutralize the system. The system was then solvated in a rectangular box of TIP3P water molecules⁴⁸ with a minimum solute wall distance of 10 Å.

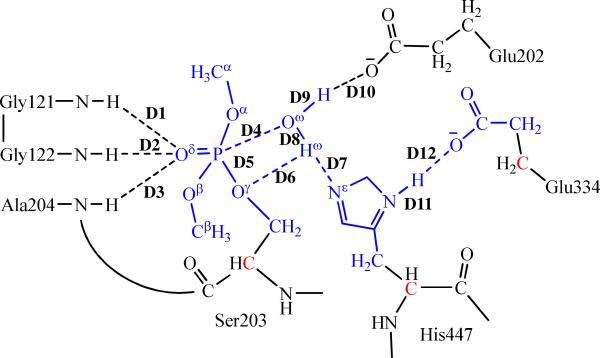
To account for possible structural reorganization and protein dynamics, the prepared system was equilibrated by gradually increasing the temperature from 10 K to 298.15 K after energy minimization. Then, the production MD simulation at 298.15 K was kept running for 2 ns. In the MD simulation, SHAKE procedure^49,50 was employed to constrain all bonds involving hydrogen atoms, and the time step of the simulation was 2 fs with a cutoff of 10 Å for nonbonded interactions. The last snapshot of the MD simulation was used to prepare pseudobond QM/MM calculations, as the structure at the last snapshot was close to the average structure simulated. Since we are interested in the reaction center, the water molecules beyond 47 Å of the P atom were removed, making the QM/MM system containing 2,220 water molecules and a total of 14,916 atoms. As illustrated in Figure 1, dimethylphosphoryl, the attacking water, and side chains of Ser203, His447, and Glu334 are defined as QM atoms. The QM/MM interface has been described by a pseudobond approach.^26,28,29 Prior to the QM/MM geometry optimization, the initial reaction system was energy-minimized with MM method by using the revised TINKER program⁵¹ with AMBER force field, where the convergence criterion is the root-mean-square deviation (RMSD) of the energy gradient of less than 0.1 kcal·mol⁻¹·Å⁻¹.

Figure 1.

Division of the QM/MM system for simulating the dephosphorylation of dimethylphosphoryl-inhibited AChE. Atoms in blue are treated by QM method. Three boundary carbon atoms (colored in red) are treated with the improved pseudobond parameters (ref.²⁸). All other atoms belong to the MM subsystem. Labeled in the figure are 12 key distances involving Glu334, Glu202, and residues in the oxyanion hole in the reaction center of dephosphorylation reaction.

Minimum Energy Path of the Enzymatic Reaction

The reaction coordinate driving method for determining a minimum energy path via pseudobond QM/MM calculations is to restrain the reaction coordinate to a specific value with a certain harmonic force constant.²⁵ The bond formation/breaking is always involved in a chemical reaction step. The internuclear distances that reflect the bond formation/breaking are therefore usually selected to represent the reaction coordinate. In the previously revised TINKER program,^25,51 the reaction coordinate can only be a linear combination of internuclear distances. However, in the present study, a spatial reorganization of the dimethylphosphoryl that is in the trigonal bipyramidal conformation was found after nucleophilic attack on the P atom by water molecule, during which no bond formation or breaking happens. Although a conformational change can usually be modeled by carrying out simpler, classical MD simulations, the lack of proper force field parameters for different trigonal bipyramidal conformations of the phosphoryl group makes such type of classical MD simulations impractical or unreliable. Furthermore, we preferred to examine all of the reaction steps at the same level of theory. Therefore, in order to also understand the spatial reorganization process, bond angles and dihedral angles are introduced in the following generalized equation for the definition of a reaction coordinate:

$$E_{res}=\frac{1}{2}k{(\sum _i{w}_{i}R\left(a_i{b}_i\right)+\sum _j{w}_j\theta \left(a_j{b}_j{c}_j\right)R\left(a_j{b}_j\right)+\sum _m{w}_m\varphi \left(a_m{b}_m{c}_m{d}_m\right)R\left(a_m{b}_m\right)-s)}^2$$ (1)

where k is the force constant. i, j, and m are the index numbers for restrained bond lengths (distances), bond angles, and dihedral angles, respectively. w_i, w_j, and w_m are the weights for each bond, angle, and dihedral angle, respectively. R(a_ib_i) is the distance between atoms a_i and b_i; θ(a_jb_jc_j) is the angle formed by atoms a_j, b_j, and c_j, of which atom b_j is the vertex of the angle. The radius of the angle movement corresponding to θ(a_jb_jc_j) is taken as R(a_jb_j), i.e. the distance between atoms a_j and b_j. φ(a_mb_mc_md_m) is the dihedral angle formed by atom a_m, b_m, c_m, and d_m, where atoms b_m and c_m form the intersection line of the dihedral angle. The radius of the dihedral angle movement corresponding to φ(a_mb_mc_md_m) is taken as R(a_mb_m), i.e. the distance between atoms a_m and b_m. s is the target value to which the reaction coordinate should be restrained.

The generalized equation, i.e. Eq.(1), proposed in this study has been implemented in a further revised version of TINKER program. Note that the more variables were used as the reaction coordinate, the more solutions to Eq.(1) could be obtained, among which not all of the solutions can lead to the minimum energy path of the reaction. Therefore, it is necessary to keep the effectiveness of this reaction coordinate driving method by selecting the geometrical variables as less as possible to best represent the reaction coordinate for each reaction step. In addition, although the distances, angles, and dihedrals can be included in a reaction coordinate as shown in Eq. (1), one must note that the weights on individual components, i.e. w_i, w_j, and w_m, may not always be +1 or −1, because the geometric changes of different types (particularly the bond lengths versus angles) may affect the energy of the reaction system in rather different energy scales. For example, the energy change with respect to changing a bond length is generally much more sensitive than that with respect to changing a bond angle or dihedral angle. Hence, when multiple types of geometric parameters are included in a reaction coordinate according to Eq. (1), the practical assignment of the weights on different types of geometric parameters must be examined carefully. Nevertheless, in the present study, we only needed to use a single type of geometric parameters (that are either the distances or the angles) in the reaction coordinate for each of the reaction steps.

With this reaction coordinate driving method and an iterative energy minimization procedure, the enzyme reaction path was determined by the pseudobond QM/MM calculations at B3LYP/6-31G*:AMBER level, in which the QM calculations were performed at the B3LYP/6-31G* level of theory and the MM calculations were performed by using AMBER force field implemented in the TINKER program. Normal mode analyses were performed to characterize the initial reactant in the dephosphorylation reaction, intermediates, transition states, and the dephosphorylated product. In addition, single-point energy calculations were carried out at the QM/MM(B3LYP/6-31+G*:AMBER) level on the QM/MM-optimized geometries to evaluate the energy barriers. Throughout the QM/MM calculations, the boundary carbon atoms are treated with improved pseudobond parameters.²⁸ The pseudobond QM/MM calculations were carried out using a modified version of Gaussian03⁵² and TINKER⁵¹ programs with AMBER force field. For QM subsystem, the convergence criterion for geometry optimizations follows Gaussian03 defaults. For MM subsystem, the geometry optimization convergence criterion is when the RMSD of energy gradient is less than 0.1 kcal·mol⁻¹·Å⁻¹. Only atoms within 20 Å of the P atom were allowed to move. No cutoff for nonbonded interactions was used in the QM/MM calculations.

Free Energy Perturbation

After the minimum energy path was determined by the QM/MM calculations, the free energy changes associated with the QM-MM interactions were determined by using FEP method.²⁵ In FEP calculations, sampling of the MM subsystem was carried out with the QM subsystem frozen at different states along the reaction path. The point charges on the frozen QM atoms used in the FEP calculation are those determined by fitting the electrostatic potential (ESP) in the QM part of QM/MM calculation. The total free energy difference between the transition state and the reactant was obtained from the following formula:

$$\Delta F(R\to TS)=\Delta F_{qm∕mm}(R\to TS)+\Delta E_{qm}(R\to TS)+\Delta F_{qm}^{fluctuation}(R\to TS)$$ (2)

where ΔF_qm/mm (R → TS) is the free energy change associated with the QM-MM interaction. ΔE_qm (R → TS) refers to the QM energy difference between the two QM subsystems, and $\Delta F_{qm}^{fluctuation}(R\to TS)$ is the change in contribution from QM subsystem fluctuation to the free energy difference.⁵³ The FEP calculations enabled us to more reasonably determine relative free energy changes due to the QM-MM interaction. Technically, the final (relative) free energy determined by the QM/MM-FE calculations is the QM part of the QM/MM energy (excluding the Columbic interaction energy between the point charges of the MM atoms and the ESP charges of the QM atoms) plus the relative free energy change determined by the FEP calculations. In FEP calculations, the time step used was 1 fs, and bond lengths involving hydrogen atoms were constrained. A twin-range cutoff method was used to treat nonbonded interactions, with a long-range cutoff of 12 Å, a short-range cutoff of 8 Å, and the nonbonded pair list updated every 20 steps. In MD simulations, the temperature was maintained at 300 K using the weak coupling method with a coupling time of 0.1 ps. Each FEP calculation consisted of 10 ps of equilibration and 50 ps of sampling. The final relative free energies were taken as the average of the “forward” and “backward” perturbation results.

Results and Discussion

Identification of a Nucleophilic Water Molecule

A water molecule is involved in the dephosphorylation reaction and it behaves as a nucleophile attacking the P atom of the OP compound. This water molecule needs to be close enough to the P atom to initiate the nucleophilic attack process. However, no such water molecule was observed in the initially modeled structure. The X-ray crystal structures of several OP-inhibited AChE conjugates (PDB ID 2JGG, 2JGH, 2JGI, 2JGE, and 2JGF)⁴⁶ also failed to give a position of nucleophilic water molecule due to the low resolution and other factors such as crystal packing. Since the position of the nucleophilic water molecule is quite essential in the dephosphorylation reaction, it is necessary to identify a nucleophilic water molecule before the QM/MM reaction coordinate calculations can be carried out.

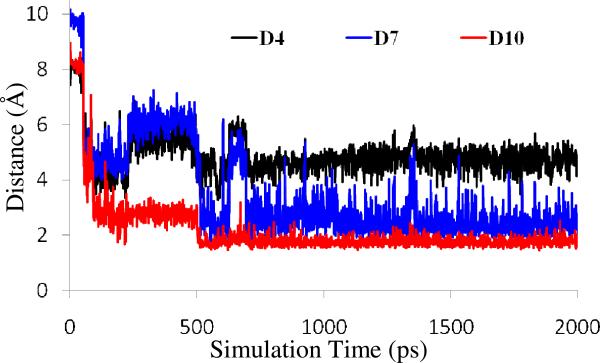
There are several possibilities for a water molecule to start the nucleophilic attack. The most possible way in gas phase for a nucleophile initiate the reaction is the inline attack from the opposite site of the leaving group. By performing the MD simulation on the initially modeled structure, a water molecule capable of initializing the inline attack on the P atom could not be found. This is because any water molecule in the inline attack position will have strong steric interactions with Phe297 and Gly202 and, therefore, cannot stably exist there. We also considered possibly different orientations of the dimethylphosphoryl group in the AChE active site, but found no alternative one since the dimethylphosphoryl structure was built by using the orientation of the diethylphosphoryl moiety in the crystal structure of mouse AChE-DFP conjugate and P atom of the dimethylphosphoryl group must covalently bond to hydroxyl oxygen of Ser203 in the phosphorylated AChE. The ~2 ns MD simulation on the phosphorylated AChE should be adequate in sampling the orientation of the dimethylphosphoryl group in the active site. Therefore, the inline attack which is very possible in gas phase can be excluded for this enzyme reaction system. Nevertheless, we observed a solvent water molecule (denoted by Wat668 below) moving toward the P atom from another direction after ~100 ps, which is on the opposite site of the methoxyl towarding acyl pocket (Trp236, Phe295, Phe297, and Phe338). It forms two hydrogen bonds with nitrogen (epsilon-N) atom of His447 side chain and carboxyl group of Glu202. Depicted in Figure 2 are the simulated key internuclear distances associated with this crucial water molecule, including the distance (D4) between the water oxygen and the P atom as well as the interacnuclear distances reflecting the two hydrogen bonds with the water (D7 and D10). As shown in Figure 2, these three key distances became stable after ~700 ps. The average values of D4, D7, and D10 after 700 ps were ~4.7, ~2.5, and ~1.8 Å, respectively. The average value of D4 reveals that Wat668 was in an appropriate location to attack the P atom. The average values of D7 and D10 indicate that Wat688 formed two hydrogen bonds with His447 and Glu202, suggesting that Wat688 was stabilized by both His447 and Glu202. In addition, the hydrogen bond between Wat688 and His447 also makes it possible for His447 facilitating the nucleophilic attack. Based on the structural information discussed above, Wat688 is the nucleophile to initiate the dephosphorylation reaction.

Figure 2.

Plots of three key internuclear distances vs simulation time in the MD-simulated dimethylphosphoryl-AChE conjugate structure. D4 is the distance between the water oxygen and the phosphorous atom, D7 refers to the distance between a hydrogen atom of the water and the nitrogen atom of His447 side chain, and D10 represents the distance between another hydrogen atom and an oxygen atom of Glu202 side chain.

As it can be seen from Figure 2, the distance represented by trace D10 was shorter and was more stable than trace D7. This means that the hydrogen bond between Wat688 and Glu202 is much stronger and more stable than the hydrogen bond between Wat688 and His447. Apparently, Glu202 is the main factor to keep Wat688 stably existing around the attacking position. Losing the interaction with Glu202 could make the structure unstable such that the active site may not be able to keep the nucleophilic water molecule close to the P atom. The role of Glu202 is thus very essential due to its stabilization effect on the nucleophilic water molecule.

Fundamental Dephosphorylatoin Reaction Pathway

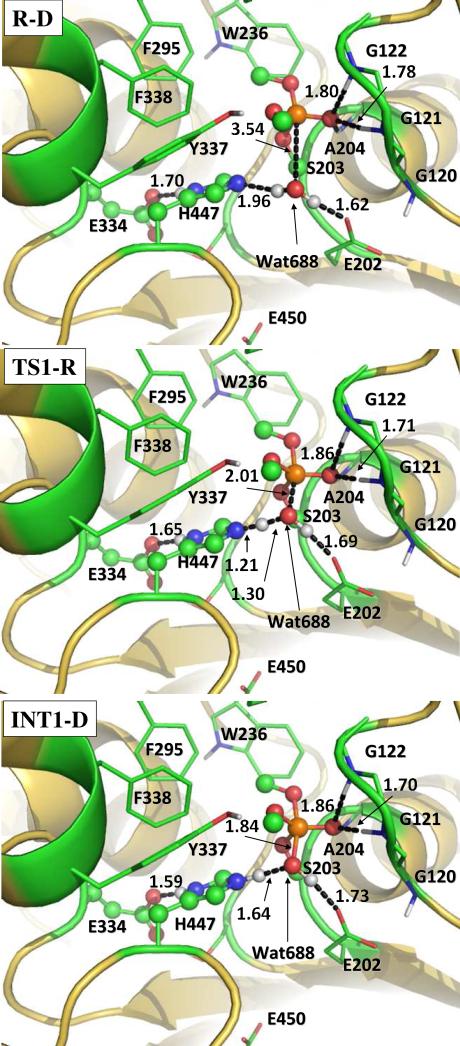
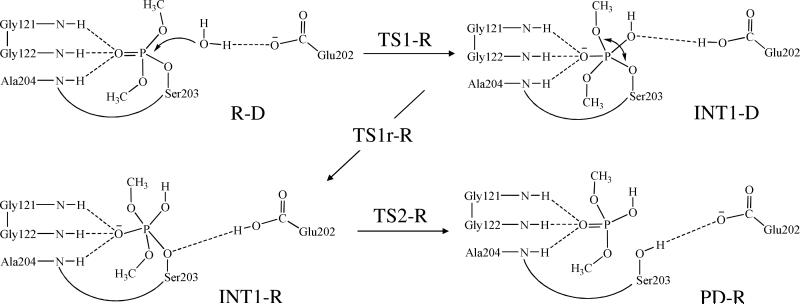
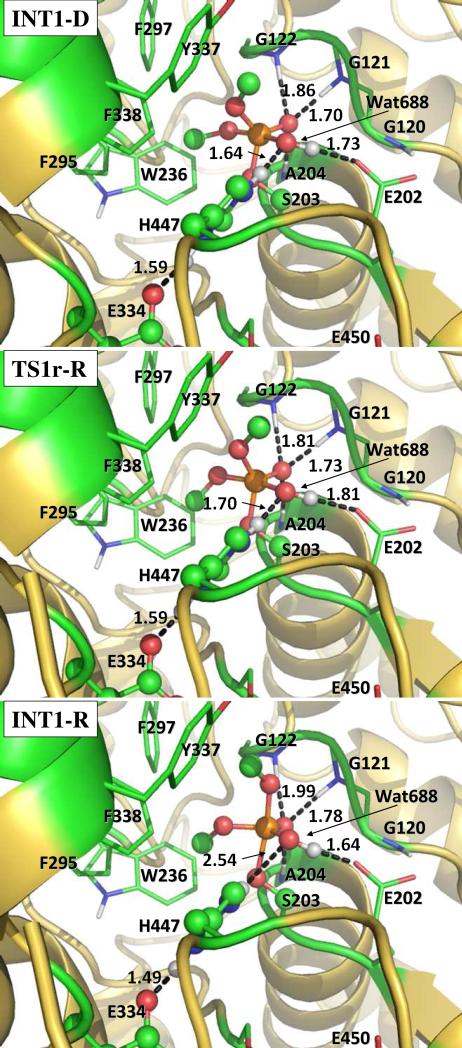
Our QM/MM reaction coordinate calculations at the B3LYP/6-31G*:AMBER level starting from the above-discussed reactant structure (with a nucleophilic water molecule in the reaction center) revealed that the dephosphorylation reaction consists of three reaction steps. The first reaction step is the nucleophilic attack on the P atom by a water molecule, just as depicted in Scheme 1. The second reaction step is dimethylphosphoryl group undergoing a spatial reorganization (conformational change). The third step is the dissociation between the dimethylphosphoryl group and Ser203. The optimized geometries of the initial reactant structure, intermediates, transition states, and dephosphorylated product are shown in Figures 3 to 5. Key distances that reflect the nature of the chemical reaction are listed in Table 1. Below we discuss each of these reaction steps in detail.

Figure 3.

The geometries optimized at the QM/MM(B3LYP/6-31G*:AMBER) level for the nucleophilic attack step. The key distances in the figure are in Å. Carbon, oxygen, nitrogen, phosphorous, and hydrogen atoms are colored in green, red, blue, orange, and white, respectively. The QM atoms are represented as ball and stick, and the surrounding residues rendered with stick. All non-polar hydrogen atoms are not shown for clarity.

Figure 5.

The geometries optimized at the QM/MM(B3LYP/6-31G*:AMBER) level for the dissociation step. The key distances in the figure are in Å. Atoms are colored and rendered in the same style as in Figure 3. All non-polar hydrogen atoms are not shown for clarity.

Table 1.

QM/MM-optimized key internuclear distances (in Å) during the dephosphorylation reaction. See Figure 1 for the definition of each key distance.

	D1	D2	D3	D4	D5	D6	D7	D8	D9	D10	D11	D12
R-D	1.78	1.80	1.94	3.54	1.60	3.01	1.96	0.98	0.99	1.62	1.05	1.70
TS1-R	1.71	1.86	1.95	2.01	1.67	2.36	1.21	1.30	1.00	1.69	1.06	1.65
INT1-D	1.70	1.86	1.91	1.84	1.70	2.28	1.06	1.64	0.99	1.73	1.07	1.59
TS1r-R	1.73	1.81	1.98	1.82	1.73	2.24	1.05	1.70	0.99	1.81	1.08	1.59
INT1-R	1.78	1.99	1.84	1.66	1.97	1.49	1.10	2.54	1.00	1.64	1.09	1.49
TS2-R	1.79	1.98	1.86	1.64	2.11	1.32	1.18	2.59	1.01	1.63	1.08	1.52
PD-R	1.78	1.93	2.06	1.59	2.96	1.00	1.65	2.97	1.02	1.55	1.06	1.57

Step 1: Nucleophilic attack on the P atom by a water molecule

In the nucleophilic attack step, the oxygen atom of the nucleophilic water molecule (Wat688) gradually approaches the P atom while a proton of Wat688 gradually transfers to a nitrogen (epsilon-N) atom of His447 side chain. D4, D7, and D8 represent the distances between the Wat688 oxygen and the P atom, between the transferring proton of Wat688 and the epsilon-N of His447, and between the transferring proton and oxygen atom of Wat688, respectively. As the changes of these three distances in the nucleophilic attack step reflect the nature of this chemical reaction step, the reaction coordinate for this reaction step was set as D4 + D7 – D8. As shown in the QM/MM-optimized geometries (Figure 3), while the Wat688 oxygen gradually approaches the P atom, the geometry of the reactant (R-D) in which the P atom is tetrahedrally coordinated by four oxygen atoms gradually changes into a pentacoordinated P geometry in an intermediate (INT1-D) through a transition state (TS1-R). In both the TS1-R and INT1-D geometries, the distribution of the five O atoms bonding with the P atom is close to a trigonal bipyramidal shape in which the oxygen atoms in Wat688 and a methoxyl group are on the axial orientation.

As residue Glu334 is a member of the well-known catalytic triad consisting of Ser203, His447, and Glu334 for AChE against the carboxylic acid esters, it is of particular interest to know whether Glu334 is involved in the formation/breaking of covalent bonds during the reaction process concerned in the present study. The answer to this essential mechanistic question can be obtained from examining two crucial internuclear distances within His447 and Glu334: one (denoted by D11 in Table 1) is the distance between the delta-nitrogen and delta-hydrogen of His447 side chain and the other (denoted by D12 in Table 1) is that between the delta-hydrogen of His447 and the nearby oxygen of Glu334 side chain. As seen in Table 1, D11 and D12 are 1.05 and 1.70 Å, respectively, in the reactant structure (R-D), revealing an expected strong hydrogen bond between Glu334 and His447. In going from R-D to TS1-R and INT1-D, D12 becomes shorter and shorter (1.65 Å in TS1-R and 1.59 Å in INT1-D) while D11 becomes slightly longer and longer (1.06 Å in TS1-R and 1.07 Å in INT1-D). The changes of these optimized geometric parameters clearly reveal that the proton (delta-hydrogen of His447) does not transfer from His447 to Glu334, but the hydrogen bond between His447 and Glu334 becomes stronger and stronger, during the reaction process. So, Glu334 stabilizes the transition state and intermediate through increasing its hydrogen bond with His447 during the currently studied reaction, instead of accepting a proton from His447 in the previously studied other reactions.^54,55 This observation on the role of Glu334 was further confirmed by performing additional QM/MM reaction coordinate calculations with D11 and D12 added to the reaction coordinate (see Figure S1 in Supporting Information).

It is also interesting to know the catalytic role of the oxyanion hole consisting of Gly121, Gly122, and Ala204. Based on the QM/MM reaction coordinate calculations, throughout the reaction process, the phosphoryl oxygen forms N-H^...O type of hydrogen bonds with the backbone NH groups of three amino acid residues (Gly121, Gly122, and Ala204), as one can see from the O^...H distances represented by D1 to D3 summarized in Table 1. These three hydrogen bonds are expected to stabilize the transition state (and also the intermediate) because the phosphoryl oxygen becomes more and more negatively charged in going from the reactant (R-D) to the transition state (TS1-R) and to the intermediate (INT1-D) while the Wat688 oxygen gradually forms a P-O covalent bond with the P atom. The catalytic role of Glu334 and the oxyanion hole in the dephsphorylation reaction of AChE is similar to that in the AChE-catalyzed hydrolysis of ACh.^31,33

Step 2: Spatial reorganization of the dimethylphosphoryl group

In the trigonal bipyramidal intermediate INT1-D resulted from the first reaction step, the oxygen atoms (O^ω and O^β) in Wat688 and a methoxyl group are on the axial orientation (see Figure 3). The hydroxyl oxygen (O^γ) of Ser203 side chain is not on the axial orientation and, thus, not suitable for a reaction step leading to breaking of the covalent bond between the P atom and the O^γ atom of Ser203. As known in literature⁵⁶ for other reactions of OP compounds and also based on our QM/MM reaction coordinate calculations for the present study, the leaving group of a pentacoordinated phosphorus intermediate with the trigonal bipyramidal conformation must stay in the axial orientation, as the P-O bonds in the axial orientation are generally weaker than the P-O bonds in the equatorial orientation. So, starting from the geometry of INT1-D, a spatial reorganization process is needed for O^γ atom to be in the axial orientation.

The spatial reorganization process can primarily be characterized as the change of a crucial dihedral angle, i.e. τ(C^βO^βPO^δ) (see Figure 1 for the used atom labels). τ(C^βO^βPO^δ) = 177.5° in the QM/MM-optimized geometry of INT1-D. Technically, τ(C^βO^βPO^δ) was multiplied by a radius R(C^βO^β) in order to define an effective reaction coordinate, τ(C^βO^βPO^δ)R(C^βO^β), in length for the practical QM/MM reaction coordinate calculations for this spatial reorganization process. R(C^βO^β) refers to the distance between atoms C^β and O^β. The results obtained from the reaction coordinate calculations indicate that INT1-D gradually changes to another trigonal bipyramidal conformation (denoted by INT1-R) through a transition state (TS1r-R). τ(C^βO^βPO^δ) = 110.1° and 39.0° in the QM/MM-optimized geometries of TS1r-R and INT1-R, respectively. It is notable that while τ(C^βO^βPO^δ) gradually decreases, three major conformational changes occur during the spatial reorganization process. One is the rotation (along the P-O^β bond) of a methoxyl group (–O^βC^βH₃) that is close to Trp236. Second, the trigonal bipyramidal intermediate undergoes a major conformational change with the O^γ atom (of Ser203) becoming to be on the axial orientation. Consequently, the P-O^γ bond becomes weaker and weaker, as the P-O^γ bond length is 1.70, 1.73, and 1.97 Å in INT1-D, TS1r-R, and INT1-R, respectively. In addition, the proton transferred to the epsilon-N of His447 gradually changes its orientation from being close to the hydroxyl oxygen (O^ω) of dimethylphosphoryl group to being close to O^γ atom of Ser203. As a result, a new hydrogen bond forms between the epsilon-hydrogen of His447 and O^γ atom of Ser203, while the old hydrogen bond between the epsilon-hydrogen of His447 and O^ω atom breaks. These three major conformational changes do not occur simultaneously. The rotation of –O^βC^βH₃ group along the P-O^β bond mainly occurs before the reaction system reaches transition state TS1r-R, whereas the other two major conformational changes mainly occur after the transition state TS1r-R is reached.

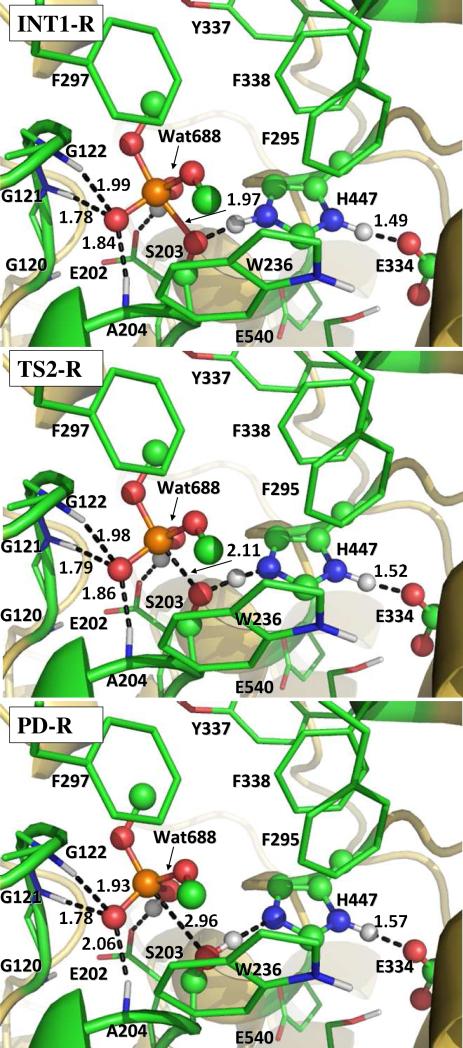
Step 3: Dissociation of dimethylphosphoryl group and Ser203

For the reaction step starting from the INT1-R structure, the epsilon-hydrogen of His447 gradually approaches O^γ atom of Ser203 side chain such that the epsilon-hydrogen gradually transfers from the epsilon-nitrogen of His447 to O^γ atom of Ser203. While the new O^γ-H bond (D6 in Figure 1) gradually forms, the old N-H bond (D7 in Figure 1) with epsilon-nitrogen of His447 and the old P-O^γ bond (D5 in Figure 1) gradually break. The changes of the lengths of these three bonds constitute the reaction coordinate which can be expressed by D5 – D6 + D7. As seen in Figure 5, D5 = 1.97 Å, D6 = 1.49 Å, and D7 = 1.10 Å in the optimized INT1-R geometry. In the optimized geometry of the transition state (TS2-R), D5 = 2.11 Å, D6 = 1.32 Å, and D7 = 1.18 Å. The distances D5, D6, and D7 become 2.96, 1.00, and 1.65 Å, respectively, in the optimized geometry of the product (PD-R). In the PD-R geometry, the P atom is tetrahedrally coordinated as the P-O^γ bond no longer exists.

Energy Barriers

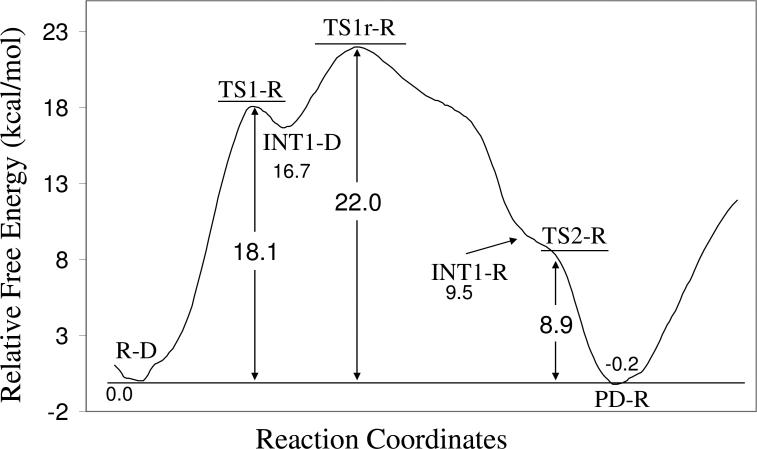
On the basis of the QM/MM-optimized geometries at the B3LYP/6-31G*:AMBER level, we carried out QM/MM single-point energy calculation at the B3LYP/6-311++G(d,p):AMBER level for each geometry along the minimum-energy path for the dephosphorylation reaction of dimethylphosphoryl-inhibited AChE. For each geometry along the minimum-energy path, the ESP charges determined in the QM part of the QM/MM single-point energy calculation were used in further FEP simulations for estimating the free energy changes along the reaction path. Depicted in Figure 6 is the energy profile determined by the QM/MM-FE calculations excluding the zero-point and thermal corrections for the QM subsystem. The relative free energy was taken as the average of the “forward” and “backward” perturbation results in which the error between “forward” and “backward” perturbation results is ±0.7 kcal/mol.

Figure 6.

Free energy profile determined by the B3LYP/6-311++G(d,p):AMBER QM/MM-FE calculations excluding the zero-point vibration and thermal corrections for the QM subsystem.

As seen in Figure 6, the energy barrier, i.e. the energy change from R-D to TS1-R, calculated for the nucleophilic attack step (the initial reaction step) is ~18.1 kcal/mol. The energy barrier, i.e. the energy change from INT1-D to TS1r-R, calculated for the spatial reorganization step is ~5.3 kcal/mol. For the last step, i.e. the dissociation of the dimethylphosphoryl group and Ser203, the calculated energy barrier, i.e. the energy change from INT1-R to TS2-R, is only ~0.4 kcal/mol on the potential energy surface determined at the QM/MM(B3LYP/6-31G*:AMBER) level. This negligible energy barrier disappears according to the final free energy calculations at the B3LYP/6-311++G(d,p):AMBER QM/MM-FE level, suggesting that the last reaction step is barrierless. So, in terms of the energy barriers for individual reaction steps, it seems like that the nucleophilic attack step is associated with the highest energy barrier. However, it is interesting to note in Figure 6 that the energy of transition state TS1r-R associated with the spatial reorganization step is actually higher than that of transition state TS1-R associated with the nucleophilic attack step by ~3.9 kcal/mol. As a result, the overall energy barrier for the entire dephosphorylation reaction is the energy change (~22.0 kcal/mol) from the initial reactant R-D to transition state TS1r-R, rather than TS1-R. So, the rate-determining transition state is TS1r-R associated with the spatial reorganization step, rather than TS1-R associated with the nucleophilic attack step. The overall energy barrier is ~3.9 kcal/mol higher than that of the nucleophilic attack step and ~16.7 kcal/mol higher than that of the spatial reorganization step.

By further including the zero-point vibration and thermal corrections for the QM subsystems to the calculated relative energies, the finally calculated overall free energy barrier is ~23.5 kcal/mol, which is close to the activation free energy of 22.3 kcal/mol derived from the experimental rate constant (k_cat = 1.01 h⁻¹)⁵⁷ by using the conventional transition state theory (CTST).^58,59 The good agreement between the computational and experimental data suggests that the reaction pathway and the free energy profile determined by the QM/MM-FE calculations are reliable.

Effects of Key Residues on the Free Energy Barrier

It is interesting for understanding the reaction mechanism of the dephosphorylation reaction to know how the amino acid residues in the active site pocket interact with the atoms that are directly involved in the dephosphorylation reaction. In order to estimate the specific role of each residue in the active site pocket, a “reaction group” was defined to consist of Wat688, the dimethylphosphoryl group, and the side chains of Ser203 and His447. The interaction energies (E_nonbond) between the reaction group and each of the other residues in the active site pocket were calculated by using the AMBER force field. Since the overall free energy barrier of the dephosphorylation reaction is the free energy difference between the R-D and TS1r-R states, the E_nonbond values were evaluated and compared for these two states. The interaction energy differences between TS1r-R and R-D were evaluated in order to roughly estimate the relative effects of the residues in the active site pocket on the free energy barrier. Theoretically, a positive value of the interaction energy difference means that the residue disfavors the reaction process (by increasing the overall energy barrier), whereas a negative value of the interaction energy difference means that the residue favors the reaction process (by decreasing the overall energy barrier). All residues in the active site pocket with an interaction energy difference larger than 1 kcal/mol are presented in Table 2.

Table 2.

Interaction energies between the reaction group and residues in the active site pocket

Residue number	Residue	R-D			TS1r-R			ΔEnonbond
		Evdw	Eele	Enonbond	Evdw	Eele	Enonbond
334	GLU	0.8	−44.2	−43.5	3.9	−59.8	−55.9	−12.5
202	GLU	0.3	−16.0	−15.7	−1.9	−3.0	−4.9	10.8
204	ALA	−0.7	−2.5	−3.1	−1.3	−7.9	−9.2	−6.0
121	GLY	−0.2	−12.2	−12.4	0.5	−17.3	−16.8	−4.4
450	GLU	−0.2	−4.0	−4.2	−0.2	−8.0	−8.2	−4.0
122	GLY	−0.5	−10.3	−10.8	−0.8	−13.7	−14.5	−3.7
236	TRP	−2.9	0.9	−2.1	−2.3	2.6	0.3	2.4
120	GLY	−1.6	−6.4	−8.0	−1.6	−8.6	−10.1	−2.1
337	TYR	−2.2	−0.5	−2.7	−2.4	1.0	−1.4	1.3

E_vdw is the van der Waals interaction; E_ele is the electrostatic interaction; E_nonbond = E_vdw + E_ele; ΔE_nonbond = E_nonbond(TS1r-R) - E_nonbond(R-D)

As can be seen in Table 2, the interaction energy between Glu334 and the reaction group in R-D and TS1r-R are about −43.5 and −55.9 kcal/mol, respectively, showing a strong stabilization effect of Glu334 on the reaction group, which is majorly due to the electrostatic interaction. The difference between the interaction energies (see Table 2) reveals that Glu334 favors the reaction process as it more favorably stabilizes the reaction group in TS1r-R.

Glu202 also plays an important role in the reaction process. From the E_nonbond values calculated for Glu202 (given in Table 2), one can see that Glu202 stabilizes the reaction group in both R-D and TS1r-R mainly through electrostatic interaction. However, Glu202 more favorably stablizes the reaction group in R-D as ΔE_nonbond = ~10.8 kcal/mol. So, Glu202 is expected to increase energy barrier within the given geometries of the reaction group. On the other hand, the role of Glu202 is essential in maintaining the structure of the reaction group. As seen in Figures 3 to 5 and Table 1, a hydrogen bond exists between the Glu202 side chain and Wat688 during the entire reaction process, suggesting that the role of Glu202 is to faciliate Wat688 performing nucleophilic attack on the phosphorous atom and hence to stabilize the trigonal bipyramid intermediate. Without the help of Glu202, it might be very difficult for Wat688 to perform nucleophilic attack. This analysis is consistent with the fact that the Glu202Gln mutation on Torpedo AChE decreased the reaction rate.⁶⁰

As discussed above, the oxyanion hole consisting of Gly121, Gly122, and Ala204 plays a stabilization role during the reaction process. This is further confirmed by the calculated interaction energies with Gly121, Gly122, and Ala204. The data in Table 2 indicate that the oxyanion hole stabilizes both R-D and TS1r-R and more favorably stabilizes TS1r-R, with ΔE_nonbond values of −3.7 to −6.0 kcal/mol.

Glu450 and Gly120 were also found to stabilize the reaction group in both R-D and TS1r-R and favor the reaction process according to the calculated interaction energies in Table 2. However, there is no direct contact between the reaction group and these two residues based on the optimized geometries. In particular, the carboxylic group of Glu450 is about 10 Å away from the P atom. It is likely that these two residues stabilize the reaction group and favor the reaction process through the long-range electrostatic interactions.

The ΔE_nonbond values calculated for Trp236 and Tyr337 are ~2.4 and ~1.3 kcal/mol, respectively (see Table 2). The positive ΔE_nonbond values suggest that both Trp236 and Tyr337 more favorably stabilize the R-D structure and increase the energy barrier for the reaction process. A detailed examination of the optimized geometries revealed that both Trp236 and Tyr337 have an obvious steric hindrance to the conformational change of the pentacoordinated phosphorus intermediate in the spatial reorganization step. In comparison between the optimized INT1-D and TS1r-R geometries, the –O^βC^βH₃ group is found to rotate toward Trp236 whereas the –O^αC^αH₃ group rotates to Tyr337 during the spatial reorganization step. Consequently, Trp236 and Tyr337 (particularly Trp236) are forced to move during the structural change from INT1-D to TS1r-R in order to accommodate the rotation of the two methoxyl groups (particularly –O^βC^βH₃). Further, when AChE interacts with a larger OP compound which has a substituent larger than the methoxyl group, the steric clash with Trp236 and Tyr337 will increase and, thus, the energy barrier will become higher. These insights are consistent with the experimental observations that the Tyr337Ala mutation increased the catalytic activity for AChE-catalyzed hydrolysis of the OP compounds⁶¹ and that the dephosphorylation/reactivation reaction rate of the AChE-OP conjugate decreased in going from paraoxon-methyl to paraoxon-ethyl and DFP.^13,57

Possible alternative reaction pathway

The above discussion reveals that Glu202 is a crucial residue which forms a hydrogen bond with Wat688, in addition to those forming the catalytic triad and oxyanion hole during the dephosphorylation reaction. A question was whether or not Glu202 takes the place of His447 for being the general base by accepting the proton from Wat688 in the nucleophilic attack process and then facilitates the dissociation between the dimethylphosphoryl group and Ser203 of AChE (Scheme 2).

Scheme 2.

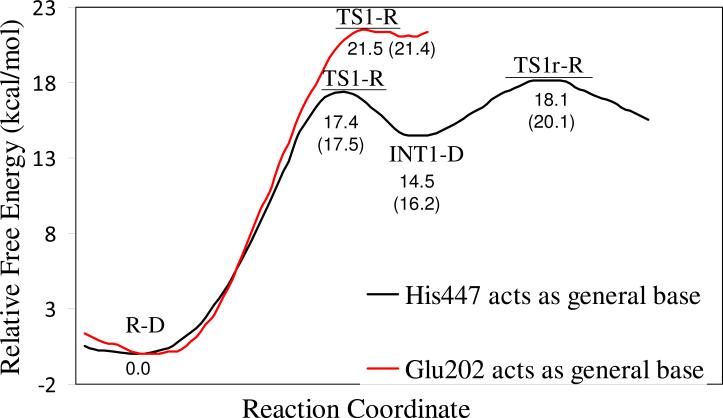
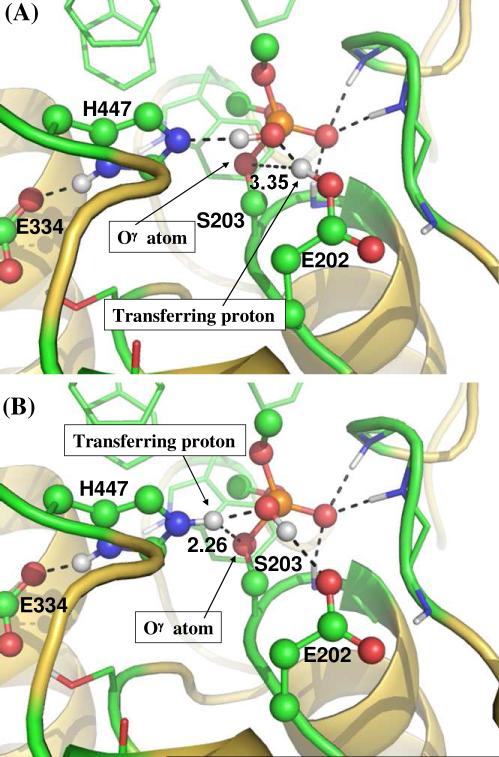
To address this critical mechanistic question, we performed further QM/MM-FE calculations to explore the alternative reaction pathway (Scheme 2) and estimate the corresponding free energy barrier. QM part of the QM/MM calculations was carried out at the B3LYP/6-31G* level for the geometry optimizations and at the B3LYP/6-311++G(d,p) level for the subsequent single-point energy calculations. Glu202 was also included in the QM part of the QM/MM calculation in order to model the proton transfer between Glu202 and Wat688. Further, to appropriately compare the calculated free energy barriers between the two competing reaction pathways at the same level of theory, additional QM/MM reaction coordinate calculations were carried out on the reaction pathway (Scheme 1) where His447 acts as the general base by also including Glu202 in the QM subsystem. For convenience, we refer “His-Reaction-Pathway” to the reaction pathway where His447 acts the general base, and refer “Glu-Reaction-Pathway” to the reaction pathway where Glu202 acts the general base. The calculated free energy profiles for these two competing reaction pathways are depicted in Figure 7 for comparison. As one can see in Figure 7, for the His-Reaction-Pathway, the calculated free energy barrier for the first reaction step is ~17.5 kcal/mol and for the calculated overall free energy barrier is ~20.1 kcal/mol; the calculated free energy barriers are systematically lower than, but reasonably close to, the corresponding free energy barriers calculated by including Glu202 in the MM part of the QM/MM calculations (Figure 6) for the same reaction pathway. As depicted in Figure 7, the free energy barrier of ~21.4 kcal/mol calculated for the first reaction step of the Glu-Reaction-Pathway is ~3.9 kcal/mol higher than that for the first reaction step of the His-Reaction-Pathway and is even ~1.3 kcal/mol higher than the overall free energy barrier calculated for the His-Reaction-Pathway at the same level of theory. In addition, in the structure of INT1-D optimized for the Glu-Reaction-Pathway, the distance of 3.35 Å (Figure 8A) between the transferring proton and the hydroxyl oxygen (O^γ) atom of Ser203 is much longer than the corresponding distance of 2.26 Å (Figure 8B) in the INT1-D structure obtained for the His-Reaction-Pathway. One may reasonably assume that a much longer distance between the transferring proton and the hydroxyl oxygen (O^γ) atom of Ser203 makes the subsequent next reaction steps much more difficult to occur. Due to this reason, and due to the observation that the free energy barrier of ~21.4 kcal/mol calculated for the first reaction step of the Glu-Reaction-Pathway is already higher than the overall free energy barrier calculated for the His-Reaction-Pathway at the same level of theory, we may safely conclude that the His-Reaction-Pathway is more favorable than the Glu-Reaction-Pathway. In other words, His447 is indeed more favorable than Glu202 to serve as the general base for the dephosphorylation/reactivation reaction of the phosphorylated AChE.

Figure 7.

Free energy profiles determined by the B3LYP/6-311++G(d,p):AMBER QM/MM-FE calculations (in which Glu202 was also included in the QM subsystem) excluding the zero-point vibration and thermal corrections for the QM subsystem. The energy curve in black refers to the reaction pathway where His447 acts as the general base (Scheme 1), whereas the energy curve in red refers to the reaction pathway where Glu202 acts as the general base (Scheme 2). The values given in parentheses are the relative free energies including zero-point vibration and thermal corrections for the QM subsystem.

Figure 8.

Structruers of INT1-D optimized at QM/MM(B3LYP/6-31G*) level in (A) the reaction pathway where Glu202 acts as the general base, and in (B) the reaction pathway where His447 acts as the general base.

Conclusion

The dephosphorylation/reactivation reaction of dimethylphosphoryl-AChE conjugate has been studied by using first-principles QM/MM-FE approach. The favorable reaction pathway has been uncovered and elucidated in detail. First, a water is stabilized at the attacking position by Glu202 and His447. Then the oxygen atom of the nucleophilic water attacks the P atom with the faciliation of a simultaneous proton transfer from the water molecule to His447, leading to the trigonal bipyramidal intermediate with the O^γ atom of Ser203 in an equatorial orientation of the trigonal bipyramid. Afterwards, the dimethylphosphoryl group undergoes a spatial reorganization process during which the O^γ atom gradually changes to an axial orientation. Finally, the dissociation between the dimethylphosphoryl group and Ser203 proceeds after the O^γ atom achieves the axial orientation. According to the calculated free energy profile, the overall free energy barrier for the entire dephosphorylation/reactivation reaction is the free energy change from the initial reactant R-D to the transition state TS1r-R associated with the spatial reorganization step. The calculated overall free energy barrier (20.1 to 23.5 kcal/mol), which covers the first two reaction steps, is reasonably close to the activation free energy of 22.3 kcal/mol derived from avaibale experimental rate constant (k_cat= 1.01 h⁻¹).

Further, our structural and energetic analyses reveal the specific roles of some key residues in the reaction process. In particular, Glu334 is a key residue in the catalytic triad as it has been well known for the AChE-catalyzed hydrolysis of its native substrate (acetylcholine). Glu334 is found to be important in stabilizing the rate-determining transition state TS1r-R through strong electrostatic interactions. However, there is no spontaneous proton transfer between Glu334 and His447 during the dephosphorylation reaction. The oxyanion hole is also essential in stabilizing the rate-determining transition state through electrostatic interactions. Another essential residue is Glu202 which stabilizes the nucleophilic water molecule attacking the P atom to initialize the dephosphorylation/reactivation reaction. Trp236 and Tyr337 are found to have steric hindrance on the rotation of the methoxyl groups of the OP compound in the spatial reorganization process.

The structural and mechanistic insights obtained from this computational study provide a valuable base for rational design of mutants of AChE with an improved catalytic activity for AChE-catalyzed hydrolysis of OP compounds. In particular, rational design of the high-activity mutants should first focus on possible mutations that can more favorably stabilize transition state TS1r-R associated with the spatial reorganization step.

Figure 4.

The geometries optimized at the QM/MM(B3LYP/6-31G*:AMBER) level for the OP spatial reorganization step. The key distances in the figure are in Å. Atoms are colored and rendered in the same style as in Figure 3. All non-polar hydrogen atoms are not shown for clarity.