Robust Covariate-Adjusted Log-Rank Statistics and Corresponding Sample Size Formula for Recurrent Events Data

Summary

Recurrent events data are frequently encountered in clinical trials. This article develops robust covariate-adjusted log-rank statistics applied to recurrent events data with arbitrary numbers of events under independent censoring and the corresponding sample size formula. The proposed log-rank tests are robust with respect to different data-generating processes and are adjusted for predictive covariates. It reduces to the Kong and Slud (1997, Biometrika 84, 847–862) setting in the case of a single event. The sample size formula is derived based on the asymptotic normality of the covariate-adjusted log-rank statistics under certain local alternatives and a working model for baseline covariates in the recurrent event data context. When the effect size is small and the baseline covariates do not contain significant information about event times, it reduces to the same form as that of Schoenfeld (1983, Biometrics 39, 499–503) for cases of a single event or independent event times within a subject. We carry out simulations to study the control of type I error and the comparison of powers between several methods in finite samples. The proposed sample size formula is illustrated using data from an rhDNase study.

1. Introduction

Many clinical trials and observational studies involve the study of events that may occur repeatedly for individual subjects. Examples of such recurrent events data include time to hospitalization for nonfatal events or resuscitated cardiac arrest. In such data, the numbers of events are different across patients and are unknown before the clinical trial. Among the methods for treatment comparisons within the recurrent events data setting, a robust log-rank test proposed by Lawless and Nadeau (1995), which shares a similar form with the log-rank test for right censored survival data, is widely used.

In the right censored survival data setting, when some auxiliary information, such as prognostic covariates or the censoring mechanism, are available, it is well known that an adjusted log-rank test statistic may improve efficiency, and/or adjust baseline imbalance, compared with that of the unadjusted log-rank test. The statistical literature contains numerous precedents on this issue (Tsiatis, Rosner, and Tritchler, 1985; Slud, 1991; Kosorok and Fleming, 1993; Chen and Tsiatis, 2001, for example). Among others, Robins and Finkelstein (2000) corrected for dependent censoring in an AIDS clinical trial with inverse probability of censoring weighted log-rank tests. Murray and Tsiatis (2001) considered adjusting a two-sample test for time-dependent covariates. Mackenzie and Abrahamowicz (2005) used categorical markers to increase the efficiency of log-rank tests. Kong and Slud (1997) and Li (2001) proposed covariate-adjusted log-rank tests for two-sample censored survival data. These works motivate us to consider adjusting covariates in log-rank statistics in the recurrent events setting.

Sample size calculations are critical in the design of clinical trials. In the recurrent event setting, Hughes (1997) and Bernardo and Harrington (2001) considered power and sample size calculations based on a multiplicative intensity model and a marginal proportional hazards model, respectively. Based on the test by Lawless and Nadeau (1995), Cook (1995), and Matsui (2005) considered sample size calculations in this context via a nonhomogeneous Poisson process model. Their methods are parametric in the sense that, conditional on a frailty, the intensity of a homogeneous Poisson process is needed as an input parameter for sample size calculations.

In this article, we propose a covariate-adjusted log-rank test to improve the power of the tests and to adjust for random imbalances of the covariates at baseline using a semiparametric approach. Based on the proposed test, we derive a nonparametric, rather than parametric, sample size formula based on the limiting distribution of the robust log-rank statistic. The idea is to base power on the corresponding proportional means local alternatives and a class of working models for the baseline covariates. This method allows for arbitrary numbers of events within subject and arbitrary independent censoring distributions.

Numerical studies show that the sample size derived from our method can maintain the type I error and achieve the desired power. Both the log-rank statistic and the sample size formula are implemented in the R software package (see www.r-project.org). The remainder of the article is organized as follows. In Section 2, we present the data structure and the model assumptions. We describe the robust covariate-adjusted log-rank statistic for recurrent events and its asymptotic distribution in Section 3. We provide the sample size formula in Section 4 and consider some design issues in Section 5. The relationship to current existing sample size formula is discussed in Section 6 and some simulation results are reported in Section 7. The methods are applied to the rhDNase study in Section 8. A discussion concludes the article in Section 9.

2. The Data and Model Assumptions

Assume that there are n = n₁ + n₂ independent subjects assigned to two treatments with n_j subjects assigned to treatment j, j = 1, 2. The observed data are {(T_ij, C_ij, V_ij), i = 1, …, n_j, j = 1, 2}, where, for subject i within treatment group j, T_ij ≡ (T_ij1, T_ij2, …), where T_ij1 < T_ij2 <… are the ordered event times of interest which constitute the recurrent event process. C_ij is a univariate right censoring time. V_ij is a p-dimensional covariate which could be time varying. We also define K_ij ≡ max {k : T_ijk ≤ C_ij} to be the total observed number of events for each subject.

We will also utilize when convenient the following counting process notation: N_ijk(t) ≡ I{T_ijk ≤ t, C_ij ≥ t}, N_ij(t) ≡ sup_k{k : T_ijk ≤ t, C_ij ≥ t}, or equivalently, $N_{ij}(t)={\sum }_{k=1}^{\infty }{N}_{\mathit{ijk}}(t)$. The at risk process is Y_ij(t) ≡ I{C_ij ≥ t}. ${\pi }_j^n(t)\equiv n_j^{-1}{\sum }_{i=1}^{n_j}EI\{C_{ij}\ge t\}$ is the probability of subjects under study at time t in treatment group j. Define $N_{\mathit{ijk}}^0(t)$ and $N_{ij}^0(t)$ as the corresponding underlying event process versions of N_ijk (t) and N_ij(t), i.e., $N_{ij}(t)={\int }_0^t{Y}_{ij}(s)d{N}_{ij}^0(s)$. We also define ${\mathrm{\Lambda }}_{ij}(t\mid V_{ij}(s),s\le t)\equiv E\{N_{ij}^0(t)\mid V_{ij}(s),s\le t\}$ to be the expected number of events for subject i by time t in treatment group j, given covariate V_ij. The following assumptions are needed:

1. We assume that T_ij and C_ij are independent given V_ij for i = 1, …, n_j and j = 1, 2.

2. lim _n→∞n_j/n = p_j ∈ (0, 1), for j = 1, 2, and ${sup}_{t\in (0,{\tau }_0)}\mid {\pi }_j^n(t)-{\pi }_j(t)\mid \to 0$ for some π_j, j = 1, 2.

3. Given the covariates {V (s), s ≤ τ₀}, where τ₀ ≡ sup{t : π₁(t)π₂(t) > 0} is the maximum observation time, the cumulative mean functions of events for subjects under study within the same treatment group are identical, i.e., ${\mathrm{\Lambda }}_{ij}(t\mid V_{ij}(s),s\le t)\equiv {\mathrm{\Lambda }}_j^n(t\mid V_{ij}(s),s\le t)$, for i = 1,2, …, n_j, t ∈ (0, τ₀). The rate function ${\lambda }_j^n(t\mid V)\equiv \partial /(\partial t){\mathrm{\Lambda }}_j^n(t\mid V)$, for j = 1, 2. Note that the superscript n permits contiguous alternatives.

4. ${sup}_{t\in (0,{\tau }_0)}\mid d{\mathrm{\Lambda }}_j^n(t\mid V(s),s\le t)/d{\mathrm{\Lambda }}_0(t\mid V(s),s\le t)-1\mid \to 0$, for some Λ₀ with Λ₀(τ₀|V (s), s ≤ τ₀) <∞. Λ₀(t | V (s), s ≤ t) can be decomposed as Λ⁰(t)h(V (t); θ₀), where Λ⁰(t) is an unspecified baseline function. h(V (t); θ₀) is a known positive integrable function containing information of V, and θ₀ is an unknown p-dimensional parameter. ${sup}_{t\in (0,{\tau }_0),\theta \in {\mathrm{\Theta }}_0}\mid {\stackrel{\sim }{\pi }}_j^n(t;\theta )-{\stackrel{\sim }{\pi }}_j(t;\theta )\mid \to 0$ for some π̃_j, j = 1, 2, where ${\stackrel{\sim }{\pi }}_j^n(t;\theta )=n_j^{-1}{\sum }_{i=1}^{n_j}EI\{C_{ij}\ge t\}h(V_{ij}(t);\theta )$, and Θ₀ is a neighborhood containing θ.

5. ${sup}_{t\in (0,{\tau }_0)}\mid \sqrt{n}\{d{\mathrm{\Lambda }}_1^n(t\mid V(s),s\le t)/d{\mathrm{\Lambda }}_2^n(t\mid V(s),s\le t)-1\}-\psi (t)\{1+\eta (t)\}\mid \to 0$, where ψ is either cadlag (right-continuous with left-hand limits) or caglad (left-continuous with right-hand limits) with bounded total variation and η is bounded and zero except at event times.

Compared with the unadjusted test statistics, h(V (t); θ) carries the information of the covariates V(t) about the cumulative mean for each individual into the test statistic. An example of the working model is h(V (t); θ) = exp(θ′V (t)). The choice of the function h(V (t) ; θ) is an interesting problem and a practical issue. Without loss of generality, assuming that the covariates to be adjusted are the same as in the correct model, the functional form h(V (t); θ) of these covariates can be chosen by certain model diagnostic techniques, such as those used in Lin et al. (2000). When there is a set of finitely many working models h_k(V (t); θ) (k = 1, …, K) available, Kong and Slud (1997) suggested computing the relative efficiency of each covariate-adjusted score statistic. The heuristic argument suggested that the working model with the maximum relative efficiency score statistic is the “best” model in the sense that the corresponding covariate-adjusted test is the most powerful test based upon the K working models under consideration. A similar idea can be carried out in our setting. As interesting as this issue is, it is, however, beyond the scope of the current article.

We also note that assumption 5 is a contiguous sequence of models for recurrent event times that will facilitate the derivation of the sample size formula. Such contiguous sequences are routinely used to derive first-order sample size formulas (Schoenfeld, 1983; Gangnon and Kosorok, 2004, for example). We will sometimes omit the superscript n for notational simplicity.

3. The Covariate-Adjusted Log-Rank Tests for Recurrent Events Data

To test H₀: Λ₁(t | V (s), s ≤ t) = Λ₂(t | V (s), s ≤ t), t ∈ (0, τ₀), the robust log-rank test we propose takes the form:

$$\begin{array}{l}{L}_n(t)=\frac{1}{\sqrt{n}}{\int }_0^t{\widehat{W}}_n(s)\frac{{\overline{Y}}_1(s;{\widehat{\theta }}_n){\overline{Y}}_2(s;{\widehat{\theta }}_n)}{{\overline{Y}}_1(s;{\widehat{\theta }}_n)+{\overline{Y}}_2(s;{\widehat{\theta }}_n)}\\ \times \left\{\frac{d{\overline{N}}_1(s)}{{\overline{Y}}_1(s;{\widehat{\theta }}_n)}-\frac{d{\overline{N}}_2(s)}{{\overline{Y}}_2(s;{\widehat{\theta }}_n)}\right\},\end{array}$$

where ${\overline{N}}_j(t)\equiv {\sum }_{i=1}^{n_j}{N}_{ij}(t)$, and Ŵ_n is caglad or cadlag with total bounded variation and is nonnegative so that L_n is sensitive to ordered alternatives. We assume sup_{t ∈ (0, τ0)}|Ŵ_n(t) − W(t) |→ 0 in probability for some uniformly bounded integrable function W(t). ${\overline{Y}}_j(t;\theta )\equiv {\sum }_{i=1}^{n_j}{Y}_{ij}(t)h(V_{ij}(t);\theta )$, j = 1, 2. θ̂_n satisfies the score equation D(θ̂_n) = 0, with

$$D(\theta )=\sum _{j=1}^2\sum _{i=1}^{n_j}{\int }_0^{{\tau }_0}\left\{\frac{h^{(1)}(V_{ij}(t);\theta )}{h(V_{ij}(t);\theta )}-\frac{{\overline{Y}}_j^{(1)}(t;\theta )}{{\overline{Y}}_j(t;\theta )}\right\}d{N}_{ij}(t),$$ (1)

where h⁽¹⁾(V (t);θ) is the first derivative of h(V (t); θ) with respect to θ, and ${\overline{Y}}_j^{(1)}(t;\theta )\equiv {\sum }_{i=1}^{n_j}{Y}_{ij}(t)h^{(1)}(V_{ij}(t);{\widehat{\theta }}_n)$.

Under some regularity assumptions, it can be shown similarly as in Struthers and Kalbfleisch (1986) that, θ̂_n is consistent for θ^★, the unique solution to

$$\begin{array}{l}\int E\left\{\sum _{j,i}{Y}_{ij}(t){\lambda }_j(t\mid V_{ij})\frac{h^{(1)}(V_{ij}(t),\theta )}{h(V_{ij}(t),\theta )}\right\}dt\\ =\int \frac{E({\sum }_j{\overline{Y}}_j^{(1)}(t;\theta )\mid V)}{E({\sum }_j{\overline{Y}}_j(t;\theta )\mid V)}E\{\sum _{j,i}{Y}_{ij}(t){\lambda }_j(t\mid V_{ij})\}dt.\end{array}$$

For variance estimation, we use the following robust variance estimator:

$${\widehat{\sigma }}_n^2\equiv \frac{1}{n}\sum _{j=1}^2\sum _{i=1}^{n_j}{\left\{{\int }_0^{{\tau }_0}{\widehat{W}}_n(s)\frac{{\overline{Y}}_{j^{\prime }}(s;{\widehat{\theta }}_n)}{{\overline{Y}}_1(s;{\widehat{\theta }}_n)+{\overline{Y}}_2(s;{\widehat{\theta }}_n)}d{\widehat{M}}_{ij}(s)\right\}}^2,$$

where ${\widehat{M}}_{ij}(t)\equiv N_{ij}(t)-{\int }_0^t{Y}_{ij}(s)h(V_{ij}(s);{\widehat{\theta }}_n)d{\overline{N}}_j(s)/{\overline{Y}}_j(s;{\widehat{\theta }}_n)$, i = 1, …, n_j, j = 1, 2 and j′ = 3 − j.

We also need to assume that ${\sigma }_n^2\to {\sigma }^2$, as n → ∞, for some 0< σ² < ∞, where

$${\sigma }_n^2\equiv \frac{1}{n}\sum _{j=1}^2\sum _{i=1}^{n_j}{\left\{{\int }_0^{{\tau }_0}W(s)\frac{p_{j^{\prime }}{\stackrel{\sim }{\pi }}_{j^{\prime }}^n(s;{\theta }^{★})}{p_1{\stackrel{\sim }{\pi }}_1^n(s;{\theta }^{★})+p_2{\stackrel{\sim }{\pi }}_2^n(s;{\theta }^{★})}d{M}_{ij}(s)\right\}}^2$$

and $M_{ij}(t)\equiv N_{ij}(t)-{\int }_0^t{Y}_{ij}(s)d{\mathrm{\Lambda }}_j(s\mid V)$, for i = 1, …, n_j, j = 1, 2. Note that this assumption does not necessarily follow from the assumptions of Section 2 because those assumptions do not restrict the variability of the recurrent event process.

We now present two asymptotic results that are needed to derive our sample size formula.

Theorem 1

Under the assumptions 1–5, L_n converges in distribution to a normally distributed random variable with mean μ and variance σ², where

$$\mu \equiv {\int }_0^{{\tau }_0}W(s)\psi (s)\{1+\eta (s)\}\frac{p_1{\stackrel{\sim }{\pi }}_1(s;{\theta }^{★})p_2{\widehat{\pi }}_2(s;{\theta }^{★})}{p_1{\stackrel{\sim }{\pi }}_1(s;{\theta }^{★})+p_2{\widehat{\pi }}_2(s;{\theta }^{★})}d{\mathrm{\Lambda }}_0(s\mid V).$$

Theorem 2

Under the assumptions 1–5, ${\widehat{\sigma }}_n^2\to {\sigma }^2$ in probability, as n → ∞.

When there is no need to adjust for covariates, the form of the test statistic and its asymptotic distribution are similar to that of the weighted log-rank test statistic for clustered survival data proposed by Gangnon and Kosorok (2004). The differences come from the definition of the at risk process. In Gangnon and Kosorok (2004), each subject within a cluster has a 0–1 valued counting process and the same marginal distribution. In contrast, we view the recurrent events from the same subject as a single counting process. M_ij(t) is not a martingale and it follows that standard martingale methods will not apply anymore. Therefore, the proofs of Theorems 1 and 2 will differ accordingly. Because the processes {M_ij(t), i = 1, …, n_j, j = 1, 2} and { ${\int }_0^{{\tau }_0}W(s)p_{j^{\prime }}{\stackrel{\sim }{\pi }}_{j^{\prime }}^n(s;{\theta }^{★})/\{p_1{\stackrel{\sim }{\pi }}_1^n(s;{\theta }^{★})+p_2{\stackrel{\sim }{\pi }}_2^n(s;{\theta }^{★})\}d{M}_{ij}(s),i=1,\dots ,n_j,j=1,2$} are manageable (Pollard, 1990; Bilias, Gu, and Ying, 1997), with the second moment of the total variation being bounded, we can utilize both Donsker and Glivenko-Cantelli results and the strong embedding theorem (van der Vaart and Wellner, 1996). Standard empirical process techniques will then yield the desired results.

4. Sample Size Formulas

We now utilize the asymptotic results of Section 3 to derive sample size formulas based on appropriate $\sqrt{n}$ local alternatives. For convenience, we only consider time independent covariates V and assume that V and the censoring time C are independent. We also assume that the treatment indicator is independent of V, which is often the case in randomized clinical trials. We consider the proportional means local alternative H_A: Λ_j(t | V ) = Λ₀(t | V ) exp {(−1)^j−1 ψ(t)/2}, j = 1, 2, ψ(t) ≠ 0, ψ(t) = o(1), t ∈ (0, τ₀), and Λ₀(t | V ) = Λ⁰(t)h(V (t);θ). Note that this alternative satisfies conditions 4 and 5 of Section 2. We now have

Theorem 3

$E(L_n(t)\mid H_A)=\sqrt{n}{\mu }_1+o(\sqrt{n})$, where

$${\mu }_1\equiv {\int }_0^{{\tau }_0}\psi (s)\{1+\eta (s)\}\frac{p_1{\pi }_1(s)p_2{\pi }_2(s)}{p_1{\pi }_1(s)+p_2{\pi }_2(s)}d{\mathrm{\Lambda }}_0(s\mid V).$$

The proof is similar to that of Theorem 1. We note that the approximation exp{ψ(s)/2} − exp{− ψ(s)/2} ≈ ψ(s) holds only when ψ(s) is very close to zero. For the variance term, the conclusion of Theorem 2 still holds under the current assumption.

We now derive the sample size formula for the log-rank test (W(s) = 1). We assume that the marginal distributions of all the censoring times C_ij are identical. Thus π₁ = π₂ ≡ π₀. The baseline cumulative mean functions are continuous and the local alternatives satisfy ψ = γ, with γ ∈ ℛ.

Corollary 1

μ₁ = γp₁p₂D_1g + o(γ), where $D_{1g}={\int }_0^{{\tau }_0}{\pi }_0(s)d{\mathrm{\Lambda }}_0(s\mid V)$.

Because π₁(s) = π₂(s) according to the assumption, p_jπ_j(s)/{p₁π₁(s) + p₂π₂(s)} = p_j, j = 1, 2, and η(s) = 0 almost everywhere, Corollary 1 follows automatically. D_1g can be interpreted as the average number of observed events per person across the two treatment groups adjusted for covariates V, because

$$\begin{array}{l}\frac{n_1}{n}\times \frac{{\displaystyle \sum _{i=1}^{n_1}}I\{C_{i1}\ge s\}}{n_1}+\frac{n_2}{n}\times \frac{{\displaystyle \sum _{i=1}^{n_2}}I\{C_{i2}\ge s\}}{n_2}=\frac{\sum I\{C_{ij}\ge s\}}{n}\\ \to P(C\ge s)=p_1{\pi }_1(s)+p_2{\pi }_2(s).\end{array}$$

D_1g can be estimated by the geometric mean

$${\widehat{D}}_{1g}\equiv \sqrt{\frac{{\displaystyle \sum _{i=1}^{n_1}}{\widehat{\mathrm{\Lambda }}}_1(C_{i1}\mid V_{i1})}{n_1}\times \frac{{\displaystyle \sum _{i=1}^{n_2}}{\widehat{\mathrm{\Lambda }}}_2(C_{i2}\mid V_{i2})}{n_2}},$$

where ${\widehat{\mathrm{\Lambda }}}_j(C_{ij}\mid V_{ij})={\int }_0^{C_{ij}}h(V_{ij}(t);{\widehat{\theta }}_n)Y_{ij}(t)d{\overline{N}}_j(t)/{\overline{Y}}_j(t;{\widehat{\theta }}_n)$, j = 1, 2. In order to compute the asymptotic variance, we assume that $N_{ij}^0$ is, conditional on a positive, latent real random variable ω_ij and covariates V_ij, a nonstationary Poisson process with cumulative intensity function w_ij Λ_j(t |V_ij), where w_ij has mean 1 and variance ${\sigma }_w^2$. We assume that w_ij is independent of the censoring process.

Corollary 2

${\sigma }^2=p_1{p}_2(D_{1a}+{\sigma }_w^2{D}_2)+o(1)$, where $D_{1a}={\sum }_{j=1}^2{\int }_0^{{\tau }_0}{p}_{j^{\prime }}{\pi }_0(s)d{\mathrm{\Lambda }}_j(s\mid V),D_2={\sum }_{j=1}^2{p}_{j^{\prime }}E[{\{{\int }_0^{{\tau }_0}{Y}_{1j}(s)d{\mathrm{\Lambda }}_j(s\mid V)\}}^2]$, and j′ ≡ 3 − j.

The proof is deferred to the Web Appendix. When p₁ = p₂ = 0.5, D_1a and D₂ are the average number and the average squared number of observed events among the two treatment groups conditional on covariates V. They can be estimated by the empirical versions ${\widehat{D}}_{1a}\equiv n^{-1}{\sum }_{j=1}^2{\sum }_{i=1}^{n_j}{\widehat{\mathrm{\Lambda }}}_j(C_{ij}\mid V_{ij})$, and ${\widehat{D}}_2\equiv n^{-1}{\sum }_{j=1}^2{\sum }_{i=1}^{n_j}{\widehat{\mathrm{\Lambda }}}_j^2(C_{ij}\mid V_{ij})$. For the estimation of ${\sigma }_w^2$, one could adopt quasi-likelihood methods as in Moore and Tsiatis (1991). However, we use instead a simpler moment estimator ${\widehat{\sigma }}_w^2\equiv {(n^{-1}{\sum }_{j=1}^2{\sum }_{i=1}^{n_j}{N}_{ij}(C_{ij})\{N_{ij}(C_{ij})-1\}/{\widehat{D}}_2-1)}^{+}$, where x⁺ denotes the maximum of x and 0. The derivation is in the Web Appendix. Therefore, the sample size required for the alternative ψ = γ for a two-sided test of size α₁ and power α₂ is

$$n=\frac{{(z_{1-{\alpha }_1/2}+z_{1-{\alpha }_2})}^2({\widehat{D}}_{1a}+{\widehat{\sigma }}_w^2{\widehat{D}}_2)}{{\gamma }^2{p}_1{p}_2{\widehat{D}}_{1g}^2}.$$ (2)

When the effect size γ is small, D_1g ≈ D_1a, the sample size formula (2) has another approximation form:

$$n\approx \frac{{(z_{1-{\alpha }_1/2}+z_{1-{\alpha }_2})}^2({\widehat{D}}_{1a}+{\widehat{\sigma }}_w^2{\widehat{D}}_2)}{{\gamma }^2{p}_1{p}_2{\widehat{D}}_{1a}^2}.$$

When the covariate V has a negligible effect on the mean frequency function, and there is no within-subject heterogeneity, i.e., ${\sigma }_w^2$ is 0, this formula reduces to Schoenfeld’s (1983) formula.

D_1g, D_1a, and D₂ need to be estimated, possibly from pilot data that have similar outcomes to the clinical trial being designed but with shorter follow-up. The value ${\sigma }_w^2$ can be readily estimated from such pilot data, because this quantity is uncorrelated with the study length. Consistent with the extra-Poisson nonstationary process assumption, we assume that there are two components of error. They are the error D_1a from a Poisson process and an extraneous variance part ${\sigma }_w^2{D}_2$. We may consider that the extraneous variance is caused by the unmeasured event dependence within subject. Thus the variance is larger than assumed by a pure Poisson process, which will lead to a larger sample size estimate than the independent events situation. We notice that in some biological processes, the heterogeneity within subject may have an opposite effect, which could lead to a shrinkage of the total variance. In this setting, our sample size formula will overestimate the sample size. Further research is needed to fully take advantage of the shrinkage variance structure, but this is beyond the scope of the present article.

5. Some Design Issues: Planning the Duration

We assume, for now, uniform recruitment of patients over the first τ_a years of the trial with a constant recruitment rate ρ. The total expected number of patients is thus ρτ_a. The goal of this section is to show how one can estimate the accrual time τ_a required to achieve power α₂ at a given type I error level α₁, for a specified rate ρ.

Let R_ij denote the real randomization time for each patient, and assume R_ij is independently uniformly distributed on [0, τ_a]. Similar to what was done in Theorem 3, we can show that $\mu =\gamma p_1{p}_2{D}_{1g}^{\prime }+o(1)$, where $D_{1g}^{\prime }=E[{\int }_R^{{\tau }_0}{\pi }_0(s)d{\mathrm{\Lambda }}_0(s)]$. $D_{1g}^{\prime }$ is the updated version of D_1g under the current trial setting. When τ_a is known, it can be estimated by

$${\widehat{D}}_{1g}^{\prime }({\tau }_a)\equiv \sqrt{\frac{{\sum }_{i=1}^{n_1}{\{{\widehat{\mathrm{\Lambda }}}_1(C_{i1}\mid V_{i1})-{\tau }_a^{-1}{\int }_0^{{\tau }_a}{\widehat{\mathrm{\Lambda }}}_1(s\mid V_{i1})ds\}}^{+}}{n_1}\times \frac{{\sum }_{i=1}^{n_2}{\{{\widehat{\mathrm{\Lambda }}}_2(C_{i2}\mid V_{i2})-{\tau }_a^{-1}{\int }_0^{{\tau }_a}{\widehat{\mathrm{\Lambda }}}_2(s\mid V_{i2})ds\}}^{+}}{n_2}},$$

Correspondingly, define $D_{1a}^{\prime }={\sum }_{j=1}^2{p}_{j^{\prime }}E\{{\int }_R^{{\tau }_0}{\pi }_0(s)d{\mathrm{\Lambda }}_j(s\mid V_{ij})\}$, and $D_2^{\prime }={\sum }_{j=1}^2{p}_{j^{\prime }}\times E[{\{{\int }_R^{{\tau }_0}{Y}_{1j}(s)d{\mathrm{\Lambda }}_j(s\mid V_{ij})\}}^2]$, j′ ≡ 3 − j. These quantities can be estimated by the following updated versions of D̂_1a and D̂₂:

$${\widehat{D}}_{1a}^{\prime }({\tau }_a)\equiv n^{-1}\sum _{j=1}^2\sum _{i=1}^{n_j}{\left\{{\widehat{\mathrm{\Lambda }}}_j(C_{ij}\mid V_{ij})-{\tau }_a^{-1}{\int }_0^{{\tau }_a}{\widehat{\mathrm{\Lambda }}}_j(s\mid V_{ij})ds\right\}}^{+},$$

and ${\widehat{D}}_2^{\prime }({\tau }_a)\equiv n^{-1}{\sum }_{j=1}^2{\sum }_{i=1}^{n_j}{\{{\widehat{\mathrm{\Lambda }}}_j(C_{ij}\mid V_{ij})-{\tau }_a^{-1}{\int }_0^{{\tau }_a}{\widehat{\mathrm{\Lambda }}}_j(s\mid V_{ij})ds\}}^2$.

Under the previous extra-Poisson variation assumption, ${\sigma }^2=p_1{p}_2({D_{1a}}^{\prime }+{\sigma }_w^2{D_2}^{\prime })+o(1)$. A simple moment estimator of ${\sigma }_w^2$ is thus

$${\left(n^{-1}\sum _{j=1}^2\sum _{i=1}^{n_j}{N}_{ij}(C_{ij})\{N_{ij}(C_{ij})-1\}/{\widehat{D}}_2^{\prime }-1\right)}^{+}.$$

Now τ_a can be obtained from the following self-consistency equation using the line search method:

$$n^{\prime }=\rho {\tau }_a=\frac{{(z_{1-{\alpha }_1/2}+z_{1-{\alpha }_2})}^2\{{\widehat{D}}_{1a}^{\prime }({\tau }_a)+{\widehat{\sigma }}_w^2{\widehat{D}}_2^{\prime }({\tau }_a)\}}{{\gamma }^2{p}_1{p}_2{\widehat{D}}_{1g}^{\prime 2}({\tau }_a)}.$$ (3)

6. Relationship to Current Existing Formula Based on Unadjusted Log-Rank Statistic

When covariates are not adjusted, Cook (1995) described a method for planning the duration of a randomized parallel group study in which the response of interest is potentially recurrent events data. Cook assumed patients accrue at a constant rate ρ in an accrual period of duration τ_a years with M denoting the random sample size and m the corresponding realization. At the end of the accrual period, subjects were assumed to be followed for an additional length of time τ_c, called the continuation period. τ = τ_a + τ_c was defined as the total study duration. The recurrent events the patients experienced over the whole study time were assumed to follow a homogeneous Poisson process with intensity λ_j, j = 0, 1. A proportional intensity model of the form λ(z_i) = λ exp{βz_i} was considered, where λ = λ₀ and β = log {λ₁/λ₀}, with z_i = 0, 1 denoting the treatment group membership. The censoring time was assumed to be exponential with rate δ_j. They derived the sample size formula based on the score tests on the regression coefficient β with respect to the hypothesis H₀ : β = 0 versus H₁: β = β_a.

Cook (1995) also considered extra-Poisson variation and proposed a revision of the variance in the original formula derived under the homogeneous Poisson process assumption. Cook (1995) used this to derive a revised variance to account for extra Poisson variation which leads to a different approximation from ours. Cook (1995) did not provide a method for estimating the extra-Poisson variance.

Proposition 1

When there are no covariates adjusted, under the parametric settings in Cook (1995) and under the same assumptions about accrual time, duration time, and censoring rate, the difference between our sample size estimate n′ and Cook’s estimate m is

$$n^{\prime }-m=\frac{4{(z_{1-{\alpha }_1/2}+z_{1-{\alpha }_2})}^2}{{\beta }_a^2}\left(\left\{k(\delta ,{\tau }_a,{\tau }_c)\frac{1+e^{2{\beta }_a}}{2e^{{\beta }_a}}-1\right\}{\sigma }_w^2\right),$$ (4)

where k(δ, τ_a, τ_c) > 1 is a function of the censoring rate δ, the accrue time τ_a and the duration time τ_c. Thus n′ > m when ${\sigma }_{\omega }^2>0$.

The proof is deferred to the Web Appendix.

When ${\sigma }_w^2=0$, Cook’s variance achieves the Cramer–Rao information lower bound and is efficient. Our sample size formula boils down to Cook’s under the same parametric setting. When there exists heterogeneity within subject, Cook (1995) treated the quantities ${\stackrel{\sim }{\lambda }}_j=N_{.}^{(j)}/T_{.}^{(j)}$ as the maximum likelihood estimators of λ_j, where $N_{.}^{(j)}$ and $T_{.}^{(j)}$ represent the total number of events and the total person years on treatment j, j = 0, 1. λ̃_j was plugged into the original score test statistic, and the sample size was derived after applying the delta method and a series approximation. Although λ̃_j is the true maximum likelihood estimate under the homogeneous Poisson model, this is not true in the presence of overdispersion, as pointed out in their paper. Thus their estimate is not in general a maximum likelihood estimate and may be inconsistent.

Matsui (2005) also considered sample size calculations with overdispersed Poisson data. His method is also parametric in the sense that λ_j is needed as an input parameter for sample size calculations. Compared with the model setting in Cook (1995) and Matsui (2005), our approach uses minimal assumptions about the data-generation process. Moreover, our sample size formula is derived based on the asymptotic normality of the covariate-adjusted log-rank test statistic. Thus our approach is more robust. In addition, we have an asymptotically unbiased estimator of the variance of the log-rank statistic, based on the estimated second moment of the cumulative mean function rather than on the square of the expected cumulative mean function as done in Cook. Therefore, our sample size is larger than Cook’s in the presence of overdispersion, as it should be.

7. Simulation Studies

The simulation study was designed in two parts. In the first part of the simulation, we study the small sample properties of the covariate-adjusted and unadjusted test statistics using simulations from overdispersed homogeneous Poisson data with intensity λ (t | V ) = λwexp{ψZ}h(V ;θ). A constant baseline intensity of λ = 0.25 is used. The heterogeneity source w is generated as a gamma distributed random variable with mean 1 and variance ${\sigma }_w^2=0$, 0.5, and 1, respectively. The treatment indicator Z takes values 0 and 1 with equal probability. The covariate V = aZ + ε, where ε follows standard normal distribution. The regression coefficient a is varied such that the correlation coefficient between V and Z are taken to be 0, 0.3, and −0.3, respectively. We consider h(V ; θ) = exp(θV ) and take θ to be 0, 0.5, and −0.5, respectively.

The censoring times follow an exponential distribution with rate λ/5 and the follow-up period is 3 years. All simulated trials involve nominal two-sided type I error α₁ = 0.05. For each setting, we simulate 2000 data sets with sample size 100 to achieve a Monte Carlo error of 0.01 for the type I error. The empirical powers are evaluated at ψ = log(0.6). The empirical type I error and the empirical power of the covariates-adjusted and unadjusted tests are recorded in Table 1.

Table 1.

Empirical type I error rates and empirical power for the robust log-rank tests unadjusted and adjusted for covariates: nominal type I error is 5%. λ = 0.25, exp(ψ) = 0.6. The Monte Carlo error is about 0.01.

		ρ = 0		ρ = 0.3		ρ = −0.3
${\sigma }_w^2$	θ	Adjusted	Unadjusted	Adjusted	Unadjusted	Adjusted	Unadjusted
Empirical type I error
0	0	0.056	0.057	0.052	0.054	0.058	0.060
	0.5	0.053	0.059	0.053	0.831	0.054	0.612
	−0.5	0.055	0.056	0.058	0.555	0.053	0.834
0.5	0	0.051	0.048	0.049	0.047	0.059	0.057
	0.5	0.046	0.049	0.055	0.575	0.051	0.435
	−0.5	0.048	0.058	0.058	0.452	0.057	0.584
1	0	0.051	0.060	0.055	0.056	0.059	0.058
	0.5	0.051	0.054	0.053	0.462	0.057	0.372
	−0.5	0.051	0.052	0.057	0.361	0.055	0.450
Empirical power
0	0	0.470	0.468	0.302	0.465	0.312	0.480
	0.5	0.524	0.453	0.404		0.281
	−0.5	0.531	0.460	0.279		0.362
0.5	0	0.367	0.368	0.243	0.379	0.221	0.376
	0.5	0.384	0.337	0.320		0.230
	−0.5	0.383	0.347	0.239		0.293
1	0	0.321	0.320	0.201	0.308	0.218	0.313
	0.5	0.321	0.286	0.209		0.213
	−0.5	0.302	0.275	0.221		0.206

When the covariate V has no effect on the time to event, the estimated type I errors are very close to the nominal levels for both statistics. When V has an effect on the event times, the empirical type I errors are still close to the nominal levels for both statistics when V and Z are uncorrelated. Due to the overly high empirical type I errors, the unadjusted log-rank test is not valid when V and Z are correlated and V has an effect on the event times, while the adjusted log-rank statistic works fine for this situation.

For the unadjusted tests, we only estimate their power when they are valid tests as indicated above. It can be seen that when V and Z are uncorrelated, using covariate-adjusted tests can increase the power, while the power using the unadjusted tests seems higher than the covariate-adjusted tests when V and Z are correlated and V has no effect on time to event.

In the second part of the simulation, we compare several sample size formulas. Cook (1995) provided several tables of trial duration and expected sample size for specified powers of two-sided tests under several scenarios. We borrow a small subset for illustration purpose. All simulated trials involve nominal two-sided type I error α₁ = 0.05 and nominal power α₂ = 0.80. The subjects are randomized to each treatment with equal probability. A constant baseline intensity of λ = 0.25 is used. We show the results from trials with no continuation period, 0.5 and 1 year continuation periods. No censoring and heavy censoring from an exponential distribution with rate δ₀ = δ₁ = λ/5 are presented. For each setting, we simulate 2000 data sets to achieve a Monte Carlo error of 0.01 for the type I error. Instead of computing the accrual time at the given accrual rate and duration period, we use the computed accrual period and duration period in Cook’s paper to compute the sample size in order to make the comparison of sample sizes more direct.

Because our sample size formula is identical with Cook’s when there is no event dependence and constant intensity, we only implement simulations to study the behavior of the methods for overdispersed homogeneous Poisson data. The heterogeneity source w is generated as a gamma distributed random variable with mean 1 and variance ${\sigma }_w^2=1$, 2 and 3, respectively. We simulate data with β = 0 for evaluating type I error rates and β = log(0.6) for evaluating power.

Table 2 records the empirical type I error and the empirical power at the corresponding sample size. Our sample size is larger than Cook’s, which, based on discussions in the previous section, is as expected. Both methods can maintain the nominal type I error of 5%. When the extra-Poisson variance increases, the power of Cook’s method is smaller than the nominal level of power, while ours performs better. This is because we have a consistent estimate of the average squared mean intensity, which is underestimated in Cook (1995).

Table 2.

Empirical type I error rates and empirical power for the robust tests and Cook’s methods: nominal type I error and nominal power is 5% and 80%, respectively, λ = 0.25, exp(β) = 0.6, “C” is Cook’s method, and “P” is the proposed method. The Monte Carlo error is about 0.01.

			${\sigma }_w^2=1$			${\sigma }_w^2=2$			${\sigma }_w^2=3$
Methods	δ	τc	τ	Sample size	Empirical type I error	τ	Sample size	Empirical type I error	τ	Sample size	Empirical type I error
C	0	0	4.83	386	0.049	5.78	463	0.050	6.85	548	0.046
P				448	0.048		586	0.047		732	0.051
C		0.5	4.95	356	0.053	5.48	439	0.048	6.62	529	0.044
P				402	0.047		536	0.041		608	0.055
C		1	5.12	330	0.057	5.23	418	0.054	6.42	513	0.048
P				367	0.056		498	0.051		641	0.054
C	0.05	0	4.99	399	0.054	5.97	478	0.055	7.06	565	0.048
P				468	0.044		618	0.054		780	0.046
C		0.5	5.11	369	0.056	5.67	453	0.055	6.82	546	0.045
P				423	0.052		568	0.050		728	0.047
C		1	5.29	343	0.052	5.41	433	0.053	6.62	530	0.054
P				388	0.049		532	0.042		690	0.054
Methods	δ	τc	τ	Sample size	Empirical power	τ	Sample size	Empirical power	τ	Sample size	Empirical power
C	0	0	4.83	386	0.766	5.78	463	0.727	6.85	548	0.712
P				448	0.813		586	0.821		732	0.827
C		0.5	4.95	356	0.777	5.48	439	0.748	6.62	529	0.732
P				402	0.811		536	0.825		608	0.775
C		1	5.12	330	0.792	5.23	418	0.763	6.42	513	0.763
P				367	0.812		498	0.823		641	0.827
C	0.05	0	4.99	399	0.783	5.97	478	0.738	7.06	565	0.728
P				468	0.841		618	0.844		780	0.851
C		0.5	5.11	369	0.792	5.67	453	0.763	6.82	546	0.747
P				423	0.848		568	0.850		728	0.850
C		1	5.29	343	0.796	5.41	433	0.763	6.62	530	0.759
P				388	0.841		532	0.839		690	0.858

8. Example: rhDNase Study

We will illustrate the test and the sample size formula through the following example. A randomized double-blind trial was conducted by Genentech Inc. (South San Francisco, CA), in 1992 to compare rhDNase to placebo (Fuchs et al., 1994). Recombinant DNase I (rhDNase or Pulmozyme) was a treatment cloned by Genentech Inc., to reduce the viscoelasticity of airway secretions and improve mucus clearance in the lung of cystic fibrosis patients.

The study enrolled 645 patients. Enrollment lasted from December 31, 1991 until March 31, 1992. The follow-up time of patients extended from March 20, 1992 to September 24, 1992. During the time patients were monitored for pulmonary exacerbations and data on all exacerbations and the baseline level of forced expiratory volume in 1 second (FEV₁) were recorded. The primary endpoint was the time until first pulmonary exacerbation (Fuchs et al., 1994). The data were analyzed by Therneau and Hamilton (1997) to compare several semiparametric methods for recurrent events data. Both the treatment effect and baseline FEV₁ are shown to be significant. Here we are interested in testing the treatment effect in terms of reducing the number of exacerbations viewed as recurrent events and calculating the sample size based on the log-rank test, for both FEV₁-adjusted and unadjusted versions.

A two-sided type I error rate of 5% and power of 80% are considered here. We test a log-rate ratio of −0.345 (or a rate ratio of 0.708), which is estimated using the marginal model by Wei, Lin, and Weissfeld (1989) as recommended in Therneau and Hamilton (1997). θ̂_n = −0.194 by solving (1). As pointed out in Section 4, we also need the extra Poisson variance ${\sigma }_w^2$, the expected number of events D_1g, D_1a and the expected squared number of events D₂ to get the sample size. We take several looks during the trial as recorded in part (i) of Table 3. We consider the trial period before each monitoring time as artificial pilot studies in order to extract the desired information. We then apply those parameter estimates to obtain the sample size for the “real” trial. By “real,” we mean the completed trial based on the actual monitoring times.

Table 3.

Interim analysis of rhDNase data at several looks starting from April 9, 1992. (i) Using log-rank statistic adjusted for FEV₁. (ii) Using log-rank statistic unadjusted for FEV₁.

Analysis date	Average study time	${\widehat{\sigma }}_w^2$	Current D̂1g	Current D̂1a	Current D̂2	Projected D̂1g	Projected D̂1a	Projected D̂2	Sample size	p-value
(i)
May 9	62	0.160	0.190	0.192	0.056	0.512	0.519	0.410	586	0.076
May 29	81	0.367	0.262	0.265	0.100	0.535	0.541	0.418	639	0.053
June 18	101	0.383	0.323	0.329	0.143	0.531	0.555	0.389	641	0.019
July 18	129	0.183	0.428	0.433	0.236	0.549	0.562	0.390	546	0.029
August 17	153	0.279	0.515	0.519	0.335	0.558	0.560	0.393	576	0.057
August 27	159	0.278	0.534	0.540	0.362	0.555	0.559	0.392	571	0.028
September 6	164	0.299	0.549	0.553	0.380	0.554	0.560	0.389	578	0.034
September 24	165	0.314	0.554	0.560	0.389	0.554	0.557	0.391	584	0.023
(ii)
May 9	62	0.452	0.185	0.187	0.045	0.499	0.505	0.326	692	0.084
May 29	81	0.703	0.257	0.260	0.080	0.525	0.532	0.334	734	0.060
June 18	101	0.693	0.320	0.325	0.117	0.525	0.534	0.317	721	0.023
July 18	129	0.437	0.425	0.430	0.194	0.545	0.551	0.319	614	0.031
August 17	153	0.554	0.513	0.517	0.275	0.555	0.559	0.322	632	0.059
August 27	159	0.552	0.532	0.537	0.298	0.552	0.558	0.321	636	0.030
September 6	164	0.571	0.547	0.552	0.314	0.552	0.557	0.320	640	0.036
September 24	165	0.595	0.551	0.557	0.321	0.551	0.557	0.321	649	0.025

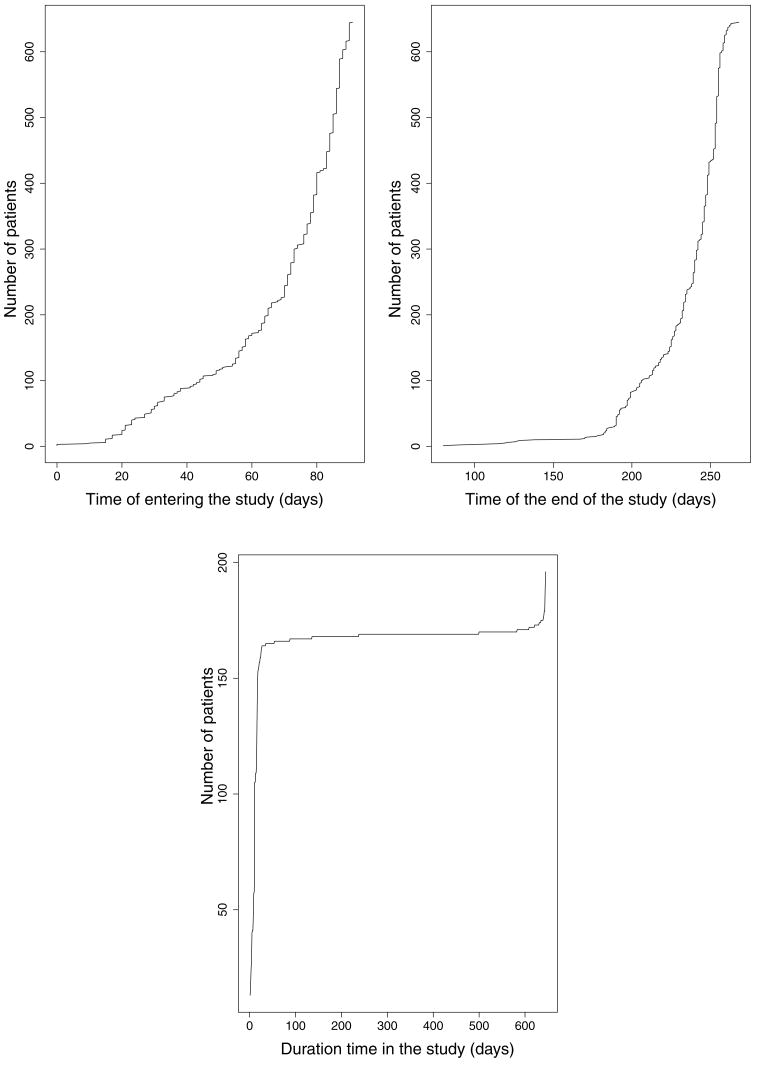
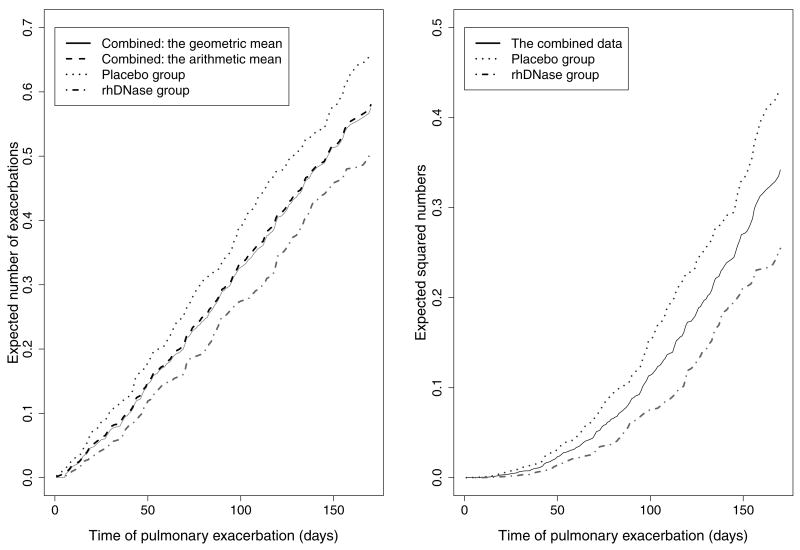
As noted earlier, the values of D_1g, D_1a, and D₂ depend on the censoring distribution and the real study length in addition to the event time distribution. Hence there is no unified, nonparametric method to specify them prior to the trial. The quantities could be determined by the investigator’s prior knowledge or biological reasoning, but this may differ according to different trial settings. As indicated in Figure 1, in this trial the timing of patient enrollment and dropout is roughly exponentially distributed and the length of follow-up time of most patients is about 165 days. We further examined the expected number of events and the expected squared number of events in Figure 2. The roughly straight lines in the left graph show that the event process appears to roughly follow a homogeneous Poisson assumption, and the approximate quadratic lines in the right graph are consistent with this presumption. Considering the above two facts, we apply linear extrapolation to estimate D_1g, D_1a and quadratic extrapolation for D₂ of the real trial using their values from the pilot study. This extrapolation procedure is generally applicable to approximately homogeneous Poisson data under uniform censoring.

Figure 1.

The number of enrolled patients versus the time of entering the study (days) (top left), the number of patients versus the time of the end of the study (days) (top right), and the number of patients versus the duration time (days) of patients stay in the study (bottom) in the rhDNase study.

Figure 2.

The expected number of events (left) and the expected squared number of events (right) over time in the rhDNase trial. In the left plot, the solid line and the dashed line are combined data with the geometric mean and with the arithmetic mean, respectively. In the right plot, the solid line is combined data. In both panels, the dotted line is the placebo group, and the dash-dotted line is the rhDNase group.

For illustration, we consider the first analysis date of May 9, 1992. The estimate of ${\sigma }_w^2$ is 0.160 based on the data collected prior to that time. The observed D̂_1g, D̂_1a, and D̂₂ are 0.190, 0.192, and 0.056 at that time, respectively. Dividing by the average trial time 62 up to May 9, 1992 and multiplying by the average total trial time 165, we obtain the projected D̂_1g = 0.512 and D̂_1a = 0.519. The value D̂₂ = 0.410 at the end of trial is obtained from the current D̂₂ times the squared ratio of 165 over 62. Therefore, the sample size is estimated as 586 using the “pilot” study data. The sample size using the information from the whole study is 584. The estimated extra Poisson variance is distributed uniformly around the value at the end of the study, 0.314, at each look, which supports the extra-Poisson variation assumption. At each look, we carry out the robust covariate-adjusted log-rank test. The p-values turn out to mostly decrease as the study length increases, as expected.

In the same manner, we evaluate the covariate unadjusted log-rank tests and calculate the corresponding sample size formulas, recorded in part (ii) of Table 3. Interestingly, the estimated variance of frailty w is larger than these FEV₁ adjusted estimates, which indicates that partial event dependence within a subject can be interpreted through the effect of FEV₁. The smaller sample needed is the main advantage of the adjusted test versus unadjusted test in this application. Although the adjusted and the unadjusted tests show similar results, the adjusted tests always produce slightly more significant results than those from the unadjusted tests, suggested by the smaller p-values. The estimated sample sizes based on the covariate unadjusted tests are higher than these based on the covariate adjusted tests, as expected.

We note that, although the pilot study and the real study are connected in this example, this is not necessary in practice. This was just done in this instance to illustrate a possible approach to estimating D_1g, D_1a, and D₂. Other approaches could be used in other settings in order to meet the required power, economic, and practical constraints.

9. Discussion

In this article, we propose a covariate-adjusted robust log-rank test. The proposed log-rank tests are robust with respect to different data-generating processes and adjustments for covariates. It reduces to Kong and Slud (1997) in the case of a single event. We also provide a sample size formula based on the asymptotic distribution of the robust covariate-adjusted log-rank test statistic and a method of estimating the extra Poisson variance. Compared with Cook (1995) and Matsui (2005), an advantage of our sample size formula is that it is nonparametric and more robust to the data-generation process. Simulation studies validate our proposed method. An rhDNase study is used to illustrate our method.

Supplementary Material

supp. 10. Supplementary Materials.

The Web Appendix, referenced in Sections 4 and 6, is available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.