Quantitative biological imaging by ptychographic x-ray diffraction microscopy

Abstract

Recent advances in coherent x-ray diffractive imaging have paved the way to reliable and quantitative imaging of noncompact specimens at the nanometer scale. Introduced a year ago, an advanced implementation of ptychographic coherent diffractive imaging has removed much of the previous limitations regarding sample preparation and illumination conditions. Here, we apply this recent approach toward structure determination at the nanoscale to biological microscopy. We show that the projected electron density of unstained and unsliced freeze-dried cells of the bacterium Deinococcus radiodurans can be derived from the reconstructed phase in a straightforward and reproducible way, with quantified and small errors. Thus, the approach may contribute in the future to the understanding of the highly disputed nucleoid structure of bacterial cells. In the present study, the estimated resolution for the cells was 85 nm (half-period length), whereas 50-nm resolution was demonstrated for lithographic test structures. With respect to the diameter of the pinhole used to illuminate the samples, a superresolution of about 15 was achieved for the cells and 30 for the test structures, respectively. These values should be assessed in view of the low dose applied on the order of ≃1.3·10⁵ Gy, and were shown to scale with photon fluence.

The need to probe the three-dimensional structure of extended biological cells and tissues at high resolution and under hydrated conditions has motivated a continuous and long-lasting effort to develop suitable x-ray microscopy techniques (1–3). Specific advantages of x-rays concern (i) the resolution (4), (ii) the kinematic nature of the scattering process enabling quantitative image analysis (5), (iii) element specific contrast variation (6), and (iv) compatibility with unsliced (three-dimensionally extended), unstained, and hydrated specimens (7, 8). Notwithstanding significant achievements, x-ray microscopy based on Fresnel zone plate lenses is severely limited by the comparatively small numerical apertures, leading to a resolution which is at least one or two orders of magnitude away from the classical diffraction barrier associated with the wavelength λ. The fabrication of high-resolution lenses poses severe technological problems, in particular for higher photon energies where the tomographic reconstruction of extended specimens can best be achieved.

To circumvent the practical resolution barrier associated with x-ray lens fabrication, different forms of lensless coherent x-ray diffractive imaging (CXDI) methods, based on iterative object reconstruction from the measured coherent diffraction patterns, have been developed (9, 10–11). CXDI has been demonstrated on biological unstained specimens by using soft (12, 13) and hard x-rays (14, 15). In its original form (9), CXDI imposes considerable limitations and preconditions to the experimental setup or the sample, excluding in particular extended samples and assuming an idealized plane wave illumination function. As a way to overcome those limitations, the concept of ptychography, which is compatible with CXDI and allows for an unlimited field of view by the use of overlapping illuminated areas on the sample, has been proposed (16, 17) and demonstrated for hard x-rays (18). Recently, several extensions of the original algorithmic scheme have been presented (19–21), which allow for a simultaneous reconstruction of both the complex object transmission and the complex illumination function (probe function) from the same dataset. In the first experimental demonstration of this ptychographic x-ray diffraction microscopy or ptychographic coherent diffractive imaging (PCDI) (19), high-resolution reconstructions with a fast and reliable convergence were obtained for a lithographically fabricated heavy-element test object.

In this article we report on a first application of PCDI to the biologically relevant case of weakly scattering cellular material. Quantitative phase maps with a phase resolution below 0.01 π have been reconstructed from diffraction data of unstained freeze-dried cells of the gram-positive bacterium Deinococcus radiodurans. In contrast to previous CXDI experiments on biological objects, the sample did not need to be isolated, and a quantitative result of high quality was obtained within comparatively short illumination time by using a mildly focused multi-keV synchrotron x-ray beam. Phase maps have been reconstructed up to a spatial frequency of 5.9 μm^-1, corresponding to a real-space half-period of 85 nm at an average fluence of ≃6.6·10⁷ photons/μm². During the imaging process a dose of ≃1.3·10⁵ Gy was applied. Quantitative area electron density maps of the cellular structure could be extracted from the reconstructed two-dimensional phase distribution. Limited here in resolution by incident photon flux, this method opens up a complementary approach to recent electron microscopy studies of the bacterial nucleoid in D. radiodurans (22, 23). The key question of these previous and ongoing structural studies aims at unraveling possible correlations of the bacterium’s extraordinary resistance to high doses of ionizing radiation and the structural arrangement of its nucleoid. Despite large efforts, this problem remains largely unsolved and highly disputed, and the application of methods complementary to electron microscopy was recommended to clarify the relationship between the nucleoid structure and radioresistance (24).

Experimental Procedure

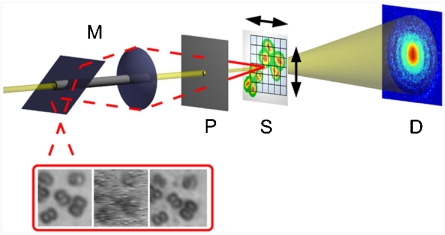
The experiment was performed at the coherent Small Angle X-ray Scattering (cSAXS) beamline of the Swiss Light Source (Villigen, Switzerland). A schematic of the setup is depicted in Fig. 1. A pinhole 1.4 μm in diameter was illuminated by a coherent beam with a photon energy of 6.2 keV. Freeze-dried, unstained cells of the bacterium D. radiodurans were mounted onto a thin Kapton film placed 1.4 mm downstream of the pinhole. The diffracted intensity was measured at a distance of 7.22 m from the sample by using a single-photon counting PILATUS 2M array with a pixel size of 172 μm (25). An optical microscope allowing for an accurate and parallax-free positioning control was placed a few centimenters upstream of the pinhole. For further details on the experimental setup and sample preparation, see SI Text).

Fig. 1.

Experimental setup. The monochromatic x-ray beam (light yellow) passes through the Molybdenum-shielded channel of the on-axis microscope M and the probe defining pinhole P. After short propagation the pinhole beam impinges on the sample S, which is translated in horizontal and vertical direction between exposures, so that the illuminated spots are distributed on a two-dimensional grid. Via a drilled lens and mirror, the optical microscope (red light path) allows for a parallax-free observation of the sample if the pinhole is moved to the side. By subsequently translating the pinhole and the sample into the fixed focal plane F of the microscope the propagation distance between pinhole and sample can be measured accurately. The two-dimensional pixel detector D is placed in the far field to collect the experimental diffraction patterns corresponding to each scan position on the grid. (Inset) Optical images of the freeze-dried D. radiodurans cells imaged in the experiment: (Left) conventional bright field microscopic image before the experiment (Z1 Observer, Zeiss, Germany), (Middle) optical image from the in situ microscope at the end of the experiment, (Right) conventional bright field microscopic image after the experiment. The reconstructions shown in Fig. 2 correspond to the same region of interest (ca. 14 × 14 μm²).

During the experiment, diffraction patterns were first collected by illuminating the sample at 51 × 51 positions on a rectangular grid with a grid spacing of 400 nm. The exposure time at each sample position was 1 s, and the incident beam intensity was I₀ ≃ 1.5·10⁵ photons per second. As a second step, a small region of interest was selected out of the previous scan area and scanned at 11 × 11 positions with the same grid spacing, but an exposure time of 60 s per scan point.

At each scanning position r_j in the sample plane, the complex-valued two-dimensional exit wave ψ_j(r) is very well approximated by a product ψ_j(r) = P(r)O(r - r_j) of the probe wave field P(r) and the object transmission function O(r) (19). The intensity distributions I_j, measured in the far field, can be written as , where 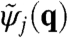is the Fourier transform of ψ_j(r) and q is the two-dimensional reciprocal space coordinate. Provided that there is sufficient overlap between neighboring illuminated regions of the object, one can reconstruct both P(r) and O(r) solely from the intensity measurements.

Results and Discussion

Ptychographic Coherent Diffractive Imaging of D. radiodurans.

As a first online analysis step, conventional differential phase contrast and dark-field images were generated by using the same procedure as in conventional scanning transmission x-ray microscopy (5). Images corresponding to a subset of 35 × 35 scan points out of the short-exposure dataset are shown in Fig. 2A and B. These micrographs have a pixel size equal to the grid spacing of the raster scan, and their resolution is limited to the size of the illumination (about 1.4 μm).

Fig. 2.

Ptychographic diffractive imaging of freeze-dried D. radiodurans cells (1-s dwell time). (A) Differential phase contrast image of a subset of the scanned region. One pixel corresponds to one scan point (pixel size is 400 × 400 nm²). (B) Dark-field contrast image of the same region as shown in A. (C) PCDI reconstruction of the object transmission function (phase) in the same region as shown in A and B. The area marked by the dashed white frame was scanned again in a subsequent scan with longer dwell time (Fig. 3). The standard deviation of the phase within the solid rectangle is 0.013 rad.

A high-resolution PCDI reconstruction from the same dataset is depicted in Fig. 2C, which shows the phase of the complex-valued object transmission function O(r), obtained after 1100 iterations. The central 128 × 128 detector pixels of each recorded diffraction pattern were used in the analysis, leading to a pixel size of Δ₁ = 66 nm in the object plane. To average out fluctuations in the reconstruction, which are due to the photon shot noise present in the experimental data, a mean object transmission function out of the final 101 iterates was generated. The resulting reconstruction is consistent with the preliminary differential phase contrast and dark-field images as well as with the optical micrographs shown in Fig. 1. D. radiodurans cells are visible as dimers and tetramers, and the separation of each monomeric part of a cell into four internal subunits, each known to contain a single copy of the bacterium’s genome, is observable for a large fraction of the cells. Actively growing and separating cells were used, so that the internal structure cannot be expected as uniform as for stationary-state cells (22).

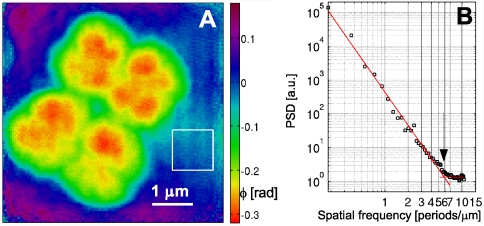
Applying the same procedure on the second, long-exposure dataset, an independent high-resolution PCDI reconstruction of a subregion from the first scan was obtained, which is marked in Fig. 2C by a dashed white frame. Here, a region of 180 × 180 central pixels on the detector was selected, corresponding to an object pixel size of Δ₂ = 47 nm. To account for fluctuations in the incident flux, all diffraction patterns for the experimental long-exposure dataset were normalized to their mean value. The resulting phase map, averaged over iterates 2400–2500 to assure an equilibrated state of the reconstruction process, is shown in Fig. 3A. The magnitudes of the phase values corresponding to the cell walls and the internal structure are in very good agreement with the short-exposure reconstruction, which is shown on the same phase scale. In addition, the reconstructions show a high degree of structural resemblance, which is best observed with both reconstructions on the same geometric scale, as shown in Fig. 4, where the phase maps have been rescaled to effective mass density per unit area (see below).

Fig. 3.

(A) Reconstructed phase map of a PCDI scan on a single, tetrameric D. radiodurans cell (60-s dwell time). The scanned region corresponds to the area marked by a dashed white frame in Fig. 2C. The standard deviation of the phase within the solid rectangle is 0.017 rad. (B) PSD of the complex object transmission function corresponding to the phase map shown in A. The result of a fit of an exponential power law to the PSD in the interval [0.1,5] μm^-1 is shown by the decaying red line. The additional red line indicates the mean value of the PSD for frequencies > 7 μm^-1. The transition point between both regions (at 5.9 μm^-1) is marked by an arrow.

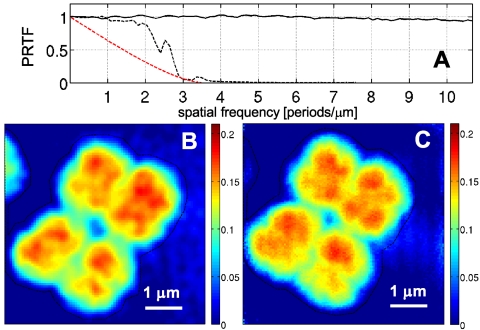
Fig. 4.

(A) PRTF, corresponding to the dataset with 1-s dwell time (black dashed line) and 60-s dwell time (solid line). The PRTF of the short-exposure dataset is compared to an ideal MTF with a cutoff frequency of 3.5 μm^-1 (red dashed line). (B) Effective area mass density distribution in the area marked by a dashed frame in Fig. 2C (short-exposure dataset). (C) Effective mass density distribution corresponding to Fig. 3A (long-exposure dataset). (Scalings in mg/cm².)

Resolution.

In principle, the resolution of PCDI reconstructions is limited only by the dimensions of the detector. In practice however, the resolution is limited by the finite amount of measured photons, leading to a fast decay of the signal-to-noise ratio at high spatial frequencies. For a cellular object without sharp features and edges, a determination of the obtained resolution is not possible from real-space line profiles alone.

The effect of noise in the reconstruction process seems to be efficiently captured with an effective transfer function called “phase retrieval transfer function” (PRTF) (13, 26). It is given here as the ratio of the reconstructed Fourier amplitude 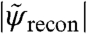and the experimental Fourier amplitude 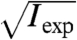, each averaged over all azimuthal angles of the diffraction pattern. ψ_recon is formed as an average out of many iterations, so that systematically reconstructed phases will add constructively, whereas random phases will add to zero. A lower limit for the smallest detectable features is then given by the cutoff frequency of an ideal modulation transfer function (MTF) that matches the experimental PRTF. For both datasets a representative diffraction pattern, recorded at a scan position where the whole beam was illuminating cellular material, was analyzed. The result of such an analysis is depicted in Fig. 4. The PRTF of the short-exposure dataset quickly decreases close to zero around a spatial frequency of 3.5 μm^-1, corresponding to a real-space half-period between 140 and 150 nm. Based on an average fluence of ≃10⁶ photons/μm², the applied dose was estimated as ≃2·10³ Gy (27, 28). For the long-exposure dataset, the PRTF remains close to one over the whole range of analyzed spatial frequencies. Although this indicates that the exit wave function ψ_recon has been consistently phased up to a spatial frequency of 1/(2Δ₂) = 10.7 μm^-1, a visual inspection of the corresponding reconstructed phase map shown in Fig. 3A indicates a lower resolution than derived from the PRTF. Therefore, for the long-exposure dataset, the resolution estimate has to be based on the reconstructed phase map itself. The angular-averaged power spectral density (PSD) corresponding to the reconstructed phase map of the long-exposure dataset is depicted in Fig. 3B. It follows a power-law decay with an exponent of -3.3 before reaching a plateau at high spatial frequencies, which corresponds to length scales where random fluctuations dominate. The smallest length scale detectable in the reconstructed phase map is thus given by the frequency, where the power-law decay changes into constant random fluctuations. Its value of 5.9 μm^-1 corresponds to a half-period of 85 nm. The dose applied here was estimated to D ≃ 1.3·10⁵ Gy, which roughly corresponds to an increase in dose by a factor of 60, leading here to an increase in resolution by a factor of about 2.

The overall phase shift introduced by a single cell is in the range of 0.25–0.3 rad. The amplitude attenuation is below the detection level of the experiment, giving rise to a homogeneously flat amplitude reconstruction. These results are in good agreement with the maximum amplitude and phase changes of 1.2·10^-3 and 0.25 rad (0.08 π), respectively, expected for an unstained biological cell of 3-μm thickness with a third of its volume filled with protein (based on assumptions presented in ref. 29).

Mass Density maps.

Reliable phase and amplitude values for a quantitative determination of the electron density can only be obtained if a sufficient part of the diffraction pattern is collected (14, 30, 31). In the present study the use of a divergent pinhole illumination function in combination with the high dynamic range (20 bit ≃ 10⁶) and single-photon–counting capability of the PILATUS detector allowed for a recording of the full diffraction data, limited only by the finite amount of measured photons. The reconstructed phase distributions ϕ(r) could thus be used for quantitative analysis (see Fig. 3B and C) after a correction was applied to a linear ramp caused by the translational invariance of the phase problem. As a first step, the phase contribution due to the substrate was obtained. It is given here by the mean of the phase outside the dashed black line depicted in Fig. 3B and C, and was subtracted to yield the phase contribution of the cell only. Based on the optical constants of biological material at 6.2-keV photon energy, one obtains a linear relation between the phase change due to a sample in the beam path and its effective mass density distribution projected along the direction of the incident beam (for a detailed derivation see SI Text):

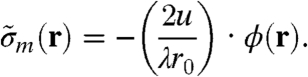[1]

Here, u denotes the atomic mass unit, r₀ the classical electron radius, and λ the wavelength of the incident radiation. 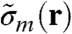is related to the absolute mass density via 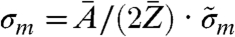. 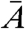and 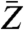denote the mass and the atomic number, respectively, of the imaged material, averaged over one resolution volume.

By using the relation in Eq. 1, the phase map from the long-exposure dataset and the corresponding area from the short-exposure dataset were converted into effective mass density distributions. A small overall offset subtraction of 0.02 mg/cm², on the order of the experimental error, from the long-exposure mass distribution was allowed to match both mass distributions. The ratio 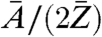, and thus the absolute mass density, is dependent on the chemical composition of the sample and generally not known in the experiment. However, on length scales of the present resolution of biological CXDI the ratio 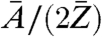can be regarded as almost constant for most biological material, which is composed to a very large extent of a few low-Z elements (32). Considering a model protein with an empiric composition H₅₀C₃₀N₉O₁₀S₁ (28) one obtains 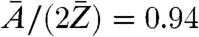. The relative deviation of the known effective mass density from the generally unknown absolute mass density can thus be expected in the range of 5–10%.

An experimental error of 0.03 mg/cm² was estimated based on reconstructions of simulated datasets and fluctuations in the substrate regions of experimental reconstructions as described above.

As most of the other cells visible in Fig. 2C, the upper two monomers of the tetrameric cell depicted in Fig. 3 contain three to four, mostly compact, dense subunits with an average linear extension of 400–600 nm. Based on their shape and size we attribute these subunits to the bacterial nucleoid, i.e., to compacted plasmid DNA. A typical value for the effective area mass density in these regions is 0.17(3) mg/cm². Assuming a cell thickness between 1.5 and 3 μm, one thus obtains an absolute volume density in the range of 0.5–1.1 g/cm³. This range is well-justified in view of the average density of a hydrated Escherichia coli cell (1.160(1) g/cm³), as determined with high accuracy from microchannel resonance measurements (33).

Certainly, the density range obtained here for the nucleoid regions of freeze-dried samples cannot be directly identified with the partial nucleoid density of a living bacterial cell. Due to the lack of depth information, only an average density value over the whole thickness of the cell could be obtained. In addition, residual water in the sample not removed in the freeze-drying process could have altered the obtained density values. However, unlike in electron microscopy, there is no systematic barrier preventing the quantitative imaging of whole (unsliced) (frozen-)hydrated cells. Accurate depth information could be assessed by an extension to tomographic imaging, so that detailed volume density maps with high density resolution can be obtained.

In previous electron microscopy studies of unstained sections of D. radiodurans cells, a very small contrast between the ribosome-rich cytoplasm and the ribosome-free nucleoid was observed (34) and interpreted as a slightly lower density in the nucleoid region compared to the surrounding medium. The low contrast generally complicates the elucidation of DNA organization in bacterial cells. A partial DNA density of 0.10(5) g/cm³ has been reported for the bacterial nucleoid in E. coli (35). This result must be carefully assessed in view of the significant difficulty to establish quantitative relationships between contrast and density in electron microscopy. Furthermore, the preparation procedure included, in contrast to the present study, sectioning and substitution of the water by a resin. The density of the nucleoid was then estimated relative to the overall cell density, determined by the protein content and the resin.

Method

The maximum phase shift measured for the cellular objects in this study is about tenfold smaller than the maximum phase shift of 2.2 rad caused by the gold test structure used as a sample in the first experimental demonstration of PCDI with simultaneous probe retrieval (19). To assure this level of phase resolution, a very careful control of all experimental and algorithmic parameters was necessary. To this end, both a numerical and experimental test of the previously described experimental procedure was performed under equivalent physical conditions.

Reconstruction of a Simulated PCDI Dataset from Biological Cells.

In contrast to a heavy-element test sample, the detailed structure and elemental composition of a biological specimen is generally not known prior to the experiment. Therefore, a quantification of the experimental error is difficult. This becomes even more important as, especially for weakly scattering samples, noise in the diffraction patterns can alter the reconstructions as well as the uniqueness properties of iterative projection algorithms quite substantially (36).

To quantify the experimental error and to find the optimum algorithmic parameters for the reconstruction of the noisy experimental data, PCDI datasets with added noise were generated and reconstructed based on an assumed phantom object function, which was adapted to preliminary reconstructions of the experimental datasets and rescaled to corrresponding phase values.

The measured data is incorporated into the reconstruction procedure by introducing the so-called ”Fourier-contraint,” i.e., by imposing an agreement between the Fourier amplitudes of the exit waves and the experimental intensities at each scan position. How to design this constraint in an optimal way to account for the complete noise statistics of the measured intensities is currently not known. In this work, the effect of noise in the measured intensities was included by introducing a relaxed Fourier constraint, which allows an exit wave candidate to obey the constraint if it is contained in a sphere around the measured Fourier amplitude. The optimal choice of the radius of this sphere was found by comparing reconstructions of simulated datasets with the true solution, both for short and long exposure times. In addition, the agreement between reconstructed and measured diffracted intensities was studied.

The experimental error of the reconstructed phase maps was estimated based on a careful comparison of the simulated and reconstructed phase maps for the same experimental and algorithmic parameters as used in the real experiment. The statistical deviation of the reconstructions from the simulated phase distributions was found to be decreasing with photon fluence (0.03 rad for the short-exposure simulation, 0.01 rad for the long-exposure simulation). For the conversion into effective area mass density an offset phase value was calculated, representing the phase contribution of the substrate. The uncertainty in determining the offset value was included in the error estimation of the mass density distributions. For further information, see SI Text.

Preparative Test Experiment.

Before the imaging experiment on the cells, a well-defined high-resolution chart (NTT-AT, Japan, model ATN/XRESO-50HC) consisting of a 500-nm-thick nanostructured tantalum layer on a SiC membrane was placed in the beam, at a distance of 1.15 mm from the pinhole as determined optically with the on-axis microscope. Diffraction patterns at 81 × 81 positions on the sample with a spacing of 250 nm and a dwell time of 1 s per step were collected at an incident beam intensity of ≃3.2·10⁵ photons per second (equivalent to an average fluence of 5.1·10⁶ photons/μm²). A region of 20 × 10 scan points around the center of the Siemens star was selected from the experimental dataset and reconstructed utilizing the central 256 × 180 pixels of each recorded diffraction pattern. In the reconstruction, the lines of the innermost circle in the segmented Siemens star, reaching a half-period of 50 nm toward the center, are clearly resolved. A line profile drawn perpendicular to a few central stripes of the Siemens star was used for an estimation of the obtained maximum resolution (see Fig. 5A). A fit of a Gaussian error function to a phase step in the central region yields a full width at half maximum of 49.6 nm. This increase in resolution with respect to the cells is mostly caused by the high phase contrast of the sample. Additional reconstructions with a wider field of view and a smaller detector area were obtained from the same dataset (SI Text). The expected phase shift of 0.34 π and amplitude transmission of 0.88 for a 500-nm-thick Ta layer at 6.2-keV incident photon energy is in very good agreement with the measured values in the reconstructed object transmission function, 0.34π and 0.86. Backpropagation of the reconstructed probe function over a distance of 1.15 mm, shown in Fig. 5B, yields a wave field with nearly flat intensity within a circular area, which agrees very well with the expectation for an ideal pinhole. This underlines the accuracy of the experimental determination of the distance between pinhole and sample as well as the high quality of the pinhole (for a scanning electron micrograph see Fig. 5C). The result further justifies the use of an ideal pinhole function, propagated over the measured distance between pinhole and sample (see Fig. 1) as an initial guess for the probe function.

Fig. 5.

Reconstruction of the complex object and probe function for a Siemens star test pattern. Phase is encoded as color and amplitude as brightness (see colorwheel in A). (Scale bars: 500 nm.) (A) Inset from a reconstruction of 20 × 10 diffraction patterns collected around the central region of the Siemens star [33 × 47 nm (h × v) pixel size]. A line profile of the phase distribution, drawn along the dashed line shown in C, is depicted in the lower part of the image. A Gaussian fit to a central gradient region of the phase profile is marked by the red line. (B) Reconstructed probe function, backpropagated over the propagation distance between pinhole and sample, as determined with the optical on-axis microscope. (C) Scanning electron micrograph of the pinhole used as the beam-defining aperture in all experiments.

Summary and Outlook

In summary, we have demonstrated the successful application of PCDI to unstained and unsliced freeze-dried D. radiodurans cells. An experimental setup and analysis procedure optimized for weakly scattering samples has been suggested and applied.

A phase map of the object transmission function could be reconstructed with an experimental error below 0.01 π, as obtained from reconstructions of a simulated PCDI dataset equivalent to the experimental situation. This allowed for a quantitative analysis of the reconstructed phase, including the extraction of a projected effective mass density map of a single D. radiodurans cell with quantified and small errors. This differs from the absolute mass density distribution in a multiplicative factor of about 0.94, which is dependent on the chemical composition of the sample, but fairly constant for biological material.

A spatial resolution around 85 nm (half-period length) was determined from the power spectral density of a phase map reconstructed from a dataset recorded at 60-s dwell time, allowing for a clear separation of the four subunits present in a typical D. radiodurans cell. The overall applied dose of ≃1.3·10⁵ Gy is well below the feature-destroying limit in an optimized sample environment (cryogenic conditions), so that substantially higher resolutions are possible, if the fluence is increased. It can be expected that also the phase resolution of the method can then be further increased above the presently achieved value. Comparison of reconstructions obtained from maps recorded at different dwell times confirm the expected scaling in spatial resolution. Furthermore, the spatial resolution was found to depend on the refractive index of the sample, yielding a value of 50 nm for a tantalum test structure.

The four compact subunits present in the density map of a single cell were attributed to the bacterial nucleoid, based on their overall size and shape. We are convinced that PCDI in particular in the tomographic mode, can help to clarify the highly debated DNA organization in bacteria (22–24), including the nucleoid structure of D. radiodurans and its possible role in radiation resistance. In particular, it provides an independent approach to sort out contradicting electron microscopy studies.

The simple and quantitative contrast mechanism of the lensless hard x-ray imaging scheme together with the high phase resolution demonstrated here opens up a unique route to determine density maps of unstained internal cellular structures with high spatial and density resolution in a single experiment. Due to the penetrating power of x-rays, the method can be applied to unsliced specimens and, with the extension to tomographic reconstruction, has the potential to provide quantitative 3D density distributions within a frozen-hydrated unsliced and unstained cell.