Abstract
The results from association studies are usually summarized by a measure of evidence of association (frequentist or Bayesian probability values) that does not directly reflect the impact of the detected signals on familial aggregation. This article investigates the possible advantage of a two-dimensional representation of genetic association in order to identify polymorphisms relevant to disease: a measure of evidence of association (the Bayes factor, BF) combined with the estimated contribution to familiality (the attributable sibling relative risk, λs). Simulation and data from the North American Rheumatoid Consortium (NARAC) were used to assess the possible benefit under several scenarios. Simulation indicated that the allele frequencies to reach the maximum BF and the maximum attributable λs diverged as the size of the genetic effect increased. The representation of BF versus attributable λs for selected regions of NARAC data revealed that SNPs involved in replicated associations clearly departed from the bulk of SNPs in these regions. In the 12 investigated regions, and particularly in the low-recombination major histocompatibility region, the ranking of SNPs according to BF differed from the ranking of SNPs according to attributable λs. The present results should be generalized using more extensive simulations and additional real data, but they suggest that a characterization of genetic association by both BF and attributable λs may result in an improved ranking of variants for further biological analyses.
Introduction
Susceptibility to rheumatoid arthritis (RA) is determined by both genetic and environmental factors, with an estimated sibling relative risk of 5-10. The HLA-DRB1 and PTPN22 genes explain approximately 50% of the familial aggregation. A recent genome-wide association (GWA) study carried out by the Wellcome Trust Case Control Consortium (WTCCC) found nine single-nucleotide polymorphisms (SNPs) with associated probability values of less than 10-5 that did not map to loci previously related to RA [1]. In agreement with the common disease-common variant hypothesis, the novel variants were common (minor allele frequencies from 0.07 to 0.41) and they showed genotype relative risks (GRRs) of less than 2.3. The authors of the WTCCC article recognized a disparity between the large population-attributable fraction (PAF) and the modest sibling relative risk (λs) explained by the newly identified variants [1]. This disparity is related to the technical characteristics of the platforms used in GWA studies, designed to scrutinize polymorphisms (common variants).
Let us assume that a polymorphism is a marker of a rarer causal variant, and the marker-specific PAF equals the PAF of the causal variant. Under this assumption, we have demonstrated that the causal variant has a higher attributable λs than the marker [2]. In other words: for a fixed PAF, causal variants contribute more to familial aggregation (λs) than the polymorphisms they are represented by.
There is much debate concerning the representation of statistical evidence in GWA studies. The frequentist p-value depends on the power of the study and it does not provide a consistent measure of evidence because identical p-values do not imply identical evidence of genetic association [3]. In contrast, the Bayes factor (BF) statistic provides a single measure of the strength of evidence of association.
We hypothesize here that the representation of genetic association by BF together with the attributable λs may help to identify polymorphisms relevant to RA, and use simulation and data from the North American Rheumatoid Consortium (NARAC) to evaluate this assumption.
Methods
Derivation of attributable risks and Bayes factors
The sibling relative risk (λs) attributable to a gene reflects the extent to which a particular genetic locus contributes to familial aggregation. The calculation of attributable λs values was first described in an early paper of James [4]. If the frequency of the high-risk allele is denoted by RAF, the relative risk of RA for high-risk allele homozygotes compared to low-risk allele homozygotes by GRRhom, the relative risk of heterozygotes compared to low-risk allele homozygotes by GRRhet and the disease prevalence among low-risk allele homozygotes by κ0, the attributable λs is given by: λs = 1+(1/2Va+1/4Vd)/K2, where Va (additive genetic variance divided by κ02) equals 2RAF(1-RAF)[(1-RAF)(1-GRRhet)-RAF(GRRhom-GRRhet)]2, Vd (dominance genetic variance divided by κ02) equals RAF2(1-RAF)2[1+GRRhom-2GRRhet]2 and K (population prevalence divided by κ0) equals RAF2GRRHom+2RAF(1-RAF)GRRhet+ (1-RAF)2. Note that if the overall disease prevalence is 50%, λs cannot exceed two by definition. However, an important property of the attributable λs is that it only depends on RAF, GRRhom, and GRRhet. That is, the attributable λs is independent of the disease prevalence among low-risk homozygotes κ0.
The BF statistic is the ratio of the probability of the observed data under the assumption that there is a true association to its probability under the null hypothesis (absence of association). A small BF provides evidence in favor of a true association. To investigate the relationship between attributable λs and the BF, we calculated the expected distribution of genotypes in 1000 cases and 1000 controls when GRRhom = 1.5, 2, 3, 4, 5 and 10. Calculations were carried out for the dominant model, which assumes that GRRhet = GRRhom, the recessive model (GRRhet = 1), and for the additive model (GRRhet = (1+GRRhom)/2). Under Hardy-Weinberg equilibrium, the expected distribution of genotypes in controls (D = 0) is: Pr(G = aa|D = 0) = (1-RAF)2; Pr(G = Aa|D = 0) = 2RAF(1-RAF); Pr(G = AA|D = 0) = RAF2 The expected distribution of genotypes in cases (D = 1) satisfies:
GRRhom = (Pr(D = 1 | G = AA)/Pr(D = 0 | G = AA))/(Pr(D = 1 | G = aa)/Pr(D = 0 | G = aa)) and GRRhet = (Pr(D = 1 | G = Aa)/Pr(D = 0 | G = Aa))/(Pr(D = 1 | G = aa)/Pr(D = 0 | G = aa)). For example, if RAF = 0.2 and GRRhom = GRRhet = 2 (dominance), the expected distribution is (aa = 640, Aa = 320, AA = 40) in controls and (aa = 471, Aa = 471, AA = 59) in cases.
The expected distributions of genotypes were investigated by Bayesian logistic regression. We considered a general three-genotype model of association. Calculation of BFs requires assumptions about effect sizes. We assumed N(0,1) priors on the mean and the two genetic effects. The function MCMClogit (R package MCMCpack [5]) was used to generate a 10,000 sample dataset from the posterior distribution using a random walk Metropolis algorithm. The BayesFactor function in the same package was used to compute log marginal likelihoods for a model 'with' compared to a model 'without' genotypic information using a Laplace approximation.
Investigated regions
This study investigated regions around the 12 signals detected in the WTCCC study with associated probability values of less than 10-5 (Table 1). The left side of Table 1 represents the 12 selected regions from the WTCCC study. For example, the most associated marker on 1p13 was rs6679677. We retrieved NARAC data from 1000-kb regions centred on the positions of the 12 signals from the WTCCC study. For example, our first region comprised the chromosomal interval (10,901,850::11,901,850) around rs6679677. The WTCCC study reported two SNPs in 6p21 that resulted in two overlapping intervals which were independently investigated.
Table 1.
Description and results from the 12 investigated regions
| WTCCC studya | NARAC datab | |||||||
|---|---|---|---|---|---|---|---|---|
| Chr | SNP | Position | MAD of log10 | Outlying SNPs, gene regions | log10 (BF) | RAF | λs Median (5th-95th) | |
| GRRhom | GRRhet | |||||||
| 1p13 | rs6679677 | 11,401,850 | 0.282 | 0.199 | rs2476601, PTPN22 | 3.91 | 0.084 | 1.048 (1.017-1.098) |
| 1p36 | rs6684865 | 2,578,391 | 0.282 | 0.199 | - | - | - | - |
| 1p31 | rs11162922 | 80,284,079 | 0.282 | 0.199 | - | - | - | - |
| 4p15 | rs3816587 | 25,093,513 | 0.255 | 0.188 | rs12505556, SLC34A2 | 3.04 | 0.112 | 1.071 (1.011-1.630) |
| 6p21a | rs6457617 | 32,771,829 | 0.306 | 0.206 | rs2395175, MHC | 16.48 | 0.148 | 1.164 (1.108-1.241) |
| rs7765379, MHC | 6.11 | 0.113 | 1.175 (1.053-1.668) | |||||
| 6p21b | rs615672 | 32,682,149 | 0.306 | 0.206 | rs2395175, MHC | 16.48 | 0.148 | 1.164 (1.108-1.241) |
| rs7765379MHC | 6.11 | 0.113 | 1.175 (1.053-1.668) | |||||
| 6q23 | rs6920220 | 138,048,197 | 0.306 | 0.206 | - | - | - | - |
| 7q32 | rs11761231 | 130,827,294 | 0.268 | 0.185 | - | - | - | - |
| 10p15 | rs2104286 | 6,139,051 | 0.290 | 0.197 | - | - | - | - |
| 13q12 | rs9550642 | 19,848,092 | 0.286 | 0.200 | rs1407961, ZMYM2 | 3.59 | 0.920 | 1.033 (1.033-1.225) |
| 21q22 | rs2837960 | 41,433,788 | 0.288 | 0.208 | rs468646, MX1 | 4.28 | 0.488 | 1.038 (1.019-1.057) |
| rs466092, MX2 | 3.59 | 0.488 | 1.030 (1.016-1.048) | |||||
| 22q13 | rs743777 | 35,876,107 | 0.283 | 0.216 | rs3218258, IL2RB | 9.63 | 0.771 | 1.061 (1.041-1.084) |
| rs710183, CSF2RB | 4.26 | 0.072 | 1.028 (1.011-1.183) | |||||
| rs8137446, KCTD17 | 3.48 | 0.903 | 1.035 (1.018-1.123) | |||||
aResults from the WTCCC study.
bResults based on NARAC.
Calculation of attributable risks and Bayes factors for NARAC data
SNPs in the 12 selected intervals were extracted from NARAC data, and the association between RA and the retrieved SNPs was represented by 1) the base 10 logarithm of the BF (log10BF) and 2) the attributable λs. RA status (affected or unaffected) was modelled by logistic regression, taking into account the covariates gender, number of HLA-DRB1 shared-epitope alleles (NN = 0, SN = 1 or SS = 2) and genotype (three levels). Individuals with missing information were excluded from the calculations. Only SNPs with the three genotypes represented in both cases and controls were considered.
As already mentioned, calculation of BFs requires assumptions on effect sizes. We calculated frequentist estimates of logistic regression coefficients over the corresponding entire chromosomes using NARAC data. Density plots and tests of goodness of fit of frequentist estimates of log10GRRHom and log10GRRHet for the seven investigated chromosomes indicated that GRR variation was better represented by the median absolute deviation (MAD) than by the standard deviation (data not shown). Therefore, we assumed N(0, MAD2) priors on the logarithms of genetic effects. MCMClogit and BayesFactor [5] were used to calculate BFs for each SNP in the selected regions based on NARAC data. The number of individuals with complete data and the observed allele frequencies in controls were used to draw 10,000 samples from a binomial distribution, which were combined with the posterior estimates of genetic effects to simulate the distribution of attributable λs for each SNP.
A bagplot is a bivariate generalization of the non-parametric univariate boxplot [6]. In a bagplot, the region which contains 50% of the observations with greatest bivariate depth is denominated the bag. Observations outside the bag expanded three times are considered outliers, they are too far away from the data's central bulk. These outliers are indicated by closed dots in univariate boxplots. Bagplots have been shown to be equivariant for linear transformations and not limited to elliptical distributions. Due to these properties and the characteristics of our data (unknown shape of the underlying distributions), we used non-parametric bagplots to identify deviating SNPs. Bagplots were determined using the function compute.bagplot in the R package aplpack [7].
Results
Theoretical relationship between Bayes factor and attributable risk
Table 1 shows the RAFs at which the maximum log10BF and λs were reached assuming several GRRhom values under the dominant, recessive and additive modes of inheritance. For example, under GRRhom = 2 and dominance, the maximum log10BF (25.3) was reached when RAF = 0.22 and the maximum λs (1.06) for RAF = 0.17. Alternative sample-sizes/priors would result in different log10BFs, but the RAF to reach the maximum log10BF would not change. The representation of log10BF versus attributable λs (data not shown) indicated that the two parameters were correlated, but they did not correspond one-to-one. In the three models, the RAF corresponding to the highest attributable λs and the RAF corresponding to the highest log10BF decreased with increasing GRRhom values. The RAF at maximum log10BF was always higher than the RAF at maximum λs, i.e., balanced designs resulted in stronger association evidences. The difference between RAF at maximum log10BF and RAF at maximum attributable λs increased with increasing GRRhom, for example (0.24-0.21) = 0.03 if GRRhom = 1.5 versus (0.14-0.05) = 0.09 when GRRhom = 10 in the dominant model.
Table 2.
Allele frequencies at maximum λs and maximum log10(BF)
| Dominant model | Recessive model | Additive model | ||||
|---|---|---|---|---|---|---|
| GRRhom | Max log10(BF) | Max λs | Max log10(BF) | Max λs | Max log10(BF) | Max λs |
| 1.5 | 0.24 | 0.21 | 0.70 | 0.66 | 0.39 | 0.40 |
| 2 | 0.22 | 0.17 | 0.64 | 0.61 | 0.38 | 0.33 |
| 3 | 0.20 | 0.13 | 0.61 | 0.54 | 0.33 | 0.25 |
| 4 | 0.17 | 0.10 | 0.59 | 0.48 | 0.26 | 0.20 |
| 5 | 0.16 | 0.08 | 0.57 | 0.45 | 0.24 | 0.17 |
| 10 | 0.14 | 0.05 | 0.49 | 0.33 | 0.17 | 0.09 |
Bayes factors and attributable sibling relative risks in the investigated regions
The analysis of complete chromosomes by frequentist logistic regression resulted in 2(GRRhom, GRRhet) × 8(chromosomes 1, 4, 6, 7, 10, 13, 21, 22) sets of genetic effects. Table 1 shows the MADs of log10GRRhom and log10GRRhet used as scale parameters in the normal prior distributions. As expected, the a priori variance of genetic effects was highest for chromosome 6 (MHC region).
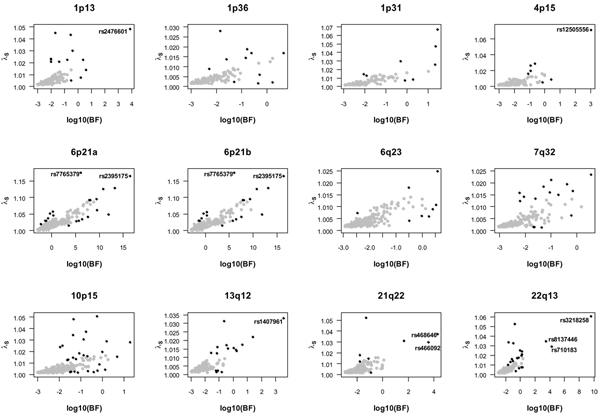
Figure 1 represents the bivariate distribution of log10BF by attributable λs based on NARAC data for individual SNPs in the 12 explored regions. Gray points show SNPs within the bulk of data, outlying observations (observations outside the bag expanded three times) are represented by black points. The right part of Table 1 shows SNP numbers and close genes for the most extreme outliers. For example, rs2476601 in the 1p13 region: based on NARAC data, the log10BF was 3.91, the high-risk allele frequency in controls is 0.084, and the estimated attributable λs with 95% confidence interval was 1.048 (1.017 to 1.098) for this SNP. The other two regions on chromosome 1 did not reveal strong associations with RA. The investigation of the two overlapping intervals in chromosome 6p21 showed practically identical results; the highest attributable λs values were found for SNPs rs7765379 (1.175) and rs2395175 (1.164). Many SNPs in this region showed a strong association with RA. The investigation of the 6q23, 7q32, and 10p15 regions resulted in log10BF values below three. The log10BF and the attributable λs for SNP rs1407961 in the 13q12 region clearly departed from the majority of data. Two extreme outlier SNPs were identified in the 21q22 region and three outliers in the 22q13 region.
Figure 1.
Scatterplots of log10 values of Bayes factors (log10(BF)) and attributable sibling relative risks (λs) for SNPs in the investigated regions. Outlying SNPs (black points) were identified by bagplots. SNP numbers are shown for most extreme outliers with log10(BF)s higher than three. Note scale differences.
Discussion
This study explored the advantage of combining BF, a measure of statistical evidence of association, and the attributable λs, a measure of contribution to familial aggregation, in order to characterize the effect of a particular polymorphism on disease risk. Both simulation and NARAC-based results showed that BF usually correlates with the attributable λs. Most markers identified in GWA studies confer a slightly increased risk of disease. For this kind of modest genetic effects (GRR ≤ 2), simulation indicated that the maximum log10BF and the maximum attributable λs were expected to be found for variants with similar frequencies: around 20% (dominant), 40% (additive) and 70% (recessive penetrances). The larger the size of the genetic effect, the lower the RAF to reach the maxima, and the larger the difference between RAFs. Causal variants generally show stronger effects than markers from GWA studies. For example, a recent GWA study identified five novel breast cancer susceptibility loci. The highest GRR was 1.6, which can be compared with GRR = 6 to 30 for carriers of BRCA1 mutations. Simulation suggested that, for this kind of strong genetic effects, attributable λs and BF are two different dimensions.
The representation of λs versus log10BF based on NARAC data confirmed that SNPs which have shown replicated associations clearly departed from the majority of polymorphisms in the selected regions. For example, the functionally relevant SNP rs2476601 was unequivocally separated from the rest of SNPs in the 1p13 region. Other genes located in the proximity of the most extreme SNPs were ZMYM2, MX1, MX2, IL2RB, and CSF2RB. This list includes SNPs which show strong evidence of association (log10BF higher than three) and outlying λs values. SNPs with high attributable λs values but relatively low BFs may also be of interest. Simulation showed that one BF value corresponds to two different λs values. In the 12 regions investigated using NARAC data, the ranking of SNPs according to BF differed from the ranking according to attributable λs. The difference was particularly clear in the low-recombination MHC region, where rs7765379 showed the maximum λs and rs2395175 showed the maximum log10BF. This difference in rankings suggests that, in addition to a measure of association evidence, the extensive fine-mapping needed to characterize etiological variants may benefit from the consideration of the attributable λs. Future studies based on more extensive simulations and additional real data should investigate this possibility.
The present study made use of Bayesian and robust statistics. The Bayesian approach has been overlooked in the analysis of GWA studies, where the adjustment for multiple testing, the relationship between power and statistical significance, and the selection of disease models are important issues [1,3]. We only considered SNPs with the three genotypes represented in both cases and controls. This strategy would initially hamper the identification of rare causal variants but, on the other hand, logistic regression has not been robust to particular types of outliers, and a three-genotype model with well represented categories would result in more robust estimates. Robust methods aim to describe the structure best fitting to the bulk of the data, and to identify deviating observations. Robust statistics are used a lot less than they ought to be in genetic epidemiology. The use of MADs and bagplots in the present article illustrates their advantage over classical methods in practical situations.
Conclusion
The association results from GWA studies are usually summarized by a measure of evidence of association (frequentist or Bayesian probability values), which do not reflect the contribution of the identified signals to familial aggregation. We propose here a two-dimensional characterization of genetic association consisting of the attributable λs and the BF.
List of abbreviations used
BF: Bayes factor; GRR: Genotype relative risk; GWA: Genome-wide association; λs: sibling relative risk; MAD: Median absolute deviation; MHC: Major histocompatibility complex; PAF: Population-attributable fraction; RA: Rheumatoid arthritis; SNP: Single-nucleotide polymorphism; WTCCC: Wellcome trust case control consortium
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
JLB designed the study, performed the statistical analyses and drafted the manuscript. CF and KH contributed to the study design and revised critically the manuscript. AS, NC, RH, LB, and JCC made substantial contributions to interpretation of results. All authors read and approved the final manuscript.
Contributor Information
Justo Lorenzo Bermejo, Email: Justo.Lorenzo@imbi.uni-heidelberg.de.
Christine Fischer, Email: Christine.Fischer@med.uni-heidelberg.de.
Anke Schulz, Email: anke.schulz@dkfz.de.
Nadine Cremer, Email: n.cremer@dkfz.de.
Rebecca Hein, Email: r.hein@dkfz.de.
Lars Beckmann, Email: l.beckmann@dkfz.de.
Jenny Chang-Claude, Email: j.chang-claude@dkfz.de.
Kari Hemminki, Email: k.hemminki@dkfz.de.
Acknowledgements
The Genetic Analysis Workshops are supported by NIH grant R01 GM031575 from the National Institute of General Medical Sciences. JLB was supported by Deutsche Krebshilfe and the Swedish Cancer Society. RH was supported by NGFN 2 (SMP-GEM, PGE-S30T09), funded by the BMBF.
This article has been published as part of BMC Proceedings Volume 3 Supplement 7, 2009: Genetic Analysis Workshop 16. The full contents of the supplement are available online at http://www.biomedcentral.com/1753-6561/3?issue=S7.
References
- Wellcome Trust Case Control Consortium. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemminki K, Försti A, Bermejo JL. The 'common disease-common variant' hypothesis and familial risks. PLoS ONE. 2008;3:e2504. doi: 10.1371/journal.pone.0002504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakefield J. Bayes factors for genome-wide association studies: comparison with P-values. Genet Epidemiol. 2009;33:79–86. doi: 10.1002/gepi.20359. [DOI] [PubMed] [Google Scholar]
- James JW. Frequency in relatives for an all-or-none trait. Ann Hum Genet. 1971;35(1):47–49. doi: 10.1111/j.1469-1809.1956.tb01377.x. [DOI] [PubMed] [Google Scholar]
- Martin AD, Quinn KM. MCMCpack: (MCMC) Package. http://mcmcpack.wustl.edu/wiki/index.php/Main_Page
- Rousseeuw PJ, Ruts I, Tukey JW. The Bagplot: a Bivariate boxplot. Am Stat. 1999;53:382–387. doi: 10.2307/2686061. [DOI] [Google Scholar]
- Wolf P. aplpack: Another Plot PACKage. http://www.wiwi.uni bielefeld.de/~wolf/software/aplpack/