Abstract
Both imprinting and maternal effects could lead to parent-of-origin patterns in complex traits of human disorders. Statistical methods that differentiate these two effects and identify them simultaneously by using family-based data from retrospective studies are available. The usual data structures include case-parents triads and nuclear families with multiple affected siblings. We develop a likelihood-based method to detect imprinting and maternal effects simultaneously using data from prospective studies. The proposed method utilizes both affected and unaffected siblings in nuclear families by modeling familial genotypes and offspring's disease status jointly. Maternal effect is usually modeled as a fixed effect under the assumption that maternal variant allele(s) has (have) identical effect on any offspring. However, recent studies report that different people may carry different amounts of substances encoded by the mother's variant allele(s) (called maternal microchimerism), which could result in heterogeneity of maternal effects. The proposed method incorporates the heterogeneity of maternal effects by adding a random component to the logit of the penetrance. Our method was applied to the Framingham Heart Study data in two steps to detect single-nucleotide polymorphisms (SNPs) that may be associated with high blood pressure. In the first step, SNPs that affect susceptibility of high blood pressure through minor allele, genomic imprinting, or maternal effects were identified by using the proposed model without the random effect component. In the second step, we fitted the mixed effect model to the identified SNPs that have significant maternal effect to detect heterogeneity of the maternal effects.
Background
The phenomenon that a trait follows a maternal or paternal lineage, instead of following the mendelian mode of inheritance, is referred to as the parent-of-origin pattern. Genomic imprinting and maternal effect could give rise to similar parent-of-origin patterns [1]. Hence, models, which are designed to identify genomic imprinting by detecting the parent-of-origin pattern, may report false positives that are actually due to maternal effect. A log-linear likelihood-ratio test (LL-LRT) [2,3] was developed to detect imprinting and maternal effects simultaneously by using case-parents triads. This approach was then extended to the parent-of-origin likelihood ratio test (PO-LRT) to detect imprinting and maternal effects at a marker that is in linkage disequilibrium with a candidate gene [4].
A case-parents triad could have 15 possible familial genotype combinations [2-4]. LL-LRT and PO-LRT model the counts of the 15 categories by using log-linear and logistic regression, respectively. It has been shown that these methods are robust for detecting imprinting effect even in the presence of maternal effect. However, when multiple affected siblings are genotyped (e.g., the North American Rheumatoid Arthritis Consortium data set [5]), trimming nuclear families to case-parents triads does not make the most of the data and thus limits the power. In contrast, the maternal-fetal genotype incompatibility (MFG) test [6] could model nuclear families with multiple affected siblings. Compared with the generalized linear models LL-LRT and PO-LRT, it does require more effort in formulating the likelihood to implement the MFG test. The MFG test was developed to detect maternal effect and an interaction effect between the mother carrying one copy of the disease susceptibility allele and the child carrying no copy under the assumption of no imprinting.
Unaffected siblings are also genotyped in many genetic studies. Although unaffected siblings have been incorporated to infer the missing parental genotypes in LL-LRT and PO-LRT [7], they do not directly contribute to model the relative risks due to genomic imprinting and maternal effect. LL-LRT, PO-LRT, and MFG tests only model affected sibling(s) because they all use the data from retrospective studies. Sampling from a retrospective study is biased because only families with affected child(ren) are recruited.
On the other hand, a prospective study like the Framingham Heart Study (FHS) does not specifically recruit subjects with a certain disease, thus the originally recruited cohort could be considered as a random sample of the general population of healthy people and patients with any disease. Therefore, a test using data from a prospective study could utilize both affected and unaffected siblings by modeling their genotypes and disease status jointly. Nevertheless, the disease of interest should not be a rare one; otherwise, the number of patients in the cohort would be too small to be sufficiently informative.
In LL-LRT, PO-LRT, and MFG tests, maternal effect is modeled as a fixed effect because it is assumed that maternal variant allele(s) has (have) identical effect on any offspring. This assumption might be invalid if we consider the cause of maternal effect more carefully. Maternal effect refers to the phenomenon that the genotype of a mother is expressed in the phenotype of her offspring, which is usually attributed to maternally produced molecules, such as mRNA that are deposited in the egg cell, and mRNA or antigens that are passed to the offspring during pregnancy. The latter case could arise from a biological process called microchimerism. Microchimerism means that two genetically distinct cells, one being at a low concentration, are present in the same individual. Microchimerism may be due to transfer of cells between mother and fetus or between two twins. Other sources of microchimerism include blood transfusions and organ transplants. Cells transferred from the mother to the fetus are referred to as maternal microchimerism (MMc). Non-inherited maternal antigen coding alleles (NIMA) [5,6] within MMc would be expressed in the offspring and increase his or her susceptibility to a certain disease. It has been found by quantitative real-time polymerase chain reaction that different individuals may have different amounts of MMc. Therefore, it is likely that the maternal effects imposed by different mothers are actually heterogeneous rather than being homogenous as assumed in the previous studies.
In this study, we will discuss a prospective likelihood formulation that will take multiple affected and unaffected siblings into consideration. Further, we will treat maternal effects as random to model heterogeneity. This method will then be applied to the high blood pressure (HBP) trait in the FHS.
Methods
Definition of HBP trait in FHS
HBP in an adult is defined as a blood pressure greater than or equal to 140 mm Hg systolic pressure or greater than or equal to 90 mm Hg diastolic pressure. High blood pressure directly increases the risk of coronary heart disease and stroke, especially when it is present with other risk factors. In the FHS, systolic pressure and diastolic pressure of the Original Cohort (the first generation) and their Offspring Cohort (the second generation) were measured at four exams, and were measured once in the Generation 3. Based on the highest measurements among all available ones, there were 1,036 individuals having high blood pressure and 1,724 individuals having normal blood pressure in the Offspring Cohort. In Generation 3, there were 379 individuals having high blood pressure and 3,618 individuals having normal blood pressure. Our analysis was based on these phenotypic data and the genotypes of nuclear families. Families with missing parental genotype(s) were omitted from our analysis because they are not informative for imprinting and maternal effects if both parents' genotypes are missing.
Moreover, only one nuclear family was selected at random to be included in the analysis from each three-generation pedigree. This selection process led to approximately 300 nuclear families (with the number of children in each family ranging from 1-8) for each single-nucleotide polymorphism (SNP).
Prospective likelihood and random effect modeling
Suppose there are N nuclear families. The ith family has two parents and ni children, i = 1, 2, ..., N. We model the genotypes of all family members and disease statuses of all children jointly. Let Mi and Fi denote the genotypes of mother and father in the ith family.
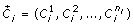 denotes the genotypes of ni children in the ith family. Mi, Fi, and
denotes the genotypes of ni children in the ith family. Mi, Fi, and 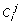 could take a value of 0, 1, or 2, indicating the number of the minor allele(s) at a SNP carried by the corresponding person, j = 1, 2, ..., n.
could take a value of 0, 1, or 2, indicating the number of the minor allele(s) at a SNP carried by the corresponding person, j = 1, 2, ..., n. 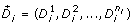 denotes the sibling's disease status, with
denotes the sibling's disease status, with 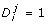 indicating that the jth child in the ith family being affected, and 0 indicating otherwise.
indicating that the jth child in the ith family being affected, and 0 indicating otherwise.
The likelihood for the ith family could be decomposed as
We use the logit model to relate the penetrance to the imprinting effect (part of the β parameters) and the maternal effect (the γ parameters):
where 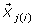 is a vector with the covariates related to the jth offspring in the ith family coded in one row:
is a vector with the covariates related to the jth offspring in the ith family coded in one row: 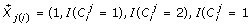 and this single copy is inherited from the mother), I(Mi = 1), I(Mi = 2)). The parameter vector
and this single copy is inherited from the mother), I(Mi = 1), I(Mi = 2)). The parameter vector 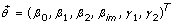 , where β0 is the logit of phenocopy rate; β1 measures the effect of the single minor allele inherited from the father; β1 + βim measures the effect of the single minor allele inherited from the mother; βim measures the imprinting effect, with βim < 0 indicating maternal imprinting and βim > 0 indicating paternal imprinting; β2 measures the effect of two copies of the minor allele; γ1 and γ2 measure the maternal effect when the mother carries one or two copies of the minor allele, respectively. Because we assume that different mothers may impose heterogeneous maternal effects, εi measures the deviation of the effect size from the mean; it also introduces correlation among the siblings within the same family. Specifically, εi is assumed to follow N(0, σ2).
, where β0 is the logit of phenocopy rate; β1 measures the effect of the single minor allele inherited from the father; β1 + βim measures the effect of the single minor allele inherited from the mother; βim measures the imprinting effect, with βim < 0 indicating maternal imprinting and βim > 0 indicating paternal imprinting; β2 measures the effect of two copies of the minor allele; γ1 and γ2 measure the maternal effect when the mother carries one or two copies of the minor allele, respectively. Because we assume that different mothers may impose heterogeneous maternal effects, εi measures the deviation of the effect size from the mean; it also introduces correlation among the siblings within the same family. Specifically, εi is assumed to follow N(0, σ2).
The parameters β0, β1, β2, βim, γ1, γ2, and σ2 are estimated by maximizing the likelihood using the procedure NLMIXED in SAS.
Selection of SNPs
SNPs that may have a minor allele effect, imprinting effect, or maternal effect are selected in the first step and the heterogeneity of maternal effects is detected in the second step. In the first step, we fit the parsimonious fixed-effect model without the random component εi and use the minimum p-value (among the tests for β1 = 0, β2 = 0, βim = 0, γ1 = 0, and γ2 = 0) being ≤ 0.00005 as the criterion to choose the SNPs. We then screen the selected SNPs by checking specific parameter constraints. The assumption that carrying minor alleles would increase the disease risk implies that β1 ≥ 0 and β1 + βim ≥ 0. Furthermore, two copies of the minor allele should have an effect at least as large as a single copy, and thus β2 ≥ max(β1, β1 + βim). Estimates of β1 and β2 being significantly less than zero indicates that labels of minor and major alleles should be reversed. SAS does not allow complex constraints such as β1 + βim ≥ 0 and β2 ≥ max(β1, β1 + βim) in its NLMIXED procedure, and as such we fit a "constraint model" and an "additive model" to check the intended constraints. In the "constraint model", we reparametrize β2 - β1 = 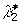 and impose β1 ≥ 0 and
and impose β1 ≥ 0 and 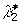 ≥ 0 to ensure that β1 ≥ 0 and β2 ≥ 0. In the "additive model", we assume an additive effect of the two copies of the minor allele, i.e., β2 = β1 + (β1 + βim), to ensure that β2 ≥ max(β1, β1 + βim). In the second step, we fit the mixed effect model to the selected SNPs with significant maternal effect and use the p-value of testing σ = 0 being less than 0.05 and reduced Akaike information criterion (AIC) value as the criterion for identifying heterogeneity of maternal effects.
≥ 0 to ensure that β1 ≥ 0 and β2 ≥ 0. In the "additive model", we assume an additive effect of the two copies of the minor allele, i.e., β2 = β1 + (β1 + βim), to ensure that β2 ≥ max(β1, β1 + βim). In the second step, we fit the mixed effect model to the selected SNPs with significant maternal effect and use the p-value of testing σ = 0 being less than 0.05 and reduced Akaike information criterion (AIC) value as the criterion for identifying heterogeneity of maternal effects.
Results
We scanned 230 k SNPs on chromosomes 1 to 6 and detected nine SNPs that may be associated with high blood pressure through minor allele, imprinting, or maternal effect. These nine SNPs are shown in Table 1. The p-values for testing β1 = 0 or β2 = 0 being less than 0.05 are shown in boldface, which signifies potential minor allele effects. For SNPs that have significant minor allele effect, we further looked at the p-value for testing βim = 0 and inferred maternal or paternal imprinting effect from the sign of 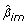 . If the p-value for testing γ1 = 0 or γ2 = 0 is less than 0.05, we further tested for heterogeneity of the maternal effects in step two. Results from the second step are shown in Table 2. There are two rows for each SNPs detected to have potential significant maternal effect. The first row shows the estimates, p-values, and AIC of the fixed effect model, while the second row shows those of the mixed effect model. If the p-value for testing σ = 0 is less than 0.05 and the AIC is reduced by fitting the mixed effect model, we concluded that the maternal effect is heterogeneous. Five SNPs were detected to have various degrees of maternal effects, of which four appears to be heterogeneous among the families (Table 2).
. If the p-value for testing γ1 = 0 or γ2 = 0 is less than 0.05, we further tested for heterogeneity of the maternal effects in step two. Results from the second step are shown in Table 2. There are two rows for each SNPs detected to have potential significant maternal effect. The first row shows the estimates, p-values, and AIC of the fixed effect model, while the second row shows those of the mixed effect model. If the p-value for testing σ = 0 is less than 0.05 and the AIC is reduced by fitting the mixed effect model, we concluded that the maternal effect is heterogeneous. Five SNPs were detected to have various degrees of maternal effects, of which four appears to be heterogeneous among the families (Table 2).
Table 1.
Parameter estimates and p-values of the fixed effect model in the first step
| Location | SNP | Association with BP |
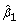 and p-value and p-value
|
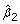 and p-value and p-value
|
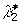 and p-value and p-value
|
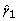 and p-value and p-value
|
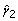 and p-value and p-value
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chr2 p22.3 | rs1979148 | Rat | 0.406 | 0.3365 | -3.579 | 0.2899 | -1.445 | 0.0200 | 1.648 | 0.0000 | 1.769 | 0.0517 |
| Chr1 q41 | rs17476063 | Rat | 0.661 | 0.0883 | -0.650 | 0.3358 | -2.201 | 0.0015 | 1.644 | 0.0000 | 0.441 | 0.7048 |
| Chr4 q26 | rs1459543 | Human | 1.957 | 0.0000a | 1.296 | 0.0146 | -1.586 | 0.0109 | 0.346 | 0.3935 | 0.100 | 0.8677 |
| Chr1 p36.22 | rs6688233 | Human, Rat | 1.573 | 0.0000 | 0.234 | 0.7368 | -1.609 | 0.0112 | 0.377 | 0.3854 | 0.747 | 0.3410 |
| Chr6 q24.1 | rs4386830 | Human | 1.046 | 0.0178 | -1.018 | 0.0809 | -2.414 | 0.0003 | 1.741 | 0.0001 | 3.031 | 0.0000 |
| Chr3 p14.1 | rs13076104 | Rat | 1.323 | 0.0000 | -0.008 | 0.9910 | -1.154 | 0.0820 | 0.141 | 0.7209 | 0.487 | 0.5428 |
| Chr2 q24.1 | rs10209732 | Human, Rat | 0.469 | 0.3301 | -1.535 | 0.1515 | -1.089 | 0.1160 | 1.632 | 0.0000 | 1.746 | 0.0619 |
| Chr3 q26.1 | rs2030350 | Human, Rat | -0.260 | 0.5752 | -0.902 | 0.1503 | -1.856 | 0.0202 | 1.422 | 0.0000 | 0.726 | 0.5396 |
| Chr3 p12.1 | rs9866277 | Rat | 1.442 | 0.0000 | 0.100 | 0.9367 | -0.488 | 0.5423 | -0.565 | 0.3501 | -0.361 | 0.7332 |
aBold font under 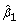 ,
, 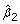 ,
, 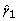 , and
, and 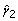 indicates p-value ≤ 0.05. Bold font under
indicates p-value ≤ 0.05. Bold font under 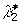 indicates p-value ≤ 0.05 and at least one p-value ≤ 0.05 for testing whether β1 = 0 and β2 = 0
indicates p-value ≤ 0.05 and at least one p-value ≤ 0.05 for testing whether β1 = 0 and β2 = 0
Table 2.
Parameter estimates, p-values, and AICs of the fixed and mixed effect models in the second step
| Location | SNP |
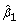 and p-value and p-value
|
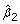 and p-value and p-value
|
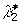 and p-value and p-value
|
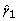 and p-value and p-value
|
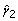 and p-value and p-value
|
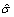 and p-value and p-value
|
AIC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chr2 p22.3 | rs1979148 | 0.406 | 0.3365 | -3.579 | 0.2899 | -1.445 | 0.0200 | 1.648 | 0.0000 | 1.769 | 0.0517 | --- | --- | 1548.1 |
| 0.807 | 0.3500 | -2.256 | 0.5740 | -2.469 | 0.0328 | 1.886 | 0.0381 | 2.273 | 0.3364 | 6.771 | 0.0000a | 1523.6 | ||
| Chr1 q41 | rs17476063 | 0.661 | 0.0883 | -0.650 | 0.3358 | -2.201 | 0.0015 | 1.644 | 0.0000 | 0.441 | 0.7048 | --- | --- | 1797.4 |
| 0.630 | 0.4079 | -2.637 | 0.2000 | -4.562 | 0.0035 | 2.041 | 0.0212 | 2.125 | 0.5012 | 6.775 | 0.0001 | 1782.0 | ||
| Chr6 q24.1 | rs4386830 | 1.046 | 0.0178 | -1.018 | 0.0809 | -2.414 | 0.0003 | 1.741 | 0.0001 | 3.031 | 0.0000 | --- | --- | 1847.1 |
| 1.950 | 0.0936 | -4.746 | 0.0027 | -3.739 | 0.0198 | 3.017 | 0.0339 | 5.217 | 0.0116 | 8.388 | 0.0000 | 1822.6 | ||
| Chr2 p24.1 | rs10209732 | 0.469 | 0.3301 | -1.535 | 0.1515 | -1.089 | 0.1160 | 1.632 | 0.0000 | 1.746 | 0.0619 | --- | --- | 1655.1 |
| 0.361 | 0.5324 | -1.589 | 0.1841 | -1.204 | 0.1482 | 1.834 | 0.0005 | 2.038 | 0.0902 | 1.596 | 0.0164 | 1653.3 | ||
| Chr3 q26.1 | rs2030350 | -0.260 | 0.5752 | -0.902 | 0.1503 | -1.856 | 0.0202 | 1.422 | 0.0000 | 0.726 | 0.5396 | --- | --- | 1704.6 |
| 0.003 | 0.9957 | -1.443 | 0.1047 | -2.709 | 0.0276 | 1.840 | 0.0033 | 1.439 | 0.3453 | 1.925 | 0.0798 | 1700.4 | ||
aBold font indicates p-value ≤ 0.05 for testing whether σ = 0
To summarize and visualize the result, we categorize the nine SNPs into a Venn diagram (Figure 1) according to how the SNPs are associated with high blood pressure. SNPs listed in the intersecting areas have the corresponding effects shown in the legend simultaneously. The locations of the nine detected SNPs in human genome are shown in the first column of Table 1.
Figure 1.
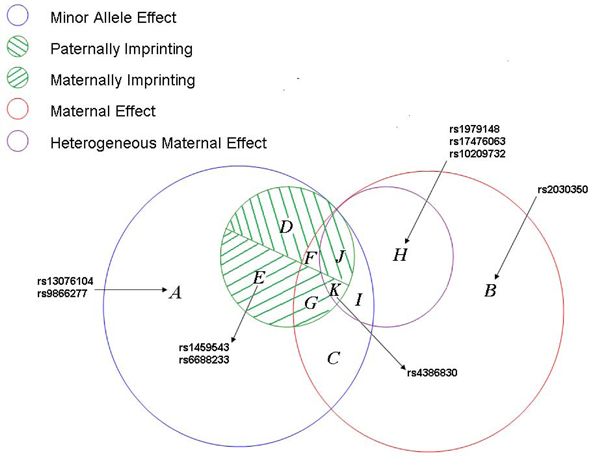
Venn diagram.
Discussion
In the Genetic Association Studies of Complex Diseases and Disorders section of the Genome Browser, we found that the association between the nine detected SNPs and blood pressure has been established either in human or in rat (see the third column of Table 1). This finding confirms the effectiveness of our method in detecting genetic association. Although the associations of five of these nine SNPs have been reported in human studies, we have found the associations of four additional SNPs in humans, rs1979148, rs17476063, rs13076104, and rs9866277, which were only reported in rat before. Furthermore, there is no previous report of imprinting or maternal effect for any of the nine detected SNPs, whereas our model detected potential imprinting effects for three and maternal effects for five of the SNPs. Finally, we note that, in our current formulation, siblings sharing the same mother have the same maternal effect component, and so it would be interesting to consider hierarchical modelling to further delineate maternal effect heterogeneity among offspring of the same mother. However, random inheritance of the minor allele from mother and father would impose different imprinting component on them, which helps to separate the maternal effect from the imprinting effect. Indeed, we found that our method could detect maternal and imprinting effects simultaneously with reasonable power via simulation.
List of abbreviations used
AIC: Akaike information criterion; FHS: Framingham Heart Study; HBP: High blood pressure; LL-LRT: Log-linear likelihood ratio test; MFG: maternal-fetal genotype incompatibility; MMc: Maternal microchimerism; NIMA: Non-inherited maternal antigen coding alleles; PO-LRT: Parent-of-origin likelihood-ratio test; SNP: Single-nucleotide polymorphism.
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
JY and SL developed the methodology and designed the analysis scheme. JY implemented the analysis and drafted the manuscript. Both authors read and approved the final manuscript.
Contributor Information
Jingyuan Yang, Email: yj@stat.osu.edu.
Shili Lin, Email: shili@stat.osu.edu.
Acknowledgements
The Genetic Analysis Workshops are supported by NIH grant R01 GM031575 from the National Institute of General Medical Sciences. This research was supported in part by NIH grant 5R01HG002657.
This article has been published as part of BMC Proceedings Volume 3 Supplement 7, 2009: Genetic Analysis Workshop 16. The full contents of the supplement are available online at http://www.biomedcentral.com/1753-6561/3?issue=S7.
References
- Hager R, Cheverud JM, Wolf JB. Maternal effects as the cause of parent-of-origin effects that mimic genomic imprinting. Genetics. 2008;178:1755–1762. doi: 10.1534/genetics.107.080697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilcox AJ, Weinberg CR, Lie RT. Distinguishing the effects of maternal and offspring genes through studies of case-parents-triads. Am J Epidemiol. 1998;148:893–901. doi: 10.1093/oxfordjournals.aje.a009715. [DOI] [PubMed] [Google Scholar]
- Weinberg CR, Wilcox AJ, Lie RT. A log-linear approach to case-parents-triad data: assessing effects of disease genes that act either directly or through maternal effects and that may be subjected to parental imprinting. Am J Hum Genet. 1998;62:969–978. doi: 10.1086/301802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberg CR. Methods for detection of parent-of-origin effects in genetic studies of case-parents triads. Am J Hum Genet. 1999;65:229–235. doi: 10.1086/302466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh H, Palmer CGS, Harney S, Chen H, Bauman L, Brown MA, Sinsheimer JS. Using the maternal-fetal genotype incompatibility test to assess non-inherited maternal HLADRB1 antigen coding alleles as rheumatoid arthritis risk factors. BMC Proc. 2007;1(suppl 1):S124. doi: 10.1186/1753-6561-1-s1-s124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinsheimer JS, Palmer CGS, Woodward JA. Detecting genotype combinations that increase risk for disease: the maternal-fetal genotype incompatibility test. Genet Epidemiol. 2003;24:1–13. doi: 10.1002/gepi.10211. [DOI] [PubMed] [Google Scholar]
- Rampersaud E, Morris RW, Weinberg CR, Speer MC, Martin ER. Power calculations for likelihood ratio tests for offspring genotype risks, maternal effects, and parent-of-origin effects in the presence of missing parental genotypes when unaffected siblings are available. Genet Epidemiol. 2007;31:18–30. doi: 10.1002/gepi.20189. [DOI] [PMC free article] [PubMed] [Google Scholar]


