Abstract
Gene × gene interactions play important roles in the etiology of complex multi-factorial diseases like rheumatoid arthritis (RA). In this paper, we describe our use of a two-stage search strategy consisting of information theoretic methods and logistic regression to detect gene × gene interactions associated with RA using the data in Problem 1 of Genetic Analysis Workshop 16. Our method detected interactions of several SNPs (single-SNP and SNP × SNP) that are located on chromosomal regions linked to RA and related diseases in previous studies.
Background
The risk of developing many common and complex diseases such as cancer and autoimmune disease involve complex interactions between multiple genes and several endogenous and exogenous environmental factors (or covariates). Rheumatoid arthritis (RA) is a complex genetic disease in which it is hypothesized that several loci contribute to disease susceptibility. Information theoretic methods are among the most promising approaches for genetic association studies and have been used for genetic analysis [1,2] and analysis of gene × gene interactions [3,4]. In this paper, we describe our use of a two-stage strategy consisting of an information theoretic search followed by logistic regression to detect gene × gene interactions associated with RA using selected genomic regions from the genome-wide scan data from the North American Rheumatoid Arthritis Consortium, which comprises 868 cases and 1194 controls. Data were provided as Problem 1 of Genetic Analysis Workshop 16.
Methods
Interaction information as measure of association
Let Xi denotes a genetic random variable representing the genotypes at locus Li. We assume Li is biallelic (with alleles A and a) with three possible genotypes (AA, Aa, and aa). The uncertainty of Xi is given by Shannon's entropy [5] as
Given a set of such genetic variables S = {X1; X2;...; Xk}, the interaction information among the k variables (referred to as k-way interaction information or KWII) is defined as the amount of information (redundancy or synergy) present in the set of variables that is not present in any subset of these variables [4]. For the variables in set S, the KWII can be written succinctly as an alternating sum over entropies (H) of all possible subsets τ of S using the difference operator [6]:
Let C be the random variable representing the disease status (phenotype variable) of RA. Then KWII(S;C) = KWII(X1; X2;...; Xk;C) is a measure of the association of the set of genetic variables in set S towards the disease phenotype variable C (i.e., how well the set explains the disease phenotype). The value of KWII(S;C) can be both positive and negative. We shall use only positive KWII values as the measure of association because larger positive values indicate stronger interaction (hence, higher association).
Redundancy between combinations of variables
Let S1 = {X1; ...; Xm} and S2 = {Y1; ...; Ym} be two sets (or combinations) of variables. Then the redundancy between S1 and S2 is given by the maximized average of pairwise linkage disequilibrium (LD) (r2) between variables from S1 and S2:
Such redundancies can arise because of LD between the variables across each set. For example, for a disease C that is caused by interactions between two untyped SNPs D1 and D2, let four marker loci be designated X1, X2, X3, and X4 such that X1 and X3 are in strong LD with D1, while X2 and X4 are in strong LD with D2. Then the KWII(X1;X2;C) and KWII(X3;X4;C) measure the association of the sets {X1;X2} and {X3;X4} for C, respectively. The redundancy between the combinations {X1;X2} and {X3;X4} is given by say, 0.5*(r2(X1, X3)+r2(X2, X4)) and existence of strong LD between X1 and X3 and between X2 and X4 will result in similar measures of KWII association for both sets, making one of the sets statistically redundant.
Stage I: Single-nucleotide polymorphism (SNP)-combination search strategy
Let S be the set of all genetic (SNPs) and environmental (non-genetic) variables (e.g., sex) and C be the variable denoting the disease phenotype. The information theoretic metric KWII(X1;...;Xk;C) is a measure of the association of the set of variables with the disease phenotype variable C (i.e., how well they explain the disease phenotype). Using this metric and a redundancy measure, we iteratively search for combinations of variables up to a fixed number (say τ) of iterations. Let the number of variables (except C) in a combination be defined as the "order" of the combination. In our method, we limit our search to up to second-order (or two-variable) combinations (i.e., we consider only {Xi;C} and {Xi;Xj;C} combinations). Let θ be the set of variables and ξ be the set of associated combinations output by our search method. Initially, both θ and ξ are empty. In iteration = 1, the variable Xk having highest KWII(Xk;C) is selected; thus θ = {Xk} and ξ = {(Xk;C)}. Also Xk is removed from S. In a subsequent iteration = i (i> 1), a new variable Xj ∈ S is considered for selection and its single variable and two-variable combinations are formed and KWII computed (using, Eq. (2)) with variables already selected in the previous iterations. At the same time each of the combinations formed are checked for redundancy with combinations already in ξ and of same order (using Eq. (3) and redundancy exceeding a threshold of 0.7). For example in iteration = 2, for Xj ∈ S, the combinations {Xj;C} and {Xk;Xj;C} are formed and {Xj;C} is checked for redundancy with {Xk;C}. From all the new variables, the variable that has maximum KWII and all non-redundant combinations is selected. A variable with a redundant combination is dropped from consideration (i.e., removed from S) in subsequent iterations. Given the computational burden of determining redundancy with combinations of variables already selected, our selection procedure stops after a maximum of τ = 50 iterations. Thus, up to 50 variables with non-redundant combinations and highest KWII are selected. This stage yields a number of single and two-variable combinations and their KWII values, which are input to the second stage.
Stage II
We conduct logistic regression analysis on the one- and two-variable combinations obtained by our information theoretic search using the methods outlined by Cordell [7] and the significance of each combination is determined. The full single-locus model is
where r is the probability of each individual being a case, μ corresponds to the mean effect, the terms a and d correspond to the additive and dominance coefficient effects of the tested SNP variable, x and z are dummy variables with x = 1, z = -0.5 for one homozygote genotype (AA), x = 0, z = 0.5 for the heterozygote genotypes (Aa), and x = -1, z = -0.5 for the other homozygote type (aa). The chi-square is used to compare the full single-locus model with the null model given by 0 values for both a and d.
For SNP × SNP interactions, fully saturated model following Cordell's notation [7] is
where r and μ are same as in Eq. (3), the terms a1, d1, a2, and d2 are the dominance and additive effect coefficients of the two SNPs, iaa, iad, ida, and idd represent their interaction coefficients, and xi and zi are dummy variables with xi = 1, zi = -0.5 for one homozygous genotype (AA or BB), xi = 0, zi = 0.5 for the heterozygous genotypes (Aa or Bb), and xi = -1, zi = -0.5 for the other homozygous genotype (aa or bb). An interaction is tested by the deviance of the full two-locus model from the model minus the interaction terms with chi-square test.
Data
We have followed a candidate-gene-based approach and selected SNPs belonging to the candidate genes/regions in Table 1 for exploring both gene × RA and gene × gene × RA interactions using our two-stage approach. The start and end base-pair positions of each gene are obtained from http://www.pharmgkb.org/. Using the genes/regions from Table 1, we created the following three data sets for analysis:
Table 1.
Candidate genes, associated genes/regions and number of SNPs (#s) in each
| Gene | Chr | No. SNPs |
|---|---|---|
| TNFRSF1B | 1 | 17 |
| PADI4 | 1 | 8 |
| PTPN22 | 1 | 10 |
| FCRL3 | 1 | 10 |
| FCGR3A | 1 | 3 |
| FCGR3B | 1 | 4 |
| IL10 | 1 | 6 |
| IL1A | 2 | 3 |
| IL1B | 2 | 9 |
| ITGAV | 2 | 27 |
| STAT4 | 2 | 2 |
| CTLA4 | 2 | 5 |
| BTLA | 3 | 2 |
| IL3 | 5 | 2 |
| SLC22A4 | 5 | 15 |
| IL13 | 5 | 4 |
| IL4 | 5 | 5 |
| HAVCR1 | 5 | 11 |
| 6p21.3 | 6 | 1702 |
| MICA | 6 | 230 |
| HLA-C | 6 | 20 |
| NFKBIL1 | 6 | 11 |
| LTA | 6 | 6 |
| TNF | 6 | 5 |
| HLA-DR | 6 | 21 |
| VEGFA | 6 | 6 |
| 6q23 | 6 | 1841 |
| OLIG3 | 6 | 2 |
| TNFAIP3 | 6 | 5 |
| IL6 | 7 | 2 |
| IRF5 | 7 | 4 |
| C5 | 9 | 8 |
| DLG5 | 10 | 20 |
| MS4A1 | 11 | 12 |
| MHC2TA | 16 | 7 |
| CARD15 | 16 | 10 |
| RUNX1 | 21 | 3044 |
| MIF | 22 | 12 |
• 7087 SNPs selected for analysis using all genes/regions (Data Set 1)
• 5385 SNPs selected using all genes/regions except those that belong to only 6p21.3 and not to any other gene (Data Set 2)
• 3263 SNPs selected using genes not on chromosome 6 (Data Set 3)
Additionally, sex of the subjects and RA status were present in each data set as the environmental variable and the phenotype variable (C).
Results
We have obtained many single-variable and two-variable interactions with the disease phenotype, only the combinations with high values of KWII are presented in Tables 2, 3, 4. The SNPs shown to be in genomic regions 6p21.3 and 6q23 do not overlap with any other gene. We found no interaction between the covariates sex and RA. Table 2 shows the single-variable combinations with KWII values greater than or equal to 95th percentile of all the single-variable KWII obtained using our method for the respective data sets. Tables 3 and 4 show the two-variable combinations with KWII values greater than or equal to 95th percentile of all the two variable KWII obtained using our method for the respective data sets. The 95th percentile value for each data set is reported with each table where  denote the 95th percentile KWII for combinations of order i and data set j. Additionally, to assess the overall strength of the KWII values we have obtained, we have calculated the KWII values of each single-variable combination for all 7088 variables, and 50,000 two-variable combinations randomly chosen from the list of 25,116,328 pairs of variables. The 95th percentile of these were found to be
denote the 95th percentile KWII for combinations of order i and data set j. Additionally, to assess the overall strength of the KWII values we have obtained, we have calculated the KWII values of each single-variable combination for all 7088 variables, and 50,000 two-variable combinations randomly chosen from the list of 25,116,328 pairs of variables. The 95th percentile of these were found to be 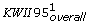 = 0.01 (one-variable combinations) and
= 0.01 (one-variable combinations) and 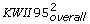 = 0.004 (two-variable combinations). All interactions reported in Tables 2, 3, 4 have KWII higher than these values. We have detected several one-variable associations in 6p21.3, HLA-DR, and RUNX1 (Table 2) and also in 6q23 and HLA-C (with
= 0.004 (two-variable combinations). All interactions reported in Tables 2, 3, 4 have KWII higher than these values. We have detected several one-variable associations in 6p21.3, HLA-DR, and RUNX1 (Table 2) and also in 6q23 and HLA-C (with 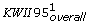 <KWII<95th percentile for respective data sets, not shown in tables). The strongest of the two-variable interactions are from the SNPs in region 6p21.3 (Table 3) obtained using Data Set 1. We have created the other two data sets because it was felt that several relatively weaker interactions are difficult to detect in the presence of the strongest interactions in 6p21.3. Using Data Sets 2 and 3, we found several two-variable KWII in genes MICA and RUNX1 (Table 3). Also several two-variable interactions are detected among SNPs in HLA-C, HLA-DR, MICA, and 6p21.3 (with
<KWII<95th percentile for respective data sets, not shown in tables). The strongest of the two-variable interactions are from the SNPs in region 6p21.3 (Table 3) obtained using Data Set 1. We have created the other two data sets because it was felt that several relatively weaker interactions are difficult to detect in the presence of the strongest interactions in 6p21.3. Using Data Sets 2 and 3, we found several two-variable KWII in genes MICA and RUNX1 (Table 3). Also several two-variable interactions are detected among SNPs in HLA-C, HLA-DR, MICA, and 6p21.3 (with 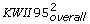 <KWII<95th percentile for respective data sets, not shown in tables). Also we observed an interaction between rs11811771 (PTPN22) with rs2828104 (RUNX1) with p-value 2.7 × 10-5 and KWII = 0.095. Separately we also calculated KWII for two-SNP combinations for Data Set 1 wherein the SNPs belong to different genes/genomic regions (Table 4).
<KWII<95th percentile for respective data sets, not shown in tables). Also we observed an interaction between rs11811771 (PTPN22) with rs2828104 (RUNX1) with p-value 2.7 × 10-5 and KWII = 0.095. Separately we also calculated KWII for two-SNP combinations for Data Set 1 wherein the SNPs belong to different genes/genomic regions (Table 4).
Table 2.
{SNP;C} interactions with KWII values ≥ 95th percentile of the 1-variable KWII obtained for Data Set 1, Data Set 2, Data Set 3
| SNP | Gene/genome region | KWII | p-Valueb |
|---|---|---|---|
Data Set 1: 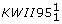 = 0.015a = 0.015a
| |||
| rs2395175 | HLA-DR | 0.195 | 0 |
| rs660895 | 6p21.3 | 0.189 | 0 |
| rs6910071 | 6p21.3 | 0.163 | 0 |
| rs3763312 | 6p21.3 | 0.151 | 0 |
Data Set 2: 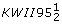 = 0.075 = 0.075 | |||
| rs2395175 | HLA-DR | 0.195 | 0 |
| rs7192 | HLA-DR | 0.094 | 0 |
| rs3129871 | HLA-DR | 0.079 | 0 |
| rs3129882 | HLA-DR | 0.075 | 0 |
Data Set 3: 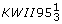 = 0.02 = 0.02 | |||
| rs731059 | RUNX1 | 0.048 | 0 |
| rs475142 | RUNX1 | 0.024 | 1.3 × 10-11 |
a denotes the 95th percentile KWII for combinations of order i and Data Set j.
denotes the 95th percentile KWII for combinations of order i and Data Set j.
b p-Value obtained using logistic regression
Table 3.
{SNP1;SNP2;C} interaction with KWII values ≥ 95th percentile of the two variable KWII obtained for Data Set 1 and consisting of SNPs only in 6p21.3 (and not in any candidate gene), for Data Set 2, and for Data Set 3)
| SNP1-SNP2 | Gene/genome region 1 - Gene/genome region 2 | KWII | p-Valueb |
|---|---|---|---|
Data Set 1: 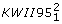 = 0.07a = 0.07a
| |||
| rs2647050-rs2858332 | 6p21.3-6p21.3 | 0.144 | 0 |
| rs9357152-rs2858332 | 6p21.3-6p21.3 | 0.098 | 0 |
| rs9275141-rs2858331 | 6p21.3-6p21.3 | 0.092 | 0 |
| rs7774434-rs2856718 | 6p21.3-6p21.3 | 0.08 | 0 |
| rs9275371-rs7765379 | 6p21.3-6p21.3 | 0.076 | 3.35 × 10-14 |
| rs660895-rs7755224 | 6p21.3-6p21.3 | 0.073 | 1.73 × 10-7 |
| rs9357152-rs9275555 | 6p21.3-6p21.3 | 0.07 | 9.98 × 10-8 |
Data Set 2: 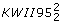 = 0.02 = 0.02 | |||
| rs9263871-rs9263969 | MICA-MICA | 0.03 | 1.35 × 10-8 |
| rs11967684-rs2523608 | MICA-MICA | 0.025 | 2.22 × 10-14 |
| rs9263871-rs2596501 | MICA-MICA | 0.022 | 1.81 × 10-5 |
| rs11967684-rs7755852 | MICA-MICA | 0.02 | 2.45 × 10-8 |
| rs3873380-rs7755852 | MICA-MICA | 0.02 | 1.39 × 10-9 |
Data Set 3: 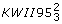 = 0.01 = 0.01 | |||
| rs1542876-rs1513737 | RUNX1-RUNX1 | 0.015 | 1.85 × 10-6 |
a denotes the 95th percentile KWII for combinations of order i and Data Set j.
denotes the 95th percentile KWII for combinations of order i and Data Set j.
b p-Value obtained using logistic regression.
Table 4.
The two-variable interactions with KWII values ≥ 95th percentile (0.01) obtained using SNPs on gene × gene pairs on Data Set 1
| SNP1-SNP2 | Gene/genome region 1 - Gene/genome region 2 | KWII | p-Valuea |
|---|---|---|---|
| rs9275596-rs1542876 | 6p21.3-RUNX1 | 0.01914 | 2.05 × 10-6 |
| rs2856725-rs1542876 | 6p21.3-RUNX1 | 0.01743 | 3.61 × 10-5 |
| rs9275596-rs1041778 | 6p21.3-RUNX1 | 0.01471 | 8.25 × 10-7 |
| rs7770216-rs563495 | 6p21.3-6q23 | 0.01444 | 4.15 × 10-7 |
| rs7755852-rs2745443 | 6p21.3-6q23 | 0.01275 | 6.22 × 10-7 |
| rs9275698-rs1883468 | 6p21.3-6q23 | 0.01262 | 4.51 × 10-7 |
| rs4673260-rs12190331 | CTLA4-6q23 | 0.01385 | 7.86 × 10-8 |
| rs1206684-rs651084 | 6q23-RUNX1 | 0.01261 | 6.12 × 10-5 |
| rs2844729-rs16984549 | 6p21.3-RUNX1 | 0.01255 | 5.71 × 10-7 |
| rs2856725-rs1041778 | 6p21.3-RUNX1 | 0.01247 | 6.54 × 10-6 |
a p-Value obtained using logistic regression.
The KWII values of two-variable combinations greater than 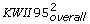 = 0.004 are used to construct the gene × gene interaction diagram (Figure 1). We have categorized these interactions as: 1) strong (KWII ≥ 0.1) in green, 2) moderate (0.1 > KWII ≥ 0.05 in light green, and 3) weak in orange. Also, bold lines indicate p-values < 10-15 while dotted lines denote 10-15 ≤ p-value ≤ 10-4.
= 0.004 are used to construct the gene × gene interaction diagram (Figure 1). We have categorized these interactions as: 1) strong (KWII ≥ 0.1) in green, 2) moderate (0.1 > KWII ≥ 0.05 in light green, and 3) weak in orange. Also, bold lines indicate p-values < 10-15 while dotted lines denote 10-15 ≤ p-value ≤ 10-4.
Figure 1.
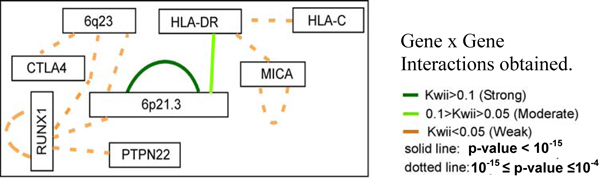
Gene × gene interactions obtained.
Discussion
We have used a two-stage strategy to search for single SNPs and SNP × SNP interactions associated with RA. Using our analysis on the candidate genes, we have found several strong interactions on 6p21.3 and interactions among SNPs on genes previously reported to be related with RA and other autoimmune diseases. For example, RUNX1 has been reported to be associated with systemic lupus erythematosus and psoriasis (two autoimmune diseases) [8,9] while associations of region 6q23 and MICA with RA has been reported by Thomson et al. [10] and Martinez et al. [11], respectively. Detecting genes and environmental factors interacting to increase the susceptibility to disease risk is a very challenging task for many reasons, particularly for the large size of the data and presence of confounding factors such as LD, presence of phenocopies, locus heterogeneity, and population stratification. Information theoretic methods have high power in detecting gene × gene interactions and have the advantage of being simpler and computationally faster; KWII-based interaction analysis has been employed in [3,4]. Also, our method can be used when the genetic and environmental variables have different numbers of classes or when the phenotype has more than two classes. Although we initially planned for a genome-wide analysis, given the large size of the data, we were able to execute only a few iterations using our computational resources. Therefore, we decided to follow a candidate-gene-based approach. We believe that with the help of additional hardware, it is possible to implement our search strategy in a distributed computing environment employing multiple processors and to explore many more interactions with moderate to low magnitudes that are potentially associated with RA.
List of abbreviations used
GAW16: Genetic Analysis Workshop 16; KWII: k-way interaction information; LD: Linkage disequilibrium; RA: Rheumatoid arthritis; SNP: Single-nucleotide polymorphism
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
PC developed the computational methods and carried out the statistical genetics analysis. AZ was involved in the development of the computational analysis. LS participated in the statistical genetics analysis and interpretations. MR conceived the study and was involved all aspects of design and coordination.
Contributor Information
Pritam Chanda, Email: pchanda@cse.buffalo.edu.
Aidong Zhang, Email: azhang@cse.buffalo.edu.
Lara Sucheston, Email: lsuchest@buffalo.edu.
Murali Ramanathan, Email: murali@buffalo.edu.
Acknowledgements
The Genetic Analysis Workshops are supported by NIH grant R01 GM031575 from the National Institute of General Medical Sciences.
This article has been published as part of BMC Proceedings Volume 3 Supplement 7, 2009: Genetic Analysis Workshop 16. The full contents of the supplement are available online at http://www.biomedcentral.com/1753-6561/3?issue=S7.
References
- Liu Z, Lin S. Multilocus LD measure and tagging SNP selection with generalized mutual information. Genet Epidemiol. 2005;29:353–364. doi: 10.1002/gepi.20092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore JH, Gilbert JC, Tsai CT, Chiang FT, Holden T, Barney N, White BC. A flexible computational framework for detecting, characterizing, and interpreting statistical patterns of epistasis in genetic studies of human disease susceptibility. J Theoret Biol. 2006;241:252–261. doi: 10.1016/j.jtbi.2005.11.036. [DOI] [PubMed] [Google Scholar]
- Chanda P, Sucheston L, Zhang A, Brazeau D, Freudenheim JL, Ambrosone C, Ramanathan M. AMBIENCE: a novel approach and efficient algorithm for identifying informative genetic and environmental interactions associated with complex phenotypes. Genetics. 2008;180:1191–1210. doi: 10.1534/genetics.108.088542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chanda P, Zhang A, Brazeau D, Sucheston L, Freudenheim JL, Ambrosone C, Ramanathan M. Information-theoretic metrics for visualizing gene-environment interactions. Am J Hum Genet. 2007;81:939–963. doi: 10.1086/521878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon CE. A mathematical theory of communication. Bell Sys Tech J. 1948;27:379–423. 623-656. [Google Scholar]
- Jakulin A. [Ph.D. Thesis] Ljubljana, Slovenia, Department of Computer Science, University of Ljubljana; 2005. Machine learning based on attribute interactions. [Google Scholar]
- Cordell HJ. Epistasis: what it means, what it doesn't mean, and statistical methods to detect it in humans. Hum Mol Genet. 2002;11:2463–2468. doi: 10.1093/hmg/11.20.2463. [DOI] [PubMed] [Google Scholar]
- Alarcon-Riquelme ME. A RUNX trio with a taste for autoimmunity. Nat Genet. 2003;35:299–300. doi: 10.1038/ng1203-299. [DOI] [PubMed] [Google Scholar]
- Yamada R, Tokuhiro S, Chang X, Yamamoto K. SLC22A4 and RUNX1: identification of RA susceptible genes. J Mol Med. 2004;82:558–564. doi: 10.1007/s00109-004-0547-y. [DOI] [PubMed] [Google Scholar]
- Thomson W, Barton A, Ke X, Eyre S, Hinks A, Bowes J, Donn R, Symmons D, Hider S, Bruce IN. Wellcome Trust Case Control Consortium; Wilson AG, Marinou I, Morgan A, Emery P. YEAR Consortium. Carter A, Steer S, Hocking L, Reid DM, Wordsworth P, Harrison P, Strachan D, Worthington J. Rheumatoid arthritis association at 6q23. Nat Genet. 2007;39:1431–1433. doi: 10.1038/ng.2007.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez A, Fernandez-Arquero M, Balsa A, Rubio A, Alves H, Pascual-Salcedo D, Martin-Mola E, de la Concha EG. Primary association of a MICA allele with protection against rheumatoid arthritis. Arthritis Rheum. 2001;44:1261–1265. doi: 10.1002/1529-0131(200106)44:6<1261::AID-ART217>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]


