Abstract
After more than 200 genome-wide association studies, there have been some successful identifications of a single novel locus. Thus, the identification of single-nucleotide polymorphisms (SNP) with interaction effects is of interest. Using the Genetic Analysis Workshop 16 data from the North American Rheumatoid Arthritis Consortium, we propose an approach to screen for SNP-SNP interaction using a two-stage method and an approach for detecting gene-gene interactions using principal components. We selected a set of 17 rheumatoid arthritis candidate genes to assess both approaches. Our approach using principal components holds promise in detecting gene-gene interactions. However, further study is needed to evaluate the power and the feasibility for a whole genome-wide association analysis using the principal components approach.
Background
It is common in candidate-gene or genome-wide association studies to perform single-gene association analysis. However, after more than 200 genome-wide association studies (GWAS), there have been fewer novel loci identified than expected [1], possibly due to small effects of individual genetic variations. By supplementing GWAS data with information from previous candidate-gene or functional studies, and considering genetic interaction effects, we may be able to identify groups of genes that contribute to a complex disease. Approaches for studying gene-environment and gene-gene interactions have been proposed for the analysis of candidate genes [2,3] and genome-wide data [4]. We extend two approaches proposed for single-gene and gene-environment interaction analyses, a principal component (PC) approach [5] and a two-step approach [6], to gene-gene interaction analysis. We compare these two approaches with the traditional approach of testing all pairwise single-nucleotide polymorphism (SNP) interactions to assess gene-gene interaction effects on rheumatoid arthritis in the North American Rheumatoid Arthritis Consortium (NARAC) data.
Methods
Data
All of our analyses utilized genotype data of the 868 cases and 1194 controls in the NARAC data set. Analyses were carried out on a set of 17 candidate genes, selected on the basis of a literature search. The candidate genes used in these analyses are listed in Table 1. We identified all SNPs in the gene and within 5 kb on each side of each of these genes. SNPs with call rate ≤ 95% or not in Hardy-Weinberg equilibrium (p < 0.001) were excluded from all analyses, leading to a final set of 135 SNPs. Before analysis, the computer program MACH [7] was used to impute missing genotypes.
Table 1.
List of candidate genes
| Gene | Chromosome |
|---|---|
| PADI4 | 1 |
| PTPN22 | 1 |
| STAT4 | 2 |
| IL1B | 2 |
| CTLA4 | 2 |
| ITGAV | 2 |
| IL13 | 5 |
| VEGFA | 6 |
| TNF | 6 |
| LTA | 6 |
| HLA-A | 6 |
| HLA-B | 6 |
| HLA-C | 6 |
| IL6 | 7 |
| TRAF1 | 9 |
| C5 | 9 |
| MS4A1 | 11 |
Approaches
Principal components
This approach was proposed by Gauderman et al. [5] to test for association between disease and multiple SNPs in a candidate gene. We extend this approach to test for gene-gene interaction. The procedure involves the following steps. 1) Let glk be the number of minor alleles at SNP k for lth subject, l = 1, ..., N, k = 1, ..., K. 2) Calculate the correlation matrix R, where Rij = cor(gi, gj) and gi and gj represent the genotypes of all subjects for SNP i and SNP j, respectively. 3) Decompose R by singular value decomposition: R = AΛAT 4) Determine the factor loading by 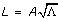 . 5) Determine the PCs by PC = GA, where G is the standardized N × K matrix of genotypes. The standardized genotypes are calculated as:
. 5) Determine the PCs by PC = GA, where G is the standardized N × K matrix of genotypes. The standardized genotypes are calculated as: 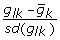 , where
, where 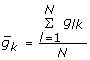 is the mean genotype across subjects and
is the mean genotype across subjects and 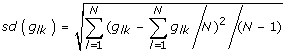 is the standard deviation.
is the standard deviation.
Then, we use PCs that explain at least 80% of the variation as the gene representation to perform a gene-gene interaction analysis, by applying logistic regression to test for interaction between every combination of two PCs. Once significant PC interactions are identified, PC loadings may be used to determine the influence of a specific SNP on the PCs because the loading represents the correlation of a SNP with a component. For better visualization of the gene-PCs and their SNPs position with the LD block plots, we created a graphical display using our own function in the statistical package R and the computer program Haploview [8].
Two-step analysis
Murcray et al. [6] proposed a two-step approach for selecting SNPs involved in significant gene-environment interactions, where Step 1 consisted of a modified version of the case-only analysis [9,10], and in Step 2, the significant SNP-environment interactions identified in Step 1 were tested using logistic regression. We modified their method to detect gene-gene interactions as follows:
Step 1
For each pair of SNPs, we perform a test of association between the two SNPs (g1, g2) based on the approximate method to screen for epistasis implemented in PLINK [11] by combining cases and controls and coding g1 and g2 as 0, 1, or 2, representing the number of minor alleles. A χ2 with 1 degree of freedom is used to test the association between each pair of SNPs. Pairs of SNPs are selected for analysis in Step 2 if they exceed a given significance threshold, p <α*. In our case, we selected α* = 0.05.
Step 2
The M significant SNP pairs from Step 1 are tested in a traditional log-additive model with gene-gene interaction
where D represents the cases (D = 1) and controls (D = 0). An interaction is considered significant when the p-value of interaction (i.e., the p-value for testing H0: β3 = 0) is less than or equal to α/M, where α = 0.05.
Results
Figure 1A shows results of all SNP-SNP interactions compared with the PC-PC interaction approach (Figure 1B) for each gene using Q values [12]. Figure 1C depicts the results of all SNP-SNP interactions for each gene using Bonferroni-corrected p-value < 5.5 × 10-6 (the α value of 0.05 divided by K(K-1)/2 with K = 135 SNPs) compared with the two-stage approach with p-value in the first stage < 0.05 and a p-value in the second stage < 3.2 × 10-5 (the α value of 0.05 divided by M = 1655 significant SNP pairs from Step 1).
Figure 1.
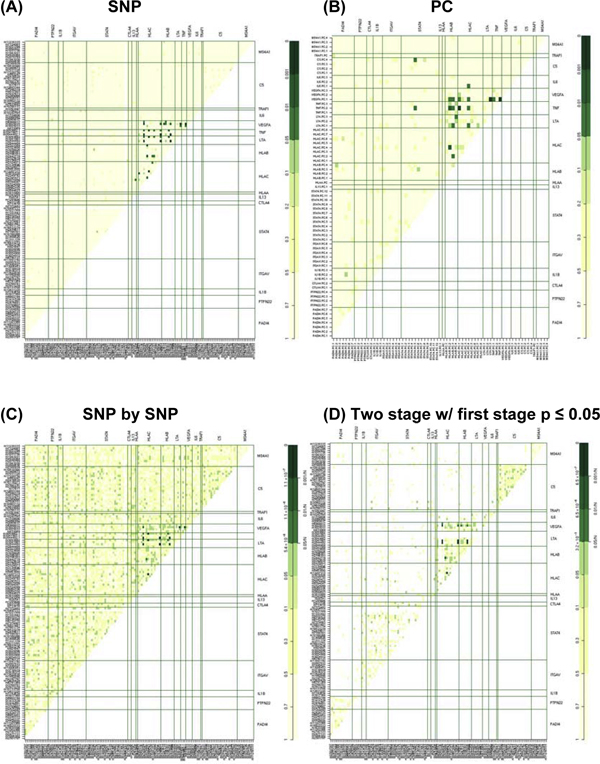
Comparison between the gene-gene interaction approaches. A, Q-values for all SNP-SNP interactions; B, PC interactions; C, p-values for all SNP-SNP interactions; and D, two-step approach. Darker shades of green represent smaller p-values.
The PC approach detected several PC interaction effects when using Q-value only. The strongest interactions were observed within the HLA region with TNF-PC3 and VEGFA-PC1 and HLA-C-PC1 and TNF-PC2 (q-value < 0.001). Outside the HLA region we observed two moderate interaction effects involving STAT4-PC5 and C5-PC4, and TNF-PC2 and STAT4-PC5 (0.001 <q-value < 0.01). Figure 2 depicts the SNP factor loadings for each PC within the genes STAT4 and C5, and the linkage disequilibrium (LD) blocks within these genes. The STAT4-PC5 interaction contains four SNPs with absolute value of loadings ≥ 0.5 and they represent their own block. The C5-PC4 interaction contains three SNPs with loadings ≥ 0.5, where the two SNPs (rs10760131 and rs10985112) with the two highest loadings, 0.9 and 0.8 respectively, belong to the same block. On the other hand, the two-step approach detected only interactions within the HLA region. The strongest interactions were between SNPs of VEGFA with HLA-C, LTA with HLA-B, and with HLA-C, and HLA-B, with HLA-C. Code to perform these analyses is available from the authors by request.
Figure 2.
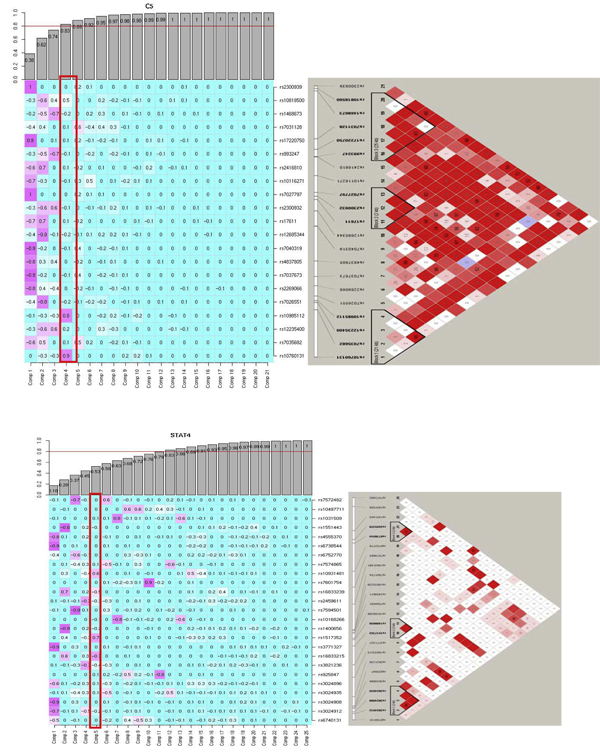
Visualization from PC to Haploview. Figures on the left depicted the C5 and STAT4 genes PCs with their respective loadings. The bar plot represents the cumulative percentage of explained data variance for each PC. The red blocks are the interactions of C5-PC4 and STAT4-PC5. Figures on the right depicted the C5 and STAT4 Haploview display.
Discussion
We extended two approaches previously used for gene-level tests or gene-environment interaction analysis to screen for gene-gene interactions in 17 candidate genes for RA using the GAW16 NARAC data. In the PC approach we calculated the SNP loadings for each PC and viewed them in the context of the gene LD structure generated using Haploview (Figure 2). This comparison is useful to identify the contribution of each SNP in the PCs and its position in the gene. For the PC gene-gene interaction analysis we used PCs that explained 80% of the variation to limit the number of PCs. Using this method we identified several gene-gene interactions. Further study to investigate the power of this PC approach is needed. This approach has potential to be used as a screening tool to detect gene-gene interaction. Subsequently, a more detailed interaction analysis should be performed using the SNPs with higher loadings [13].
We could not identify any significant interactions using the two-step approach. There are several possibilities, including the elimination of SNPs with low allele frequency, and the choice of α* in Stage 1. Recently, a similar two-step method was proposed and shown to be more powerful than a one-step approach [14]. Further evaluation of this approach is warranted.
Conclusion
Using PCs is a promising approach to screen for potential interactions. As shown in our results, it can detect interactions not observed based on SNP-SNP interactions assessed using either a single-step or a two-step approach. Furthermore, the method used to correct for multiple comparison also plays an important role.
List of abbreviations used
GAW16: Genetic Analysis Workshop 16; GWAS: Genome-wide association studies; LD: Linkage disequilibrium; NARAC: North American Rheumatoid Arthritis Consortium; PC: Principal components; SNP: Single-nucleotide polymorphism
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
JL carried out the candidate genes selection, programming, and performed the statistical analysis. RT participated in the candidate genes selection and programming. JMB participated in the design of the study and helped to draft the manuscript. MdA conceived of the study, participated in its design and coordination, and drafted the manuscript. All authors read and approved the final manuscript.
Contributor Information
Jia Li, Email: jiajiaysc@gmail.com.
Rui Tang, Email: rtang@mtu.edu.
Joanna M Biernacka, Email: biernacka.joanna@mayo.edu.
Mariza de Andrade, Email: mandrade@mayo.edu.
Acknowledgements
The Genetic Analysis Workshops are supported by NIH grant R01 GM031575 from the National Institute of General Medical Sciences. We thank Jason Sinnwell and David Rider for their assistance in MACH (JS) and SNP selection for the candidate genes (DR) and the two reviewers for their insightful comments. Partial funding for this study was provided by NIH grant HL87660 (MdA and JL) and the S.C. Johnson Genomics of Addiction Program at Mayo Clinic (JMB and RT).
This article has been published as part of BMC Proceedings Volume 3 Supplement 7, 2009: Genetic Analysis Workshop 16. The full contents of the supplement are available online at http://www.biomedcentral.com/1753-6561/3?issue=S7.
References
- Office of Population Genomics. Overview: A catalogue of genome-wide association studies. http://www.genome.gov/gwastudies/
- Kallberg H, Padyukov L, Plenge RM, Ronnelid J, Gregersen PK, Helm-van Mil AH van der, Toes RE, Huizinga TW, Klareskog L, Alfredsson L. Epidemiological Investigation of Rheumatoid Arthritis study group. Gene-gene and gene-environment interactions involving HLA-DRB1, PTPN22, and smoking in two subsets of rheumatoid arthritis. Am J Hum Genet. 2007;80:867–875. doi: 10.1086/516736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao J, Jin L, Xiong M. Test for interaction between two unlinked loci. Am J Hum Genet. 2006;79:831–845. doi: 10.1086/508571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J, Donnelly P, Cardon LR. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat Genet. 2005;37:413–417. doi: 10.1038/ng1537. [DOI] [PubMed] [Google Scholar]
- Gauderman JW, Murcray C, Gilliland F, Conti DV. Testing association between disease and multiple SNPs in a candidate gene. Genet Epidemiol. 2007;31:383–395. doi: 10.1002/gepi.20219. [DOI] [PubMed] [Google Scholar]
- Murcray C, Lewinger JP, Gauderman JW. Gene-environment interaction in genome wide association study. Am J Epidemiol. 2009;169:219–226. doi: 10.1093/aje/kwn353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Abecasis GR. Proceedings of the American Society of Human Genetics: 2006 October 9-13; New Orleans. Rockville, MD: American Society of Human Genetics; 2005. Mach 1.0: rapid haplotype reconstruction and missing genotype inference [abstract 2290/C]http://www.ashg.org/genetics/ashg/annmeet/2006/call/pdf/2390 Abstracts, 6-per-page.pdf. [Google Scholar]
- Barrett JC, Fry B, Maller J, Daly MJ. Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics. 2005;21:263–265. doi: 10.1093/bioinformatics/bth457. [DOI] [PubMed] [Google Scholar]
- Piegorsch WW, Weinberg CR, Taylor JA. Non-hierarchical logistic models and case-only designs for assessing susceptibility in population-based case-control studies. Stat Med. 1994;13:153–162. doi: 10.1002/sim.4780130206. [DOI] [PubMed] [Google Scholar]
- Clayton D, McKeigue PM. Epidemiologic methods for studying genes and environmental factors in complex diseases. Lancet. 2001;358:1356–1360. doi: 10.1016/S0140-6736(01)06418-2. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ, Sham PC. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey JD, Tibshirani R. Statistical significance for genomewide studies. Proc Natl Acad Sci USA. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee N, Kalayioglu Z, Moslehi R, Peters U, Wacholder S. Powerful multilocus tests of genetic association in the presence of gene-gene and gene-environment interactions. Am J Hum Genet. 2006;79:1002–1016. doi: 10.1086/509704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kooperberg C, LeBlanc M. Increasing the power of identifying interactions in genome-wide association studies. Genet Epidemiol. 2008;32:255–263. doi: 10.1002/gepi.20300. [DOI] [PMC free article] [PubMed] [Google Scholar]


