Lab-on-chip FIA system without an external pump and valves and integrated with an in line electrochemical detector

Abstract

Surface energy in small droplets can be used to drive samples through micro-channels. When a sample fluid is spontaneously driven through a solution filled micro-channel with liquid droplets on its entry (sample) and exit (reservoir) ports it is termed as a passive pumping device. A passive pump driven micro-fluidic system integrated with microfabricated planar electrodes or electrode arrays (e.g., interdigitated electrode arrays, or microband electrode arrays) can be considered as a manifold for flow injection analysis without external pump and injector valve. Factors affecting the passive pump driven flow rate in a polydimethylsiloxane (PDMS) – glass hybrid micro-fluidic system, including the volume, viscosity and surface tension of the sample solution and the tilt of the microfluidic channel are analyzed. By placing 2 μL hexacyanoferrate (II) solutions at the entry port of the device peak shaped transients were recorded. The peak heights showed linear dependence on the sample concentrations between 3·10⁻⁷ and 10⁻⁵ M.

Introduction

Flow injection analysis (FIA) has been introduced as a simple analytical method to perform complex time dependent analytical tasks with high sampling rates and excellent reproducibility.¹ In general, FIA systems consist of a pump, an injection valve, a mixing coil or column and a flow through detector cell. Since its inception FIA was developed through stages and gradually miniaturized. Simple flow injection (FI) methods were developed into sequential injection (SI) and a wide range of operations were integrated on the valve (laboratory on the valve, LOV systems).² The next level of miniaturization has been the utilization of FI principles in micro-fluidic devices. In these systems, only few nano-liters of the sample are loaded into the channel and analyzed.^3–8 These lab on a chip devices unite the advantages of the previous FIA systems and offer fast and controllable analysis in portable (hand-held) format with minimal reagent consumption, energy need and waste generation. However, FI in a micro-fluidic format comprised a variety challenges.^9–11 These challenges are due to lack of micropumps that could be integrated onto the analytical chips,⁸ difficulties of the precise time and volume control in microscopic channels with short analysis time,³ complicated flow patterns, bulky actuators and analytical instrumentation required for low detection limits and good reproducibility, etc.

Recently it has been shown that the surface energy in small droplets can be utilized to drive solutions through solution filled microchannels with controlled flow rates.^{4, 12–14} When a sample fluid is spontaneously driven through a solution filled micro-channel with liquid droplets on its entry (sample) and exit (reservoir) ports it is termed as a passive pumping device. In passive pumps, potential and interfacial energies are converted into kinetic energy and heat. A passive pump has no moving parts, needs no external energy or equipment to initiate or maintain flow. Since the sample droplet drives the flow in a reproducible way, a passive pumping manifold integrated with an in-line electrochemical detector can be considered as the simplest single line FIA system without an external pump and a precision injection valve.

Microscopic electrochemical cells can be patterned onto silicon wafers or glass slides with conventional thin-film photolithography. Microfabrication of planar electrochemical cells is cost effective and the reproducibility of the electrode dimensions and surface properties is excellent. Thus, microfabricated electrodes are ideal candidates for single use devices without calibration, short analysis time in combination with minimal sample and reagent consumption.

The flow rates in passive pump driven micro-fluidic systems can be controlled by the (i) material properties of the micro-fluidic manifold (e.g., hydrophilic or hydrophobic), (ii) geometrical parameters of the channel (e.g., shape, length, width, height), the sample and the reservoir wells (i.e., the diameters of these wells), (iii) tilt of the channel, (iv) the sample properties (e.g., viscosity, density, surface tension), and (v) volumes (radiuses) of the sample and reservoir droplets at the beginning of a pumping experiment. This paper shows the feasibility of a passive pump driven single line flow injection system without an external pump and/or injection valve. The bottom of the micro-fluidic device is a glass slide with an amperometric microcell patterned onto its surface with 1 μm thick polyimide insulation layer. The microfluidic channel is made from polydimethylsiloxane (PDMS) by soft lithography. We report on the influence of the experimental conditions on the induced flow rate in this PDMS-glass hybrid device including the volume, viscosity, and surface energy of the sample solution and the tilt of the channel (gravitational energy). In addition, we show the performance characteristics of the system as a flow injection manifold in combination with a planar amperometric detector cell using potassium hexacyanoferrate (II) as a model compound. To the best of our knowledge this is the first report on passive pump driven FIA system.

Passive pump driven FIA system

A schematic view of a simple, single line FIA system utilizing the passive pumping principle is shown in Figure 1. The channel has a rectangular cross section which is about 192 μm wide and 96 μm high. The 10 mm long channel connects two cylindrical ports (sample and reservoir) with φ₁ between 1.2 and 1.4 mm and φ₂ between 1.2 and 2.9 mm. The depth (d) of both microwells was 2 mm. The volumes of the sample and reservoir wells and the micro-fluidic channel were equal or smaller than 1.4, 13.0, and 0.2 μL, respectively.

Figure 1.

(a) Schematic cross sectional view of the polydimethylsiloxane (PDMS)-based micro-fluidic system used in passive pumping experiments. L is the channel length, d is the depth of the entry and reservoir ports, while Φ₁ and Φ₂ are the diameters of the sample and reservoir ports, respectively. (b) Photograph of a glass slide with three electrochemical cells patterned onto its surface and a microchannel in the middle of the glass slide above the electrochemical cell in the center. (c) Schematic representation of the electrochemical cells and the placement of the ~200 μm wide channel over the reference (E_R), interdigitated working (E_w), and counter electrodes (E_A).

During the pumping process, the sample droplet descends into the sample port and the solution flows toward reservoir port. The flow rate in the channel can be acquired from the volume change of the sample droplets¹³ or the chronoamperometric current in the presence of an electrochemically active mediator of constant concentration.¹⁵ The volumetric flow rate (Q) is determined by the overall pressure difference (ΔP_tot) between the sample and reservoir ports and the hydrodynamic resistance (Ω) of the system (Eq. 1).

$$Q=\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}=\frac{\mathrm{\Delta }{P}_{\text{tot}}}{\mathrm{\Omega }}$$ (Eq. 1)

The total pressure difference (ΔP_tot) is determined by three pressure differences in the system: pressure difference of the sample droplet (ΔP_s), pressure difference of reservoir droplet (ΔP_R) and hydrostatic pressure difference between the two ends of the channel (ΔP_h), i.e. the sample and reservoir ports:

$$\mathrm{\Delta }{P}_{\text{tot}}=\mathrm{\Delta }{P}_{\text{S}}-\mathrm{\Delta }{P}_{\text{R}}+\mathrm{\Delta }{P}_{\text{H}}$$ (Eq. 2)

The pressure differences at sample (S) and reservoirs (R) droplets can be calculated from Young-Laplace Equation:

$$\mathrm{\Delta }{P}_{\text{i}}=\frac{2{\gamma }_{\text{i}}}{R_{\text{i}}}$$ (Eq. 3)

where γ is the surface tension of the liquid, R is the radius of the droplet and the subscript i can be S or R indicating the sample and reservoir droplets. The hydrostatic (gravitational) pressure difference (ΔP_H) between the droplets is determined by the height difference between the centers of gravity in the sample and reservoir droplets:

$$\mathrm{\Delta }{P}_{\text{H}}=\rho \text{g}(h_{\text{S}}-h_{\text{R}})$$ (Eq. 4)

where ρ is the density of the liquid, g is the gravitational constant, while h_S and h_R are the heights of the apexes (indeed the heights of the centers of gravity) of the sample and reservoir droplets, respectively. The hydrodynamic resistance of a channel (Ω) with rectangular cross section is a function of channel height (h_c), width (w), and length (L) and the viscosity (μ) of the fluid:¹⁶

$$\mathrm{\Omega }\approx \frac{12\mu L}{w{h_{\text{c}}}^3}{\left[1-\frac{h_{\text{c}}}{w}\left(\frac{192}{{\pi }^5}\sum _{\text{n}=1,3,5}^{\infty }\frac{1}{{\text{n}}^5}tanh(\frac{\text{n}\pi w}{2h_{\text{c}}})\right)\right]}^{-1}$$ (Eq. 5)

Since the hydrodynamic resistance of the microchannel is about six orders of magnitude larger than that of the wells, the influence of the wells (entry and reservoir ports) was neglected in calculating the overall hydrodynamic resistance of the system.

Experimental

Chemicals

All water-based solutions were prepared with 18.2 MΩ cm⁻¹ resistivity deionized water provided by a Milli-Q Gradient A-10 water purification system (Millipore Corp., Bedford, MA). Glycerol from Acros, (Morris Plains, NJ) was used to adjust the viscosity of aqueous solutions. The viscosities of the solutions were determined with an Ostwald U-tube viscosimeter at 20 °C using deionized water as standard. Hexacyanoferrate (II) from Sigma-Aldrich (St. Louis, MO), was used as model compound in voltammetric and chronoamperometric experiments. NaNO₃ and NaCl from Fisher (Fair Lawn, NJ) were used to prepare the background electrolytes. Sylgard 184 Polydimethylsiloxane (Dow Corning, Midland, MI.) was used to fabricate microchannels.

Instruments

A Harrick Scientific (Pleasantville, NY) PDC-32G plasma cleaner, in combination with an Emerson (St. Louis, MO) PDC-VP-1 model vacuum pump, was used for the surface treatment of PDMS specimens¹⁷ and cleaning the Au electrodes. The volumes of the sample and reservoir droplets over the circumference of the sample and reservoir ports were determined by capturing their images with VCA Optima surface analysis system (Advanced Surface Technology, Billerica, MA). The voltammetric and chronoamperometric measurements were performed with CH Instrument 900 bipotentiostat (CH Instruments Inc., Austin, TX). The planar electrochemical cells, patterned onto the surfaces of glass slides (Fig. 1b) with recessed microband (1 μm recess depth)^{18, 19} and interdigitated working electrodes were custom made by AEgis Technologies (Huntsville, AL). All three microfabricated electrodes were gold. One of the rectangular gold electrodes in the electrochemical cell was electroplated with Ag/AgCl and was used as a reference electrode in the electrochemical measurements. First silver was electroplated onto the bare gold surface with 10mA/cm² current density for 10 minutes using a cyanide-free plating solution from Technic Inc.(Cranston, RI, Cat. #31807). Next, about one third of the silver layer was turned into AgCl by oxidizing the Ag at 10mA/cm² current density for 3 minutes in 0.1 M NaCl.

As shown in Figure 1, the electrochemical cell was about 0.5 cm from both the sample and reservoir ports. To simplify the channel alignment with the electrochemical cell, the sizes of the working, reference and counter electrodes perpendicular to the channel were ~3 times of the channel width (600 μm vs. ~200 μm, respectively, Fig. 1C). In this work, interdigitated electrode arrays (IDA) (~1 μm recessed, with 5 μm finger widths and 5 μm separation) and individually addressable microband electrodes (~1 μm recessed, 5 μm wide with 100 μm separations) were used.

Passive pump-driven micro-fluidic manifolds

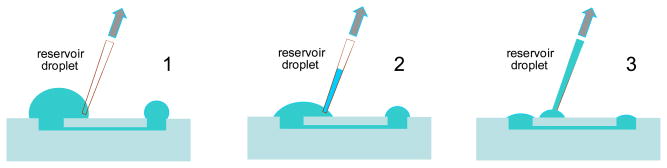
The preparation of the microchannels was described in our previous paper.¹³ The protocol of loading the passive pump and starting an experiment in a highly reproducible fashion is shown in Fig. 2. First, the microchannel is filled with an adequate solution. In FIA experiments with electrochemical detection the microchannel is filled with a background electrolyte (0.1mM NaCl/0.1M NaNO₃). Next, the excess of solution around the sample and reservoir wells is carefully removed by using a manual micropipette and the volumes of the protruding residues of solution droplets over the circumference of the sample and reservoir ports are determined by capturing their images. These volumes were very close to 0.2 ± 0.1 μL and 1.0 ± 0.1 μL, respectively. After that, a solution droplet with desired volume (8.5 or 16 μL) and viscosity is placed over the reservoir well. Finally, the sample solution is dispensed over the sample port of the device. The surface tension in the sample droplet generates a pressure difference (400 dyne/cm²<ΔP_tot<800 dyne/cm²) between the two ends of the microchannel and initiates the flow from the sample port towards the reservoir port. When a 2 μL droplet is placed at the sample port the initial flow rate decreases from 0.14 to 0.05 μL/s during the first 12 s of measurement. The flow stops after approximately 40 s when ΔP_tot = 0 and approximately 1 μL sample has been transported towards the reservoir.

Figure 2.

Protocol for setting reproducible initial conditions in the passive flow-driven micro-fluidic system through the removal of excess supporting electrolyte from a filled channel.

The device-to device variations in the generated flow rates and/or in the recorded electrochemical transients were at first relatively large related to our difficulties in producing flow channels with identical sample and reservoir wells. By using metal punchers (e.g. Harris Uni-Core) to drill the sample and reservoir port the device-to device reproducibility was significantly improved. The relative standard deviation of the well diameters using the metal punchers was reduced to 2% which is negligible compared to other sources of errors.

Results and discussions

Effect of viscosity on the flow rate

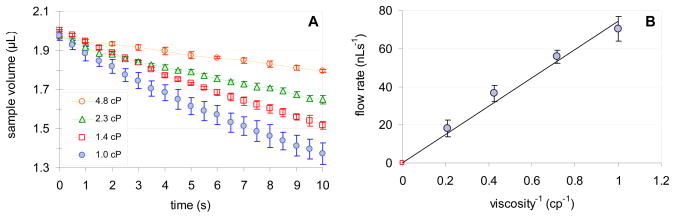
To assess the feasibility of utilizing the passive pump driven micro-fluidic manifold as a simple FIA system, first the influence of the solution viscosity on the flow rate has been evaluated. Considering the viscosity of the sample is of primary importance in analyzing biological samples, such as whole blood, plasma, etc., which are non-Newtonian fluids and have a broad range of viscosity (between 1.3 to 3.7 cp).^{20, 21} To model solutions with viscosities ranging between 1 and 4.9 cP glycerol and deionized water mixtures with 0, 10, 15, 20 30 and 50 wt% glycerol were used. First the device was filled with one of the model solutions. Next, 2 μL of these solutions were dispensed over the sample port of an already filled device. Then, images of the sample droplets were captured every 0.5 second for at least 10 seconds. The sample volumes were calculated from the recorded images.¹³ Fig. 3A shows the changes in the sample droplet volumes as function of time. The slopes of the curves provide the volumetric flow rates (Q). In Fig. 3B these flow rates are plotted against the reciprocal value of the sample solution viscosities. As expected, the induced flow rate is inversely proportional to the sample solution viscosity.

Figure 3.

Effect of viscosity on the sample flow rate in passive pump driven micro-fluidic systems. Symbols represent the mean values of n=3 parallel measurements performed in the same device. The bars correspond to the standard deviation of the data. (A) Change in the sample droplet volume as function of time using samples of different viscosities (◆ 1.0 cP; □ 1.4 cP; △ 2.3 cP; ○ 4.8 cP) (B) Dependence of the volumetric flow rates on the reciprocal value of the sample viscosity (1/μ). Data points (flow rates in the first 5 s of flow) are plotted with the best fit line Q = m·1/μ.

The linear flow rates were calculated from the volumetric flow rates and the cross sectional area of the channel. The linear flow rates in the system ranged from 0.35 cm/s to 0.09 cm/s and the Reynolds numbers were always smaller than 1, indicating that the passive pump generated flow is laminar in our system.

Upon the quantitative evaluation of the effect of the sample viscosity on the flow rates the variations in the surface tension of the sample (Eqs. 1, 3 and 5) should also be considered. However, for the glycerol/water mixtures these changes are almost negligible. By changing the sample from pure water to a 50 % water/glycerol mixture the surface tension changes from 72 dyne/cm to 68.5 dyne/cm.

Effect of surface tension and the droplet volume on the flow rate

Samples with different surface tensions and droplets with diverse sizes generate different ΔP_tot values between the sample and reservoir ports of the device (Eqs.2 and 3). Consequently, the induced flow rates can be influenced by controlling these parameters on both droplets. Surfactants commonly decrease the surface tension of solutions. Thus, the presence of proteins in the sample droplet decreases ΔP_tot and the induced flow rate. This decrease in ΔP_tot and flow rate however can be compensated by decreasing the surface tension in the reservoir droplet. Conversely, the presence of surfactants in the reservoir droplet increases the total pressure difference and induced flow rate. Accordingly, the influence of the surface tension on the flow rates is expected to be significant with biological samples. Albumin concentration in human serum samples can vary between 34 mg/mL and 54 mg/mL. The normal range of total protein concentration in blood is between 60 and 83 mg/mL. 60 mg/mL bovine serum albumin (BSA) in water decreases the surface tension from 72 dyne/cm to 60 dyne/cm.^{22, 23}

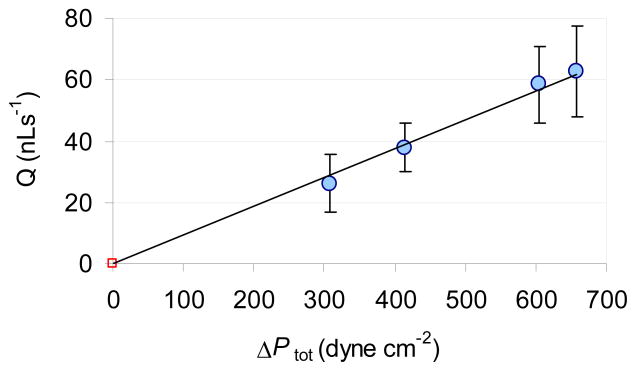
In passive pump driven system the pressure difference and flow rate are also affected by the radiuses (volumes) of the sample and reservoir droplets (Eq. 3). With increasing reservoir droplet volume ΔP_tot and the flow rate are increasing in the channel. Experimental conditions providing ΔP_tot pressure differences between 657 and 309 dyne/cm² with 3.3 μL sample droplet volumes are summarized in Table 1.

Table 1.

Effect of surface tension and droplet volume on the total pressure difference between the sample and reservoir wells.

Experiment	Sample		Reservoir
	solution	volume (μL)	solution	volume (μL)	ΔPtot at t0 (dyne/cm2)
A	DI water	3.3	DI water	8.5	415
B	DI water	3.3	BSA†	8.5	657
C	BSA†	3.3	BSA†	8.5	309
D	DI water	3.3	DI water	16	605

^†The BSA concentration was 60 mg/ml

The effect of decreased surface tension in the reservoir droplet on ΔP_tot can be assessed by comparing A and B data sets. The comparison of B and C data sets shows the effect of decreased surface tension in the sample droplet. The influence of the reservoir droplet volume on ΔP_tot can be evaluated by comparing A and D data sets. As shown in Fig. 4, the measured flow rates are proportional to the calculated total pressure differences in Table 1. The ΔP_tot values in the table were calculated with Eqs. 2 to 4. They represent the total pressure differences at the beginning of the passive pumping experiments (t=0). The flow rates induced in experiments A through D are shown in Fig. 4.

Figure 4.

Correlation between the total pressure difference and the induced flow rate. The data points (flow rates in the first 5 s of flow) are plotted with the best fit line Q = m·ΔP_tot The symbols represent the mean values of n=3 parallel measurements performed in the same device. They are plotted with their standard deviation. The ΔP_tot values are from Table 1.

Effect of hydrostatic pressure on the flow rate

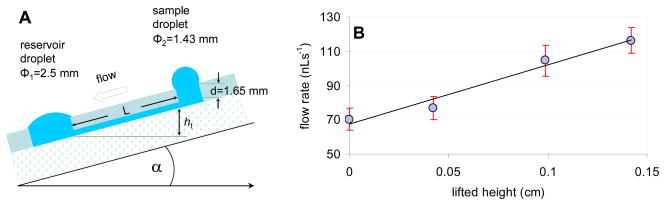
As stated in Equations 2 and 4, the total pressure difference between the sample and reservoir ports of the microchannel is influenced by the hydrostatic pressure difference, which is related to the height difference between the sample and reservoir droplets. The hydrostatic pressure difference can be enhanced by pitching the channel (Fig. 5A). Morier et al.¹⁵ utilized gravity induced flow in micro-fluidic systems in combination with electrochemical detectors. We have found a similar effect by tilting the channel at an angle α. By placing the channel on an incline, the height difference (Δh=h_S−h_R) between the centers of gravity of the sample and reservoir droplets increases with h_t height, which increases the hydrostatic pressure difference with ρgh_t. The tilting angles tested in this work were 2.4, 5.7 and 8.2° with h_t values of 0.4, 1.0 and 1.4 mm, respectively. The correlation between the flow rate in the microchannel and the elevation (h_t) of the sample port is shown in Fig. 5B. As expected, the flow rate in the microchannel increased proportionally to the tilting angles. However, for α > 12°, the shape of the droplets changed (their spherical shape became distorted) and consequently their volumes could not be estimated from the recorded images with enough accuracy.

Figure 5.

Effect of the hydrostatic (gravitational) pressure difference (ΔP_H) on the induced flow rate. A: Schematics of the tilted microchannel with tilting angle α and h_t elevation of the sample port. B: Correlation between the induced flow rate and the elevation height (h_t) of the sample port in a passive pump driven micro-fluidic system. Symbols represent average flow rate values in the first 5 s of the induced flow while error bars represent the standard deviation of the data (n=3).

Passive pump-based FIA system with electrochemical detection

The most essential parts of a conventional FIA system are a pump, a flow channel, a sampling valve and a detector. In passive pump driven micro-fluidic manifolds the surface energy in the sample droplet drives the flow. Consequently, in these systems there is no need for external pump or a sophisticated injection valve. However, a passive pump-based FIA system still needs an adequate detector for recording the sample dispersion in the channel filled with a buffer or reagent solution. To keep the simplicity of the system, we chose planar electrochemical cells for detection during the pumping process. These planar cells were patterned onto glass microscope slides which served as the bottom of the rectangular channel (Figure 1).

To show the performance of the passive pump driven FIA system hexacyanoferrate (II) was used as model compound in combination with an interdigitated array (IDA) type working electrode. First, the micro-fluidic channel was filled with 0.1 mM NaCl/0.1 M NaNO₃ background electrolyte solution. Next, potentials of the IDA electrodes were set to 0.35 V and −0.10 V and the current recording was started. After 30 seconds, 2μL sample solution was loaded on the sample port of the device to induce flow. The sample solution concentrations were between 0.0 M (background) and 10⁻⁵ M of hexacyanoferrate (II). The transient current was recorded until the flow stopped. Between the individual sample injections 2 μL aliquots of background electrolyte (up to 5 times, i.e., a total of 10 μL) were passively pumped across the channel to remove residues of a previous injection. The clearance could be monitored by recording the chronoamperometric current during these washing steps (See supporting information).

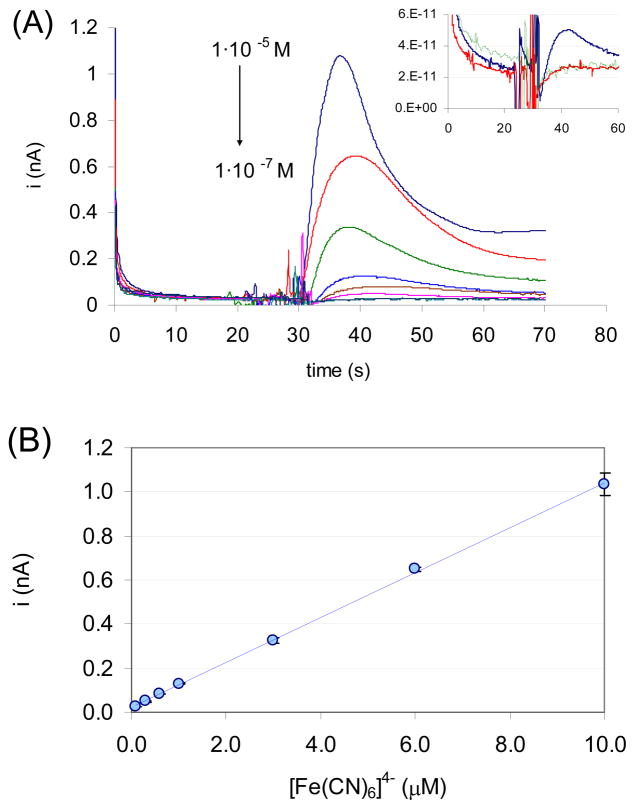
The current-time transients recorded in the passive pump driven FI system are shown in Fig. 6A. Very similar to FIA experiments, the transients are peak shaped representing the sample dispersion during the FI process. However, the interpretation of the transient current is more complicated since the sample flow rate gradually decreases during the process and the amperometric current is a function of flow rate. Once the flow stopped, the sample in the channel is gradually diluted in a diffusion controlled process with the background electrolyte primarily in the reservoir droplet. Nevertheless, the peak heights were proportional to the injected sample concentrations between 3 · 10⁻⁷ M and 1 · 10⁻⁵ M (Fig. 6B)

Figure 6.

Response characteristics of the passive pump driven FIA system. The sample and reservoir port diameters were 1.22 and 2.88 mm, respectively. An interdigitated gold electrode array with 5 μm finger widths and 5 μm separations was used as working electrode. The applied potentials on the two electrodes in the IDA were 0.35 V and −0.1 V vs. the Ag|AgCl reference electrode in the channel. The background electrolyte composition was 0.1 mM NaCl + 0.1M NaNO₃. (A) Current-time transients recorded with the passive pump driven FI system following the introduction of 2 μL hexacyanoferrate (II) solutions of 1·10⁻⁵, 6·10⁻⁶, 3·10⁻⁶, 1·10⁻⁶, 6·10⁻⁷, 3·10⁻⁷, 1·10⁻⁷ M concentrations. The inset shows i-t transients following the injections of the background electrolyte, (green), 1·10⁻⁷ M (red) and 3·10⁻⁷ (blue) hexacyanoferrate (II) solutions. (B) Correlation between the peak currents and the injected sample concentration. The data points represent the mean values of n = 3 parallel measurements performed in the same device. They are plotted with their standard deviations (apparent only at 10⁻⁵ M). R² of the correlation equation was 0.9996.

Similar calibration curves were generated from the current time transients that were recorded with gold microband working electrodes using different concentrations of ascorbic acid solutions as analyte or by pumping ascorbic acid phosphate through a microchannel in which alkaline phosphatase (ALP) enzyme has been immobilized on the gold electrode surface (see supporting information). The peak heights of the recorded transients were proportional to the ascorbic acid concentration pumped through the device or generated in situ on the working electrode surface in the ALP enzyme catalyzed reaction. These preliminary results suggest that the passive pump driven FI system with on board enzyme microsensors may be adequate for the simple analysis of microliter volume samples or for the development of simple electrochemical immunoassays where the label enzyme activity is the analytically relevant information. Analogous, power-free microfluidic immunoassays were reported earlier using capillary pumps in combination with fluorescence-labeled antibodies.^24–26

Similar to FIA, the sample flow rate influences the analyte dispersion in the flow channel and the recorded transient. Consequently, the influence of the solution characteristics on the flow rate in passive pump driven FI experiments is a concern and can limit the fields of application. The detrimental influence of sample viscosities on the induced flow rate can be minimized by diluting the samples with an adequate “masking reagent”. The dilution of the sample with a masking reagent will also reduce the differences in the surface tensions and sample densities of the individual samples. The microfluidic manifold offers possibilities to perform this dilution in situ.

Conclusion

Passive pumps provide low flow rates with good reproducibility by utilizing the surface energy of small droplets. The induced flow rates can be controlled by proper design (dimensions and tilt of the channel) and experimental conditions associated with sample properties such as surface tension, density and viscosity. A passive pump driven micro-fluidic system with electrochemical sensors inside the micro-fluidic channel can be considered as a lab-on-chip flow injection manifold that does not require an external pump or an injector valve. With this extremely simple FIA system a detection limit smaller than 3 · 10⁻⁷ M has been achieved with hexacyanoferrate (II) as analyte (corresponding to the injection of less than 6·10⁻¹³ moles). The utilization of the system for the analysis of microliter volume samples with on board enzyme microsensors or for assessing label enzyme activities in enzyme linked immunoassays are exciting potential applications.