Semi-automated Region of Interest Generation for the Analysis of Optically Recorded Neuronal Activity

Abstract

Bath-applied membrane-permeant Ca²⁺ indicators offer access to network function with single-cell resolution. A barrier to wider and more efficient use of this technique is the difficulty of extracting fluorescence signals from the active constituents of the network under study. Here we present a method for semi-automatic region of interest (ROI) detection that exploits the spatially compact, slowly time-varying character of the somatic signals that these indicators typically produce. First, the image series is differenced to eliminate static and very slowly varying fluorescence values, and then the differenced image series undergoes low-pass filtering in the spatial domain, to eliminate temporally isolated fluctuations in brightness. This processed image series is then thresholded so that pixel regions of fluctuating brightness are set to white, while all other regions are set to black. Binary images are averaged, and then subjected to iterative thresholding to extract ROIs associated with both dim and bright cells. The original image series is then analyzed using the generated ROIs, after which the end-user rejects spurious signals. These methods are applied to respiratory networks in the neonate rat tilted sagittal slab preparation, and to simulations with signal-to-noise ratios ranging between 1.0 – 0.2. Simulations established that algorithm performance degraded gracefully with increasing noise. Because signal extraction is the necessary first step in the analysis of time-varying Ca²⁺ signals, semi-automated ROI detection frees the researcher to focus on the next step: selecting traces of interest from the relatively complete set generated using these methods.

Introduction

Optical recording of neuronal activity has been in use for a generation now, starting with voltage-sensitive dyes (Cohen et al., 1974), Ca²⁺ indicators (Grynkiewicz, Poenie et al. 1985), and more recently genetically encoded fluorescent sensors (Palmer and Tsien, 2006). Perhaps the simplest way to sample network activity using fluorescent indicators is by bath application of membrane-permeant high-affinity Ca²⁺ indicators that change fluorescence amplitude (such as Calcium-Green AM or fluo-4 AM) to a slice preparation (Yuste and Konnerth, 2005), which loads cells at or near the surface of the tissue sample (Funke et al., 2007), whose activity is recorded as a series of images.

With these dyes, changes in fluorescence accompanying changes in intracellular Ca²⁺ ([Ca²⁺]_i) can be detected in the raw image series, and their salience can be enhanced by simple filtering, such as subtraction of the first image from the rest of the images in the series. By these methods, the activity of a large number of neurons can be recorded in parallel (Takahashi et al., 2007), confronting the experimenter with the task of identifying and extracting the signals of interest.

In general, the process of extracting neuronal signals from a series of images showing localized time-varying changes in brightness is done by hand: a region of interest (ROI) is defined on the screen using a tool that allows a user to draw a box or circle around regions of the image where brightness is seen to fluctuate. The disadvantages of this approach are: it is time-consuming; it is difficult to tightly fit the ROI to the area from which optical signal is to be extracted, and it is prone to produce different results depending on who does the analysis.

Manual analysis becomes still more difficult as sampling rate increases via the use of sensitive but noisy electron-multiplier CCDs, and/or binning of CCD elements, which lowers spatial resolution. Thus, increased temporal resolution comes at the cost of reduced image quality, and gives rise to very large image series, rendering the task of manual ROI detection still more difficult.

The problem of automatic generation of ROIs around regions in which Ca²⁺ transients occur has been addressed by others (Ikegaya et al., 2005), but not in detail. The specific problem of fitting ROIs to somatic Ca²⁺ signals is a special case of the more general problem of image change detection (Radke et al., 2005), in which changes in fluorescence as a function of time in an otherwise static image series are targeted. We apply our methods to the activity of medullary networks responsible for respiratory rhythm generation, recorded in vitro from a neonate rat tilted slab preparation (Barnes et al., 2007; Mellen, 2008). This preparation provides access to medullary networks involved in respiratory rhythm generation, as well as phrenic motor output, recorded from ventral roots C1–C4, which serves as the criterion signal for the identification of optically recorded respiratory neurons. The methods we have developed are designed to minimize the likelihood of missing neurons active in the field of view, at the cost of generating false positives, which the user can reject manually.

Methods

Brainstem preparation

In accordance with methods approved by the Institutional Animal Care and Use Committee, neonate Sprague-Dawley rat pups (P0–P4) were anesthetized with isoflurane, and, according to methods described elsewhere (Barnes et al., 2007; Mellen, 2008), the neuraxis was isolated, in chilled aCSF made up of (in mM) 128.0 NaCl, 3.0 KCl, 1.5 CaCl₂, 1.0 MgSO₄, 21.0 NaHCO₃, 0.5 NaH₂PO₄, and 30.0 glucose, equilibrated with 95% O₂-5% CO₂, and a thick sagittal slab was cut (Mellen, 2008), exposing respiratory networks at the surface, with the highest concentration of respiratory neurons ventral, dorsal, and caudal to the facial nucleus (VIIn), and approximately 500 µm caudally in the pre-Bötzinger Complex (preBötC). The preparation was then incubated for 2 hours in an aerated solution containing the high affinity cell-permeant Ca²⁺ indicator fluo-4 AM (50 µg, K_d= 350 nM; Invitrogen), or the lower affinity fluo-8L (50 µg, K_d= 1.86 µM, ABD Bioquest), solubilized in 25 µL of the surfactant pluronic F-127 (2g/10 ml DMSO; Invitrogen), and diluted in 750 µL aCSF for a final concentration of 60 µM. The preparation, stabilized on a Sylgard block was then transferred to the recording chamber (JG 23 W/HP, Warner Instruments, Hamden CT), mounted on an upright microscope (Axioskop 2, Zeiss instruments), which in turn was mounted on a digital translation stage (MT-2000, Sutter Instruments, Novato CA). The preparation was perfused at 4 ml/min with aCSF warmed to 27° C and aerated with a 95%-5% O₂-CO₂ gas mixture. Synaptic blockade was obtained by perfusing the preparation with the AMPA receptor blocker 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX; 20 µM), the NMDA receptor blocker 2-amino-5-phosphopentanoic acid (APV; 20 µM), the GABA_A receptor blocker bicucculine (10 µM), and the glycine receptor blocker strychnine (1 µM).

Data acquisition

Respiratory activity was recorded extracellularly from ventral root C2 at 1 kHz, and optical signals, visualized using an upright microscope (Axioskop 2 FS, Carl Zeiss AG, Oberkochen, DE) through 10X or 20X water-immersion lenses (Achroplan 20x/0.5W/0; Achroplan 10x/0.3 W Ph1, Carl Zeiss AG, Oberkochen, DE), illuminated using a xenon arc lamp (Lambda DG-4, Sutter Instruments, Novato CA) and filtered (480 nm excitation / 505 nm long-pass dichroic mirror / 535 emission; Chroma Technology Corp., Rockingham VT). Images were recorded using an electron- multiplier CCD camera (EM-CCD 9100-13, Hamamatsu Corp, Bridgewater NJ) in a 826 × 826 µm (10 X) or 413 × 413 µm (20 X) area, with pixel sizes of 1.6 µm (10 X and 20 X with 2 × 2 binning) or 0.8 µm (20 X, 1 × 1 binning). At these spatial resolutions, pixels/soma were roughly 160 (20X, 1×1) and 40 (20X, 2×2 or 10X, 1×1). The camera was operated in normal and electron multiplier mode. In normal mode, noise was minimized due to very low dark current and noise read-out (0.69 MHz pixel clock, 8 electron readout noise), and long integration times, and spatial resolution was maximized (1 × 1 binning) at the cost of a low sampling rate (3 Hz). In electron multiplier mode, speed was maximized (30 Hz), at the cost of spatial resolution (2 × 2 binning), higher noise read-out (11 MHz pixel clock, 25 electron readout noise), and excess noise due to noise associated with the multiplication register (see http://sales.hamamatsu.com/assets/pdf/hpspdf/e_imagemtec.pdf for details). These two modes of operation are referred to henceforth as low-noise, and high-noise. Images were captured using a frame grabber (Active Silicon PHX-D48CL, Chelmsford MA), and written to hard drive using image acquisition software developed in LabView (National Instruments, Austin TX) as a directory of tag image files (TIF). Motor output was digitized at 1 kHz and written to disk using an A/D board (PCI-MIO-16XE-10, National Instruments, Austin TX). To ensure accurate synchronization of voltage and optical recordings, the 1 kHz voltage acquisition time-base was used to trigger image acquisition, so that an image was acquired with every nth voltage sample, to obtain image sampling rates of 3–30 Hz.

ROI generation

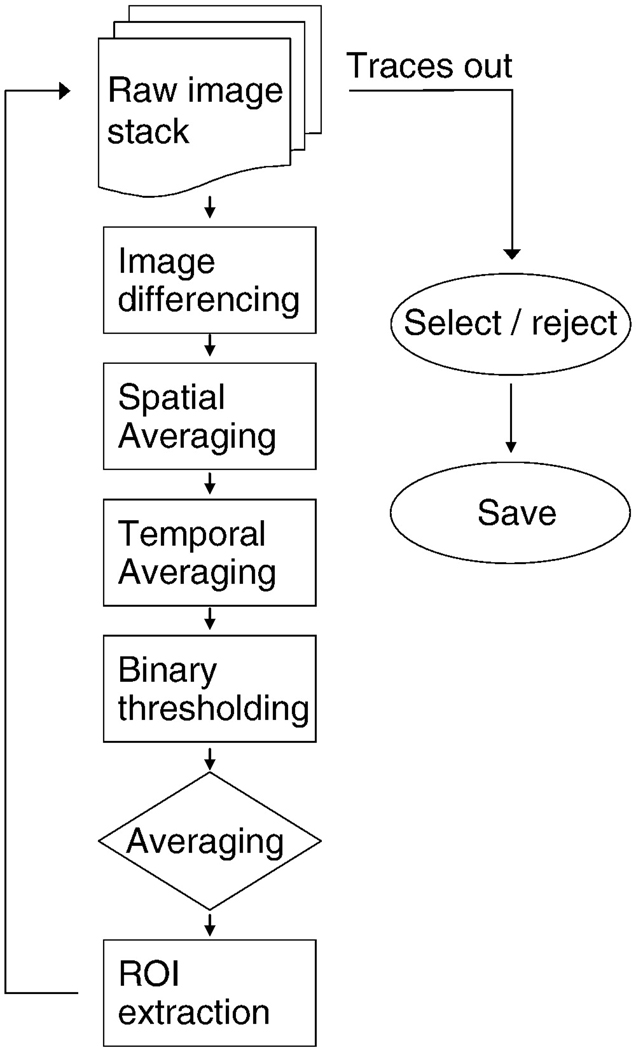
All data were analyzed on a generic personal computer equipped with a 2.4 GHz single core processor and 4 GB RAM running Microsoft Windows XP (SP2), using an application developed in LabView (National Instruments, Austin TX). While we were able to take advantage of the image-processing subroutines included in this development package, all these subroutines reduce to matrix manipulations, and thus could straight-forwardly be implemented in development environments such as MatLab (MathWorks Inc., Novi MI). Implementing these routines in the widely-used Java-based image processing environment Image-J would be complicated by memory use limitations for Java-based applications running in a 32-bit Windows environment. In our experience, large image series are difficult to work with using Image-J because of these memory limitations. An overview of the processing steps that follow is shown in figure 1.

Figure 1.

Image processing sequence for ROI extraction. Boxes indicate processing steps applied to single images, the rhombus indicates processing carried out on the image stack generated by the earlier processing steps, and ovals indicate operations on traces. At the end of the ROI extraction process, mean luminance values associated with each ROI are measured from every raw image. These traces are then screened by the end-user, and good traces are saved.

Qualitatively, the methods we have developed minimize background fluorescence, and apply both spatial and temporal averaging to enhance the salience of somatic Ca²⁺ transients, while minimizing other sources of variation in pixel values. These filtering steps are used to automatically extract ROIs; once the ROIs are generated, the ROIs are used to extract luminance changes in the raw image series associated with those regions.

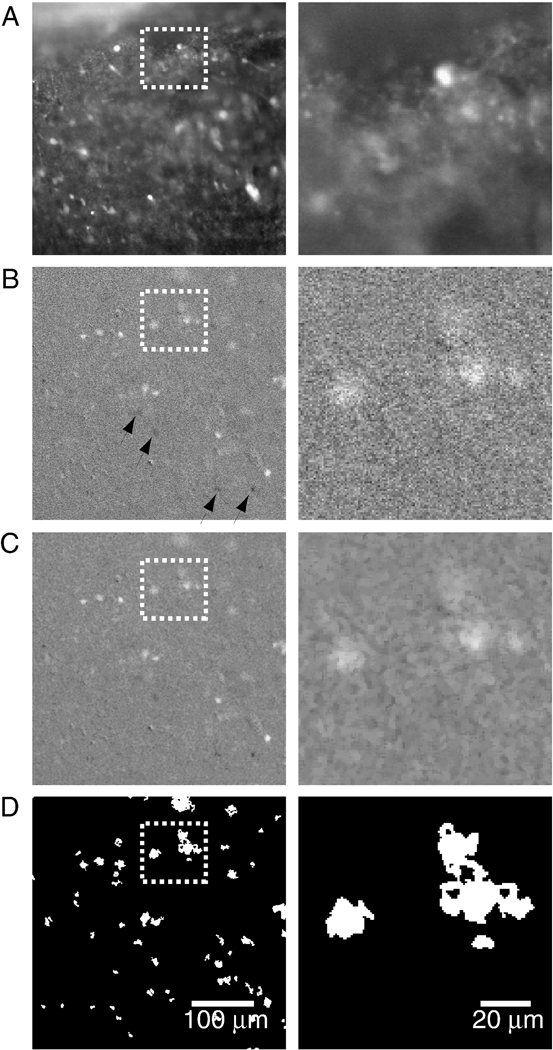
To eliminate static or slow variation in pixel values over each image, for every image in the series, we subtract the target image A_j (Figure 2 A) from an image obtained at a lag T (the subtracted image); the result of this filtering is denoted as the differenced image D_j in what follows.

$${\mathrm{D}}_{\mathrm{j}}={\mathrm{A}}_{\mathrm{j}}-{\mathrm{A}}_{\mathrm{j}-\mathrm{T}}$$

Figure 2.

Temporospatial image-processing enhances salience of Ca²⁺ transients associated with neuronal activity. A. Raw image shows the wide dynamic range of static fluorescence signals that complicates detection of small amplitude Ca²⁺ transients. Boxed region is expanded on the right to highlight image changes accompanying filtering steps. B. “Derivative” image obtained by subtracting the target image (low-pass filtered using a 0.5 s moving average) from the image obtained 1.5 s earlier (low-pass filtered using a 1.0 s moving average). In this image, fluorescence changes during Ca²⁺ influx are more salient, pixels within bright regions are still quite variable, with active regions showing up as going towards white (during Ca²⁺ influx) or towards black after return to baseline (arrows). C. Spatial averaging homogenizes pixel values within regions of cellular activity, as well as in quiescent regions. D. Binary thresholding sets regions of static fluorescence to black, and regions of dynamic fluorescence to white.

To preserve the relatively slow Ca²⁺ transients in the differenced image, the lag between target and subtracted image should be greater than the indicator’s peak-to-baseline time-course (for a high-affinity indicator like fluo-4, > 1 s), so as to minimize the likelihood that the subtracted and the target frames contain a signal generated by the same event. It should be stressed that if the interval between target and subtracted image is too short, signal detection is impacted; but not if the interval is too long, since in general, fluorescence signals separated by longer delays will be unrelated. Thus the lag between target and subtracted frame used here (1.5 s), which was chosen for fluo-4, worked well for the lower affinity indicator fluo-8L, which has a faster signal roll-off.

In the resulting differenced image, slowly changing and static fluorescence signals are eliminated, and faster pixel values fluctuations are accentuated. These faster pixel fluctuations in part also reflect shot noise, which leads to pixel value fluctuations uncorrelated image-to-image. We strongly attenuate these by taking a 0.5 s moving average of the target image prior to differencing. In addition, the subtracted image undergoes a 1 s moving average low-pass filtering, which is intended to mitigate not only shot noise, but also to reduce the signal related to intracellular Ca²⁺ dynamics, since the goal is to enhance the Ca²⁺-related fluorescence fluctuations in the target. If the low-pass filtering of target and subtracted image were identical then the differenced image would give equal weight to the target and subtracted image Ca²⁺ transients. By applying a larger smoothing window to the subtracted image, the physiologically relevant Ca²⁺ transients in the target are given greater salience by attenuation of the subtracted image’s Ca²⁺ transients, so that only the slowly varying and static fluorescence values in the target image are removed. The size of the moving average window must be adjusted to the Ca²⁺ signal roll-off of the indicator being used, with smaller moving average windows selected for lower affinity indicators. It should be noted that all these filtering approaches are subject to edge effects, since images at the beginning and the end of the series cannot be processed in the same way as images in the middle of the series. Thus at the edges of the image series, the lag between target and subtracted image increase (decrease) from 0 (n) to n (0), where n represents the number of images spanned by the lag between target and subtracted images. A similar increase / decrease of the moving average window size is also implemented. Finally, a simple unweighted moving average window is used here, which has no effect on signal phase; better results may be obtainable using other low-pass filtering approaches. Because all of these filtering steps serve the purpose of generating ROIs, which are then applied to the raw image series, any phase-shifts caused by the filter used to generate the ROIs is without importance.

In the resulting differenced image series, all areas of the image where fluorescence values are constant or slowly changing have near zero intensity values (grey), In regions of changing fluorescence, pixel values are high (going towards white) during Ca²⁺ influx; and then take on negative values (going towards black) thereafter (Figure 2 B).

In much the same way that Ca²⁺ signals of interest can be distinguished from both slower and faster components of the optical signal in the time domain, they can also be distinguished spatially: neuronal activity gives rise to elevated [Ca²⁺]_i throughout the soma, thus, signals of interest occur over contiguous pixels, whereas changes in pixel values due to noise will be spatially uncorrelated. For the purpose of facilitating ROI detection therefore, spatial low-pass filtering is applied to the differenced image series, with the goal of accentuating regions where contiguous pixels are either near-white or near-black, while attenuating isolated pixels whose values are far from the image mean. To this end, pixel values are recalculated based on the values of neighboring pixels, using a square pixel kernel (K_ij) of sizes 3×3, 5×5 and 7×7, centered on the pixel of interest (Px_ij). The basic operations used are erosion (E), which sets a given pixel’s value to the minimum value of its neighbors; and dilation (D), which sets a given pixel’s value to maximum of its neighbors. These simple operations are combined in opening (O) and closing (C) functions, which consists of erosion followed by dilation, and dilation followed by erosion, respectively.

$$\begin{array}{c}\mathrm{E}({\text{Px}}_{\text{ij}})=\text{min}({\mathrm{K}}_{\text{ij}})\hfill \\ \mathrm{D}({\text{Px}}_{\text{ij}})=\text{max}({\mathrm{K}}_{\text{ij}})\hfill \\ \mathrm{O}({\text{Px}}_{\text{ij}})=\mathrm{\text{D}}(\mathrm{\text{E}}({\text{Px}}_{\text{ij}}))\hfill \\ \mathrm{C}({\text{Px}}_{\text{ij}})=\mathrm{E}(\mathrm{D}({\text{Px}}_{\text{ij}}))\hfill \end{array}$$

Opening does not significantly alter the morphology of shapes spanning many pixels, since bright borders reduced by erosion are restored by dilation, but isolated pixels far from the mean that are set to the mean by erosion do not reappear after the dilation, thus O eliminates isolated bright pixels. By similar logic, closing eliminates dark pixels. Here, spatial averaging is achieved using the proper opening (POPEN) function, which consists of a series of openings and closings, in which for a given image, each pixel is set to the lesser of either the pixel value of the unfiltered image, or the value of that same pixel after having undergone sequential opening, closing, and opening:

$$\text{proper}-\text{opening}({\text{Px}}_{\text{ij}})=\text{min}({\text{Px}}_{\text{ij}},\text{OCO}({\text{Px}}_{\text{ij}}))$$

or

$$\text{proper}-\text{opening}({\text{Px}}_{\text{ij}})=\text{min}({\text{Px}}_{\text{ij}},\text{DEEDDE}({\text{Px}}_{\text{ij}}))$$

In the resulting image, active regions can clearly be distinguished from background (Figure 2C).

After having undergone a differencing, as well as spatial and temporal low-pass filtering, each image is transformed from a gray-scale image to a binary (B) image by setting pixels with values close to the mean to black (−255), and values far from the mean to white (255), using an ad hoc threshold of 1.3 times the image’s standard deviation (Figure 2 D):

$$\begin{array}{cc}\mathrm{B}({\text{Px}}_{\text{ij}})\hfill & =255\text{if}\text{abs}({\text{Px}}_{\text{ij}})>\text{Avg}(\text{Px})+{1.3}^{*}\text{SD}(\text{Px})\hfill \\ \hfill & =-255\text{otherwise}\hfill \end{array}$$

This black-and-white image again undergoes low-pass POPEN spatial filtering, which preserves grouped white pixels associated with neuronal activity, but eliminates isolated white pixels.

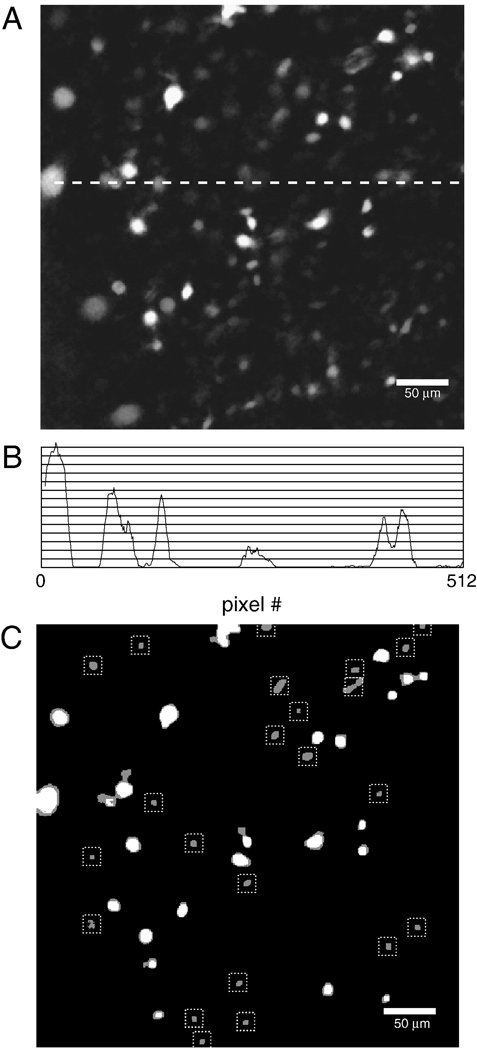
When all the binary images obtained in this manner are averaged pixel-by pixel, a gray-scale image is generated in which inactive regions are black, weak and/or infrequent Ca²⁺ transients show up as close to black, while strong and/or frequent Ca²⁺ transients show up as near to white (Figure 3 A). Because regions of interest are generated from a simplified, black and white version of this grey scale image, the grey scale image must be thresholded. The problem is that a threshold set high enough to identify two bright cells close together (as in the upper right-hand corner of Figure 3 A) would miss dimmer cells; conversely, a threshold set low enough to detect dim cells (as in the top left corner of Figure 3 A) would merge bright cells close together. Thus, for an image series containing both bright and dim cells no single threshold will work. This problem is apparent when the luminance profile of one row of pixels in this image is examined (Figure 3 B).

Figure 3.

Average of binary image series undergoes successive thresholding to identify ROIs. A. In the average of the binary images, regions of intense and/or regular neuronal activity are near-white, while regions of weak and/or intermittent activity are near-black. B. Intensity profile of a row of pixels indicated by dotted line in A. Using the methods described here, an ROI will be generated for points where a lower threshold intersects a peak in the intensity profile, but where the threshold above it does not. C. Superimposed binary images generated by a low threshold (grey blobs) and the threshold above it (white blobs). Only blobs retained using the lower threshold, but missed by the upper threshold are stored as ROIs (dotted boxes).

In order to pick out all peaks, the averaged image is thresholded sequentially. The lowest threshold used is set at the bottom 5% of the dynamic range of the averaged binary images, and the highest is just above the brightest pixel value in that image, and 5–80 thresholds are used. Images generated by neighboring pairs of thresholds are compared, starting from the lowest two, and ending with the highest two. For each image, all pixels below threshold are set to black, and all pixels above threshold are set to white. Using subroutines provided as part of the development environment used here (LabView IMAQ; National Instruments, Austin TX) each convex, bounded, hole-free white region -- referred to henceforth as a blob (Lindeberg, 1994) -- is detected, and a descriptor containing the perimeter and location of each blob is generated and stored to an array for subsequent comparison.

With each pair of thresholds, there are the same or fewer blobs in the binary image obtained with the higher threshold than in the one obtained with the lower threshold (Figure 3 B). The strategy is to retain blobs that are captured by the lower threshold, but missed by the upper threshold in each pair-wise comparison of thresholds. These blobs are identified by mapping the center of mass of blobs identified using the upper threshold onto the perimeter of blobs identified using the lower threshold.

By only retaining lower threshold blobs whose perimeter does not encompass the center of mass of a higher threshold blob, luminance peaks are identified (Figure 3 C). The descriptors associated with these lower threshold blobs are converted to ROIs, that is to say, into an array of masks, which when applied to an image set pixel values outside of the mask to zero, allowing for sampling of pixel values in a circumscribed portion of the image.

Signal Extraction and storage

Once candidate ROIs have been generated, they are applied to the raw image series: mean luminance values of pixels within each ROI are measured in every image in the image stack. Because optical signals generated by the Ca²⁺ indicator used here do not provide estimates of [Ca²⁺]_i in absolute terms, we focus our analysis on peak times rather than peak amplitudes, treating our signals in much the same way as extracellular recordings are treated. To facilitate peak detection, and to generate reasonably compact figures in which peaks can clearly be detected, traces associated with each ROI are subjected to high-pass filtering as follows: each trace is subjected to a 14 s moving average to eliminate physiologically interesting transients from the signal but retain slow fluctuations in luminance associated with photobleaching. This low-pass filtered signal is then subtracted from the raw signal, to obtain a high-pass filtered version of the signal (Figure 6 C). At higher sampling rates, in which tissue movement and/or arc-lamp flicker contribute to variation in fluorescence (Movie 2, Supplemental Materials), low-pass filtering is achieved by taking a 0.1 s moving average of intensity values.

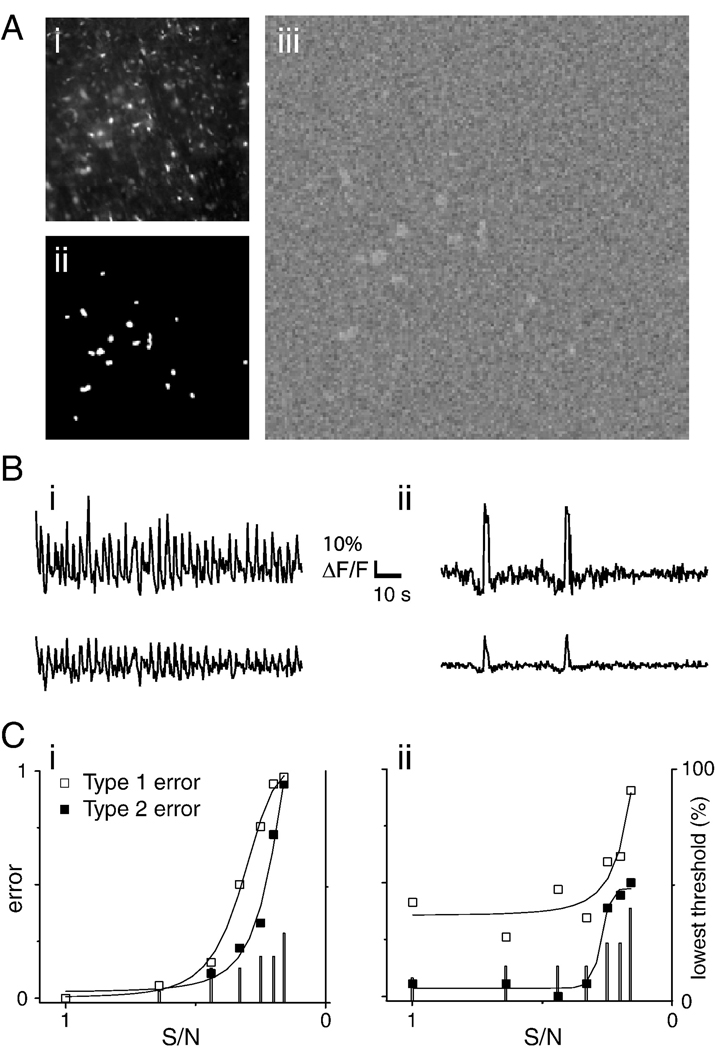
Figure 6.

Simulated data were used to estimate type 1 and type 2 error under conditions of varying noise. A. i. simulated image series were based on a 20X image of indicator- loaded tissue. ii. Regions of time-varying fluorescence retained naturalistic morphology and distribution, as they were defined by thresholding the raw image to generate a binary image. iii. Pixels in black regions of the binary image were assigned random values; pixels in white regions were assigned values representing the sum of a time-varying signal and noise; so as to maintain constant dynamic range, as noise was increased the amplitude of the time-varying signal was decreased. B. Time-varying signals assigned to white regions of the binary image were obtained from fluorescence measurements from a respiration modulated neuron (i) or from simulation of sparse activity generated by splicing two peaks associated with inspiratory activity between epochs of random values scaled to 10% of burst amplitude (ii). Upper traces show traces in which signal and noise components were of equal amplitude (S/N=1); lower traces were obtained at S/N=0.33. Traces were scaled so that ΔF/F bars matched. C. Plot of type 1 (□) and type 2 (■) errors as a function of S/N for rhythmic (i) and sparse (ii) simulated datasets. Type 1 error was calculated as the ratio of ROIs that picked out “cells” to the total number of ROIs generated; type 2 error was calculated as the ratio of identified “cells” to the actual number of “cells” in the simulation. Both errors are minimized as these ratios approach 1; to convey conditions under which both types of error are minimized, (1-ratio) is plotted. As S/N decreased the lowest threshold applied to the summed image was increased so as to reduce type 1 error, and more accurately estimate type 2 error (with sufficiently high ROI numbers, all “cells” will be identified). Lowest thresholds are expressed as percent of the simulated image’s dynamic range (right axis), and are indicated by bars.

To estimate the amplitude of fluorescence changes associated intracellular Ca²⁺ fluxes as a ratio of other sources of fluorescence (ΔF/F), other groups use the first frame of the image series as the estimator of F, and ΔF is calculated as the difference between all subsequent images and the first image (Beltran-Parrazal et al., 2006), thus:

$$\mathrm{\Delta }\mathrm{F}/\mathrm{F}=(\mathrm{F}-{\mathrm{F}}_0)/{\mathrm{F}}_0$$

Consistent with our lagged differencing approach to signal extraction, rather than use the static luminance values of the first frame, we estimate F using the mean of the 14 s moving average (F_slow) calculated for the high-pass filtering described above as our estimator of F, and use the high- or band-passed raw image (F_filtered) as ΔF thus:

$$\mathrm{\Delta }\mathrm{F}/\mathrm{F}={\mathrm{F}}_{\text{filtered}}/{\mathrm{F}}_{\text{slow}}$$

For F_slow constant or stationary, F_slow ≈ F₀. We set the scale bar height to the difference between baseline and the trace maximum, and then divide or multiply that height so that it is scaled to 1% of ΔF/F. In either case, ΔF/F does not allow estimation of [Ca²⁺]_i, but it does provide a way of comparing signal amplitude within and across datasets. In order to assess whether the observed ΔF/F approaches the maximum obtainable with a given indicator, after loading tissue using standard methods, application of aCSF with 15 mM [K+]o can be used to elicit a brief epoch of maximal fluorescence. If maximal fluorescence is associated with low ΔF/F, different loading methods or indicators should be tested.

Simulation

A basic question about this algorithm’s performance that can not be tested using real data is the number of units missed (type 2 error), since the actual number of neurons in the field of view is unknown. To address this question we generated a 300 element image series, containing 18 units whose luminance varied with time.

In order to approximate the spatial distribution and morphology found in actual data, the image series was generated using a single frame from a 20 X dataset, thresholded to generate a binary image in which the brightest regions in the image (typically associated with dead or dying cells no longer able to buffer Ca²⁺) were set to white and all other parts of the image set to black, resulting in 18 white blobs on a black ground (Figure 6 Ai, Aii). A 300 frame image series was then constructed using this binary image. In each image, pixels in black regions of the binary image were assigned random values, scaled to fall within 45% of the image type’s dynamic range (16 bits). In each image, pixels contained within the white blobs were assigned values designed to approximate Ca²⁺ transients. This was done using two 300 element template arrays. The first array contained the signal obtained from a single ROI in an actual dataset, consisting of 33 respiratory cycles, recorded over 100 s at 3 Hz. The second array contained two bursts from the first array, separated by baseline activity, simulated by random pixel values falling within the 15% of the two bursts’ amplitude. These two arrays were used to simulate the signals of a periodically active and sparsely active cell respectively, and each array was scaled so that signal values ranged between −0.5 and 0.5. In each simulation, for each frame in the image series, all pixels within all the white blobs of the binary image were assigned a value as follows:

$${\mathrm{S}}_{\mathrm{i}}(\mathrm{x},\mathrm{y})={\mathrm{s}}_{\mathrm{i}}+\mathrm{\xi }(\mathrm{x},\mathrm{y})$$

Where for frame i in an image series, each pixel (x,y) in the white blobs was assigned a value S_i(x,y), which was the sum of the value s_i obtained from the ith element of the signal array, and a noise term ξ(x,y), obtained from a uniform distribution of random numbers falling between [−0.5,0.5].

In order to vary the signal-to-noise ratio, a term m was incorporated:

$${\mathrm{S}}_{\mathrm{i}}(\mathrm{x},\mathrm{y})=({\mathrm{s}}_{\mathrm{i}}/\mathrm{m})+(\mathrm{\xi }{(\mathrm{x},\mathrm{y})}^{*}\mathrm{m})$$

where m varied between 1 and 2.5 in increments of 0.25. By dividing the signal term and multiplying the noise term by the same variable m, the signal to noise ratio (S/N) was reduced, but the dynamic range of S_i(x,y) was kept constant. So as to match the dynamic range of pixel values assigned to the white blobs to pixel values assigned to the black ground, values within the white blobs were values were then scaled so that they also fell within 45% of the image type’s dynamic range (16 bits).

For each simulation, the signal-to-noise ratio for each value of m was estimated by the ratio:

$$S/N=\frac{\text{max}(s_i)/m}{\text{max}(\mathrm{\xi })\times m}\approx 1/m^2$$

Thus, for the values of m used here, S/N varied between 1 and 0.16.

Algorithm performance at varying levels of noise was quantified by measuring type 1 (false positive) and type 2 (false negative) errors. Type 1 error was estimated by taking the ratio of ROIs that picked out “cells” to the total number of ROIs generated; type 2 error was estimated by taking the ratio of identified “cells” to the actual number of “cells” in the simulation. Curves were fitted to these data using the “sigmoid fit” function within Origin (OriginLab Corp., Northampton MA).

An executable version of this software can be obtained by contacting the Corresponding Author.

Results

The software was tested using a low-noise, high-spatial resolution dataset acquired at 3 fps, and then on a series of low-spatial resolution, noisy datasets obtained at 30 fps.

In the first case, we analyzed: 90 s of activity, acquired at 3 fps at 200× magnification (Movie 1, Supplemental Materials), from the caudal pole of the facial nucleus (VIIn) (Figure 4 B, inset). This first dataset was used to determine the sensitivity of ROI detection to analysis parameters. We varied the size of the spatial averaging kernel (3×3, 5×5, and 7×7), and for each kernel size, we varied the number of thresholding steps (5, 10, 20, 40, and 80 steps). We found the highest number of respiratory neurons using 80 threshold steps and a 3×3 kernel, resulting in 58 ROIs. Although the number of respiratory neurons identified in this dataset increased with the number of thresholds, nearly 50% of the respiratory neurons identified with 80 thresholds were found using 5 thresholds (Figure 4 A left). Further, as the number of thresholds increased, the ratio of ROIs associated with respiration-modulated signals to ROIs arising from extraneous signals decreased steeply (Figure 4 A right). Cell-permeant AM ester dyes load not only neurons of interest, but also other neurons and glia, which were correctly identified by the algorithm. Thus, this graph over-estimates type 1 error associated with the signal processing methods described here.

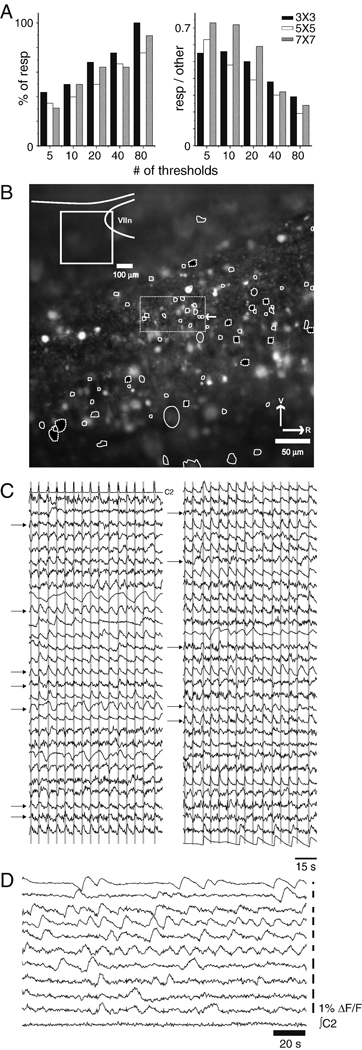
Figure 4.

Using 80 thresholds, 58 ROIs are identified in a high spatial resolution low-noise, slow optical recording data series. A. As the number of thresholds increases, the number of ROIs associated with respiration-modulated activity goes up (left); conversely, the ratio of respiration modulated ROIs to false positives decreases as the number of thresholds increases. B. View of the tissue, with ROIs under control (white outlines) and synaptic blockade (black fill, dotted white outlines) conditions, and location of recording (inset; VIIn: facial nucleus). C. Traces of respiration-modulated activity obtained from the ROIs shown in A; top left trace is rectified integrated motor output (C1). Gray bars indicate inspiratory activity; neurons active at a variety of phases, and both strongly and weakly respiration-modulated are included. Because of space constraints ΔF/F scale bars have been omitted. Traces contained in dotted rectangle in the center of B are indicated by arrows; although all these traces share respiratory modulation, they are sufficiently different to suggest that they are generated by separate units. D. Traces of spontaneous activity recorded under conditions of synaptic blockade. Under these conditions, neurons active once in 180 s, and neurons active at frequencies higher than control respiratory frequencies were observed.

Execution time is strongly dependent on threshold number, ranging from 238±15 s for 5 threshold steps, to 778 ± 79 s for 80 threshold steps, and as the number of false positives increases, the time taken by the end-user to select traces to be saved increases as well. Choice of binning also impacted software performance: although the largest number of ROIs were detected with 3×3 binning, the number of respiratory neurons identified using 7×7 binning closely matched those identified using the more sensitive 3×3 binning (figure 4 A), and the number of false positives was lower with 7×7 binning at all threshold levels.

Taken together, these findings suggest that this algorithm’s performance is relatively insensitive to choice of kernel, but more sensitive to the number of thresholds used. The lack of sensitivity to choice of kernel may be due to the magnification used here. Certainly, as the number of pixels spanning a soma increases, the size of the smoothing kernel would need to be increased. For magnifications of 65× or greater, the usefulness of the methods described here will likely decrease, as the field of view will only contain a handful of cells, obviating the need for automated ROI detection.

The recording was made at the caudal pole of the facial nucleus (Figure 4 B inset). Traces reveal respiratory modulation at a variety of phases (Figure 4 C). The high threshold number used to generate these traces allows resolution of units close to one another; traces generated by the tightly clustered ROIs contained in the dotted rectangle at the center of 4 B are indicated by arrows. Because these traces all differ slightly from one another, we present them here as separate units, but cannot rule out that some of the traces are generated by a common unit. Using fewer thresholds or changing the spatial averaging would likely lead to fewer ROIs, raising the probability of type 2 error.

To establish that these methods can detect a cell even if it is intermittently active or active only once in a recording epoch, ROIs obtained from the same network under conditions of synaptic blockade are shown (Figure 4 F; black-filled, dotted white ROI outlines Figure 4 B). Thus, while the behavior under study here generates periodic optical signals, these methods are not restricted to rhythmically active networks.

To test whether these methods remain viable as image quality degrades, we applied them to four image series obtained at 30 frames per second for 500 seconds with lower spatial resolution due to 2×2 binning, with a less favorable signal-to-noise ratio due to electron multiplication, and with a lower-affinity indicator (fluo-8L, K_d= 1.86 µm). These datasets of 15,000 images were processed with 3×3 binning, using 40 thresholds, and generating traces in 2 hours and 13 minutes ± 8 minutes.

In Figure 5 A, one of the datasets, and the ROIs associated with 13 respiration-modulated cells are shown. Of the 13 good traces, 2 ROIs are most likely from a single unit (Figure 5 A arrow); this is supported by the close match between the associated traces (Figure 5 B, arrows). It is worth noting that the ROI traces do not match perfectly (Figure 5 B, boxes). As with the earlier dataset, respiration-modulated ROIs constitute roughly 10% of the total number of ROIs detected (figure 5 A inset panel). To facilitate detection of respiratory modulation, the traces shown in Figure 5 B have been filtered. The top trace in Figure 5 C shows a portion of one optical trace (dotted box, Figure 5 B, second optical trace from the bottom) raw (Figure 5 C top), high-pass filtered (Figure 5 C middle) and band-pass filtered (Figure 5 C bottom). Because changes in Ca²⁺ indicator intensity is relatively slow (due to the relatively high Ca²⁺ affinity of the dyes used here), high-frequency luminance fluctuations are likely due to arc-lamp flicker (See Movie Clip 2, Supplemental Materials), and are attenuated here using low-pass filtering. The superimposed high-pass and band-pass filtered traces of one inspiratory burst (dotted box, Figure 5 C right) reveals close correspondence in peak times (Figure 5 C left). Because arc-lamp jitter will be the same across the image, it can likely be corrected using deconvolution techniques, obviating the need for low-pass filtering.

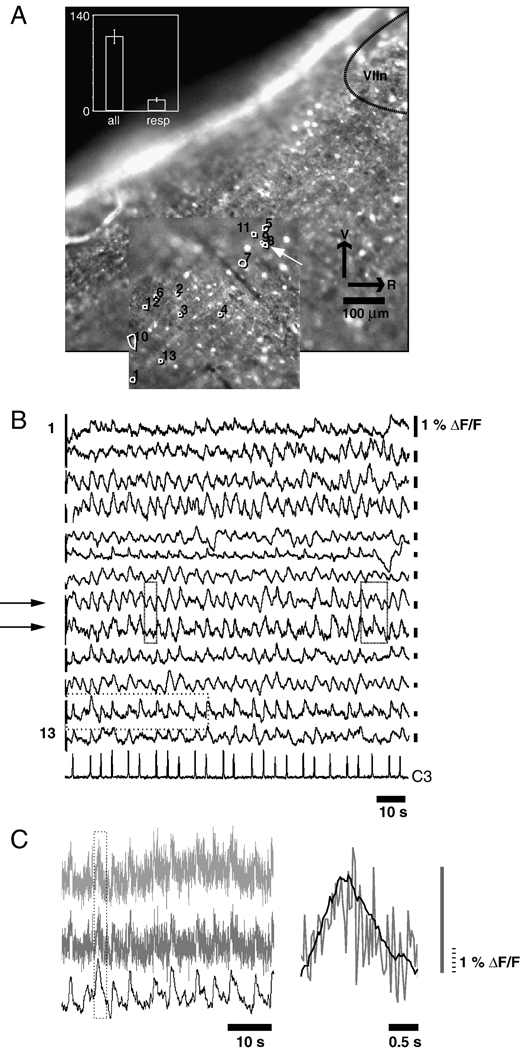
Figure 5.

ROIs can be generated using noisy, low spatial resolution datasets. A. anatomical location of recording overlaps with the preBötC, which has been identified as lying 500 µm caudal to the VIIn (Ruangkittisakul et al., 2005). Two juxtaposed ROIs are likely generated by the same cell (arrow). In the 4 datasets analyzed, the number of respiration modulated ROI traces remained at approximately 10% of the total number of ROIs identified (inset). B. Traces sorted to match ROI numbering reveal closely matched activity in 2 adjacent ROIs (arrows), suggesting that one cell has been misidentified as 2. Despite the fact that traces 8 and 9 are likely generated from the same cell, the two traces do not match exactly (boxes). C. Effects of high- and band-pass filtering on the optical recording from one ROI (dotted box, 2^nd optical trace from the bottom, Figure 5 B). Top trace: the raw optical signal, obtained by calculating the mean of pixels within the ROI for each frame in the data series. High-pass filtering (via subtraction of the trace low-pass filtered using a 14 s moving average) eliminates slow time-course fluorescence fluctuations (middle trace); subsequent low-pass filtering (by taking a 0.6 s moving average of the signal) gives rise to a band-pass fitered signal in which high-frequency fluctuations in brightness associated with arc-lamp jitter is attenuated (bottom trace), but in which the underlying Ca²⁺ signal is retained. The effect of low-pass filtering on one Ca²⁺ peak associated with an inspiratory burst (dotted box, left) is shown on an expanded time-scale (right panel).

Simulated datasets were generated based on a 20X image of Ca²⁺-loaded tissue (Figure 6 Ai) converted to a binary image (Figure 6 Aii), which was used to generate image series with transient noisy luminance fluctuations (Figure 6 Aiii). Luminance fluctuations were obtained from an actual optical recording of an inspiratory neuron to which increasing levels of noise were added in successive simulations (rhythmic activity, Figure 6 Bi). In order to simulate an optical recording from a sparsely active neuron, two peaks from the first dataset were incorporated into a dataset which otherwise contained noisy baseline activity with increasing amounts of noise (sparse activity; Figure 6 Bii).

The signal to noise ratios were varied between 1.0 and 0.16. With the exception of the low threshold cut-off used on the summed image, ROIs for all simulated datasets were generated using the same parameters: spatial averaging was carried out with 7×7 binning, temporal averaging was applied over 2 images, and 40 thresholds were used. As noise levels increased, when we held the minimum threshold at 5% of the summed image’s luminance range, the number of false positives increased steeply. As the number of false positives increased, it became ambiguous whether correct identification of “cells” was due to the algorithm, or was occurring by chance. To clarify this issue, the minimum threshold was increased from 5% up to 30% of the summed image’s luminance (bar graphs, Figure 6 C). By this means, false positives were kept as low as possible; at lowest S/N large numbers of false positives could not be prevented however.

In the simulation of rhythmic activity, although type 2 error stayed low for S/N values ranging from 1.0 – 0.33, at S/N=0.33, type 1 error showed a sharp increase (Figure 6 Ci). At S/N=0.25 (Movie Clip 3, Supplemental Materials), 12/18 of simulated cells were identified, but the number of false positives increased steeply. At lower S/N algorithm performance fell off, effectively defining the lower bound on signals analyzable with these methods. These simulations suggest that that these methods are robust over a range of S/N values, but that as noise increases past a certain point, performance deteriorates sharply. A comparison of movies from actual optical recordings (Movie Clip 1 and Movie Clip 2, Supplemental Materials) and the movie of the simulated data reveals that most of the units discernible in the real data are brighter than those in the simulation. Although algorithm performance on sparse data was qualitatively similar, type 2 error increased at lower noise levels, but then leveled off (Figure 6 Cii). This discrepancy may be due to the fact that the two bursts in the sparse dataset both reached the maximum amplitude (0.5), whereas in the rhythmic simulation, only one of the peaks reached this amplitude, while the other 32 peaks were smaller. Because of how differenced images were thresholded to generate binary images, this amplitude difference could account for why type 2 error was lower in the sparse simulation than in the rhythmic simulation at low S/N.

Discussion

We describe here methods for automated detection of cellular activity in neural tissue loaded with membrane-permeable Ca²⁺ indicators. The premise of this approach is that it is easier and quicker for the experimenter to identify a cell of interest from a plot of fluorescence variation as a function of time, than from the time-varying fluorescence itself apparent in the raw or high-pass filtered play-back of a series of images acquired by a CCD camera.

In extracting neuronal signals from an image series, there are two possible sources of error: false positives (type 1 error), and false negatives (type 2 error). Minimizing these two kinds of error is achieved by proper selection of the number of thresholds, which can be identified iteratively by comparing the results from successively larger number of thresholds.

Multiple thresholds are used to pick out local luminance maxima in the summed image, associated with fluorescence emitted by cells in the tissue recorded from. With too few thresholds, cells close together will be contained in a single ROI (type 2 error), since the luminance trough separating them will be missed. With too many thresholds, a single cell will generate multiple ROIs (type 1 error), because of small differences in brightness within the region spanning the cell’s soma in the summed image. Another important parameter is the value of the lowest threshold: if the lowest threshold is set too high, dim cells will be missed (type 2 error); if it is set too low, ROIs will be assigned to local maxima generated by noise (type 1 error).

Selection of proper threshold number should be arrived at iteratively. In our experience, for a given magnification and indicator, there is typically a range of thresholds over which the number of ROIs generated are similar. In our use of these methods, this is the signal-processing parameterization we look for in analyzing data, since it defines filtering and thresholding values that fit the data. As S/N deteriorates, the number of ROIs identified becomes increasingly sensitive to parameterization; in our simulations at low S/N, slight changes in minimal threshold or number of thresholds generated dramatic changes in ROI numbers, because there were no well-formed peaks in the luminance landscape for the algorithm to pick out.

With membrane permeant indicators such as those used here, neurons of interest are loaded, but so are neurons involved in behaviors other than those under study, as are glia. Signals from these sources will also generate ROIs and thus will give rise to false positives that must be excluded using criteria that depend on the behavior or the question under study. This problem presents itself irrespective of how ROIs are generated. In the context of the system under study here, identification of respiratory neurons can be done by inspection, but is facilitated by online calculation of a burst-triggered average, using inspiratory drive recorded from the phrenic nerve as the reference signal. Our operating assumption is that the rapid Ca²⁺ influx accompanying action potentials is not seen in glia, thus we exclude signals that are slowly-varying and smooth, on suspicion that these signals are glial in origin. In addition, cells whose Ca²⁺ signals show marked increases in amplitude are also excluded, as this likely reflects intracellular Ca²⁺ homeostasis failure.

Because of how candidate ROIs are generated, the methods described here will degrade as the number of frames in the image series decreases, since as binary images are averaged noise is attenuated; conversely, a cell that is active only once will be less and less likely to generate an ROI as the recording epoch lengthens, since its activity will fade from the averaged image. Practically speaking, these limitations are not insurmountable. In the first instance, generically, as sample number decreases, the ability to distinguish between signal and noise decreases, thus regardless of how one analyses the data this problem arises and can be solved by acquiring more samples; in the second instance, our methods identified a cell active once in 180 s (Figure 4 F), thus only cells with very low levels of activity are likely to be missed.

A key component of our method is spatial averaging. Our exploration of kernel size suggests that on one hand, the cost of choosing a kernel that is too small is an increase in type 1 error, and in conjunction with too many thresholds, the generation of multiple ROIs for a given soma. On the other hand, too much spatial averaging leads to type 2 error. Thus, for the data acquired with 2×2 binning resolution, only the 3×3 kernel captured all regions where somatic signal could be seen. For these data, if one compares pixels/kernel (9) to pixels/soma (~40), this suggests that kernel area should not greatly exceed 0.25 of soma area. In image series acquired at higher spatial resolution (1×1 binning, 20X), results were less sensitive to smoothing kernel size: in these data, the program identified very close to the same number of ROIs at 7×7 binning as with 3×3 binning. Under these conditions, pixels/kernel=49, and pixels/soma ≈ 160, resulting in a ratio of kernel area/soma area of 0.3. Thus at pixels/soma values different than those studied here, a kernel whose area is 0.2–0.3 of the area of a typical soma is a good initial choice. A modification to this algorithm that may save computation time without impacting performance would be to spatiotemporally bin images according to signal time-course and ROI size. After ROI selection, the image series can be reanalyzed at full spatiotemporal resolution.

By applying these methods to simulated datasets, we were able to show that our methods are relatively robust to type 2 error (false negatives), generating similar results over a range of noise levels; as the S/N ratio fell below 0.4, however performance deteriorated steeply. Nonetheless, the algorithm detected some units at all noise levels. If the lowest threshold applied to the summed image was kept fixed, type 2 error is reduced but at the cost of much higher type 1 error (data not shown); if robust criteria exist for excluding false positives (as is the case for the identification of respiration-modulated neurons), then the algorithm can be applied to data with low S/N. It should be stressed that even at low noise levels, 1/18 units were missed. Although with more careful choice of kernel, number of thresholds, and lowest threshold cut-off, the algorithm will perform perfectly, when working with real data, prior knowledge of the actual number of units in the data is not available, so we chose to test the algorithm’s performance using a reasonable rather than optimal parameter set, since this is closer to normal operating conditions.

These simulations are particularly useful because they provide a benchmark against which optimizations of the methods described here, or qualitatively different methods can be measured. Because these methods worked similarly for simulated sparse and rhythmic activity, these simulations suggest that the methods described here will detect sparsely active networks as well as rhythmically active networks.

When using these methods on real data however, it cannot be excluded that a subset of signals will remain undetected by any automated approach to their detection, and that some subset of automatically generated ROIs will be associated with cells that should be excluded from the analysis (dead/unhealthy cells; glia). These errors are (at least in part) irreducibly ambiguous however, as the experimenter generally does not know more about the neuronal activity under study than the optical signals provide. An advantage of automated detection is that insofar as the program errs, it errs without bias, based on the parameters selected for the processing of the image series. One source of error is inappropriate parameterization, another is the subjective process of choosing which cells to reject, add, merge, or split. These decisions will likely be made differently by each individual attempting to analyze the data, and are likely an important source of error in the analysis of optical data, irrespective of how ROIs are generated. The methods described here reduce the burden of analyzing optical data, but do not eliminate the risk of error associated with inappropriate inclusion or exclusion criteria applied to signals obtained with automatically generated ROIs. .

Do these methods have general applicability? We have used this program under rather narrow conditions, namely for the analysis of cells labeled by bath application of membrane-permeant Ca²⁺ indicators that change in intensity and not wavelength as a function of [Ca²⁺]_i. Other loading methods, such as pressure ejection (Garaschuk et al., 2006; Koshiya and Smith, 1999; Stosiek et al., 2003); electroporation (Bonnot et al., 2005) or ballistic delivery (Kettunen et al., 2002) will likely generate signals in a three-dimensional volume of tissue; depending on the technology used to acquire the images, this could lead to stronger diffuse signal and hence a deterioration in performance. In addition, other classes of indicators, such as ratiometric Ca²⁺ indicators (such as Fura-2), or voltage sensitive indicators (such as di-4-ANEPPS) have not been tested here and may generate different results. Here, we have tested our methods on optical signals obtained at different spatial resolutions, sampling rates, with low- and high-affinity indicators, and with different spatio-temporal characteristics. Thus, we have shown that the utility of these methods is neither restricted to the spatially dispersed, coupled, rhythmic activity characteristic of respiratory networks, nor to data acquired at narrowly specified spatio-temporal resolutions, nor to indicators with similar kinetics.

Although this software was developed to analyze the rhythmic activity generated by the relatively sparse networks involved in respiratory rhythm generation, using a particular class of indicators and dye-loading methodology, these methods may have more general use. Assuming that neurons are healthy and well-loaded with indicator, the ubiquitous biophysical properties (low [Ca²⁺]_i levels or hyperpolarized V_m during quiescence; rapid and large Ca²⁺influx or depolarized V_m during action potentials) responsible for the optical signals we record will generally produce the somatic signals our algorithms are designed to detect, albeit with different temporal characteristics and/or sign.

Because in ventrolateral medulla, respiratory networks are heterogeneous, and in-terdigitated by neurons that show no respiratory modulation, optical recording using membrane permeant Ca²⁺ indicators is an attractive option that has been pursued by numerous groups both in the neonate (Barnes et al., 2007; Eugenin et al., 2006; Funke et al., 2007; Hartelt et al., 2008; Koshiya and Smith, 1999; Onimaru and Homma, 2003; Potts and Paton, 2006; Ruangkittisakul et al., 2008), as well as the embryo (Thoby-Brisson et al., 2005). By enabling simultaneous recording from network constituents, progress in understanding the functional organization of these physiologically critical networks can accelerate, as has occurred in other systems (Ohki et al., 2005; Ohki et al., 2006). Unfortunately, as temporal resolution and camera sensitivity provide ever richer datasets, the burden of their analysis increases as well. It is hoped that these methods will facilitate that process.