Learning by Doing, Scale Effects, or Neither? Cardiac Surgeons after Residency

Abstract

Objective

To examine impacts of operating surgeon scale and cumulative experience on postoperative outcomes for patients treated with coronary artery bypass grafts (CABG) by “new” surgeons. Pooled linear, fixed effects panel, and instrumented regressions were estimated.

Data Sources

The administrative data included comorbidities, procedures, and outcomes for 19,978 adult CABG patients in Florida in 1998–2006, and public data on 57 cardiac surgeons who completed residencies after 1997.

Study Design

Analysis was at the patient level. Controls for risk, hospital scale and scope, and operating surgeon characteristics were made. Patient choice model instruments were constructed. Experience was estimated allowing for “forgetting” effects.

Principal Findings

Panel regressions with surgeon fixed effects showed neither surgeon scale nor cumulative volumes significantly impacted mortality nor consistently impacted morbidity. Estimation of “forgetting” suggests that almost all prior experience is depreciated from one quarter to the next. Instruments were strong, but exogeneity of volume was not rejected.

Conclusions

In postresidency surgeons, no persuasive evidence is found for learning by doing, scale, or selection effects. More research is needed to support the cautious view that, for these “new” cardiac surgeons, patient volume could be redistributed based on realized outcomes without disruption.

Learning by doing is a very well-known mechanism by which health care providers achieve improvements in patient outcomes with increased production experience (Luft, Bunker, and Enthoven 1979). Scale effects driven, for example, by indivisibilities in critical investments may similarly impact patient outcomes. However, in cardiac surgery most recent work fails to document substantial and/or significant relationships between individual operator volume and patient outcomes (California Office of Statewide Health Planning and Development 2007; Shahian et al. 2007; Huesch and Sakakibara 2009; Sfekas 2009;) at any except the lowest output levels. Nevertheless, some payor and patient advocates and some in the medical community argue that high minimum scale thresholds lead to lower mortality, morbidity, and costs (Birkmeyer et al. 2003).

Since coronary artery bypass graft (CABG) operations are still the most common major surgical procedure in the United States today, with substantive mortality, morbidity, and cost impacts, these unsettled questions of learning by doing and scale economies have clear relevance to multiple stakeholders in the health care system. This study examines these questions in an underexplored empirical setting, focusing on “new” surgeons in practice following completion of specialist surgical residencies. One might expect both experience and scale economies to have substantial impact here, given fast diminishing returns to high cumulative experience,1 and given changes in scale with practice growth.

Experience may drive several independent sets of skill: those of technical competence2 as well as decision making capabilities,3 and also those of collaboration and coordination with other health care professionals (e.g., intensivists). However, experience may suffer from “forgetting” or other causes of depreciation of experience.

The benefits of scale at the individual surgeon level are less intuitive. Higher current practice volume may justify and facilitate discrete investments in office support and in regular training. Higher current volume necessarily implies closer spacing of practice, well known in other fields to improve technical proficiency. Indirect effects may be in preferred operating room (OR) slots and a more stable team structure with preferred anesthesiologists and OR staff. Scale may also be accompanied by a closer integration into hospital processes of care as surgeons increasingly spend time in pre- and postoperative ward consultations.

PRIOR RESEARCH

Ho (2002) analyzed hospital-level angioplasties and mortality and admission cost outcomes, finding that scale generally dominates experience economies. Gaynor, Seider, and Vogt (2005) used panel data at the CABG hospital level and also found that static scale economies were the dominant effect driving the volume–outcome relationship. However, Reagans, Argote, and Brooks (2005) examine procedure time spent in the OR and related this inversely to cumulative experience.

New surgeons are examined by two papers with opposing conclusions. Bridgewater et al. (2004) find significant improvement in mortality rates in CABGs performed postresidency by 15 cardiac surgeons over 4 years in the United Kingdom. They suggest that this improvement might be due to an improved stock of nontechnical skills.4 However, their surgeon-level analysis did not control for the possibility of selective referral effects.5 In contrast, Ramanarayanan (2007) uses a patient-level panel instrumental variables model and finds no significant impact of cumulative volume on mortality. Neither study examines the possible impact of scale, current volume, or “forgetting.”

Finally, Gowrisankaran, Ho, and Town (2006) examine the impact of hospital-level cumulative experience on patient mortality. Allowing for organizational forgetting, their model estimated an almost complete depreciation of experience from one quarter to the next. Such forgetting may make more sense in an organizational context (e.g., labor turnover; Darr, Argote, and Epple 1995); it is not immediately obvious how one ought to conceive of forgetting at the level of the individual surgeon.

DATA AND DESCRIPTIVE STATISTICS

The data are commercially available from the Agency for Health Care Administration in Florida, and they represent all discharges for CABG surgery performed in state-regulated hospitals in the 36 quarters between 1998 and 2006. These data contain unique operating surgeon medical license identifiers, which were linked to publicly available statutory physician data maintained by the Florida Department of Health.

Only operating surgeons who were both positively identified as surgeons (residency training in general, vascular surgery and/or thoracic surgery, and/or fellowships in cardio-thoracic surgery) and completed their residency in 1998 or subsequently were included in the analyses below. These sample restrictions, further described in Appendix SA1, resulted in 57 operating surgeons and their 19,978 patient admissions.

Dependent variables analyzed were postoperative mortality (averaging 3.6 percent) and other measures hypothesized to reflect the significant noncardiac morbidity. In the United States, as many as 3 percent of CABG patients suffer strokes, around 2 percent experience kidney damage severe enough to require dialysis, and a further 3 percent survive a prolonged chest wall wound site infection (Eagle et al. 2004). In the panel, the incidence of these unobserved major morbidity events may lead to longer of stay (average 10.6 days), discharge elsewhere than home (22.6 percent), prolonged mechanical ventilation >96 hours (3.2 percent), and postoperative dialysis (2.2 percent in patients not diagnosed preoperatively with acute kidney failure).

Additionally, a proxy for OR time was constructed from the list of OR charges. Conditional on a particular facility and time period, such list charges are a “noisy” function of time spent in the OR. Shorter OR time relative to other cases in that facility in that period may represent more skilled and/or more efficient surgical operations after controlling for procedure type.

Summary Surgeon Statistics

The 57 new surgeons were observed on average for 15 quarters each and performed an average of 350 total cases over the panel. In Table 1, an analysis of mortality by cross-sectional volume categories is made to facilitate comparison with other studies. Moderate positive correlation between surgeon current volume and surgeon cumulative experience (0.39) will not disallow reasonably precise estimates of the relative impacts of current scale and experience economies.6 In contrast, very substantial hospital serial correlation exists in volume (0.92), while contemporaneous surgeon and hospital volume is more modestly positively correlated (0.26).

Table 1.

Average Annual Volume–Outcomes Relationship

	Yearly Volume Categories
	Low	Medium	High
	<50	50–75	>75 Cases
Number of surgeons	22	23	12
Annual CABG cases	24.5	68.0	144.8
Preoperative expected mortality (%)	7.6	4.0	3.1
Length of stay (days)	17.0	11.2	9.7
Discharge alive but not home (%)	33.6	23.2	21.6
In-hospital mortality (%)	10.1	3.9	3.0

Notes. Fifty-seven “new” operating cardiac surgeons treating 19,978 patients over 1998–2006.

CABG, coronary artery bypass grafts.

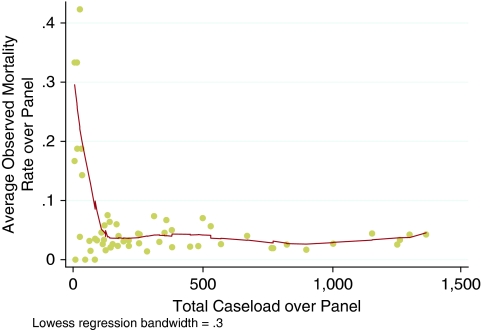
In Figure 1, the panel aggregate relationship between total caseload and average crude mortality rate is shown. Over a wide range around the average caseload the relationship is relatively flat. This figure is not suggestive of obvious cumulative experience economies, unless one conjectures rapidly plateauing learning curves.

Figure 1.

Total Panel Volume–Outcome Relationship

Supporting Figure SA1 shows the relationship between average quarterly caseload and average crude mortality rate, and it is similarly not suggestive of obvious scale economies unless the minimum scale threshold is very low. However, these figures do not provide definitive evidence one way or another because they do not control for possible differences inter alia in preexisting risk. This adjustment procedure is further described below.

Surgical Risk Adjustments

The importance of risk adjustment of case mix is well known. Tsai et al. (2006) demonstrate the additional importance of using clinical covariates (e.g., chart data such as lab tests) where available, showing attenuation of volume coefficients when such clinical covariates are incorporated. In CABG surgery the leading cardiac risk models include Parsonnet, Euroscore, and ACC/AHA, which were used to inform the choice of risk adjustments.7 As shown in Table SA1 of Appendix SA1, the patient records were searched for 37 medical diagnosis risk factors (e.g., left ventricular failure) and 20 surgical procedural risk factors (e.g., concomitant valve operation). Additionally, eight other patient demographic variables (e.g., age) and patient ecologic variables (e.g., county median family income) were obtained from the patient records and U.S. Census bureau data, respectively. Finally, calendar year of operation dummy variables were generated.

A parsimonious risk model was constructed from these 77 covariates using forward stepwise probit and logit regressions (cutoff for inclusion of covariate was p<.2, the two specifications agreed on 41 of the final 45 covariates). The final logit model generated an area under the receiver–operating characteristic curve of 0.92, indicative of a well-discriminating model.8 A linear probability model variance inflation factor analysis showed mean VIF of 1.76, max VIF of 6.92, indicating the absence of serious multicollinearity.

Surgeon Attributes

In Table 2 more detailed information on surgeon characteristics is given, arranged by quintiles of total panel caseload. It is apparent, for example, that surgeons with higher panel caseloads tend to have fewer faculty appointments, tend to work in nonteaching hospitals, and see patients more electively while operating less on weekends. Those surgeons in the lowest quintile for total panel caseload also operated on the sickest patients on average (7.8 percent expected mortality in quintile 1 versus 3.2 percent in quintile 5).

Table 2.

Characteristics of Surgeons by Quintiles of Surgeon Total Cases Treated over Panel

	Quintiles of Surgeon Panel Cases
	1	2	3	4	5
Quintile (Range)	(6–67)	(84–144)	(145–285)	(312–569)	(670–1,359)
Mean cases	42.8	118.7	216.0	438.8	1,076.8
Total cases in quintile	348	1,266	2,479	4,647	11,238
Observed panel mortality rate (%)	10.6	3.9	3.2	4.3	3.2
Quarters observed	6.6	7.9	13.4	22.4	28.3
Mean cumulative cases at quarter of operation	14.8	49.4	97.0	207.3	516.8
Holds faculty appointment(s) (%)	10.0	35.6	25.5	41.6	0.0
Number of other state licenses	1.6	1.5	1.7	1.8	1.8
Number of surgical boards	1.5	1.5	1.5	1.7	1.8
Thoracic Board (%)	60.0	89.7	68.6	56.1	82.5
General Surgical Board (%)	56.0	23.8	43.4	35.6	18.8
Last residency ended	2002	2000	2001	2000	1999
Medical school ended	1992	1993	1992	1992	1988
Operating surgeon is also attending (%)	22.4	49.9	44.8	38.9	49.0
Mean attending quarterly cases	6.6	12.4	9.7	10.1	20.6
Patient outcomes
Preoperative expected mortality (%)	7.8	4.2	3.8	4.1	3.2
In-hospital mortality (%)	10.6	3.9	3.2	4.3	3.2
Normalized OR charges	0.4	0.1	0.0	0.1	−0.1
Ventilated more than 96 hours (%)	12.6	3.6	4.1	3.5	2.5
Received dialysis postoperatively (%)	3.9	1.2	1.4	1.8	1.1
Discharge alive but not home (%)	35.9	17.5	22.0	20.4	23.9
Length of stay	16.2	11.3	11.7	10.9	10.0
Demographics and acuity
Age	65.9	64.2	67.1	66.3	67.1
Female (%)	31.0	28.3	28.4	29.4	29.6
County population: bachelors degree (%)	23.8	25.6	25.2	24.8	23.3
Elderly (%)	16.8	14.9	19.0	17.7	18.3
Below poverty line (%)	12.6	14.1	13.6	13.0	12.1
Emergency presentation (%)	37.1	39.7	26.7	28.8	30.3
Transfer presentation (%)	49.1	51.5	40.5	45.6	46.2
Operation day of the week	3.4	3.1	3.1	3.2	3.1
Hospital characteristics
Average quarterly CABG volume	121.8	121.0	89.5	93.6	124.7
Observed CABG mortality rate (%)	3.9	3.7	4.5	4.2	3.7
Risk-adjusted CABG mortality rate (%)	3.5	3.7	3.8	3.9	4.1
PTCA/CABG ratio	1.8	2.5	2.3	2.2	1.5
CABG/admission ratio (%)	1.4	0.8	1.2	1.5	1.5
Beds	650.9	767.5	451.1	454.4	525.0
Designated “adult open heart” (%)	96.6	99.8	98.3	98.5	99.4
Designated “teaching” (%)	28.4	38.0	25.2	19.6	0.8

Notes. All means are calculated at the patient level. Total patients included 19,978, treated by a total of 57 operating surgeons with last residency since 1998. Hospital volume and mortality rate based on all CABG operations at hospital, whether performed by these operating surgeons or not. Operation day of week >3 (i.e., Wednesday) implies some weekend operations. Dialysis measure restricted to patients not diagnosed with acute kidney failure preoperatively.

CABG, coronary artery bypass grafts; OR, operating room.

The drivers of this increased ex ante probability of in-hospital death are clearer in Table SA1 of Appendix SA1. Here one may note that lower volume surgeons are operating on patients with substantially higher degrees of comorbidities (e.g., fluid, electrolyte, and coagulation disorders) and higher cardiovascular risk (e.g., congestive heart failure, dysrhythmiae, and pacemakers in situ). They are also clearly performing a larger number of more complex operations on average (e.g., concomitant valve operations) while tending to lower use of the “gold standard” of the single mammary artery as graft material.

These descriptive statistics suggest that the appropriate empirical strategy is to use surgeon unobservable effects models,9 and to control rigorously for input and process differences. The next section details this analytical strategy.

ECONOMETRIC SPECIFICATION AND ESTIMATION

The base specification for patient outcomes has the following generic functional form:

where f (.) represents either a linear probability model or nonlinear functional forms, for dichotomous-dependent variables. Results below were not qualitatively different by functional form. Accordingly, the more intuitive marginal effects from linear models are presented below.

The dependent variable d_i,h,s,p is at the patient level, and it reflects the outcome of patient i in hospital h after operation by operating surgeon s in quarterly period p. The controls are a constant α₀, the vector of patient level demographic, acuity, medical, and surgical risk factors X_i described in Table SA1 of Appendix SA1. Hospital characteristics X_h comprised teaching hospital status and “adult open heart” designation. All disturbances ɛ_i,h,s,p were presumed to be orthogonal to all covariates for all i, for all h, for all s and for all p.

Other available hospital measures such as number of nurses, number of beds, number of total admissions, ratio of PTCA to CABG were found to be too closely correlated with the Hospital_Vol variable below. Given the very high serial correlation in lags of Hospital_Vol, one may usefully view this variable as essentially a hospital fixed effect. Year dummies X_y were rolled up such that y was the year corresponding to quarter p.

The focal independent variables are Surgeon_Vol_s,p and Hospital_Vol_h,p performed by operating surgeon s or facility h in current quarter p and the number of patients seen cumulatively as at quarter p since residency completion, Surgeon_Cumul_Vol_s,p.

Pooled linear probability regressions were performed in initial data analysis, but standard tests convincingly reject pooled models in favor of models with unobserved surgeon effects, and reject the consistency of random effects models. Accordingly, all specifications below included surgeon fixed effects c_s.

Additional specifications considered different robustness controls. For example, a number of researchers control for a measure of time-varying surgeon or hospital quality that may be independent of volume (Farley and Ozminkowski 1992; Huckman and Pisano 2006;). Although the main specifications below include surgeon fixed effects, it is plausible that surgeons may have (time varying) poorer and better quarters in performance. Accordingly, the lagged risk-adjusted mortality rate by the surgeon s in the period p−1 was added to control for this, as well as a similarly defined measure for hospital h in period p−1.10

Finally, to allow for the possibility of depreciation of experience, the model was also separately estimated with a free parameter, λ, and fitted using nonlinear least squares. Here instead of cumulative volume, surgeon experience evolves as a function of a nonlinear combination of quarterly period volume:

If λ is estimated as close to 1, then there is little depreciation of experience, whereas a “forgetting” parameter of zero would represent complete degradation of the prior period's volume. Alternatives forms modeled for g (.) were linear, square root, or logarithmic functional forms.

Endogeneity of Volume and Experience

This paper is identifying the impact of surgeon volumes on outcomes via within-surgeon changes in volume over time. If there are unobservable, unvarying effects at the surgeon level that are associated with outcomes and volumes, then the fixed effects approach will satisfactorily deal with these. However, unobservable, time-varying effects at the surgeon level that are correlated with both outcomes and volumes may still lead to biased estimates of the parameters β₅ and β₆.

An example of such time-varying effects could be reputational effects: as a surgeon performs more he or she becomes more well known and is sought out by more patients. In one scenario, these patients could be unobservably healthier and more likely to survive the CABG operation. Alternatively, as a surgeon performs more volume and becomes a senior attending, he or she may be on call for fewer nights or be able to choose schedules to avoid seasonal peaks of high-mortality admissions. Failing to control for these could lead to an omitted variable bias in the same negative direction as a hypothesized learning-by-doing mechanism. In a different scenario, it is possible that such unobservable, time-varying effects at the surgeon level lead to biases in the other direction, toward zero. This might happen, if, for example, reputational effects driven by higher volume led to unavoidable exposure to patients who were sicker in unobservable ways.

Under either scenario there is correlation between the actual surgeon volume and a time-varying surgeon-specific component η_s,p of the compound error ɛ_i,h,s,p. In this observational data, patients are not randomly assigned to surgeons, so we must address this potential confounding problem (Harris and Remler 1998).

While natural experiments such as volume shocks caused by hospital or surgeon entries or exits have been used (e.g., Ramanarayanan 2007), substantial noise in quarterly operating volumes and observable mortality is observed in this data. This noise might effectively swamp the exogenous shock's impact at a clinical level, making it less plausible. This is particularly important given the low mean value of such instruments relative to typical caseloads.

This paper relies instead on a plausibly exogenous instrument for surgeon volume derived from choice models. The predictions of surgeon volume rest here on a utility-maximizing model of selection (Escarce et al. 1999; Kessler and McClellan 2000; Chernew, Gowrisankaran, and Fendrick 2002; Tsai et al. 2006;). The choice of surgeon is assumed to be influenced by attributes of the patient, by attributes of the particular surgeon, by whether the surgeon is the closest, and by the distances between patient and possible surgeons. Using a tractable conditional logit specification due to McFadden (1973), this study's approach yields predicted probabilities of treatment for every patient by every surgeon in a feasible choice set. These probabilities of treatment are aggregated by surgeon to construct expected patient volume in a period.

Identification Assumptions

Choice models should be constructed using an exhaustive set of observable, plausibly exogenous determinants of surgeon choice. The expected volumes by surgeon resulting from the choice model would then serve as exogenous instruments for the potentially endogenous actual surgeon volume. One may then use two-stage least squares in a linear probability model to consistently estimate β₅ and β₆ in the main model. Using a similar approach, Gowrisankaran, Ho, and Town (2006) point out the three crucial assumptions for identification: the predicted volumes do not separately affect patient outcomes conditional on actual volumes, the instruments are conditionally correlated with the potentially endogenous volumes, and the instruments are uncorrelated with the time-varying surgeon-specific error component η_s,p. The first assumption is reasonable and assumed to hold; the second is reasonable and will be tested using standard tests of instrument strength.

The third maintained assumption of instrument exogeneity may be violated if any of the assumed determinants of choice are in fact endogenous or any are missing. For example, if surgeon quality were observable and wrongly included in the choice model, then predicted volumes might be correlated with the η_s,p error in the specification of patient outcomes. In our approach, we do not include surgeon risk-adjusted mortality in the specification of patient utility. In another example (Gowrisankaran, Ho, and Town 2006), suppose “higher quality” providers with a lower value of the η_s,p error move to an area closer to larger numbers of potential patients (or vice versa, suppose patients move to an area with “higher quality” surgeons).11 This could render distance an endogenous determinant in the choice model. Suppose furthermore that this type of surgeon faced little competition from any other surgeon. Then the choice model would necessarily predict higher volumes for him or her, and this would preserve unwanted correlation between the instrument and the error component. This violation is possible but seems unrealistic, and it is not supported by descriptive statistics of the choice set. This study finds that the lower the mean and median observed quality of surgeons, the larger is the number of alternatives in their patients' choice set (Pearson correlations −0.051 and −0.163, respectively, both p<.001). The approach here maintains the key assumption that such economic behavior (whether surgeons or potential patients or both moving) does not happen.

In a different example, suppose some types of insurers curtail the access of unobservably sicker patients to higher volume, higher cost, and possibly “higher quality” providers. A choice model that fails to capture this plausible determinant of choice might lead to a violation of the maintained assumption of instrument exogeneity. This problem is approached by estimating separate choice models for patients in different classes of insurance status (Medicare, Medicare Advantage, Indemnity, PPO, and HMO) and in different periods of time to account for changes in preferences over time. In a similar vein, healthier patients might systematically have different preferences than less healthy patients. To account for such differences in tastes, the approach here is to divide patients by quintiles of ex ante probability of mortality and to separately estimate the above choice models to construct an alternative instrument.

Choice Model Specifications

Using a conditional logit specification, if a patient i were to receive treatment from surgeon s, then utility U_is accrues to the patient. Utility was specified as a linear additive function of covariates, chiefly of the transformed distance between surgeon and patient. Following Chernew, Gowrisankaran, and Fendrick (2002), the great circle distance in miles between zipcode centroids was transformed using the natural logarithm of the sum of the distance and 1 (because a substantial number of surgeons and patients shared the same zipcode and thus had zero distance). Utility was specified as the sum of the transformed distance, the square of the transformed distance, an indicator representing the closest surgeon, and the surgeon's 12-month lagged operating volume as covariates, and a Gumbel-type independently and identically distributed error.

By a revealed preference argument, the observed choice of surgeon s^* implies that U_is^* is greater than U_is for any other surgeon in the choice set. By the logit functional form, the probability of a particular match is^* was then computed as the ratio of the exponentiated fitted value Û_is^* to the sum of the exponentiated fitted values Û_is for all the surgeons s in i's choice set. The sum of expected patient flows for each surgeon s in each time period was then calculated by adding these match probabilities across all i within that period.

In estimating these choice models, the patient sample was expanded to include all 80,324 nonemergency, nontransferee CABG patients who sought treatment within 75 miles from home. All cardiac surgeons practicing in the quarter of the patient's admission were included in the choice sets, not just new surgeons. The choice set size averaged 17 surgeons (range 2–38).

FINDINGS

Misspecified pooled regressions that inappropriately ignore the panel structure (not reported) reveal a small but highly significant scale effect for current surgeon volume on mortality (elasticity −0.2), but no impact of cumulative surgeon volume on mortality.

Uninstrumented Panel Models

In Table 3 the estimated coefficients on focal volume variables of interest are given for the surgeon fixed effects linear probability models. The most striking finding is the absence in Model V of significant effects of scale or cumulative volume on the probability of in-hospital mortality.

Table 3.

Impact on In-Hospital Mortality and Morbidity: Current Volume, Cumulative Volume

	CABG Patient Outcome
	Model I	Model II	Model III	Model IV	Model V	Model VI
			Probability of …
	Proxy for OR Time (Charges z Score)	Length of Stay (Days)	Dialysis Postoperatively	Prolonged Mechanical Ventilation (>96 Hours)	In-Hospital Mortality	Discharged Elsewhere Than Home
Surgeon current volume	0.123	10.900*	0.220**	−0.082	−0.092	−0.859
t statistic	0.22	1.79	2.44	−0.65	−0.71	−3.15
Surgeon cumulative volume	−0.028	1.650***	0.009	−0.015	0.012	−0.016
t statistic	−0.49	2.73	0.96	−1.20	0.92	−0.60
Hospital current volume	0.322***	0.197	−0.038***	−0.008	0.004	−0.038
t statistic	3.59	0.21	−2.69	−0.40	0.21	−0.88
(Suppressed patient, hospital, year controls)
Specification check
Pooled model rejected	Yes***	Yes***	Yes**	Yes**	Yes**	Yes***
Random effects model rejected	Yes***	Yes^	Yes***	Yes**	Yes***	Yes***
Surgeon fixed effects linear model	Yes	Yes	Yes	Yes	Yes	Yes
Model fit
R2 within (%)	40.1	29.5	3.5	9.7	17.4	24.5
F test	229***	143***	13***	37***	72***	111***
Observations	19,978	19,978	18,194	19,978	19,978	19,978

Notes. Estimated marginal coefficients (× 1,000) with t statistics. (^***), (^**), and (^*) denote estimated coefficients' significance at p=.01, .05, and .10 level, respectively. See “Econometric specification and estimation” and Appendix SA1 for full details on model controls. All standard errors are conventional. Loss of observations in Model III due to dialysis specification including only patients not diagnosed with preoperative acute kidney failure. No qualitative differences when corrected for clustering by surgeon or corrected for heteroskedasticity. (^) denotes use of single-estimate t test (on focal volume variable) to evaluate Hausman-like test given other assumptions not met.

CABG, coronary artery bypass grafts; OR, operating room.

For the other outcome measures in Models I–IV and Model VI, generally mixed results are obtained. Higher surgeon scale, as measured by total patients treated in a quarter, is associated with a small but significant decrease in the probability of being discharged to a subacute or convalescent hospital rather than home (elasticity −0.13). Higher surgeon scale slightly increased the length of stay (elasticity +0.04) and appeared to increase the use of dialysis in his or her patients (elasticity +0.34). Because the discharge date and use of dialysis is partially at the discretion of the surgeon, it is not immediately clear whether these represent more prudent treatment, or diseconomies of scale.

Cumulative surgeon operating experience fails to significantly impact any of the measures of patient outcome, except for patient length of stay, where a small positive impact is estimated (elasticity of +0.06). This may represent more prudent treatment mediated by greater experience or just mirror the impact of current volume on length of stay.

Hospital scale as measured by total patients treated in a quarter (by all surgeons regardless of residency dates) is seen to slightly reduce the probability of receiving postoperative dialysis, which may imply enhanced hospital-level processes of care. The finding that larger hospital scale is associated with a proxy for OR time may reflect either OR management complexity (i.e., diseconomies of scale) or more time-consuming OR-level processes of care. However, hospital scale was not associated with improved risk-adjusted mortality in Model V.

Instrumented Models

Using in-hospital mortality as the dependent variable, analyses were repeated using instrumented current and cumulative surgeon volume based on the patient choice model instrument.

In Table 4, Models VII and VIII show that both instruments were strong in all specifications (Staiger 2002). Using these instruments, no significant selection effects were identified, and estimates of the focal coefficients on current and cumulative volume were statistically indistinguishable from zero. The Davidson–MacKinnon tests failed to conclusively reject the exogeneity of either of the potentially endogenous focal volume variables (p=.37). One explanation may be that at the beginning of their career these new surgeons have yet to build sufficient stocks of reputation, and that their actual volume is truly exogenous.

Table 4.

Impact on In-Hospital Mortality: Instrumented Volume, Depreciating Experience

	Probability of In-Hospital Mortality
	Model V	Model VII	Model VIII	Model IX	Model X	Model XI
		Instrumented Volume		Experience Is a … Function of Depreciated Volume
	Base Specification	Choice	Choice, by Risk	Linear	Square Root	Logarithmic
Instrumented surgeon current volume		0.976	1.123
t statistic		0.89	0.82
Instrumented surgeon cumulative volume		0.020	0.034
t statistic		0.23	0.32
Surgeon current volume	−0.092			−0.040	−0.065	−0.059
t statistic	−0.71			−0.29	−0.47	−0.43
Surgeon experience	0.012			−3.905	−5.376	−6.447
t statistic	0.92			−0.03	−0.01	−0.13
Depreciation parameterλ	(=1)			0.029	0.013	0.018
t statistic				0.03	0.01	0.08
(Suppressed patient, hospital, year controls)
First-stage checks
First-stage R2: current; cumulative volume (%)		15.9; 87.9	16.0; 88.0
t test on instrument: current; cumulative vol		9.0***; 18.5***	10.6***; 19.3***
Model fit
R2 within (%)	17.4	16.8	16.7	21.7	21.7	21.7
F test or Wald	72***	4,371***	4,366***	NA	NA	NA
Specification check
Exogeneity assumption rejected		No	No
Davidson–MacKinnon p-value			.37	.37
Observations	19,978	17,489	17,489	19,978	19,978	19,978

Notes. Estimated marginal coefficients (× 1,000) with t statistics. Model V estimated by OLS, Models VII–VIII by 2SLS, Models IX–XI by NLLS. Model fit is for second stage in instrumented specifications. Loss of observations in Models VII–VIII due to choice model exclusions of emergency and transferee patients and maximum 75-mile distance between patient and surgeon. Surgeon experience specified as a function of a nonlinear combination of past volumes with geometric decay driven by ë. (^***), (^**), and (^*) denote estimated coefficients' significance at p=.01, .05, and .10 level, respectively. See “Econometric specification and estimation” and Appendix SA1 for full details on model controls and specification. All standard errors are conventional.

Alternatively, the reduced form approximation to the patient choice model of surgeon selection may be flawed. For example, the surgeon–patient match may not determined by patients or referring cardiologists, but by hospital administrators and senior surgeons who allocate patients to surgeons (Huesch and Sakakibara 2009). Nonrandomness in such allocation mechanisms may lead to unobservably healthier or sicker patients being treated by new surgeons with unobservably lower or higher quality. This study's instruments were constructed from expected flows based on patient choice models and would thus fail to correct for such omitted variables biases.

Depreciating Experience Models

Using the alternative specification in which prior period experience is allowed to depreciate, Models IX–XI in Table 3 show that very substantial depreciation is estimated. The point estimates on λ are consistent with almost complete forgetting of prior period experience, irrespective of functional form assumptions. Comparing estimates with the base specification in Model V, one may observe that neither current nor historical operating volume—however modeled—appears to have any significant impact on current patient outcomes.

Robustness Checks

Given the correlation between hospital and surgeon scale (0.26 for current quarter volumes) and the correlation between surgeon current volume and cumulative volume (0.39), the results were repeated using different combinations of these three focal volume variables. No qualitative differences were obtained. Variance inflation factor analyses on pooled linear probability models indicated the absence of severe multicollinearity. Relaxing the linear probability model specification and using nonlinear (probit) functional forms (with dummies for surgeons to preserve the panel structure) did not impact these results for dependent variables with binary outcomes.12 Correcting standard errors for clustering at the operating surgeon level did not lead to qualitative differences in results. Robustness checks with specifications including controls for lagged risk-adjusted mortality also did not qualitatively affect these results.

Limitations

This study's limitations are due to data sources, data constraints, and to critical assumptions made. The underlying discharge data are administrative in nature, and in particular not clinically audited, and hence prone to well-known concerns about data integrity (Torchiana and Meyer 2005). As indicated in Appendix SA1, slightly more than 1 percent of the data was discarded due to potential miscoding of physician identifiers, while additionally nearly 2 percent of the data was discarded due to operating surgeon fields containing nonsurgeon license identifiers. A key maintained assumption in this paper is that any remaining data errors are not systematically related to surgeon volume variables.

The underlying data also does not allow observation of pre- or extra-panel experience. While operating surgeon residency completion dates were identified, it is not clear how much each surgeon practiced before completion of residency. A lower bound of 75 adult cardiac cases required during residency may still mask substantial preresidency experience, or general surgical exposure to thoracic cases. Similarly, contemporaneous practice in non-state-regulated hospitals in Florida (e.g., VA) or any hospitals in contiguous states is not observed.

Lastly, a key assumption underpins this paper's analyses. It is assumed that the operating surgeon is substantially responsible for outcomes, and that singling out this individual is valid. It is important to note that the profession sees CABG surgery as a team-based endeavor (Shahian et al. 2007) and disagrees with sole identification of the operating surgeon.

DISCUSSION

Learning, scale, and selection effects were investigated in a large group of cardiac surgeons recently completing residency. Apart from allowing information on the total cumulative experience of these surgeons, this is a group in which one might most fruitfully look for learning effects. Similarly this is a phase of their career where scale is changing dramatically, and this variation in scale should allow identification of the impacts of contemporaneous volume.

Unexpectedly, learning effects (whether from simply cumulating operating experience or allowing for depreciation) appeared to play no significant role in driving patient outcomes. The finding of high rates of apparent depreciation of experience in one specification was not necessarily inconsistent with the finding of an insignificant impact of summed up, undepreciated period volumes in another specification.

Indeed, this paper is unable to econometrically distinguish between learning by doing with very rapid forgetting on the one hand, and insignificant experience effects with some scale effect on the other. However, these models examined individual surgeons. It is thus not immediately clear what forgetting ought to be measuring in this clinical context. By construction, the focus on individuals means labor force turnover is not a meaningful construct. By the focus on younger physicians, there is unlikely to be significant true (i.e., cognitive) forgetting. One may also reasonably rule out obsolescence (and hence apparent depreciation) of technology-specific skills, because these new physicians possess state-of-the-art skills, again by construction of the dataset. Given these factors, the preferred assumption of this paper is that learning-by-doing effects are insignificant.

Also unexpectedly, contemporaneous surgeon scale effects had no significant impact on patient in-hospital mortality, with inconclusive effects on other proxies for patient in-hospital morbidity. It is to be noted that by focusing on younger surgeons, such scale effects may have been systematically underestimated. That is, if unobserved patient risk factors differed systematically in older surgeons, these results may not apply more generally (Waljee et al. 2006).

Finally, no patient selection effects were identified by strong and plausibly exogenous instruments based on patient choice models. These findings should be viewed as holding only in the context of selective referral (self, or by physician) mechanisms. If selective allocation mechanisms exist at the level of hospital or group practice, these instruments are unable to identify them (Huesch and Sakakibara 2009).

One implication of these results is that learning effects may have a low upper bound in the broader profession, in which surgeons have been practicing for one or two decades and seen their learning curve likely reach a plateau. This echoes similar findings previously noted at the hospital level by Ho (2002) and Gaynor, Seider, and Vogt (2005), but not rigorously established at the individual surgeon level.

This paper also supports the view, first noted by Gaynor, Seider, and Vogt (2005) in the context of hospitals, that there are apparently no compelling reasons to favor higher cumulative experience providers either when making marginal volume allocation decisions (e.g., personally choosing physicians, or hospitals shifting patients between different providers) or making discontinuous volume allocation decisions (e.g., closing centers, and regionalizing provision).

In conclusion, CABG surgery is a clinical context with particularly small volume–outcome relationships, in contrast to other high-risk and smaller-volume procedures. A cautious view is that the time for volume–outcome CABG studies may well be close to over. As noted by Shahian (2004), future research on drivers of patient quality and treatment costs ought to focus less on volume and more closely on processes of care at the institutional level and on conformance of practice with evidence-based clinical guidelines.

Supporting Information

Additional supporting information may be found in the online version of this article:

Appendix SA1: Data Appendix.

Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.