Inference for Cumulative Incidence Functions with Informatively Coarsened Discrete Event-Time Data

Summary

We consider the problem of comparing cumulative incidence functions of non-mortality events in the presence of informative coarsening and the competing risk of death. We extend frequentist-based hypothesis tests previously developed for non-informative coarsening and propose a novel Bayesian method based on comparing a posterior parameter transformation to its expected distribution under the null hypothesis of equal cumulative incidence functions. Both methods use estimates derived by extending previously published estimation procedures to accommodate censoring by death. The data structure and analysis goal are exemplified by the AIDS Link to the Intravenous Experience (ALIVE) study, where researchers are interested in comparing incidence of human immunodeficiency virus seroconversion by risk behavior categories. Coarsening in the forms of interval and right censoring and censoring by death in ALIVE are thought to be informative, thus we perform a sensitivity analysis by incorporating elicited expert information about the relationship between seroconversion and censoring into the model.

1. Introduction

In prospective studies examining incidence of non-mortality outcomes, event times are often assessed at regular pre-scheduled appointments. These event times can be interval censored when study participants miss visits and return after a hiatus having experienced the event of interest. Censoring also occurs when participants never return or die before returning after missing visits. Such data are usually analyzed by assuming non-informative censoring, a special case of coarsening at random (CAR) [1–3]. However, the censoring process may be related to the event process. That is, the coarsening mechanism may be coarsened not at random (CNAR). Unfortunately, observed data are not sufficient to estimate the relationship between these processes. Therefore, analyzing coarsened data involves making unverifiable assumptions about the relationship between coarsening and event incidence.

There have been several recent methodologic developments to address coarsening not at random. Bayesian and frequentist methodologies were developed for interval-censored data to estimate cumulative incidence for (potentially) CNAR data by incorporating elicited expert information into the model [4]. A tool for quantifying local sensitivity to informative coarsening in the context of censoring has been proposed [5]. A test for dependent censoring has been developed using auxiliary visit-compliance information outside of the censoring interval [?]. Assuming a proportional hazards model, inference methods based on the collection of all attainable hazards ratios have been proposed [7]. The book by Sun [8] provides a compendium of analytical methods to handle noninformative interval censoring and a brief treatment of informative interval censoring. However, none of the aforementioned developments includes hypothesis assessment methods for informatively interval-censored data without imposing a proportional hazards model.

In this paper, we aim to develop formal hypothesis assessment procedures for comparing cumulative incidence functions using estimates derived by extending previously published methods [4] to accommodate censoring by death. For frequentist inference, we extend the logrank [9] and a two-sided version of the integrated weighted difference (IWD) [10] tests to allow informative censoring. We also generalize IWD to more than two groups. For Bayesian inference, we propose parameter transformations of posterior event-time probabilities, motivated by the logrank and IWD tests.

We apply our methods to AIDS Link to the Intravenous Experience (ALIVE), an ongoing prospective observational study of risk factors for human immunodeficiency virus (HIV) infection among injection drug users (IDUs) in Baltimore, Maryland [11–13]. In this study, HIV serostatus, a proxy for HIV infection status, was determined by subsequent regularly scheduled laboratory blood tests. For those who attended every visit on schedule, time to seroconversion (operationalized as years from enrollment here) is known, resulting in discrete event-time data. However, ALIVE participants often missed visits or attended visits off schedule, sometimes resulting in interval-censored seroconversion times only known within a range of years. Also, some seropositive participants never tested positive during the study due to loss to follow up, administrative censoring, or death. We compare ten-year seroconversion incidence (1988-1998) between those who self-reported sharing needles for injecting drugs during the six months prior to enrollment and those who did not. To perform a sensitivity analysis, we use information about the relationship between incidence and censoring elicited from ALIVE investigators and an AIDS epidemiologist. After estimating cumulative incidence functions, we assess the null hypothesis of equal HIV incidence between needle sharers and non-sharers.

2. Data Structure, Coarsening Models, and Inference

2.1. Data structure

Let T = t denote seroconversion during year t, where E = {t : t = 1, …, M + 1} is the support of T. M denotes last year of follow-up from enrollment, and T is arbitrarily set to be M + 1 for individuals who did not seroconvert during follow-up. Observed data for an individual may be a set of years from E, [L, R] = {t ∈ E : L ≤ t ≤ R}, where [L, R] is a coarsening of T because T ∈ [L, R]. For example, if a participant tests negative for HIV at a visit in year 2, returns for a visit in year 5 and tests positive, then serconversion could have occurred as early as year 2 (after the year 2 visit) and as late as year 5 (before the year 5 visit). Therefore L = 2, R = 5, and T ∈ [2, 5]. However, if the participant never returned after the year 2 visit, then seroconversion could have occurred anytime during or after year 2 within the study period, after the end of the study, or never. Therefore, L = 2, R = M + 1, and T ∈ [2, M + 1]. If seroconversion is known to occur in year t, t=1, …, M, then L = R = t. For example, if the participant would have returned later in year 2 and tested positive, then L = 2, R = 2, and thus T = 2. In general, if seroconversion did not occur during follow-up, then L = R = M + 1, and if knowledge about T is incomplete, then L < R. Those with L < R = M + 1 are right-censored drop-outs, and those with L < R < M + 1 are interval-censored returners [4].

We generalize the above ideas to accommodate the competing risk of death encountered in ALIVE. Those with first missed visit in year l who die in year r (r > l) either seroconverted in [L = l, R = r] or died seronegative. For those censored by death, [L = l, R = r] has an altered interpretation: R = r denotes death at year r, and possible event times are {l, …, r, M + 1}. Therefore, T = M + 1 denotes not seroconverting while at risk. For example, if a participant who tested negative during year 2 and missed subsequent visits died with unknown serostatus during year 5, then seroconversion either did not occur (T = M + 1) or occurred between years 2 and 5, inclusive. Therefore T ∈ {2, …, 5, M + 1}. Let Δ = δ, δ ∈ {0, 1}, indicate whether R is year of death. Thus, the aforementioned participant would have L = 2, R = 5, and Δ = 1. In general, if R < M + 1 and serostatus is unknown at year R due to death, then Δ = 1, otherwise Δ = 0.

Let G denote number, and denote the set, of groups to compare. We assume that, for those in group g, g ∈ 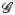, we observe n_g i.i.d. copies of the data. P_g(·) refers to probabilities for those in group g. Where necessary, the subscript i will denote subject-specific data.

2.2. Coarsening Models

2.2.1. Coarsening at random

Given L = l, R = r, and Δ = δ, let A(l, r, δ) denote possible values of T induced by censoring, where A(l, r, 0) = [l, r] and A(l, r, 1) = {[l, r], M + 1}. Within group g, CAR means

$$P_g(L=l,R=r,\Delta =\delta |T=t)\text{is constant in}t\in A(l,r,\delta ),$$ (1)

for all [l, r] ∈ E* = {[l, r] : l ≤ r, l, r ∈ E} and δ ∈ {0, 1}. Using Bayes' rule with 1, it can be shown that CAR also means

$$P_g(T=t|L=l,R=r,\Delta =\delta )=P_g(T=t|T\in A(l,r,\delta )),$$

for all t ∈ A(l,r,δ) [3].

In words, CAR means that among those in group g, the coarsening process provides no information about the seroconversion process beyond knowing that the true year of seroconversion resides in the set of years induced by censoring. As a result, estimated event-time probabilities for censored individuals only depend on estimated probabilities for years in that set.

2.2.2. CNAR models

The coarsening (in this case, censoring) mechanism cannot be identified from observed data [3], therefore we consider a class of CNAR models indexed by a (possibly group-specific) censoring bias function that allows elicited expert information to determine whether event probabilities for coarsened event times should be made stochastically larger at later times (seroconversions tend to occur late in the censoring set) or earlier times (seroconversions tend to occur early in the censoring set) relative to CAR [4]. We ‘exponentially tilt’ [14] the model assuming CAR for each group g, g ∈ :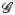

$$P_g(T=t|L=l,R=r,\Delta =\delta )=\frac{P_g(T=t|T\in A(l,r,\delta ))exp\{q_g(t,l,r,\delta )\}}{c_g(l,r,\delta ;q_g)}$$ (2)

where c_g(l, r, δ; q_g) = Σ_{s∈A(l,r,δ)} P_g(T = s | T ∈ A(l, r, δ)) exp{q_g(s, l, r, δ)}, and q_g(t, l, r, δ) is a specified censoring bias function of (t, l, r, δ) for those in group g. If q_g(·) does not depend on t, no tilting is performed, and CAR is assumed for group g. Information about death is only utilized to define possible seroconversion times and in q_g(·) to allow estimation of the seroconversion process without requiring estimation of the death process.

Using Bayes' rule, equation (2) can be represented as a selection model:

$$\text{log}\left\{\frac{P_g(L=l,R=r,\Delta =\delta |T=t)}{P_g(L=l,R=r,\Delta =\delta |T=t\prime )}\right\}=q_g(t,l,r,\delta )-q_g(t\prime ,l,r,\delta ),$$ (3)

for t, t′ ∈ A(l, r, δ). From (3), q_g(t, l, r, δ) is the group-g difference in log probability of having censoring set A(l,r,δ) comparing those with T = t to those with T equal to some reference value, t_ref, such that q_g(t_ref, l, r, δ) = 0.

2.2.3. Low-dimensional parameterization of q_g(·)

We temporarily return to ALIVE to describe a proposed censoring bias function. To facilitate a sensitivity analysis, we parameterize a censoring bias function by a small set of unidentified censoring bias parameters to capture key features of ALIVE. The function parameters differentiate between those who are interval censored, right-censored alive, and censored by death. We allow the censoring mechanism to differ between non-sharers (g = n) and needle sharers (g = s). Let ϕ = {ϕ_g: g = n, s} denote group-specific censoring bias parameters. The proposed censoring bias function is

$$\begin{array}{c}{q}_g(\varphi ,t,l,r,\delta )=\frac{9}{4}{\varphi }_{g1}\text{I}(r<M+1)(1-\delta )\frac{(t-l)}{(M-1)}+{\varphi }_{g2}\text{I}(r=M+1)\frac{(t-l)}{M}\\ +{\varphi }_{g3}\text{I}(r<M+1)(\delta )\frac{(t-l)}{M},g=n,s,\end{array}$$ (4)

where ϕ_g = {ϕ_g1, ϕ_g2, ϕ_g3}, and I(·) denotes the indicator function. From equation (3), exp{ϕ_g1} is the probability ratio of having L = 1, R = 5, and Δ = 0 comparing those with T = 5 to those with T = 1, among those in group g, g = n, s. The factor 9/4 is used to attain this interpretation for elicitation. Similarly, exp{ϕ_g2} is the needle sharing-specific probability ratio of having L = 1, R = M + 1, and Δ = 0, comparing those with T = M + 1 to those with T = 1. Lastly exp{ϕ_g3} is the needle sharing-specific probability ratio of having L = 1, R = M + 1, and Δ = 1, comparing those with T = M + 1 to those with T = 1. Note that ϕ_g1, ϕ_g2, and ϕ_g3 refer to returning, dropping out alive, and being censored by death, respectively, for those in group g.

From (2), we see that when exp{ϕ_g1} > 1 (< 1), returners are assumed to be more (less) likely to seroconvert late than seroconvert early. When exp{ϕ_g2} > 1 (< 1), drop-outs who remain alive are assumed more (less) likely to seroconvert late or never than seroconvert early. Lastly, When exp{ϕ_g3} > 1 (< 1), drop-outs who die with unknown serostatus are assumed more (less) likely to seroconvert late or never than seroconvert early.

The form of Equation 4 was chosen to capture key features of ALIVE, such as the presence of both interval-censoring and drop-outs as well as the competing risk of death. Equation 4 also allows us to explore sensitivity to different assumptions about needle sharers and non-sharers because the purpose of the analysis is to compare HIV incidence between these two groups. Lastly, we specified Equation 4 to be a scientifically interpretable low-dimensional function to facilitate elicitation from subject matter experts. Thus, for specifying a censoring bias function for other applications, one should consider study design features, scientific hypotheses, interpretability of parameters, and ease of elicitation.

2.3. Inference

2.3.1. Frequentist inference

Let p_gj be the event probability during year j among those in group g. Frequentist estimation of p_g = p_g1, …, p_g(M+1) is performed via the expectation-maximization algorithm [15] by replacing coarsened event times with their expected values given L, R, and Δ [4]. See Appendix I for details.

Probability estimates are used to estimate F_g(·), the cumulative incidence function for group g, $F_g(t)\equiv P_g(T\le t)={\sum }_{j=1}^t{p}_{gj}$. Once estimates of p = {p_g, g ∈ 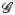}, denoted p̂, and standard errors are obtained, statistics can be derived for testing the null hypothesis H₀ : F_g(·) = F_g′(·), g = g′ ∀g, g′ ∈ 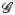using the delta method, including logrank (LR) and IWD tests.

Let LR = {LR_g, g ∈ 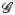}^t be a vector of length 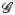with gth component $L{R}_g={\sum }_{j=1}^M(d_{gj}-n_{gj}{d}_j/n_j)$, where d_gj = n_gp̂_gj is the estimated number of seroconverts in group g during year j, $n_{gj}=n_g{\sum }_{k=j}^{M+1}{\widehat{p}}_{gk}$ is the estimated number at risk in group g during year j, d_j = Σ_g∈Gd_gj, and n_j = Σ_g∈Gn_gj. Thus LR_g takes the form of the logrank test numerator. The variance of LR, Σ_LR, is a 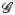× 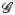matrix estimated by Σ̂_LR (see Appendix I). The test statistic is ${\chi }_{\mathit{\text{LR}}}^2={\mathbf{\text{LR}}}^t{\widehat{\sum }}_{\mathit{\text{LR}}}^{-}\mathbf{\text{LR}}$, where ${\widehat{\sum }}_{LR}^{-}$ denotes generalized inverse of Σ̂_LR. Under the null hypothesis, ${\chi }_{LR}^2$ has a χ² distribution with G − 1 degrees of freedom. The generalized inverse is needed owing to the loss of one degree of freedom from estimating p_j by d_j/n_j.

The IWD test was originally proposed to perform a one-sided hypothesis for G = 2 [10]. We generalize it to a two-sided test. The two-sample test with weight w(·), estimated by ŵ(·), has numerator $\mathit{\text{IWD}}={\sum }_{j=1}^M\widehat{w}(j)\left[{\widehat{F}}_g(j)-{\widehat{F}}_{g\prime }(j)\right]$, where ${\widehat{F}}_g(j)={\sum }_{k=1}^j{\widehat{p}}_{gk}$. Let ${\mathit{\sigma }}_{\mathit{\text{IWD}}}^2$ denote the variance of IWD, estimated by ${\widehat{\mathit{\sigma }}}_{\mathit{\text{IWD}}}^2$ (Appendix I). The test statistic, Z_obs = IWD/σ̂_IWD, can be compared to a standard normal distribution [10]. When G ≥ 2, we modify the test by comparing F̂_g(j), g∈ 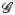, to the estimated overall cumulative function: F̂(j) = Σ_g∈Gn_gF̂_g(j)/n. Let IWD = {IWD_g, g ∈ 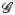}^t be a vector of length G with gth component $IW{D}_g={\sum }_{j=1}^M\widehat{w}(j)\left[{\widehat{F}}_g(j)-\widehat{F}(j)\right]$. The variance of IWD is a G × G matrix, Σ_IWD, estimated by Σ̂_IWD (Appendix I). The test statistic, ${\chi }_{\mathit{\text{IWD}}}^2={\mathbf{\text{IWD}}}^t{\widehat{\sum }}_{\mathit{\text{IWD}}}^{-}\mathbf{\text{IWD}}$, is distributed χ² with G − 1 degrees of freedom under the null hypothesis due to estimation of F̂(j)

2.3.2. Bayesian inference

We specify a Dirichlet prior density for p_g to obtain posterior cumulative incidence. Conjugate analysis cannot be performed, therefore we use a Markov Chain Monte Carlo (MCMC) algorithm described in Appendix II [4]. Simulated p's are then transformed into an interpretable one-dimensional quantity summarizing the difference between G cumulative incidence functions.

One proposed quantity is motivated by the logrank test. Let N_sim denote the Markov chain length. Let p^(s) be the vector of simulated p at iteration s, and let LR(p^(s)) denote the posterior logrank transformation, a vector of length G with gth component $L{R}_g({\mathbf{\text{p}}}^{(s)})={\sum }_{j=1}^M\left(d_{gj}^{(s)}-n_{gj}^{(s)}{d}_j^{(s)}/n_j^{(s)}\right)$, where $d_{gj}^{(s)}=n_g{p}_{gj}^{(s)},n_{gj}^{(s)}=n_g{\sum }_{k=j}^{M+1}{p}_{gj}^{(s)},d_j^{(s)}={\sum }_{g\in \mathcal{G}}{d}_{gj}^{(s)}$, and $n_j^{(s)}={\sum }_{g\in \mathcal{G}}{n}_{gj}^{(s)}$. Let Σ_LR(p^(s)) be a G × G matrix motivated by the variance of the logrank test numerator when the null hypothesis is true (Appendix II). The transformation involves calculating ${\chi }_{\mathit{\text{LR}}}^2({\mathbf{\text{p}}}^{(s)})=\mathbf{\text{LR}}{({\mathbf{\text{p}}}^{(s)})}^t{\sum }_{\mathit{\text{LR}}}^{-}({\mathbf{\text{p}}}^{(s)})\mathbf{\text{LR}}({\mathbf{\text{p}}}^{(s)})$. The median of this posterior parameter transformation under the null hypothesis is the median of a χ² distribution with G − 1 degrees of freedom, approximately μ_G = G − 1 − 2/3 + 4/[27(G − 1)] − 8/[729(G − 1)²]. The vector of logrank parameter transformations is denoted by ${\mathbf{\chi }}_{LR}^2(\mathbf{\text{p}})=\{{\chi }_{LR}^2({\mathbf{\text{p}}}^{(1)}),\cdots {\chi }_{LR}^2({\mathbf{\text{p}}}^{(N_{\mathit{\text{sim}}})})\}$. Let ω denote the observed data, where ω_igj is the indicator that t_j ∈ [L_ig, R_ig], i.e., that time t_j is a possible event time for person i in group g. A posterior tail probability summarizing the degree of overlap between the observed distribution and expected distribtution under the null can be calculated by $2P({\mathbf{\chi }}_{LR}^2(\mathbf{\text{p}})\le {\mu }_G|\omega )$. For a visual representation, the ${\mathbf{\chi }}_{LR}^2(\mathit{\text{p}})$ can be plotted with a ${\chi }_{G-1}^2$ kernel, the distribution of the logrank test statistic when all G event-time distributions are equal. When G = 2, a transformation can be calculated by Z_LR(p^(s)) = LR_g(p^(s))/σ_LR(p^(s)), where σ_LR(p^(s)) is the standard deviation of LR_g(p^(s)). Let Z_LR(p) = {Z_LR(p⁽¹⁾), ⋯, Z_LR(p^(N_sim))}; Z_LR(p) can be plotted with a standard normal kernel, and the tail probability can be calculated as 2 [min{P (Z_LR(p) ≥ 0 | ω), P (Z_LR(p) ≤ 0 | ω)}].

The second quantity considered is motivated by the IWD test. Let IWD(p^(s)) denote the posterior IWD transformation, a vector of length G with gth component $IW{D}_g({\mathbf{\text{p}}}^{(s)})={\sum }_{j=1}^M{w}^{(s)}(j)\left[F_g^{(s)}(j)-F^{(s)}(j)\right]$, where $F_g^{(s)}(j)={\sum }_{k=1}^j{p}_{gk}^{(s)},F^{(s)}(j)={\sum }_{g\in \mathcal{G}}{n}_g{F}_g^{(s)}(j)/n$, and w(^s)(j) is a weight function. Let Σ_IWD(p^(s)) be a G × G matrix motivated by the variance of the IWD test numerator (Appendix II). The parameter transformation is ${\mathbf{\chi }}_{\mathit{\text{IWD}}}^2({\mathbf{\text{p}}}^{(s)})=\mathbf{\text{IWD}}{({\mathbf{\text{p}}}^{(s)})}^t{\sum }_{\mathit{\text{IWD}}}^{-}({\mathbf{\text{p}}}^{(s)})\mathbf{\text{IWD}}({\mathbf{\text{p}}}^{(s)})$. When G = 2, inference is performed like that for Z_LR(p) using Z_IWD(p) = {Z_IWD(p⁽¹⁾), ⋯, Z_IWD(p^(N_sim))}, where Z_IWD(p^(s)) = IWD₂(p^(s))/σ_IWD(p^(s)), and σ_IWD(p^(s)) is the same form as the standard deviation of IWD₂(p^(s)).

These posterior tail probabilities are interpreted differently from frequentist p-values. Instead of calculating the tail probability of a test statistic under H₀ at the observed value, we calculate the posterior tail probability of a parameter transformation at its expected value when H₀ is true. This tail probability summarizes the degree of overlap between the observed posterior parameter transformation distribution and that expected under H₀, where tail probabilities of 1 and 0 denote perfect and no overlap, respectively. Comparing the posterior distribution to some reference posterior (in this case, the expected posterior under H₀) to assess Bayesian hypotheses is thought to be more appropriate than inference by Bayes' factors for continuous parameters, because calculating Bayes' factors requires hypotheses to have strictly positive prior probabilities [16]. The reference posterior approach has the additional benefit of being simpler to perform than calculation Bayes' factors because it does not require running the MCMC multiple times.

3. Simulation Study

Simulations were performed for two-sample and G-sample logrank and IWD tests with G = 3 and 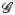= {1, 2, 3}, allowing left, interval, and right censoring, but no competing risks. Event times were simulated from a multinomial distribution using the continuation ratio logistic model with M = 4. Let ρ_ij = P(T_i = j | T_i ≥ j, Z_i) for j = 0, …, M + 1. The continuation ratio model for the three-sample simulation is logit $({\rho }_{ij})={\theta }_j+\mathbf{\beta }{\mathbf{\text{Z}}}_i^t$, j = 0, …, M, where β = {β₁, β₂} and Z_i = {Z_i1, Z_i2}, where Z₁ = I(g = 2) and Z₂ = I(g = 3). Replacing $\mathbf{\beta }{\mathbf{\text{Z}}}_i^t$ with β₁Z_1i results in the continuation ratio model used for the two-sample simulation study. For the three-group simulation study, groups two and three are assumed to have the same distribution (e.g., a control group and two exchangeable treatments), β₁ = β₂ = β. For each group, censoring intervals were simulated given T. The function q(·) and the distribution of T for group g do not identify P(L_i = l, R_i = r | Z_i, T_i) = P_g(L_i = l, R_i = r | T_i). The number of free parameters in this distribution for each group equals (M + 2)(M + 1)/2, the number of intervals minus the number of event times. These parameters (interval probabilities) were fixed at values satisfying the constraints P_g(T = t) > P_g(T = t, L = l, R = r), for g ∈ 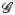. The strict inequality allows positive probability for each combination of l and r including t. The remaining M + 2 interval probabilities were identified from the constraints Σ_l≤rP_g(L = l, R = r) = 1 and Σ_{{l,r}: l≤t≤r}P_g(T = t | L = l, R = r)P_g(L = l, R = r) = P_g(T = t).

True event times, T, were drawn given g, with β ∈ {0, 0.75} and θ = {−0.65, −0.55, −0.45, −0.15, −0.05}. Let ϕ = {ϕ_g: g ∈ 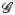} be the vector of group-specific censoring bias parameters for the censoring bias function q_g(t, l, r) = ϕ_g(t−l)/(r−l). The true censoring bias parameters were combinations of {−log(2), 0, log(2)}. In this study, ϕ₂ = ϕ₃.

The empirical sizes of the tests were estimated assuming β = 0. Empirical power was estimated for the alternative hypothesis H₁ : F_g(·) ≠ F_g′ (·) when β = 0.75, where g = 1 and g′ = 2 for the two-sample test and where g ≠ g′ for some g, g′ ∈ 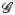for the G-sample test. We chose n_g = 100, 200, 500 and performed 1000 simulations for each specification. Simulations were also performed on uncensored data. Values of the true parameters were chosen to produce between 86% and 97% censoring (i.e., P(L ≠ R)), depending on ϕ and β. For censored data, two weight functions were used for the IWD test, ŵ(j) = 1, and ŵ(j) = w*(j), where $w\ast (j)\equiv {\prod }_{g=1}^G{\widehat{K}}_g(j)/\left[{\sum }_{g=1}^G(n_g/n){\widehat{K}}_g(j)\right]$, and K̂_g(j) is the sample proportion of individuals in group g with known serostatus in year j [10]. When data are uncensored, w*(j) simplifies to 1.

Simulation test results are shown in Tables I and II. The first row of each sample size-specific study shows results for uncensored data. The first column shows the true ϕ that generated the censoring intervals for simulations with censoring. The second column shows the assumed ϕ for the model with censored data, either CAR or the true ϕ. Both tables show results for six tests: the IWD test with w = 1 and w = w* and the logrank test, all for G = 2 and G = 3. The empirical size results in Table I show the tests perform well with no censoring, and the performance improves as the sample size increases. When ϕ are correctly specified, or when the bias for both parameters is of equal magnitude in the same direction (e.g., true ϕ are {−log(2), −log(2)}, but CAR is assumed), the tests perform well. Empirical size differs most from nominal size when ϕ are biased in different directions (e.g., true ϕ are {−log(2), log(2)}, but CAR is assumed). No single test performs uniformly better than the others, however, the logrank test tends to be more anticonservative than the IWD test for smaller samples sizes, even with no censoring. When the data are censored, the three-group IWD test produces the most conservative (n = 500, true ϕ = {−log(2), −log(2)}) and most anticonservative (n = 200, true ϕ = {−log(2), 0}) results. Empirical power is shown in Table II. In general, the test with weight w* is more powerful than the analogous test with w = 1. With no censoring, the logrank test is more powerful than the IWD test. However, with censoring in smaller sample sizes, the IWD test tends to be more powerful. In larger sample sizes, the difference is negligible. The true underlying distribution has hazard ratio 2.12 (exp{0.75}) comparing groups 2 and 3 to group 1. When groups 2 and 3 are biased to have greater (lower) hazards relative to group 1, power is increased (decreased).

Table I.

Simulation results: empirical size of integrated weighted difference (IWD) and logrank (LR) tests with nominal size 0.05. 1000 iterations, M = 4, n₁ = n₂ = n₃ = n., ϕ₂ = ϕ₃ when G = 3, no censoring or 86% censoring.

n.	True {ϕ1, ϕ2}	Modeled ϕ	2 groups w = 1	2 groups w*	2 groups LR	3 groups w = 1	3 groups w = w*	3 groups LR
100	(no censoring)		0.054		0.061	0.055		0.064
	−log(2), −log(2)	Truth	0.043	0.038	0.048	0.043	0.042	0.059
		CAR	0.055	0.056	0.066	0.063	0.060	0.075
	−log(2), 0	Truth	0.050	0.058	0.048	0.052	0.052	0.057
		CAR	0.129	0.127	0.131	0.128	0.131	0.137
	−log(2), log(2)	Truth	0.058	0.059	0.062	0.050	0.054	0.061
		CAR	0.311	0.292	0.297	0.311	0.306	0.304
200	(no censoring)		0.054		0.055	0.055		0.059
	−log(2), −log(2)	Truth	0.044	0.044	0.036	0.049	0.054	0.051
		CAR	0.060	0.059	0.059	0.054	0.058	0.054
	−log(2), 0	Truth	0.055	0.052	0.051	0.072	0.071	0.066
		CAR	0.208	0.201	0.209	0.197	0.198	0.204
	−log(2), log(2)	Truth	0.053	0.052	0.058	0.052	0.055	0.050
		CAR	0.500	0.490	0.464	0.528	0.518	0.511
500	(no censoring)		0.050		0.049	0.052		0.054
	−log(2), −log(2)	Truth	0.054	0.052	0.053	0.062	0.062	0.061
		CAR	0.045	0.043	0.050	0.061	0.059	0.059
	−log(2), 0	Truth	0.054	0.056	0.056	0.059	0.060	0.063
		CAR	0.389	0.377	0.366	0.364	0.364	0.365
	−log(2), log(2)	Truth	0.047	0.048	0.049	0.034	0.035	0.040
		CAR	0.891	0.880	0.863	0.917	0.909	0.894

Table II.

Simulation results: empirical power of IWD and LR tests with size 0.05. 1000 iterations, β = 0.75 (hazard ratio = 2.12), M = 4, n₁ = n₂ = n₃ = n, ϕ₂ = ϕ₃ when G = 3, 97% censoring when Z = 1 and 86% censoring when Z = 0 or no censoring.

n.	True {ϕ1, ϕ2}	Modeled ϕ	2 groups w = 1	2 groups w*	2 groups LR	3 groups w = 1	3 groups w*	3 groups LR
100	(no censoring)		0.966		0.972	0.976		0.982
	−log(2), −log(2)	Truth	0.860	0.860	0.850	0.909	0.900	0.907
		CAR	0.638	0.668	0.601	0.697	0.723	0.684
	−log(2), 0	Truth	0.810	0.837	0.785	0.867	0.884	0.865
		CAR	0.929	0.939	0.912	0.970	0.976	0.963
	−log(2), log(2)	Truth	0.756	0.784	0.750	0.820	0.841	0.823
		CAR	1.000	1.000	0.999	1.000	1.000	1.000
200	(no censoring)		0.999		0.999	1.000		1.000
	−log(2), −log(2)	Truth	0.993	0.989	0.991	0.998	0.998	0.999
		CAR	0.916	0.931	0.893	0.953	0.968	0.941
	−log(2), 0	Truth	0.973	0.979	0.971	0.992	0.994	0.988
		CAR	0.996	0.997	0.996	0.999	0.999	0.997
	−log(2), log(2)	Truth	0.961	0.973	0.959	0.982	0.991	0.985
		CAR	1.000	1.000	1.000	1.000	1.000	1.000
500	(no censoring)		1.000		1.000	1.000		1.000
	−log(2), −log(2)	Truth	1.000	1.000	1.000	1.000	1.000	1.000
		CAR	1.000	1.000	1.000	1.000	1.000	1.000
	−log(2), 0	Truth	1.000	1.000	1.000	1.000	1.000	1.000
		CAR	1.000	1.000	1.000	1.000	1.000	1.000
	−log(2), log(2)	Truth	1.000	1.000	1.000	1.000	1.000	1.000
		CAR	1.000	1.000	1.000	1.000	1.000	1.000

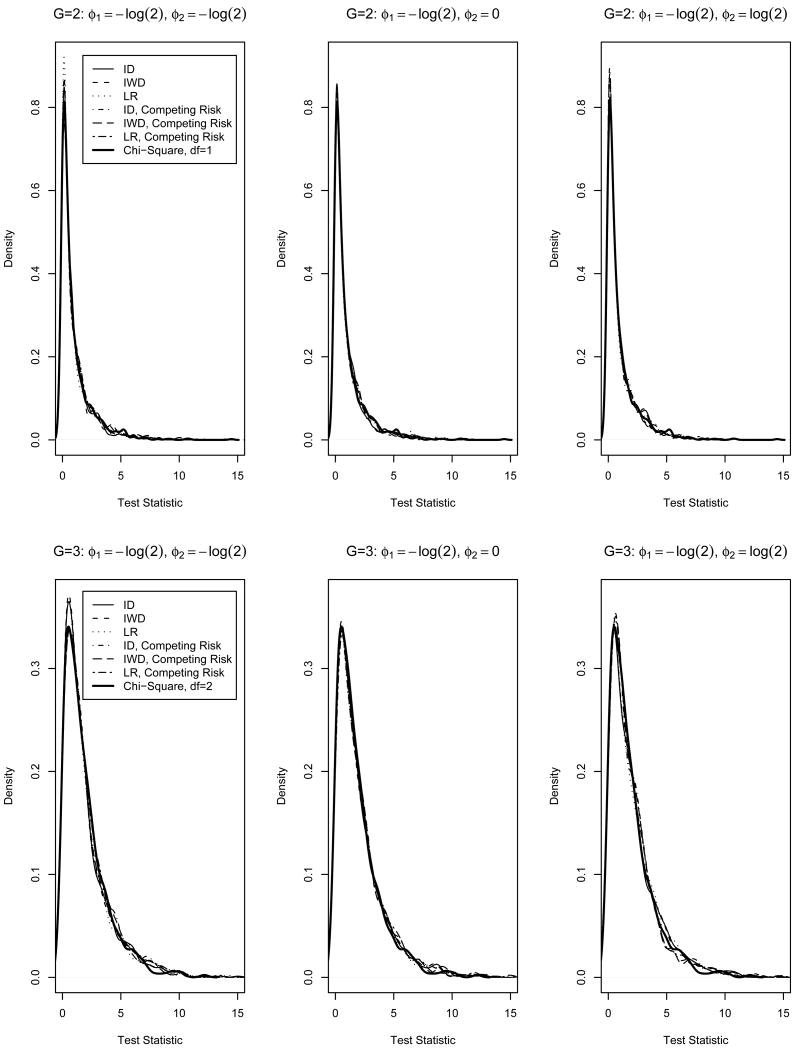
We repeated the simulation study with n=500 and 1000 iterations by including a competing risk. In this case, the number of free parameters is (M + 2)² because there are twice as many intervals with a competing risk than without a competing risk i.e., specify probabilities for intervals L = l, R = r, Δ = 0 and L = l, R = r, Δ = 1 rather than only L = l, R = r. Interval probabilities were fixed at values satisfying the constraints P_g(T = t) > P_g(T = t, L = l, R = r, Δ = δ), for g ∈ 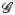. Analogous to the case with no competing risk, the strict inequality allows positive probability for each combination of l, r, δ including t. Similarly, the remaining M + 2 interval probabilities were identified from the constraints Σ_δ∈{0,1}Σ_l≤rP_g(L = l, R = r, Δ = δ) = 1 and Σ_δ∈{0,1} Σ_{{l,r}:t∈A(l,r,δ)} P_g(T = t | L = l, R = r, Δ = δ)P_g(L = l, R = r, Δ = δ) = P_g(T = t). The empirical type I error from this simulation ranged from 0.048 (ϕ = {−log(2), 0}, IWD test with w = w* and G = 2) to 0.062 (ϕ = {−log(2), −log(2)}, IWD test with w = w* and G = 2; ϕ = {−log(2), 0}, IWD test with w = 1 and logrank test, both with G = 3). The empirical type I errors were, on average, closer to the nominal type I error than those in Table I obtained without the competing risk. Trends in empirical power with the competing risk were similar to those without the competing risk in Table II (not shown). The empirical distribution of the test statistic is graphically compared with the chi-square distribution in Figure 1. Regardless of ϕ, number of groups, and presence of a competing risk, Figure 1 shows that the distributions of all three test statistics (ID, IWD, and LR) approximate a chi-square distribution well.

Figure 1.

Simulation study results, N_g = 500, N_sim = 1000. Empirical distribution of integrated weighted difference (ID, w = 1; IWD, (w = w*) and logrank (LR) tests compared to a chi-square distribution (two groups, df=1; three groups, df=2), with and without a competing risk.

4. Example Data Analysis: ALIVE

We apply our proposed inference methods to ALIVE to compare ten-year cumulative incidence functions of seroconversion between those who self-reported needle sharing at enrollment and those who did not. Among the 2,205 ALIVE participants with complete needle-sharing information, 1,527 reported sharing needles, and 678 did not. Among those reporting sharing needles, 190, 1,135, 144, and 58 participants were censored by death, right-censored by drop-out or end of study, interval censored, and exactly observed, respectively. The respective numbers among those reporting not sharing needles were 73, 522, 54, and 29. Among needle sharers, 242 (15.8%) total died within ten years of enrollment. Similarly, 100 (14.7%) total non-sharers died during the study. The relationship between needle-sharing and seroconversion may be driven by differential death rates between groups. However, logrank test results (p = 0.52) do not support this hypothesis. Death as a primary endpoint was not addressed in the sensitivity analysis.

4.1. Elicitation and sensitivity analysis

To elicit values of ϕ in equation (4), two ALIVE investigators were seperately interviewed to obtain ranges of the parameters and hyperparameters found in Table III (columns 4-5, and 6-7, respectively). Prior distributions of p and ϕ were elicited from an external AIDS epidemiologist and an ALIVE investigator, respectively. The AIDS epidemiologist was interviewed regarding the expected seroconversion time distribution and the weight of expert opinion relative to ALIVE data. An expert unaffiliated with ALIVE was consulted to obtain opinion prior to ALIVE. The elicited weight of prior opinion was 10 percent of final results (ALIVE data weighted 90 percent). Prior information about seroconversion probabilities was not specific to needle-sharing status to reflect the “null” hypothesis of equal cumulative incidence functions. Elicited ranges of exp{ϕ} were centered and scaled parameters ranged 0 to 1 with assumed beta distributions. Plots of beta distributions were used to elicit the beta hyperparameters from an ALIVE investigator. To accommodate correlations between the parameters, we consider the normal approximation to the beta distribution. Using scatterplots of pairwise correlations between parameters to elicit covariances, the ALIVE investigator's prior variance-covariance matrix involved positive correlations for several combinations of needle-sharing group and censoring type:

Table III.

Elicited range of exp (ϕ) and hyperparameters for beta distributions used in Bayesian analyses.

(1)	(2)	(3)	(4)	(5)	(6)	(7)
Needle-sharing	Censoring	ϕ	Range of exp (ϕ)		Shape	Scale
Yes	Interval-censored	ϕs1	1.75−1	2.75	2.00	7.75
	Dropped out	ϕs2	1.50	3.00	5.25	2.75
	Dead	ϕs3	2.00	2.50	2.00	1.00
No	Interval-censored	ϕn1	1.15−1	2.50	2.00	9.50
	Dropped out	ϕn2	1.75	2.50	3.75	2.00
	Dead	ϕn3	2.00	2.50	2.00	1.00

$$\text{correlation}(exp\{\varphi \})=\left[\begin{array}{cccccc}exp\{{\varphi }_{s1}\}& & & & & \\ 0.00& exp\{{\varphi }_{s2}\}& & & & \\ 0.00& 0.60& exp\{{\varphi }_{s3}\}& & & \\ 0.75& 0.00& 0.00& exp\{{\varphi }_{n1}\}& & \\ 0.00& 0.75& 0.45& 0.00& exp\{{\varphi }_{n2}\}& \\ 0.00& 0.50& 0.75& 0.00& 0.55& exp\{{\varphi }_{n3}\}\end{array}\right]$$

Additional details about the elicitation process and rationale for ranges of parameters and their hyperparameters can be found elsewhere [17].

4.2. Frequentist results

Frequentist inference was performed using estimates assuming CAR and combinations of minimum and maximum elicited values of ϕ [4]. For each combination, needle-sharing specific seroconversion probabilities were estimated, and logrank and IWD tests were performed with weights w(j) = 1 and w*(j).

Table IV shows estimated needle-sharing specific one-, five-, and ten-year cumulative incidence and 95 percent confidence intervals (using the complementary log-log transformation), and p-values for three values of ϕ: ϕ = 0 (CAR assumed), {max(ϕ_n), min(ϕ_s)}, and {min(ϕ_n), max(ϕ_s)}. When CAR is assumed, estimated probabilities are similar across groups, corroborated by large p-values for IWD and logrank tests. The minimum p-values were produced when needle sharers are assumed to seroconvert stochastically early in their observed sets (minimum ϕ_s) and non-sharers are assumed to seroconvert stochastically late in their observed sets (maximum ϕ_n) according to elicited ranges for ϕ. Estimated cumulative incidence is lower for non-sharers than for needle-sharers under this assumption. Similarly, when the opposite assumption is made (minimum ϕ_n, maximum ϕ_s), estimated cumulative incidence was higher for non-sharers than for needle sharers. Test results were most sensitive to values of ϕ_s2 (not shown), because needle-sharing drop-outs alive at the end of year ten is the largest needle-sharing group-by-censoring type category in ALIVE, and experts expressed the most uncertainty about them.

Table IV.

ALIVE frequentist results. Estimated cumulative incidence (F̂) and 95% confidence intervals (CI) at years 1, 5, and 10; logrank and integrated weighted difference (IWD) p-values across censoring assumptions.

							IWD
		Non Sharers		Needle Sharers		Logrank	w=1	w = w*
Assumption	Year	F̂	95% CI	F̂	95% CI	p-value	p-value	p-value
CAR	1	0.07	0.05, 0.10	0.05	0.04, 0.07	0.68	0.86	0.87
	5	0.16	0.13, 0.20	0.18	0.15, 0.20
	10	0.23	0.19, 0.28	0.24	0.22, 0.28
Max ϕn, Min ϕs	1	0.05	0.03, 0.07	0.05	0.03, 0.06	0.11	0.17	0.18
	5	0.11	0.09, 0.14	0.14	0.12, 0.17
	10	0.17	0.14, 0.21	0.21	0.18, 0.24
Min ϕn, Max ϕs	1	0.06	0.04, 0.08	0.03	0.02, 0.05	0.68	0.53	0.52
	5	0.12	0.10, 0.16	0.12	0.10, 0.14
	10	0.19	0.15, 0.23	0.18	0.16, 0.20

4.3. Bayesian results

Prior beliefs about seroconversion probabilities and censoring bias parameters were converted into Dirichlet and multivariate normal hyperparameters, respectively. First, exp{ϕ} were centered and scaled to have range [0, 1] and marginal beta distributions, inducing means and variances used to make normal approximations to beta densities. Elicited correlation coefficients induced an approximate multivariate normal joint distribution for centered and scaled exp{ϕ}, and the logit transformation was used for simulating from a multivariate normal distribution.

Bayesian analysis was first performed for fixed ϕ. We examined results assuming CAR and the same two extreme specifications used in frequentist analysis, {max(ϕ_n), min(ϕ_s)} and {min(ϕ_n), max(ϕ_s)}. MCMC was run for 500 burn-in and 5000 additional iterations. A previously published diagnostic scheme was used for all Bayesian analyses [18]. Needle-sharing specific mean posterior one-, five-, and ten-year cumulative incidence, 95 precent credible intervals, and parameter transfomation tail probabilities are shown in Table V. The IWD parameter transformation was only calculated for w = 1 because, given imputed complete data, w* = 1. Mean posterior cumulative incidence was higher than analogous results from frequentist analyses due to shrinkage to the prior, which suggested more accelerated seroconversion than estimates from data alone. Also, credible intervals are slightly narrower than analogous confidence intervals, especially for the ten-year cumulative incidence, due to additional information from the prior and many drop outs. The tail probabilities were similar to analogous frequentist p-values.

Table V.

ALIVE Bayesian results. Mean posterior cumulative incidence (F̂) and 95% credible intervals (CI) at years 1, 5, and 10; logrank (LR) and integrated weighted difference (IWD) with w = 1 tail probabilities (tail prob.) across censoring assumptions.

Assumption	Year	Non Sharers		Needle Sharers		LR	IWD
		F̂	95% CI	F̂	95% CI	tail prob.	tail prob.
CAR	1	0.07	0.05, 0.10	0.06	0.04, 0.07	0.74	0.84
	5	0.18	0.15, 0.22	0.19	0.16, 0.22
	10	0.26	0.22, 0.30	0.26	0.24, 0.29
Max ϕn, Min ϕs	1	0.05	0.03, 0.07	0.05	0.06, 0.04	0.12	0.13
	5	0.13	0.11, 0.16	0.16	0.14, 0.18
	10	0.20	0.16, 0.23	0.23	0.20, 0.26
Min ϕn, Max ϕs	1	0.06	0.04, 0.08	0.04	0.03, 0.05	0.63	0.47
	5	0.14	0.12, 0.16	0.14	0.12, 0.16
	10	0.21	0.18, 0.25	0.20	0.18, 0.22
Random ϕ	1	0.05	0.04, 0.07	0.04	0.03, 0.06	0.74	0.82
	5	0.14	0.11, 0.17	0.14	0.12, 0.16
	10	0.20	0.17, 0.24	0.21	0.18, 0.23

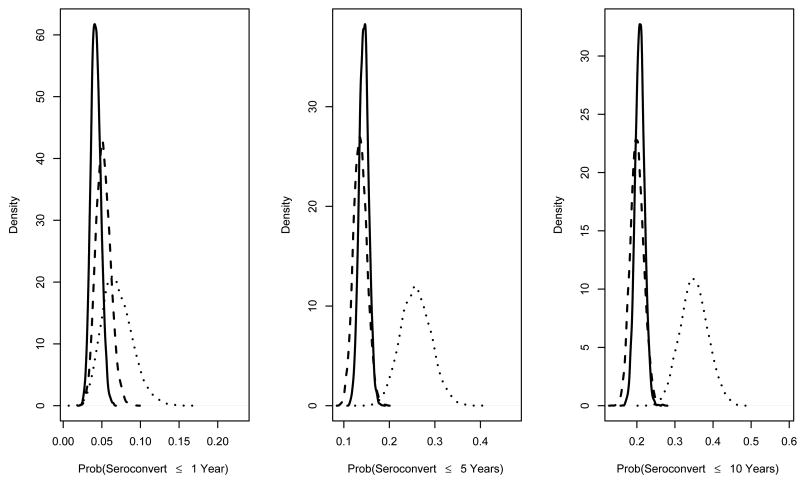
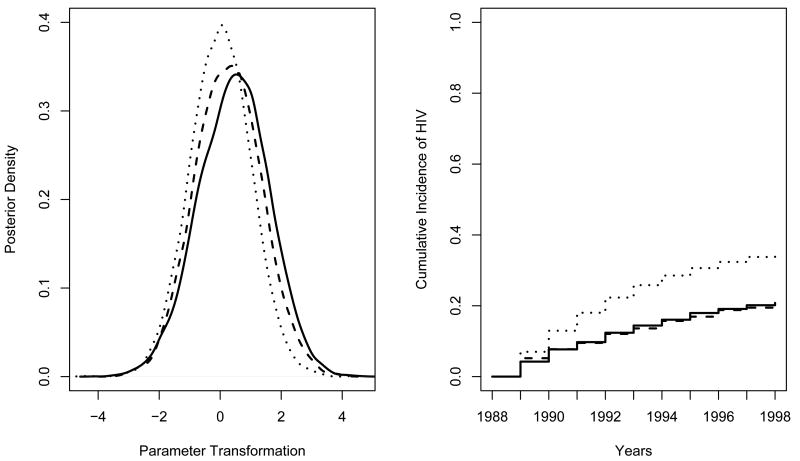
Fully Bayesian analysis was then performed, averaging over the posterior distribution of ϕ. MCMC was burned in for 1000 iterations and run for 10000 more. Metropolis-Hastings [19] acceptance was 64 and 86 percent for needle sharers and non-sharers, respectively. Prior and posterior densities for exp {ϕ} were approximately equal, reflecting no information about these parameters in the data (not shown). Prior and posterior densities for one-, five-, and ten-year cumulative incidence are reported in Figure 2. Posterior densities are tighter than priors, due to small weight given to elicited information relative to the data. Cumulative incidences are between those obtained using extreme elicited censoring bias parameter values, and tail probabilities were similar to those assuming CAR (Table V). Figure 3 shows that the LR and IWD posterior parameter transformations differ little from a standard normal kernel, suggesting seroconversion cumulative incidence functions do not differ across needle-sharing status. Posterior mean cumulative incidence and tail probabilities in Table V corroborate this conclusion.

Figure 2.

ALIVE Bayesian results. Posterior (solid line, needle sharers; dashed line, non-sharers) and prior (dotted line) densities of one-, five-, and ten-year cumulative incidence.

Figure 3.

ALIVE Bayesian Inference. Posterior density for Z_LR(p) (solid line) and Z_IWD(p) (dashed line) parameter transformations with standard normal kernel (dotted line). Mean posterior (solid line, needle sharers; dashed line, non-sharers) and prior (dotted line) cumulative incidence.

5. Discussion

We developed two approaches for comparing cumulative incidence functions for informatively coarsened event-time data using estimates derived from previously published methods [4] and applied them to ALIVE. We accounted for the competing risk of death in the analysis, extended two test statistics to accommodate informatively coarsened data, and proposed a novel approach for Bayesian hypothesis assessment that is interpretable and easily calculated after performing a single MCMC run. We also extended the IWD test to be two sided and to accommodate more than two groups. We showed that these tests perform well when the censoring mechanism is correctly specified. The simulation study was performed using a regression model appropriate for discrete event-time data. Future research includes estimation and variable selection using this model in the presence of informative coarsening.

CAR-based analyses of ALIVE data suggest baseline needle sharing is not associated with time to seroconversion. These conclusions are robust to elicited assumptions about the visit-compliance process. CAR-based and random-ϕ posterior cumulative incidence varied little. Had our sensitivity analysis results produced conflicting conclusions, the test results could be displayed using contour plots like in [20] to allow readers to see conclusions as a function of ϕ. Needle sharing status poses a short term risk for HIV and may change over time, thus future research involves developing methods to accommodate time-varying risk factors.

The proposed inference methods are beneficial in that they facilitate a sensitivity analysis across assumptions about the censoring mechanism using results from a previously published estimation method. The methods are generalizable to any scientific application where the goal is to compare cumulative incidence across groups in the presence of informative censoring. However, the form of the censoring bias function should differ as appropriate, and interpretations of the censoring bias parameters would be context specific. The approaches proposed here are preferable to other ad hoc sensitivity analyses involving single imputation of interval endpoints or interval midpoint imputation, because these approaches underestimate standard errors [21]. Also, interval endpoint imputation involves extreme assumptions that may not be scientifically plausible. In particular, imputing L and R for T is equivalent to specifying ϕ = −∞ and ϕ = ∞, respectively.

Despite the benefits, these methods have limitations. In particular, results may be sensitive to distributional assumptions. For example, the correlation structure of Dirichlet priors does not take advantage of time ordering of visits. Also, the proposed methods are limited to small numbers of groups. Lastly, utilizing these methods requires a potentially challenging elicitation process and difficult choice of censoring bias function.

Despite these challenges, assumptions must be made to analyze coarsened data, because the coarsening process is not identifiable from observed data [22], thus statistical methods that can incorporate ranges of assumptions are needed. Our methods fulfill this need by allowing investigators to explicitly communicate their assumptions and perform a sensitivity analysis to explore the impact of these assumptions on analysis results, facilitating more honest reporting of results from scientific studies.

6. Appendix I: Frequentist Methods

6.1. Estimation

The complete-data likelihood is $L(p)={\prod }_{g\in \mathcal{G}}{\prod }_{i=1}^{n_g}{\prod }_{j=1}^{M+1}{p}_{gj}^{I_{\mathit{\text{igj}}}}$, where I_igj is the event indicator at time j for person i in group g. Initial estimates of p_g are used to evaluate the expected complete-data log likelihood, given observed data (E-step). The E-step at iteration s is

$$Q(\mathbf{\text{p}};{\mathbf{\text{p}}}^{(s-1)})=\sum _{g\in \mathcal{G}}\sum _{i=1}^{n_g}\sum _{j=1}^{M+1}{I}_{\mathit{\text{igj}}}^{(s-1)}log(p_{gj})-\sum _{g\in \mathcal{G}}[{\lambda }_g(\sum _{j=1}^{M+1}{p}_{gj})-1],$$

where λ_g are Lagrange multipliers, and

$$I_{\mathit{\text{igj}}}^{(s-1)}=\frac{{\omega }_{\mathit{\text{igj}}}{p}_{gj}^{(s-1)}\text{exp}\{q_g(j,l,r,\delta )\}}{{\sum }_{k=1}^{M+1}{\omega }_{\mathit{\text{igk}}}{p}_{gk}^{(s-1)}{c}_{ig}^{(s-1)}(l,r,\delta ;q_g)}.$$

Q(p; p^(s−1)) is maximized (M-step) to obtain updated estimates of p_g. The M-step results in a reweighted version of Turnbull's self-consistency equation [23] for each group g, g ∈ :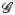

$$p_{gj}^{(s)}=\frac{1}{n_g}\sum _{i=1}^{n_g}\frac{{\omega }_{\mathit{\text{igj}}}{p}_{gj}^{(s-1)}\text{exp}\{q_g(j,l,r,\delta )\}}{{\sum }_{k=1}^{M+1}{\omega }_{\mathit{\text{igk}}}{p}_{gk}^{(s-1)}\text{exp}\{q_g(k,l,r,\delta )\}}.$$

Estimated standard errors for probabilities in each group can be calculated using Louis's [24] method for estimating the observed information matrix.

To derive the observed information matrix for group g, Ip_g, let ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_{\mathit{g}}}^{\mathit{\text{comp}}}$ denote the complete-data information matrix, and let ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_{\mathit{g}}}^{\mathit{\text{mis}}}$ denote the missing-data information matrix, where ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_g}={\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_g}^{\mathit{\text{comp}}}-{\mathbf{\text{I}}}_{{\mathbf{p}}_g}^{\mathit{\text{mis}}}$. Using Louis's method, ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_g}^{\mathit{\text{comp}}}={\sum }_{i=1}^{n_g}\text{E}\{\frac{{\partial }^{2}log[L_i({\mathbf{\text{p}}}_g)]}{\partial {\mathbf{\text{p}}}_g^2}|{\mathbf{\omega }}_{ig}\}$, where log[L_i(p_g)] is the complete-data log likelihood and ω_ig is the observed information for individual i in group g. Also, ${\mathbf{\text{I}}}_{{\mathbf{p}}_g}^{\mathit{\text{mis}}}={\sum }_{i=1}^{n_g}\mathbf{\text{E}}\{{\mathbf{S}}_i({\mathbf{\text{p}}}_g){\mathit{\text{S}}}_i^t({\mathbf{\text{p}}}_g)|{\omega }_{ig}\}$ where $S_i({\mathbf{\text{p}}}_g)=\frac{\partial log[L_i({\mathbf{\text{p}}}_g)]}{\partial {\mathbf{\text{p}}}_g^2}$, the complete-data score equation for individual i in group g. Then, ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_{\mathit{g}}}^{\mathit{\text{comp}}}$ is a (M + 1) × (M +1) diagonal matrix with jth diagonal element ${\sum }_{i=1}^{n_g}E(I_{\mathit{\text{igj}}}|{\omega }_{ig})/p_j^2$. Next, ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_{\mathit{g}}}^{\mathit{\text{mis}}}$ is a (M + 1) × (M + 1) matrix with j, k element ${\sum }_{i=1}^{n_g}[I(j=k)E(I_{\mathit{\text{igj}}}|{\omega }_{ig})/p_j^2-E(I_{\mathit{\text{igj}}}|{\omega }_{ig})/p_j-E(I_{\mathit{\text{igk}}}|{\omega }_{ig})/p_k+1]$. The variance-covariance matrix for p̂_g is then ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_g}^{-1}/n_g$, estimated by plugging p̂_g into ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_{\mathit{g}}}^{\mathit{\text{comp}}}$ and ${\mathbf{\text{I}}}_{{\mathbf{\text{p}}}_{\mathit{g}}}^{\mathit{\text{mis}}}$.

6.2. Test Statistics

To calculate Σ̂_IWD, let ${\widehat{\sigma }}_g^2$ be the estimated variance of ${\sum }_{j=1}^M\widehat{w}(j){\widehat{F}}_g(j)$, where

$${\widehat{\sigma }}_g^2=\sum _{j=1}^M\sum _{k=1}^M\widehat{w}(j)\widehat{w}(k)\sum _{j\prime =1}^j\sum _{k\prime =1}^k\widehat{cov}({\widehat{p}}_{gj\prime },{\widehat{p}}_{gk\prime }),$$ (5)

and $\widehat{cov}({\widehat{p}}_{gj\prime },{\widehat{p}}_{gk\prime })$ is the estimated covariance between p̂_gj′ and p̂_gk′, the j′, k′ entry of ${\widehat{I}}_{{\mathbf{\text{p}}}_g}^{-1}$, the inverse estimated observed information matrix for group g.

Let f̂_g = n_g/n. Then, the g,h (g h ∈ 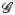) entry of Σ̂_IWD equals

$${\widehat{\sigma }}_g^2/n_{g}I(g=h)-{\widehat{f}}_g{\widehat{\sigma }}_g^2/n_g-{\widehat{f}}_h{\widehat{\sigma }}_h^2/n_h+\sum _{g\prime \in \mathcal{G}}{\widehat{f}}_{g\prime }^2{\widehat{\sigma }}_{g\prime }^2/n_{g\prime }.$$ (6)

To calculate Σ̂_LR, we define ${\widehat{\mathit{I}}}_{\mathbf{\text{p}}}^{-1}$ to be the block-diagonal G(M + 1) × G(M + 1) inverse estimated observed information matrix. Then, using the multivariate delta method,

$${\widehat{\sum }}_{\text{LR}}=\left(\frac{\partial \mathbf{\text{LR}}}{\partial \mathbf{\text{p}}}\right){\widehat{I}}_{\mathbf{\text{p}}}^{-1}{\left(\frac{\partial \mathbf{\text{LR}}}{\partial \mathbf{\text{p}}}\right)}^T,$$

where $\frac{\partial \mathbf{\text{LR}}}{\partial \mathbf{\text{p}}}$ is a G × G(M + 1) matrix with g, (h − 1)(M + 1) + j′ entry, i.e., $\frac{\partial L{R}_g}{{\partial }_{p_{hj\prime }}}$, equal to $n_{g}I(j\prime \le M)I(g=h)-\text{∑}_{j=1}^M[n_g{d}_j/n_{j}I(j\prime \ge j)I(g=h)-n_{gj}{n}_h/n_j+n_{gj}{d}_j{n}_{h}I(j\prime \ge j)/n_j^2]$

7. Appendix II: Bayesian Methods

7.1. Estimation

The Bayesian algorithm is a G-group version of that previously described [4]. Let I_g be complete data and ω_g be observed data (e.g., L, R, and Δ) for all individuals in group g.

For the Dirichlet prior, let B_g = {b_g1, ⋯, b_g(M+1)} be a base measure defined on E for those in group g, the prior mean of p_g. A precision parameter, α*, describes concentration of the distribution around B_g, where elements of B_g sum to 1. Let α_gj = α*b_gj, for j = 1, …, M +1. The Dirichlet density is given by:

$$f({\mathbf{\text{p}}}_g)=\frac{\Gamma ({\alpha }_{g1}+\dots +{\alpha }_{g(M+1)})}{\Gamma ({\alpha }_{g1})\dots \Gamma ({\alpha }_{g(M+1)})}\prod _{j=1}^{M+1}{p}_{gj}^{{\alpha }_{gj}-1},$$

where p_g1, ⋯, p_g(M+1) ≥ 0; ${\sum }_{j=1}^{M+1}{p}_{gj}=1$; the α_g = {α_g1,…, α_g(M+1)} are all positive; and α_gj's are interpreted as ‘prior counts’ of seroconverts during year j in group g. Data are incomplete, thus we use the Gibbs sampler [25] with data augmentation [26] and a Metropolis-Hastings step [19].

First, starting values are chosen for censoring bias parameters, ϕ⁽⁰⁾, and event-time probabilities, p⁽⁰⁾. The Gibbs sampler involves three simulation steps per iteration. For iteration s = 1, …, N_sim simulate:

1. $I_g^{(s)}$ from $\mathit{\text{p}}(I_g|{\mathbf{\omega }}_g,{\mathbf{p}}_g^{(s-1)},{\mathbf{\varphi }}^{(s-1)})$,

2. ${\mathit{\text{p}}}_g^{(s)}$ from $\mathit{\text{p}}({\mathbf{\text{p}}}_g|{\mathbf{\omega }}_g,{\mathbf{\varphi }}^{(s-1)},I_g^{(s)})=p({\mathbf{p}}_g|I_g^{(s)})$,

3. ϕ^(s) from $\mathbf{\text{p}}(\mathbf{\varphi }|{\mathbf{\omega }}_g,I_g^{(s)},{\mathbf{p}}_g^{(s)})$,

where p(·) denotes the density.

The vector of imputed event indicators, ${\mathbf{\text{I}}}_{ig}^{(s)}$, for person i in group g are simulated from a truncated multinomial distribution,

$${\prod _{j=1}^{M+1}\left[\frac{{\omega }_{\mathit{\text{igj}}}{p}_{gj}^{(s-1)}\text{exp}\{q_g(j,l,r,\delta ,{\varphi }^{(s-1)})\}}{{\sum }_{k=1}^{M+1}{\omega }_{\mathit{\text{igk}}}{p}_{gk}^{(s-1)}\text{exp}\{q_g(k,l,r,\delta ,{\varphi }^{(s-1)})\}}\right]}^{I_{\mathit{\text{igj}}}}.$$

The ${\mathbf{\text{I}}}_g^{(s)}$ are aggregated into group-by-time frequencies. Let $n_{gj}^{(s)}$ denote the simulated event count during interval j among those in group g at iteration S, and ${\mathbf{\text{n}}}_g^{(s)}=\{n_{g1}^{(s)}\dots n_{g(M+1)}^{(s)}\}$. Conditional on ${\mathbf{n}}_g^{(s)}$, p_g is independent of ϕ and ω_g. Therefore, ${\mathbf{\text{p}}}_g^{(s)}$ can be simulated in Step 2 from $\mathit{\text{p}}({\mathbf{\text{p}}}_g|{\mathbf{\text{I}}}_g^{(s)})=p({\mathbf{p}}_g|{\mathbf{\text{n}}}_g^{(s)})$, a Dirichlet distribution with hyperparameters ${\mathbf{\alpha }}_g+{\mathbf{\text{n}}}_g^{(s)}$. Metropolis-Hastings is used in Step 3 to simulate ϕ. Let I^(s) denote the iteration s vector of simulated event indicators and ω denote observed data across all groups. The candidate, ϕ*, is simulated from the jumping distribution at iteration s, J_s(ϕ* | ϕ^(s−1)), and is accepted with probability min(1,r_MH), where

$$r_{MH}=\frac{\mathit{\text{p}}({\mathbf{\text{I}}}^{(s)}|\mathbf{\omega },{\mathbf{\text{p}}}_g^{(s)},\mathbf{\varphi }\ast )p(\mathbf{\varphi }\ast )J_s({\mathbf{\varphi }}^{(s-1)}|\mathbf{\varphi }\ast )}{p({\mathbf{\text{I}}}^{(s)}|\mathbf{\omega },{\mathbf{p}}_g^{(s)},{\mathbf{\varphi }}^{(s-1)})p({\mathbf{\varphi }}^{(s-1)})J_s(\mathbf{\varphi }\ast |{\mathbf{\varphi }}^{(s-1)})}.$$

In this application, J_s(ϕ* | ϕ^(s−1)) was a multivariate normal distribution.

7.2. Posterior Parameter Transformations

To calculate the logrank parameter transformation, let

$${\sum }_{LR}({\mathbf{\text{p}}}^{(s)})=\sum _{j=1}^M\frac{d_j^{(s)}(n_j^{(s)}-d_j^{(s)})(n_j^{(s)}{n}_{g\prime j}^{(s)}I(g=g\prime )-n_{gj}^{(s)}{n}_{g\prime j}^{(s)}}{{(n_j^{(s)})}^2(n_j^{(s)}-1)}.$$

For the IWD parameter transformation, elements of Σ_IWD(p^(s)) take the same form as Equation (6), with $\left[p_{gj\prime }^{(s)}I(j\prime =k\prime )-p_{gj\prime }^{(s)}{p}_{gk\prime }^{(s)}\right]$ /n_j replacing $\widehat{cov}({\widehat{p}}_{gj\prime },{\widehat{p}}_{gk\prime })$ in Equation (5).