Abstract
Dematin is an actin-binding protein abundant in red blood cells and other tissues. It contains a villin-type `headpiece' F-actin-binding domain at its extreme C-terminus. The isolated dematin headpiece domain (DHP) undergoes a significant conformational change upon phosphorylation. The mutation of Ser74 to Glu closely mimics the phosphorylation of DHP. We investigated motions in the backbone of DHP and its mutant DHPS74E using several complementary NMR relaxation techniques: laboratory frame 15N NMR relaxation, which is sensitive primarily to the ps–ns time scale, cross-correlated chemical shift modulation NMR relaxation detecting correlated μs–ms time scale motions of neighboring 13C′ and 15N nuclei, and cross-correlated relaxation of two 15N–1H dipole–dipole interactions detecting slow motions of backbone NH vectors in successive amino acid residues. The results indicate a reduction in mobility upon the mutation in several regions of the protein. The additional salt bridge formed in DHPS74E that links the N- and C-terminal subdomains is likely to be responsible for these changes.
Keywords: Dematin headpiece, NMR relaxation, Model-free, Cross-correlation, Slow motions, Backbone dynamics
Introduction
Dematin (also known as band 4.9) is an actin-binding and bundling protein first isolated as a component of the junctional complex that supports the red blood cell membrane, but dematin is also abundant in human brain, heart, blood, skeletal muscle, lung, and kidney (Kim et al. 1998). Dematin consists of 383 amino acids, with a unique N-terminal domain and a 76-residue C-terminal `headpiece' domain. The N-terminal domain has one actin binding site. The C-terminal domain belongs to the villin-type headpiece family and also binds actin. Knock-out mice lacking only the headpiece domain of dematin have a fragile red cell phenotype and develop compensated anemia (Khanna et al. 2002). This phenotype becomes even more dramatic in double knockout mice that lack both dematin headpiece and the adducin protein, another component of the junctional complex (Chen et al. 2007). Thus, the headpiece domain of dematin plays a key role in the junctional complex of the red cell membrane.
The structure, folding and dynamics of villin-type headpiece proteins have been characterized in several works (McKnight et al. 1996; Vugmeyster et al. 2002; Meng et al. 2005; Grey et al. 2006; Tang et al. 2006; Vermeulen et al. 2006). The structure of dematin headpiece (DHP) was determined by solution NMR (Frank et al. 2004). DHP is composed of a well-folded helical subdomain, which is very similar to the analogous region in the villin headpiece, and a more mobile N-terminal subdomain, consisting of mainly loops and turns.
In addition to an actin-binding site, dematin headpiece contains a phosphorylation site that reversibly regulates the actin bundling activity of the intact dematin, in vitro. The phosphorylation of the headpiece domain reduces the actin-binding activity (Azim et al. 1995; Vardar et al. 2002). Studies of phosphorylated DHP are complicated by low production yield and multiple phosphorylation reactions. Jiang et al. solved the structure of a DHP mutant (DHPS74E) in which Ser74 is replaced with Glu (Jiang and McKnight 2006). They have shown that the mutant protein closely mimics the conformation of the phosphorylated DHP. The orientation and conformation of the N-terminal subdomain of DHPS74E are dramatically altered, while the C-terminal subdomain remains very similar to the wild-type DHP. Figure 1 shows the change in conformation of the flexible loop region and an additional salt bridge that is formed between Lys24 and Glu74.
Fig. 1.
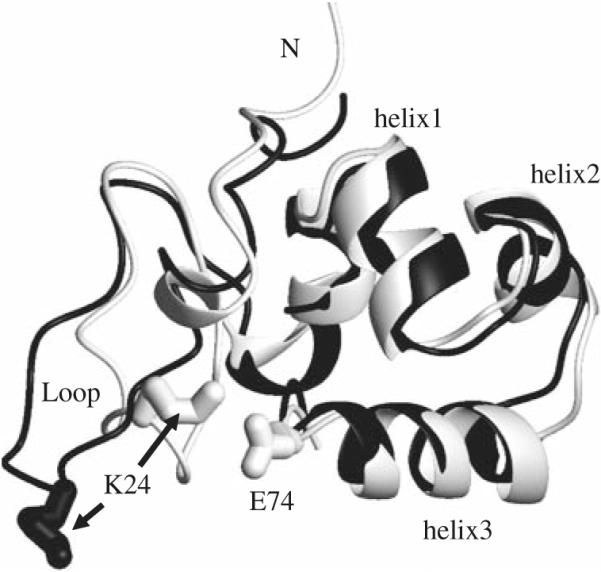
Comparison of the structures of DHP (black) and DHPS74E (white). The side chains of Lys24 and Glu74 that are involved in the salt bridge between the N- and C-terminal subdomains are shown as sticks. This figure was produced with MOLMOL (Koradi et al. 1996)
In this work we investigate the backbone dynamics of wild-type DHP and its mutant DHPS74E using several NMR relaxation techniques. Dynamics has been shown to play a significant role in many important biological functions of proteins (Palmer 2004; Eisenmesser et al. 2005; Mittermaier and Kay 2006; Gardino and Kern 2007). In recent years the importance of complementary NMR approaches for studies of protein dynamics has been stressed in several works (Engelke and Ruterjans 1997; Yang et al. 1998, 2006; Palmer 2004; Lundstrom et al. 2005; Wang et al. 2005, 2006; Mittermaier and Kay 2006). While traditional laboratory frame relaxation measurements on 15N nuclei can provide valuable information on protein dynamics, especially on the ps–ns time scale, in order to obtain a wider picture it is useful to perform additional experiments that encompass other nuclei and/or reveal slower μs–ms timescales of motions. For example, Wang et al. (2006) probed the dynamics of ubiquitin and calmodulin proteins by looking at 13CO relaxation. Their data indicate that the CO order parameters report on slower, and sometimes different, motions than the 15N relaxation order parameters. Chang and Tjandra (2005) studied temperature dependence of protein backbone motion from carbonyl 13C and amide 15N NMR relaxation. Their results suggest that fast local motion experienced by these nuclei cannot be easily described by one single type of motion over a broad range of temperatures.
In addition to the autocorrelated relaxation experiments, several cross-correlated experiments involving dipolar, chemical shift anisotropy (CSA), and isotropic interactions are now available for assessing protein dynamics. Of particular importance is the 13C′–15N cross-correlated isotropic chemical shift modulation relaxation experiment (CSM/CSM). The experiment probes concerted slow motions of carbonyl-nitrogen nuclei by looking at the correlated isotropic chemical shift modulations of the C′ and N nuclei belonging to the same peptide bond. This relatively simple and sensitive experiment was developed by Wist et al. (2004) and Pellecchia et al. (1999) and applied to ubiquitin and binase, respectively. It has been recently used to study μs–ms dynamics of the C-terminal domain of human centrin 2 complexed with P1-XPC by Kateb et al. (2006) and major urinary protein in the presence or absence of a pheromone (Perazzolo et al. 2005). The changes in the isotropic chemical shift can be caused by a variety of phenomena. Examples include variations of φ and ψ dihedral angles of the backbone, slow collective motions of protein domains, dynamic intramolecular interactions, the existence of transient hydrogen bonds, and transient interactions between complexes or fluctuating interactions with metal ions (Arnold and Oldfield 2000; Frueh 2002; Kateb et al. 2006).
Another type of experiment which will be also used in the present work was developed by Pelupessy et al. (2003) in order to investigate correlated fluctuations of two NH bonds in neighboring residues. The technique (we will refer to it as the NH–NH experiment) relies on the measurements of cross-correlated relaxation rates caused by the correlation of two N–H dipole–dipole interactions. Unlike the CSM/CSM experiment where the internal correlation times of slow μs–ms motions enter explicitly into the spectral density, in the NH–NH experiment the spectral density is independent of internal correlation times of motions slower than the overall tumbling of the macromolecule. Rather, the motions are observed as an ensemble average over different conformations, which allows the extraction of cross-correlated order parameters of slow motions (Vugmeyster et al. 2004).
We combine laboratory frame 15N R1, R2, and heteronuclear NOE NMR relaxation, 13C′–15N cross-correlated chemical shift modulation relaxation, and NH–NH cross-correlated experiments to perform a detailed investigation of backbone dynamics in DHP and DHPS74E. We show that the mutation leads to reduction in mobility in several regions of the protein.
Materials and methods
Sample preparation
15N/13C labeled DHP and DHPS74E proteins were prepared as described in Jiang and McKnight (2006) and Frank et al. (2004). NMR samples were prepared in 20 mM sodium phosphate, 0.02% sodium azide, 10% D2O and adjusted to pH 6.0. Final concentration of the samples were 1.5 mM for DHP and 2.5 mM for DHPS74E.
NMR spectroscopy
NMR spectra were acquired on a Bruker DMX500 spectrometers equipped with a triple-resonance TXI probe with a Z-gradient coil for 15N laboratory frame and CSM/CSM experiments and with a triple-axes gradient coil for the NH–NH experiment. The temperature was set to 25°C with 100% methanol sample used as a temperature standard. The data were processed by the NmrPipe/NmrDraw/NlinLS package (Delaglio et al. 1995). Each dimension was apodized by a 90° phase-shifted sine-bell window function and zero-filled once.
Laboratory frame 15N NMR relaxation measurements and model-free analysis
Longitudinal, R1, transverse, R2, and heteronuclear NOE 1H–15N σNH, relaxation rates were measured using standard pulse sequences (Farrow et al. 1994). The σNH rates were measured from pairs of spectra recorded with (NOE) and without (control) proton saturation during the recycle delay. The saturation period was 5 s in the NOE experiment and the recycle delay was 5 s in the control experiment. Each NOE experiment was repeated three times. For the determination of R1 and R2 rates the peak volumes were fitted to a mono-exponential function using CurveFit software available at http://www.cumc.columbia.edu/dept/gsas/biochem/labs/palmer/software.html. The uncertainties in rates were obtained by jack-knife simulations (Mosteller and Tukey 1977).
The initial estimation of the molecular diffusion tensors was performed using r2r1_diffusion program (A.G. Palmer, Columbia University. The program is available at the web page indicated above) on the basis of R2/R1 ratio and structural coordinates from pdb files 1QZP for DHP and 1ZV6 for DHPS74E. Fast ModelFree Software (Mandel et al. 1995; Cole and Loria 2003) was used to perform the modelfree analysis using the extended modelfree formalism described by Lipari and Szabo (1982) and Clore et al. (1990). The modelfree procedure optimizes both the diffusion tensor parameters and the parameters of internal motions (Mandel et al. 1995). The modelfree procedure first attempts to fit spectral densities (which determine experimental R1, R2 and σNH rates) using order parameters and relaxation times for fast and slower time scales but without the use of the phenomenological chemical exchange term Rex. If the results of the fits are unsatisfactory, the Rex term is included.
Several residues had to be excluded from modelfree calculations due to either spectral overlap or very low signal intensity.
To follow the standard protocols for the analysis of laboratory frame relaxation data, the N–H bond length was taken as 1.02Å and the 15N CSA tensors for each site were assumed to be axially symmetric with the value of anisotropy −172 ppm (Kroenke et al. 1999). The assumption of the constant value of the CSA and N–H bond length introduces apparent errors in the values of the order parameters. As shown by Hall and Fushman (2006) the site-to-site variability can be as much as 21 ppm, leading to average uncertainties of about 0.03 in the values of order parameters for experiments performed at 500 MHz. These uncertainties are not expected to affect the comparison of the dynamics of our two very similar proteins.
13C–15N cross-correlation experiments
In the 13C′–15N CSM/CSM experiment one measures the differential auto-relaxation rates of the double-quantum (C′+N+ + C′−N−) and zero-quantum (C′+N− + C′−N+) coherences involving C′ and N nuclei:
| (1) |
The RZQ and RDQ rates were obtained using the pulse sequence described in Wist et al. (2004, 2005) and Perazzolo et al. (2005). Six to eight relaxation delays were used. 2D spectra with 1024 × 64 complex points and a 1.5 s recycle delay were collected. For the determination of RZQ and RDQ rates the peak volumes were fitted to a mono-exponential function using the CurveFit software. The uncertainties in rates were obtained by jack-knife simulations. Several auto- and cross-correlated relaxation mechanisms contribute to the relaxation rates RDQ and RZQ. However, the difference in the rates depends only on cross-correlated mechanisms, given by:
| (2) |
RDD/DD represents the contributions of cross-correlated dipole–dipole mechanisms and RCSA/CSA is the contribution of the cross-correlated mechanism due to the chemical shift anisotropies of C′ and N nuclei. The third term, RCSM/CSM, which is of main interest in this work, is due to correlated isotropic chemical shift modulations of the two nuclei. The first two terms were calculated on the basis of protein structure and CSA tensor components.
The dipolar contributions were calculated using the following expression:
where each term in the sum gives the contribution to the relaxation rate from two dipole-dipole mechanisms involving C′i−1, Ni, and any 13C, 1H, or 15N nucleus in a protein, denoted by Xk. They were estimated using the bond distances and angles extracted from the NMR structures (pdb entries 1QZP for DHP and 1ZV6 for DHPS74E).
Calculation of the RCSA/CSA rates requires the knowledge of N and C′ CSA tensor components. Since 13C′ CSA tensors have a strong rhombicity (Tang and Case 2007), one has to take into account all of the components of the CSA tensor. For consistency we treat 15N CSA tensors as fully anisotropic as well. The components of the 15N and 13C CSA tensors were estimated using the empirical rules derived by Loth et al. (2005) from the sets of auto- and cross-correlated relaxation rates in ubiquitin. These empirical rules allow the calculations of the fully anisotropic CSA tensor components (denoted by σαα) from the values of isotropic chemical shift based on the specific motional models. In analogy to recent works performed by Perzzalo et al. (2005) and Kateb et al. (2006) we have chosen the following tensor components: , and for C′ and , and for amide 15N. Here σiso stands for the isotropic chemical shift. The chemical shifts were taken from the previously reported assignments (Frank et al. 2004; Jiang and McKnight 2006). As noted in Perazzolo et al. (2005), the differences in the values of the CSA components between various models are minor and do not affect the interpretation of the C′N cross-correlated relaxation rates. Note that these empirical rules do not allow the estimation of site-specific 15N CSA if one assumes an axially symmetric model for CSA tensor: one can see that is independent of isotropic chemical shift. The same conclusion regarding the absence of correlation between Δσ and isotropic chemical shift was reached by Hall and Fushman (2006). The value of ΔσN calculated using the empirical rules of Loth et al. is −158 ppm, which is somewhat different from the value of −172 ppm used in the model-free procedure. This difference has a negligible effect (less than 3%) on the estimated RCSA/CSA rates.
Further details on the calculations of RDD/DD and RCSA/CSA rates are available in the supplementary material.
The RCSM/CSM rate is related to the spectral density by (Frueh 2002)
| (3) |
The spectral density associated with the CSM/CSM contribution is given by
| (4) |
where ωC (t) and ωN (t) are instantaneous chemical shifts for C′ and 15N nuclei, respectively, and <…> represents the ensemble average.
Two factors contribute to the magnitude of the spectral density: the amplitude of the modulation of the chemical shifts and the extent of correlations between the modulations of the two chemical shifts. When the modulations of the chemical shifts are anticorrelated, the spectral density can be negative.
NH–NH cross-correlation experiment
The experiment developed by Pelupessy et al. (2003) for the measurements of NH/NH dipole–dipole cross-correlated relaxation rates is based on the interconversion between the DQ coherences: and . The main mechanism of the interconversion is due to correlated fluctuations of two dipole–dipole interactions between hydrogen and nitrogen spins in neighboring residues denoted by indices u and v. In principle, the rates can also be measured using both DQ and ZQ coherences. However, by selecting only the DQ coherence, one avoids the effects of cross-relaxation involving the two amide protons.
The rates are obtained from the results of two experiments. In the first experiment the decay of the initial coherence is detected and the volumes of the peaks in the resulting spectrum Iref are taken. In the second experiment the coherence resulting from the two dipole–dipole interactions is detected. The volumes of the resulting peaks in this spectrum are denoted by Icross. The rate is then obtained from the ratio of Icross and Iref:
| (5) |
where T is a relaxation delay. Note that for a specific residue the magnetization transfer starts from the amide proton and INEPT-like transfers are utilized to create the double-quantum coherence involving two nitrogen spins in successive residues. After the relaxation period the magnetization is returned to the original amide proton .
Data were acquired with a single relaxation delay of 43 ms. 2D spectra experiments were taken in an interleaved manner with 256 scans for the reference and 1,536 for the cross-peak experiments. 512 × 40 complex points were collected with a spectral width of 14 and 25 ppm in the 1H and 15N dimensions, respectively. Three to four data sets were taken for each of the samples and the data reported represents the average of the data sets. The errors in were calculated by the propagation of the errors in the cross-correlated relaxation rates.
The experimental cross-correlated relaxation rates reflect the fluctuations of dipole–dipole interactions for two NH bonds in successive amino acid residues (Pelupessy et al. 2003) denoted by unit vectors u and v. We will assume the existence of three time scales of motions: fast ps–ns time scale τf, slow μs–ms timescale τs, and ns timescale of the overall molecular tumbling τc.
The rate is proportional to the spectral density at zero frequency Juv (0):
| (6) |
where rNH is the distance between N and H nuclei, μ0 is the permeability of free space, and γH and γN are the gyromagnetic ratios. In the case of a rigid backbone and isotropic overall tumbling the spectral density is equal to
| (7) |
where P2(x) = (3x2 − 1)/2 is the second order Legendre polynomial, and is the equilibrium angle between bond vectors u and v.
In the presence of internal backbone motions the spectral density was obtained using a two-component relaxation model (Vugmeyster et al. 2004) for the fast and slow motions of the NH bonds. The fast component describes the relaxation of bond orientations on ps–ns time scale toward an intermediate quasiequlibium state, characterized by an instantaneous random position of the slow fluctuating bond environment. The slow component describes the relaxation of the bond environment on the μs–ms timescale to its equilibrium conformation. Thus, we assume that the limit τf<<τc<<τs is satisfied. Then for axially symmetric fast motions the expression for spectral density is given by
| (8) |
where and are the Lipari-Szabo 15N model-free order parameters for fast motions, and θuv is the instantaneous angle between slow fluctuating local environment axes of the NH vectors u and v for a given conformation. <…> indicates the statistical average over possible conformations in the molecular reference frame.
The term ⟨P2(cosθuv)⟩ thus contains both structural and dynamic contributions. A pure structural contribution corresponds to the rigid backbone such that θuv has a fixed value, which also corresponds to its equilibrium value . Dynamic contribution characterizes the effect of slow fluctuations of the angle θuv. The equilibrium angle can be obtained from either X-ray or NMR structural coordinates.
In the case of uncorrelated bond fluctuations separation of ⟨P2(cosθuv)⟩ into the structural and dynamic contributions can be done exactly with the use of addition theorem for spherical harmonics under the assumption of axially symmetric slow fluctuations with respect to the equilibrium bond vector orientations (Vugmeyster et al. 2004), and the spectral density can be written in the form
| (9) |
is the dynamic slow motion cross-correlated order parameter, which in the absence of correlations in slow motions of different bond vectors is equal to
| (10) |
where and are the order parameters characterizing the slow motion of NH vectors with respect to the molecular reference frame. These order parameters can be extracted from the residual dipolar coupling experiments.
It has been recently shown by numerical simulation with the use of a model potential constraining the amplitude of fluctuations (Vugmeyster and McKnight 2008) that the validity of Eq. 9 can be extended for correlated slow motions as well, if the angle is at least 10° away from the magic angle of 54.7°. Thus, the dynamic cross-correlated order parameter in the general case can be represented as
| (11) |
where Δuv is a measure of the actual strength of the correlations between the local conformational fluctuations. Note, however, that the NH–NH cross-correlated relaxation experiments alone cannot determine the actual strength of correlations in the slow motions. Additional residual dipolar coupling experiments, which can detect fluctuations of individual N–H bond vectors on a wide time scale range, would be useful for this purpose.
Results and discussion
Model-free order parameters and chemical exchange rates at 15N sites
The initial estimation of the global diffusion tensors was made using the criteria for residue retention outlined in Pawley et al. (2001). Model-free analysis was performed with both isotropic and axially symmetric global diffusion models using the Fast-Modelfree program (Cole and Loria 2003). We have found no statistically significant improvement in the quality of the fits for the axially symmetric model over the isotropic model of global diffusion, as judged by P value of at least 0.35 for F-test. In addition, the choice of the diffusion tensor model had no effect on the values of the order parameters and chemical exchange terms within the experimental errors. The only exception was L61 in DHPS74E which was fitted with a different motional model without any chemical exchange contribution when the axially symmetric model was used, while the isotropic case yielded a very small chemical exchange term. Therefore, we use the isotropic model for both proteins in the subsequent analysis of experimental data. The optimized values of the molecular tumbling times τc are 5.2 for 1.5 mM DHP and 5.7 ns for 2.5 mM DHPS74E.
To check for the possibility of a concentration dependence of the molecular tumbling times, the DHPS74E sample was diluted in half and yielded the molecular tumbling time of 5.5 ns, indicating a slight propensity toward aggregation at high concentration. To exclude any possible effect of the aggregation on the comparative dynamics of DHP and DHPS74E, the model-free analysis of R1, R2 and heteronuclear NOE rates and the C′–N CSM/CSM experiments were performed at 1.3 and 2.5 mM concentrations of DHPS74E and yielded very similar results. Hence, we conclude that the slight propensity of the samples toward aggregation has a negligible effect on their internal backbone dynamics. All data shown are for the 2.5 mM DHPS74E sample to take advantage of its higher signal to noise ratio.
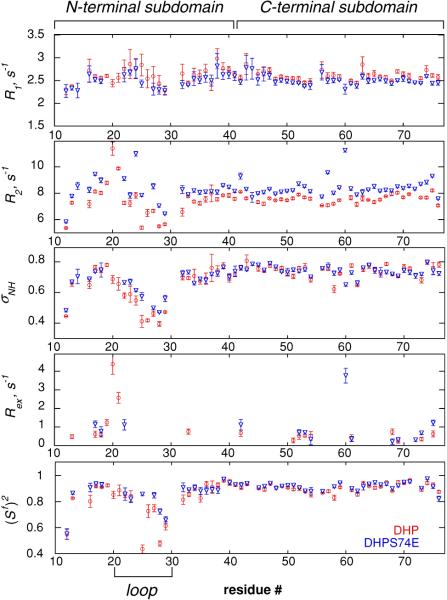
The model-free order parameters which characterize the amplitude of motion on the fast ps–ns time scale are shown in Fig. 2. Note, that the numbering of the residues starts with P9 in order to be consistent with the numbering in the full-length C-terminal domain of dematin headpiece protein. One can see that both proteins display a similar extent of fast backbone motions with the exception of the loop region (residues 20–30). In the loop region the order parameters are on the average lower in DHP, indicating larger amplitudes for the fast motions. The latter observation is consistent with the earlier results of Jiang and McKnight (2006). Residue K24 participating in the additional salt bridge could not be fit with any of the standard motional models in either protein, suggesting a more complex motion.
Fig. 2.
Experimental R1, R2 and heteronuclear NOE rates, Rex contributions, and generalized 15N model-free autocorrelated order parameters (Sf)2 representing ps–ns time scale motions of N–HN backbone bond vectors in DHP (red circles) and DHPS74E (blue triangles) versus residue number
The chemical exchange contribution to transverse relaxation rate Rex, which indicates the presence of motions on the time scale slower than the overall tumbling of the molecule, can be observed as an anomalous increase in R2 relative to that predicted for the dipolar and CSA relaxation mechanisms. Most residues in both proteins were fitted with the motional models that do not include a contribution due to Rex (see Fig. 2), meaning that this contribution is negligible. Seventeen residues in DHP and 13 residues in DHPS74E required fitting with motional models with Rex ≠ 0. However for all residues in the N- and C-terminal subdomains of both proteins Rex contributions are small, ranging between 0.2 and 1.2 s−1, with the exception of K60 in DHPS74E for which Rex = 3.8 s−1. V20 and V21 in the loop region of DHP yielded Rex contributions 2.6 and 4.5 s−1, respectively. In DHPS74E, V21 was fit without the Rex term and V20 was excluded due to very low initial intensity. Note that negligible Rex contributions for most residues have been reported in a number of other proteins as well. Examples include basic pancreatic trypsin inhibitor (Millet et al. 2000), human ubiquitin (Tjandra et al. 1995), and chicken villin headpiece subdomain (Vugmeyster et al. 2002).
The few obtained values of the chemical exchange rates do not allow one to make a definite conclusion on the comparative slow motions in DHP and DHPS74E. This calls for other techniques for the assessment of slow motions.
Slow motions detected by 13C–15N cross-correlation chemical shift modulation experiments
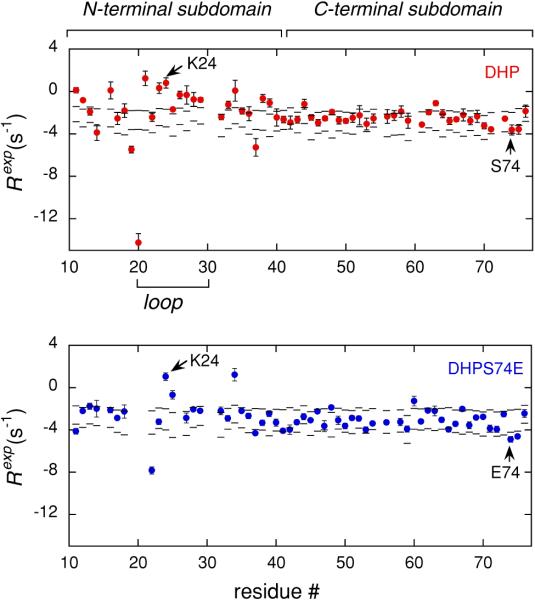
Figure 3 presents the experimental results for C′–N cross-correlated relaxation rates given by Eq. 1, which are plotted as a function of residue number. The sum of the contributions from cross-correlated dipole–dipole mechanisms (DD/DD) and the cross-correlated mechanism due to the chemical shift anisotropies of C′ and N nuclei (CSA/CSA), estimated as described in “Materials and Methods” section, are represented by the dashed lines. The lower line indicates a limit of totally rigid molecule with the square of the order parameters of 1. The upper line is drawn for the CSA/CSA and DD/DD contributions scaled by the square of the order parameters of 0.5, which represent a limit of a very flexible molecule. The Rexp rates of residues that fall within the dashed lines can be explained solely by the CSA/CSA and DD/DD contributions. However, the rates of the residues that are outside the band of the dashed lines have significant contributions due to the CSM/CSM mechanism and therefore participate in slow concerted motions.
Fig. 3.
Experimental rates Rexp (circles) as defined in Eq. 1 versus residue number for DHP (red) and DHPS74E (blue). The band between the two dashed lines represents the range of rates that can be explained by the contributions from CSA/CSA and DD/DD cross-correlated mechanisms
Almost all of the residues belonging to the C-terminal subdomains in both proteins do not show contributions due to CSM/CSM mechanisms. By contrast, the N-terminal subdomains have a large number of residues with significant CSM/CSM contributions, which provides direct evidence for the enhanced mobility of the N-terminal subdomains on μs–ms time scale. Further, the comparison of the two proteins reveals that for many residues in the N-terminal subdomain, including the flexible loop region, RCSM/CSM contribution is reduced in DHPS74E compared to DHP. This indicates a reduction in mobility upon the mutation. One of the possible reasons for this difference can be the formation of the extra salt bridge between K24 and E74 in DHPS74E. It is interesting that for these two residues the mobility of the backbone remains similar in both proteins. Hence, the sites of changes in dynamics are not directly correlated with the point of mutation.
It is worth noting that the residue V20 in DHP has a very large Rexp rate of −14.2 ± 0.9 s−1, indicating extensive slow dynamics. It is likely that this residue acts as a hinge between the more structured region of the N-terminal domain and the loop residues. Unfortunately, no quantitative comparison could be made to V20 in DHPS74E due to low initial intensity of the signal. However, the loss of the signal intensity indicates extensive dynamics for this residue.
Using the expression for the RCSM/CSM rate given by Eqs. 3 and 4, it can be shown that in the fast exchange limit assuming a two-site exchange between two conformations, the C′N CSM/CSM cross-correlated contribution is given by (Wist et al. 2004)
| (12) |
where pa and pb are the populations of the two sites (pa + pb = 1), ΔωN and ΔωC are differences in isotropic chemical shifts (in frequency units) between the two conformations for 15N and 13C, respectively, and kex is the rate of exchange between the two conformations.
It is interesting that the majority of residues show positive RCSM/CSM contributions (these residues are above the dashed line region of Fig. 3), whereas a few show negative ones. Since 15N has a negative gyromagnetic ratio and 13C a positive one, using Eq. 12 we conclude that negative RCSM/CSM rates indicate correlated motions, and positive rates indicate anticorrelated motions. This is in contrast to the conclusions made about rates involving nuclei with the same sign of gyromagmetic ratios (Fruh et al. 2001; Frueh 2002), when negative RCSM/CSM rates reflect anticorrelated motions.
All residues that have large 15N Rex contributions (V20 and V21 in DHP and K60 in DHPS74E) also show RCSM/CSM contributions. On the other hand, many residues in the N-terminal domain that show the presence of slow motions by the means of C′–N CSM/CSM experiment have negligible 15N Rex contributions. As has been argued in several works (Massi et al. 2005; Kateb et al. 2006) whether or not the chemical exchange contribution with a given kinetic constant kex is seen in a specific type of NMR relaxation experiments depends on the type of nuclei involved; whereas in a single-quantum 15N relaxation experiment the exchange contribution is weighted by the square of the isotropic chemical shift differences , in the C′–N experiment both 15N and 13C chemical shift differences come into play and the exchange contribution is weighted by the product ΔωNΔωC. As a result, it is possible that the same motional process remains invisible by single quantum relaxation experiments, while the multiple quantum C′N relaxation rates are able to detect it when |ΔωN|<|ΔωC|.
A question remains (which is out of scope of the present paper) regarding the exact time scale of the detected slow correlated motions. Relaxation dispersion on the multiple quantum C′–N coherences would be a logical step to undertake, but the approach yet has to overcome a number of technical challenges (Wist et al. 2004). It would be interesting to perform the C′–N experiments as a function of temperature for the two proteins in order to further explore the differences in the dynamics. Regardless of the exact time scale of motions, it is clear that the C′–N CSM/CSM experiment is a powerful tool in assessing the differences in dynamics of DHP and its phosphorylation-mimicking analog DHPS74E.
Slow motions detected by NH–NH cross-correlation experiment
To further examine the differences in the motions of DHP and DHPS74E, the NH–NH cross-correlation experiments were performed.
Because of the inherent insensitivity of this experiment, signals from many residues are missing.
A careful analysis of the spectra shows that the signal intensities of all N-terminal subdomain residues are either greatly reduced or within the noise in the auto-correlated spectra (which is denoted by Iauto in Eq. 5) and are completely within the noise for all residues in the cross-correlated spectra (denoted by Icross in Eq. 5). The signal to noise ratios of the N-terminal subdomain residues are diminished by approximately a factor of two or more in the autocorrelated spectra compared to the helical C-terminal subdomain residues. Typical signal to noise ratios in the cross-correlated spectra for the C-terminal domain residues are no larger than ~4:1, while they are ~7:1 in the auto-correlated spectra. We thus conclude that the most probable factor leading to the absence of signals of the N-terminal residues in the cross-correlated spectrum are the losses during the lengthy magnetization transfer steps due to enhanced relaxation of various coherences, likely because of more pronounced motions.
In contrast, the C-terminal subdomains in both proteins are significantly more structured and hence we were able to detect the signals for most residues.
Table 1 contains raw experimental rates for the C-terminal subdomains and angles calculated from the NMR structures. Most missing residues are in the loop regions or at the very end of secondary structure elements. Possible reasons for large dynamic contribution in these residues are weaker H-bonds or their role as hinges between the structural elements and less ordered loops. In addition, A73 in DHP and L42 in DHPS74E are expected to have a low intensity due to the structural factor, since their NH–NH angles lie very close to the magic angles of 54.7° and 125.3°. Residue 55 is a proline, and therefore S54 and P55 are nondetectable.
Table 1.
Experimental cross-correlated relaxation rates Rexpand NH–NH angles , for the C-terminal subdomain of DHP and DHPS74E
| Residue | 2° | DHP |
DHPS74E |
||
|---|---|---|---|---|---|
| Rexp (s−1) | Rexp (s−1) | ||||
| 42 | Loop | 105.4 ± 0.9 | 123.0 ± 0.2 | ||
| 43 | Helix 1 | 107.6 ± 0.9 | 107.1 ± 0.7 | ||
| 44 | 27.7 ± 0.1 | 3.0 ± 0.5 | 28.6 ± 1.1 | 4.5 ± 0.4 | |
| 45 | 41.0 ± 0.5 | 2.0 ± 0.4 | 16.6 ± 1.1 | 5.7 ± 0.4 | |
| 46 | 28.2 ± 0.5 | 2.7 ± 0.3 | 15.3 ± 0.7 | 6.0 ± 0.4 | |
| 47 | 11.0 ± 0.9 | 5.9 ± 0.1 | 9.2 ± 0.8 | 6.7 ± 0.4 | |
| 48 | 29.1 ± 0.7 | 3.2 ± 0.2 | 44.3 ± 0.4 | 2.6 ± 0.3 | |
| 49 | 47.5 ± 0.2 | 5.7 ± 0.5 | 35.5 ± 0.6 | 5.7 ± 0.3 | |
| 50 | 25.1 ± 0.5 | 5.8 ± 0.4 | 34.1 ± 0.5 | 6.0 ± 0.4 | |
| 51 | 69.5 ± 0.8 | 40.5 ± 0.5 | |||
| 52 | Loop | 24.4 ± 0.6 | 3.5 ± 0.2 | 49.2 ± 1.4 | 4.2 ± 0.1 |
| 53 | 163 ± 3 | 7.1 ± 0.2 | 147.9 ± 2.3 | 6.3 ± 0.5 | |
| 54 | Helix 2 | ||||
| 55 | |||||
| 56 | 23.8 ± 0.5 | 4.9 ± 0.1 | 37.3 ± 1.9 | 4.9 ± 0.2 | |
| 57 | 21.6 ± 0.7 | 5.7 ± 0.1 | 15.3 ± 0.9 | 6.0 ± 0.5 | |
| 58 | 19.3 ± 0.5 | 5.1 ± 0.3 | 15.7 ± 0.5 | 6.7 ± 0.4 | |
| 59 | 40.5 ± 0.9 | 3.5 ± 0.4 | 35.3 ± 0.5 | 4.1 ± 0.3 | |
| 60 | 46.2 ± 1.2 | 63.7 ± 0.6 | |||
| 61 | Loop | 77.7 ± 0.5 | 71.2 ± 0.4 | ||
| 62 | Helix 3 | 106.3 ± 0.7 | –3.2 ± 0.7 | 140.8 ± 1.4 | |
| 63 | 42.5 ± 0.4 | 3.0 ± 0.2 | 36.0 ± 0.6 | 3.7 ± 0.7 | |
| 64 | 18.1 ± 0.3 | 4.2 ± 0.3 | 37.4 ± 0.2 | 3.9 ± 0.6 | |
| 65 | 22.8 ± 0.5 | 5.1 ± 0.5 | 10.5 ± 0.3 | 5.4 ± 0.4 | |
| 66 | 22.0 ± 0.3 | 6.1 ± 0.6 | 20.8 ± 0.2 | 7.4 ± 0.6 | |
| 67 | 20.0 ± 0.5 | 5.9 ± 0.3 | 1.7 ± 0.3 | 6.1 ± 0.9 | |
| 68 | 37.8 ± 0.7 | 4.2 ± 0.5 | 27.3 ± 0.4 | 6.9 ± 0.4 | |
| 69 | 26.0 ± 0.7 | 4.5 ± 0.5 | 5.2 ± 0.3 | 5.6 ± 0.9 | |
| 70 | 30.6 ± 0.6 | 5.7 ± 0.4 | 35.7 ± 0.4 | 6.3 ± 0.9 | |
| 71 | 32.9 ± 0.8 | 5.1 ± 0.5 | 37.5 ± 0.5 | 5.5 ± 0.2 | |
| 72 | 29.7 ± 0.9 | 3.15 ± 0.04 | 47.5 ± 0.5 | 5.4 ± 0.6 | |
| 73 | 55.0 ± 0.7 | 63.3 ± 0.4 | |||
| 74 | Loop | 46.2 ± 0.9 | 44.4 ± 0.8 | ||
| 75 | 60 ± 3 | −6 ± 3 | 116.0 ± 0.5 | ||
Residues with in the vicinity of the magic angles of 54.7° and 125.3° are shown in bold. The errors in the angles were calculated from the ensemble of the several models present in the NMR-derived coordinates
Note that residues with angles in the vicinity of the magic angle (where Eq. 9 is invalid) had to be excluded from the analysis. These residues were R49 and L75 in DHP and A52 and K72 in DHPS74E. In addition, due to the absence of value for K60 in DHP (K60 was not included in the analysis of the 15N laboratory frame rates due to signal overlap) the neighboring residue G59 had to be excluded as well.
Dynamic cross-correlated order parameters were extracted from the experimental rates using Eqs. 4 and 6. Figure 4 summarizes the values of for the C-terminal subdomains of both proteins. For the majority of residues the values of are smaller than 1, which clearly indicates that the C-terminal subdomains of both proteins participate in slow motions. As summarized in Table 2, the amplitudes of these motions are on the average comparable for the two proteins for residues belonging to the second (residues 54–60) and third (residues 62–73) helices. In contrast, the first helix (43–51) shows larger amplitudes of slow motions in DHP, as indicated by lower values of .
Fig. 4.
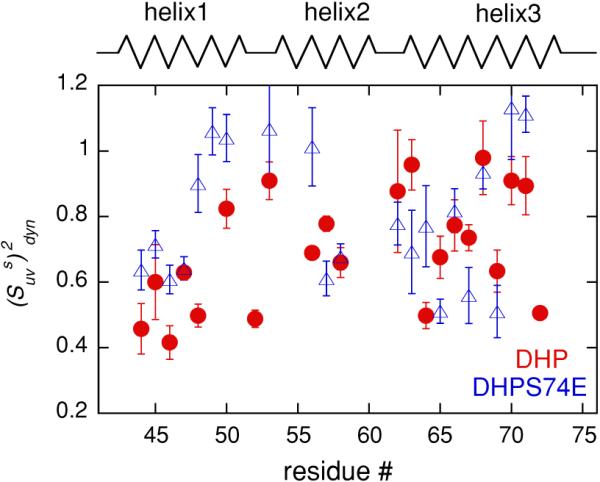
Dynamic cross-correlated order parameters for slow motions describing the amplitude of fluctuations of two N–HN dipole–dipole interactions involving successive residues. The data are shown for the C-terminal subdomains of DHP (red circles) and DHPS74E (blue triangles) as a function of residue number. Helices are represented by zigzag lines and unstructured regions by straight lines
Table 2.
Average values of the dynamic cross-correlated slow motions order parameters for secondary structure elements of the C-terminal subdomains of DHP and DHPS74E
| DHP | DHPS74E | |
|---|---|---|
| Helix 1 | 0.57 ± 0.06 | 0.80 ± 0.07 |
| Helix 2 | 0.71 ± 0.04 | 0.77 ± 0.09 |
| Helix 3 | 0.77 ± 0.05 | 0.78 ± 0.08 |
As can be seen from Fig. 1, the first helix forms an interface between the flexible N-terminal subdomain and the C-terminal subdomain. Since the N-terminal subdomain changes its structure and dynamics upon the mutation, its interaction with the first helix very likely governs the observed changes in the dynamics of this helix. Table 1 highlights the fact that the values of NH–NH angles for equivalent residues in the two proteins can be quite different, despite almost identical amino acid compositions and secondary structures of DHP and DHPS74E. It is therefore possible that the low values of observed in the first helix of DHP imply that it samples a number of conformational states with different inter-bond angles. Since there are no stringent constraints on the values of the NH–NH angles in an alpha-helix, it can accommodate relatively large changes in these angles without being destroyed.
The errors in the NH–NH angles were obtained from the ensemble of several models present in the NMR-derived structural coordinates. While it is possible that actual experimental errors in the NH–NH angles may be larger than the estimate obtained from the dispersion of the NMR structure ensemble, it is clear that all of the differences between DHP and DHPS74E cannot be attributed solely to the errors in the angles. If this were the case, experimental rates given in Table 1 would be very close for corresponding residues of the two proteins. For many residues the relative differences in experimental rates between DHP and DHPS74E are much larger than the reported differences in .
Note that the first helix hosts two key residues of the hydrophobic core: F47 and F51 (Frank et al. 2004). Low order parameters for slow motions in the first helix of DHP suggest that the conformational fluctuations are characterized by a somewhat different rearrangement of the hydrophobic core geometry. In DHPS74E due to diminished flexibility of the N-terminal subdomain new hydrophobic contacts are formed by L19, V20, V21, and L75 (Jiang and McKnight 2006), thus rendering the hydrophobic core more rigid.
The NH–NH experiment turned out to be a more informative technique for detecting slow μs–ms motions in the C-terminal subdomains compared to either the 15N single quantum or the C′–N CSM/CSM experiments. The spectral density expression given by Eq. 8 is independent of the internal correlation times and the slow motions enter as a “quasistatic” distribution of conformations, where each conformation is characterized by the angles θuv between two NH bonds belonging to neighboring peptide planes. On the contrary, the CSM/CSM experiment detects the motions of the nuclei belonging to the same peptide plane and the magnitudes of the RCSM/CSM rates given by Eq. 12 are explicitly dependent on the internal correlation times, as well as the product of the populations and the chemical shift differences.
We have thus observed a reduction in dynamics in several regions upon the mutation. We can describe these changes in terms of the population shift model (Monod et al. 1965; Gardino and Kern 2007). It is likely that DHP samples a variety of states with higher free energies within the free energy landscape of conformations, but in DHPS74E the mutation stabilizes the ground state and shifts the equilibrium toward this state. While the single quantum 15N and C′–N CSM/CSM measurements highlighted the differences in the N-terminal subdomains, the NH–NH experiment demonstrates that the differences in the ground and higher energy states are also likely to involve changes in the hydrophobic core.
Phosphorylation in DHP serves as a switch controlling the conformational state of DHP and the actin bundling activity of dematin (Jiang and McKnight 2006). The availability of a larger variety of conformational states in DHP compared to its phosphorylation-mimicking analog DHPS74E may be an indication that these conformations are facilitating the acting bundling activity.
Conclusion
Below we summarize the findings on the comparative backbone dynamics of DHP and its phosphorylation-mimicking analog DHPS74E. Three techniques were used: 15N laboratory frame R1, R2, and 1H–15N heteronuclear NOE experiments, 13C′–15N cross-correlated chemical shift modulation relaxation, and cross-correlated relaxation of two 15N–1H dipole–dipole interactions involving neighboring residues. These techniques turned out to be complementary for the comparison of the dynamics of DHP and DHPS74E.
Fast backbone motions of NH vectors are comparable in both proteins except for the flexible loop region, where DHP shows larger amplitude motions. Few residues yield non-negligible chemical exchange contributions and hence it is not possible to compare slow μs–ms motions based on this information.
Correlated slow motions of adjacent C′–N nuclei show an overall reduction in mobility for the N-terminal subdomain of DHPS74E, including the flexible loop region. With the exception of few residues, slow μs–ms motions are not seen in the C-terminal subdomains.
In the NH–NH experiment the N-terminal subdomain is not observed because of enhanced dynamics in these residues. Slow motions have been detected in the C-terminal subdomains of both proteins. The amplitudes of slow motions of successive NH bond vectors are similar in both protein in helices 2 and 3 of the C-terminal subdomains, whereas helix 1 is more flexible in DHP.
The additional salt bridge formed between K24 and E74 in DHPS74E is likely to stabilize its ground state and reduce the number of the conformations available within the free energy landscape, thus rendering the mutant less flexible compared to the wild-type DHP. The backbone mobility of K24 and E74 themselves remains roughly the same, indicating that the changes in dynamics are not directly related to the site of mutation.
Supplementary Material
Acknowledgements
We thank Zhenghui G. Jiang and Benjamin S. Frank for preparation of the protein samples. We are grateful to Prof. Arthur Palmer for a critical reading of the manuscript, Prof. Geoffrey Bodenhausen's laboratory for the assistance with the pulse sequences and to Prof. Milo Westler for technical assistance. The study made use of the National Magnetic Resonance Facility at Madison, which is supported by NIH grants P41RR02301 (BRTP/NCRR) and P41GM66326 (NIGMS). Additional equipment was purchased with funds from the University of Wisconsin, the NIH (RR02781, RR08438), the NSF (DMB-8415048, OIA-9977486, BIR-9214394), and the USDA. This work has been supported by the University of Alaska Anchorage fund number 104110-11970 to L.V. and National Institute of Health grant number GM26335 to C.J.M.
Footnotes
Electronic supplementary material The online version of this article (doi:10.1007/s10858-008-9289-4) contains supplementary material, which is available to authorized users.
References
- Arnold WD, Oldfield E. The chemical nature of hydrogen bonding in proteins via NMR: J-couplings, chemical shifts, and AIM theory. J Am Chem Soc. 2000;122:12835–12841. [Google Scholar]
- Azim AC, Knoll JH, Beggs AH, Chishti AH. Isoform cloning, actin binding, and chromosomal localization of human erythroid dematin, a member of the villin superfamily. J Biol Chem. 1995;270:17407–17413. doi: 10.1074/jbc.270.29.17407. [DOI] [PubMed] [Google Scholar]
- Chang SL, Tjandra N. Temperature dependence of protein backbone motion from carbonyl C-13 and amide N-15 NMR relaxation. J Magn Reson. 2005;174:43–53. doi: 10.1016/j.jmr.2005.01.008. [DOI] [PubMed] [Google Scholar]
- Chen HQ, Khan AA, Liu F, Gilligan DM, Peters LL, Messick J, Haschek-Hock WM, Li XR, Ostafin AE, Chishti AH. Combined deletion of mouse dematin-head piece and beta-adducin exerts a novel effect on the spectrin-actin junctions leading to erythrocyte fragility and hemolytic anemia. J Biol Chem. 2007;282:4124–4135. doi: 10.1074/jbc.M610231200. [DOI] [PubMed] [Google Scholar]
- Clore GM, Szabo A, Bax A, Kay LE, Driscoll PC, Gronenborn AM. Deviations from the simple 2-parameter model-free approach to the interpretation of N-15 nuclear magnetic-relaxation of proteins. J Am Chem Soc. 1990;112:4989–4991. [Google Scholar]
- Cole R, Loria JP. FAST-Modelfree: a program for rapid automated analysis of solution NMR spin-relaxation data. J Biomol NMR. 2003;26:203–213. doi: 10.1023/a:1023808801134. [DOI] [PubMed] [Google Scholar]
- Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. NMR Pipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- Eisenmesser EZ, Millet O, Labeikovsky W, Korzhnev DM, Wolf-Watz M, Bosco DA, Skalicky JJ, Kay LE, Kern D. Intrinsic dynamics of an enzyme underlies catalysis. Nature. 2005;438:117–121. doi: 10.1038/nature04105. [DOI] [PubMed] [Google Scholar]
- Engelke J, Ruterjans H. Backbone dynamics of proteins derived from carbonyl carbon relaxation times at 500, 600 and 800 MHz: application to ribonuclease T1. J Biomol NMR. 1997;9:63–78. doi: 10.1023/A:1018675618785. [DOI] [PubMed] [Google Scholar]
- Farrow NA, Muhandiram R, Singer AU, Pascal SM, Kay CM, Gish G, Shoelson SE, Pawson T, Forman-Kay JD, Kay LE. Backbone dynamics of a free and phosphopeptide-complexed Src homology 2 domain studied by 15N NMR relaxation. Biochemistry. 1994;33:5984–6003. doi: 10.1021/bi00185a040. [DOI] [PubMed] [Google Scholar]
- Frank BS, Vardar D, Chishti AH, McKnight CJ. The NMR structure of dematin headpiece reveals a dynamic loop that is conformationally altered upon phosphorylation at a distal site. J Biol Chem. 2004;279:7909–7916. doi: 10.1074/jbc.M310524200. [DOI] [PubMed] [Google Scholar]
- Frueh D. Internal motions in proteins and interference effects in nuclear magnetic resonance. Prog Nucl Magn Reson Spectrosc. 2002;41:305–324. [Google Scholar]
- Fruh D, Tolman JR, Bodenhausen G, Zwahlen C. Cross-correlated chemical shift modulation: a signature of slow internal motions in proteins. J Am Chem Soc. 2001;123:4810–4816. doi: 10.1021/ja003487k. [DOI] [PubMed] [Google Scholar]
- Gardino AK, Kern D. Functional dynamics of response regulators using NMR relaxation techniques. Methods Enzymol. 2007;423:149–156. doi: 10.1016/S0076-6879(07)23006-X. [DOI] [PubMed] [Google Scholar]
- Grey MJ, Tang Y, Alexov E, McKnight CJ, Raleigh DP, Palmer AG. Characterizing a partially folded intermediate of the villin headpiece domain under non-denaturing conditions: contribution of His41 to the pH-dependent stability of the N-terminal subdomain. J Mol Biol. 2006;355:1078–1094. doi: 10.1016/j.jmb.2005.11.001. [DOI] [PubMed] [Google Scholar]
- Hall JB, Fushman D. Variability of the N-15 chemical shielding tensors in the B3 domain of protein G from N-15 relaxation measurements at several fields. Implications for backbone order parameters. J Am Chem Soc. 2006;128:7855–7870. doi: 10.1021/ja060406x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang ZG, McKnight CJ. A phosphorylation-induced conformation change in dematin headpiece. Structure. 2006;14:379–387. doi: 10.1016/j.str.2005.11.007. [DOI] [PubMed] [Google Scholar]
- Kateb F, Abergel D, Blouquit Y, Duchambon P, Craescu CT, Bodenhausen G. Slow backbone dynamics of the C-terminal fragment of human centrin 2 in complex with a target peptide probed by cross-correlated relaxation in multiple-quantum NMR spectroscopy. Biochemistry. 2006;45:15011–15019. doi: 10.1021/bi061469v. [DOI] [PubMed] [Google Scholar]
- Khanna R, Chang SH, Andrabi S, Azam M, Kim A, Rivera A, Brugnara C, Low PS, Liu SC, Chishti AH. Headpiece domain of dematin is required for the stability of the erythrocyte membrane. Proc Natl Acad Sci USA. 2002;99:6637–6642. doi: 10.1073/pnas.052155999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim AC, Azim AC, Chishti AH. Alternative splicing and structure of the human erythroid dematin gene. Biochim Biophys Acta. 1998;1398:382–386. doi: 10.1016/s0167-4781(98)00078-5. [DOI] [PubMed] [Google Scholar]
- Koradi R, Billeter M, Wuthrich K. MOLMOL: a program for display and analysis of macromolecular structures. J Mol Graph. 1996;14:51–55. doi: 10.1016/0263-7855(96)00009-4. [DOI] [PubMed] [Google Scholar]
- Kroenke CD, Rance M, Palmer AG. Variability of the N-15 chemical shift anisotropy in Escherichia coli ribonuclease H in solution. J Am Chem Soc. 1999;121:10119–10125. [Google Scholar]
- Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. J Am Chem Soc. 1982;104:4546–4559. [Google Scholar]
- Loth K, Pelupessy P, Bodenhausen G. Chemical shift anisotropy tensors of carbonyl, nitrogen, and amide proton nuclei in proteins through cross-correlated relaxation in NMR spectroscopy. J Am Chem Soc. 2005;127:6062–6068. doi: 10.1021/ja042863o. [DOI] [PubMed] [Google Scholar]
- Lundstrom P, Mulder FAA, Akke M. Correlated dynamics of consecutive residues reveal transient and cooperative unfolding of secondary structure in proteins. Proc Natl Acad Sci USA. 2005;102:16984–16989. doi: 10.1073/pnas.0504361102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandel AM, Akke M, Palmer AG. Backbone dynamics of Escherichia coli ribonuclease Hi—correlations with structure and function in an active enzyme. J Mol Biol. 1995;246:144–163. doi: 10.1006/jmbi.1994.0073. [DOI] [PubMed] [Google Scholar]
- Massi F, Grey MJ, Palmer AG. Microsecond timescale backbone conformational dynamics in ubiquitin studied with NMR R-1p relaxation experiments. Protein Sci. 2005;14:735–742. doi: 10.1110/ps.041139505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKnight CJ, Doering DS, Matsudaira PT, Kim PS. A thermostable 35-residue subdomain within villin headpiece. J Mol Biol. 1996;260:126–134. doi: 10.1006/jmbi.1996.0387. [DOI] [PubMed] [Google Scholar]
- Meng J, Vardar D, Wang Y, Guo HC, Head JF, McKnight CJ. High-resolution crystal structures of villin headpiece and mutants with reduced F-actin binding activity. Biochemistry. 2005;44:11963–11973. doi: 10.1021/bi050850x. [DOI] [PubMed] [Google Scholar]
- Millet O, Loria JP, Kroenke CD, Pons M, Palmer AG. The static magnetic field dependence of chemical exchange linebroadening defines the NMR chemical shift time scale. J Am Chem Soc. 2000;122:2867–2877. [Google Scholar]
- Mittermaier A, Kay LE. Review—new tools provide new insights in NMR studies of protein dynamics. Science. 2006;312:224–228. doi: 10.1126/science.1124964. [DOI] [PubMed] [Google Scholar]
- Monod J, Wyman J, Changeux JP. On nature of allosteric transitions—a plausible model. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- Mosteller F, Tukey JW. Data analysis and regression: a second course in statistics. Reading; Addison-Wesley: 1977. [Google Scholar]
- Palmer AG. NMR characterization of the dynamics of biomacromolecules. Chem Rev. 2004;104:3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- Pawley NH, Wang CY, Koide S, Nicholson LK. An improved method for distinguishing between anisotropic tumbling and chemical exchange in analysis of N-15 relaxation parameters. J Biomol NMR. 2001;20:149–165. doi: 10.1023/a:1011249816560. [DOI] [PubMed] [Google Scholar]
- Pellecchia M, Pang YX, Wang LC, Kurochkin AV, Kumar A, Zuiderweg ERP. Quantitative measurement of cross-correlations between N-15 and (CO)-C-13 chemical shift anisotropy relaxation mechanisms by multiple quantum NMR. J Am Chem Soc. 1999;121:9165–9170. [Google Scholar]
- Pelupessy P, Ravindranathan S, Bodenhausen G. Correlated motions of successive amide N–H bonds in proteins. J Biomol NMR. 2003;25:265–280. doi: 10.1023/a:1023076212536. [DOI] [PubMed] [Google Scholar]
- Perazzolo C, Wist J, Loth K, Poggi L, Homans S, Bodenhausen G. Effects of protein–pheromone complexation on correlated chemical shift modulations. J Biomol NMR. 2005;33:233–242. doi: 10.1007/s10858-005-3355-y. [DOI] [PubMed] [Google Scholar]
- Tang S, Case DA. Vibrational averaging of chemical shift anisotropies in model peptides. J Biomol NMR. 2007;38:255–266. doi: 10.1007/s10858-007-9164-8. [DOI] [PubMed] [Google Scholar]
- Tang Y, Grey MJ, McKnight J, Palmer AG, Raleigh DP. Multistate folding of the villin headpiece domain. J Mol Biol. 2006;355:1066–1077. doi: 10.1016/j.jmb.2005.10.066. [DOI] [PubMed] [Google Scholar]
- Tjandra N, Feller SE, Pastor RW, Bax A. Rotational diffusion anisotropy of human ubiquitin from N-15 NMR relaxation. J Am Chem Soc. 1995;117:12562–12566. [Google Scholar]
- Vardar D, Chishti AH, Frank BS, Luna EJ, Noegel AA, Oh SW, Schleicher M, McKnight CJ. Villin-type headpiece domains show a wide range of F-actin-binding affinities. Cell Motil Cytoskeleton. 2002;52:9–21. doi: 10.1002/cm.10027. [DOI] [PubMed] [Google Scholar]
- Vermeulen W, Van Troys M, Bourry D, Dewitte D, Rossenu S, Goethals M, Borremans FAM, Vandekerckhove J, Martins JC, Ampe C. Identification of the PXW sequence as a structural gatekeeper of the headpiece C-terminal subdomain fold. J Mol Biol. 2006;359:1277–1292. doi: 10.1016/j.jmb.2006.04.042. [DOI] [PubMed] [Google Scholar]
- Vugmeyster L, McKnight CJ. Slow motions in chicken villin headpiece subdomain probed by cross-correlated NMR relaxation of Aamide NH bonds in successive residues. Biophys J. 2008;95(12) doi: 10.1529/biophysj.108.134320. doi:10.1529/biophysj.108.133462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vugmeyster L, Pelupessy P, Vugmeister BE, Abergel D, Bodenhausen G. Cross-correlated relaxation in NMR of macromolecules in the presence of fast and slow internal dynamics. C R Phys. 2004;5:377–386. [Google Scholar]
- Vugmeyster L, Trott O, McKnight CJ, Raleigh DP, Palmer AG. Temperature-dependent dynamics of the villin headpiece helical subdomain, an unusually small thermostable protein. J Mol Biol. 2002;320:841–854. doi: 10.1016/S0022-2836(02)00537-5. [DOI] [PubMed] [Google Scholar]
- Wang TZ, Frederick KK, Igumenova TI, Wand AJ, Zuiderweg ERP. Changes in calmodulin main-chain dynamics upon ligand binding revealed by cross-correlated NMR relaxation measurements. J Am Chem Soc. 2005;127:828–829. doi: 10.1021/ja045743p. [DOI] [PubMed] [Google Scholar]
- Wang T, Weaver DS, Cai S, Zuiderweg ERP. Quantifying Lipari–Szabo modelfree parameters from 13CO NMR relaxation experiments. J Biomol NMR. 2006;36:79–102. doi: 10.1007/s10858-006-9047-4. [DOI] [PubMed] [Google Scholar]
- Wist J, Frueh D, Tolman JR, Bodenhausen G. Triple quantum decoherence under multiple refocusing: slow correlated chemical shift modulations of C′ and N nuclei in proteins. J Biomol NMR. 2004;28:263–272. doi: 10.1023/B:JNMR.0000013699.48099.38. [DOI] [PubMed] [Google Scholar]
- Wist J, Perazzolo C, Bodenhausen G. Slow motions in nondeuterated proteins: concerted chemical shift modulations of backbone nuclei. Appl Magn Reson. 2005;29:251–259. [Google Scholar]
- Yang DW, Mittermaier A, Mok YK, Kay LE. A study of protein side-chain dynamics from new H-2 auto-correlation and C-13 cross-correlation NMR experiments: application to the N-terminal SH3 domain from drk. J Mol Biol. 1998;276:939–954. doi: 10.1006/jmbi.1997.1588. [DOI] [PubMed] [Google Scholar]
- Yang A, Miron S, Mouawad L, Duchambon P, Bloquit Y, Craescu CT. Flexibility and plasticity of human centrin 2 binding to the xeroderma pigmentosum group c protein (XPC) from nuclear excision repair. Biochemistry. 2006;45:3653–3663. doi: 10.1021/bi0524868. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.