Dimension Reduction of Microarray Gene Expression Data: The Accelerated Failure Time Model

Abstract

The construction of the components of Partial Least Squares (PLS) is based on the maximization of the covariance/correlation between linear combinations of the predictors and the response. However, the usual Pearson correlation is influenced by outliers in the response or in the predictors. To cope with outliers, we replace the Pearson correlation with the Spearman rank correlation in the optimization criteria of PLS. The rank-based method of PLS is insensitive to outlying values in both the predictors and response, and incorporates the censoring information by using an approach of Nguyen and Rocke (2004) and two approaches of reweighting and mean imputation of Datta et al. (2007). The performance of the rank-based approaches of PLS, denoted by Rank-based Modified Partial Least Squares (RMPLS), Rank-based Reweighted Partial Least Squares (RRWPLS), and Rank-based Mean-Imputation Partial Least Squares (RMIPLS), is investigated in a simulation study and on four real datasets, under an Accelerated Failure Time (AFT) model, against their un-ranked counterparts, and several other dimension reduction techniques. The results indicate that RMPLS is a better dimension reduction method than other variants of PLS as well as other considered methods in terms of the minimized cross-validation error of fit and the mean squared error of fit in the presence of outliers in the response, and is comparable to other variants of PLS in the absence of outliers.

1. Introduction

An important aspect of microarray analysis is the modeling of patient survival times, in the presence of censoring, taking into account the patients’ microarray gene expression data. One popular regression model that incorporates the censoring information is the Cox Proportional Hazards (PH) model.¹ However, when the Cox model is not appropriate, an alternative is the Accelerated Failure Time (AFT) model. Both the Cox and AFT models require less covariates than cases. A typical microarray gene expression data consists of thousands of genes, but only a small number of cases, often in the order of hundreds, is available. In this setting, the estimates obtained from the Cox and AFT models are nonunique and unstable. A two-stage procedure aims to cope with this issue by first reducing the dimension of the microarray data matrix from N × p to N × K where K < N using dimension reduction techniques, and then applying the regression model in the reduced subspace. ^{2,3,4,5,6,7,8,9}

The performance of the different dimension reduction methods employing the two-stage procedure was investigated extensively in the literature using the Cox model in the second stage.^{4,5,6,7,8,9,10,11,12} However, there are only a few comparison studies of the different methods under the AFT model.^13,14 In this paper, we apply a rank-based method of PLS to three variants of PLS: 1) Modified PLS (MPLS)⁴, 2) Reweighted PLS¹⁴ and 3) Mean Imputation PLS¹⁴. Both the rank-based approaches of Partial Least Squares (PLS) and their un-ranked counterparts incorporate the censoring information. We compare the variants of PLS (ranked and unranked versions) under an AFT model to several well-known dimension reduction methods: Principal Component Analysis (PCA), Univariate Selection (UNIV), Supervised Principal Component Regression (SPCR), and Correlation Principal Component Regression (CPCR). The algorithm for rank-based PLS is implemented in R, and is available upon request.

2. Methods

Let X be the N × p matrix of gene expression values with the p columns of X centered about the mean, where N is the number of cases (patients), and p is the number of genes with N ≪ p. Let y be the N × 1 vector of true survival times, c be the N × 1 vector of right-censoring times, and let y and c be independent. The observed data consists of the gene expression data matrix X, the survival times T_i = min(y_i, c_i), and censoring indicators δ_i = I(y_i ≤ c_i) for i = 1,…, N (δ_i = 1 if the true survival time for the i^th individual is observed, and δ_i = 0 otherwise).

Accelerated Failure Time (AFT) Model

The Accelerated Failure Time (AFT) model represents the logarithm of the true survival time for the i^th individual as a linear regression model. That is,

$$\mathit{\text{log}}(y_i)=\mu +z_i^{\prime }\beta +\sigma u_i$$ (1)

where the y_i’s are the true survival times, z_i’s are the vector of covariates corresponding to the i^th individual, β is the vector of regression coefficients, μ is a location parameter or intercept, and σ is a scale parameter. The errors u_i are i.i.d. with some distribution. The model in Eq. (1) can be written in terms of the survival function,

$$S(t,z_i;\beta )=S_0\left(\frac{1}{\sigma }\mathit{\text{log}}\left(t{e}^{-\mu -z_i^{\prime }\beta }\right)\right)$$ (2)

where S₀(t) denotes the survival function for u_i. The AFT model models the survival times directly, and thus, the regression coefficients have a linear regression interpretation.^15,16,17

Several papers in the literature have explored semiparametric estimation of the coefficients in the AFT model with an unspecified error distribution. The least-squares method of Buckley-James¹⁸ used the Kaplan-Meier estimator to adjust for the censored observations. Another popular method is the rank-based estimator using the score function of the partial likelihood.^19,20 Using the two-stage procedure, the semiparametric AFT model can be used in conjunction with the dimension reduction methods. For instance, the method of PLS can be used in the first stage to reduce the dimension of the data. Adopting the modified version of PLS⁴, the semiparametric AFT model is used in the construction of the PLS weights to incorporate the censoring. In the second stage, the reduced data are fitted to a multivariate AFT model, where the coefficients are obtained semiparametrically. Once the coefficients are estimated, the log of the lifetimes can be estimated. However, a drawback of the semiparametric approach is the difficulty in computing such estimators, even if there are only a few covariates.²⁰

In this paper, we focus on the parametric AFT model where the distribution of the error is known. The AFT likelihood function for right-censored data is given as

$$L(\mu ,\beta ,\sigma )={{\displaystyle \prod _{n=1}^N{\left[\frac{1}{\sigma }{f}_0\left(\frac{y_n-\mu -z_n^{\prime }\beta }{\sigma }\right)\right]}^{{\delta }_n}\left[S_0\left(\frac{y_n-\mu -z_n^{\prime }\beta }{\sigma }\right)\right]}}^{(1-{\delta }_n)}$$ (3)

Estimates for μ, β and σ are found by maximizing the likelihood function given in Eq. (3).¹⁶

We next describe the dimension reduction methods to be discussed. One approach to select K, the number of components or the dimension of the reduced data after dimension reduction, is to use Principal Component Analysis (PCA) to choose K components that explain a certain percentage of total variation in the original data, and then use the same K across all the dimension reduction methods.^3,4 However, choosing the same number of components K for all the methods may not reflect the inherent nature of the methods. A more popular approach to select K for each method is to allow adaptive tuning, i.e. cross-validation, so as optimize a certain criteria (for example, minimizing the mean squared error of prediction). In this paper, we select K using cross-validation based on the minimization of the squared error of fit or squared residuals.

2.1. Principal Component Analysis (PCA)

PCA constructs the set of orthogonal components sequentially by maximizing the variance of the linear combinations of the original predictors. In other words, a sequence of weight vectors is obtained as,

$$w_k=\text{arg}\text{max}\text{Var}(Xw)=\text{arg}\text{max}w\prime X\prime Xw$$ (4)

subject to the constraints w′ w = 1 and $w_k^{\prime }X\prime X{w}_j=0$ for all 1 ≤ j < k, where k = 1,…, min(N,p). Here, X′ denotes the transpose of the matrix X. The k^th Principal Component (PC) is x̃_k = Xw_k. The constraints $w_k^{\prime }X\prime X{w}_j=0$ ensure that the PCs are orthogonal. Geometrically, the PCs represent a new coordinate system obtained by rotating the original coordinate system such that the new axes represent the directions of maximum variability in the original data, and these PCs are ordered in terms of the amount of variation explained in the original data.⁶ We should observe that the construction of the PC’s does not involve the response, and hence, the components with the highest variation explained to be included in the AFT model are not necessarily predictive of the response.

2.2. Univariate Selection (UNIV)

Univariate Selection (UNIV) fits a univariate regression model of y against each gene j, and obtains a p-value from the test of the null hypothesis β_j = 0 versus the alternative β_j ≠ 0.7 The genes are then ranked according to increasing p-values, and the top-ranked K genes are selected. In this paper, we use the AFT model as the regression model.

2.3. Supervised Principal Component Regression (SPCR)

The method of SPCR consists of two steps: first pick out a subset of the top λ_spcr percent of the original genes that are correlated with patient survival using UNIV, and then apply PCA to this subset of genes to obtain K SPCR components.^12,5 We should note that SPCR incorporates the response y in the dimension reduction stage while PCA does not. There is no set rule for selecting λ_spcr. In practice, λ_spcr can be chosen by cross-validation. We choose λ_spcr= 20% in this paper.

2.4. Correlation Principal Component Regression (CPCR)

Another variant of PCA that considers the response y is Correlation Principal Component Regression (CPCR).²¹ The method first uses PCA on the gene expression data matrix X, and then uses UNIV to pick out the top-ranked K PC’s.

2.5. Modified versions of Partial Least Squares (PLS)

The components of PLS are constructed sequentially by maximizing the covariance between linear combinations of the original predictor variables X and the response variable y such that these components are uncorrelated. In other words, a sequence of weights w_k is obtained as,

$$w_k=\text{arg}\text{max}\text{Cov}(Xw,y)=\text{arg}\text{max}w\prime X\prime y$$ (5)

subject to the constraints w′ w = 1 and $w_k^{\prime }X\prime X{w}_j=0$ for all 1 ≤ j < k, where k = 1,…, min (N,p). The k^th PLS component is x̃_k = Xw_k.

Although PLS considers both the response y and predictors X in its construction of the weights, it does not take into account the censoring information, which induces bias in the estimates. Various approaches to incorporate the censoring into the construction of PLS components were proposed in the literature by combining the construction of PLS components and the Cox regression model.^3,22,23 These approaches were proposed under the Cox model, and thus, are not appropriate for the AFT model. In this paper, we consider one approach proposed by Nguyen and Rocke,³ and two approaches proposed by Datta et al.¹⁴ to incorporate the censoring information in PLS.

The method of Modified Partial Least Squares (MPLS) modifies the PLS weights in the dimension reduction step by use of the Cox regression model to incorporate the censoring.³ In other words, the weights w_k, can be written as

$$w_k={\displaystyle \sum _{i=1}^N{\theta }_{ik}{\upsilon }_i}$$ (6)

where υ_i is the i^th eigenvector of X′X. The constants θ_ik depend on the response y only through the dot product $a_i={\gamma }_i^{\prime }y$, where γ_i’s are the eigenvectors of XX′. When X is centered, a_i is the estimated slope coefficient of the simple linear regression of y on γ_i. To incorporate the censoring information, Nguyen and Rocke proposed to replace this dot product a_i by the slope coefficient obtained from the univariate Cox PH regression of y on γ_i. However, since we adopt the AFT regression model instead, we propose to replace a_i by the slope coefficient obtained from the univariate AFT regression of y on γ_i. The error distribution in the AFT model is discussed in section 3. We also denote this modified version of PLS by MPLS.

Datta et al. applied three nonparametric approaches to incorporate right-censoring in the PLS method: reweighting, mean imputation and multiple imputation.¹⁴ Since mean imputation and multiple imputation perform relatively the same,¹⁴ we focus on the approaches of reweighting and mean imputation. Although the mean imputation scheme outperforms the reweighting scheme in terms of mean squared error of prediction of the estimated log survival times, it is not clear that a similar relationship between the performance of the two approaches holds for measures discussed in section 3. We now describe the reweighting and mean imputation schemes.

1) Reweighting (RWPLS) (or Inverse Probability of Censoring Weighted): Under this method, we replace the censored response with 0, but reweigh the uncensored response by the inverse of the probability that it corresponds to an uncensored observation. In other words, let ỹ_i = 0 for δ_i = 0 and ỹ_i = T_i/Ŝ_c(T_i–) for δ_i = 1, where T_i = min(y_i,c_i), Ŝ_c is the Kaplan-Meier estimator of the survival function of the censoring time c and – denotes the left limit. PLS is then applied to (y˜, X). We denote this method by RWPLS.

2) Mean Imputation (MIPLS): We keep the uncensored response T_i, but replace the censored T_i by its expected value given that the true survival time y_i exceeded the censoring time c_i. This conditional expectation can be estimated by the Kaplan-Meier curve,

$$y_i^{*}=\frac{{\displaystyle {\sum }_{t_j>c_i}{t}_j\text{Δ}\widehat{S}(}{t}_j)}{\widehat{S}(c_i)}$$ (7)

where t_j are the ordered death times, ΔŜ(t_j) is the jump of Ŝ at t_j, and Ŝ is the Kaplan-Meier estimator of the survival function of y. Under this method, we let ỹ_i = y_i if δ_i = 1 and ${\tilde{y}}_i=y_i^{*}$ if δ_i = 0. As in the case of reweighted PLS, we apply the usual PLS method to (ỹ, X), and denote this approach by MIPLS.

2.6. Rank-based versions of Partial Least Squares

The optimization criteria of PLS involves the usual Pearson covariance/correlation measure between a linear combination of the predictors X and the response y. We replace the usual Pearson correlation with the Spearman rank correlation in the optimization criteria of PLS.

The orthogonal scores algorithm for PLS²⁴ is:

1. The p columns of X and vector y are standardized (mean 0 and variance 1).

2. Let w̃ = X′y define the weight vector w as $w=\frac{\tilde{w}}{\sqrt{\tilde{w}\prime \tilde{w}}}$.

3. Let t̃ = Xw, define the scores vector t as $t=\frac{\tilde{t}}{\tilde{t}\prime \tilde{t}}$

4. Find q₁ = y′t, and q₂ = X′t

5. Deflate X and y: $X=X-t{q}_2^{\prime }$ and $y=y-t{q}_1^{\prime }$

The K weight vectors are obtained sequentially by repeating the algorithm.

Our modification to the above algorithm is as follows. Since X and y are standardized, we have cor(X, y) = X′y. In step 2, we then redefine w̃ = X′y by w̃ = ρ(X,y), where ρ_j(X, y) = ρ(X_j, y), for j = 1,...,p, denotes the Spearman correlation between the j^th column of X and y. In step 4 of the algorithm, q₂ can be expressed as $q_2=X\prime t=\frac{X\prime Xw}{\tilde{t}\prime \tilde{t}}$. Since cor(X) = X′X, we change q₂ = X′t to $q_2=\frac{\rho (X,X)w}{\tilde{t}\prime \tilde{t}}$. In step 5, we update R_X and R_y instead of X and y. Here, the columns of R_X correspond to the ranks of the columns of X, and R_y denotes the ranks of y.

The rank-based approach is applied to the three variants of PLS considered in this paper, MPLS, RWPLS, and MIPLS. Both the rank-based PLS methods and their corresponding un-ranked versions take into account the censoring information. We should observe that for MPLS, the q₂’s in step 4 of the orthogonal scores algorithm are exactly the same as the dot product a_i’s mentioned by Nguyen and Rocke (2004). We denote the rank-based methods of PLS as Rank-based Modified Partial Least Squares (RMPLS), Rank-based Reweighted Partial Least Squares (RRWPLS) and Rank-based Mean Imputation Partial Least Squares (RMIPLS). Note that both the reweighting and mean imputation schemes generally reduce the effect of outliers in the response when these outliers are censored. Thus these rank-based methods may not show improvement over their un-ranked counterparts. Derivation of the weight vectors for RMPLS as solutions to an optimization problem is described in detail in Nguyen and Rojo.⁹

3. Assessment of the Methods

We assess the performance of the different dimension reduction methods in a simulation study and four real datasets.

3.1. Simulation Procedure

We follow the simulation setup from Nguyen and Rocke,³ which consists of generating the gene expression values, and generating the lifetimes and censoring times.

3.1.1. Generating gene expression values

Let x_ij be the ij^th entry of the gene expression data matrix X, where i = 1,…, N denote the indices for the sample, and j = 1,…,p denote the indices for the genes. As in Nguyen and Rocke,³ the gene expressions are generated as a linear combination of d independent underlying components and an error component.

In other words, the ij^th entry of the gene expression data matrix X is $x_{ij}=exp(x_{ij}^{*})$, where $x_{ij}^{*}={\displaystyle {\sum }_{k=1}^d{r}_{ki}{\tau }_{kj}+{\epsilon }_{ij}}$, for k = 1,…, d, with i.i.d. underlying components ${\tau }_{kj}\sim N({\mu }_{\tau },{\sigma }_{\tau }^2)$, and error components ${\epsilon }_{ij}\sim N({\mu }_{\epsilon },{\sigma }_{\epsilon }^2)$. Here, r_ki are the weights for the underlying components τ_kj, which we simulate r_ki ∼ Unif(− 0.2,0.2) once to use in all the simulations (see Nguyen and Rojo⁹ for discussion of the choice of r_ki’s). We fix the sample size N = 50, d = 6, μ_ε = 0, μ_τ = 5/d, σ_τ = 1, and σ_Є = 0.3. For each p ε 100, 300, 500, 800,1000,1200,1400,1600, we generate 5000 datasets.

We generate the true regression parameters, β_j with j = 1,… ,p from a $N(0,{\sigma }_{\pi }^2)$ distribution once to use in all the simulations. We fix σ_π =0.2 for all values of p ∈ 100, 300, 500, 800, 1000, 1200, 1400, 1600.

3.1.2. Generating life and censoring times

The lifetime of the i^th individual, y_i, is generated independently from the censoring time, c_i, with (i = 1,…, N), as follows:

$$\mathit{\text{log}}(y_i)=\mu +X_i^{\prime }\beta +u_i,\text{and}\mathit{\text{log}}(c_i)=\mu +X_i^{\prime }\beta +w_i.$$

Here, X_i is the vector of covariates corresponding to the i^th individual. In this paper, we consider an exponential, lognormal, log-t, and lognormal mixture model for the true lifetimes. For example, in the case of the exponential model, the errors ui are taken to be from a standard extreme value distribution, with density f_ui (t) = e^t−et for –∞ < t < ∞. The error for the censoring times w_i are taken to be from an exponential distribution, i.e. w_i ∼ Exp(λ_c), with density f_wi(t) = λ_ce^λ_ct. We pick λ_c in these simulations to obtain a censoring rate of 1/3. The true censoring rate is $P[y_i>c_i]=P[u_i>w_i]={\displaystyle {\int }_0^{\infty }{S}_{u_i}(t)f_{w_i}(t)dt}$. The observed survival time for the i^th individual is T_i = min(y_i,c_i), and the corresponding censoring indicator is δ_i = I(y_i < c_i). In the case of the lognormal mixture model, the errors u_i are taken to be from a normal mixture distribution, with density $f_{u_i}(x)=0.9\varphi (x)+\frac{0.1}{10}\varphi \left(\frac{x}{10}\right)$. The error for the censoring times w_i are taken to be from a gamma distribution Gamma(a_C, s_C), with a_C = 3, and s_C chosen such that the censoring rate is 1/3. The results of the simulation study for the exponential and lognormal mixture models are presented in this paper, where outliers in the response are present for large values of p and absent for small values of p. The results for other models for the true lifetimes, such as lognormal and log-t models are given in the Supplementary Materials.

In these simulations, we want to assess the performance of the different dimension methods in the presence of outliers in the response. By fixing σ_π = 0.2, we increase the absolute values of $X_i^{\prime }\beta$ for large values of p. Since both the true and censoring times for the i^th individual depend on $X_i^{\prime }\beta$ the observed survival times will have outliers for large values of p (see Nguyen and Rojo⁹ for detail on the β’s). The distribution of the errors for the true lifetimes and censoring times, u_i and w_i respectively, also influence on the behavior of the outlying observations of the observed survival times. For example, we would expect the observed survival times to have less outliers under the exponential model than under the lognormal mixture model since the lognormal mixture distribution has a longer tail than the exponential distribution.

Performance Measures

We select K, the dimension of the reduced data matrix after applying dimension reduction techniques to the original data, based on the minimization of the cross-validation squared error of fit or squared residuals of the log lifetimes, denoted by CV (fit.error), for each method under the AFT model. The CV (fit.error) is defined as:

$$CV(fit.error)=\frac{1}{sM}{\displaystyle \sum _{i=1}^s{\displaystyle \sum _{m=1}^M\left[\frac{{\displaystyle {\sum }_{l=1}^{N_m}{\delta }_{m,l}(i){\left({\widehat{y}}_{m,l}^{*}(i)-y_{m,l}^{*}(i)\right)}^2}}{{\displaystyle {\sum }_{l=1}^{N_m}{\delta }_{m,l}(i)}}\right]}}$$ (8)

where i = 1,…, s is the index for the simulation run, s = 5000 simulations, m = 1,…, M is the index for the cross-validation fold, M = 2, l = 1,…, N_m is the index for the individual in the m^th fold, N_m = 25 is the number of individuals in the m^th fold, and δ_m,l(i) denotes the censoring indicator for the l^th individual in the m^th fold of the i^th simulation. The $y_{m,l}^{*}(i)’\mathrm{s}$’s are defined as

$$y_{m,l}^{*}(i)=log(y_{m,l}(i))$$ (9)

where the y_m,l(i)’s are the actual lifetimes. The ${\widehat{y}}_{m,l}^{*}(i)$ are the estimates of $y_{m,l}^{*}(i)$, and are given by

$${\widehat{y}}_{m,l}^{*}(i)={\widehat{\mu }}_{-m,AFT}(i)+{\tilde{X}}_{m,l}(i)\prime {\widehat{\beta }}_{-m,AFT}(i)$$ (10)

where μ̂_−m,AFT(i) and β̂_−m,AFT(i) are the coefficients estimated from the AFT model when the m^th fold is removed, and X̃ corresponds to the reduced data matrix after applying dimension reduction techniques. Note that after dimension reduction, we first split the data into a training set and a test set, then use the training set to obtain estimates for the coefficients in the AFT model, and finally use the estimated coefficients to validate the test set.

Since the logarithm of the lifetimes is represented as a linear regression model, it is natural to examine the squared error of fit or squared residual of the log lifetimes. For each dimension reduction method, a CV (fit.error) is obtained for each value of λ, where λ < min(N_m, N_–m). In this paper, we let λ = 1,…, 15. Since CV (fit.error) is a measure of squared distance of the error of fit, it is appropriate to select the K that corresponds to the minimal CV (fit.error). Thus, K is the value of the optimal λ that minimizes CV (fit.error).

For microarray data, it is important to select the relevant genes that relate to biological processes as well as accurately predicting the patients’ lifetimes. Thus, we are interested in assessing the performance of the different dimension reduction methods based on the mean squared error of the estimated coefficients of the genes, and the mean squared error of fit. In other words, once K is selected for each method, we compute the following measures.

The first measure, MSE(β), is the mean squared error of the estimated weights placed on the genes,

$$MSE(\beta )=\frac{1}{s}{\displaystyle \sum _{i=1}^s{\displaystyle \sum _{j=1}^p({\beta }_j-{\widehat{\beta }}_j}}(i){)}^2$$ (11)

where i = 1,…, s indicates the i^th simulation, and j = 1,…,p indicates the j^th gene. For the i^th simulation, the p × 1 vector β^ is obtained by β^ = W β^_AFT where W is the vector of weights obtained from the dimension reduction step (such as PCA, PLS,…), and β^_AFT are the coefficient estimates obtained from the AFT model.

The next measure, MSE(fit), is the average of the squared residuals of the true lifetimes,

$$MSE(fit)=\frac{1}{s}{\displaystyle \sum _{i=1}^s\left[\frac{{\displaystyle {\sum }_{n=1}^N{\delta }_n(i){({\widehat{y}}_n^{*}(i)-y_n^{*}(i))}^2}}{{\displaystyle {\sum }_{n=1}^N{\delta }_n(i)}}\right]}$$ (12)

where for the i^th simulation and n^th individual,

$$y_n^{*}(i)=log(y_n(i))$$ (13)

and

$${\widehat{y}}_n^{*}(i)={\widehat{\mu }}_{AFT}(i)+{\tilde{X}}_n(i)\prime {\widehat{\beta }}_{AFT}(i)$$ (14)

3.2. Real Datasets

We also investigate the performance of the different dimension reduction methods on four real datasets. The Diffuse Large B-cell Lymphoma (DLBCL) dataset consists of 240 cases and 7399 genes, and 42.5% of the cases are censored.^25,12 Five of the survival times are 0, so we set these survival times to 0.001 in order to apply the AFT model. The Harvard Lung Carcinoma dataset consists of 84 cases, 12625 genes, and 42.9% of the cases are censored.²⁶ The Michigan Lung Adenocarcinoma consists of 86 cases, 7129 genes, and 72.1% of the cases are censored.²⁷ The Duke Breast Cancer dataset consists of 49 cases, 7129 genes, and 69.4% of the cases are censored.²⁸ We used a 3–fold CV for the four datasets: 80 samples in test set and 160 in the training set for the DLBCL data, 28 in test set and 56 in the training set for the Harvard data, 28 in test set and 58 in the training set for the Michigan data, and 16 in test set and 33 in the training set for the Duke data. For the Harvard data, we first screened out the genes using UNIV under an AFT model to retain 7189 top-ranked genes. The cross-validation is based on 1000 repetitions. The comparison of the different dimension reduction methods is based on the minimized CV (fit.error).

4. Results

4.1. Simulation

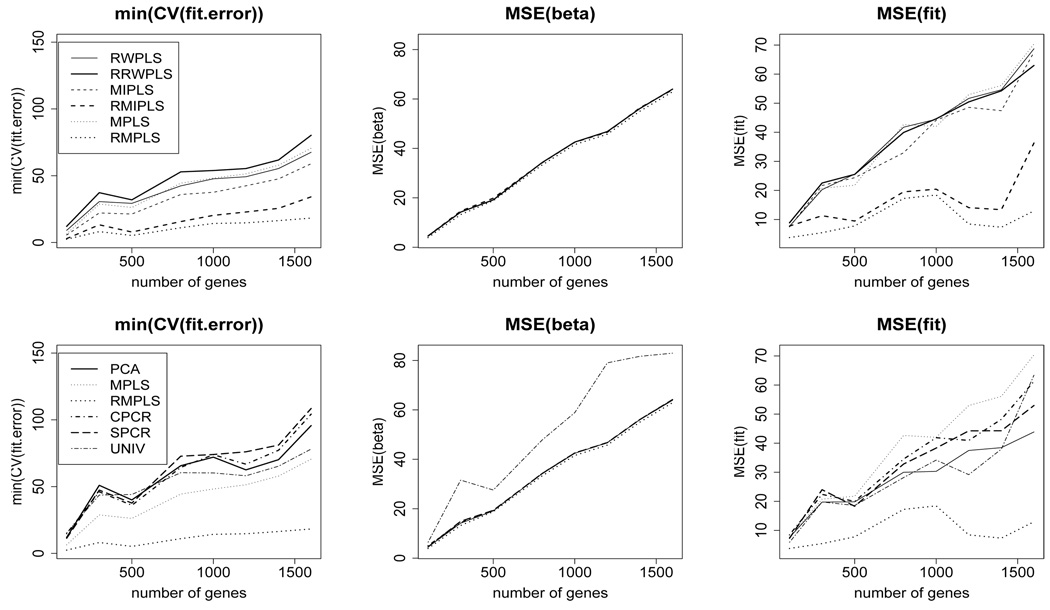
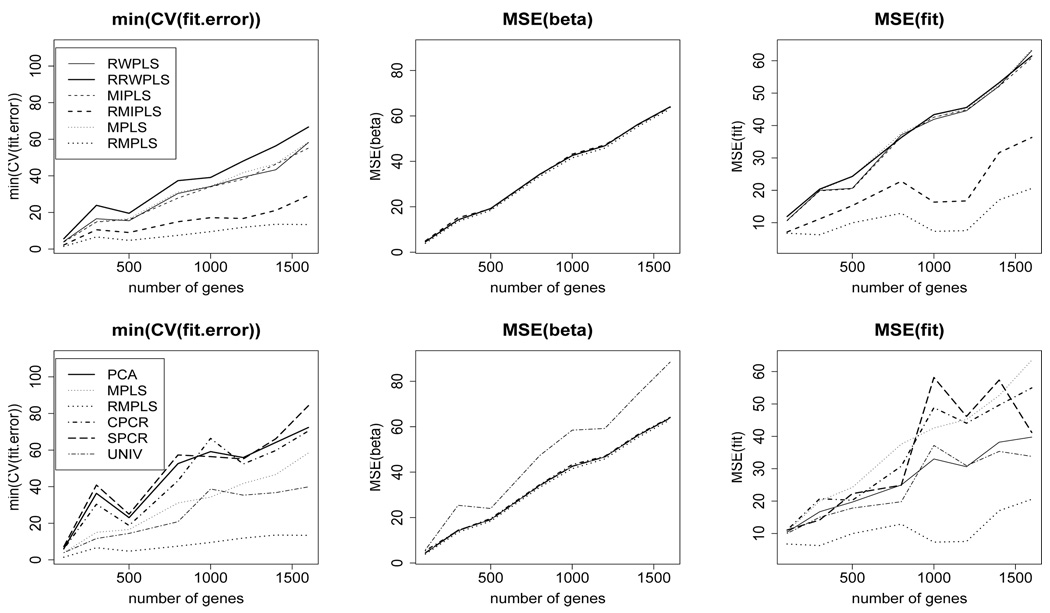
Figure 1 (top row) compares the CV (fit.error), MSE(β), and MSE(fit) for RW-PLS, RRWPLS, MIPLS, RMIPLS, MPLS, and RMPLS for censoring rate of 1/3 under the AFT exponential model. In terms of MSE(β), the ranked versions of PLS are comparable to their un-ranked counterparts. RMPLS outperforms other methods, including MPLS, in terms of CV (fit.error) and MSE(fit) for both cases when outliers are absent (p = 100) and present (p ≥ 300) in the response. In the absence of outliers in the response (p = 100), the ranked versions of RWPLS and MIPLS are comparable to their un-ranked counterparts in terms of CV (fit.error) and MSE(fit). RMPLS and RMIPLS significantly improve their un-ranked counterparts in terms of CV (fit.error) and MSE(fit) in the presence of outliers, while RRWPLS does not necessarily outperform its un-ranked version. Similar results are obtained for the lognormal mixture model (Figure 2), lognormal model and log-t models (Figures 4 and 5 in Supplementary Materials).

Fig. 1.

AFT exponential model: 1/3 censored. K is chosen by CV. min(CV (fit.error)), MSE(β), and MSE(fit) comparing RWPLS, RRWPLS, MIPLS, RMIPLS, MPLS, and RMPLS (top row), and comparing PCA, MPLS, RMPLS, SPCR, CPCR, and UNIV (bottom row) based on 5000 simulations.

Fig. 2.

AFT lognormal mixture model: 1/3 censored. K is chosen by CV. min(CV (fit.error)), MSE(β), and MSE(fit) comparing RWPLS, RRWPLS, MIPLS, RMIPLS, MPLS, and RMPLS (top row), and comparing PCA, MPLS, RMPLS, SPCR, CPCR, and UNIV (bottom row) based on 5000 simulations.

Figure 1 (bottom row) compares the CV (fit.error), MSE(β), and MSE(fit) for PCA, MPLS, RMPLS, CPCR, SPCR, and UNIV for censoring rate of 1/3 under the AFT exponential model. In terms of MSE(β), PCA, MPLS, RMPLS, CPCR and SPCR perform relatively the same when outliers are absent (p = 100) and present (p ≥ 300) in the response. UNIV performs worst among the methods in terms of MSE(β). RMPLS outperforms all other methods in terms of CV (fit.error) and MSE(fit) in the presence of outliers in the response. Similar results are obtained for the lognormal mixture model (Figure 2), lognormal model and log-t models (Figures 4 and 5 in Supplementary Materials).

4.2. Real Datasets

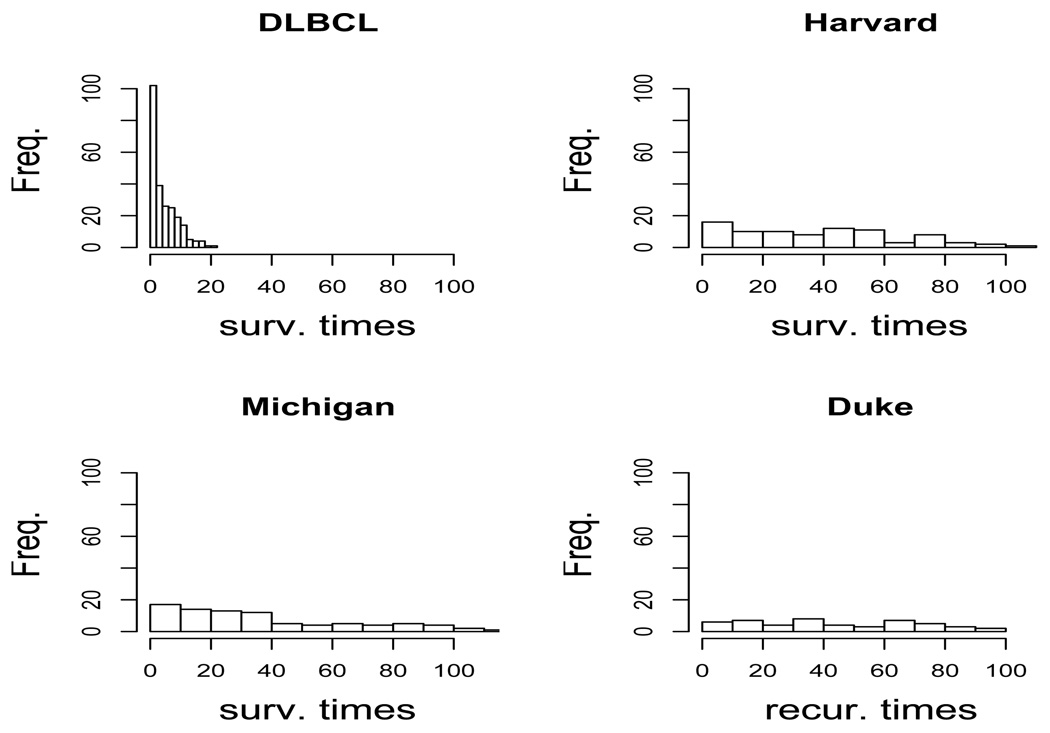
Note that the survival times in the Harvard, Michigan and Duke datasets have longer tails than those of the DLBCL dataset (Figure 3). Table 1 and Table 2 show the minimized CV (fit.error) and the standard error of the 1000 repeated runs for the different methods under the AFT exponential model and lognormal mixture model, respectively. Under the lognormal mixture model, RMPLS outperforms other methods. Under the exponential model, RMPLS generally outperforms other methods, except for the DLBCL (short tail) and Harvard datasets in which the method is slightly outperformed by RMIPLS. The standard error for the minimized CV (fit.error) over the 1000 repeated runs for RMPLS is comparable to other variants of PLS. Results for the lognormal and log-t models (tables 4 and 5 in Supplementary Materials) are similar to the results for the lognormal mixture model.

Fig. 3.

Histograms of the survival times for DLBCL, Harvard, Michigan and Duke datasets.

Table 1.

AFT exponential model: DLBCL, Harvard, Michigan and Duke datasets. K chosen by CV for the different methods. The min(CV (fit.error)) and the standard error of the 1000 repeated runs are shown.

	DLBCL			HARVARD			MICHIGAN			DUKE
Method	K	error	SE	K	error	SE	K	error	SE	K	error	SE
PCA	7	5.9975	0.9198	3	3.5506	0.6048	5	6.8389	1.4619	5	20.2349	5.7284
MPLS	3	2.9528	0.5285	2	1.2639	0.4307	3	3.1026	1.0491	1	12.4282	3.7951
RMPLS	3	2.4344	0.434	1	1.1679	0.2532	3	2.3919	0.7124	2	5.8008	2.4583
RWPLS	1	6.2211	0.8641	1	2.5704	0.2964	2	4.3526	0.9748	1	11.6507	2.7335
RRWPLS	1	5.7951	0.7833	1	2.6999	0.5653	2	3.2623	1.2633	2	6.9515	2.6657
MIPLS	3	3.1403	0.4513	2	1.1875	0.6105	2	3.1731	1.5248	2	11.8239	4.9705
RMIPLS	5	2.2963	0.4302	1	1.1585	0.2791	1	2.4789	1.5366	1	8.409	2.9436
CPCR	1	6.6413	1.1556	1	3.48	0.9098	1	7.2268	1.601	2	17.4874	5.3907
SPCR	1	6.3594	0.9723	1	3.8267	1.4767	1	10.6534	2.047	2	18.9023	5.5066
UNIV	9	6.5043	1.0576	9	2.9802	1.0017	5	7.1902	2.6427	4	17.5441	5.5117

Table 2.

AFT Lognormal Mixture model: DLBCL, Harvard, Michigan and Duke datasets. K chosen by CV for the different methods. The min(CV (fit.error)) and the standard error of the 1000 repeated runs are shown.

	DLBCL			HARVARD			MICHIGAN			DUKE
Method	K	error	SE	K	error	SE	K	error	SE	K	error	SE
PCA	5	5.3338	0.6355	6	1.4313	0.2179	4	4.1421	0.8324	4	19.1543	6.5068
MPLS	3	2.5578	0.4013	1	0.5081	0.1749	3	1.0418	0.4578	1	15.9075	4.6314
RMPLS	5	1.619	0.3016	2	0.3644	0.1295	4	0.6373	0.2462	3	5.4052	3.1271
RWPLS	1	5.5406	0.6855	1	1.3515	0.2165	1	4.9017	0.8752	1	13.1164	2.4758
RRWPLS	1	5.3157	0.7607	1	2.0553	0.3194	1	4.073	0.7727	2	9.5983	3.4348
MIPLS	3	2.795	0.43	2	0.5784	0.1639	2	1.7188	0.4036	2	11.7866	3.9348
RMIPLS	4	1.9231	0.638	2	0.5573	0.1549	2	1.1113	0.7714	1	10.4242	3.9714
CPCR	7	4.5904	0.8113	5	1.1098	0.2223	4	2.4685	0.5096	4	9.8773	3.6931
SPCR	1	5.4759	0.6712	1	2.1183	0.349	2	5.099	1.0204	2	22.1386	7.1154
UNIV	5	4.0944	0.7591	6	0.8381	0.38	6	1.7173	0.4515	7	10.8	4.0594

We compared the ranking of the significant genes based on the absolute value of the estimated weights on the genes (AEW) between the ranked versions of PLS and their un-ranked counterparts. The AEW is defined as,

$$AEW=\left|W{\widehat{\beta }}_{AFT}^{*}\right|$$ (15)

where W are the weights obtained from the dimension reduction step using the whole datasets, and ${\widehat{\beta }}_{AFT}^{*}=\frac{{\widehat{\beta }}_{AFT}}{se({\widehat{\beta }}_{AFT})}$. Table 3 shows the number of top-ranked genes in common between MPLS and RMPLS, RWPLS and RRWPLS, and MIPLS and RMIPLS, out of K considered top-ranked genes for the four datasets using only the first component. The number of common genes selected by the ranked versions of PLS and their un-ranked counterparts for the Harvard, Michigan and Duke datasets is generally less than that of the DLBCL dataset because the survival times of the Harvard, Michigan and Duke datasets have longer tails than those of the DLBCL dataset.

Table 3.

Number of top-ranked genes in common between the ranked versions of PLS and their un-ranked counterparts for DLBCL, Harvard, Michigan and Duke datasets using the absolute of the estimated weights for the genes for 1st component. The first row shows the number of considered top-ranked genes.

	K top-ranked genes	25	50	100	250	500	1000
DLBCL	MPLS and RMPLS	15	33	74	188	397	802
	RWPLS and RRWPLS	0	0	1	32	140	405
	MIPLS and RMIPLS	18	36	76	201	409	843
HARVARD	MPLS and RMPLS	12	28	58	171	368	822
	RWPLS and RRWPLS	0	0	3	15	80	273
	MIPLS and RMIPLS	14	28	69	170	371	804
MICHIGAN	MPLS and RMPLS	10	20	46	117	273	601
	RWPLS and RRWPLS	0	0	0	2	20	126
	MIPLS and RMIPLS	0	0	1	12	45	158
DUKE	MPLS and RMPLS	3	3	3	21	73	210
	RWPLS and RRWPLS	0	3	7	36	105	287
	MIPLS and RMIPLS	0	0	2	18	59	194

5. Conclusion

The results from the simulation study indicate that RMPLS outperforms all other methods in terms of min(CV (fit.error)) and MSE(fit) in the presence of outliers in the response under the AFT exponential, lognormal mixture, lognormal and log-t models. RMIPLS significantly improves its un-ranked counterpart, while RRWPLS does not necessarily perform as well as its un-ranked counterpart in terms of min(CV (fit.error)) and MSE(fit) in the presence of outliers. In the absence of outliers, the method of RMPLS is comparable to other methods, including other variants of PLS. The results from the real datasets indicate that RMPLS is a better variant of PLS compared to MPLS, RWPLS, RRWPLS, MIPLS and RMIPLS in terms of min(CV (fit.error)) under the considered AFT models.