Computational analysis of membrane proteins: the largest class of drug targets

Abstract

Given the key roles of integral membrane proteins as transporters and channels, it is necessary to understand their structures and, hence, mechanisms and regulation at the molecular level. Membrane proteins represent ~30% of all proteins of currently sequenced genomes. Paradoxically, however, only ~2% of crystal structures deposited in the protein data bank are of membrane proteins, and very few of these are at high resolution (better than 2 Å). The great disparity between our understanding of soluble proteins and our understanding of membrane proteins is because of the practical problems of working with membrane proteins – specifically, difficulties in expression, purification and crystallization. Thus, computational modeling has been utilized extensively to make crucial advances in understanding membrane protein structure and function.

Introduction

Integral membrane proteins (IMPs) have essential roles in numerous physiological functions, such as molecular recognition, energy transduction and ion regulation. Despite the experimental challenges of studying these proteins, understanding them is crucial because they represent more than 60% of drug targets [1,2]. For example, G-protein-coupled receptors (GPCRs) form the largest family of drug targets among membrane proteins because the malfunction of these receptors results in serious disorders, such as hypertension, congestive heart failure, stroke and cancer. On a similar scale, genetic disorders of ion channels result in ‘channelopathies’ such as cystic fibrosis, Bartter syndrome and paralysis. Therefore, ongoing technological advances are exploited to study membrane proteins to improve or develop novel drugs.

The availability of complete or partial genome sequences for several organisms from several domains including the eubacterial, archaean and eukaryotic domains now makes possible much more detailed studies of membrane proteins. Compounded by their genomic abundance, the use of computational tools to study membrane proteins is essential and timely. In combination with the advancement of simulation techniques, the advent of structural genomics has spurred the membrane protein field to consider high-throughput methods, which can help redress the disparity between our understanding of soluble proteins and membrane proteins. Indeed, numerous bioinformatics and proteomic analyses (e.g. Refs. [3–6]) have been carried out to examine membrane protein architecture and even to closely analyze detailed stabilizing and mediating interactions between transmembrane (TM) helices in membrane proteins. GPCRs have been intensively studied using computational tools such as comparative modeling, docking calculations, molecular dynamics (MD) simulations and normal mode analysis [7–9].

Membrane proteins, in many respects, are easier to investigate computationally than experimentally, owing to the uniformity of their structures and interactions [10,11]. The high propensity to form secondary structures reduces the number of degrees of freedom that determine the protein’s fold and, hence, lowers the complexity of predicting the structures of these proteins. Computational techniques represent key methods for relating the few static experimental membrane protein structures to dynamic biological systems, thereby yielding maximum benefit from the limited structural and mechanistic information available. Structure-based drug design for membrane proteins involves obtaining a structural model for the protein if a high-resolution structure is not available and design of small molecules that bind the protein. The computational techniques employed toward these aims are dizzyingly vast. Thus, in this review, although we discuss the various techniques briefly, we will focus on one intensively utilized technique: MD simulations.

Membrane protein structure

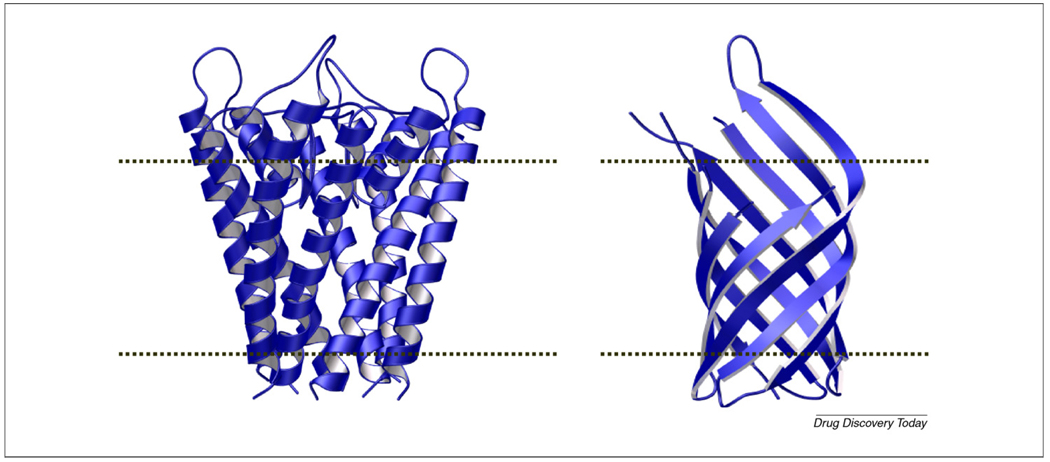
Membrane proteins are divided into two main classes: some contain a significant portion of their mass within the interior of the membrane (intrinsic or integral membrane proteins, or IMPs), whereas other proteins are only associated to the membrane surface (extrinsic or peripheral proteins). For IMPs, two common structural motifs have been observed for the TM domains: an α-helical or a β-sheet topology [12]. These two folds (Fig. 1) are the simplest solutions to satisfying the hydrogen-bonding potential of the polypeptide backbone amide groups within the lipid bilayer. The majority of IMPs display α-helical TM segments and can be further divided into two types: bitopic (those that traverse the lipid bilayer with a single α-helix) and polytopic (an α-helical bundle). Membrane proteins that are α-helical typically form well-packed bundles as found in, for example, bacteriorhodopsin, photosynthetic reaction centers and cytochrome C oxidase. Formation of β-sheets is seen in bacterial outer membrane proteins (e.g. OmpA [13] and FecA [14]), which span the membrane as β-barrels.

FIGURE 1.

Two examples of membrane proteins. KcsA (left) (PDB: 1K4C) is a voltage-gated K⁺-selective α-helical protein. OmpA (right) (PDB: 1QJP) is an example of a β-barrel membrane protein. The dashed lines indicate the position of the bilayer.

Experimental structure determination

Despite the inherent difficulties in studying the structure of membrane proteins, as discussed below, they remain a crucial area of study because of their essential role in the control of important biochemical processes. Several experimental methods exist and are continually being developed to extract structural information on membrane proteins. Spectroscopic methods, such as vibrational spectroscopy, Raman, FTIR and circular dichroism, have been utilized to determine their secondary structure and to help distinguish between competing models of structure or function [15,16]. Bacteriorhodopsin [17], the acetylcholine receptor [18], lactose permease [19] and the outer membrane proteins of Escherichia coli [20] are examples of membrane proteins whose secondary structure content has been determined with such techniques. Various techniques have been used to determine high-resolution structures. Under this category, three methods are generally employed: electron microscopy, NMR and X-ray crystallography. Despite the difficulties involved in generating large and sufficiently well-ordered 3D crystals, X-ray crystallography is still the most successful and least difficult technique for obtaining high-resolution structures. Crystallography gives the greatest information content, although the resolution is generally less than for typical soluble protein structures. Electron crystallography [21] and atomic force microscopy [22] are also used to study membrane proteins whose natural propensity is to form 2D arrays [23], and these methods can have the advantage of showing proteins in a more native-like lipid bilayer environment that is generally absent in crystals prepared for X-ray analysis.

The disparity between our knowledge of soluble proteins and membrane proteins is largely because of the practical difficulties involved in expressing and crystallizing the latter [24]. Their inherent membrane-bound nature makes structure determination a particular challenge and, thus, requires special treatment. This is particularly true for α-helical membrane proteins because they tend to be hydrophobic and, therefore, are difficult to unfold and refold in vitro. β-barrel proteins, however, are more hydrophilic and amenable to the traditional methods of denaturation and refolding into detergents or directly into lipids [25].

Three major bottlenecks exist for obtaining structural information of membrane proteins. First, it is difficult to obtain the protein of interest because membrane proteins are usually present in the cell at low concentrations. Overexpression, therefore, is a necessity for the majority of membrane proteins that cannot be readily obtained in sufficient amounts from their native environments [25]. Many different expression systems are used, although each has its drawbacks, including low yield (often because of toxicity), heterogeneous post-translational modification, low stability and partial proteolysis [24]. The majority of membrane protein crystal structures result from proteins that occur naturally at high concentrations or have been overexpressed in a homologous system. Second, membrane proteins are naturally embedded in a heterogeneous dynamic environment of the mosaic lipid bilayer (Fig. 2) and it is extremely difficult to use high-resolution experimental techniques in their native environment. The proteins, therefore, need to be extracted from the native membrane and studied in a detergent or lipid environment in vitro, which leads to difficulties in sample preparation for biophysical methods, such as X-ray crystallography and NMR. However, cryo-electron microscopic analysis differs from these techniques in that it can be used to study membrane proteins in a crystalline or noncrystalline state at intermediate resolution [26]. This has enabled, for example, the structure of bacteriorhodopsin to be analyzed to a resolution of 2.8 Å [27]. Third, membrane proteins are generally insoluble in aqueous solution; hence, detergents are required in concentrations above the critical micellar concentration. Too much detergent can denature the protein or impede crystallization by phase separation, but too little and the protein might become insoluble. The production of 3D or 2D crystals remains one of the major challenges in obtaining structural information.

FIGURE 2.

Illustration of a membrane protein (KcsA, shown in purple) embedded in a lipid bilayer. For clarity, the water molecules on either side of the lipid bilayer have not been included. The hydrocarbon core of a membrane is typically ~25–30 Å wide with the headgroups spanning ~10 Å. The polar head groups of the lipids face the aqueous environment on both sides of the membrane, whereas their hydrophobic chains form the insulating interior of the bilayer. Owing to the ester carbonyls and water associated to the lipid headgroups, lipid molecules possess electrical dipoles, which result in a considerable electrical potential (positive inside the bilayer). Figure generated using KcsA crystal structure, PDB: 1K4C.

Each experimental method has its own advantages and, hence, the structural data obtained are complementary. All methods are generally used in parallel in an attempt to achieve the best structural description of a membrane protein. In addition, methods are continually being developed, with the use of computational resources, leading to an increasing rate of membrane protein structure determination. As noted recently by White, the first atomic structure of a membrane protein was solved in 1985 and now, with an exponential increase in the cumulative number of structures, more than 180 unique high-resolution structures are available [28]. In the past two years, significant progress has been made in solving the crystal structures of GPCRs: the structures of opsin, an active form of rhodopsin, and ligand-activated GPCRs (avian β1-adrenergic receptor, human β2-adrenergic receptor and human adenosine A_2A receptor) are now available [29]. However, as noted by White, at the current pace it will take approximately 30 years to obtain the 1700 membrane protein structures that are needed to account for each structural family [28]. Hence, despite the increasing rate of experimental structure determination, improved structure prediction methods using computational tools are important in studying membrane proteins.

Computational structure determination and ligand docking

In the absence of high-resolution 3D structures, computational methods are used for the structure prediction of membrane proteins. These methods can be broadly divided into two categories: homology modeling and ab initio modeling [29,30]. Homology modeling (also known as comparative modeling) methods rely on sequence similarity with known protein structures, whereas ab initio modeling methods can be used when little or no experimental information is available for the protein or its homologs. An ensemble of low-energy conformations is obtained by ab initio modeling. Various software packages available for homology modeling and ab initio modeling have been discussed by Vaidehi et al. [29] and Punta et al. [30].

After a high-resolution structure or a low-resolution model for the membrane protein is available, the next step in drug discovery is modeling small-molecule binding to the active sites. Many different methods for protein–ligand docking are available [29,31,32]. The docking problem includes the search for precise ligand conformations at the protein-binding site. Different scoring functions are used to compute the protein–ligand binding affinity. MD simulations enable the study of protein–ligand interaction with both the protein and ligand being flexible [31]. They are increasingly being used to compute standard free energies of protein–ligand binding [33].

Computational approaches most commonly used to understand protein structure dynamics include normal mode analysis [34] and simulations. MD simulations are used for structure prediction under the ab initio structure prediction approach, computation of protein–ligand-binding free energies, and they are widely used for the study of membrane protein dynamics. Below, we discuss the application of MD simulations to the study of membrane proteins in detail.

Computer simulations of membrane proteins

Once a structural model is obtained, computer simulation methods provide key insights into the general nature of protein motions and aspects of motion linked to the functions of proteins in their native state. They are rapidly becoming a standard tool for studying the structure and dynamics of membrane proteins. While X-ray structures of membrane proteins provide static, spatially and temporally averaged snapshots of the proteins in specific crystal environments, simulations enable us to explore the structural dynamics of the proteins in an attempt to bridge the gap between structure and function of proteins and to include influences of the native-like lipid bilayer environment that is generally absent in the crystal structures. Relating molecular structures to the physiological properties of the protein is a major challenge in the field. Ion channels are membrane proteins that transport ions across membranes. They are regulated by voltage (e.g. some potassium channels), by ligand binding (e.g. nicotinic acetylcholine receptor) or by some other means. A wide variety of computational approaches such as MD simulations (e.g. Refs. [16,35,36]), continuum electrostatic Poisson–Boltzmann theory [37], Brownian dynamics (BD) [38,39] and electrodiffusion theory [40] have helped to refine our understanding of the molecular determinants of channel function. Among these techniques, MD arguably provides the most detailed information.

In a fully atomistic MD simulation, all atoms in the system (including ions and water molecules) are represented explicitly and simulations are typically carried out using empirically determined pairwise interaction potentials between the atoms. Another approach, known as QM/MM, that combines quantum mechanics (QM) and molecular mechanics (MM) has also been used for the study of membrane proteins [41]. Under this hybrid approach, most of the system is treated by empirical force fields (MM); however, the parts of the system where the phenomena of interest cannot be studied by classical MM description are treated by first-principles quantum chemistry (QM).

Among all structurally known membrane proteins, the ion channels (KvAP and KcsA), transporters (AQP, GlpF and the ABC transporter) and outer membrane proteins (OmpA) have been examined via computational modeling [42] and particularly via simulation in detail. The simulation methods described will be compared using the bacterial K⁺ channel, KcsA, as a case study. This is the first biological ion channel whose tertiary structure was elucidated [43] and has been studied extensively in terms of ion selectivity, permeation and gating.

MD simulations of KcsA have been employed to examine channel selectivity, ion permeation and ion transport energetics in potassium channels, with the main focus being on the selectivity filter and understanding the permeation properties of K⁺ ions in the filter and cavity regions. Many of the results from MD simulations based on realistic all-atom models have been consistent with the information obtained from high-resolution structural data, thereby showing that MD simulations can be used to provide crucial information in the absence of high-resolution structural data [44].

Although the significant increase in computational power and the improvement in parallel techniques used in MD codes have now made possible the use of MD simulations for the routine study of systems consisting of thousands of atoms for multi-nanoseconds [45], there are many events of interest that occur on the temporal and spatial scales that still remain a challenge for atomistic MD simulations. For example, the typical timescale for allosteric effects is usually from microseconds to milliseconds. During such complex events, the transitions between two stable states are separated by high free-energy barriers. Modified MD techniques are used for the study of such events, such as using coarse-grained models instead of fully atomistic ones [46,47] and computing free energies for the events of interest. Examples of biased MD approaches applied to KcsA include umbrella sampling [48], using an expanding sphere inside the pore at the gate region of the KcsA channel to induce gating [49], steered MD [50], targeted MD [51] and alchemical free-energy perturbation [52,53]. Although results from these techniques increase our confidence in MD, we cannot build a complete picture of ion permeation if ion fluxes cannot be simulated or if channel conductance cannot be calculated. Single-channel measurements reveal the net translocation of one ion in KcsA to be 10–20 ns [54], which is the order of timescales accessible by atomistic MD simulations [52,55].

The time-scale limitation of MD is the strength of BD. The drawback of BD, however, is the comparatively poor description or parameterization of the biological system simulated. In BD, ion permeation can be simulated for sufficiently long to measure channel conductance without having to treat the system in fully atomic details explicitly. BD simulations (e.g. on KcsA [39]) treat protein atoms forming the channel as rigid and the water implicitly as a dielectric continuum performing Brownian motion. Despite these severe limitations of the continuum electrostatic approximation and the assumption of a rigid channel structure, BD simulations confirmed the multi-ion mechanism to be in agreement with the ion flux determined experimentally [56]. The ability to compute current flow across ion channels confers a distinct advantage to BD simulations over other techniques with the application of BD to calculate current and voltage conductance in ion channels. The assumptions in BD of treating the water–protein interface as a rigid boundary and the treatment of water in a narrow pore as a continuum are simplifications because proteins (and lipid bilayers) are, in fact, dynamical, undergoing fluctuations on a picosecond timescale, which is much more rapid than the timescale for ion permeation.

The treatment of the water–protein boundary has been modified in some studies in an attempt to reduce its simplified stochastic nature. For example, an elaborate treatment of boundaries was proposed [56,57] using a grand canonical Monte Carlo (GCMC) method. However, comparison of BD using a simple stochastic boundary and the GCMC boundary [58] revealed no significant differences with the results obtained when the boundaries were at a reasonable distance from the channel. MD is also the preferred technique for size-dependent selectivity among ions with the same valence because such ions cannot be distinguished in BD. Although microscopic quantities can be deduced from BD, the increased high-level detail adopted by MD and Monte Carlo algorithms enables the analysis of large-scale conformational changes. For example, one study explored the conformational changes between the open KcsA crystal structure and a model of the closed form [59]. The simulation of the large-scale conformational transition was run by imposing lateral forces to the C termini of the inner helices and minimizing the energy at each step. As a result of the applied forces, the inner helices converged to form a tightly packed structure, with a change in backbone geometry in the central region.

Often, the results obtained from simulation methods rely on the assumptions made in the underlying models, as well as the approach used. Hence, the user should be aware of these assumptions made and draw conclusions that are within the scope of the models. Most of the currently used empirical biomolecular force fields contain fixed charge distribution for the atoms and do not include effects of induced electronic polarization. Efforts to include polarization into biomolecular force fields by using methods such as fluctuating charge model, Drude oscillator model and induced point dipole model are ongoing, and with the advent of these force fields, the scope of MD simulations will probably enhance significantly [60].

Although MD provides the most detailed information about the dynamics of ion channels, currently accessible simulation times are its greatest limitation. However, this problem might be surmounted in the future with the doubling of computer speeds over the years. In the meantime, as discussed above, faster, more coarse-grained methods and application of free-energy methods are becoming increasingly viable with increasing computational power. Despite such hurdles, MD simulations – in combination with other tools discussed above, such as homology modeling and experimental studies – have proved to be essential in the study of membrane protein structure and function, which, in turn, enables the development of novel drugs.

Concluding remarks and future perspectives

IMPs perform key functions in regulating the physiological state of the cell. This is especially true for receptors and ion channels that control, for example, the TM potential. The scarcity of IMP structures is because the route from membrane protein sequences to atomic-resolution structures is not as straightforward as for their soluble counterparts. This, in turn, is primarily because of the substantial difficulties with overexpression and crystallization of IMPs. Thus, the use of computational tools such as protein simulation methods, in combination with experimental and structural genomics studies, is becoming increasingly valuable in studying the structure and function of membrane proteins.

The explosion of genomic data, in combination with huge advances in computational resources and experimental techniques, is leading to a greater understanding of biological structure, function and mechanisms. Considering the dramatic advancements in MD simulation methodologies in recent years, it is probable that current drawbacks will be overcome considerably in the near future. Over the past few years, there has also been a dramatic increase in the number of membrane protein crystal structures obtained, with the total number of solved membrane protein structures being above 180.

Unsurprisingly, given the immense computing power and wealth of genomic and structural data, recent years have seen a rise in structural genomics initiatives primarily focusing on membrane proteins in an attempt to harness the synergy between the growing data and technology available. Examples of such initiatives include the Swiss National Center of Competence in Research (http://www.structralbiology.ethz.ch/), the Membrane Protein Network (http://www.mepnet.org/), European Membrane Proteins (http://www.e-mep.org/), Protein Wide Analysis of Membrane Proteins (http://www.pst-ag.com/), the Biological Information Research Center, Japan (unit.aist.go.jp/birc) and the Membrane Protein Structure Initiative (http://www.mpsi.ac.uk/). At present, the large majority of crystallized membrane proteins are bacterial proteins; thus, there is an urgent need to obtain structures of eukaryotic membrane proteins as these could be potential drug targets. In this respect, structural genomics initiatives are essential for rapidly increasing the structure determination throughput of eukaryotic membrane proteins. Interestingly, this situation is analogous to that of soluble proteins; slow structure determination in the 1970s was followed by an exponential increase of structures generated owing to improved experimental protocols.

The paradox posed by the sheer number of potential helical membrane proteins and the lack of high-resolution structural and thermodynamic information for them emphasizes the extensive work that remains to be done in the field of membrane proteins. The potential payoff might be great; this class of proteins has historically contained excellent targets for therapeutics, and advances in our ability to understand and manipulate membrane proteins are essential for the discovery or design of novel pharmaceutical agents that can modulate their functions.