Human Reinforcement Learning Subdivides Structured Action Spaces by Learning Effector-Specific Values

Abstract

Humans and animals are endowed with a large number of effectors. Although this enables great behavioral flexibility, it presents an equally formidable reinforcement learning problem of discovering which actions are most valuable because of the high dimensionality of the action space. An unresolved question is how neural systems for reinforcement learning—such as prediction error signals for action valuation associated with dopamine and the striatum—can cope with this “curse of dimensionality.” We propose a reinforcement learning framework that allows for learned action valuations to be decomposed into effector-specific components when appropriate to a task, and test it by studying to what extent human behavior and blood oxygen level-dependent (BOLD) activity can exploit such a decomposition in a multieffector choice task. Subjects made simultaneous decisions with their left and right hands and received separate reward feedback for each hand movement. We found that choice behavior was better described by a learning model that decomposed the values of bimanual movements into separate values for each effector, rather than a traditional model that treated the bimanual actions as unitary with a single value. A decomposition of value into effector-specific components was also observed in value-related BOLD signaling, in the form of lateralized biases in striatal correlates of prediction error and anticipatory value correlates in the intraparietal sulcus. These results suggest that the human brain can use decomposed value representations to “divide and conquer” reinforcement learning over high-dimensional action spaces.

Introduction

The number of effectors with which the body is endowed is both blessing and curse. Having many effectors permits flexible actions, but the task of deciding between candidate movements must compare many movement combinations: the number of possible combinations scales exponentially with the number of effectors. This is a vivid problem for prominent accounts of the brain's mechanisms for reinforcement learning (RL) (Daw and Doya, 2006; Dayan and Niv, 2008), which envision that the brain learns to map each candidate action to its expected consequences, to choose the best one. Although such action–value learning mechanisms work well for experiments involving choice between a few options (Sugrue et al., 2004; Lau and Glimcher, 2005; Samejima et al., 2005; Daw et al., 2006a; Behrens et al., 2007), for movements comprising multiple effectors, they would require unrealistic amounts of experience to adjudicate between the many combinations of choices.

One approach to this “curse of dimensionality” (Bellman, 1957) is to “divide and conquer” (Ghahramani and Wolpert, 1997; Doya et al., 2002), subdividing a complicated problem into simpler subproblems. A subject in a visuomotor task might realize that rewards depend solely on eye movements, whereas other tasks reward multiple effectors independently, like driving while talking on the phone. Work in computational RL (Chang et al., 2003; Russell and Zimdars, 2003) uses decomposition to simplify learning tasks such as controlling fishing by a fleet of boats. These approaches focus on cases in which each overall “joint” action can be subdivided into a set of subactions (e.g., what sort of net each boat casts), and the reward received can be approximated as a sum of rewards received for each subchoice (the fish of each boat, assuming the “credit assignment” problem of matching fish to boats is solved). In such cases, joint actions can be evaluated more simply by assessing each subaction separately.

The topographic organization of the sensorimotor systems of the brain seems a promising substrate to support a similar decomposition of the values of actions between effectors. For instance, eye-specific value maps (Platt and Glimcher, 1999; Sugrue et al., 2004) might represent the value of a saccade separately from the value of any other movements made with the saccade, although this remains to be tested. If true, the choice of multieffector actions could be simplified by decomposing them into separate choices for individual effectors. In contrast, the mechanisms by which the brain learns these valuations are often envisioned as unitary. RL theories hypothesize that learning is driven by a “prediction error” (PE), typically assumed to be a single signal broadcast by dopaminergic projections (Houk et al., 1995; Schultz et al., 1997; Daw and Doya, 2006). However, learning effector-specific action values is facilitated when the PE also decomposes into a separate PE for each subaction (Chang et al., 2003).

We used a bimanual choice task to investigate whether humans can decompose value between conjoint multieffector actions, and to probe decomposition of value- and PE-related neural signaling. The movements in the study were all multieffector in the motor sense of involving near-simultaneous movements of both hands. We asked whether the underlying reasons for the movements (the values of the actions and their neural correlates) were decomposed as though for two parallel single-effector choices. In functional magnetic resonance imaging (fMRI), correlates of value and PE have often been observed in medial prefrontal cortex (mPFC) and striatum (Pagnoni et al., 2002; McClure et al., 2003; O'Doherty et al., 2003; Daw et al., 2006a; Delgado, 2007; Schönberg et al., 2007; Hare et al., 2008). However, previous designs were not suited to identifying values localized to particular effectors, let alone those executing subcomponents of a multieffector action.

Subjects made paired choices in a probabilistic bandit task, indicated simultaneously with left- and right-hand movements. Rewards for each hand were computed independent of the other's choice, and displayed separately. This allowed the task to be decomposed into two hand-specific learning problems. We investigated whether subjects exploited this decomposition by comparing the fit to subjects' choice behavior of RL models using decomposed or unitary value representations, by comparing the results to additional behavioral tasks with different reward structures, and by searching for lateralized neural correlates for the subvalues of either hand.

Materials and Methods

Subjects.

Eighteen right-handed subjects participated in the study. All were free of neurological or psychiatric disease and fully consented to participate. Two subjects' data were lost because of technical failures during the experiment, so results are reported for 16 subjects. Informed consent was obtained in a manner approved by the New York University Committee on Activities involving Human Subjects. Subjects were paid for their participation, with a portion of their payment determined by their actual winnings in the choice task.

Behavioral procedure.

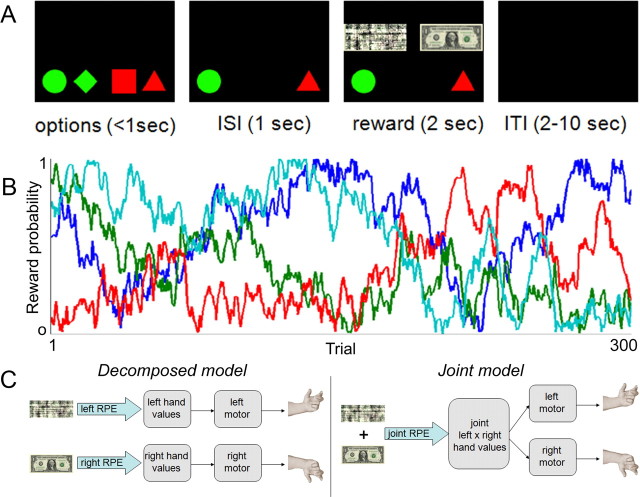
In the task (Fig. 1A), subjects were presented on each trial with four shapes and asked to pick two of them. Each hand could choose between two shapes (from triangle, circle, square, and diamond; the assignment of shapes to hands was counterbalanced between subjects and fixed over the course of the task). Shapes were colored uniquely for each hand and presented on the side of the screen ipsilateral to the corresponding hand. Thus, there were 2 × 2 = 4 possible joint actions. Responses were entered via presses on two magnetic resonance-compatible button boxes, one in either hand. Subjects were given 1 s to respond, and were required to make both responses within 100 ms of each other. Once a response was made, the nonchosen shapes disappeared and the chosen shapes remained on screen for 1 s, after which the rewards won by each hand were displayed above the corresponding shape. Rewards were binary, with a “win” represented by a dollar bill and a “lose” represented by a phase-scrambled dollar bill. The rewards were displayed on screen for 2 s, followed by a pseudorandomly jittered intertrial interval chosen uniformly between 2 and 10 s. Each subject was presented with 300 trials. If choices were not obtained in time, or if the two hands did not respond within 100 ms of each other, the trial entered the intertrial interval.

Figure 1.

Task design. A, On each trial, subjects chose simultaneously between green shapes with their left hand and between red shapes with their right hand. Monetary reward was then sampled from separate choice-dependent Bernoulli distributions (one for each hand). Rewards for each hand were presented simultaneously. In this example trial, the left reward is $0 (indicated by a phase-scrambled dollar bill), and the right reward is $1. ISI, Interstimulus interval; ITI, intertrial interval. B, Reward probability for each of the shapes is shown in a different color. Each probability diffused in a Gaussian random walk with reflecting boundaries at 0 and 1. C, Schematic depiction of the decomposed model (left) and joint model (right). RPE, Reward prediction error.

Reward was delivered, or not, for each shape chosen pseudorandomly according to a probability associated with each shape. Subjects could learn these probabilities only by trial and error. The probabilities determining the chance each shape would be rewarded were changed slowly and independently throughout the experiment (Fig. 1B). Specifically, the probabilities each diffused stochastically from trial to trial according to a Gaussian random walk (at each trial, noise is added with mean of 0 and SD of 0.05) with reflecting boundaries at 0 and 1 (to ensure the parameters stayed in the appropriate range). This diffusion was intended to incentivize subjects to learn continuously throughout the experiment rather than reaching a steady-state level of performance, thus facilitating study of their learning (Daw et al., 2006a). Since each shape (that is, each hand's choice) was independently rewarded, total rewards expected on a trial could be decomposed into independent hand-specific components. Moreover, the hand-specific rewards actually obtained were displayed at the end of the trial.

Subjects were instructed to make choices so as to maximize rewards, and received 7% of the money won during the task at the conclusion of the experiment. The task was presented using the Psychophysics Toolbox (Brainard, 1997), projected onto a screen that was visible via an angled mirror on top of the fMRI head coil.

We also performed two additional behavioral experiments to examine choice behavior under different reward structure and feedback conditions. The methods and results of these experiments are presented in the supplemental material (available at www.jneurosci.org).

Reinforcement learning model-based analysis.

Two alternative RL models were fit to the choice data (Fig. 1C), both based on the temporal difference (TD) algorithm (Sutton and Barto, 1998). The first, which we will call the “joint” model, was a traditional TD model defined on the space of joint actions. Specifically, the model assigns a value Q to each joint action; these are learned according to the following update on each trial t:

In this equation, a_t represents the combination of two shapes chosen on trial t (that is, it takes four possible values corresponding to the possible combinations of a choice from the left and the right hand). The free parameter α controls the learning rate, and δ_t is the prediction error on trial t. This is defined as follows:

Here, r_L,t and r_R,t are the rewards received by each effector on trial t. Thus, the joint model is the same TD algorithm that has been used to model human and animal decision making in many other studies, but treating the multidimensional action as a unitary choice over both effectors and for reward summed over both choices.

The second model we considered, which we call the “decomposed” model, modifies the first model to incorporate knowledge about structure in the action space. It assumes that the joint value function can be decomposed into a sum of effector-specific components, one for each hand as follows:

This allows us to define a separate TD update for each effector, with its own prediction error in its own reward as follows:

and similarly for Q_R and δ_R. Because the updates for each effector are independent of one another, they can be performed in parallel. Thus, this model applies the standard TD model twice, in parallel, to learn valuations for each effector separately.

For both models, we assume that the action values Q control the probabilities P by which joint actions a are chosen on trial t, according to a “softmax” (logistic) rule as follows:

Here, β is a free “inverse temperature” parameter controlling how exclusively choices are focused on the highest valued actions. The additional factors M_t are action traces included to capture residual autocorrelation in choice behavior (Lau and Glimcher, 2005; Schönberg et al., 2007). These capture a tendency to repeat (positive ϕ) or avoid (negative ϕ) recently chosen actions, weighted according to the free parameter ϕ. Traces are assumed to decay exponentially, with a free decay parameter θ. Thus, in the joint model, if k(a_t) is the time since joint action a_t was last chosen, M_t(a_t) = θ^ka_t. In the decomposed model, traces for the actions of each hand are maintained separately, and M_t(a_t) = θ^ka_L,t + θ^ka_R,t. Note that, although Equation 6 expresses the choice probability in terms of the four joint actions a_t, in the case of the decomposed model this may equivalently be treated as the product of a probability for the action of each hand separately (since both M and Q factor into sums over each hand); thus, the decomposed model could be implemented using independent, effector-specific choice mechanisms.

For a setting of the free parameters, the likelihood of a subject's choice dataset under either model was computed as the product over all trials of the probability of the choice made on that trial (Eq. 6) given action values computed from the subject's experience thus far. Maximum-likelihood estimates of the parameters α, β, θ, and ϕ were found for each model by constrained nonlinear optimization, so as to maximize the choice likelihoods. To avoid local optima, the search was repeated from 20 different starting points. For behavioral analysis, we estimated a separate set of parameters for each subject (treating the individual parameters as random effects). To generate regressors for fMRI analysis (below), we refit the behavioral model to estimate a single set of the parameters that optimized choice likelihood aggregated over all subjects (i.e., treating the behavioral parameters as fixed effects). This is because in our experience (Daw et al., 2006a; Schönberg et al., 2007) unregularized random-effects parameter estimates tend to be too noisy to obtain reliable neural results.

To compare the fit of models to choice behavior, we used likelihood ratio tests for comparisons involving nested models, and, when the models being compared were not nested, compared models using Bayes factors (Kass and Raftery 1995), approximated using Bayesian information criterion (BIC) (Schwartz, 1978) scores. BIC is as follows:

where LL_m is the log-likelihood of model m, K_m is the number of parameters of model m, and N is the number of data points (choices). The log Bayes factor between the two models can then be approximated by the difference in BIC scores (in which a smaller BIC score indicates a superior model fit).

Note that, for the main comparison of interest here, that between the joint and decomposed model, both models considered have equivalent sets of free parameters (α, β, ϕ, and θ). As a result, the models are effectively matched in complexity, and so comparing the BIC, the AIC (Akaike information criterion) score, or simply the uncorrected log-likelihoods will give the same rank ordering of the models.

For additional tests of model fit, we compared the RL models to a parameter-free “null model” that assumes all choices are random and equiprobable. We also use the random choice model to compute a standardized metric of model fit, a pseudo-R² statistic (Camerer and Ho, 1999; Daw et al., 2006a), defined as (R − L)/R, where R is the log data likelihood under the chance model and L is that under the fit model.

Imaging procedure.

Functional imaging was performed on a 3T Siemens Allegra head-only scanner and a Nova Medical NM-011 head coil to acquire gradient echo T2* weighted echoplanar images (EPIs) with blood oxygenation level-dependent (BOLD) contrast. Thirty-three contiguous oblique-axial slices (3 × 3 × 3 mm voxels) were obtained, tilted 23° off the anterior commissure–posterior commissure axis so as to optimize sensitivity in the orbitofrontal cortex. This provided coverage from the base of the orbitofrontal cortex and temporal lobe to the superior parietal lobule. Slices were acquired with a repetition time of 2 s. A high-resolution T1-weighted anatomical image (magnetization-prepared rapid acquisition with gradient echo sequence, 1 × 1 × 1 mm) was also acquired for each subject.

Imaging analysis.

Preprocessing and data analysis were performed using Statistical Parametric Mapping software (SPM5; Wellcome Department of Imaging Neuroscience, Institute of Neurology, London, UK). Images were realigned to correct for subject motion, spatially normalized by estimating a warping to template space from each subject's anatomical image (SPM5, “segment and normalize”) and applying the resulting transformation to the EPIs, resampled to 2 × 2 × 2 mm voxels in the normalized space, and smoothed using an 8 mm full-width at half-maximum Gaussian kernel. High-pass filtering with a cutoff period of 128 s was also applied to the data.

Each trial was modeled with impulse regressors at two time points: the time of the presentation of the options (shapes), which was taken to be the time of the decision, and the time of presentation of the outcome. The options event was modulated by two parametric regressors, representing the left and right chosen action values (Q_L,t and Q_R,t, respectively) for the action chosen on each trial, derived from the decomposed model fits. The outcome event was modulated by two parametric regressors, representing the left and right prediction errors (δ_L,t and δ_R,t, respectively). Importantly, because left and right rewards are determined by independent random processes, these regressors are mostly uncorrelated from each other between sides, which improves statistical power to search for any lateralized neural correlates.

These regressors were then convolved with the canonical hemodynamic response function and entered into a general linear model (GLM) of each subject's fMRI data. The left and right parametric modulators were orthogonalized separately to their corresponding events but not to one another. The six scan-to-scan motion parameters produced during realignment were included as additional regressors in the GLM to account for residual effects of subject movement. Linear contrasts of the resulting SPMs were taken to a group-level (random-effects) analysis. We report whole-brain results at an uncorrected threshold of p < 0.001 for areas in which we had a previous hypothesis, and whole-brain corrected for familywise error elsewhere. All voxel locations are reported in Montreal Neurological Institute coordinates, and results are overlaid on the average over subjects' normalized anatomical scans.

Interaction analysis of region of interest data.

We used univariate statistical parametric maps (SPMs) to identify voxels for additional study. Specifically, we found maxima of the contrasts Q_L + Q_R and δ_L + δ_R in anatomically defined regions of interest (ROIs). Because this analysis was specifically concerned with detecting lateralized value decomposition, we attempted to group voxels into well aligned pairs in clusters with multiple maxima. To help to compensate for between-subject variability in anatomy or normalization, we searched for individual-subject local maxima within a small sphere (9 mm) around the group maxima.

We then performed a two-way repeated-measures ANOVA on the strength of value-related BOLD effects in the selected maxima with factors hemisphere (left/right) and effector (left hand/right hand). The data tested were per-subject effect sizes (betas from the first-level GLM) for effector-specific chosen action values (Q_L and Q_R) in the case of intraparietal sulcus (IPS) and mPFC, or prediction errors (δ_L and δ_R) in the case of ventral striatum. Note that, because the contrast used to select the voxels was unbiased with respect to the interaction test, it is unnecessary to correct for multiple comparisons involved in the selection. However, when multiple maxima within a region were identified, we grouped them into left/right hemisphere pairs and applied a Bonferroni correction for the number of pairs tested.

Results

Behavioral results

Subjects were able on most trials to complete the bimanual movements within the time constraints; on average 12 ± 2.9 (mean ± SEM over subjects) of 300 trials were eliminated because of subjects failing to enter responses for both hands within 100 ms of each other and within 1 s total. On correct trials, response times for the left and right hands were 456 ± 15 ms for left-hand responses and 457 ± 15 ms for right-hand responses (grand means ± SEMs across subjects). Collapsed across left and right hands, the mean was 457 ± 15 ms.

Over the course of the game, subjects won 360 ± 9.4 (mean ± SEM) points. This was significantly higher (paired-sample t test, t₍₁₅₎ = 10.27, p < 0.00001) than the amount that would be expected assuming random choices (281 ± 4.5 points, computed for each subject in expectation over his or her reward probabilities).

Reinforcement learning model results

To investigate behaviorally whether subjects took advantage of the decomposition of the task across left and right hands to learn choices, we fit computational models to the behavioral data. A key difference between the joint and decomposed hypotheses is that, if an agent learns the hands' values separately, then the net expected value of a particular joint action (such as left, circle; right, square) will depend on the agent's experience with the outcomes of other joint actions that share the same subactions (such as left, triangle; right, square). In contrast, if learning is over joint actions, value is expected to depend only on past experience with the same joint action, and not to “generalize” between joint actions that share the same left- or right-hand choices. We tested this prediction using a conditional logit regression analysis (see supplemental material, available at www.jneurosci.org), which indicated that subjects' choice of joint action was better predicted not just by the rewards received for particular joint actions on the previous trial, but in addition by the rewards received for the left and right hand's subactions.

To examine learning in more detail, we compared the fit to subjects' choices of RL models that learn action values either jointly or decomposed across the effectors. For reasons such as that discussed above, these two models generalize from experience to action preferences in different ways and thus predict different trial-by-trial patterns of choices.

Parameter estimates and BIC measures for the joint and decomposed models are summarized in Table 1. For additional discussion of the parameter values, see supplemental material (available at www.jneurosci.org). We first tested whether both models performed better than random chance at explaining the choices; they did (likelihood ratio tests, 64 df; values of p not numerically different from zero at machine precision). Comparing the two models, the observed choices were more likely under the decomposed than the joint model for 15 of the 16 subjects. Summing BIC scores across subjects, the estimated log Bayes factor was 572 in favor of the decomposed model, indicating that the choices were approximately exp(572) times more probable given the decomposed model than the joint model. Conventionally (Kass and Raftery, 1995), a log Bayes factor of 4.6 (100:1 ratio) constitutes “decisive” evidence in favor of one model over another.

Table 1.

Reinforcement learning model fits

Model	−LL	BIC	p-R2	α	β	θ	Φ
Joint	3553	3734	0.44	0.53 ± 0.06	4.37 ± 0.48	0.46 ± 0.10	1.43 ± 0.30
Decomposed	2981	3162	0.53	0.72 ± 0.15	4.43 ± 0.60	0.56 ± 0.11	0.12 ± 0.94
Random	6378	6560	—	—	—	—	—

Shown are negative log-likelihood (−LL), BIC, pseudo-R² (p-R²), and random-effects maximum-likelihood parameter estimates (mean ± SEM across subjects) for the joint and decomposed RL models. The bottom row shows summary statistics for the random (null choice) model in which all joint actions have equal probability.

Finally, we wanted to further verify the sensitivity of our methods and to test the broader prediction of our framework that effector-specific decomposition should depend on task factors such as actual value separability and task instructions. For this, we repeated the model-based analysis for two additional behavioral experiments, in one of which the reward structure (and also the visual display of the options) could not be decomposed into separate contributions from each hand's choice. In this case, we hypothesized that subjects would be encouraged to learn action valuations in the space of joint rather than decomposed actions; model fits (see supplemental material, available at www.jneurosci.org) supported this interpretation.

Together, these results indicate that, in the fMRI study in which the choice problem could be decomposed across effectors, subjects learned action values in a way that respected this decomposition. That is, subjects learned in an intuitively plausible way appropriate to the task, even though the rejected joint RL model is arguably the more straightforward application to this task of standard theories.

Imaging results

We next sought evidence whether neural valuation or value learning signals reflected the decomposition of the action values across effectors. We hypothesized that value-related neural signals would exhibit lateralized signaling. Such a hypothesis posits an interaction between the strength of value effects for the left and right hands in areas in the left and right hemispheres. Since this is inherently a claim about multiple voxels, the hypothesis cannot be tested via standard univariate analysis. Instead, we first used univariate contrasts to locate paired functional ROIs in left and right hemispheres with value-related signaling, and then tested within these pairs of areas for an interaction of effector by hemisphere. It is crucial that the contrast used to identify ROIs be unbiased with respect to the subsequent interaction test (Kriegeskorte et al., 2009). Thus, we selected maxima from the univariate net value contrasts Q_L + Q_R and δ_L + δ_R, which indicate regions of neural chosen value or error signaling but are indifferent (since they sum equally over these) as to the relative strength of left- or right-effector related signals. Note that our Q_L and Q_R value regressors represent the value of the chosen action for each hand, and their sum thus represents net value for the joint choice. We tested our hypotheses concerning decomposition using the chosen action value (rather than, say, the option-specific action value for some particular option such as the triangle) since this is the value most often reported to correlate with BOLD signaling (Daw et al., 2006a; Behrens et al., 2007; Gläscher et al., 2009).

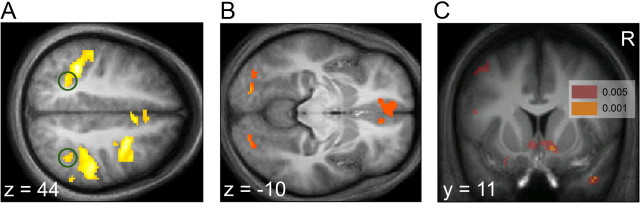
On the basis of previous studies (Platt and Glimcher, 1999; Pagnoni et al., 2002; O'Doherty et al., 2003; Sugrue et al., 2004; Daw et al., 2006a; Delgado, 2007; Schönberg et al., 2007; Hare et al., 2008; Gläscher et al., 2009; Seo and Lee, 2009), we focused on three regions that have been repeatedly implicated in value-based learning and decision making: the IPS, ventral striatum, and mPFC. We found significant correlations between net chosen value Q_L + Q_R and neural activity in bilateral parietal (Fig. 2A) (left hemisphere, peak p = 6e-9, uncorrected; right hemisphere, peak p = 5e-8, uncorrected) and medial prefrontal regions (Fig. 2B) (left hemisphere, peak p = 4e-6, uncorrected; right hemisphere, peak p = 1e-4, uncorrected). The mPFC activations extended from dorsal mPFC down through ventral regions of the structure, similar to activations sometimes identified as ventral mPFC or medial orbitofrontal cortex (supplemental Fig. S1, available at www.jneurosci.org as supplemental material) (Daw et al., 2006a; Hare et al., 2008). Note that, in IPS, the correlation was negative, that is, BOLD activity was lower for actions with a larger Q_L + Q_R. We found a significant correlation between net prediction error δ_L + δ_R and neural activity bilaterally in ventral striatum (Fig. 2C) (left hemisphere, peak p = 6e-4, uncorrected; right hemisphere, peak p = 6e-4, uncorrected). Supplemental Table 3 (available at www.jneurosci.org as supplemental material) summarizes uncorrected Z values for the left and right chosen value regressors separately for each of these coordinates. We also noted correlations with net chosen value and prediction error in a number of additional areas in which we did not have previous hypotheses; these are summarized in supplemental Tables 1 and 2 (available at www.jneurosci.org as supplemental material).

Figure 2.

Random-effects analysis of fMRI. A, Axial slice showing voxels in parietal cortex correlating with net chosen value, thresholded at p < 0.00001, uncorrected. The caudal pair of coordinates is circled in green. A stringent threshold was selected to highlight the peak of interest. B, Axial slice showing voxels in medial prefrontal cortex correlating with net chosen value, thresholded at p < 0.001, uncorrected. C, Coronal slice showing voxels in ventral striatum correlating with net prediction error, shown thresholded at p < 0.005 (red) and p < 0.001 (orange), uncorrected.

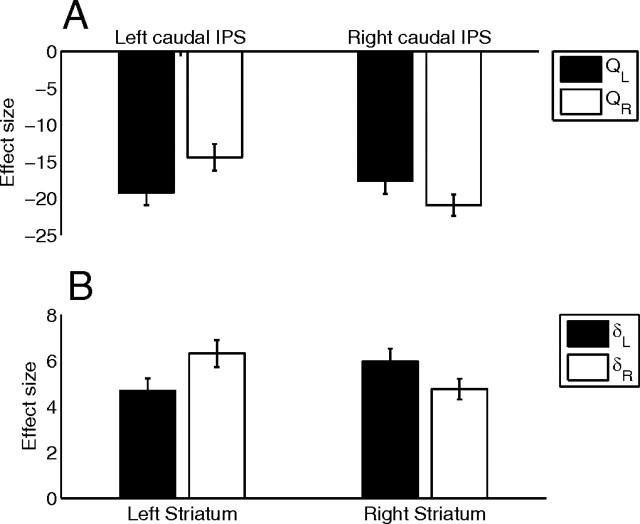
We then tested for hemispheric interactions at the maxima of the chosen value contrast in IPS and mPFC and the prediction error contrast in ventral striatum. In left and right IPS (Fig. 2A), we identified two distinct pairs of maxima for the net chosen value contrast, which were well aligned bilaterally and which we label caudal [left (−32, −50, 38); right (40, −50, 44)] and rostral [left (−34, −38, 38); right (38, −34, 44)]. The ANOVA analysis (Fig. 3A; supplemental Fig. S2A, available at www.jneurosci.org as supplemental material) revealed that only the caudal pair exhibited an interaction (Fig. 3A): F_(1,15) = 6.28, p < 0.025 (Bonferroni corrected for two comparisons).

Figure 3.

Parameter estimates in functional ROIs. A, Responses in caudal IPS to the left and right chosen value regressors, separated by left (−32, −50, 38) and right (40, −50, 44) hemisphere. B, Responses in ventral striatum to the left and right prediction error regressors, separated by left (−4, 14, −8) and right (10, 10, −8) hemisphere.

In mPFC (Fig. 2B), there were several maxima for the net chosen value contrast, but only one pair that was clearly well aligned across hemispheres [left (−10, 40, −10); right (8, 40, −12)]. The ANOVA analysis (supplemental Fig. S2B, available at www.jneurosci.org as supplemental material) failed to reveal a significant interaction between hemisphere and effector: F_(1,15) = 0.0025, p = 0.96.

In the ventral striatum (Fig. 2C), we identified only one maximum in each hemisphere for the net prediction error contrast [left (−4, 14, −8); right (10, 10, −8)]. The ANOVA analysis (Fig. 3B) revealed a significant crossover interaction between hemisphere and effector, with each hemisphere responding preferentially to the contralateral hand's prediction error: F_(1,15) = 11.16, p < 0.005.

Together, the findings that both chosen value- and learning-related neural signals show a lateralized pattern of activation support the hypothesis that the RL systems of the brain decompose values across effectors.

Discussion

Using a bimanual decision task, we found that subjects exploited structure in the rewards to learn action valuations that decomposed into independent effector-specific components whose neural correlates exhibited a lateralized bias. Neurally, this bias was evident in a multivoxel pattern of interaction between hemisphere and effector in the strength of value-related BOLD effects in two areas. Although voxels in both hemispheres correlated with values for both effectors (Fig. 3; supplemental Table 3, available at www.jneurosci.org as supplemental material)—that is, value-related effects on the BOLD signal were not entirely segregated to the contralateral hemisphere—the significant biases observed imply that the brain must represent the subcomponents of values separately, since a pattern of differential signaling would not be expected to arise if only net values (and scalar errors in these net values) were represented.

Of course, it has long been known that the sensory and motor systems of the brain are organized topographically and contralaterally. Here, we report evidence that neural representations of the values of movements may follow a similar organization, as would be expected if “value maps” for decision are overlaid on “motor maps” for execution (Platt and Glimcher, 1999). Furthermore, and more importantly, we show evidence that the brain maintains such decomposed effector-specific action values even in the context of simultaneous bimanual movements, implying the ability to divide and conquer the problem of learning to evaluate simultaneous multieffector movements. We chose a bimanual task because much evidence supports a contralateral organization in the motor systems of the brain, and should this be respected by the value representations of the brain, it would be expected to be observable at a spatial scale detectable by fMRI. A fruitful avenue of research may be to explore more fine-grained forms of decomposition with single-unit recordings.

The ability to decompose values of multieffector actions would greatly simplify the RL problem of learning valuations for multidimensional actions. This is indeed what is suggested by our behavioral finding that subjects' trial-by-trial choices are better explained by a computational learning model that exploits such decomposition than by one that treats multieffector actions jointly. Note that, in the present study, in order not to confound task difficulty with value structure, we used a two effector by two action design that matched the number of values learned between decomposed (2 + 2) and joint (2 × 2) approaches. This approximately equated the task complexity from the viewpoint of our two hypothetical models, and also with the version of the task in which values were not decomposable (supplemental material, available at www.jneurosci.org). Thus, in the present study, subjects did not actually face or resolve a curse of dimensionality. Nevertheless, since in higher dimensions, decomposing a problem as appropriate to the task structure will be more efficient, such an ability to decompose learning may suggest how simple computational and neural mechanisms for value learning studied previously in one-dimensional action choice problems (Platt and Glimcher, 1999; O'Doherty et al., 2003; Sugrue et al., 2004; Daw et al., 2006a; Schönberg et al., 2007; Lau and Glimcher, 2008; Pesaran et al., 2008; Seo and Lee, 2009) might “scale up” to more realistic multidimensional movements.

If values are learned using prediction errors, as commonly supposed, then decomposed values are most efficiently learned using separate prediction errors (Chang et al., 2003). We thus sought evidence of such a decomposition in the oft-reported (Pagnoni et al., 2002; McClure et al., 2003; O'Doherty et al., 2003; Daw et al., 2006a; Schönberg et al., 2007; Hare et al., 2008) prediction error correlates of ventral striatal BOLD, and our results demonstrate a contralateral bias to these signals. This result stands in contrast to the predominant assumption from computational models that a unitary dopaminergic prediction error broadcast supports value learning throughout the forebrain (Houk et al., 1995; Schultz et al., 1997; Bayer and Glimcher, 2005) (but see Daw et al., 2006b; O'Reilly and Frank, 2006; Bertin et al., 2007). The basis for this assumption is the relatively coarse organization of the ascending dopaminergic projection (Haber et al., 2000), in which relatively few dopamine neurons innervate a very large territory of forebrain (Schultz, 1998; Matsuda et al., 2009). Moreover, in recordings, different dopaminergic neurons respond with considerable (Schultz, 1998), although not perfect (Roesch et al., 2007; Brischoux et al., 2009), homogeneity.

Although there is some evidence suggesting prediction error correlates in striatum may reflect dopaminergic input (Pessiglione et al., 2006; Knutson and Gibbs, 2007), we cannot identify whether the contralateral bias in BOLD signaling we report reflects dopaminergic activity or some other lateralized neural source. Nevertheless, this result suggests a particular sort of response heterogeneity that might fruitfully be sought in dopaminergic unit recordings. The possibility that the prediction error signal is vector-valued, encoding decomposed effector-specific signals, means that the brain has recourse to a wider range of learning algorithms than would be possible with a scalar signal (Chang et al., 2003; Russell and Zimdars, 2003).

The cortical results reported here are consistent with a wide range of neuroimaging and single-unit studies that have implicated parietal cortex in value-based learning and decision making (Platt and Glimcher, 1999; Coe et al., 2002; O'Doherty et al., 2003; Sugrue et al., 2004; Daw et al., 2006a; Pesaran et al., 2008). The posterior parietal cortex is a key candidate for effector-specific value signaling. There is evidence that the lateral intraparietal (LIP) area in the posterior parietal cortex contains a “spatial map” for guiding eye movements (Snyder et al., 1997) and neurons in area LIP encode the value associated with eye movements (Snyder et al., 1997; Platt and Glimcher, 1999; Sugrue et al., 2004). Other areas in the posterior parietal cortex show activity that is specialized for other effectors such as reaching and grasping (Murata et al., 1996; Connolly et al., 2003; Kalaska et al., 2003; Pesaran et al., 2006; Cui and Andersen, 2007), and more work is needed to identify the relationship of these areas to expected value (but see Musallam et al., 2004).

We identified an area of IPS whose left and right maxima showed differential sensitivity to left and right chosen action values. Although we hypothesized that value representations would show a contralateral bias, reflecting the underlying motor organization, the value modulation effect we observed in IPS is larger for the ipsilateral action. This may relate, in turn, to another seemingly inverted aspect of our parietal results: the correlation between BOLD response and chosen action value throughout IPS is negative. Although the underlying neural source of this negative modulation remains to be understood, the sign of the effect may explain why value correlates have not to our knowledge previously been reported in IPS using fMRI [but see Daw et al. (2006a) for a related result, in which the increased IPS activity on exploratory compared with exploitative trials implies a negative relationship to value, since exploitative choices by definition are more valuable], despite strong evidence that the activity of parietal neurons is modulated by value in primates (Platt and Glimcher, 1999; Coe et al., 2002; Sugrue et al., 2004).

The negative parametric effect of chosen action value on IPS is unlikely to be simply a confound of response time (e.g., preparatory activity accumulated for longer on lower valued trials), since it remains highly significant even when RT is included as a nuisance covariate (data not shown; the IPS results are essentially identical). Also, although we did not track eye position, we think it is unlikely that the value-related modulations in IPS are driven by uncontrolled saccadic eye movements, since the area most commonly associated with saccades—the putative human analog of primate LIP—is generally more medial and posterior to the areas we report here (Koyama et al., 2004; Grefkes and Fink, 2005). The area in which we see lateralized activation may correspond to the putative human homolog of the nonhuman primate parietal reach region (Astafiev et al., 2003; Connolly et al., 2003; Grefkes et al., 2004), which has been associated with visually guided arm movements (Batista et al., 1999; Cohen and Andersen, 2002; Kalaska et al., 2003; Pesaran et al., 2006).

Although we also observed value-related BOLD modulations in mPFC, as seen in many other studies (O'Doherty, 2004; Hampton et al., 2006; Plassmann et al., 2007; Boorman et al., 2009; Gläscher et al., 2009), we did not find evidence that these were lateralized. However, such a negative result must be interpreted with caution. Indeed, one question that cannot be statistically addressed by our design is whether there are areas in which value signals are explained by net chosen action values, but not biased toward one effector or the other (e.g., a monolithic, net chosen action value). The existence of such a net (chosen, or chosen relative to unchosen; Boorman et al., 2009) action value signal is the underlying assumption of most studies of neural value signaling in the fMRI literature, including those mentioned above. But in the present study, this plays the role of a “null hypothesis” to the alternative entertained here: that, under appropriate conditions, the brain can decompose value signals. Given our results, one candidate for such a net chosen action value signal is the medial PFC, since it correlated with net chosen action values but showed no evidence for laterality. However, from a failure to reject the null hypothesis that there is no pattern of effector-by-value interaction, we cannot affirmatively conclude that the two effectors are really equally weighted in the medial prefrontal value representation.

Another important limitation of our study concerns the timing of events. Because there is <2 s between the trial onset and the onset of feedback, we are not able to distinguish between brain activity related to the decision, response, or outcome periods.

Finally, a significant lacuna of the computational model presented here, and an opportunity for future work, is that it offers no explanation of how the decomposition of value between effectors is learned from experience. Indeed, because our primary question was whether or not subjects were capable of treating RL problems in a decomposed manner, we explained the reward structure to them in detail before their participation in the task. Additionally, our supplemental behavioral data (available at www.jneurosci.org as supplemental material) indicate that subjects are also able to learn values jointly over multieffector actions under other conditions. However, because that study differed from the separable value studies on more than one dimension—including the actual reward structure, the instructed reward structure, and the decomposability of the visual stimuli—additional experiments will be needed to determine how these variables each contribute to whether subjects decompose an RL problem. More generally, future experimental and computational work should address how structure learning, which has often been studied in the context of Bayesian models of inference (Griffiths and Tenenbaum, 2005; Courville et al., 2006; Kemp and Tenenbaum, 2008) can be integrated with reinforcement learning.