Exemplary Dataset Sample Size Calculation for Wilcoxon-Mann-Whitney Tests

Abstract

Zhao, Rahardja and Qu consider sample size calculation for Wilcoxon-Mann-Whitney (WMW) tests for data with ties, and present a straightforward formula. We observe that the “exemplary dataset” approach, usually applied in more complex situations, has a close relationship to the Zhao-Rahardja-Qu method for WMW sample size estimation and they are asymptotically equivalent. Therefore, the exemplary dataset approach can be used to easily obtain estimates similar to those the closed formula gives. We illustrate application of both methods for a WMW sample size estimation example, and also extend the simulation study presented by Zhao, et al. We find that the Zhao-Rahardja-Qu formula (and by extension the exemplary dataset method) can give estimates just as accurate as those obtained using either the Kolassa approach (via nQuery Advisor) or the O’Brien-Castelloe approach (via SAS 9.2 PROC POWER), for 1:1 and 1:2 allocation ratios. However, the latter two methods can be more accurate for a ratio of 1:4 or 1:19. Finally, we note the general utility of the exemplary dataset approach for sample size estimation, even in other situations where closed form sample size formulae exist.

Background

The exemplary dataset approach

Ralph O’Brien [1] [2] [3] and others have advocated the use of exemplary datasets to facilitate sample size and power calculations. While this has usually been in relatively complex situations such as linear models [2], log-linear models [1], Poisson regression [4] [5], or genetic analysis [6], there should be nothing to prevent its application in simpler circumstances, even when closed form sample size and power formulae are available.

The exemplary dataset approach uses sample or synthesized data and a preliminary analysis to generate an estimate of the effect size of interest, usually in the form of a non-centrality parameter. Since a non-centrality parameter is directly proportional to the sample size, and the analysis provides an easy link to the power for a given N, the sample size and power calculation using an exemplary dataset can be straightforward.

Wilcoxon-Mann-Whitney Sample Size Calculation

Noether [7] gave a useful sample size formula for the Wilcoxon-Mann-Whitney (WMW) test. However, it was based upon an assumption that the variable of interest was continuous, having no tied observations. Lesaffre, et al, [8] evaluated Noether’s formula and others when the outcome variable is bounded and ties are present. They noted in particular that a sample size calculation based upon a t-test and using a shift alternative can give drastically inaccurate sample size or power estimates in this situation. However, they did not provide a sample size formula. Instead they required a simulation-based approach to obtain estimates.

Whitehead [9] and Kolassa [10] presented formulae for WMW sample size calculation when ties are present, but the formulations are framed in terms of the proportional odds and its standard error. The O’Brien-Castelloe formulation [11] is used in PROC POWER in SAS 9.2. Their approach expresses the effect size in terms of the log(WMWodds) = log[(p″/(1−p″)] and its standard error. Using Noether’s notation, p″=Pr(X<Y), where X and Y are random observations from the two distributions being compared.

Finally, Zhao et al [12] present a generalization of the Noether formulation, but with an explicit modification for ties. Their formula is:

$$\text{N}=\frac{{(Z_{\alpha }+Z_{\beta })}^2(1-{\sum }_{c=1}^D{((1-t)p_c+t{q}_c)}^3)}{12t(1-t){({\sum }_{c=2}^D{p}_c{\sum }_{d=1}^{c-1}{q}_d+0.5{\sum }_{c=1}^D{p}_c{q}_c-0.5)}^2}$$ (1A)

where D is the number of unique outcome levels, p_c and q_c are the hypothesized proportions at level c for the two populations being compared, m and n are the sample sizes for the two populations, N=m+n, t = n/N is the proportion of observations in the second population, and z_α and z_β are the z-values associated with the type I and type II error levels of interest. If the weighted average of p_c and q_c is denoted as P_c and the expression for ${\text{p}}^{″}={\sum }_{c=2}^D{p}_c{\sum }_{d=1}^{c-1}{q}_d+0.5{\sum }_{c=1}^D{p}_c{q}_c$, is replaced by that symbol, formula (1A) becomes:

$$\text{N}=\frac{{(Z_{\alpha }+Z_{\beta })}^2}{12t(1-t){(p^{″}-0.5)}^2}(1-{\sum }_{c=1}^D{P_c}^3)$$ (1B)

Here $1-{\sum }_{c=1}^D{P_c}^3$ reflects the reduction in variance that is associated with ties.

The Zhao-Rahardja-Qu paper notes that formula (1A) is flexible enough to handle either tied or untied data, as well as data that include a mixture of tied and untied or continuous observations. In fact, in the latter situation they point in a direction consistent with use of the exemplary dataset method when they suggest that “In this case one needs to obtain (a table of proportions) from existing data in order to compute N using formula” (1A).

To compute power starting with the Zhao-Rahardja-Qu formula, the relevant equation would be:

$$Z_{\beta }=\sqrt{\frac{N12t(1-t)}{(1-{\sum }_{c=1}^D{P_c}^3)}}(p^{″}-0.5)-Z_{\alpha }$$ (2)

Derivations of the Noether and Zhao-Rahardja-Qu WMW Sample Size Formulae

The Noether and Zhao, et al papers begin their sample size derivations by solving an equation of the form:

$${\left[\frac{{\mu }_1-{\mu }_0}{{\sigma }_0}\right]}^2={({\text{z}}_{\alpha }+\frac{{\sigma }_1}{{\sigma }_0}{\text{z}}_{\beta })}^2$$ (3)

where μ and σ² reflect the expected value and variance for a statistic used for the test. (For Noether it was the rank sum statistic, while Zhao, et al used p̂″.) Here the subscripts 0 and 1, denote the null and alternative, respectively. It is assumed thatσ₁≈σ₀ (and hence the ratio σ₁/σ₀=1), and expressions appropriate to the WMW test are substituted for μ₁, μ₀ and σ₀.

We may replace ${\left[\frac{{\mu }_1-{\mu }_0}{{\sigma }_0}\right]}^2$ by the symbol X² to denote the formula for a chi square statistic. The Noether and Zhao-Rahardja-Qu sample size formulae are based upon factoring the algebraic expression for X² into N and a second term which will be denoted as G. Therefore, we have X² = NG, and formula (3) becomes:

$$\text{N}=\frac{{({\text{z}}_{\alpha }+{\text{z}}_{\beta })}^2}{\text{G}}$$ (4)

There can be considerable effort required to factor the formula for X² to isolate N. For WMW testing, notable instances of this are the original work of Noether [7] for the general case without ties, Whitehead [9] with ties assuming proportional odds, and Zhao, et al [12] for the situation with ties.

In Noether’s case he found G=12t(1−t)(p″−0.5)². For Zhao-Rahardja-Qu, as reflected in formulae (1A) and (1B), they derived:

$$G=\frac{12t(1-t){(p^{″}-0.5)}^2}{(1-{\sum }_{c=1}^D{P_c}^3)}$$

Derivation of the Exemplary Data Set Formula

To obtain the parallel derivation for the exemplary dataset formula, we can use equation (3), but instead of using an algebraic expression for the left hand side, we can use an actual value of a chi square test statistic. If the sample size for this calculation was N_obs and we denote the chi square statistic by $X_{\mathit{obs}}^2$, we have $X_{\mathit{obs}}^2={\text{N}}_{\text{obs}}\text{G}$. If both sides of equation (4) are divided by N_obs, we have:

$$\frac{N}{N_{\mathit{obs}}}=\frac{{(z_{\alpha }+z_{\beta })}^2}{N_{\mathit{obs}}G}$$ (5)

Multiplying both sides by N_obs then yields:

$$\text{N}=\frac{N_{\mathit{obs}}{(z_{\alpha }+z_{\beta })}^2}{X_{\mathit{obs}}^2}$$ (6)

That is, if $X_{\mathit{obs}}^2$ is an actual realization of the test statistic, but using data which reflects the alternative hypothesis of interest and which has a sample size of N_obs, it follows that equation (6) gives the desired exemplary dataset sample size estimate. The “exemplary dataset” provided the data used to calculate $X_{\mathit{obs}}^2$.

Although the validity of equation (6) is immediate when a version of equation (4) exists, it is merely the potential existence of a factorization of X² into the product of N and G that is required for equation (6) to work. It is important to note that formula (6) may need to rely upon an approximation where the term G may retain or omit components which are low order with respect to N, and therefore, may be ignored for moderate to large sample sizes. The derivation for the Zhao-Rahardja-Qu formula incorporates one such approximation.

If an estimate of power is needed using the exemplary data approach, starting with the sample size of N_obs, and the effect size implicit in the test statistic $X_{\mathit{obs}}^2$, equation (6) may be solved for z_β, giving:

$$Z_{\beta }=\sqrt{\frac{{NX}_{\mathit{obs}}^2}{N_{\mathit{obs}}}}-Z_{\alpha }$$ (7)

Finally, to consider the relationship of the effect size to sample size and power, we note that under the alternative X² has a non-central chi square distribution. If we write X² = NG = Nθ/K, the whole expression has an interpretation as the non-centrality parameter. Here θ= (p″−0.5)² (or its square root) might be thought of as the effect size and $\text{K}=(1-{\sum }_{c=1}^D{P_c}^3)/12t(1-t)$ represents the variance for p″. If it is reasonable to assume that θ can vary without a major change in ( $1-{\sum }_{c=1}^D{P_c}^3$), a change in the effect size from θ_a to θ_b would call for a corresponding change in N, from N to Nθ_a/θ_b. Put another way, for a given power, N ∝ 1/θ, so N and 1/θ must vary together.

Illustration of Exemplary Dataset Sample Size Estimation for a WMW Test

Wilcoxon Mann-Whitney Test

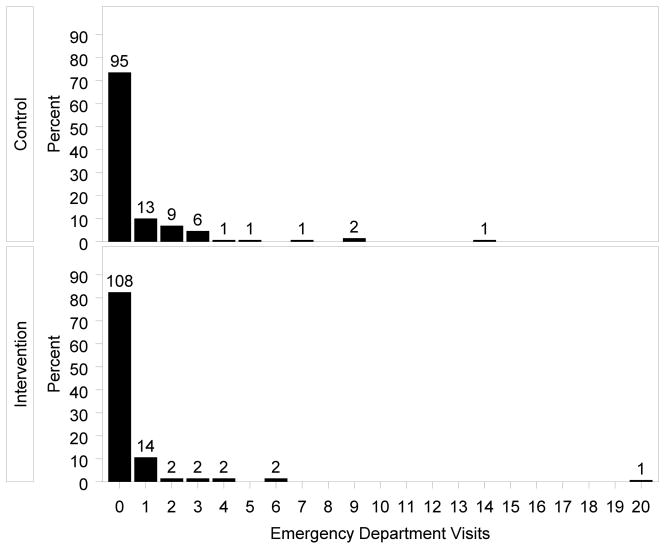
The Puff City [13] randomized trial of a tailored asthma management program for urban African-American high school students, had among its outcome variables, the 12 month post-intervention number of emergency department (ED) visits among the study participants. Figure 1 shows the observed distribution of visits for the two study groups. As might be expected among subjects not selected on the basis of ED use, majorities have no visits in the follow-up period. However, overall the distribution appears to be shifted toward zero for the intervention group. The WMW chi square test statistic for the comparison of the two groups is 3.393 (p=0.0655), for the total sample size of 260. The observed value for p″, the probability that an intervention subject has a lower number of ED visits compared to a control, is 0.54778. The associated WMWodds value is 1.21. A follow-on trial might be contemplated, with a goal of definitively demonstrating that the intervention results in a reduction in ED visits. For the sample size calculation, it could be assumed that the difference in ED visit distributions is comparable to that in the observed data. To apply the Zhao-Rahardja-Qu formula, in this circumstance we also need the quantity ( $1-{\sum }_{c=1}^D{P_c}^3$), which for the data in this example equals (1−0.47718). Applying formula (1B) for equal group sizes, two-tailed alpha=0.05 and 80% power, gives:

$$\text{N}=\frac{{(1.96+0.8416)}^2}{12t(1-t){(0.54778-0.5)}^2}(1-0.47718)=\frac{7.849}{3{(.04778)}^2}(0.52282)=599.2$$

Figure 1.

Distributions of Emergency Department Visits During 12 Month Follow-up for Puff City Trial Intervention and Control Groups

Or N=600.2 using formula (1B). More straightforwardly, formula (6) can be used, giving its estimate for the total sample size, which is 260*7.849/3.393 = 601.4, or ~301 per group.

It should be noted that the proportion of the observations in this example which are equal to zero was 0.78077. When this proportion is cubed, the resulting quantity, 0.4759, represents 99.7% of the total reduction in variance due to ties.

There are 11 unique visit count values observed in this example, but nQuery Advisor only accommodates up to 8 outcome levels. Therefore, nQuery Advisor was not used to estimate a sample size estimate. PROC POWER in SAS 9.2 gave an estimate of 598 (299 per group). However, to get PROC POWER to produce this estimate, the proportions were expressed using up to 9 digits¹. Also, an adjustment (made to the zero cell proportions), was required to get the sum of the probabilities to add up to “exactly” 1.0 for each group, even when the proportions were expressed using a large number of digits².

When 10,000 simulations with N=602 and 598 were carried out for the proportions shown in Figure 1, the observed power estimates were 80.2% and 79.4% respectively, suggesting that both methods worked well for this example.

Extension of the Zhao-Rahardja-Qu Simulations

Methods

Zhao, et al illustrated their formula using data published by Bender [14] for smoking and retinopathy status among diabetes patients. They also evaluated the accuracy of the sample size estimates using simulations for two allocation ratios and for 12 different alternative hypotheses cases. The first 6 cases required sample sizes up to 45,264, and may not be of major additional interest given how close the p″ values were to the null (0.5) and the fact that the power estimates agreed closely with the simulation estimates. The last 6 cases, however, may be more interesting, in particular for the last three instances for the 1:19 (t=0.95) allocation ratio. For these latter cases, there was evidence that the sample size estimates could be too large.

The distributions being compared for the last six cases are presented in Table 1A. We undertook simulations for these 6 cases, with allocation ratios of 1:1, 1:2, 1:4 and 1:19. The first and last ratios respectively, almost and exactly replicate those used by Zhao, et al, but the middle two represent other unbalanced allocation ratios that might realistically be considered for use in randomized trials. As was the case for the Zhao-Rahardja-Qu simulations, we used 10,000 replications.

Table 1.

Table 1A: Hypothetical Distributions of Retinopathy Status Used for Zhao-Rahardja-Qu, Simulations
	Retinopathy Status			P″
Group/Alternative Case	None	Non-proliferative	Advanced
Non-Smokers	0.66	0.15	0.19
Versus
Smokers Case 7	0.55	0.23	0.22	0.550
Smokers Case 8	0.55	0.20	0.25	0.555
Smokers Case 9	0.55	0.15	0.30	0.563
Smokers Case 10	0.55	0.00	0.45	0.589
Smokers Case 11	0.45	0.00	0.55	0.646
Smokers Case 12	0.40	0.00	0.60	0.675

Table 1B: Observed Power Estimates From a) 10,000 Simulations, b) nQuery Advisor v6.0 (nQa) and c) SAS v9.2, All Using N’s Calculated Using the Zhao-Rahardja-Qu formula for 80% Power for Cases 7–12
		Allocation Ratio
Case	P″	1:1					1:2					1:4					1:19
		n1	n2	a) SIM	b) nQa	c) SAS	n1	n2	a) SIM	b) nQa	c) SAS	n1	n2	a) SIM	b) nQa	c) SAS	n1	n2	a) SIM	b) nQa	c) SAS
7	0.550	405	405	0.798	0.800	0.801	311	621	0.789	0.805	0.804	263	1052	0.807	0.807	0.805	225	4281	0.816	0.809	0.806
8	0.555	333	333	0.804	0.801	0.802	255	511	0.803	0.807	0.806	216	865	0.814	0.811	0.809	185	3517	0.812	0.816	0.812
9	0.563	249	249	0.798	0.802	0803	190	381	0.804	0.811	0.809	161	644	0.803	0.818	0.815	138	2615	0.820	0.826	0.823
10	0.589	124	124	0.816	0.802	0.803	93	187	0.815	0.818	0.817	78	311	0.831	0.834	0.831	65	1238	0.845	0.848	0.846
11	0.646	48	48	0.804	0.812	0.814	36	71	0.816	0.826	0.826	29	118	0.823	0.832	0.834	24	460	0.852	0.845	0.850
12	0.675	34	34	0.805	0.817	0.818	25	50	0.800	0.826	0.827	21	82	0.840	0.842	0.847	17	314	0.857	0.851	0.862

nQa–nQuery Advisor uses the Kolassa method to estimate WMW power

SAS–PROC POWER in SAS v9.2 uses the O’Brien-Castelloe method to estimate WMW power (based upon the log(WMWodds) statistic)

Since nQuery Advisor and SAS version 9.2 are two software options to do sample size and power estimation for WMW testing with ties, they were evaluated as well as the Zhao-Rahardja-Qu approach. To compare methods, but to avoid having to undertake three very similar sets of simulations, one set of simulations was performed using the sample size(s) estimated to give 80% power using the Zhao-Rahardja-Qu formula. As expected, power estimates computed using the exemplary dataset method were nearly identical to the Zhao-Rahardja-Qu values (all were within 0.03% of 80%), so those two methods will be considered as being the same for this analysis.

nQuery Advisor and SAS were then used to calculate power estimates, given the Zhao-Rahardja-Qu sample sizes. Accordingly, good performance of the Zhao-Rahardja-Qu formula and the exemplary dataset method would be reflected in simulation estimates close to 80%, while good performance of nQuery Advisor (using the Kolassa formula) or SAS (using the O’Brien-Castelloe method) would be reflected in their power estimates being close to the simulation estimates (whether or not the latter are close to 80%). With n=10,000, the simulation based power estimates can be expected to have 95% confidence intervals of ±0.8%.

Simulation Results

Table 1B shows power estimates from a) 10,000 simulations, b) nQuery Advisor v6.0, and c) SAS 9.2. In all cases, nQuery Advisor and SAS gave comparable estimates. For cases 10–12, the nQuery Advisor and SAS estimates are better than Zhao for allocation ratios of 1:4 and 1:19 (t=0.8, t=0.95). For instance, for case 12 and an allocation ratio of 1:4, the observed power is 4.0% higher than estimated by the Zhao-Rahardja-Qu formula, while nQuery Advisor and SAS give power estimates within 0.2% and 0.7% of the observed power, respectively. In cases 7–9 for all allocations ratios, and for allocation ratios of 1:1 and 1:2 for all 6 cases, the three different estimation methods all appear to match the empirical power relatively well (within 3.0%). From these results, we would conjecture that the Zhao-Rahardja-Qu formula may be quite suitable when the allocation ratio is 1:1 or 1:2, but that the nQuery Advisor and SAS formulae might be better when the ratio is larger than 1:2. Given the fact that the Zhao-Rahardja-Qu formula may overestimate the sample size requirement and a major component of randomized trial costs can be a function of the sample size requirement, it could be worthwhile using the nQuery Advisor/Kolassa or the SAS/O’Brien-Castelloe formula in such cases. In other situations, convenience may suggest that a Zhao-Rahardja-Qu estimate is preferable.

Discussion

Exemplary Dataset Method Application

In a situation where the hypothesized alternative distribution is well expressed by preliminary data, use of the exemplary dataset method for sample size estimation can be seen to be very natural and straightforward. Since software to compute a test statistic might be much more accessible than software for sample size, the only essential extra step is a simple calculation using formula (6). If calculation of power is of interest, using the exemplary dataset formula for Z_β is also convenient, as can be seen when formula (2) and formula (7) are compared. If calculation of a detectable “effect size” is the goal, the exemplary dataset calculation can again be helpful. That is, if along with the p-value for the test, the Mann-Whitney U statistic or the rank sum statistic is obtained, p″ may be easily computed as U/nm (noting that U can easily be computed from the rank sum). In this situation all the important quantities are in hand, since N is directly proportional to 1/(p″−0.5)².

Even if preliminary data are not readily available, there are some situations where an exemplary dataset might be a natural way to express the alternative hypothesis. A very simple example of this might be comparison of two proportions, where the percentages could be used to fill in a two-by-two table with 100 observations per group, and the associated chi square statistic could be used with formula (6) for a sample size estimate. Extension to a small number of ordered categories for a WMW test need not be conceptually different. Kruskal-Wallis test sample size estimation could be approached the same way. Other, related tests with less commonly available sample size solutions, such as a Jonckheere-Terpstra procedure might also benefit from the exemplary dataset approach. Finally, it should be clear that the potential utility of the exemplary data method for basic sample size estimation is not limited to tests related to the Wilcoxon.

One limitation of the exemplary dataset method is that it is generally only well suited to asymptotic tests. Where a small sample size is planned, requiring an exact test, another method such as simulations might be required. Another limitation of the exemplary dataset method is that the test statistic will likely make the assumption that the null hypothesis holds, while its distribution under the alternative may be important for an accurate power estimate. Since the exemplary dataset method incorporates the test statistic assumptions, it may also only assume the variance under the null. For instance, for the WMW test statistic considered here, the null is assumed. This point might partially explain the somewhat better performance of the Kolassa and O’Brien- Castelloe estimates for some of the simulations represented in Table 1B, since both of those methods take the variance under the alternative into account.

Mixed Tied and Untied (Continuous) Wilcoxon-Mann-Whitney Sample Size Estimation

A very minor technical limitation of formula (1A), is that although it handles a fixed number of tied and untied categories, when increasing the sample size implies additional unique outcome categories, the formula becomes slightly inaccurate. That is, additional untied observations would increase the value of D. This implies that D becomes a function of N. However, since D is still on the right hand side of formula (1A), the formula technically fails to provide a completely closed form solution for N. Fortunately, it can be argued that the inclusion or exclusion of such additional categories does not appreciably affect the estimate for N.

If pilot data are not readily available for an outcome that will include both tied and untied data, and generation of hypothetical data is not easy, this would be a situation where the Zhao-Rahardja-Qu formula (1B) could be more useful than the exemplary dataset approach. For instance, as long as it might be possible to do a reasonable prediction of the proportions of tied observations for the planned study, these might be used to generate an estimate for ΣP_c³. If an estimate for a biologically important value for p″ can be made, these might be combined using formula (1B), to give a useful sample size estimate for the study.

An example of a situation where such an approach might be used, would be for a laboratory value outcome, where a significant proportion of the observations will be zero (or equivalently, below the limits of detectability). In this case, a WMW test might be contemplated, and sample size estimated using formula (1B). In this case, if there will be a few small sets of ties other than at zero, the quantity $\mathrm{\sum }{P}_i^3$ could still be closely approximated by P₀³, where P₀ is the proportion of observations expected at zero. That is, even a very large number of small proportions, when cubed and summed, will not add up to a very large amount. An extension of this argument suggests that the potential of the number of outcome categories D to be a function of N is of little, if any consequence with respect to the variance contribution to the sample size estimate. Thus, the Zhao-Rahardja-Qu formula should remain a good approximation, as long as p″ is estimated reasonably.

Summary

An exemplary dataset sample size estimate for a Wilcoxon-Mann-Whitney test is basically identical to what can be computed using the Zhao-Rahardja-Qu formula. In an example with real data, and for simulations with a group size ratio not more unbalanced than 1:2, these sample size calculation options performed as well as the Kolassa and O’Brien-Castelloe methods. Most usefully, the exemplary dataset approach to sample size estimation can be much easier to apply for WMW estimation, despite the availability of closed form solutions. Finally, the same considerations suggest that the exemplary dataset method should be considered in other circumstances, whether or not a closed form solution is known.