Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Jan 1.
Published in final edited form as: Genet Epidemiol. 2010 Jan;34(1):100–105. doi: 10.1002/gepi.20430

Avoiding the high Bonferroni penalty in genome-wide association studies

Xiaoyi Gao 1,†, Lewis C Becker 2, Diane M Becker 2, Joshua D Starmer 3,4, Michael A Province 1
PMCID: PMC2796708  NIHMSID: NIHMS141684  PMID: 19434714

Abstract

A major challenge in genome-wide association studies (GWASs) is to derive the multiple testing threshold when hypothesis tests are conducted using a large number of single nucleotide polymorphisms. Permutation tests are considered the gold standard in multiple testing adjustment in genetic association studies. However, it is computationally intensive, especially for GWASs, and can be impractical if a large number of random shuffles are used to ensure accuracy. Many researchers have developed approximation algorithms to relieve the computing burden imposed by permutation. One particularly attractive alternative to permutation is to calculate the effective number of independent tests, Meff, which has been shown to be promising in genetic association studies. In this study, we compare recently developed Meff methods and validate them by the permutation test with 10,000 random shuffles using two real GWAS data sets: an Illumina 1M BeadChip and an Affymetrix GeneChip® Human Mapping 500K Array Set. Our results show that the simpleM method produces the best approximation of the permutation threshold, and it does so in the shortest amount of time. We also show that Meff is indeed valid on a genome-wide scale in these data sets based on statistical theory and significance tests. The significance thresholds derived can provide practical guidelines for other studies using similar population samples and genotyping platforms.

Keywords: multiple testing correction, genome-wide significance, genetic association studies

With the advent of high throughput genotyping technology, genome-wide association studies (GWASs) are becoming more common. One of the major challenges in GWASs is to derive the multiple testing correction threshold. There are two simple methods in practice: Bonferroni and Šidák corrections[Šidák 1967]. These methods try to keep the experimental-wise error rate (αe) at a nominal level, e.g. 0.05, by adjusting the point-wise error rate (αp). Suppose that there are M independent tests, Šidák correction gives αp = 1−(1−αe)1/M and Bonferroni correction gives αp = αe/M. These two methods are very closely related and lead to similar results. Unfortunately, they can be conservative if the independence assumption does not hold, and this is usually the case for densely typed single nucleotide polymorphisms (SNPs) in current genetic association studies.

In genetic association studies, researchers treat permutation tests as the gold standard for multiple correction adjustment. For the permutation tests of population-based studies, phenotypes are randomly shuffled while the SNP genotypes are kept the same [Churchill and Doerge 1994]. Hence, the correlation structure among SNPs is preserved and the phenotype is permuted to simulate the null hypothesis of no association. However, permutation tests are hindered by the large number of random shuffles required, which take considerable computing time and resources. If a large number of SNPs, e.g. 1M or 500K, are involved in the genetic association study, permutation tests become impractical for GWASs because it can take years to finish on a single modern PC if a substantial number of random shuffles are carried out [Conneely and Boehnke 2007; Gao, et al. 2008]. Reducing the number of random shuffles to make the computation feasible results in thresholds that suffer from high levels of variation. If we increase the number of random shuffles, the computing time increases tremendously. Therefore, less computationally demanding methods that can approximate permutation tests with a large number of shuffles are desirable.

One particularly attractive alternative to permutation tests is to calculate the effective number of independent tests, Meff [Cheverud 2001; Gao, et al. 2008; Li and Ji 2005; Moskvina and Schmidt 2008; Nyholt 2004; Nyholt 2005]. Despite criticism from Salyakina et al. [2005], the validity of Meff has been shown by many researchers. The idea of Meff-based approaches is simple: “filter out” the correlation among tests, leaving only the effective number of independent ones, Meff, and then use the Bonferroni or the Šidák correction by replacing M with Meff in the corresponding formula.

Meff-based corrections have been shown to be effective and fast. The Meff approach was first proposed in genetic studies by Cheverud [2001] and later refined by Nyholt [2004]. Later, it was found that Nyholt’s approach can be conservative when haplotype block structure exists [Salyakina, et al. 2005]. Salyakina et al. [2005] also reported some anti-conservative behavior for Nyholt’s approach for data with strong linkage disequilibrium (LD) though these observations have not been seen by the other investigators. Li and Ji [2005] proposed another Meff estimation formula and showed an improvement in power over Nyholt’s approach but at the expense of the type I error rate. Cheverud’s, Nyholt’s and Li and Ji’s Meff methods, however, were validated using only a small number of SNPs, and it remained to be seen how well they performed using a large number of correlated SNPs. Recently, Gao et al. [2008] proposed to a principal component approach to derive Meff, named simpleM, and showed that it provided a better estimate than Li and Ji’s method in the presence of a large number of SNPs. Moskvina and Schmidt [2008] derived a new Meff estimation formula, calling it Keff, and validated it using a GWAS data set.

Gao et al’s simpleM method performed accurately and efficiently when a large number of SNPs were involved, even under different LD situations and showed potential for GWASs [Gao, et al. 2008]. It uses composite LD among SNPs to capture the correlation and derives the Meff using the number of principal components that contribute to 99.5% of variation. When a large number of SNPs are used, they need to be partitioned into smaller blocks in order to calculate eigenvalues effectively [Gao, et al. 2008]. The authors tested two partition methods, fixed length and haplotype blocks inferred from HaploView software [Barrett, et al. 2005]. Partitions based on haplotype blocks gave slightly better Meff estimations than fixed length partitions. However, computing haplotype blocks is slow and impractical on the genome-wide scale. Moskvina and Schmidt’s Keff algorithm estimates the overall type I error probability using pair-wise correlations among SNPs[Moskvina and Schmidt 2008]. However, it can be very time consuming to derive the full correlation matrix among SNPs and the authors developed an approximation method by using only small window sizes, e.g. 20, for the correlation matrix. The Keff approach was shown to be able to give a relatively accurate though slightly conservative estimation when tested using a GWAS data set.

In this study, we evaluate the simpleM (available at https://dsgweb.wustl.edu/rgao/) as tested in the original paper [Gao, et al. 2008], and the Keff algorithm (available at http://x001.psycm.uwcm.ac.uk/) as tested in the original paper [Moskvina and Schmidt 2008], using two real GWAS data sets: an Illumina 1M BeadChip and an Affymetrix GeneChip® Human Mapping 500K SNP data set. We also show that Meff is indeed valid on a genome-wide scale in these data sets based on statistical theory and significance tests.

In our evaluation of the permutation approximation algorithm, we first used the Illumina 1M BeadChip data, from our genetic study of aspirin responsiveness (GeneSTAR) project (https://dsgweb.wustl.edu/genestar/). In total, 1,004,037 SNPs were genotyped. For the multiple testing evaluations, we only used common SNPs with a minor allele frequency greater than or equal to 0.05, reducing the set to 778,629 SNPs. 656 unrelated white individuals were used. The missing value rate among these common SNPs was about 0.26%. We used the K-nearest neighbor (KNN) approach [Hastie, et al. 2001] to fill in missing genotypes. Other imputation algorithms, e.g. Mach [Li and Abecasis 2006], IMPUTE [Marchini, et al. 2007], Beagle [Browning and Browning 2007] and BimBam [Servin and Stephens 2007], should work well too, but can take more computing time. For the second data set, we used the Affymetrix GeneChip® Human Mapping 500K Array Set, from the Framingham Heart Study [Splansky, et al. 2007] (http://www.ncbi.nlm.nih.gov/sites/entrez?Db=gap). In total, there are 485,424 SNPs in the database. We also only used common SNPs, reducing the set to 383,213 SNPs. 698 unrelated white individuals were used. The missing value rate was about 1.4% among these common SNPs and we used the KNN approach to fill in missing genotypes.

We compared the simpleM and the Keff methods to permutation and Bonferroni corrections. We conducted permutation tests with 10,000 random shuffles using the Cochran-Armitage trend test[Armitage 1955; Cochran 1954]. We set experiment-wise error rates to be 0.05. Details of permutation tests have been described previously[Gao, et al. 2008]. Results for each chromosome (chromosome-wide αe = 0.05) and genome-wide (genome-wide αe = 0.05) are shown in Table 1 for the Illumina 1M data and Table 2 for the Affymetrix 500K data. For each chromosome, we calculated the permutation threshold and derived the αps for the simpleM, Keff and Bonferroni methods by setting chromosome-wide αes to 0.05. For the simpleM and Keff methods, we inferred the effective number of independent tests first and then applied the Šidák formula to derive the corresponding αps (see the Table 1 and 2). The simpleM method gives the best approximation (the smallest distance) to the permutation thresholds, while the Keff method gives more conservative estimations, and Bonferroni gives the most conservative results. We also derived the thresholds for the whole genome by setting genome-wide αes to 0.05. In Table 1 (the Illumina 1M data), the genome-wide permutation threshold is 1.36e–7 and the corresponding estimated Meff is log(1-0.05)/log(1–1.355645e–7) = 378368. The simpleM, Keff and Bonferroni methods give the thresholds as 1.24e–7, 9.70e–8 and 6.42e–8, respectively. Again, we see that Bonferroni is very conservative, Keff is better and simpleM gives the best approximation. For the genome-wide estimation of the Meff, the simpleM and Keff estimate 34992 and 150656 more tests than the permutation, respectively. The Keff estimates 115664 more tests than the simpleM method, and hence is more conservative. In Table 2 (the Affymetrix 500K data), the permutation threshold is 2.46e–7 and the corresponding estimated Meff is log(1-0.05)/log(1–2.46119e–7) = 208408. The simpleM, Keff and Bonferroni methods give the thresholds as 2.23e–7, 1.95e–7 and 1.30e–7, respectively. In order to see their difference clearly, we can treat the permutation threshold as the “true” baseline. The simpleM, Keff and Bonferroni thresholds are 91%, 79% and 53% of the “true” value. Therefore, we continue to see that Bonferroni is conservative, Keff is better and simpleM gives the best approximation. For the genome-wide estimation of the Meff, the simpleM and Keff estimate 21352 and 54306 more tests than the permutation, respectively. The Keff estimates 32954 more tests than the simpleM method, and thus is more conservative.

Table 1.

Derived significance thresholds for the Illumina 1M data.

Chromo-
some		 Number
of SNPs		 Permutation simpleM Keff Bonferroni
Meff αp Meff αp w=20 αp αp
1 63560 30881 1.66E-06 31898 1.61E-06 41438 1.24E-06 7.87E-07
2 64367 31760 1.62E-06 33386 1.54E-06 43538 1.18E-06 7.77E-07
3 53622 26328 1.95E-06 27675 1.85E-06 36009 1.42E-06 9.32E-07
4 47096 24292 2.11E-06 24474 2.10E-06 31651 1.62E-06 1.06E-06
5 48758 24187 2.12E-06 25229 2.03E-06 32699 1.57E-06 1.03E-06
6 52870 25667 2.00E-06 26165 1.96E-06 34945 1.47E-06 9.46E-07
7 43084 23040 2.23E-06 23123 2.22E-06 29607 1.73E-06 1.16E-06
8 41932 23254 2.21E-06 22314 2.30E-06 28809 1.78E-06 1.19E-06
9 35591 20078 2.55E-06 20061 2.56E-06 25505 2.01E-06 1.40E-06
10 40195 21186 2.42E-06 21277 2.41E-06 27575 1.86E-06 1.24E-06
11 39420 21101 2.43E-06 20359 2.52E-06 26188 1.96E-06 1.27E-06
12 38787 20875 2.46E-06 21318 2.41E-06 26644 1.93E-06 1.29E-06
13 28656 14936 3.43E-06 15087 3.40E-06 19624 2.61E-06 1.74E-06
14 26026 14414 3.56E-06 13829 3.71E-06 17749 2.89E-06 1.92E-06
15 23896 12277 4.18E-06 13312 3.85E-06 16477 3.11E-06 2.09E-06
16 24517 14346 3.58E-06 14626 3.51E-06 17627 2.91E-06 2.04E-06
17 23054 11558 4.44E-06 12578 4.08E-06 15360 3.34E-06 2.17E-06
18 22885 11629 4.41E-06 12583 4.08E-06 15935 3.22E-06 2.18E-06
19 16918 9152 5.60E-06 9646 5.32E-06 11389 4.50E-06 2.96E-06
20 19995 10177 5.04E-06 11169 4.59E-06 13971 3.67E-06 2.50E-06
21 11012 6150 8.34E-06 6247 8.21E-06 7747 6.62E-06 4.54E-06
22 12388 6708 7.65E-06 7004 7.32E-06 8537 6.01E-06 4.04E-06
genome-
wide		 778629 378368 1.36E-07 413360 1.24E-07 529024 9.70E-08 6.42E-08
Open in a new tab

The permutation thresholds were calculated using 10,000 random shuffles.

The experiment-wise error rates for each chromosome and the genome-wide adjustment was set at αe = 0.05.

αp: point-wise error rate.

Meff: the effective number of independent tests.

w=20: window size is set equal to 20.

Table 2.

Derived significance thresholds for the Affymetrix 500K data.

Chromo-
some		 Number
of SNPs		 Permutation simpleM Keff Bonferroni
Meff αp Meff αp w=20 αp αp
1 30655 17011 3.02E-06 18079 2.84E-06 20980 2.44E-06 1.63E-06
2 32107 18474 2.78E-06 19193 2.67E-06 22041 2.33E-06 1.56E-06
3 26573 15279 3.36E-06 15704 3.27E-06 18054 2.84E-06 1.88E-06
4 24773 13534 3.79E-06 14363 3.57E-06 16603 3.09E-06 2.02E-06
5 25414 12829 4.00E-06 14941 3.43E-06 17209 2.98E-06 1.97E-06
6 25552 14610 3.51E-06 14638 3.50E-06 17077 3.00E-06 1.96E-06
7 20655 12108 4.24E-06 12470 4.11E-06 14243 3.60E-06 2.42E-06
8 21494 12268 4.18E-06 12749 4.02E-06 14617 3.51E-06 2.33E-06
9 18140 9519 5.39E-06 11194 4.58E-06 12737 4.03E-06 2.76E-06
10 22293 12681 4.04E-06 13017 3.94E-06 14980 3.42E-06 2.24E-06
11 20621 10719 4.79E-06 11931 4.30E-06 13654 3.76E-06 2.42E-06
12 19487 10214 5.02E-06 11626 4.41E-06 13326 3.85E-06 2.57E-06
13 14859 8070 6.36E-06 8766 5.85E-06 10073 5.09E-06 3.36E-06
14 12151 6592 7.78E-06 7438 6.90E-06 8439 6.08E-06 4.11E-06
15 10997 6832 7.51E-06 7112 7.21E-06 7945 6.46E-06 4.55E-06
16 11808 7067 7.26E-06 7692 6.67E-06 8539 6.01E-06 4.23E-06
17 8900 5371 9.55E-06 5743 8.93E-06 6372 8.05E-06 5.62E-06
18 11421 7134 7.19E-06 6981 7.35E-06 7890 6.50E-06 4.38E-06
19 5062 3052 1.68E-05 3437 1.49E-05 3762 1.36E-05 9.88E-06
20 9739 5851 8.77E-06 6024 8.51E-06 6744 7.61E-06 5.13E-06
21 5668 3084 1.66E-05 3439 1.49E-05 3854 1.33E-05 8.82E-06
22 4844 3042 1.69E-05 3223 1.59E-05 3575 1.43E-05 1.03E-05
genome-
wide		 383213 208408 2.46E-07 229760 2.23E-07 262714 1.95E-07 1.30E-07
Open in a new tab

The permutation thresholds were calculated using 10,000 random shuffles.

The experiment-wise error rates for each chromosome and the genome-wide adjustment was set at αe = 0.05.

αp: point-wise error rate.

Meff: the effective number of independent tests.

w=20: window size is set equal to 20.

With the empirical distribution from permutation available, we can also derive the corresponding type I error rate for each correction threshold. For the Illumina 1M BeadChip, the type I error rate is 0.05 for the genome wide permutation threshold, 1.36e–7, since we set αe = 0.05. The genome-wide type I error rate for the simpleM method is 0.045 because 450 permutation tests out of 10,000 have p-values less than the derived threshold, 1.24e–7. Similarly, the Keff and Bonferroni genome-wide thresholds, 9.70e-8 and 6.42e–8, correspond to type I error rates of 0.035 and 0.022, respectively. Again, we see that the simpleM method gives the best approximation to the desirable type I error rate, 0.05. For the Affymetrix 500K data set, the type I error rate is 0.05 for the genome-wide permutation threshold, 2.46e–7. Similarly, the simpleM, Keff and Bonferroni genome-wide thresholds, 2.23e–7, 1.95e–7 and 1.30e–7, correspond to type I error rates of 0.046, 0.040 and 0.026, respectively. Again, we see that the simpleM method gives the best approximation to the desirable type I error rate, 0.05. We also see that the Bonferroni correction produces a more conservative type I error rate, 0.026 (the 500K data) vs. 0.022 (the 1M data), when the LD among SNP increases, while the simpleM method gives consistent type I error. As the SNP density goes higher and higher, e.g. some imputed datasets can contain up to 2.5M SNPs, the advantage of simpleM over Bonferroni would be more apparent.

To demonstrate the computing time required for each method, we will use the Illumina 1M BeadChip chromosome 1 data as an example. There were 63560 common SNPs in chromosome 1. Permutation tests with 10,000 random shuffles took more than 200 hours on a personal computer (PC) (Intel® Core™2 Duo 2.6G CPU with 3GB memory). Calculating Keff, with a window size of 20 (w = 20), took about 18 minutes. We also calculated Keff using different window sizes, because bigger window sizes should result in better estimations [Moskvina and Schmidt 2008]. It took about 48 minutes to calculate Keff when we used a window size of 50. The Keff = 41155 (w = 50) estimation did not significantly improve over Keff = 41438 (w = 20) even though the computing time more than doubled. Therefore, we did not try larger window sizes for Keff. In comparison, it took less than one minute for the simpleM method to infer Meff for the chromosome 1 data. If we extended these calculations on a single PC for the entire genome for the Illumina 1M BeadChip, it would take about 15 weeks for the permutation method with 10K shuffles, about 221 minutes for the Keff and only about 13 minutes for the simpleM.

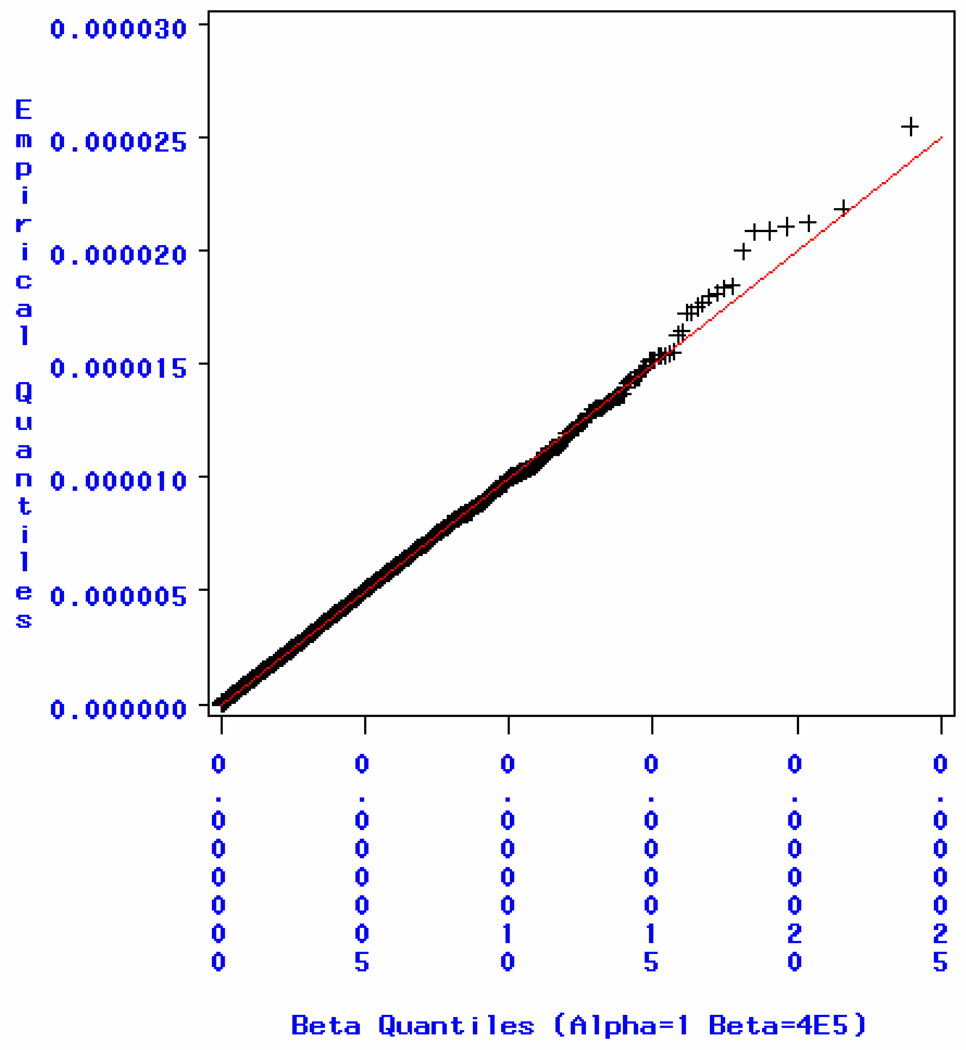
It is known that the minimum P value in each permutation should follow a beta(1, M) distribution if the M markers are statistically independent [Casella and Berger, 2001]. This allows us to verify the consistency between observed minimum p-values with their theoretical distribution. Hence, we fitted a Beta distribution to the observed 10,000 minimum p-values from the permutation tests for each GWAS data set and estimated the two beta parameters by maximum likelihood estimation (MLE) using SAS version 9.1.3 (SAS Institute, Cary, NC, USA). For the Illumina 1M BeadChip, the MLEs for the two beta parameters, α and β, are α̂ = 1.02 and β̂=413549.7. If we fix α=1 and only estimate β, then the MLE β̂=404001, which is in line with the Meff suggested by the permutation tests, 378368. Goodness-of-fit tests based on empirical distribution function (EDF) statistics did not reject the null hypothesis (the data follow a specified distribution) at the 0.25 significance level, which suggests that the data (minimum p-values) follow the specified beta distribution. The p-values are >0.25, >0.25 and >0.25 for the EDF tests: Kolmogorov-Smirnow, Cramér-von Mises and Anderson-Darling statistic, respectively. The quantile-quantile plot for minimum p-values from the permutation tests is shown in Figure 1. From the plot, we see that the empirical distribution and theoretical distribution agree with each other and the data points fall on the diagonal line, indicating that the minimum p-values follow the beta distribution very well. In Table 1, we also find that the genome-wide Meff estimation from the simpleM, 413360, gives a better (closer) approximation to the MLE estimate β̂ and the permutation suggested Meff than the Keff estimate.

Figure 1.

Figure 1

Open in a new tab

Quantile-Quantile plot for minimum p-values using the Illumina 1M data.

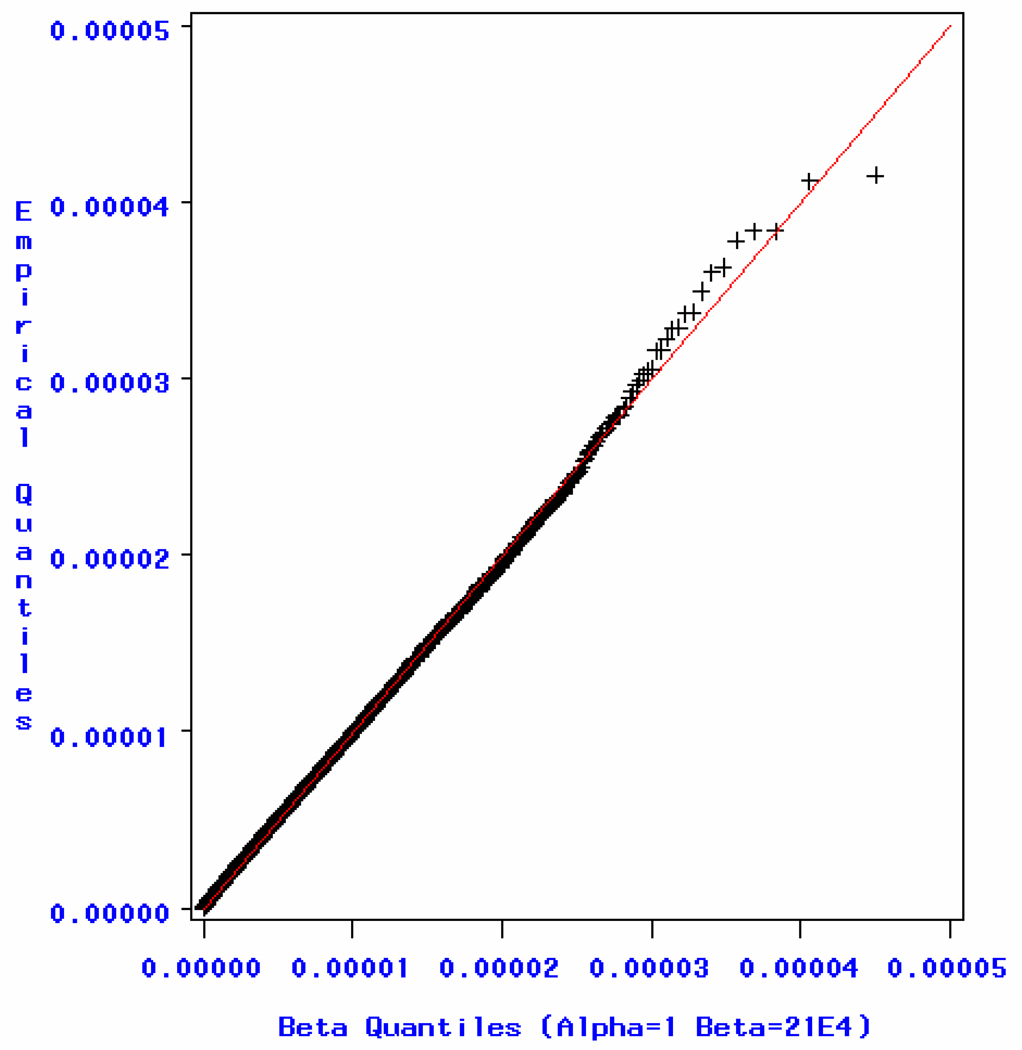
For the Affymetrix 500K data, we saw a pattern similar to the Illumina data. The MLEs for the two beta parameters, α and β, are α̂ = 1.03 and β̂ = 222043.9. The MLE β̂ = 214986.2 if we fix α=1, which is consistent with the Meff suggested by the permutation tests, 208408. Goodness-of-fit tests based on EDF statistics did not reject the null hypothesis at the 0.1 significance level, which suggests that the data follow the specified beta distribution. The p-values are 0.19, 0.13 and 0.13 for the EDF tests: Kolmogorov-Smirnow, Cramér-von Mises and Anderson-Darling statistic, respectively. The quantile-quantile plot for minimum p-values from the permutation tests is shown in Figure 2. From the plot, we see that the empirical distribution and theoretical distribution agree with each other, indicating that the minimum p-values follow the beta distribution very well. In Table 2, we find that the genome-wide Meff estimation from simpleM, 229760, gives a better approximation to the MLE estimate β̂ and the permutation suggested Meff than the Keff estimate. Therefore, the effective number of independent tests is indeed valid for these data sets based on statistical theory and significance tests and is a reasonable approach in multiple testing corrections for GWASs.

Figure 2.

Figure 2

Open in a new tab

Quantile-Quantile plot for minimum p-values using the Affymetrix 500K data.

Many other multiple testing correction methods exist. Lin [2005] proposed using a Monte Carlo approach to approximate the joint distribution of test statistics and then using a Monte Carlo distribution to adjust p-values. Seaman and Müller-Myhsok [2005] proposed a direct simulation approach that approximates p-values from permutation tests. Both methods avoid permutation by simulating test statistics directly from the asymptotic distribution. Conneely and Boehnke [2007] developed a p-value adjustment method through numerical integration assuming an asymptotic multivariate normal distribution for the test statistics and achieved even greater speed compared to simulation approaches. However, the numerical integration can only handle up to 1,000 dimensions at present. Furthermore, these methods can take much longer to compute than the simpleM method. Conneely and Boehnke [2007] estimated that it would take several hours for a 400K genome-wide scale, and for the Affymetrix 500K data, the simpleM method only took about 7 minutes. Moreover, the simpleM method is a non-parametric method that does not rely on the joint distribution of test statistics to be known.

With the increasing popularity of GWASs, the simpleM algorithm can serve as a fast approximation to the computationally intensive permutation procedure. It gives a highly accurate estimation of the permutation threshold for multiple testing correction while greatly reducing the computing time and resources required. We validated the method using each individual autosomal chromosome and together in a genome-wide format. We believe the simpleM method, an effective number of independent tests approach, can be useful to current large-scale genetic association studies for quickly estimating the permutation threshold. Moreover, the multiple testing thresholds derived in this study can provide practical guidelines for other GWASs using similar population samples, genotyping platforms and quality control protocols.

Acknowledgments

We thank Drs. Ingrid Borecki and Aldi Kraja for help in gaining access to the data sets analyzed. This work was supported in part by NIH grants 5R01HL08770002, 1R01HL08768801, 5R01HL087698, HL088655, HL087700, HL088215 and AG023746 and NIEHS T32 ES007126.

Reference List

  1. Armitage P. Tests for Linear Trends in Proportions and Frequencies. Biometrics. 1955;11(3):375–386. [Google Scholar]
  2. Barrett JC, Fry B, Maller J, Daly MJ. Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics. 2005;21(2):263–265. doi: 10.1093/bioinformatics/bth457. [DOI] [PubMed] [Google Scholar]
  3. Browning SR, Browning BL. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. Am J Hum Genet. 2007;81(5):1084–1097. doi: 10.1086/521987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cheverud JM. A simple correction for multiple comparisons in interval mapping genome scans. Heredity. 2001;87(1):52–58. doi: 10.1046/j.1365-2540.2001.00901.x. [DOI] [PubMed] [Google Scholar]
  5. Churchill GA, Doerge RW. Empirical Threshold Values for Quantitative Triat Mapping. Genetics. 1994;138(3):963–971. doi: 10.1093/genetics/138.3.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cochran WG. Some Methods for Strengthening the Common X2 Tests. Biometrics. 1954;10(4):417–451. [Google Scholar]
  7. Conneely KN, Boehnke M. So Many Correlated Tests, So Little Time! Rapid Adjustment of P Values for Multiple Correlated Tests. American journal of human genetics. 2007;81(6):1158–1168. doi: 10.1086/522036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gao X, Starmer J, Martin ER. A multiple testing correction method for genetic association studies using correlated single nucleotide polymorphisms. Genetic Epidemiology. 2008;32(4):361–369. doi: 10.1002/gepi.20310. [DOI] [PubMed] [Google Scholar]
  9. Hastie T, Tibshirani R, Friedman J. The elements of statistical learning. New York: Springer; 2001. [Google Scholar]
  10. Casella G, Berger RL. Statistical Inference. 2nd Edition. Pacific Grove, CA: Duxbury Press; 2001. p. 230. [Google Scholar]
  11. Li J, Ji L. Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlation matrix. Heredity. 2005;95(3):221–227. doi: 10.1038/sj.hdy.6800717. [DOI] [PubMed] [Google Scholar]
  12. Li Y, Abecasis GR. Mach 1.0: Rapid haplotype reconstruction and missing genotype inference. Am J Hum Genet. 2006:S79. [Google Scholar]
  13. Lin DY. An efficient Monte Carlo approach to assessing statistical significance in genomic studies. Bioinformatics. 2005;21(6):781–787. doi: 10.1093/bioinformatics/bti053. [DOI] [PubMed] [Google Scholar]
  14. Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet. 2007;39(7):906–913. doi: 10.1038/ng2088. [DOI] [PubMed] [Google Scholar]
  15. Moskvina V, Schmidt KM. On multiple-testing correction in genome-wide association studies. Genetic Epidemiology. 2008;32(6):567–573. doi: 10.1002/gepi.20331. [DOI] [PubMed] [Google Scholar]
  16. Nyholt DR. A Simple Correction for Multiple Testing for Single-Nucleotide Polymorphisms in Linkage Disequilibrium with Each Other. American journal of human genetics. 2004;74(4):765–769. doi: 10.1086/383251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Nyholt DR. Evaluation of Nyholt's procedure for multiple testing correction - author's reply. Hum Hered. 2005;60(1):61–62. doi: 10.1159/000087919. [DOI] [PubMed] [Google Scholar]
  18. Salyakina D, Seaman SR, Browning BL, Dudbridge F, Muller-Myhsok B. Evaluation of Nyholt's procedure for multiple testing correction. Hum Hered. 2005;60(1):19–25. doi: 10.1159/000087540. discussion 61–2. [DOI] [PubMed] [Google Scholar]
  19. Seaman SR, Müller-Myhsok B. Rapid Simulation of P Values for Product Methods and Multiple-Testing Adjustment in Association Studies. American journal of human genetics. 2005;76(3):399–408. doi: 10.1086/428140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Servin B, Stephens M. Imputation-based analysis of association studies: candidate regions and quantitative traits. PLoS Genet. 2007;3(7):e114. doi: 10.1371/journal.pgen.0030114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Šidák Z. Rectangular confidence regions for the means of multivariate normal distributions. J Am Stat Assoc. 1967;62:626–633. [Google Scholar]
  22. Splansky GL, Corey D, Yang Q, Atwood LD, Cupples LA, Benjamin EJ, D'Agostino RB, Sr, Fox CS, Larson MG, Murabito JM, et al. The Third Generation Cohort of the National Heart, Lung, and Blood Institute's Framingham Heart Study: Design, Recruitment, and Initial Examination. Am. J. Epidemiol. 2007;165(11):1328–1335. doi: 10.1093/aje/kwm021. [DOI] [PubMed] [Google Scholar]

RESOURCES