Bayesian Mixture Modeling of Gene-Environment and Gene-Gene Interactions

Abstract

With the advent of rapid and relatively cheap genotyping technologies there is now the opportunity to attempt to identify gene-environment and gene-gene interactions when the number of genes and environmental factors is potentially large. Unfortunately the dimensionality of the parameter space leads to a computational explosion in the number of possible interactions that may be investigated. The full model that includes all interactions and main effects can be unstable, with wide confidence intervals arising from the large number of estimated parameters. We describe a hierarchical mixture model that allows all interactions to be investigated simultaneously, but assumes the effects come from a mixture prior with two components, one that reflects small null effects and the second for epidemiologically significant effects. Effects from the former are effectively set to zero, hence increasing the power for the detection of real signals. The prior framework is very flexible, which allows substantive information to be incorporated into the analysis. We illustrate the methods first using simulation, and then on data from a case-control study of lung cancer in Central and Eastern Europe.

INTRODUCTION

Complex diseases such as cancers are the result of a multifactorial process, and the interplay between many risk factors including environmental exposures and genetic susceptibility (Adami et al., 2008; Weinberg, 2007). Specifically, the biological dosage of environmental exposures may be modified by an individuals biological response to the exposures, including their specific metabolism, DNA repair capacity and cell cycle control. On the other hand, genetic expression of specific cancer-related genes can be induced or altered by specific environmental exposures, and the extent of this alteration can be influenced by sequence variation. Thus it is important to identify interactions between various etiological factors for better understanding of the disease mechanism. A number of important gene-environment interactions have already been identified. One example concerns the interaction between alcohol dehydrogenase (ADH) genetic variants and alcohol consumption for upper aerodigestive cancer, in which increased alcohol consumption strengthens the association between ADH genetic variants and upper aerodigestive cancer risk (Hashibe et al., 2008). As a second example, Boccia et al. (2008) describe the interaction between methylenetetrahydrofolate reductase (MTHFR) and folate intake with respect to gastric cancer risk, in which a more prominent genetic effect was observed when the folate intake level was low. Clayton and McKeigue (2001) provide a discussion of the differences between biological and statistical interpretations of “interaction”. Here we concentrate on case-control data and refer to an interaction as a departure from main effects only in a logistic model.

In this paper we describe a method for modeling interactions when the number of single nucleotide polymorphisms (SNPs) is moderate (we have experimented with up to 100 SNPs and 5 exposures), for example in a candidate gene study, or following an initial screen in a genome-wide association study. An obvious strategy in such a situation is to fit separate models for each SNP/exposure combination. This requires a large number of models to be fitted, and a formal comparison between these models is not straightforward under a frequentist approach since the models are not nested. An additional, and more significant, problem is that the exposures will often be correlated and so fake associations will be induced due to confounding, since there is no control for additional exposures in a model containing a single exposure. These drawbacks suggest that a better approach is to include all of the SNPs, exposures and interactions in a single model. Unfortunately this leads to an increase in the standard errors of estimates, since there are a large number of parameters to simultaneously estimate, an example of the usual bias-variance trade-off in regression modeling. Numerical instability may also result, particularly with a large number of correlated exposures. In general, multiple comparisons issues must be considered, though common approaches such as the control of the family-wise error rate through a Bonferroni correction lead to a loss of power due to their overly conservative nature. A stepwise strategy in which main effects models are first fitted and then interactions are considered when the main effects are significant is fraught with problems in terms of interpretation, since the search through model space is data driven, which causes standard type I and type II error probability calculations to be incorrect (Miller, 1984).

Many methods have been suggested for the modeling of interactions (Motsinger et al., 2007). These range from conventional, parametric logistic regression driven approaches (Kraft et al., 2007; Marchini et al., 2005), to exploratory approaches such as multifactor dimensionality reduction (MDR) (Ritchie et al., 2001, 2003). MDR is a popular technique which we briefly describe in the context of detecting SNP-SNP interactions. For a fixed number of factors (SNPs), K, to include in the model MDR finds the optimal set by first splitting the data into multiple training and validation sets. Based on the training data, contingency tables corresponding to each possible combination of K factors are then constructed, with each cell in the table being labeled as high/low risk depending on whether the case/control ratio is >/< 1 within that cell. The “training error” is then calculated for each set of factors, and the set producing the lowest error is deemed the best for this value of K. Prediction errors and the consistency across different training sets are then computed for different values of K, to give the “best” K. MDR has recently been critiqued by Park and Hastie (2008). In particular they highlight that the power of MDR will suffer when the real effects are additive (since no structure is imposed on the form of the model). In addition, for high-dimensional tables many of the cells will contain zero cells, and the classification to high/low risk may be highly unstable. We would add the lack of flexibility in allowing prior information to be incorporated, and the ad hoc nature in labeling each cell as high/low risk.

Several tree-based methods have also been proposed to detect subgroups of interest, for example, classification and regression trees (CART) and random forests (Lunetta et al., 2004; Strobl et al., 2008; Wu et al., 2006). These type of methods have the advantage of dealing with large number of parameters with small sample sizes. However they too cannot take into account available prior information (Ziegler et al., 2008). An additional critique is that subgroup effects detected in the tree-based methods are often difficult to interpret.

A number of methods have been proposed that build a semi-parametric model based on a logistic regression framework with a flexible regression model. Kooperberg and Ruczinski (2005) use logic regression, a technique for finding interesting combinations of binary regressors. Chen et al. (2007) proposed a method based on trees to detect gene-gene and gene-environment, while Chen et al. (2008) suggest another algorithmic method, support vector machines, to detect interactions. Again these approaches do not use prior information, and so cannot be tuned to specific applications.

Alternative suggestions begin by assuming independence of SNPs and exposures, in order to increase power. Methods for the case-only design that assumes and exploits the independence between SNPs and exposure, in order to increase power, have been proposed by a number of authors (Piegorsch et al., 1994: Umbach and Weinberg, 1997). Other methods assume independence and use case and control data (Chatterjee and Carroll, 1995; Chatterjee et al., 2006). The presence of gene-environmental non-independence can greatly bias the interaction estimates in this design, however (Albert et al., 2001: Kraft et al., 2007). To overcome this a hybrid estimator has recently been proposed (Mukherjee and Chatterjee, 2008), and appears promising in comparative simulation studies (Mukherjee et al., 2008). These methods have not been used in the multiple SNP/multiple exposure scenario.

Throughout we assume a rare disease and refer to odds ratios as relative risks. The approach we follow is Bayesian and is based on a mixture prior for the effect sizes. Specifically we assume that with probability 1 − π a single log relative risk arises from a normal prior centered at zero with a small variance (the null component of the prior), and with probability π the log relative risk arises from a zero mean normal with a larger variance reflecting anticipated effects (the non-null component). Such mixture priors have a long history in Bayesian linear model selection contexts (George and McCulloch, 1993, 1997; Mitchell and Beauchamp, 1988). The extension of such models in the context of modeling interactions in a linear model was suggested by Chipman (1996). Here we use a hierarchical model for the case-control context with a logistic regression model at the first stage of the hierarchy, with the mixture prior on the coefficients at the second stage. A similar model has been proposed in this context by Conti et al. (2003), though there are differences in the prior set-up, and in the reporting, as we will highlight.

We briefly describe two approaches to the detection of gene-environment interactions that we consider in detail later in the paper. The first is to fit single models containing a single SNP main effect, a single exposure main effect, and the interaction. Alternatively the full model containing all main effects and all interactions may be fitted. Unfortunately both of these strategies have serious drawbacks. The single models do not control for other variables, which can lead to serious problems of false positives, due to dependence between exposures. In the full model the standard errors can be very large due to the estimation of multiple parameters, which leads to a loss of power. The supplementary material contains a more formal critique of the full and single model strategies, and describes the difficulties of controlling meaningful criteria such as the false discovery rate (FDR) in a correlated multiple testing setting.

The structure of this paper is to first describe the Bayesian mixture model, before examining its behavior on simulated data. We then apply the model to data from a case-control study of lung cancer, before concluding with a discussion.

METHODS

Conventional Hierarchical Approach

Although we are primarily interested in modeling interactions, we motivate the mixture model by initially considering models for estimating the effects of multiple SNPs only. Let Y_i = 1/0 denote a case/control indicator with i = 1, …, n₁ corresponding to cases and i = n₁ + 1, …, n₁+ n₀ = n to controls. Further let x_is = 0/1/2 be the minor allele count for SNP s, s = 1, …, S, i = 1, …, n.

A standard three-stage hierarchical model is given by:

Stage 1 Data Model: Y_i|α, β ~ Binomial(1, p_i) where β = (β₁, …, β_S) and

$$\text{logit}{p}_i=\alpha +\sum _{s=1}^S{x}_{is}{\beta }_s$$

so that we have a linear predictor in the number of minor allele copies with exp(β_s) corresponding to the relative risk associated with a single copy of the minor allele for SNP s, s = 1, …, S.

Stage 2 Prior for Log Relative Risks: Assume a common prior for the log relative risks:

$${\beta }_s\mid {\sigma }_{\text{s}}^2\sim N(0,{\sigma }_{\text{s}}^2),s=1,\dots ,S.$$

The s subscript is necessary here since later we will extend the notation to incorporate environmental exposures and interaction effects. We assign an improper flat prior to α.

Stage 3 Hyperprior: ${\sigma }_{\text{s}}^{-2}\sim \text{Gamma}(a_{\text{s}},b_{\text{s}})$ for suitable a_s, b_s

The latter stage may be neglected if ${\sigma }_{\text{s}}^2$ are fixed a priori, or if they are estimated from the data via empirical Bayes, or related methods (Greenland, 1992, 1993; Witte and Greenland, 1996). In the remainder of the paper we will fix the parameters of the prior model based on the context, since the majority of SNPs will be null, and so there will be limited information available to estimate the parameters of the prior.

We relate this model to the penalized logistic regression method of Park and Hastie (2008) which maximizes

$$L(\alpha ,\mathit{\beta })-\frac{\lambda }{2}\left|\right|\mathit{\beta }\mid {\mid }^2$$

for fixed λ where L(α, β) = log p(y|α, β) denote the log-likelihood. This method can be viewed from a Bayesian standpoint as finding the posterior mode with independent priors β_s ~ _iid N(0, 1/λ), s = 1, …, S, so that λ is the reciprocal of the variance. Sandwich estimation is used to obtain standard errors (which is more difficult to justify via a Bayesian argument), and cross-validation is used to choose λ.

A difficulty with the above three stage model is that it assumes that the prior is the same for all of the log relative risks β_s, when in the present context the vast majority of SNP effects will be zero, or very close to zero. We now describe a model that allows for each parameter to be effectively set to zero, thus aiding in interpretation, and allowing the remaining parameters to be estimated with greater power.

Mixture Hierarchical Approach

We describe a hierarchical mixture model which extends the above model by assuming that a proportion π_s of SNPs are non-null, with a common prior for their effects, while the remaining proportion 1 − π_s of null SNPs arise from a distribution with its mass very close to zero. Mixture models, with components corresponding to null and non-null signals, were suggested in an epidemiologlcal multiple testing situation by Thomas et al. (1985, 1992). A similar logistic model to that described below was proposed in the gene-environment context by Conti et al. (2003). Stage 1 is as in the conventional model with Stages 2 and 3 given by:

Stage 2 Prior for Log Relative Risks: We assume the mixture prior:

$${\beta }_s\mid T_s,{\sigma }_{\text{s}}^2\sim N\left(0,T_s{\sigma }_{\text{s}}^2+(1-T_s){\sigma }_{{\epsilon }_{\text{s}}}^2\right)$$

where T_s is an indicator for SNP s that takes the value 1 for a non-null SNP, and the value 0 for a null SNP. We assume that the non-null effects arise from $N(0,{\sigma }_{\text{s}}^2)$ with the null effects from $N(0,{\sigma }_{{\epsilon }_{\text{s}}}^2)$. The latter is chosen so relative risks in the range e^±ε_s for small ε_s can be treated as null. In what follows we choose ${\sigma }_{{\epsilon }_{\text{s}}}^2={0.012}^2$ which corresponds to the belief that the null relative risks lie in the range (0.98, 1.02) with probability 0.9. It is useful to allow values slightly either side of 1 in order to “soak up” small amounts of bias arising from, for example, small differential genotyping errors, or confounding due to population stratification.

Stage 3 Prior for Non-Null/Null Indicators: Without additional information we assume that

$$T_s\mid {\pi }_{\text{s}}\sim \text{Bernoulli}({\pi }_{\text{s}}),s=1,\dots ,S,$$

so that π_s is the proportion of non-null SNPs.

As we have noted, often the number of non-null SNPs will not be large, and so it will not be possible to estimate ${\sigma }_{\text{s}}^{-2}$ and π_s from the data, so we fix them in advance. We set the standard deviation so that we expect 100(1 − q)% of non-null SNPs to have relative risks that lie within exp(±R), to give σ_s = log R/Φ⁻¹(1 − q/2). As an example, for 90% within [e^−2.5, e^2.5] we obtain σ_s = log 2.5/1.645 = 0.557. The anticipated proportion of non-null SNPs is given by S × π_s, which aids in the fixing of π_s. For example, with S = 50 SNPs in total a best guess of 5 non-null SNPs gives π_s = 0.10. Note that under this prior set-up, the prior on the number of non-null SNPs is binomial with parameters S and π_s, which allows the prior probability of a particular number of non-null SNPs to be evaluated.

We note the following about this model:

1. Setting T_s = 1 for all s gives the conventional hierarchical model.

2. If we average out over the T_s (i.e. collapse stages 2 and 3 into a single stage) we obtain the mixture model

   $${\beta }_s\mid {\pi }_{\text{s}},{\sigma }_{{\epsilon }_{\text{s}}}^2,{\sigma }_{\text{s}}^2\sim (1-{\pi }_{\text{s}})N(0,{\sigma }_{{\epsilon }_{\text{s}}}^2)+{\pi }_{\text{s}}N(0,{\sigma }_{\text{s}}^2)$$

3. If we have prior information on particular SNPs being non-null we can relax the Stage 3 assumption that the indicators T_s are independent and identically distributed to independent with π_ss, for s = 1, …, S. Such information may reflect information such as whether the SNP is missense, or has been previously implicated with the disease. Setting π_ss = 1 indicates that we believe SNP s is important.

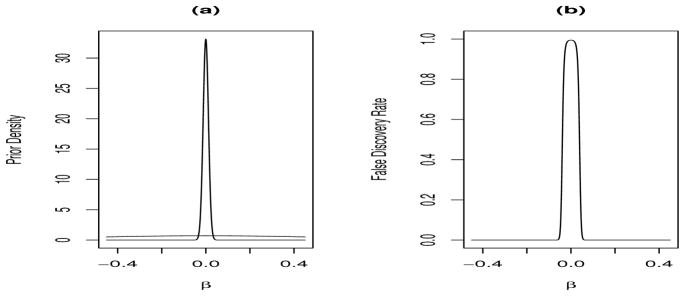
Figure 1(a) shows the two components of the prior (for the choices discussed above, namely 95% points of 1.02 and 2.5 for the null and non-null components). The densities cross at a log relative risk value of 0.033 so that |β|’s less than this are more likely to be null, with values larger more likely to be non-null. For a given log relative risk β, one can evaluate the false discovery rate (FDR):

$$Pr(T=0\mid \beta )=\frac{p(\beta \mid T=0){\pi }_{\text{s}}}{p(\beta \mid T=0){\pi }_{\text{s}}+p(\beta \mid T=1)(1-{\pi }_{\text{s}})}$$

and this quantity is displayed in Figure 1(b) (with π_s = 0.8). The FDR associated with this prior shows desirable behavior in that it is monotonic decreasing from zero (Rice and Spiegelhalter, 2008). This is desirable since it means that as |β| increases it becomes increasingly less likely that the coefficient corresponds to a false discovery.

Figure 1.

(a) Two component mixture prior, and (b) false discovery rate Pr(null |β).

Gene × Environment Interactions

Turning now to gene-environment interactions we let z_ie denote exposure e on individual i, i = 1, …, n, e = 1, …, E. We assume that continuous exposures are standardized to have mean 0 and standard deviation 1, so that associated log relative risks are on the same scale. We extend the model of the previous section:

Stage 1 Data Model: Y_i|α, β, γ, δ ~ Binomial(1, p_i) where

$$\text{logit}{p}_i=\alpha +\sum _{s=1}^S{x}_{is}{\beta }_s+\sum _{e=1}^E{z}_{ie}{\gamma }_e+\sum _{s=1}^S\sum _{e=1}^E{x}_{is}{z}_{ie}{\delta }_{se}$$

so that γ = (γ₁, …, γ_E) are the main effects associated with exposure, and δ = (δ₁₁, …, δ_SE) are the interactions. We have assumed that the interactions act in the same fashion on 1 or 2 copies of the minor allele, though the mixture formulation is easily extended to other interaction models.

Stage 2 Prior for Non-Null/Null Indicators:

$$\begin{array}{l}{\beta }_s\mid T_s,{\sigma }_{\text{s}}^2\sim N\left(0,T_s{\sigma }_{\text{s}}^2+(1-T_s){\sigma }_{{\epsilon }_{\text{s}}}^2\right),s=1,\dots ,S\\ {\gamma }_e\mid T_e,{\sigma }_{\text{e}}^2\sim N\left(0,T_e{\sigma }_{\text{e}}^2+(1-T_e){\sigma }_{{\epsilon }_{\text{e}}}^2\right),e=1,\dots ,E\\ {\delta }_{se}\mid T_{se},{\sigma }_{\text{se}}^2\sim N\left(0,T_{se}{\sigma }_{se}^2+(1-T_{se}){\sigma }_{{\epsilon }_{\text{se}}}^2\right)s=1,\dots ,S,e=1,\dots ,E\end{array}$$

Stage 3 Priors for Non-Null/Null Indicators:

$$\begin{array}{l}{T}_s\mid {\pi }_{\text{s}}{\sim }_{\mathit{iid}}\text{Bernoulli}({\pi }_{\text{s}}),s=1,\dots ,S\\ T_e\mid {\pi }_{\text{e}}{\sim }_{\mathit{iid}}\text{Bernoulli}({\pi }_{\text{e}}),e=1,\dots ,E\\ T_{se}\mid {\pi }_{\text{se}}{\sim }_{\mathit{iid}}\text{Bernoulli}({\pi }_{\text{se}}),s=1,\dots ,S,e=1,\dots ,E\end{array}$$

We also assume that the collections T_s, T_e and T_se are independent. Again we fix ${\sigma }_{\text{s}}^2,{\sigma }_{\text{se}}^2,{\sigma }_{\text{se}}^2$, π_s, π_s and π_se.

We make four observations:

1. A special case of this model is to take T_se = T_sT_e, which equals 1 only if both main effects are in the model, and is zero otherwise, thus obeying the “hierarchy principle” in which an interaction term is only included if the main effect is present. A further extension is to take T_se = T_sT_eΔ where Δ < 1 so that we have a reduced probability of an interaction, relative to the product of the SNP and exposure interactions (Chipman, 1996). In both the simulations and the real data example, the number of exposures is small, and we will assume that π_e = 1 so that we do not have a null prior for exposures, and we take T_se = T_sT_e = T_s. In this case we only need to specify π_s.

2. The above model can be applied in an obvious fashion to three- and higher-way interactions, and to the analysis of SNP-SNP interactions.

3. Interpretation of the results requires care in situations in which the majority of the probability mass of Pr(T|y) is not at T = 0 or T = 1. If the mass is distributed more equally between these points then interval estimates for the corresponding regression coefficient may be deceptive. One possibility is to report posterior intervals given that T = 1, along with Pr(T = 1|y).

4. The model of Conti et al. (2003) differs from the above in the following respects. We place a tight normal prior around the log odds ratio under the null, while Conti et al. set the parameter to zero. Under the alternative (T = 1) we fix the variance of the effect sizes, while Conti et al. estimate these variances and have a specific prior on variance inflation parameters. We fix these variances because we want to be as context-specific as possible. In the situations in which we are envisaging, the number of non-null effects will be small, and so the variance will be difficult to estimate. Similarly, Conti et al. assign Beta prior distributions to, and estimate, the mixture probabilities, whereas we fix these a priori. In terms of reporting, Conti et al. recommend, for a generic parameter θ, tabulation of E[θ|T = 1, y], var(θ|T = 1, y) and Pr(θ < 0|T = 1, y), whereas we will examine credible intervals for the unconditional parameter, for example, we report those values (l, u) such that Pr(l < θ < u|y) = 0.95, along with Pr(θ > 0|y). Conti et al also explicitly emphasize model averaging and calculate posterior probabilities of each model (where the class of models is obtained by considering all values of T = 0/1). We view the analysis as more exploratory in nature and hence concentrate on the posterior probabilities of coefficients being “significantly” different from zero.

Computation

The posterior distribution is given by

$$p(\alpha ,\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{T}\mid \mathit{y})\propto p(\mathit{y}\mid \alpha ,\mathit{\beta },\mathit{\gamma },\mathit{\delta })p(\alpha )p(\mathit{\beta }\mid {\mathit{T}}_{\text{se}})p(\mathit{\gamma }\mid {\mathit{T}}_{\text{e}})p(\mathit{\delta }\mid {\mathit{T}}_{\text{se}})p({\mathit{T}}_{\text{se}})$$

The first stage logistic model means that marginalization short-cuts available for the linear model (which allow the random effects to be integrated out analytically) are not possible here, but Markov chain Monte Carlo (MCMC) techniques, in which a Markov chain is constructed whose stationary distribution is the posterior distribution, may be utilized.

As noted by George and McCulloch (1997) it is important that the ratios ${\sigma }_{\text{s}}^2/{\sigma }_{{\epsilon }_{\text{s}}}^2,{\sigma }_{\text{e}}^2/{\sigma }_{{\epsilon }_{\text{e}}}^2,{\sigma }_{\text{se}}^2/{\sigma }_{{\epsilon }_{\text{se}}}^2$, should not be made too large since this will lead to poor convergence of the Markov chain, because the sampler can become “stuck” at values of β close to zero. Intuitively, if the two variances are not too different then the sampler will move easily between the T = 0 and T = 1 models, but if one is highly peaked it is difficult to move since the ratio of the peaked to the flatter densities is too large.

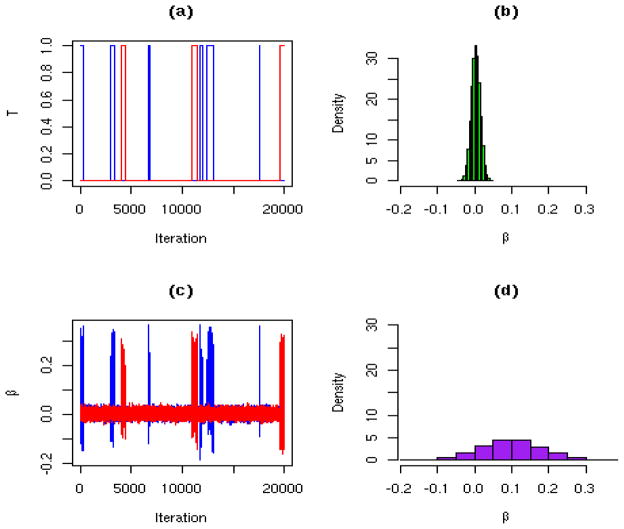
To assess convergence we recommend that multiple chains be run. In the examples that follow we run two chains, one with starting values T = 0 and each regression parameter set initially to zero, and the other setting T = 1 for those parameters that are significantly different from zero from the fit of the full model (with initial values for the significant regression parameters set to the estimates from this model). Figure 2 illustrates the mixing for a particular parameter, β, with associated indicator variable T, from two chains. These data were taken from one of the simulations of the next section. Panel (a) shows that T = 0 for the majority of the iterations, but there are visits to the T = 1 state. Panel (c) shows how β is more varied when T = 1. Panels (b) and (d) display histogram representations of the conditional posterior densities, β|y, T = 0 and β|y, T = 1, respectively. When T = 0 the posterior for β essentially corresponds to the narrow prior.

Figure 2.

(a) Realizations of indicator variable T associated with parameter β, for two Markov chains (displayed in blue and red). (b) Histogram representation of the posterior of the conditional β|y, T = 0. (c) Realizations of the parameter β, for two Markov chains (displayed in blue and red). (d) Histogram representation of the posterior of β|y, T = 1.

RESULTS

Simulation Study

We assume binary exposures and to simulate data, first fixed SNP and exposure prevalences, and then set a number of relative risks for SNP and exposure main effects, and interactions to be non-null. There are clearly many characteristics of the simulation that can be varied, and we explored only a subset. Null SNP minor allele frequencies (MAFs) were set to 0.3, with non-null SNPs having MAFs of 0.1 and relative risks of 1.2. The prevalences of exposed individuals was 0.1 in all cases and non-null exposure and interaction relative risks were set to 2. In the dependent exposure simulations the correlation was approximately 0.75. We examine the performance of three models: (1) S × E “single” models that contain four parameters only (the intercept, main effects for SNP and exposure, and the interaction); (2) the full model that contains all SNPs/exposures and interactions; (3) the Bayesian mixture model. We set π_s = 0.2 and π_e = 1 so that the non-null exposure prior is always used; we also have T_se = T_s so that the hierarchy principle is obeyed.

For the mixture models a pair of Markov chains were run for a minimum of 50,000 iterations, discarding the first 10,000 as burn-in. A number of the models with a larger number of SNPs/exposures required longer runs.

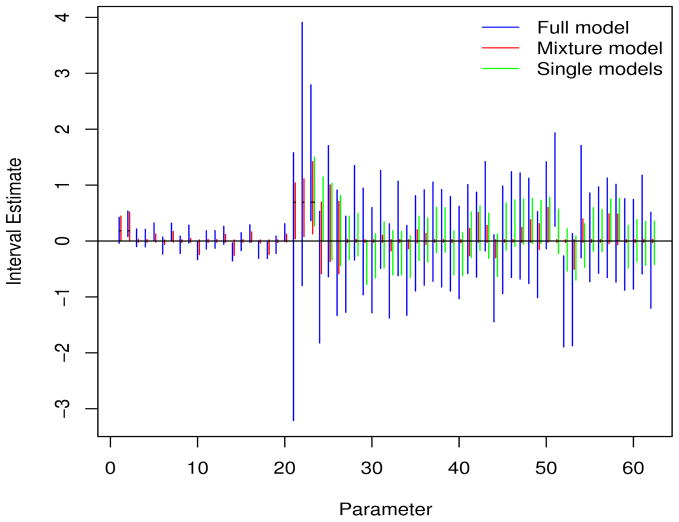
Figure 3 displays 95% interval estimates for each parameter for simualtion 9 (since the same main effects are estimated multiple times under the single models, we report the interactions only for these models). This figure clearly shows the wide intervals that result from the full model, and the effective setting to zero of the majority of parameters under the mixture model. The supplementary material contains plots analogous to Figure 3, for all of the simulations.

Figure 3.

Summaries of three modeling approaches for simulation 9. Parameters 1–20 represent SNP main effects, 21–22 are the exposure main effects, and 23–62 are the 40 interactions. The latter are ordered so that 23 and 24 correspond to the interaction between SNP 1 and exposures 1 and 2, respectively, etc. The five short horizontal lines represent the true effect sizes.

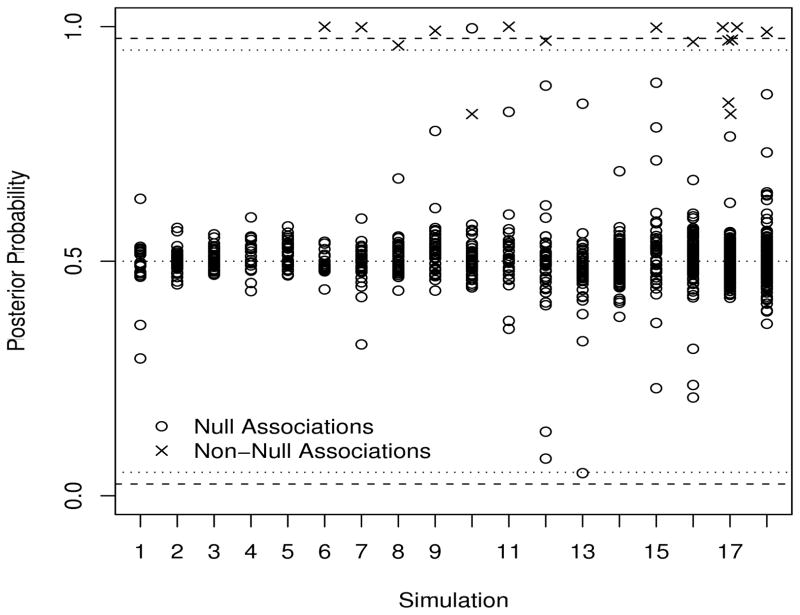
Table 1 summarizes the results for each of the combinations of parameters we examine. We concentrate on inference for the interactions and report the number of false discoveries (type I errors), and missed signals (type II errors), where these are (somewhat arbitrarily) evaluated based on 95% confidence/credible intervals. In each simulation, and for each of the interactions we also evaluate the posterior probabilities of exceedence of 0, and these are presented in Figure 4. For true null signals these should be close to 0.5, and for true non-null signals they will be close to zero (for protective effects) or one (for detrimental effects, which is the case in our simulations). We also consider the mean squared error of the interactions, which is given by the sum of the variance and the square of the bias:

$$\text{MSE}=\frac{1}{S\times E}\sum _{s=1}^S\sum _{e=1}^E{({\widehat{\delta }}_{se}-{\delta }_{se})}^2=\frac{1}{S\times E}\sum _{s=1}^S\sum _{e=1}^E\left[var({\widehat{\delta }}_{se})+{({\widehat{\delta }}_{se}-{\delta }_{se})}^2\right]$$

where S × E is the number of interactions, and δ_se is the interaction parameter corresponding to SNP s and exposure e.

Table 1.

Simulated data settings and summaries. For the non-null SNPs the relative risks are 1.2, while the relative risks for the non-null exposure main effects and interactions are 2. Exposure prevalences are 10%, as are MAFs for non-null SNPs. All other SNPs have MAFs of 0.3.

		Number/Non-null			Single			Full			Mixture
	n	SNPs	Exposures	Interactions	MSE	Type I Errors	Type II Errors	MSE	Type I Errors	Type II Errors	MSE	Type I Errors	Type II Errors
1	1000	20/0	1/0	20/0	0.113	1 (0.05)	—	0.253	3 (0.15)	—	0.0110	0 (0)	—
2	1000	20/0	2/0★	40/0	0.0866	0 (0)	—	0.255	2 (0.05)	—	0.00291	0 (0)	—
3	1000	20/2	2/0★	40/0	0.100	0 (0)	—	0.580	2 (0.05)	—	0.00272	0 (0)	—
4	1000	20/1	1/1	20/0	0.0865	1 (0.05)	—	0.106	1 (0.05)	—	0.00302	0 (0)	—
5	1000	20/1	2/2★	40/0	0.0796	0 (0)	—	0.343	3 (0.08)	—	0.0150	0 (0)	—
6	1000	20/1	1/1	20/1	0.0664	0 (0)	0 (0)	0.121	0 (0)	0 (0)	0.00561	0 (0)	0 (0)
7	1000	20/2	2/1	40/1	0.105	1 (0.03)	0 (0)	0.183	2 (0.05)	0 (0)	0.00806	0 (0)	0 (0)
8	1000	20/2	2/1★	40/1	0.0934	2 (0.05)	0 (0)	0.154	0 (0)	1 (100)	0.0108	0 (0)	1 (100)
9	1000	20/2	2/2★	40/1	0.108	2 (0.05)	0 (0)	0.464	2 (0.05)	0 (0)	0.0185	0 (0)	0 (0)
10	2000	20/2	2/2★	40/1	0.0606	2 (0.05)	0 (0)	0.234	4 (0.10)	1 (100)	0.0226	1 (0.05)	1 (100)
11	2000	20/1	5/1	100/1	0.0576	7 (0.07)	0 (0)	0.0891	11 (0.11)	0 (0)	0.0149	0 (0)	0 (0)
12	2000	20/1	5/1★	100/1	0.0635	8 (0.08)	0 (0)	0.391	9 (0.09)	1 (100)	0.0163	0 (0)	1 (100)
13	2000	50/1	1/0	50/0	0.0581	3 (0.06)	—	0.0763	3 (0.06)	—	0.00556	0 (0)	—
14	2000	50/1	2/0★	100/0	0.0547	6 (0.06)	—	0.184	3 (0.03)	—	0.00673	0 (0)	—
15	2000	50/5	1/1	50/1	0.0477	6 (0.12)	0 (0)	0.0676	4 (0.08)	0 (0)	0.00704	0 (0)	0 (0)
16	2000	50/2	2/2★	100/1	0.0405	7 (0.09)	0 (0)	0.159	1 (0.01)	0 (0)	0.00481	0 (0)	1 (100)
17	2000	50/5	5/3★	250/6	0.101	9 (0.04)	1(17)	1.71	32 (0.13)	3 (50)	0.0427	0 (0)	4(67)
18	2000	100/2	2/2★	200/1	0.0418	7 (0.04)	0 (0)	0.718	20 (0.10)	0 (0)	0.00381	0 (0)	0 (0)

^★denotes correlated exposures, with correlation approximately 0.75. The mean-squared errors (MSE) are averages over the interaction parameters. The number of type I and type II errors are given as an absolute number and as a percentage (in brackets), and are based on a 95% interval estimate.

Figure 4.

Posterior probabilities that interactions exceed 0, Pr(δ > 0|y). The null signals should cluster around 0.5. The top dashed line is at 0.975, which corresponds to the cut-off for a 95% credible interval. Horizontal lines are also drawn at probabilities of 0.95, 0.5, 0.05 and 0.025.

We make some general conclusions, and discuss each simulation in more detail in the supplementary material. In general:

• The single models perform better, in terms of MSE, than the full models, with the mixture models having orders of magnitude lower MSEs than either.

• The 95% interval estimates are widest for the full model, and shortest for the mixture model.

• There is slight bias towards zero in the Bayesian mixture model, due to the prior being centered at zero, but so far as MSE is concerned, this is more than offset by the reduced variance.

• The full model approach tends to have higher type I error rates than the single model analyses, while in only one simulation did the mixture model give a type I error.

• Using the 95% credible interval criteria the mixture model has a number of Type II errors. However, as Figure 4 shows, the mixture model is ranking the associations reasonably well. Figure 4 shows the posterior probability of exceedence of 0, for all of the interaction parameters. We see that although for a number of the simulations (numbers 8, 12, 16 and 17 in particular) signals are missed at the 95% level, they are detected at level 90% without any increase in the number of type I errors. In simulation 10, in which the exposures are correlated, the “wrong” SNP-exposure interaction is detected, but the correct signal is the second most significant. Figures 1 and 2 of the supplementary material give the p-values associated with each interaction and for each simulation for the single and full model examples, respectively. An advantage of examination of Pr(δ > 0|y) is that for null signals these posterior probabilities tend to concentrate around 0.5. In contrast, under the null p-values are uniform on (0,1) and so it is more difficult to discern the true non-null signals from the null effects.

• Simulation 18 represents a situation similar to many in practice with 100 SNPs, two correlated exposures, and a single non-null interaction. For this simulation all three of the methods correctly identify the interaction, though the full model gives a very wide interval estimate. The full model also gives 20 false positives, while the single models give 7 and the mixture model 0.

Real Data

We analyze data previously described in Hung et al. (2004), from a study conducted in centers within six countries of Central and Eastern Europe including the Czech Republic, Hungary, Poland, Romania, Russia and Slovakia. Within each country an identical protocol was followed with a consecutive group of newly diagnosed cases of lung cancer and a comparable group of controls being recruited between 1998 and 2002. Controls in all centers except Warsaw were chosen among subjects admitted as in-patients or out-patients in the same hospital as the cases, and were frequency matched with the case group by sex, age (+/− 3 years), center and referral (or residence) area. The eligible diseases for controls were non-tobacco related diseases including minor surgical conditions, benign disorders, common infections, eye conditions (except cataract or diabetic retinopathy) common orthopaedic diseases (except osteoporosis), etc. In Warsaw, population controls were selected by random sampling from the Polish Electronic List of Residents. Both cases and controls underwent an identical face-to-face interview during which they completed a detailed questionnaire including sections on: (a) demographic variables; (b) medical history; (c) family history of cancer; (d) tobacco smoking and involuntary smoking; (e) alcohol drinking; (f) intake frequency of selected food items: (g) occupational history. Blood samples were collected at the time of interview.

For illustration of the model we here examine 20 SNPs, two of which, CHEK2I157T (rs17879961, Brennan et al. 2007) and loc123688 (rs8034191, Hung et al. 2008), are known to be associated with lung cancer. As exposure we take a binary smoking variable (0=never, 1=ever) which has a known and strong association with lung cancer. The model we fit has 48 parameters (plus an intercept): 20 main effects for SNPs, a main effect for smoking, 20 interactions between the SNPs and smoking, and seven additional variables coding countries 1–5 (so that country 6 is the baseline), gender and age. Since CHEK2I157T and loc123688 are known to be associated we set T = 1 for these SNPs, and for the remainder we take π_s = 0.2. We placed flat priors on the intercept and the log relative risks corresponding to age, gender and the country indicators. For simplicity we consider the 1752 individuals with full data.

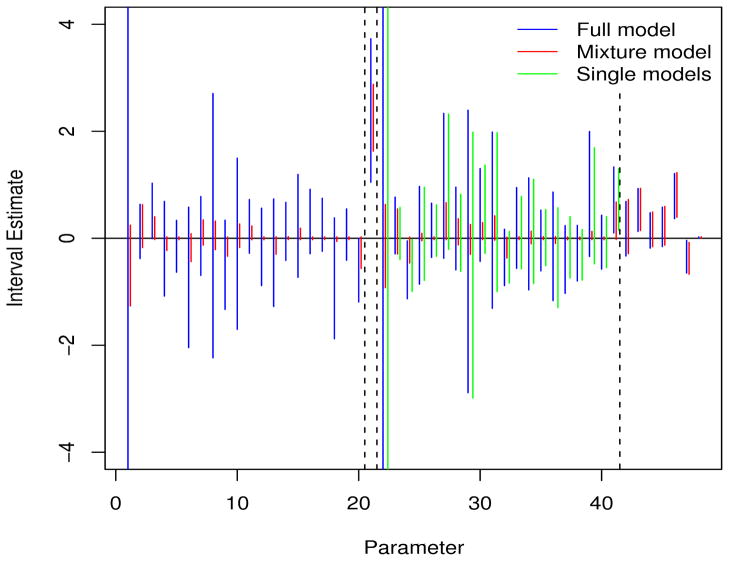
Figure 5 shows 95% interval estimates for each of the 48 parameters from the full logistic model and single models (all fit via MLE), and the Bayes mixture model. There was numerical instability for the logistic models — for example, the standard errors for the main effect of CHEK2I157T, and the interaction between CHEK2I157T and smoking were both 395 (the y-axis in Figure 5 is truncated) for the full model. The single model containing this interaction was also highly unstable. Two interactions were flagged as “just” significant under the full model, and one by the single model. Under the Bayesian mixture model (for which the results are stable) no signal interaction was categorically flagged as “significant”. For 18 of the 20 interactions, the values of Pr(δ|y) lay between 0.38 and 0.61 indicating no evidence of an interaction. Of the remaining SNPs, NAT2C282T gave a probability of 0.83. However, the interaction between loc123688 and smoking gave a posterior probability of 0.93 giving a hint of significance, and indicating that the harmful allele combined with ever smoking further increased the risk of lung cancer.

Figure 5.

95% interval estimates under the full and mixture models. The dashed vertical lines denote distinct sets of parameters: 20 main effects for SNPs, a main effect for smoking, 20 interactions between the SNPs and smoking, and seven additional variables coding centers 1–5, gender and age.

DISCUSSION

In this paper we have proposed the use of a Bayesian mixture model for modeling interactions, and have shown, via simulation, that this model has good performance when compared to fitting a full model, or multiple single models. All of the Bayesian mixture models were fitted using the freely-available WinBUGS software (Spiegelhalter et al., 1998). Example code is presented in the supplementary material, and is also available at: http://faculty.washington.edu/jonno/cv.html

In practice there are often missing genotype data, the MCMC approach is ideally suited to imputing these missing data see, for example, Lunn et al. (2006). We have assumed a binary phenotype (case-control data) but the hierarchical model could easily be altered for continuous phenotypes including survival data. Often in studies of environment and occupation the exposures are subject to measurement error. The incorporation of a parametric measurement error model is also straightforward within the Bayesian framework.

The choice of the π parameters will determine the operating characteristics (type I errors and power) and varying these parameters will give a more or less conservative procedure. For example, if we are in exploration mode we should set the π’s to be relatively large, since we would rather have a longer list of possible interactions to investigate. Sensitivity of the results to the specific values of π chosen is an important step.

In the hierarchical model that we have described the number of relative risks is fixed and equal to the maximum number of main effects and interactions that we wish to consider. An alternative approach is to allow the model dimension to change as terms are “dropped” and “added” to the model. This is an attractive strategy but requires specialized reversible jump MCMC (Green, 1995) and great care in diagnosis of convergence/posterior summarization. Some progress has been made in the former with the WinBUGS software (Lunn et al., 2006), though logistic regression models are not currently available.

The implementation for the model we use is computationally expensive and so the use of the model in a genome-wide association study (GWAS) is not currently feasible. However, Lewinger et al. (2007) use a similar mixture model for prioritizing signals in a GWAS.

In summary, we have described a Bayesian mixture model framework to assess gene-environment and gene-gene interactions in higher dimensional case-control studies. We have shown that this framework performs much better than traditional methods, and dramatically reduces both the MSE and the number of false positives, especially when exposures are correlated. The discovery of interactions in the setting we have considered is an intrinsically difficult endeavor, however, and so we would recommend the use of the mixture model in tandem with complementary alternative methods such as recently-proposed tree-based approaches.