Stochastic Spatio-Temporal Dynamic Model for Gene/Protein Interaction Network in Early Drosophila Development

Abstract

In order to investigate the possible mechanisms for eve stripe formation of Drosophila embryo, a spatio-temporal gene/protein interaction network model is proposed to mimic dynamic behaviors of protein synthesis, protein decay, mRNA decay, protein diffusion, transcription regulations and autoregulation to analyze the interplay of genes and proteins at different compartments in early embryogenesis. In this study, we use the maximum likelihood (ML) method to identify the stochastic 3-D Embryo Space-Time (3-DEST) dynamic model for gene/protein interaction network via 3-D mRNA and protein expression data and then use the Akaike Information Criterion (AIC) to prune the gene/protein interaction network. The identified gene/protein interaction network allows us not only to analyze the dynamic interplay of genes and proteins on the border of eve stripes but also to infer that eve stripes are established and maintained by network motifs built by the cooperation between transcription regulations and diffusion mechanisms in early embryogenesis. Literature reference with the wet experiments of gene mutations provides a clue for validating the identified network. The proposed spatio-temporal dynamic model can be extended to gene/protein network construction of different biological phenotypes, which depend on compartments, e.g. postnatal stem/progenitor cell differentiation.

Introduction

An early embryonic stage in Drosophila embryogenesis, i.e. the syncytial blastoderm stage, is completed two hours after the onset of fertilization and periodic segments are then characterized. Before the determination of periodic segments, the embryo is not yet separated by membranes, and macromolecules such as transcription factors (TFs) can diffuse freely and regulate downstream target genes in neighboring nucleus. Hence, at the syncytial blastoderm stage diffusion mechanism is fast enough to vary the concentrations of TFs in transcription regulations. Through a series of high/low affinity bindings of transcription regulations, downstream genes are dictated to express in their corresponding space of an embryo. Therefore, we assume that the transcription regulation and diffusion mechanism may play a cooperative role in characterizing embryonic segments.

Although some topics about protein diffusion have been well studied,^1,2 gradient dynamics of concentrations of transcription factors is still hard to be analyzed without quantitative inference under dynamic modeling. For example, critical boundaries settled by protein concentration gradient in dynamic models of early embryogenesis have allowed investigators to re-examine quantitatively concentration gradient dynamics.³ Jaeger and his colleagues have used mRNA spatial-temporal data and dynamic model to characterize the establishment of gap domains.⁴ Therefore, in order to analyze the diffusion mechanisms of transcription factors at different domains of Drosophila embryo, a spatio-temporal model is needed. In recent studies, early embryogenesis in Drosophila includes at least 31 genes in subdividing the embryonic patterns into 14 segmental primordia along the anterior-posterior (A-P) axis .⁵ In the past several decades, the spatio-temporal expressions of the early development-related genes (bicoid (bcd), caudal (cad), hunchback (hb), giant (gt), knirps (kni), Krüppel (Kr), tailless (tll), even-skipped (eve), fushitarazu (ftz), hairy, odd-skipped (odd), paired (prd), runt and sloppy-paired (slp)) have been provided and studied during the early developmental stages of Drosophila melanogaster. The 14 early development-related genes can be roughly divided into three classes, i.e. maternal genes, gap genes and pair-rule genes, which have been regarded as hierarchical transcription regulations with positive auto-regulations to generate and refine the constitutions of segments.^6,7 At the beginning of early embryogenesis, gap genes are regulated by high-level expressions of maternal TFs to initiate an early embryo development. Gene expression boundaries are determined by thresholds of protein concentration, while gene expression borders are refined by autoregulation and repression.^8,9

Three classified genes (i.e. maternal genes, gap genes and pair-rule genes) into which the 14 early development-related genes can be divided are described in detail in the following. The maternal genes, i.e. bcd, cad and hb, diffuse and regulate gap genes with different expression levels in each spatial region along the A-P axis of the Drosophila embryo. The gap genes, i.e. gt, hb, kni, Kr and tll, define roughly the differences between two neighboring stripes by protein diffusion. The pair-rule genes, i.e. eve, ftz, hairy, odd, prd, runt and slp, define periodic patterns of the embryo by transcription regulation and protein diffusion. Two of these pair-rule genes, i.e. eve and ftz, are involved in defining even and odd segments of the 14 segmental primordia along the A-P axis.^10,11 The odd and even segments of concern are the seven eve stripes and seven ftz stripes, respectively. Moreover, at the blastoderm stage, along the D-V axis, three main regions, i.e. non-neural ectoderm (prospective epidermis), neurectoderm (prospective nervous system and larval ventral epidermis) and mesoderm (prospective muscle and connective tissue) are also divided.¹² The genes, which determine the three primary regions along the D-V axis, are different from these 14 early development-related genes which determine periodic segments along the A-P axis. In this study, for the convenience of analysis and system identification we will define spatial regions in the two-dimensional (2-D) space of the embryo along the A-P and D-V axes according to the above information. However, we only analyze the A-P formation of embryo after system modeling of transcriptional regulatory network, and the D-V formation can be analyzed by a similar procedure.

At the early developmental stages of Drosophila, the three-dimensional (3-D) spatio-temporal expression data of 14 early development-related proteins (http://flyex.ams.sunysb.edu/flyex/),^13–16 genome-wide mRNA time-course expression data¹⁷ and mRNA 3-D spatio-temporal expression data (http://flyex.ams.sunysb.edu/lab/gaps.html)^4,6 have been published and can be used for a system dynamic modeling of early Drosophila development. Interestingly, by comparing the normalized protein spatio-temporal expression data with mRNA spatio-temporal expression data, the trends of gene expressions along the A-P axis are found.³ In this study, we incorporate the mRNA 3-D data with protein 3-D data to construct the gene/protein interaction network for the transcription regulations and diffusion mechanisms of early embryogenesis via our stochastic 3-D dynamic model. However, there are some expression data within the 14 early development-related genes are unavailable in mRNA 3-D spatio-temporal expression database. In recent studies, Neural-Network (NN) model, which could be trained to optimize its internal network to learn the behaviors of complex systems, has been used to not only infer gene network regulatory relationships based on genome-wide microarray data¹⁸ but also build the relationship between input and output information by using a back-propagation algorithm to learn from the training data.^19–22 Therefore, for the unavailable mRNA data, we will use the back-propagation NN training method to obtain the mimic mRNA data according to the available protein and mRNA 3-D data.

In recent years, since the development of experimental techniques has increased the quality and amount of available mRNA and protein expressions, many approaches, e.g. fuzzy logic,^23,24 recurrent neural networks,^25–27 Bayesian networks,^28,29 Boolean networks^30,31 and differential equations,^32–34 have been widely exploited to unravel regulation networks from the perspective of systems biological. For the well available protein spatio-temporal data in early Drosophila development, nonlinear 2-D dynamic models have been employed to analyze the transcription regulation properties and effect of gap genes on eve stripe formation.^{3,6,16,35–38} However, more efforts are needed to incorporate these pathways and gene networks with a spatio-temporal gene/protein interaction network to interpret the dynamic system behavior in early Drosophila development since not only protein but also mRNA 3-D spatio-temporal data are both available for dynamic interplay of genes and proteins at different compartments of Drosophila embryo in early embryogenesis. The mechanisms of early Drosophila development in the whole embryo can be unraveled clearly if the dynamic interactions of genes and proteins are considered at different compartments in early embryogenesis. Therefore, in this study, we propose a stochastic 3-D dynamic model for constructing the gene/protein interaction network of early Drosophila development.

In this study, we focus on the topic of investigating the possible mechanisms for the eve stripe formation of Drosophila embryo. In this biological development approach, it is assumed that transcription regulations consist of cis-effect and trans-effect. Since edges, i.e. transcription regulations, in a gene regulatory network must be constantly selected in order to survive randomization forces, trans-effects, which are the binding affinities of specific transcription factors to cis-regulatory regions in the promoter of the target gene, would be varied rapidly while cis-effects, which are regulated directly by physical attachment of TF’s binding cis-regulatory regions, are relatively fixed.³⁹ Thus, we assume that regulation abilities, i.e. trans-effects, should vary with different spatial regions of the embryo, which results from different binding affinities of diffusible TFs. Based on the constructed stochastic 3-D Embryo Space-Time model (stochastic 3-DEST model), we analyze the transcription regulations and diffusion mechanisms for gene/protein interaction network. The stochastic 3-DEST model with 28 state variables is employed to represent the transcription/translation regulation process between 14 mRNA genes and the corresponding TFs in early embryogenesis. Moreover, because we consider both the environmental noises and the intrinsic noises in mRNA and protein data, stochastic partial differential equations (PDEs) are employed for the transcriptional and translational regulatory model of early embryogenesis. In order to understand the roles of TFs in each spatial region, according to the signs of diffusion parameters of the stochastic 3-DEST model, a TF can be considered as a donor (>0) or an acceptor (<0) in each spatial region to balance instant concentrations of the whole embryo. Hence, the TF in a spatial region that diffuses to (from) the neighboring spatial regions, is called a donor (acceptor). In addition, from previous studies we know that transcription regulations can be inferred by a dynamic model via microarray data.^33,36,40 However, how to sieve out the insignificant transcription regulations from the whole gene/protein interaction network is still a problem. For this reason, according to the stochastic 3-DEST model, the Akaike Information Criterion (AIC)⁴¹ for model order detection combined with the maximum likelihood (ML) for parameter estimation in system identification is used in this study to detect significant upstream regulators and to prune insignificant transcription regulations for refining the gene/protein interaction network of early Drosophila development. From the identified stochastic 3-DEST model, we can not only find the significant transcription regulations of the corresponding TFs, which control the anterior/posterior border formation of eve stripes, but also validate these results with wet experiments. In order to validate the identified effect of transcription regulation and diffusion on early Drosophila development, the wet experiments, i.e. gene mutations,^{7,9,10,42–46} regulatory module classification⁴⁷ and cis-regulatory module detection,⁴⁸ have been employed to trace back the direct or indirect transcription regulations and protein diffusions in early Drosophila development. From the perspective of the network motifs of the identified gene/protein interaction network in the embryo, we find that transcription regulations and protein diffusion mechanisms may play a cooperative role in the formation of eve stripes in early Drosophila development.

Methods

System modeling and identification for gene/protein interaction network

To identify the dynamic behavior of the early development-related genes, the procedure of system identification in early embryogenesis is divided into four steps. First, utilizing fully the well-published spatio-temporal data and the prior knowledge of early embryogenesis, we construct a stochastic 3-DEST model to identify the molecular dynamics of gene/protein interaction network in early embryogenesis. Second, for system modeling, we use Eve’s spatial expression at the cleavage cycle 14A temporal class 8 (c14A8) of the nuclear cleavage to settle stripe boundaries and region boundaries of each stripe for dividing the embryo into seven eve stripes along the A-P axis and into three spatial regions (i.e. anterior part, middle part and posterior part) along the D-V axis, respectively. Third, for the early development-related genes, since a part of the mRNA spatio-temporal data are unavailable, we incorporate the available mRNA and protein spatio-temporal expression data with the back-propagating NN training method to train and simulate the mimic data for the unavailable mRNA spatio-temporal expression data (see Appendix I). Fourth, we identify the model parameters and select the significant regulatory parameters for the stochastic 3-DEST model to construct the transcriptional regulatory network in every spatial region by the ML estimation method and the AIC backward elimination method, respectively. Finally, the transcriptional regulatory networks in every spatial region are connected together to construct the entire spatio-temporal gene/protein interaction network for early Drosophila development.

Remark: If the information of cooperation bindings is richer in future, the transcriptional regulations due to cooperation binding can be easily extended to the regulation candidates of the 3-DEST model, which can improve the proposed model of gene/protein network but with increased computation burden when using the AIC method in early embryogenesis.

Stochastic PDEs model in eve stripe formation

In previous studies, dynamic models with protein synthesis, protein diffusion and protein decay have been utilized in the description of the mechanism of embryonic development.^{3,4,6,35–38} To analyze the dynamic interplay of genes and proteins in early embryogenesis, six stochastic molecular dynamics are incorporated in the 3-DEST model, i.e. (1) protein synthesis, (2) protein decay, (3) mRNA decay, (4) protein diffusion, (5) transcription regulations, and (6) autoregulation. In addition, in order to differentiate mRNA expressions from protein expressions, we define two state variables X_i and Y_i to represent the 3-D spatio-temporal mRNA profiles of the ith target gene and its corresponding TFs, respectively. According to the transcription regulation model proposed in previous studies,^6,33,36,40 the stochastic 3-DEST model for the ith target gene and their upstream regulatory TFs in the gene/protein interaction network of Drosophila development is proposed as follows:

$$\begin{array}{l}\frac{\partial X_i(t,x,y)}{\partial t}={\kappa }_i(x,y)-{\alpha }_i(x,y)X_i(t,x,y)\\ +\sum _{j=1}^{14}{\beta }_{ij}(x,y)f(Y_j(t-{\tau }_j,x,y))\\ +{\upsilon }_i(t,x,y)\\ \frac{\partial Y_j(t,x,y)}{\partial t}={\varpi }_j(x,y)+{\alpha }_j(x,y)X_i(t,x,y)\\ -{\lambda }_j(x,y)Y_j(t,x,y)\\ +{\gamma }_j(x,y){\nabla }^2{Y}_j(t,x,y)+{\zeta }_j(t,x,y),\\ i,j=1,2,\dots ,14\end{array}$$ (1)

where X_i(t, x, y) represents the mRNA expression of the ith target gene, Y_j(t, x, y) denotes the expression of the jth TF of the target gene, and f(Y_j.(t, x, y)) defined as f(Y) = Yⁿ/(Pⁿ + Yⁿ) is a sigmoid function to denote the regulatory bindings of TFs on the promoters of targets.^39,49,50 Here, P is defined as the means of protein expressions, which imply cis-effects of transcription regulations. The term ${\Sigma }_{j=1}^{14}{\beta }_{ij}(x,y)f(Y_j(t-{\tau }_j,x,y))$ denotes the transcription regulation, i.e. trans-effect, on the ith target gene from its TFs. α_i(x, y) stands for mRNA decay rate for the ith gene and is equal to the synthesis rate of the ith protein, and λ_j(x, y) stands for protein decay rate. κ_i(x, y) and ϖ_j(x, y) are basal level of mRNA and protein generation, respectively, and they satisfy κ_i(x, y), ϖ_j(x, y) ≥ 0. The diffusion operator ▿² = ∂²/∂x² + ∂²/∂y² is the Laplacian operator in 2-D to denote the diffusion of protein at the location (x, y). In Eq. (1), mRNA expressions are transcriptionally regulated by TFs (i.e. ${\Sigma }_{j=1}^{14}{\beta }_{ij}(x,y)f(Y_j(t-{\tau }_j,x,y)$ and translated for protein synthesis α_i(x, y) X_i(t, x, y) in the downstream translation process. In the second equation of Eq. (1), the jth TF, Y_j(t, x, y), is assumed to be produced in the translation process by the corresponding mRNA α_i(x, y) X_i(t, x, y) from the upstream transcription process and decayed by degradation λ_j(x, y) Y_j(t, x, y) and diffusion γ_j(x, y)▿²Y_j(t, x, y).⁵¹ Diffusion coefficients of the jth TF are represented by γ_j(x, y). β_ij(x, y) denotes the regulatory ability of the jth TF (or regulatory protein), Y_j, on the promoter region of the target gene X_i. β_ij(x, y) > 0 stands for the ith target gene activated by the jth TF (prospective activator) or not repressed by the jth TF (prospective repressor) while β_ij(x, y) < 0 stands for the ith target gene not activated by the jth TF (prospective activator) or repressed by the jth TF (prospective repressor).³⁹ Therefore, the gene/protein interaction network of early Drosophila development is constructed by linking up all target genes through the regulations of their upstream TFs, ${\Sigma }_{j=1}^{14}{\beta }_{ij}(x,y)f(Y_j(t-{\tau }_j,x,y))$ in Eq.(1). Moreover, the productions of Y_j in Eq.(1)are synthesized by the corresponding mRNA X_j and diffused from Y_j in the neighborhood. Model uncertainty, fluctuations of the basal levels and measurement noises in the mRNA (transcription) dynamics and protein (translation) dynamics are denoted by stochastic noise υ_i(t, x, y) and ζ_j(t, x, y), respectively. x and y denote the location of the embryo in the 2-D space, i.e. the coordination in the x-axis and y-axis.

Remark: The dynamic model in Eq. (1) is to interpret the transcription/translation regulation processes of 14 genes in early embryogenesis. The first Equation of Eq. (1) describes the transcription regulation of the ith gene; and the mRNA productive rate is mainly due to the transcription regulations of 14 proteins (i.e. TFs), the influence of basal level and degradation of mRNA. The noise υ_i(t, x, y) denotes the fluctuation of basal level, measurement noise and modeling residue. Since the expression levels of TFs can be altered with different spatial regions of the whole embryo by diffusion mechanism, the relationship of transcription regulation between one TF and its target gene is also different in different spatial regions. The second equation of Eq. (1) describes protein production in the translational diffusion process at the location (x, y). The protein productive rate is mainly influenced by the translation of mRNA, diffusion from the neighboring space, and degradation rate of the protein. The noise ζ_j(t, x, y) is due to the fluctuation of the basal level of protein, measurement noise and modeling error. The model in Eq. (1) describes the interplay of gene/protein interactions at the location (x, y). The parameters of the stochastic spatio-temporal dynamic model in Eq. (1) can be estimated by the spatio-temporal profile of mRNA data and protein data in each spatial region. The regulatory gene/protein network can be linked gene by gene through the transcription regulations ${\Sigma }_{j=1}^{14}{\beta }_{ij}(x,y)f(Y_j(t-{\tau }_j,x,y))$ to other regulatory TFs iteratively.

In the proposed stochastic dynamic model in Eq. (1), the interplay of six stochastic processes, i.e. protein synthesis, protein decay, mRNA decay, protein diffusion, transcription regulations and autoregulation, mimics the dynamics in early embryogenesis. We are the first to combine mRNA dynamic equations with protein dynamic equations to mimic the dynamic interaction network of target genes and their regulatory proteins via 3-D mRNA and protein data at different compartments in early Drosophila development. Our main purpose is to infer the possible mechanisms of eve stripe formation by investigating the estimated parameters κ_i, ϖ_j, α_j, β_ij, λ_j and γ_j, i = 1, 2, ..., 14 of the system dynamic model in Eq. (1) via mRNA and protein data. Since it is hard to solve directly the identification problem of the continuous 3-DEST model in Eq. (1), we discretize the continuous 3-DEST model in Eq. (1)⁵² and the location (x, y) on the continuous plane is transformed into the location (l, m) on the discrete plane. The discrete 3-DEST model is shown as follows:

$$\begin{array}{l}{X}_i(k+1,l,m)=d_{i,l,m}+(1-a_{i,l,m})X_i(k,l,m)+\sum _{j=1}^{14}{b}_{ij,l,m}f(Y_j(k-k^{\prime },l,m))+{\varepsilon }_i(k,l,m)\\ Y_i(k+1,l,m)=w_{i,l,m}+a_{i,l,m}{X}_j(k,l,m)+c_{j,l,m}{Y}_j(k,l,m) i,j=1,2,\dots ,14\\ +{\rho }_{j,l,m}(\frac{Y_j(k,l,-1,m)-2Y_j(k,l,m)+Y_j(k,l+1,m)}{h_x^2} l=1,2,3\\ +\frac{Y_j(k,l,m-1)-2Y_j(k,l,m)+Y_j(k,l,m+1)}{h_y^2})+{\delta }_j(k,l,m) m=1,2,\dots ,21\end{array}$$ (2)

with the stability constraints d_i,l,m ≥ 0, w_j,l,m ≥ 0, $\left|1-a_{j,l,m}\right|\le 1,\{\begin{array}{cc}|c_{j,l,m}-4{\rho }_{j,l,m}(h_x^{-2}+h_y^{-2})|\le 1& \text{if} {\rho }_{j,l,m}<0\\ \left|c_{i,l,m}\right|\le 1& \text{if} {\rho }_{j,l,m}\ge 0\end{array}$ (see Appendix II), where k denotes the kth time point, l and m denote the location (l, m) on the discrete plane, and h is the distance between two locations along two axes, i.e. A-Paxis (h_x) and D-V axis (h_y). The parameters are defined as follows: d_i,l,m = k_i(x_l, y_m)· Δt, w_j,l,m = ϖ_j (x_l, y_m)·Δt a_j,l,m = α_j(x_l, y_m)·Δt, b_ij,l,m = β_ij(x_l, y_m)·Δt, c_j,l,m = 1 – λ_j(x_l, y_m)· Δt, and ρ_j,l,m = γ_j(x_l, y_m)·Δt where Δt ≈ 2.568 minutes. Then, by using the discrete 3-DEST model in Eq. (2) and mRNA and protein data, the parameters k_i(x_l, y_m), ϖ_j(x_l, y_m), α_i(x_l, y_m), β_ij(x_l, y_m), λ_j(x_l, y_m) and γ_j(x_l, y_m) in Eq. (2) can be estimated by the system identification method in a spatial region one by one, which will be described in the sequel. Therefore, before the system identification of discrete 3-DEST model in Eq. (2), we need to define the 2-D spatial regions of Drosophila embryo in the following section.

Specification of 2-D spatial regions of Drosophila embryo

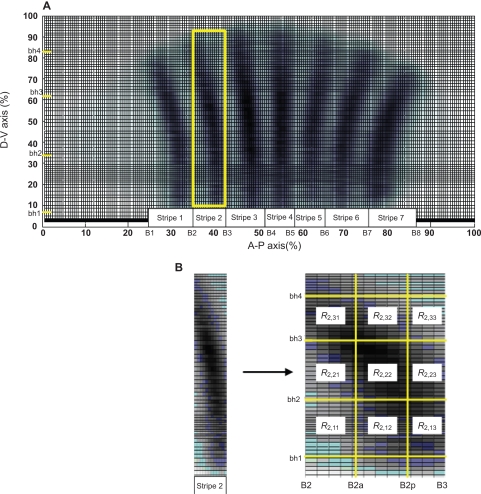
To identify the discrete 3-DEST model in Eq. (2), we have to define (l, m) as the center of the spatial regions of the embryo by specifying the boundaries of the spatial regions. Along the A-P axis, two boundaries of the ith eve stripe are denoted by Bi and Bi + 1, respectively. The boundaries of seven eve stripes along the A-P axis are denoted by {B1, B2, ..., B8} (Fig. 1a). Each of the eve stripes along the A-P axis is separated into three parts, and the boundaries of middle part of the eve stripe i are denoted as Bia and Bip (Fig. 1b). Therefore, there are totally 21 spatial regions (i.e. m + 1, 2, ..., 21 in Eq. (2)) within seven eve stripes along the A-P axis, and the 22 boundaries of the 21 spatial regions are specified as follows:

{B1, B1a, B1p, B2, B2a, B2p, …, B7 B7a, B7p, B8} = {25%, 29%, 32.5%, 35%, 38.26%, 40.44%, 42.17%, 47%, 49%, 50%, 54.5%, 55.5%, 57.5%, 62%, 64%, 67%, 69%, 72%, 75%, 79%, 81%, 85%}.

Figure 1.

Determination of eve stripe boundaries at c14A8. A) Along the A-P axis and D-V axis, seven eve stripe boundaries {B1, B2, ..., B8} and three spatial region boundaries {bh1, bh2, bh3, bh4} are defined, respectively. B) The yellow square frame as shown in (a) is enlarged for the second eve stripe. Nine spatial regions with symbol R_stripe,lk are defined in each stripe.

Additionally, three spatial regions (i.e. l = 1, 2, 3 in Eq. (2))along the D-Vaxis are defined with their boundaries {bh1, bh2, bh3, bh4} = {8.54%, 33.67%, 61.40%, 82.25%} (Fig. 1b). For the convenience of illustration, we define a symbol, R_stripe,lk, to be a spatial region of the location (l, k) in the stripe-th eve stripe. The transformation from (l, m) in the whole embryo to (l, k) in the stripe-th eve stripe, i.e. R_stripe,lk, is given by m = k + 3*(stripe-1). For example, (l, k) = (3, 3) in the second eve stripe, i.e. the spatial region R_2,33 corresponds to (l, m) = (3, 6) in the whole embryo, with l = 3 and m = 3 + 3*(2–1) = 6 (Fig. 1b). After the determination of the spatial regions, expression levels of protein and mRNA are interpolated to the determined spatial regions, which will be used for model identification of Eq. (1).

System identification for stochastic 3-DEST gene/protein interaction networks in different spatial regions of Drosophila embryo

When the data points {X_i(k, l, m), Y_j(k, l, m)} for i,j ∈ {1, 2, ..., 14}, k ∈ {1,2, ..., N}, l = {1, 2, 3}, m = {1, ..., 21} are ready, the parameters of stochastic 3-DEST model can be estimated using Eq. (2) for gene/protein interaction networks in each spatial region of Drosophila embryo. For the convenience of parameter estimation, Eq. (2) with N data points can be translated into the following linear regression matrix form:

$$Y_{l,m}={\Phi }_{l,m}{\Theta }_{l,m}+E_{l,m},l=\{1,2,3\},m=\{1,2,\dots ,21\}$$ (3)

where

$$\begin{array}{l}{Y}_{l,m}=\left[\begin{array}{c}{\chi }_{1,l,m}\\ {\chi }_{2,l,m}\\ ⋮\\ {\chi }_{14,l,m}\\ {\psi }_{1,l,m}\\ {\psi }_{2,l,m}\\ ⋮\\ {\psi }_{14,l,m}\end{array}\right],\hspace{0.17em}{\Phi }_{l,m}=\left[\begin{array}{cccccc}{H}_{l,m}& 0& -Z_{l,m}& 0& 0& \Sigma {\Upsilon }_{l,m}\\ 0& H_{l,m}& Z_{l,m}& {\Upsilon }_{l,m}& \Delta {\Upsilon }_{l,m}& 0\end{array}\right],\hspace{0.17em}{\Theta }_{l,m}=\left[\begin{array}{c}{D}_{l,m}\\ {\Omega }_{l,m}\\ M_{l,m}\\ N_{l,m}\\ {\Xi }_{l,m}\\ O_{l,m}\end{array}\right],\\ E_{l,m}=\left[\begin{array}{c}{\xi }_{1,l,m}\\ {\xi }_{2,l,m}\\ ⋮\\ {\xi }_{14,l,m}\\ {\varsigma }_{1,l,m}\\ {\varsigma }_{2,l,m}\\ ⋮\\ {\varsigma }_{14,l,m}\end{array}\right],\hspace{0.17em}{\chi }_{i,l,m}=\left[\begin{array}{c}{X}_i(2,l,m)-X_i(1,l,m)\\ X_i(3,l,m)-X_i(2,l,m)\\ ⋮\\ X_i(N,l,m)-X_i(N-1,l,m)\end{array}\right],\hspace{0.17em}{\psi }_{i,l,m}=\left[\begin{array}{c}{Y}_j(2,l,m)\\ Y_j(3,l,m)\\ ⋮\\ Y_j(N-1,l,m)\end{array}\right],\\ H_{l,m}=\mathit{\text{block}}\hspace{0.17em}\mathit{\text{diag}}(1_{N-1},\hspace{0.17em}{1}_{N-1},\dots 1_{N-1}),\hspace{0.17em}{Z}_{l,m}=\\ \left[\begin{array}{cccc}{X}_1(1,l,m)& 0& \cdots & 0\\ X_1(2,l,m)& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮\\ X_1(N-1,l,m)& 0& ⋮& ⋮\\ 0& X_2(1,l,m)& ⋮& ⋮\\ ⋮& X_2(2,l,m)& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮\\ ⋮& X_2(N-1,l,m)& 0& ⋮\\ ⋮& 0& \ddots & 0\\ ⋮& ⋮& 0& X_{14}(1,l,m)\\ ⋮& ⋮& ⋮& X_{14}(2,l,m)\\ ⋮& ⋮& ⋮& ⋮\\ 0& \cdots & 0& X_{14}(N-1,l,m)\end{array}\right],\\ {\Upsilon }_{l,m}=\left[\begin{array}{cccc}{Y}_1(1,l,m)& 0& \cdots & 0\\ Y_1(2,l,m)& ⋮& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮\\ Y_1(N-1,l,m)& 0& ⋮& ⋮\\ 0& Y_2(1,l,m)& ⋮& ⋮\\ ⋮& Y_2(2,l,m)& ⋮& ⋮\\ ⋮& ⋮& ⋮& ⋮\\ ⋮& Y_2(N-1,l,m)& 0& ⋮\\ ⋮& 0& \ddots & 0\\ ⋮& ⋮& 0& Y_{14}(1,l,m)\\ ⋮& ⋮& ⋮& Y_{14}(2,l,m)\\ ⋮& ⋮& ⋮& ⋮\\ 0& \cdots & 0& Y_{14}(N-1,l,m)\end{array}\right],\hspace{0.17em}\Delta {\Upsilon }_{l,m}=\left[\begin{array}{cccc}\delta {\Upsilon }_{1,l,m}& 0& \cdots & 0\\ 0& \delta {\Upsilon }_{2,l,m}& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& \delta {\Upsilon }_{14,l,m}\end{array}\right],\\ \Sigma {\Upsilon }_{i,m}=\left[\begin{array}{cccc}\sigma {\Upsilon }_{1,l,m}& 0& \cdots & 0\\ 0& \sigma {\Upsilon }_{2,l,m}& \ddots & ⋮\\ ⋮& \ddots & \ddots & 0\\ 0& \cdots & 0& \sigma {\Upsilon }_{14,l,m}\end{array}\right]\\ \delta {\Upsilon }_{i,l,m}=\left[\begin{array}{c}\frac{Y_i(1,l-1,m)-2Y_i(1,l,m)+Y_i(1,l+1,m)}{h_x^2}+\frac{Y_i(1,l,m-1)-2Y_i(1,l,m)+Y_i(1,l,m+1)}{h_y^2}\\ \frac{Y_i(2,l-1,m)-2Y_i(2,l,m)+Y_i(2,l+1,m)}{h_x^2}+\frac{Y_i(2,l,m-1)-2Y_i(2,l,m)+Y_i(2,l,m+1)}{h_y^2}\\ ⋮\\ \frac{Y_i(N-1,l-1,m)-2Y_i(N-1,l,m)+Y_i(N-1,l+1,m)}{h_x^2}+\frac{Y_i(N-1,l,m-1)-2Y_i(N-1,l,m)+Y_i(N-1,l,m+1)}{h_y^2}\end{array}\right],\\ \sigma {\Upsilon }_{i,l,m}=\left[\begin{array}{cccc}{Y}_1(1,l,m)& Y_2(1,l,m)& \cdots & Y_{14}(1,l,m)\\ Y_1(2,l,m)& Y_2(2,l,m)& \cdots & Y_{14}(2,l,m)\\ ⋮& ⋮& \cdots & ⋮\\ Y_1(N-1,l,m)& Y_2(N-1,l,m)& \cdots & Y_{14}(N-1,l,m)\end{array}\right],\hspace{0.17em}{D}_{l,m}=\left[\begin{array}{c}{d}_{1,l,m}\\ d_{2,l,m}\\ ⋮\\ d_{14,l,m}\end{array}\right],\hspace{0.17em}{\Omega }_{l,m}=\left[\begin{array}{c}{w}_{1,l,m}\\ w_{2,l,m}\\ ⋮\\ w_{14,l,m}\end{array}\right],\\ M_{l,m}=\left[\begin{array}{c}{a}_{1,l,m}\\ a_{2,l,m}\\ ⋮\\ a_{14,l,m}\end{array}\right],\hspace{0.17em}{N}_{l,m}=\left[\begin{array}{c}{c}_{1,l,m}\\ c_{2,l,m}\\ ⋮\\ c_{14,l,m}\end{array}\right],\hspace{0.17em}{\Xi }_{l,m}=\left[\begin{array}{c}{\rho }_{1,l,m}\\ {\rho }_{2,l,m}\\ ⋮\\ {\rho }_{14,l,m}\end{array}\right],\\ O_{l,m}=\left[\begin{array}{c}{o}_{1,l,m}\\ o_{2,l,m}\\ ⋮\\ o_{14,l,m}\end{array}\right],\hspace{0.17em}{o}_{i,l,m}=\left[\begin{array}{c}{b}_{i1,l,m}\\ b_{i2,l,m}\\ ⋮\\ b_{i14,l,m}\end{array}\right],\hspace{0.17em}{\xi }_{i,l,m}=\left[\begin{array}{c}{\varepsilon }_i(2,l,m)\\ {\varepsilon }_i(3,l,m)\\ ⋮\\ {\varepsilon }_i(N,l,m)\end{array}\right],\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\varsigma }_{j,l,m}=\left[\begin{array}{c}{\delta }_i(2,l,m)\\ {\delta }_i(3,l,m)\\ ⋮\\ {\delta }_j(N-1,l,m)\end{array}\right]\end{array}$$

Suppose the noise components ɛ_i(k, l, m) and δ_j(k, l, m) are normally distributed, and the noise matrix E_l,m has an unknown covariance matrix ∑_l,m to be estimated. Then we use the ML method to solve the parameter estimation problem with the optimum solution Θ̂_l,_m and ∑̂_l,m. The likelihood function of Y_l,m is defined as follows:⁴¹

$$\begin{array}{l}{p}_{l,m}(Y_{l,m}|{\Theta }_{l,m},{\Sigma }_{l,m})=\frac{1}{\sqrt{2\pi }}\text{det}{({\Sigma }_{l,m})}^{-M/2}\\ \text{exp}\{-\frac{1}{2}{[Y_{l,m}-{\Phi }_{l,m}{\Theta }_{l,m}]}^T\\ \times {\Sigma }_{l,m}^{-1}[Y_{l,m}-{\Phi }_{l,m}{\Theta }_{l,m}]\}\end{array}$$ (4)

The log-likelihood function for the given M data points in Y_l,m, i.e. M = 2·14(N – 1), can be defined as⁴¹

$$\begin{array}{l}{L}_{l,m}({\Theta }_{l,m},{\Sigma }_{l,m})=\text{constant} -\frac{M}{2}\text{ln}[\text{det}({\Sigma }_{l,m})]\\ -\frac{1}{2}{[Y_{l,m}-{\Phi }_{l,m}{\Theta }_{l,m}]}^T\\ {\Sigma }_{l,m}^{-1}[Y_{l,m}-{\Phi }_{l,m}{\Theta }_{l,m}]\end{array}$$ (5)

We can estimate the unknown parameters Θ_l,m and the covariance matrices of noise ∑_l,m by maximizing the log-likelihood function L_l,m(Θ_l,m, ∑_l,m), i.e. $\frac{\partial L_{l,m}({\Theta }_{l,m},{\Sigma }_{l,m})}{\partial {\Theta }_{l,m}}=0$ and $\frac{\partial L_{l,m}({\Theta }_{l,m},{\Sigma }_{l,m})}{\partial {\Sigma }_{l,m}}=0$, as follows:

$${\widehat{\Sigma }}_{l,m}=\frac{1}{M}{[Y_{l,m}-{\Phi }_{l,m}{\Theta }_{l,m}]}^T[Y_{l,m}-{\Phi }_{l,m}{\Theta }_{l,m}]$$ (6)

$${\widehat{\Theta }}_{l,m}={({\Phi }_{l,m}^T{\Theta }_{l,m})}^{-1}{\Phi }_{l,m}^T{Y}_{l,m}$$ (7)

In order to satisfy the following stability constraints d_i,l,m ≥ 0, w_j,l,m ≥ 0, |1 – a_j,l,m| ≤ 1, $\{\begin{array}{cc}|c_{j,l,m}-4{\rho }_{j,l,m}(h_x^{-2}+h_y^{-2})|\le 1& \text{if} {\rho }_{j,l,m}<0\\ \left|c_{i,l,m}\right|\le 1& \text{if} {\rho }_{j,l,m}\ge 0\end{array}$ in the discrete 3-DEST model (Eq. 2), a Matlab function, lsqlin, is used in the estimation procedure of the parameter identification of the stochastic 3-DEST model (see Appendix III). For the stochastic 3-DEST model of gene/protein interaction network in each spatial region of embryo, the number of estimated regulatory parameters is 266. We have a total of 28 dynamic equations which will be solved simultaneously. To avoid overfitting in parameter estimation and to find a more robust solution, we should interpolate these data points by the cubic spline method. Hence, we will test the robustness of system parameters on different numbers of interpolating data points from four times to six times the number of estimated parameters in the sequel.

According to the Akaike Information Criterion (AIC) method, we will let b_ij,l,m = 0 while the transcription regulation between the jth transcription factor and the ith target gene in the spatial region R_stripe,lk is insignificant. We use the AIC to prune some insignificant regulatory parameters of TFs in Eq. (7). The AIC is defined to include both the residual variance in parameter estimation and the model complexity into one statistics for model order detection as⁴¹

$$AI{C}_{l,m}(p)=\text{log}\left(\frac{1}{M}{(Y_{l,m}-{\widehat{Y}}_{l,m})}^T(Y_{l,m}-{\widehat{Y}}_{l,m})\right)+\frac{2p}{M}$$ (8)

where p is the number of reserved parameters in the backward elimination method of the AIC. Regulatory parameters are pruned one by one as p is decreased until the smallest AIC_l,m in the smaller p is larger than the AIC_l,m value of the previous pruning step. While the minimum AIC_l,m is achieved, the most adequate transcription regulations for each target gene could be obtained from the most adequate model order point of view.⁵³

Data and Materials

In this study, we incorporate two spatial-temporal data, protein data (http://flyex.ams.sunysb.edu/flyex/)^13–16 and mRNA data (http://flyex.ams.sunysb.edu/lab/gaps.html),^4,6 into the stochastic 3-DEST model to investigate how the transcription regulations and diffusion mechanisms cooperatively pattern eve stripes in the early embryogenesis of Drosophila. The spatial regions are first defined as shown in Figure 1 by Eve at cleavage cycle 14A and temporal class 8 (c14A8) in the embryo. Subsequently, the NN model combined with the method is trained by the available protein and mRNA data to simulate and mimic the unavailable mRNA data. The training of the NN model by the available data is achieved by minimizing the training error and maximizing the output correlations. Additionally, to avoid overfitting in system identification, we must interpolate the data points to an adequate number. However, over-interpolated data will lose the low-frequency (or long-range) behavior of the development system. Moreover, using different numbers of interpolated data in system identification may also cause significant differences in parameter estimations, especially in the AIC method. Hence, the robustness of the stochastic 3-DEST model will also be tested by different numbers of interpolated data as an assessment to choose an adequate number of interpolation in the sequel, because the robustness principle has been employed to check if a model can work in the real cell and is employed to narrow down the range of models to the few in the modeling procedure of biological networks, i.e. robustness can help theorists identify the correct dynamic model.³⁹ From the ML parameter estimation method, the dynamic model in early Drosophila development is constructed. Then, we incorporate the AIC method into the identification process to prune the insignificant regulatory parameters and refine the model. This allows us to pick up the TFs, which are the most significant regulators for controlling the downstream genes in the early development of Drosophila.

The real biological systems are always robust. Therefore the model of a biological system should be robust and the robustness is a validation of dynamic models for biological systems.³⁹ To test the robustness of the 3-DEST model by different number of data points, we interpolate the time-course data from 38 data points (i.e. four times the number of parameters) to 57 data points (i.e. six times the number of parameters), i.e. there are 20 test cases. However, among the 20 test cases only six test cases, which are respectively those with 38, 39, 40, 41, 42 and 44 interpolated data points, meet the model’s stability constraints d_i,l,m ≥ 0, w_j,l,m ≥ 0, |1 – a_j,l,m| ≤ 1, $\{\begin{array}{cc}|c_{j,l,m}-4{\rho }_{j,l,m}(h_x^{-2}+h_y^{-2})|\le 1& \text{if} {\rho }_{j,l,m}<0\\ \left|c_{i,l,m}\right|\le 1& \text{if} {\rho }_{j,l,m}\ge 0\end{array}$ in Eq. (2), when the AIC values of the model are minimized. Therefore, only six kinds of data interpolations to meet robustness test can be used for the parameter identification of the 3-DEST model. Here, only the robustness test of the 3-DEST system in the spatial region R_2,22 is discussed for further choice of data interpolations. The robustness of the estimated basal levels and the regulatory abilities in the six test cases in the spatial region R_2,22 are shown in Table 1. As can be seen, there are a few changes such as basal levels (κ̂_i (x₂, y₅)) of runt at N = 39 and hairy at N = 41 (N represents number of interpolated data points), and there is no significant change in basal levels of protein (ϖ̂_j (x₂, y₅)). In addition, the regulatory abilities (β̂_eve,j (x₂, y₅)) of both runt and slp at N = 38 and 39 are pruned by the AIC method when compared with the others. Therefore, except a few variations in N = 38, 39 and 41 the other cases, i.e. N = 40, 42 and 44, are robust for system identification. Here, mRNA and protein data with 44 interpolation time points are chosen for parameter estimation of the stochastic 3-DEST model of the whole embryo. When spatio-temporal data are ready and the number of interpolated data points is decided (N = 44), system identification for parameter estimation in Eqs. (6)(7) and (8) can be performed.

Table 1.

Robustness tests of parameters, κ̂_i (x_l, y_m), ϖ̂_j (x_l, y_m) and β̂_eve,j (x_l, y_m) (shown in Eq. (9)), of R_2,22 (i.e. l = 2 and m = k + 3*(stripe-1) = 2 + 3*(2 – 1) = 5) in the six test cases, i.e. the six test cases individually have 38, 39, 40, 41, 42 and 44 interpolated data points denoted by N = 38, N = 39, N = 40, N = 41, N = 42 and N = 44, respectively.

Parameters	κ̂i(x2,y5)						ϖ̂i(x2,y5)						β̂eve,j(x2,y5)
N	38	39	40	41	42	44	38	39	40	41	42	44	38	39	40	41	42	44
bicoid	8.18	8.26	8.34	8.41	8.47	8.60	29.54	29.15	28.75	28.39	28.05	27.37	584.11	580.97	714.09	794.65	721.02	719.16
caudal	30.73	30.69	30.59	85.11	30.39	30.22	58.60	58.12	57.78	22.43	57.25	56.67	0	0	0	0	0	0
eve	0	0	0	0	0	0	0	0	0	0	0	0	−1040.69	−1063.51	−1972.63	−1881.88	−1763.69	−1590.02
ftz	0	0	0	0	0	0	37.59	37.69	37.79	37.88	37.96	38.08	1340.85	1343.18	3338.48	3172.99	3112.51	2913.20
giant	0.72	0.72	0.72	1.65	2.07	0.72	19.82	19.64	19.43	13.85	15.33	16.72	−101.86	−106.81	−445.25	−414.64	−439.09	−429.87
hairy	18.58	17.65	60.80	0	65.51	66.21	58.03	58.66	80.99	80.91	80.84	80.69	0	0	−1178.98	−1039.98	−1101.73	−1033.91
hunchback	10.32	11.45	12.41	13.13	14.03	15.65	105.69	104.42	103.70	103.26	102.40	100.84	227.98	245.25	194.56	73.79	86.04	2.15
knirps	3.40	3.53	3.38	3.56	3.43	3.45	5.03	4.56	5.51	4.02	4.83	4.25	163.00	164.28	638.90	546.26	566.78	505.28
krüppel	0.86	0.86	0.86	0.86	0.86	0.86	23.05	22.54	22.05	21.60	21.16	20.33	−1010.23	−1003.42	−2153.69	−1946.24	−1980.59	−1827.30
odd	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
paired	0	0	0	0	0	0	0	0	0	0	0	0	0	0	557.86	497.67	555.37	549.33
runt	0	17.94	0	0	0	0	0	0	0	0	0	0	0	0	589.60	467.39	522.54	465.37
slp	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
tailless	0	0	0	0	0	0	20.74	20.50	20.29	20.09	19.89	19.53	0	0	0	0	0	0

Results

After the parameters in Eq. (1) are estimated by ML and pruned by the AIC in Eqs. (6)–(8), the identified 3-DEST models for gene/protein interaction networks in the spatial regions of Drosophila embryo are given in the following.

$$\begin{array}{l}\frac{\partial X_i(t,x_l,y_m)}{\partial t}={\widehat{\kappa }}_i(x_l,y_m)\\ -{\widehat{\alpha }}_i(x_l,y_m)X_i(t,x_l,y_m)\\ +\sum _{j=1}^M{\widehat{\beta }}_{ij}(x_l,y_m)f(Y_j(t-{\tau }_j,x_l,y_m))\\ +{\phi }_i(t,x_l,y_m)\\ \frac{\partial Y_j(t,x_l,y_m)}{\partial t}={\widehat{\varpi }}_j(x_l,y_m)\\ +{\widehat{\alpha }}_j(x_l,y_m)X_j(t,x_l,y_m)\\ -{\widehat{\lambda }}_j(x_l,y_m)Y_j(t,x_l,y_m)\\ +{\widehat{\gamma }}_j(x_l,y_m){\nabla }^2{Y}_j(t,x_l,y_m)\\ +{\phi }_j(t,x_l,y_m),\end{array}$$ (9)

where i, j = 1, 2, ..., 14, l = 1, 2, 3, m = 1, 2, ..., 21. κ̂_i ϖ̂_j, α̂_i, β̂_ij, λ̂_j, and γ̂_j are estimated by Eq. (7) and the covariance matrices of the stochastic noises ϕ_i and ϕ_j can be estimated in Eq. (6).

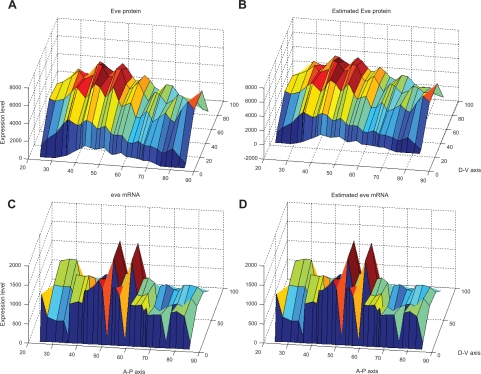
After system identification, the simulation results of the system model obtained using the ML estimation method and the AIC method are shown in Figure 3(b) (protein) and 3(d) (mRNA) compared with the original data in Figure 3(a) (protein) and 3(c) (mRNA), respectively. The 3-DEST gene/protein interaction networks in different spatial regions are constructed in Figure 4 through the diffusion coefficients γ̂_j and regulatory abilities β̂_ij of the identified 3-DEST dynamic model in Eq. (9). The changes in these diffusion coefficients and regulatory abilities in eve stripes will be simultaneously investigated to see whether there are some cooperative effects on them, which may give a clue of eve stripe formation.

Figure 3.

Original data and estimated results by our proposed dynamic model. The original eve mRNA and protein spatial data at c14A8 are shown in A) and C), respectively. After system identification, the estimated eve mRNA and protein spatial data generated by the dynamic model are shown in B) and D), respectively.

Figure 4.

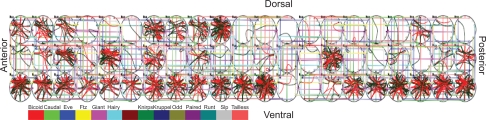
3-DEST dynamic gene/protein interaction network for diffusion and transcriptional regulation mechanisms in different spatial regions in the whole embryo. The notations, R_1,11, R_1,12, R_1,13, R_1,21, ..., R_7,31, R_7,32, R_7,33, are the 63 spatial regions of the whole embryo which is specified by Figure 1(a). In each spatial region R_stripe,ij, the colors of the outer ring in the color circle are specified by the 14 gene names, which are given by the color bar below the figure, respectively. Each color of the outer ring is specified by each gene. The solid lines that connect color circles stand for transcription regulation between genes in each spatial region based on regulatory abilities β̂_ij of the identified 3-DEST dynamic model in Eq. (9). Positive and negative regulations are denoted by arrows and bars at the end of solid lines, respectively. Additionally, the colors of the inner circle, i.e. the black and white circle, inside the color circle stand for the TFs’ roles, i.e. donor or acceptor of the transcriptional regulation network, respectively. The bold color lines that connect the same genes in neighboring spatial regions with different roles stand for protein diffusions from donor (black inner circle) to acceptor (white inner circle) in neighboring spatial regions based on the diffusion coefficients γ̂_j of the identified 3-DEST dynamic model in Eq. (9). The specification of the colors in bold color lines is consistent with the colors in the outer ring of the color circle, which are specified by the color bar. For example (see also Fig. 5a), Caudal in R_4,11 with green color in outer ring and black color in inner circle found regulates ftz (yellow) and runt (navy blue) and plays as a donor, which can diffuse to the neighboring regions. A clearer figure is available online at the website, http://www.ee.nthu.edu.tw/bschen/Drosophila_Fig4.pdf.

Previous research⁴⁸ on cis-regulatory module detection shows that the enhancer element of the second eve stripe contains the binding sequences of Krüppel, Giant, Bicoid and Hunchback, and the second eve stripe can be activated by Bicoid, Hunchback, and repressed by Giant and Krüppel (Table 1 and Fig. 4).

In the analysis of eve stripe formation, the boundaries of eve stripe can be affected by diffusion from the neighboring regions where Eve serves as a donor to the regions where it plays the role of an acceptor. Figure 4 shows that Hunchback in R_2,22, R_3,11, R_3,33, R_4,31, R_6,11, R_6,13, and R_7,31 and Knirps in R_1,12, R_4,13, R_5,23 and R_7,13 positively and negatively regulate eve, respectively, and Eve in these regions simultaneously serves as a donor which diffuses through and affects the boundaries, i.e. stripe 1–2, stripe 3–4, stripe 4–5, stripe 5–6 and stripe 7-terminal (Fig. 4). Therefore, it shows that stripe boundaries are broken in the embryo with hunchback and knirps double mutant and the phenotype is similar to the embryo with a strong eve mutant.¹⁰ In addition, eve in R_2,11 and R_2,23, which plays the role of donor and is repressed by Giant and Krüppel respectively, would locally affect the anterior and posterior of the second eve stripe, respectively (Fig. 4).^7,45,54 Moreover, the effect of Giant and Krüppel respectively on the anterior and posterior of the second eve stripe should be diffusively reinforced by the same repressive transcription regulations in R_2,22. In the boundaries of the third eve stripe, eve in R_3,31 and R_4,31, which is negatively regulated by Hunchback and Knirps respectively, would diffuse to and affect on anterior and posterior boundaries of the third eve stripe, respectively (Fig. 4).^7,45,54 Moreover, we find that Giant and Hairy have no effect on the boundaries stripe 4–5 and stripe 5–6, respectively.

From the transcription regulations shown in Figure 4, we believe that most of them are new predicted except those discussed here because most of genetic studies in Drosophila are not easy to find direct transcription regulations without chromatin immunoprecipitation microarray (ChIP-chip) experiments. In this study, we provide a direction for other biologists at the wet experiments of transcription regulations especially in ChIP-chip experiments. For example, according to the robustness tests in Table 1, we show that eve in R_2,22 is positively regulated by Ftz and Knirps and is negatively self-regulated. The robust regulations are the most probable suggestion in transcription regulations of eve stripe formation.

Moreover, in the large network, there exist a huge number of interaction patterns. Only a few types of interaction patterns called network motifs, which are embedded in the network and connected to each other, allow them to carry out their functions even in the presence of additional interactions. Mangan and Alon⁵⁵ have analyzed two feedforward network motifs, i.e. coherent feedforward loops (C-FFL) and incoherent feedforward loops (I-FFL), and found that C-FFL acted as sign-sensitive delays, and I-FFL acted as sign-sensitive accelerators.⁵⁵ Moreover, Han et al⁵⁶ propose that a signaling module composed of a C-FFL and an I-FFL causes an early transient response and a delayed prolonged response after a short stimulus.⁵⁶ The early transient responses and delayed prolonged responses plausibly depend on post-translation modification of existing proteins and new protein synthesis, respectively. The combinative signaling module is suggested and found in drug therapy. Therefore, we obtain C-FFL and I-FFL from the constructed network (Fig. 5) according to the following rules. One relationship of the transcription regulations in Figure 5 serves as an edge of FFL, when the regulation relationship exists in at least four neighboring regions among its nine neighboring regions. For example (Fig. 5a), a C-FFL C15 found in Figure 5 is composed of three transcription regulations (Caudal->Ftz in R_3,13, Runt->Ftz in R_3,13 and Caudal->Runt in R_4,11) and two diffusions (Caudal and Runt are both diffused from R_4,11 to R_3,13). In addition, these three regulatory relationships exist respectively in at least four neighboring regions, i.e. Caudal->Ftz in R_3,13, R_3,12, R_4,11 and R_4,31, Runt->Ftz in R_3,13, R_3,12, R_3,33 and R_4,31 and Caudal->Runt in R_4,11, R_3,13, R_4,12 and R_4,31. Therefore, C15 is one of the FFLs (Fig. 5b) found in our network. By the same procedure, not only can we find 25 C-FFLs and 18 I-FFLs (Fig. 5b) but also 13 possible combinative signaling modules among 25 C-FFLs and 18 I-FFLs, i.e. Odd in R_1,12, R_1,11 (C3 and I1 in Fig. 5b), R_1,13 and R_1,23 (C1 and I1), Slp in R_2,12, R_2,22 (C7 and I5), R_3,31 (I12 and C18) and R_3,12 (C19 and I4), Eve in R_3,12, R_3,13 (C14 and I9) and R_4,11 (C13 and I9), and Ftz in R_3,13 (C21 and I15) and R_6,13 (C25 and I17). Among these modules, we find that Hunchback acts as a source of FFLs to activate Ftz as an output expressed in eve stripes 3, 4, 6 and 7. From the embryo with hb⁻ mutants, eve stripes 2, 3, 4 and 7 are partially or completely deleted.¹⁰ Although Ftz in R_6,12 and R_6,13 is activated respectively by I-FFL and combinative signaling module with Hunchback as an input source, Ftz in R_6,12 and R_6,13 is respectively negatively regulated and does not regulate eve. Therefore, we suggest that C-FFL, I-FFL and combinative signaling module are respectively important in activating speedy responses in R_4,11, R_4,12 and R_7,11, activating a delayed response in R_7,13 with the ability of noise filtering and activating a delayed prolonged response in R_3,13.

Figure 5.

Coherence and incoherence feedforward loops of 3-DEST dynamic gene/protein interaction network. (A) According to the rule that each of the regulation relationships of FFLs must exist in at least four neighboring spatial regions, parts of gene/protein interaction network (left) in R_3,2, R_3,3, R_4,1 and R_4,2 are examples of feedforward loops, and can be redrawn as C15 (right). (B) From the above rule, we find the network motifs, i.e. 25 C-FFLs (C1∼C25) and 18 I-FFLs (I1∼I18), for the cooperation of transcription regulations with diffusions in early embryogenesis. The color bars denote diffusions, which are the same as those in Figure 4. A clearer figure is available online at the website, http://www.ee.nthu.edu.tw/bschen/Drosophila_Fig5.pdf.

Discussion and Conclusion

In this study, we are the first to combine mRNA dynamic equation with protein dynamic equation using spatio-temporal model to construct the gene/protein interaction network to investigate the gene/protein regulatory mechanisms of eve stripe formation in the early development of Drosophila. However, there are still three mechanisms of concern in Drosophila embryogenesis, i.e. protein-protein interactions, translation regulations and epigenetic regulations. In a recent study, protein-protein direct interactions are not found between the 14 early development-related TFs of Drosophila embryo,⁵⁷ although there may exist some interactions which require a co-factor(s). For example, Bicoid has self-inhibitory property which requires a co-factor(s), and the binding site at the N-terminal region of Bicoid is evolutionarily conserved.⁵⁸ However, the understanding of protein–protein interactions via a co-factor(s) is limited. Moreover, cooperative bindings through sigmoid function have been implicitly concerned in previous models.³⁸ However, since the prior information of cooperative bindings in early embryogenesis is also limited, cooperative binding is not considered in our model. If the information of cooperative binding is most available, cooperative bindings can be considered easily as regulation candidates in the 3-DEST model, i.e. the cooperation regulation $\sum _{j,k}{\beta }_{ijk}f(Y_j(t,x,y))f(Y_k(t,x,y))$ could be considered in Eq. (1). In addition, there are two translation regulations of concern in early embryogenesis.⁵⁹ The first is Bicoid which binds to maternal caudal to repress its translation,^60,61 and the second is Nano which binds to the nanos response element (e.g. Pumilio) located within the 3’ untranslated region of maternal hunchback and then results in maternal hunchback, which cannot be translated.^62–64 Since the understanding of translation regulations is limited so far, translation regulations are not yet included in the stochastic 3-DEST dynamic model yet. Finally, epigenetic regulations, such as DNA methylation, histone modification and RNAi, are able to play important roles in the regulation of gene expression, but they always interact to accomplish their responsibilities. Combinations of several epigenetic regulations conduct complex silencing such as chromosome inactivation and gene imprinting. For example, during Drosophila embryogenesis the proteins of the trithorax (trxG) and Polycomb groups (PcG) modify chromatin via interacting with chromosomal elements, Cellular Memory Modules (CMMs). A nearby gene can be continuously transcribed through mitotic cell division and meiosis by a switched activated state of CMMs during Drosophila embryogenesis. Thus, CMMs could affect the patterning of cells by the transcriptional control of genes involved in embryonic patterning. In conclusion, trxG and PcG confer epigenetic regulations for different binding affinities of transcription regulation, i.e. trans-effect, that result in embryonic patterning throughout Drosophila embryogenesis.^65–67 In the 3-DEST model, the space-variant parameters of regulatory abilities β_ij(x, y) and basal levels of protein generation ϖ_j(x, y) have implied the affection of epigenetic regulations on transcription regulations throughout eve stripe patterning of Drosophila embryogenesis. An example is shown in Table 1. As seen in N = 40, 41, 42 and 44, epigenetic regulation of Hairy, which has been speculated by⁶⁸ in the terminal system of the larvae, is probably identified that Hairy is encoded to transcriptionally regulate eve in R_2,22 in eve stripe formation.

In early embryogenesis, diffusion mechanism is needed not only for maternal genes but also for gap genes and pair-rule genes to regulate their target genes in the neighboring spatial regions, which can determine the roles of TFs in each region, i.e. donor/acceptor. Without the dynamic space-time model, the dynamics of TFs’ diffusions may not be easily observed from a system point of view, especially in 2-D space. The contributions of this study include the following. (1) Construction of a stochastic 3-DEST dynamic model for gene/protein interaction network which not only contains the concentration-dependent transcriptional abilities but also includes six stochastic processes to mimic the spatio-temporal dynamic interplay among the target genes and their regulatory TFs at the early embryonic stage (i.e. the following six processes (i) protein synthesis, (ii) protein decay, (iii) mRNA decay, (iv) protein diffusion, (v) transcription regulations, and (vi) autoregulation are involved in our dynamic model). (2) Utilization of the AIC to refine the stochastic 3-DEST dynamic model for gene/protein interaction network via pruning the insignificant transcription regulations in each spatial region. (3) Findings of transcription regulations in the seven eve stripes in the stochastic 3-DEST gene/protein interaction network. (4) Validating of the identified gene/protein interaction network by literature reference with the wet experiments of gene mutations. (5) Inference of transcription regulations and diffusion mechanisms for playing a cooperative role in the creation of FFLs to build eve stripes by speedy responses, delayed responses with the ability of noise filtering and delayed and prolonged responses. For the possible experimental validation of the feedforward loops (FFLs) in 3-DEST dynamic gene/protein interaction network, biologists can follow the similar experimental design in⁶⁹ and.^{9,10,43,45,46} For example, if the two FFLs, 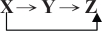and are considered, biologists can examine gene Z’s expression in the corresponding region found in Figure 5 of cellular blastoderm wild-type and Y⁻ embryos by filtered flu-orescence imaging after immunoperoxidase staining with polyclonal antibodies specific for Z. By comparing gene Z’s expression in wild-type with Y⁻ embryos, the suggested FFLs in Figure 5 can be validated. In the future, the proposed spatio-temporal dynamic model and construction algorithm can be extended to gene/protein network construction of different biological phenotypes, which depend on compartments, especially in early embryonic development, e.g. post-natal stem/progenitor cell regulation and differentiation, differentiation of Hematopoietic stem cells (HSCs), the segmentally modulated Hox expression patterns and patterning of the wing in Drosophila development.

However, one of the weaknesses in system identification is the increase in computation burden due to the use of the AIC method. Because one of our main purposes is to extract the significant transcription/translation regulations via pruning the insignificant transcription/translation regulations by using the AIC method, we use an explicit scheme with some stability constraints on the parameters to construct and then refine the gene/protein interaction network. Additionally, computation complexity will be increased, when the spatial regions are precisely specified. Moreover, a plenty of spatio-temporal data are needed in parameter estimation of the 3-DEST model. Although we know that eve stripes of the Drosophila embryo is probably not just built by the 14 early development-related genes, it is not a problem to estimate a more complicated dynamic regulatory network by the proposed method if much more mRNA and protein data are available in the future.

Appendix I: Reconstruction of Unavailable Data by Neural-Network Learning

Because there are some deficiencies in the mRNA data, recovery of these missing data is needed when the data are used for system identification. For the deficiencies of mRNA data, a back-propagation NN training method is employed to reconstruct them. Three classes of genes, i.e. maternal genes, gap genes, and pair-rule genes, into which the 14 early development-related genes are divided, are utilized for the reconstruction of these unmeasured data in their classes of genes, individually. For each data reconstruction process, we individually train and reconstruct these data in each class of genes along the A-P axis, since the protein and mRNA data of each class of genes along the A-P axis are roughly similar (Fig. 2).³ Note that the downstream class of genes with missing mRNA data is reconstructed by the upstream class of genes via the back-propagation NN training method. The training methods, i.e. Broyden, Fletcher, Goldfard and Shanno (BFGS), Levenberg-Marquardt, Powell-Beale Restarte, Polak-Ribiere, Fletcher-Reeves, and Rprop, have been employed to test the performance of data reconstruction. In this study, NN combined with the BFGS method is used for training and simulating the unmeasured mRNA data,⁷⁰ because the NN plus BFGS method has the best performance in our tests (data not shown). In order to obtain an optimal NN training results, we maximize the output correlations and minimize the training errors in the training processes. A few of the unmeasured protein data points are also reconstructed by the same learning and simulating processes. For example, if the mRNA data of gene A is unknown, a back-propagation NN is trained by the protein data of the upstream class of gene A as input and the protein data of gene A as output. Then the mRNA data of gene A can be simulated by the mRNA data of the upstream class of gene A through the well-trained back-propagation NN. After these missing data are simulated, the parameter estimation for the system identification of stochastic 3-DEST gene/protein interaction network model in Eq. (1) or Eq. (2) is introduced in the following section.

Figure 2.

Normalized mRNA and protein expressions. Solid line and dashed line denote protein and mRNA expressions, respectively. The expressions of knirps (cyan line), krüppel (green line) and giant (black line) are plotted in time profiles.

Appendix II: Stability of Discrete 3-DEST Model

Lemma 1⁷¹

Let $X(k,l,m)=g_1^k{e}^{il\Phi }{e}^{im\Phi }$ and $Y(k,l,m)=g_2^k{e}^{il\Theta }{e}^{im\Theta }$ where X(k, l, m) ∈ Ω_x : = {X_i(k, l, m)} and Y(k, l, m) ∈ Ω_y := {Y_j(k, l, m)} for i, j + 1, 2, ... 14 in Eq. (2).

An one-step finite difference scheme (with constant coefficient) is stable if and only if |g₁(Φ)| ≤ 1, |g₂(Θ)| ≤ 1 and g₁(Φ) and g₂(Θ) both are independent of l and m.

Substituting $X(k,l,m)=g_1^k{e}^{il\Phi }{e}^{im\Phi }$ and $Y(k,l,m)=g_2^k{e}^{il\Theta }{e}^{im\Theta }$ in Eq. (2), we obtain $g_1^{k+1}{e}^{il\Phi }{e}^{im\Phi }=(1-a_{l,m})g_1^k{e}^{il\Phi }{e}^{im\Phi }$ and

$$\begin{array}{l}{g}_2^{k+1}{e}^{il\Theta }{e}^{im\Theta }=c_{l,m}{g}_2^k{e}^{il\Theta }{e}^{im\Theta }+{\rho }_{l,m}[(g_2^k{e}^{i(l-1)\Theta }{e}^{im\Theta }\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-2g_2^k{e}^{il\Theta }{e}^{im\Theta }+g_2^k{e}^{i(l+1)\Theta }{e}^{im\Theta })/h_x^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+(g_2^k{e}^{il\Theta }{e}^{i(m-1)\Theta }-2g_2^k{e}^{il\Theta }{e}^{im\Theta }\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+g_2^k{e}^{i(l+1)\Theta }{e}^{i(m+1)\Theta })/h_y^2].\end{array}$$

We can obtain g₁ = 1 – a_l,m and g₂ = c_l,m – 4ρ_l,m ( $h_x^{-2}+h_y^{-2}$) sin² (Θ/2).

Thus, according to Lemma 1, the scheme is stable if and only if |1 – a_l,m| ≤ 1 and

$$\{\begin{array}{cc}|c_{l,m}-4{\rho }_{l,m}(h_x^{-2}+h_y^{-2})|\le 1& \text{if} {\rho }_{l,m}<0\\ \left|c_{l,m}\right|\le 1& \text{if} {\rho }_{l,m}\ge 0\end{array}.$$

Appendix III: Procedure of Stability Constrained Estimation

The stability constrained estimation of parameters can be performed by a Matlab function, lsqlin.

A procedure for the parameter estimation is given as follows:

1. First, assume ρ_j,l,m ≥ 0 with the constraint |c_j,l,m| ≤ 1 for j = 1, 2, ... 14 in Eq. (2) and estimate the parameters, {d̂_i,l,m, ŵ_j,l,m â_i,l,m ĉ_j,l,m ρ̂_j,l,m b̂_ij,l,m}, under the constraints, d_i,l,m ≥ 0, w_i,l,m ≥ 0, |c_j,l,m| ≤ 1 and |1 – a_j,l,m| ≥ 1.

2. Change the assumption of ρ_j,l,m according to the estimated ρ̂_j,l,m of the previous step, and estimate the parameters under the constraints, d_i,l,m ≥ 0, w_j,l,m ≥ 0, |1 – a_j,l,m| ≤ 1 and |c_j,l,m| ≤ 1 if the diffusion coefficient estimated by the previous step for some j (i.e. some TFs) is non-negative, ρ̂ ≥ 0. But otherwise the constraints of the other TFs with negative diffusion coefficients, ρ̂_j,l,m < 0, estimated by the previous step are changed to be d_i,l,m ≥ 0, w_j,l,m ≥ 0, |1 – a_j,l,m| ≤ 1 and $\left|c_{j,l,m}-4{\rho }_{j,l,m}(h_x^{-2}+h_y^{-2})\right|\le 1$

3. Stop and obtain the estimated parameters if the sign of the estimated ρ̂_{j,l,m ,} for each j is not changed anymore in the last two estimation steps, otherwise go back to step 2.