High skill in low-frequency climate response through fluctuation dissipation theorems despite structural instability

Abstract

Climate change science focuses on predicting the coarse-grained, planetary-scale, longtime changes in the climate system due to either changes in external forcing or internal variability, such as the impact of increased carbon dioxide. The predictions of climate change science are carried out through comprehensive, computational atmospheric, and oceanic simulation models, which necessarily parameterize physical features such as clouds, sea ice cover, etc. Recently, it has been suggested that there is irreducible imprecision in such climate models that manifests itself as structural instability in climate statistics and which can significantly hamper the skill of computer models for climate change. A systematic approach to deal with this irreducible imprecision is advocated through algorithms based on the Fluctuation Dissipation Theorem (FDT). There are important practical and computational advantages for climate change science when a skillful FDT algorithm is established. The FDT response operator can be utilized directly for multiple climate change scenarios, multiple changes in forcing, and other parameters, such as damping and inverse modelling directly without the need of running the complex climate model in each individual case. The high skill of FDT in predicting climate change, despite structural instability, is developed in an unambiguous fashion using mathematical theory as guidelines in three different test models: a generic class of analytical models mimicking the dynamical core of the computer climate models, reduced stochastic models for low-frequency variability, and models with a significant new type of irreducible imprecision involving many fast, unstable modes.

The climate is an extremely complex, coupled system involving significant physical processes for the atmosphere, ocean, and land over a wide range of spatial scales, from millimeters to thousands of kilometers, and time scales, from minutes to decades or centuries (1, 2). Climate change science focuses on predicting the coarse-grained, planetary scale, longtime changes in the climate system due to either changes in external forcing or internal variability, such as the impact of increased carbon dioxide (3). For several decades, the predictions of climate change science have been carried out with some skill through comprehensive computational, atmospheric, and oceanic simulation (AOS) models (1–3) that are designed to mimic the complex, physical, and spatio-temporal patterns in nature. Such AOS models, either through lack of resolution due to current computing power or through inadequate observation of nature, necessarily parameterize the impact of many features of the climate system such as clouds, mesoscale and submesoscale ocean eddies, sea ice cover, etc. There are intrinsic errors in the AOS models for the climate system and a central scientific issue is the effect of such model errors on predicting the coarse-grained, large-scale, longtime quantities of interest in climate change science. The potentially high skill of systematic algorithms based on the fluctuation dissipation theorem (FDT), whereby climate change projections are made on the basis of statistics calculated from the present climate (4–15), is the approach advocated to address these issues in this paper. There are important practical and conceptual advantages for climate change science when a skillful FDT algorithm can be established for suitable low-frequency variables in a climate model. The linear statistical response operator produced by FDT can be utilized directly for multiple climate change scenarios, multiple changes in force and other parameters, and inverse modelling directly without the need for running a complex climate model in each case, often a computational problem of overwhelming complexity. In particular, FDT has been demonstrated to have high skill for the mean and variance responses in the upper troposphere for changes in tropical heating in a prototype atmospheric, general circulation model and when utilized for complex, multiple force, and inverse modelling issues of interest in climate change science (8, 9).

In a recent, stimulating article, McWilliams (16) has termed the impact of the errors in AOS models as the change in the probability density functions (PDFs) in the climate equilibrium compared with the true PDFs from nature as “irreducible imprecision.” The main hypothesis advocated in ref. 16 is that structural instability is the main source of irreducible imprecision for climate change science. In other words, small changes in AOS model parameters or formulation result in significant differences in the longtime PDFs or the phase-space attractor and these can effect climate change projections. Virtually all physical systems have structural instability. For example, the dynamical core of AOS models can be written abstractly (7, 17) as the quadratic nonlinear system for a vector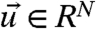

[1]

with α(t) the damping or dissipation coefficient, 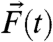the external forcing, L a skew-symmetric matrix representing rotation, and 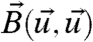a quadratically nonlinear operator arising from nonlinear advection. Physical conservation of energy principles (7, 17) dictate that 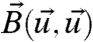satisfies

[2]

and this is an immediate source of structural instability since AOS models often do not satisfy A and B due to finite mesh discretization errors (16). In fact, the principal example utilized (16) to demonstrate irreducible imprecision and structural instability is the special case of 1 with and α(t), a constant diffusion operator involving decaying two-dimensional turbulence (17, 18). The other primary example discussed (16) regarding irreducible imprecision and structural instability is Lorenz’s famous three-dimensional chaotic system (19) where the attractor properties are known to exhibit sensitive dependence on small changes in the coefficients of this model.

The main point of this paper is to demonstrate that systematic algorithms for low-frequency climate response based on FDT have significant, high skill for coarse-grained climate change projections despite structural instability and various types of irreducible imprecision. Simplified models with both firm mathematical underpinning and some relevance to central issues in climate change science, as well as (16), are utilized here to demonstrate this high skill of judicious FDT algorithms. There is no doubt that comprehensive AOS models in regimes to model realistic climate science are turbulent, chaotic, dynamical systems, but the nature of their chaotic dynamics is radically different from Lorentz’s famous three-equation model (19), which is weakly mixing with one unstable direction on the attractor and high symmetry. In contrast, realistic AOS models (7, 10, 12, 20) have high-dimensional, unstable manifolds, mix strongly with exponential decay of correlations, and have coarse-grained PDFs in the climate equilibrium that are smooth and often nearly Gaussian (12, 20–23). Furthermore, the coarse-grained, large-scale dynamics often acquire an intrinsic stochastic noise due to interaction with rapidly changing, small-scale variables (20, 24–26). In climate change science, the main interest involves predictions of the coarse-grained, large-scale climate impacts and the above effects in turbulent, large-dimensional, dynamical systems ameliorate the impact of structural instability and irreducible imprecision for the coarse-grained, large-scale variables. This has been established in recent literature. Two of the authors (10, 12) have developed a unique, blended response algorithms for FDT that explicitly demonstrate, for a wide range of forcings, the high skill of linear response theory despite structural instability for large-dimensional dynamical system models with the form in 1 of relevance to atmospheric science, such as the L-96 model (10, 27), and truncated barotropic flow on the sphere with realistic orography (12). With this background, we outline the remainder of this paper. First, we discussed the general FDT framework as background. Then, a general family of mathematically exact statistical solutions for the general models in 1 and 2 were utilized to explicitly demonstrate the high skill of FDT in predicting climate change despite explicit structural instability. The ameliorating effects of stochastic noise, despite deterministic structural instability for FDT climate change projections, were discussed by developing analytic formulas for FDT in a scalar, nonlinear stochastic model that arises as the canonical, scalar model for low-frequency, atmospheric or oceanic regimes (28). Then, the high skill of FDT for low-frequency climate variables is explicitly demonstrated for a toy AOS model that acquires a different type of irreducible imprecision through a large-dimensional space of short-time instabilities representing gravity waves or moist convection. The paper ends with a brief discussion.

General Properties of FDT

Consider a dynamical system with noise like an AOS model written as

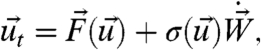[3]

for 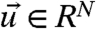, where σ is an N × K noise matrix and 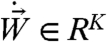is a K-dimensional white noise. We assume that 3 is written in the Ito sense so that the associated Fokker–Planck equation for the probability density 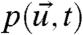is

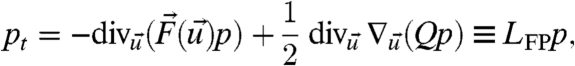[4]

where Q = σσ^T. The climate state associated with 3 is the probability density 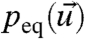that satisfies L_FPp_eq = 0 and the climate statistics of some functional 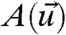are determined by

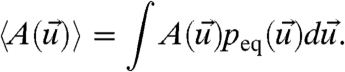[5]

Next, perturb the system in 3 by the change 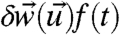, that is, consider the perturbed equation

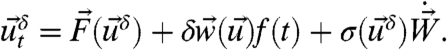[6]

Calculate perturbed climate statistics by utilizing the Fokker–Planck equation associated with 6 with initial data given by the unperturbed climate equilibrium. Then, FDT (7) states that if δ is small enough, the leading order correction to the statistics in 5 becomes

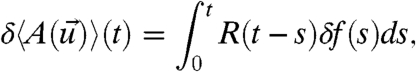[7]

where R(t) is the linear response operator that is calculated through correlation functions in the unperturbed climate

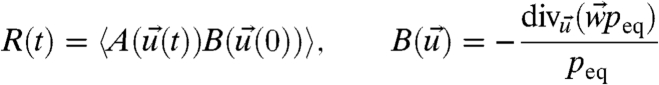[8]

The noise in 3 is not needed for FDT to be valid but, in this form, the equilibrium measure needs to be smooth.Tthere is an alternative formulation of FDT for σ ≡ 0 in 3 that avoids this smoothness requirement or even explicit knowledge of 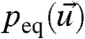and is useful for developing short-time FDT algorithms based on a linear, tangent model (10–13). There are useful generalizations of FDT that apply to ensemble predictions of time-dependent systems and even allow for noise perturbations to assess model error (14, 15). FDT does not require any linearization of the underlying dynamics in 3. One major stumbling block in applying FDT directly in the form in 8 is that the equilibrium measure 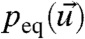is not known exactly. In the quasi-Gaussian (qG-FDT) approximation, one utilizes an approximate Gaussian equilibrium measure, 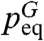, with mean and covariance matrix that match those in the climatology, p_eq. One then calculates

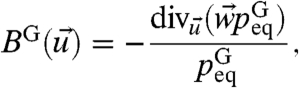[9]

and replaces 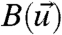by 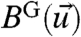in 8 in the qG-FDT (4, 6–10, 12). The correlation in 8 is calculated, usually, by integrating the original system in 3 over a long trajectory or an ensemble of trajectories covering the attractor for shorter times assuming mixing and ergodicity for 3.

Prototype Models with Transparent Structural Instability and High Skill of the FDT Climate Response

The unperturbed model climate system that is studied here is generated by the undamped unforced version of 1 so that α(t) ≡ 0 and 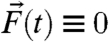. There are many examples of inviscid geophysical models satisfying 1 without damping and forcing as well as the structural conditions in 2. These include multilayer, quasi-geostrophic models with topography in pseudo-energy variables on the sphere or with periodic geometry (17) as well as important test models such as the Lorenz-96 model, the truncated Burgers-Hopf, and Kruskal-Zabusky models (7). Numerical experiments show that, with a sufficiently high number of degrees of freedom, all these truncated, undamped, unforced models are turbulent, dynamical systems that are strongly mixing (7, 17). The structural properties in 2 guarantee (17) that the energy 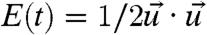is conserved for solutions of 1 and also that the climatology of this system is a Gaussian invariant measure, 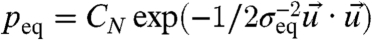where σ_eq is the climate variance. We claim that this climatology provides a transparent example of structural instability as defined in ref. 16 with respect to changes in the damping coefficient δα(t) that is switched on at time t = 0 and can have any magnitude and form. By using 2 and the radial symmetry of the unperturbed climate as the initial data, the Fokker–Planck equation associated with the perturbation of damping in the present setting from 6, simplifies for radially symmetric solutions and becomes

[10]

The equation in 10 is easily solved explicitly and yields the exact statistical solution

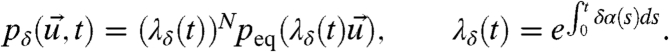[11]

The explicit, statistical perturbations, by damping of the climatology, yield a Gaussian statistical solution with variance :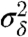

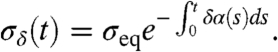[12]

We claim that these perturbations transparently manifest structural instability of the unperturbed climate. First, if there is any small, fixed value of δ so that 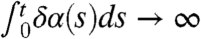as t → ∞, for example, if δα is a positive constant, then the variance σ_δ(t) tends to zero with time and the new equilibrium climate has the trivial attractor concentrated at zero with no climate variability. On the other hand, if there is enough amplification so that 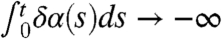, the variance σ_δ(t) grows without bound as time increases so that there is climate runaway. These two radically different climate change scenarios, arising from small perturbations of a coefficient, provide unambiguous and transparent, explicit examples of structural instability of the climate state (16). Only in the case when 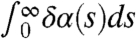is finite does a finite climate state with nontrivial variability emerge.

The crucial issue addressed next is whether FDT has high skill in predicting the response in this setting with transparent structural instability. For changes in dissipation, 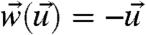in 6 and with the Gaussian equilibrium measure, p_eq, the linear response operator from 8 is given by

[13]

The shorthand notation for averages over the unperturbed equilibrium measure from 5 has been utilized in 13. Functionals of interest in climate change science include the mean, 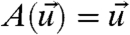, the variance, 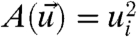, and the total variance, 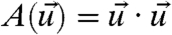. The mean response to changes in dissipation is the integral of a triple correlation. This is, essentially, the same functional needed as the linear response of the variance to a change of external forcing. Detailed numerical simulations (7) with the Kruskal–Zabusky model confirm the rapid decay of the integral of such triple correlations and the excellent skill of FDT despite structural instability. On the other hand, the total variance, 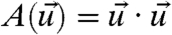, projects directly onto the key mechanism of structural instability in the present models. Recall that in the unperturbed system, energy is conserved so that 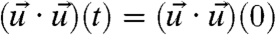and the linear response operator for the total variance to changes in dissipation from 13 becomes a constant, 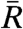, independent of time,

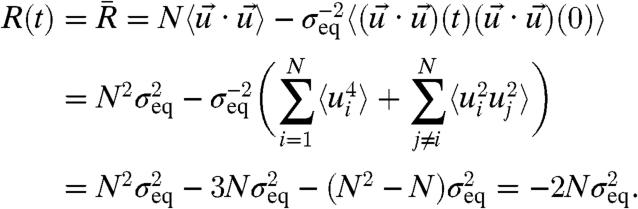[14]

In the penultimate equality in 14, we have used the relation 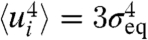valid for a Gaussian random variable. With 7 and 14, the linear response predicted by FDT of the total variance to the changes in dissipation is given by

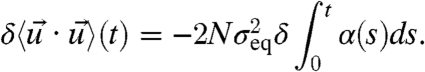[15]

Note the high skill of FDT in predicting the distinct climate change scenarios: If 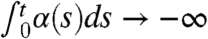, FDT predicts climate runaway whereas, if 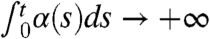, FDT predicts continuing decrease in variance in the climate. Furthermore, if 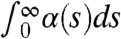is finite, FDT predicts a finite climate change. In fact, the direct, nonlinear ideal response can be calculated using 11 and compared with 15. This nonlinear ideal response is

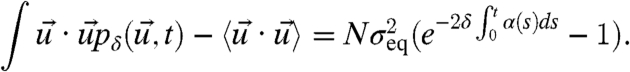[16]

The leading order expansion of the nonlinear response 16 is exactly the prediction from FDT. This provides quantitative evidence of the high skill of FDT in predicting the manifestations of structural instability in the present models. The models discussed here are quite similar to the primary example of two-dimensional decaying turbulence (16) with one important difference. In decaying, two-dimensional turbulence it can be proved with full mathematical rigor (17) that the attractor is always trivial and concentrates at zero for a wide range of dissipative mechanisms. The primary example from (16) describes irreducible imprecision in the approach to a trivial attractor rather than structural instability in a nontrivial attractor as presented here.

Stochastic Models for Low-Frequency Climate Dynamics, Structural Instability, and FDT

There is recent interest in deriving reduced, stochastic models for climate and extended-range weather prediction. An attractive property of atmospheric, low-frequency variability is that it can be efficiently described by just a few large-scale, teleconnection patterns (20–22, and references therein). These patterns exert a huge impact on surface climate and seasonable predictability. An application of the blended response algorithm for FDT to the climate change of the mean and variance of such low-frequency, teleconnection patterns with high skill has been developed recently in a barotropic model on the sphere with realistic orography (12). Reduced stochastic models are an attractive alternative for climate sensitivity studies via FDT (15) because they are computationally much more efficient than state-of-the-art climate models and have been shown to have comparable long-range prediction skill (29, 30). Systematic, mathematical, stochastic-mode reduction strategies (24–26) have been utilized recently to develop normal forms for reduced, stochastic climate models (28). The one-dimensional, normal form was applied in a regression strategy in (28) for data from a prototype AOS model (20) to build one-dimensional stochastic models for low-frequency patterns such as the North Atlantic Oscillation (NAO) and the leading principal component (PC-1) that has features of the Arctic Oscillation. These one-dimensional, normal form stochastic models are utilized to show the high skill of FDT algorithms despite deterministic, structural instability to both changes in external forcing and dissipation parameters. Also illustrated below is another facet of irreducible imprecision where higher order statistics of the mean climate substantially effect the FDT response to the changes in the dissipation parameter.

The canonical, one-dimensional stochastic models for low-frequency variability (28) are given by the scalar stochastic equation

[17]

with corresponding Fokker–Planck equation

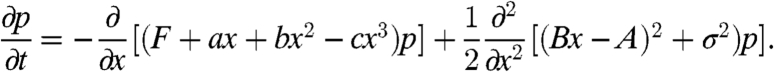[18]

As developed (28), the Fokker–Planck equation in 18 has an explicit, smooth equilibrium distribution p_eq(x) with a Gaussian tail provided that the physically imposed restriction, c > 0, is satisfied. In this section, the notation x rather than u is utilized to emphasize the scalar nature of the present problem. The explicit form of the PDF, p_eq(x), will allow us to calculate explicit forms of the ideal response operator to perturbations in forcing, F, or the dissipation parameter, a, as well as explicit analytic expressions for the FDT linear response operator from 7, 8, and the linear response operator for qG-FDT in 7 and 9 that utilizes only the mean and variance statistics of the unperturbed climate in an approximation.

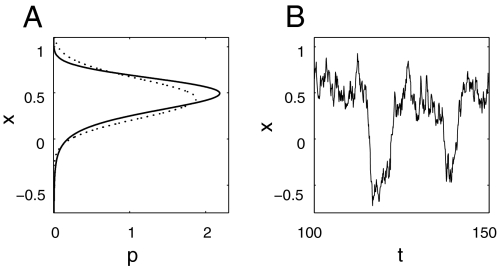
One of the striking features of atmospheric general circulation models is that there are different regimes of low-frequency behavior despite uni-modal, nearly-Gaussian PDFs for the low-frequency variables (21–23, 29, 30). The stochastic models from 17 are studied here in parameter regimes where this behavior occurs and in the vicinity of where there is deterministic, structural instability. The deterministic ODE associated with 17 is given by 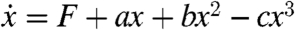. If b and c are fixed with c < 0, the two-dimensional forcing dissipation parameter space, (a,F), for the ODE is naturally divided into two separate regions of dynamical behavior with either one stable equilibrium or two stable and one unstable equilibria. The dividing curve, B, between these two different types of behavior is clearly a boundary with structural instability and is determined analytically by the formula F = -ab/(3c) - 2b³/(27c²) ± 2c(a/(3c) + b²/(9c²))^3/2. In Table 1, we list five different cases of 17 that are studied below. The first three cases correspond to a single stable equilibrium, S, the boundary of structural instability, B, and the region with three equilibria, U. The next two parameter values for 17 arise from the physical regressed data for PC-1 and the NAO (28) that have been discussed earlier. Note that the additive noise variance in Table 1 for the first three cases has a comparable magnitude to the noise variance in the regression plots for PC-1 and NAO for the low frequency data. In Fig. 1, the uni-modal PDF in the case S is shown as well as a piece of the time series that shows the distinct regimes of behavior (29, 30) despite the nearly-Gaussian statistics in the PDF that has a moderate skewness. The PDFs for both B and U as well as the respective time series show similar behavior. A key issue here is the skill of the FDT algorithm in this regime of deterministic structural instability. An advantage of the present models is that the ideal response to the changes in forcing or dissipation can be calculated analytically through simple, quadrature involving moments of PDFs and their derivatives with respect to parameters. In calculating linear response theory, as predicted by FDT, we consider the functionals A_M(x) = x and A_Var(x) = (x - 〈x〉)² that correspond to the mean and the variance response. In 6, the perturbation in the external forcing, F, leads to the functional w_F(x)p = -∂p/∂x and the perturbation in the dissipation, a, correspond to the functional w_a(x)p = -∂(xp)/∂x. Using the explicit PDF from (28) required in 8 yields

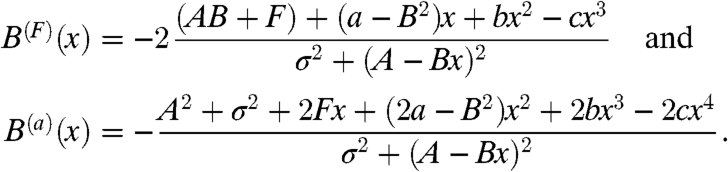[19]

For the approximate qG-FDT, it is straightforward to calculate B^G in 9. The FDT and qG-FDT responses are computed by integrating a long-time series using the second-order Milstein method and computing the statistics “on the fly” (7). The comparison of the ideal response and the responses predicted by both the FDT algorithm and qG-FDT are reported in Table 2 for the response of the mean and variance to the changes in forcing or dissipation. First, the deterministic structural instability plays no role and there is high skill of the FDT response compared to the exact ideal response for the mean and variance to both changes in dissipation and forcing for all five examples. The reader should note that the rare, high-percentage errors in Table 2 for S,B, and U are a reflection of small values in the ideal response that are remarkably well captured by FDT. For the physical low-frequency patterns, PC-1 and NAO, the FDT response has high skill with errors of, at most, a few percent for all four response scenarios. The qG-FDT has high skill for the mean response to the change in forcing and in all other cases except the mean response to changes in dissipation for PC-1, the variance response to the change in forcing for both PC-1 and the NAO, and the variance response to the change in dissipation for NAO. The skill of qG-FDT is much poorer for the cases S, B, and U. These results all indicate that the subtle non-Gaussian statistics in the climate (15) as reflected by the skewness in the equilibrium climate are needed to get an accurate low-frequency climate response. This is another instance of the impact of irreducible imprecision for the present, idealized setting for climate change science. As shown here and in other applications to climate science, the qG-FDT algorithms often have very high skill for the mean response to the change in forcing (8, 9, and 12) even when there are significant non-Gaussian effects in the PDFs (15).

Table 1.

Parameters and corresponding skewness and flatness for model 17, A = 0 and B = 0 for all five cases

Case	F	A	B	C	σ	Skew	Flat
S	1.8	0	−5.4	4		−1.35	8.56
B	2.0	0	−6.0	4		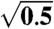−1.50	10.8
U	2.2	0	−6.6	4		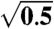−2.05	17.5
PC-1	−0.005	−0.018	0.006	0.003	0.226	0.27	2.72
NAO	−1.44	−0.55	−0.073	0.003	0.253	0.21	3.11

Fig. 1.

(a) Solid line shows the equilibrium PDF for system 17 with parameters from case S from Table 1, dotted line shows the Gaussian PDF with the same mean and variance as the equilibrium PDF; (b) sample trajectory with distinct regimes of behavior.

Table 2.

Ideal, FDT, and qG-FDT mean and variance response to the change in forcing or dissipation with the corresponding percentage errors for the five cases given in Table 1

	Case	Ideal	FDT	qG-FDT	FDT % error	qG-FDT % error
	S	0.1814	0.1827	0.3197	0.70	76
	B	0.1621	0.1633	0.3425	0.72	111
	U	0.1555	0.1591	0.8655	2.29	457
	PC-1	40.54	40.52	41.84	0.05	3.21
	NAO	5.41	5.46	5.51	0.93	1.84
	S	0.0533	0.0536	−0.0937	0.57	276
	B	0.0486	0.0499	−0.1639	2.55	437
	U	0.0401	0.0334	−0.8988	16.71	2339
	PC-1	6.13	6.66	16.91	8.69	176
	NAO	−71.00	−71.16	−71.37	0.22	0.51
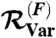	S	−0.0522	−0.0540	−0.2331	3.4	346
	B	−0.0490	−0.0463	−0.3218	5.5	557
	U	−0.0630	−0.0702	−1.2797	11.5	1932
	PC-1	11.23	11.24	16.02	0.08	42
	NAO	0.470	0.473	0.715	0.72	52
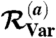	S	0.0083	0.0071	0.157	15	1798
	B	0.0104	0.0107	0.291	3.1	2714
	U	0.0207	0.0304	1.56	47	7431
	PC-1	36.25	36.16	34.30	0.23	5.4
	NAO	−5.185	−5.186	−8.1	0.03	56

Validity of the FDT Response of Climate Variables Despite Irreducible Imprecision at Fast Scales

We provide a definition of irreducible imprecision as applied to the linear response framework, outline main factors affecting irreducible imprecision, and design a test setup where the irreducible imprecision is explicitly controlled through a time-scale separation parameter in a model with large-scale, “climate” variables and small-scale, fast, “unresolved” variables. We demonstrate a remarkable precision of the linear response for the climate variables despite irreducible imprecision from the fast variables. The linear response operator from 7 can be computed using both the FDT formulas in 8 and by a series of direct perturbations of a large statistical ensemble of solutions (6, 7, 10–12) with different directions and magnitudes of the small, forcing parameter, in which case R is called the “ideal”, that is, directly measured linear response operator that is used to verify the response computed via an FDT formula. Clearly, due to the fact that the ideal response is computed through direct perturbations of the nonlinear dynamics, it can stay “linear” only for a limited time that is determined by the extent to which the linearized dynamics around the unperturbed solution remain valid that is, in turn, governed by the Lyapunov characteristic time of the dynamical system. Thus, the time of validity of the ideal response is proportional to the product of the Lyapunov characteristic time, T_Lyap, and the logarithm of the magnitude of the external perturbation 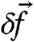with a negative sign,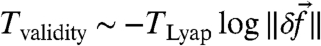, where 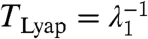, with λ₁ being the first Lyapunov exponent. Thus, for a fixed validity time of the ideal response (that for convenience we set to 1 here), the magnitude of external perturbations must decrease exponentially with the first Lyapunov exponent, 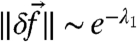. On the other hand, the external perturbation 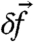cannot be too small due to the natural noise in the statistical ensemble of solutions (6, 7, and 10–12), whose level is inversely proportional to the square root of the ensemble size N. For a fixed perturbation/noise ratio, the size of the ensemble should grow as 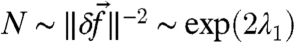. From the computational standpoint, the exponential growth of the ensemble size N places practical limits on the validity time of the ideal response proportional to the Lyapunov characteristic time. There is an operational definition of the irreducible imprecision for linear response:

Definition 1:

The irreducible imprecision for linear response is the practical inability to compute the ideal response beyond time limits determined by the Lyapunov characteristic time, and, as a result, to validate the predictions of FDT response formulas beyond these time limits.

How much of an impact can irreducible imprecision have on the linear response framework? Remarkably, there are known examples of the FDT response predictions, such as the truncated Burgers–Hopf, the Kruskal–Zabusky, the Lorenz 96, and the T21 models (7, 10–12), where irreducible imprecision does not manifest itself due to the fact that the autocorrelation decay times (that govern the active stage of the linear response development) are comparable to the Lyapunov characteristic time and the response is fully developed before the above feature of irreducible imprecision starts having an impact.

On the other hand, contemporary climate models are typically characterized by a set of fast “weather” variables that describe small-scale interactions on a short time scale of a few hours, nonlinearly coupled with the large-scale slow “climate” variables. This setup causes the largest Lyapunov exponents and, consequently, the characteristic Lyapunov time to be extremely short and associated with the fast variables, whereas the response of the mean climate state is tied to the decorrelation times of the slow-climate variables. Therefore, it is likely that the typical time of climate response development will be much longer than the Lyapunov characteristic time, and the irreducible imprecision noted above may potentially have a remarkable impact. To model such a situation, we employ a nonlinear model with time-scale separation explicitly controlled by an external parameter.

Controlled Irreducible Imprecision: A Test Setup

The inviscid full Lorenz 96 (IFL96) model is given by

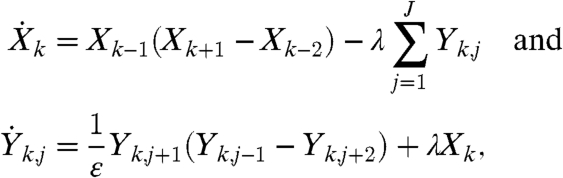[20]

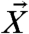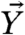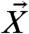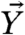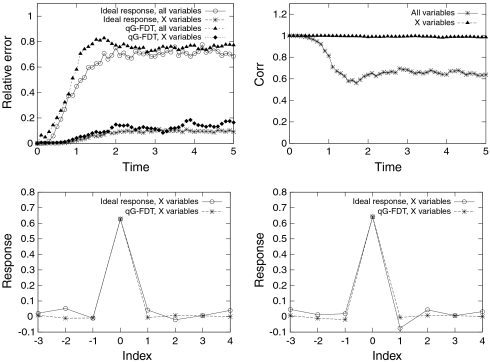
where ε > 0, λ > 0, 1 ≤ k ≤ K, 1 ≤ j ≤ J, and appropriate periodic boundary conditions are utilized (27). The IFL96 model is characterized by two sets of variables: is a set of slow-climate variables of size K and is a set of fast weather variables of size KJ with explicit time-scale separation parameter ε whereas λ is the nonlinear coupling parameter between and . In the current work, we set K = J = 8, so that there are 72 variables in total (8 X_k and 64 Y_kj), and the value of the coupling parameter λ = 1. The IFL96 model in 20 satisfies 2 and preserves the quadratic total energy. The classical Gaussian equilibrium state with zero mean and uniform energy spectrum defines the climate statistical equilibrium (7, 17). As a result, the qG-FDT formula in 7 and 9 is exact for the IFL96 model and the development of the linear response is governed by the decorrelation time. For the value of ε = 0.1, the Lyapunov characteristic time, T_Lyap = 0.1356, whereas the largest correlation time, T_corr = 0.6634. The Lyapunov characteristic time is one order of magnitude shorter than the decorrelation time suggesting that irreducible imprecision should obstruct validation of the linear response prediction for times longer than one. To confirm this claim, in Fig. 2 we show the intrinsic relative errors in the ideal response operator (7, 10–12) and relative errors between the ideal and qG-FDT response operator for the simplest linear response function 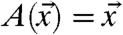that corresponds to the response of the mean state. Observe that the error growth between the ideal and qG-FDT response correlates to a very high extent with the error growth in the ideal response operator that in turn, is governed by the Lyapunov characteristic time (errors start growing after the time interval of roughly T_Lyap = 0.1356 passes). By the time the linear response is fully developed, which is beyond the decorrelation time T_corr ≈ 1, the intrinsic errors in the ideal response operator are about 80%, which is a clear manifestation of irreducible imprecision for the linear response as sketched in the Definition. Additionally, the physical space correlations (7, 17) between the ideal and qG-FDT response operators, show only moderate correlation with value around 0.6.

Fig. 2.

Upper left: errors in the ideal response and between the qG-FDT and ideal response, ε = 0.1 and λ = 1. Upper right: the physical space correlations between the ideal response and qG-FDT for the same regime. Lower left and right: snapshots of the ideal and qG-FDT response operators for X-variables at time t = 2 and t = 4, respectively.

Validity of Linear Response for Climate Variables

We have just demonstrated that irreducible imprecision obstructs the computation of the ideal linear response for the full set of IFL96 variables. However, in practical situations for climate change, one is interested only in the response of the slow-climate variables, with the same set of variables being forced by a change of external parameters. In Fig. 2 we show the errors in both the ideal response operator and between the ideal and qG-FDT response operator, restricted to the 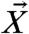(slow climate) variables in both forcing and response. Remarkably, in this case the errors in the ideal response never exceed 12% over the full measured response time interval of five time units (that is about 37 times the Lyapunov characteristic time), whereas the errors between the ideal and qG-FDT response only reach magnitudes of about 20%. In addition, the physical space correlations between the ideal and qG-FDT response operators are about one, which is a perfect correlation. In Fig. 2, we also show two snapshots of linear response operators for the X-variables at times t = 2 and t = 4, both significantly beyond the longest correlation time in the system where one can observe that there is, visually, a good correspondence between the ideal and qG-FDT response operators. This is a vivid demonstration of the fact that irreducible imprecision does not necessarily affect the low-frequency response of the slow-climate variables, while clearly obstructing the computation of the response for the full set of variables.

Conclusions

Recently, it has been suggested (16) that there is irreducible imprecision in comprehensive AOS models that manifests itself as structural instability in the climate statistics and that can significantly hamper the skill of these computer models for climate change projections. A systematic approach to deal with this irreducible imprecision is advocated through algorithms based on FDT.