High-DQE EPIDs based on thick, segmented BGO and CsI:Tl scintillators: Performance evaluation at extremely low dose

Abstract

Purpose: Electronic portal imaging devices (EPIDs) based on active matrix, flat-panel imagers (AMFPIs) have become the gold standard for portal imaging and are currently being investigated for megavoltage cone-beam computed tomography (CBCT) and cone-beam digital tomosynthesis (CBDT). However, the practical realization of such volumetric imaging techniques is constrained by the relatively low detective quantum efficiency (DQE) of AMFPI-based EPIDs at radiotherapy energies, ∼1% at 6 MV. In order to significantly improve DQE, the authors are investigating thick, segmented scintillators, consisting of 2D matrices of scintillating crystals separated by septal walls.

Methods: A newly constructed segmented BGO scintillator (11.3 mm thick) and three segmented CsI:Tl scintillators (11.4, 25.6, and 40.0 mm thick) were evaluated using a 6 MV photon beam. X-ray sensitivity, modulation transfer function, noise power spectrum, DQE, and phantom images were obtained using prototype EPIDs based on the four scintillators.

Results: The BGO and CsI:Tl prototypes were found to exhibit improvement in DQE ranging from ∼12 to 25 times that of a conventional AMFPI-based EPID at zero spatial frequency. All four prototype EPIDs provide significantly improved contrast resolution at extremely low doses, extending down to a single beam pulse. In particular, the BGO prototype provides contrast resolution comparable to that of the conventional EPID, but at 20 times less dose, with spatial resolution sufficient for identifying the boundaries of low-contrast objects. For this prototype, however, the BGO scintillator exhibited an undesirable radiation-induced variation in x-ray sensitivity.

Conclusions: Prototype EPIDs based on thick, segmented BGO and CsI:Tl scintillators provide significantly improved portal imaging performance at extremely low dose (i.e., down to 1 beam pulse corresponding to ∼0.022 cGy), creating the possibility of soft-tissue visualization using MV CBCT and CBDT at clinically practical dose.

INTRODUCTION

During the past decade, electronic portal imaging devices (EPIDs) based on active matrix, flat-panel imagers (AMFPIs) have largely replaced portal film and earlier EPID technologies and have become the gold standard for portal imaging.¹ These AMFPI-based EPIDs, which are referred to as conventional EPIDs in this article, utilize a detector consisting of a phosphor screen (typically 133 mg∕cm² of Gd₂O₂S:Tb) and a Cu plate to detect megavoltage (MV) X rays.² Given the low quantum efficiency (QE) of such detectors at radiotherapy energies (∼2% at 6 MV), the detective quantum efficiency (DQE) of conventional EPIDs is only ∼1%, compared to ∼40%–80% for kV AMFPIs.^{3, 4, 5}

The low DQE of conventional EPIDs constrains the practical execution of volumetric imaging techniques, such as MV cone-beam computed tomography (CBCT)^{6, 7, 8, 9, 10, 11, 12, 13} and cone-beam digital tomosynthesis (CBDT).^{14, 15} These techniques are under examination for providing 3D visualization of soft tissues — information that could help ensure accurateexecution of advanced treatment plans for 3D conformal radiotherapy¹⁶ and intensity modulated radiotherapy (IMRT),¹⁷ in which dose delivery is precisely shaped to the tumor treatment volume.¹⁸ However, due to the low DQE of conventional EPIDs, MV CBCT and CBDT would require high doses to achieve soft-tissue visualization. For example, as reported by Groh et al.¹⁹ in a phantom study, an MV CBCT system using a conventional EPID requires a dose of 32 cGy to delineate electron density differences of ∼4%–5% between soft tissues for a reconstruction slice thickness of 5 mm. In a patient study, Morin et al.⁸ reported that an irradiation of 14.4 MU was needed to visualize soft tissues in the pelvic region. In order to significantly reduce the dose required for MV CBCT and CBDT, it is necessary to greatly improve the DQE of EPIDs.

DQE depends on QE, the modulation transfer function (MTF), and the noise power spectrum (NPS) in the following manner:

$$\text{DQE}\left(f\right)\propto \text{QE}\times \frac{{\text{MTF}}^2\left(f\right)}{\text{NPS}\left(f\right)},$$ (1)

where f is spatial frequency. In order to significantly improve DQE, the most efficient strategy is to greatly increase detector QE, while maintaining or improving MTF and limiting additional noise contributions, such as Swank noise originating from the variation in the X ray to secondary quanta conversion gain.²⁰ For this reason, high-efficiency x-ray detectors have been widely examined. Those detectors that directly detect MV X rays include a 1D arc array of tungsten cavities filled with high-pressure xenon gas,²¹ 2D gas chambers formed by microstructured tungsten spacer plates²² and thick HgI₂ photoconductors.²³ For indirect detection, some of the detectors considered include thick optical fibers detecting Cerenkov radiation,²⁴ 2D polymer matrices filled with Gd₂O₂S:Tb phosphor,²⁵ as well as 1D and 2D crystalline scintillators (e.g., CsI:Tl, Bi₄Ge₃O₁₂, CdWO₄, and ZnWO₄), employing the concept of segmentation.^{26, 27, 28, 29, 30, 31, 32, 33, 34}

A series of theoretical and empirical studies has been previously reported on 2D segmented crystalline scintillators, which consists of matrices of scintillating crystals separated by septal walls to limit the lateral spread of optical photons.^{25, 35, 36, 37, 38, 39, 40} Monte Carlo simulations of radiation and optical transport have suggested that EPIDs employing segmented CsI:Tl and Bi₄Ge₃O₁₂ (BGO) detectors up to 40 mm thick can offer DQE values of up to 29% and 42%, respectively.^{36, 38} Such significant improvement in DQE should allow acquisition of MV CBCT images with soft-tissue visualization at doses as low as ∼3 cGy.³⁸ In a previous investigation, we reported that an EPID employing a 40 mm thick, segmented CsI:Tl scintillator provided a measured DQE of ∼22% at zero spatial frequency with a 6 MV beam.³⁷ However, at higher spatial frequencies, the MTF and DQE performance of this initial prototype exhibited significant falloff due to insufficient optical isolation between scintillator elements, as well as suboptimal alignment between scintillator elements.

Building upon the experience gained from this earlier prototype, three new CsI:Tl prototypes and one BGO prototype, employing thinner polymer septal walls, have been fabricated and examined. In the development of these prototypes, the objectives were to improve element-to-element alignment, explore the use of BGO scintillating crystals, and evaluate CsI:Tl detector performance as a function of scintillator thickness. The signal and noise properties, as well as phantom images, acquired from these prototype EPIDs are reported and compared to the results obtained from a conventional EPID. Finally, the performance limitations for these prototype EPIDs and the direction for future scintillator development are discussed.

METHODS AND MATERIALS

Physical description of prototype EPIDs

The segmented scintillators reported in this article include an 11.3 mm thick BGO scintillator and three CsI:Tl scintillators, referred to as CsI-1, CsI-2 and CsI-3, with thicknesses of 11.4, 25.6, and 40.0 mm, respectively. (CsI-1 and CsI-2 were obtained by slicing CsI-3 into two independent, thinner parts.) Each segmented scintillator consists of 120×60 scintillator elements (each element comprising a scintillating crystal and the surrounding septal walls) with an element-to-element pitch of 1.016 mm, providing an active area of ∼12.2×6.1 cm². The septal walls are 0.05 mm thick and consist of polymer reflectors glued to the crystals. The reflectors, having a reflectivity of ∼90%, are not entirely opaque to optical photons, resulting in some light sharing between adjacent scintillator elements. Note that the thickness of the septal walls was chosen to be less than that used in the earlier CsI:Tl prototype (0.1 mm)³⁷ with the expectation that this would facilitate improved alignment of the scintillator elements. As previously reported, considering radiation transport only, thinner walls result in a larger fill factor, leading to increased DQE.³⁶ The top and bottom surfaces of the scintillators reported in this article were polished using the same technique. However, since BGO is a much harder material than CsI:Tl, polishing resulted in the top and bottom surfaces of the BGO scintillator being much smoother than those of the CsI:Tl scintillators. Figure 1 shows pictures illustrating the transparency of the BGO and CsI-1 scintillators. While the BGO scintillator is seen to be highly transparent, the CsI-1 scintillator (having a similar thickness) is much less so and exhibits an ivory color. It is believed that the difference in light transmission between the two scintillators is due to the difference in optical scattering. Such a difference is the result of the inherently higher degree of self-scattering in the CsI:Tl crystal, as well as higher scattering at the much rougher surfaces of that scintillator.

Figure 1.

Pictures showing a top view of the segmented (a) BGO (11.3 mm thick) and (b) CsI-1 (11.4 mm thick) scintillators overlying the same photograph of two flamingos. Note that the photograph is narrower than the scintillators. The light grid of the horizontal and vertical lines corresponds to the septal walls of the prototypes. The BGO scintillator is seen to be more transparent than the CsI-1 scintillator. Also note that the BGO and CsI-1 scintillators were assembled from seven and five subassemblies (each consisting of 60 rows of elements), respectively. Although the transparencies of the various subassemblies are very similar for the BGO prototype, this is not the case for the CsI-1 prototype.

Each segmented scintillator was covered by a 1 mm thick copper plate with a polished mirror surface, forming a segmented scintillating detector. The copper plate absorbs scattered radiation and also serves as a radiation build-up layer. Each segmented detector was configured with a mirror or a black top reflector. The mirror top reflector configuration utilizes the mirror surface of the copper plate, resulting in a reflectivity of ∼60%–70%. The black top reflector configuration employs a sheet of black paper positioned between the copper plate and the segmented scintillator.

The segmented detectors were evaluated using an indirect detection, active matrix, flat-panel array (Cyclops II, with a format of 512×512 pixels and a pixel pitch of 0.508 mm).² The detector and array were housed in a custom-built, precision alignment jig.³⁷ This jig allowed horizontal, vertical, and rotational adjustment of the segmented scintillator with respect to the underlying array. Prior to x-ray measurements, each scintillator was aligned to the array with the goal of registering each scintillator element with a block of 2×2 array pixels. In addition, given the high optical conversion gain of CsI:Tl (∼54000 photons∕MeV),³⁸ a 0.05 mm thick neutral density filter with 12% light transmission was placed between the CsI:Tl scintillator and the array so as to help avoid pixel signal saturation. Finally, for each prototype, the segmented scintillator was brought to close, mechanical contact with the array (using the alignment jig), eliminating any unintended air gap. The absence of any significant air gap ensured negligible contributions from optical glare, irrespective of the degree of polishing performed on the bottom surfaces of the prototype scintillators.

For comparison, x-ray measurements were also performed with a conventional EPID, consisting of a Lanex Fast-B screen (∼133 mg∕cm² Gd₂O₂S:Tb, Eastman Kodak, Rochester, NY) and a 1 mm thick copper plate coupled to the same flat-panel array used for the prototype EPIDs.

Measurement methods

The prototype and conventional EPIDs were evaluated using a 6 MV photon beam from a Varian 21EX linear accelerator (LINAC). The radiation output of the machine is measured in monitor units (MU) and, for each MU, the LINAC delivers ∼36 beam pulses. The LINAC was calibrated so that at 6 MV with a field of 10×10 cm², an irradiation of 1 MU deposits a dose of ∼0.8 cGy in water at a source-to-detector distance (SDD) of 100 cm, with 10 cm of overlying water. Unless otherwise stated, for the reported measurements the size of the x-ray field was 15×15 cm² at the isocenter and the LINAC was operated at a dose rate of 100 MU∕min. The radiation measurements consist of x-ray sensitivity, MTF, NPS, DQE, and phantom images. Note that all measurements involving the BGO prototype were immediately preceded by irradiating the scintillator to a total dose of ∼2000 MUs. This preirradiation was necessary to stabilize the radiation signal of the prototype, which exhibited an initial sharp decline of ∼17% with increasing cumulative dose until reaching an asymptotic, stable level. Independent measurements using blocks of BGO crystals of the same type and quality as that used in the prototype indicated that this undesirable behavior is due to short-term radiation-induced changes to the BGO material itself, which resulted in visible discoloration of the material. The reduction in sensitivity and discoloration were observed to gradually recover over time (in the absence of radiation) and this behavior was found to be highly reproducible.

X-ray sensitivity and normalized noise power spectrum (NNPS)

X-ray sensitivity and NPS were determined using the same set of data acquired both in the presence and absence of radiation, in the form of flood and dark frames, respectively. In these measurements, the EPIDs were placed 130 cm from the radiation source. The flood frames were obtained in a fluoroscopic mode, which involves the acquisition of consecutive data frames in synchronization with the delivery of the beam pulses. Synchronization was achieved using the “target I” output from the LINAC control logic to trigger array readout. Data were obtained under various irradiation conditions corresponding to the delivery of a constant number of beam pulses (i.e., 1–4) per frame. Note that the radiation delivered by one beam pulse corresponds to a calibration dose of ∼0.022 cGy. Synchronization of radiation delivery with array readout resulted in the frame time, defined as the time between consecutive frames, varying with dose and ranging from 16.7 to 66.7 ms. For each dose, 900 frames consisting of 512 data lines by 100 gate lines were acquired. The first 400 frames were not saved as they were used to allow stabilization of both the LINAC output and the signal from array pixels. The last 500 frames were used for sensitivity and NPS determination. For each dose, in order to allow correction of dark signal contributions in the flood frames, the same number of dark frames (i.e., 500) was obtained under similar conditions. A smaller region of interest (ROI) located away from the edges of the scintillator (consisting of 180×100 and 140×100 pixels for the BGO and CsI:Tl prototypes, respectively) was selected from the image frames. Although all scintillators have the same active area, the more aggressive cropping for the CsI:Tl prototypes was performed so as to exclude a small region within the scintillators where the signal was significantly lower. It is suspected that this region was mistakenly constructed with septal walls having different optical properties compared to those in other regions.

As a first step in processing of the data, gain and offset corrections were applied to the ROI in the flood frames. Subsequently, defective array pixels were corrected by a 3×3 median filter affecting less than 0.2% of the total number of pixels. The corrected frames were then binned in a 2×2 format, resulting in a synthesized pixel area equal to the size of the scintillator elements. These processing steps were applied to all flood frames and images obtained from the prototypes as well as from the conventional EPID. The signal, measured in analog-to-digital converter (ADC) units, was converted to electrons using a calibration factor of 1 ADC=7480 electrons.²⁵ For each prototype and for the conventional EPID, the average signal per binned pixel $\left(\overline{S}\right)$ plotted as a function of calibration dose was fit with a linear function, the slope of which yielded the x-ray sensitivity.

NPS was determined from the processed flood frames using the synthesized slit technique.^{41, 42, 43} For each dose, the 500 processed flood frames (consisting of 90×50 and 70×50 binned pixels for the BGO and CsI:Tl prototypes, respectively) were averaged along the gate line direction, forming 500 independent, 1D realizations. After removing low-frequency background trends and applying a Hanning window, a 1D Fourier transform was applied to each of the 500 realizations, the results for which were averaged to yield 1D NPS. A correction for lag (i.e., frame-to-frame signal carryover, estimated to be ∼3%) was applied to each NPS, yielding a lag-corrected NPS, NPS_L.^{5, 36, 37, 44} In this article, the normalized NPS (NNPS) was determined from

$$\text{NNPS}\left(f\right)=\frac{{\text{NPS}}_L\left(f\right)\times {\overline{q}}_0}{{\overline{S}}^2},$$ (2)

where ${\overline{q}}_0$ is the incident x-ray fluence for the corresponding dose. For a calibration dose of 1 cGy, ${\overline{q}}_0$ is approximately equal to 1.024×10⁷ X rays∕mm² at a SDD of 130 cm.

MTF

Spatial resolution of the prototype EPIDs was characterized in terms of the presampled MTF, using the angled slit technique.^{36, 37, 45} In these measurements, a custom-made slit,⁴⁶ consisting of two blocks of tungsten each having dimensions of 4.25×8.5×19 cm³, was used. A polymer shim with dimensions of 0.01×8.5×19 cm³ sandwiched between the two tungsten blocks formed a narrow gap. The slit was attached to the LINAC using an accessory mount, with the longest dimension of the slit oriented along the direction of the beam. The gap was positioned at an angle of ∼3° with respect to the direction of the data lines of the flat-panel array. The entrance surface of the slit was ∼119 cm from the radiation source (resulting in a SDD of 138 cm) and the radiation field was 4.0×5.5 cm² at the isocenter. The LINAC was operated at a dose rate of 600 MU∕min. Prior to each measurement, the slit was positioned at the center of the field so as to allow maximum radiation transmission through the gap. A total of 10 images of the slit was obtained in radiographic acquisition mode, which involves the acquisition of a single flood frame following x-ray irradiation. For each prototype, ten additional images, referred to as radiation dark images, were acquired after displacing the gap ∼5 mm away from the centered position so that no direct radiation could transit the gap. These images were used to correct for the small amount of radiation that penetrates through the tungsten blocks in the slit images. After image processing, the average of the radiation dark images was subtracted from the average of the slit images, resulting in an image from which a line spread function (LSF) was determined. Application of a Fourier transform to the LSF yielded the MTF.

DQE

For each dose at which NPS data were acquired, the DQE for each prototype EPID was determined using the measured MTF and NNPS:

$$\text{DQE}\left(f\right)=\frac{{\text{MTF}}^2\left(f\right)}{\text{NNPS}\left(f\right)}.$$ (3)

Phantom images

A contrast-detail phantom^{37, 47} was imaged using the prototype EPIDs. The phantom is made of aluminum and consists of holes at ten different depths and ten different diameters.⁴⁷ Due to the limited size of the prototype EPIDs, only a portion of the phantom was imaged, corresponding to a set of 8×3 holes providing the highest contrasts (0.18%–1.91% at 6 MV) and largest diameters (0.5–1.3 cm). In addition, part of a human head phantom (model 76–018DT, Nuclear Associates, Long Island, NY) was also imaged using the BGO prototype. For comparison, images of the phantoms were also obtained using the conventional EPID operated under similar irradiation conditions. For all images, the EPIDs were placed at a SDD of 130 cm with the phantoms sitting ∼20 cm nearer to the x-ray source.

Simulation methods

In order to compare the measured performance of the prototype EPIDs to theoretical predictions, Monte Carlo simulations of radiation transport were performed to determine MTF, NNPS, and DQE using the EGSnrc (Ref. ⁴⁸) and DOSXYZnrc (Ref. ⁴⁹) codes. The resulting simulated MTF and DQE values represent theoretical upper limits for the prototype EPIDs. Each simulated EPID consists of a segmented scintillator covered by a 1 mm thick copper plate. (The flat-panel array was not included in the simulation geometry given its negligible impact on the deposition of radiation energy in the scintillator.) The x-ray source employed a 6 MV photon beam representing a spectral output of a Varian LINAC.⁵⁰ The scintillator thickness and element-to-element pitch correspond to those of the prototype scintillators. The septal walls were simulated as 0.05 mm thick layers of polystyrene. In order to determine MTF and NNPS, the simulated scintillators were chosen to consist of 300×300 and 600×600 elements, respectively. The imaging signal was extracted from the radiation energy deposited in each scintillating crystal.

For the MTF simulation, a parallel beam of 30×0.01 cm² was generated perpendicularly incident on the center of each detector, forming a thin radiation slit. This slit beam was oriented at a small angle (∼1°) with respect to the column direction of the scintillators. The Fourier transform of the resulting simulated LSF, extracted from the slit image (using the angled slit technique),⁴⁵ yielded the simulated MTF.³⁶ For the NPS simulation, a 60×60 cm² parallel beam was generated perpendicularly incident on the central part of each detector. A total of 50 flood frames was simulated for each EPID, with 360 million x-ray histories carried out for each frame. Data from ten nonoverlapping blocks, each consisting of 250×100 elements, were obtained from the central 500×500 elements of each flood frame. Data in each of the resulting 500 blocks ware averaged along the shorter dimension, resulting in 500 realizations from which NPS was determined (using the synthesized slit technique).^{41, 42, 43} NNPS was obtained using Eq. 2 and a fluence of 1000 X rays∕mm² (corresponding to 360 million X rays over 60×60 cm²), and with no electronic noise contribution. Finally, DQE was calculated with Eq. 3 using the results for the simulated MTF and NNPS. Note that the absence of electronic noise in the simulations leading to the NNPS makes those results, as well as the associated DQE values, independent of dose.

RESULTS

For the various types of measurements reported for the prototype EPIDs, comparisons are made with the performance of the conventional EPID described in Sec. 2A. The results for the conventional EPID were either acquired for the present study (in the case of x-ray sensitivity and phantom images) or obtained from previously published data obtained from that EPID (in the case of MTF and DQE).² In all cases, the data were binned in a 2×2 format to match the element-to-element pitch of the segmented scintillators.

X-ray sensitivity

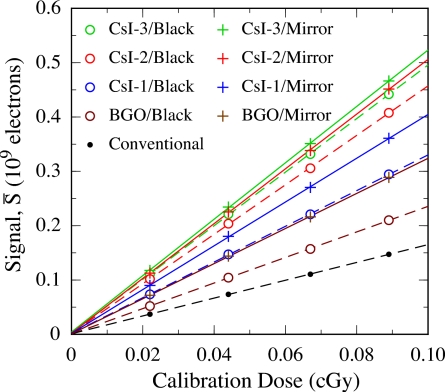
Figure 2 shows the average signal per binned pixel $\left(\overline{S}\right)$ presented as a function of calibration dose for the prototype EPIDs. Results are shown for the prototypes configured with the black and the mirror top reflectors, as well as for the conventional EPID. The signal response for each of the prototypes is seen to be highly linear. The corresponding x-ray sensitivities, determined from linear fits to the signal response data, are summarized in Table 1. For each prototype configuration, the sensitivity is found to be higher than that for the conventional EPID, even with the neutral density filter used to attenuate signal in the case of the CsI:Tl prototypes. In addition, for a nearly identical scintillator thickness, CsI-1 offers higher sensitivity than the BGO prototype. For BGO, CsI-1, CsI-2, and CsI-3, the substitution of the black top reflector with the mirror top reflector results in sensitivity enhancements of ∼37%, 23%, 11%, and 5%, respectively. The enhancement for the CsI-1 prototype is smaller than that for the BGO prototype due to less efficient light transmission in the CsI-1 scintillator. In addition, for the three CsI:Tl prototypes, the enhancement of sensitivity decreases with increasing thickness, indicating a reduction in the efficiency of optical transport with increasing scintillator thickness.

Figure 2.

Average signal per binned pixel as a function of calibration dose for the four prototype EPIDs. Results for each prototype, configured with the black top reflector (open circles) and with the mirror top reflector (plus symbols), are shown. (Note that, for a given type of reflector, the legend is organized, from top to bottom, in order of decreasing prototype sensitivity). For comparison, the average signal for the conventional EPID is also plotted (black dots). The dashed lines (which correspond to results with the black reflector and the conventional EPID) and solid lines (which correspond to results with the mirror reflector) are linear fits to the data.

Table 1.

X-ray sensitivities, derived from the EPID signal data appearing in Fig. 2, are listed in the first two rows. The percentages reported in the third row correspond to the degree of sensitivity enhancement that results from the replacement of the black top reflector with the mirror top reflector.

	BGO	CsI-1	CsI-2	CsI-3	Conventional
Black top reflector (109e∕cGy)	2.35	3.29	4.55	4.93	1.64
Mirror top reflector (109e∕cGy)	3.23	4.03	5.04	5.19	–
Enhancement using mirror top reflector (%)	37	23	11	5	–

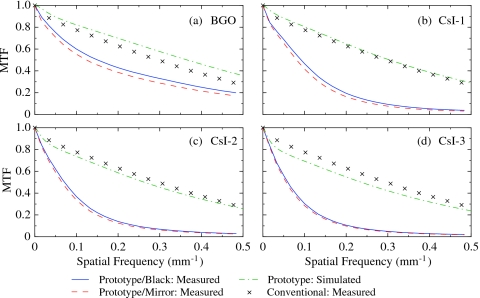
MTF

Figure 3 shows presampled MTF results measured from the prototype EPIDs. Results are shown for the prototypes configured with the black and the mirror top reflectors, along with the corresponding theoretical upper limits obtained through simulation, as well as the MTF measured from the conventional EPID. The theoretical upper limits show that, as scintillator thickness increases [from Figs. 3b, 3c, 3d] or scintillator density decreases [from Figs. 3a, 3b], the MTF decreases due to increased lateral spreading of secondary radiation. The measured MTFs of the prototype EPIDs are seen to be much lower than both the corresponding theoretical upper limits and the MTF of the conventional EPID. The difference between the measured and the simulated prototype MTF results is believed to be the combined result of lateral optical spreading, as well as misalignment between scintillator elements and misregistration between the scintillator elements and the array pixels — none of which is accounted for in the simulations. The latter two effects will be referred to as “misalignment” and “misregistration” in the remainder of this article, and those photons that enter neighboring elements will be referred to as lateral spreading photons.

Figure 3.

Presampled modulation transfer function (MTF) for the (a) BGO, (b) CsI-1, (c) CsI-2 and (d) CsI-3 prototype EPIDs. The results are shown for configurations with the black top reflector (blue lines) and the mirror top reflector (red dashed lines). The maximum estimated error in these MTF results is ∼3%. The green dot-dashed lines correspond to the MTF obtained from simulation of the various prototypes. The black crosses correspond to MTF results measured from the conventional EPID (adapted from data appearing in Ref. 2).

The BGO prototype empirically demonstrates significantly higher MTF than the CsI-1 prototype. Given the similar degree of misalignment and misregistration present in these two, similarly thick, prototypes, the difference in MTF performance is likely due to differences in the amount of lateral optical spreading. Since the same polymer reflector and optical glue were nominally used in all prototype scintillators, it is suspected that the superior element-to-element optical isolation demonstrated by the BGO scintillator is the combined result of its higher refractive index and lower optical scattering. Given that the refractive indices of the optical glue (∼1.55) and the flat-panel array (∼1.70) are both lower than that of BGO (∼2.15) and CsI:Tl (∼1.79), total internal reflection can occur at the scintillator-glue interface (i.e., at the side surfaces of the scintillator crystals) and the scintillator-array interface (i.e., at the bottom surfaces of the scintillator crystals). At the scintillator-glue interface, photons incident at angles larger than the critical angle (∼46° and ∼60° for BGO and CsI:Tl, respectively) cannot exit the crystal and cannot spread into neighboring elements. This limiting effect on lateral optical spreading is stronger for the BGO scintillator due to its smaller critical angle. At the scintillator-array interface, photons incident at angles larger than the critical angle (∼52° and ∼72° for BGO and CsI:Tl, respectively) cannot enter the flat-panel array. For the BGO scintillator (having little or no optical scattering), the lateral spreading photons (those with incident angles smaller than ∼46° at the scintillator-glue interface) have incident angles larger than ∼44° at the scintillator-array interface. A significant portion of those lateral spreading photons cannot enter the flat-panel array and thus do not contribute to imaging signal. This effect, which helps improve MTF for the BGO scintillator, is strongly suppressed for the CsI:Tl prototypes due to its lower refractive index and greater optical scattering.

From Fig. 3, the EPID configurations with the mirror top reflector are seen to exhibit slightly lower MTF performance than the configurations with the black top reflector. This is probably due to a greater degree of lateral spreading of those photons reflected by the mirror top reflector. In addition, as expected, the spatial resolution for the CsI:Tl prototypes decreases with increasing scintillator thickness due to increased lateral spreading of secondary radiation and optical photons. Finally, although the MTF measured from each prototype EPID is lower than that for the conventional EPID, the BGO prototype nevertheless demonstrates relatively good performance — for example, providing an MTF of ∼20% near the Nyquist frequency of 0.49 mm⁻¹.

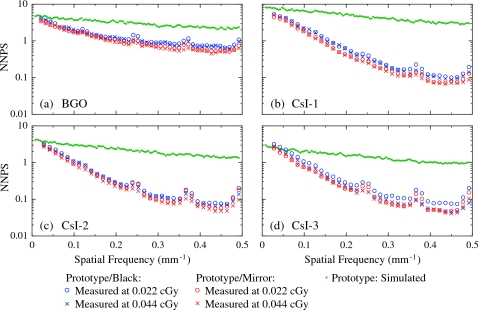
NNPS

Figure 4 shows the measured and simulated NNPS for the prototype EPIDs. For each prototype, the NNPS measured at 0.022 and 0.044 cGy (corresponding to 1 and 2 beam pulses) are generally similar, indicating a noise performance dominated by x-ray quantum noise. In addition, the configurations with the black top reflector exhibit slightly higher NNPS — likely the result of two contributing factors. The first is an increase in Swank noise at all frequencies for the black reflector configurations, originating from the increase in the difference in optical gain for photons generated at different depths in the scintillator.³⁸ The second factor is a higher degree of optical spreading for the mirror reflector configurations (see Fig. 3), leading to a stronger element-to-element signal correlation and thus a lower NNPS. Compared to the CsI:Tl prototypes, the BGO prototype exhibits significantly less decline in NNPS at higher spatial frequencies, indicating a much smaller element-to-element signal correlation — a consequence of less optical cross-talk. At four specific spatial frequencies, all NNPS results for the various prototypes show small bumps, the origin of which is not understood — but which are possibly associated with pickup of ambient electromagnetic noise. Finally, the large difference observed between the measured and the simulated NNPS is the combined result of three effects that have not been included in the simulations: Stochastic optical Swank noise, noise reduction caused by lateral optical spreading, and deterministic noise caused by misalignment and misregistration.

Figure 4.

NNPS for the (a) BGO, (b) CsI-1, (c) CsI-2, and (d) CsI-3 prototype EPIDs. The results are shown for configurations with the black top reflector (blue symbols) and the mirror top reflector (red symbols), at both 0.022 and 0.044 cGy. The maximum estimated error in the NPS results is ∼5%. The green dots correspond to simulated NNPS for the prototype EPIDs.

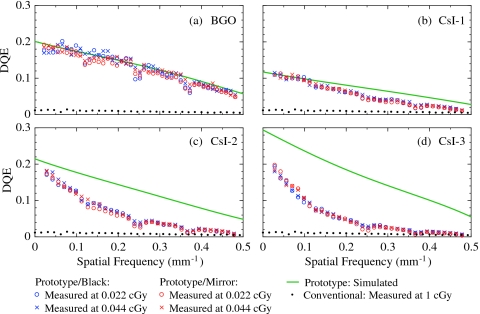
DQE

Figure 5 shows measured DQE results at 0.022 and 0.044 cGy for the prototype EPIDs configured with the black and the mirror top reflectors, along with corresponding DQE values determined using Monte Carlo simulations. The DQE for the conventional EPID, measured at 1 cGy, is also shown. (Note that this result represents the maximum DQE that can be obtained from the conventional EPID at 6 MV.) Quantum limited DQE performance is observed for the prototypes at a dose as low as 0.022 cGy, as indicated by the nearly overlapping DQE results at different doses. It is also observed that the choice of top reflector does not significantly affect the DQE results. Note that the small dips in the measured DQE for the prototypes originate from the previously noted anomalies in the NNPS results.

Figure 5.

DQE for the (a) BGO, (b) CsI-1, (c) CsI-2, and (d) CsI-3 prototype EPIDs. The results are shown for configurations with the black top reflector (blue symbols) and the mirror top reflector (red symbols), at both 0.022 and 0.044 cGy. The maximum estimated error in these DQE results is ∼7%. The green lines correspond to polynomial fits to the DQE results obtained through simulation. The black dots correspond to DQE results measured from the conventional EPID at 1 cGy (adapted from data appearing in Ref. 2).

As shown in Fig. 5a, the measured DQE for the BGO prototype is very close to the simulated results for frequencies up to ∼0.3 mm⁻¹, indicating that contributions of optical Swank noise (which degrade DQE at all frequencies) are small. At higher frequencies, the measured DQE is slightly lower than the simulations. For example, at the Nyquist frequency, the measured DQE is ∼80% that of the simulations. This is likely a result of the presence of some element-to-element optical cross-talk. The overall similarity of the measured and simulated DQE results suggests that the large differences between the corresponding MTF results shown in Fig. 3 are primarily due to misalignment and misregistration. Since these effects lead to deterministic noise propagation, which results in modulation of the NNPS by the square of the MTF,⁵¹ their impact on DQE is muted, as can be anticipated through an examination of Eq. 3. Finally, compared to the conventional EPID, the BGO prototype provides DQE improvements of up to a factor of ∼20 at zero frequency (i.e., ∼20% compared to 1%), and ∼10 at the Nyquist frequency of 0.49 mm⁻¹ (i.e., ∼5% compared to 0.5%).

Figure 5b shows that the measured DQE results for the CsI-1 prototype approach the theoretical upper limit at low frequencies, indicating the presence of negligible levels of optical Swank noise. However, at frequencies beyond ∼0.1 mm⁻¹, the measured DQE is significantly lower than the simulated DQE due to degradation caused by lateral optical spreading. Nevertheless, CsI-1 offers greatly improved DQE compared to the conventional EPID at all frequencies — for example, ∼12% and ∼1.5% compared to ∼1% and ∼0.5% at zero frequency and the Nyquist frequency, respectively.

As demonstrated in Figs. 5c, 5d, further increases in CsI:Tl scintillator thickness lead to higher DQE at low spatial frequencies. Using polynomial extrapolation, the measured DQE for CsI-2 and CsI-3 at zero frequency is estimated to be up to ∼20% and ∼25%, respectively. These values are lower than those predicted by the corresponding simulations due to degradation caused by optical Swank noise.³⁸ Such degradation is observed to be more pronounced for thicker scintillators due to their higher degree of optical absorption. In addition, the DQE of these two prototypes exhibits a strong falloff at higher frequencies, resulting in even larger differences with the corresponding simulated results. At the Nyquist frequency, the measured DQE for these two prototypes is not quite twice that for the conventional EPID. As a result of the more significant drop in DQE for the thicker CsI:Tl scintillators, CsI-1 exhibits higher DQE compared to CsI-2 and CsI-3 at frequencies above ∼0.2 and 0.1 mm⁻¹, respectively. In addition, CsI-2 provides higher DQE than CsI-3 above ∼0.03 mm⁻¹. These complicated and unanticipated behaviors are the result of lateral optical spreading in the CsI:Tl scintillators.

Phantom images

Figure 6 shows x-ray images of the contrast-detail phantom obtained using the prototype EPIDs configured with the mirror top reflector, as well as using the conventional EPID. As observed from Figs. 6a, 6c, 6e, 6g, 6i, at a dose of 0.022 cGy, all prototype EPIDs offer significantly improved contrast resolution compared to the conventional EPID. (For example, for the 1.3 cm hole at 1.91% contrast, all prototype EPIDs offer contrast-to-noise performance more than nine times higher than that of the conventional EPID.) Moreover, even at this extremely low dose, the prototype EPIDs allow delineation of objects having contrast as low as ∼0.2%. In addition, the contrast resolution offered by the BGO prototype at 0.044 cGy [Fig. 6d] is at least comparable to, and perhaps slightly better than, that provided by the conventional EPID at 20 times more dose [Fig. 6b]. Although the spatial resolution provided by the BGO prototype is seen to be slightly inferior to that of the conventional EPID, the boundaries of the objects shown in Fig. 6d are still clearly distinguishable. It is also interesting to note that, despite its lower DQE, CsI-1 provides object visibility [Fig. 6f] similar to that of the BGO prototype [Fig. 6d]. However, the spatial resolution is noticeably poorer in the image obtained with CsI-1. For the thicker scintillators (CsI-2 and CsI-3), the corresponding phantom images [Figs. 6h, 6j] are even more blurred. As a result, it becomes progressively more difficult to distinguish the boundaries of the low-contrast objects, and increasing CsI:Tl scintillator thickness does not lead to improvement in object visibility.

Figure 6.

X-ray images of a contrast-detail phantom. Images acquired using the conventional EPID at (a) 0.022 and (b) 0.889 cGy. Images acquired using the (c) BGO, (e) CsI-1, (g) CsI-2, and (i) CsI-3 prototypes at 0.022 cGy; and the (d) BGO, (f) CsI-1, (h) CsI-2, and (j) CsI-3 prototypes at 0.044 cGy. All prototype EPIDs were configured with a mirror top reflector. Due to the limited size of the segmented scintillators, each image is formed by stitching two separately acquired images (left and right) corresponding to adjacent parts of the phantom. In addition, in order to optimize object visibility, the two images were enhanced separately using different windows and levels. For consistency, the same image enhancement method was applied to the corresponding parts of the images acquired with the conventional EPID. The legend above (a) and (b) indicate the estimated contrast of the holes at 6 MV (Ref. ³⁷). The diameters of the three rows of holes are 1.3, 0.8, and 0.5 cm.

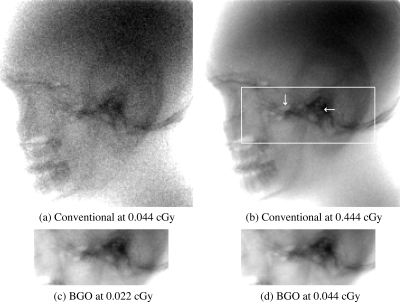
Figure 7 shows x-ray images of the human head phantom obtained using the BGO prototype configured with the mirror top reflector, as well as using the conventional EPID. A comparison of the images in Figs. 7d, 7a indicates that the BGO prototype offers significantly improved image quality compared to the conventional EPID at a dose of 0.044 cGy. This improvement is the result of more x-ray quanta sampled, as well as a lower contribution from additive electronic noise relative to x-ray quantum noise. Moreover, for the low-contrast features of the phantom, the BGO prototype images at doses of 0.022 and 0.044 cGy [Figs. 7c, 7d] demonstrate contrast-detail visibility similar to that obtained with the conventional EPID at 0.444 cGy [Fig. 7b].

Figure 7.

X-ray images of a human head phantom acquired using the conventional EPID at (a) 0.044 and (b) 0.444 cGy, and the BGO prototype (with the mirror top reflector) at (c) 0.022 and (d) 0.044 cGy. The white rectangle superimposed in (b) corresponds to the region imaged by the BGO prototype, while the two white arrows point to a pair of low-contrast features.

SUMMARY AND DISCUSSION

The development of high-DQE EPIDs based on thick, segmented scintillators is motivated by the desire to obtain 3D visualization of soft tissue in radiotherapy using the treatment beam. This article presents an empirical investigation of four prototype EPIDs employing such scintillators — a BGO scintillator (11.3 mm thick) and three CsI:Tl scintillators, CsI-1, CsI-2 and CsI-3 (11.4, 25.6, and 40.0 mm thick, respectively). The portal imaging performance of these prototypes was compared to the corresponding theoretical upper limits obtained through Monte Carlo simulation, as well as to values measured from a conventional EPID.

Compared to the conventional EPID, the BGO prototype demonstrates somewhat lower MTF and significantly improved DQE at all spatial frequencies, as well as the ability to delineate low-contrast objects at a dose of only 0.022 cGy (corresponding to a single LINAC beam pulse). Moreover, given the relatively modest thickness of the BGO scintillator, the performance of a large-area version of such a scintillator would not be expected to be limited by radiation incident at oblique angles³³ — removing the need for a focused geometry for the scintillator elements.³⁶ The three CsI:Tl prototypes also showed significantly improved low-frequency DQE and image quality at 0.022 cGy. However, the MTF and DQE of these prototypes are considerably lower than theoretical expectations at higher spatial frequencies due to the effect of lateral optical spreading. Consequently, the increasing thickness of these nonoptimized CsI:Tl scintillators did not provide the progressive improvement in DQE expected at high frequencies. In order to circumvent this limitation, lateral optical spreading in such scintillators needs to be reduced through modifications of the septal walls (e.g., through the use of more opaque polymer reflectors or replacing polymer reflectors with metal reflectors).^{36, 38} In addition, further improvement in the alignment between scintillator elements is required to provide more accurate registration between the segmented scintillator and the underlying flat-panel array, thus improving the spatial resolution.

While the BGO prototype offered, by far, the best imaging performance, it also exhibited dose-dependent sensitivity. The sharp decline in scintillator sensitivity (∼17%) within the first few hundred cGy of radiation exhibited by the prototype would complicate clinical use of such a scintillator. Previous examinations of the effect of radiation on the performance of BGO have indicated widely varying results — ranging from negligible to significant effects^{52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62} — possibly due to differences in the crystal quality and irradiation conditions. Some studies suggested the possibility that high-energy X rays knock out electrons from oxygen atoms, forming color centers that increase optical absorption in the BGO crystal.^{52, 54, 56} A possible way to reduce such undesirable radiation effects involves the introduction of Eu³⁺ as a doping agent, which can donate electrons to the oxygen atoms to prevent the formation of color centers.^{52, 56} Therefore, achieving a stable light output for future segmented scintillators based on BGO is crucial for the practical implementation of such detectors in a clinical setting.

In conclusion, prototype EPIDs based on thick, segmented BGO and CsI:Tl scintillators demonstrated significantly improved portal imaging performance at extremely low doses. Except for CsI-1, the prototypes reported in this article provide DQE(0) values above ∼20%. Such an increase in DQE(0) compared to that of conventional² as well as an earlier experimental prototype¹³ reflects the more efficient use of the incident x-ray quanta, which should lead to better contrast-to-noise ratio and thus better soft-tissue delineation in MV CBCT images.³⁹ Although the present prototypes are far from optimal, it is anticipated that, through further iteration of design, fabrication, and characterization, MV CBCT systems based on high-efficiency, segmented scintillators can provide high quality images for soft-tissue delineation at clinically practical doses.