Differential direct coding: a compression algorithm for nucleotide sequence data

Abstract

While modern hardware can provide vast amounts of inexpensive storage for biological databases, the compression of nucleotide sequence data is still of paramount importance in order to facilitate fast search and retrieval operations through a reduction in disk traffic. This issue becomes even more important in light of the recent increase of very large data sets, such as metagenomes. In this article, I propose the Differential Direct Coding algorithm, a general-purpose nucleotide compression protocol that can differentiate between sequence data and auxiliary data by supporting the inclusion of supplementary symbols that are not members of the set of expected nucleotide bases, thereby offering reconciliation between sequence-specific and general-purpose compression strategies. This algorithm permits a sequence to contain a rich lexicon of auxiliary symbols that can represent wildcards, annotation data and special subsequences, such as functional domains or special repeats. In particular, the representation of special subsequences can be incorporated to provide structure-based coding that increases the overall degree of compression. Moreover, supporting a robust set of symbols removes the requirement of wildcard elimination and restoration phases, resulting in a complexity of O(n) for execution time, making this algorithm suitable for very large data sets. Because this algorithm compresses data on the basis of triplets, it is highly amenable to interpretation as a polypeptide at decompression time. Also, an encoded sequence may be further compressed using other existing algorithms, like gzip, thereby maximizing the final degree of compression. Overall, the Differential Direct Coding algorithm can offer a beneficial impact on disk traffic for database queries and other disk-intensive operations.

Introduction

The field of bioinformatics necessitates a particular set of considerations, with respect to database management systems. A fundamental requirement is the capacity to warehouse large amounts of biological sequence data that are currently inundating the publicly available database resources. As of January 2009, the Nucleic Acids Research online Molecular Biology Database Collection listed 1170 publicly available biological databases (1). GenBank, a major sequence database and a component of the International Nucleotide Sequence Databases (INSD), doubles in size roughly every 18 months (2). Furthermore, biological data is distinct in that it requires accompanying annotation data in order for it to be useful (3). While modern hardware can provide vast amounts of inexpensive storage, the compression of biological sequence data is still of paramount concern in order to facilitate fast search and retrieval operations, primarily by reducing the number of required I/O operations. Therefore, the effective management and compression of both sequence data and corresponding annotation data are indispensable considerations for biological database management systems.

Data compression requires two fundamental processes: modeling and coding (4). Modeling involves constructing a representation of the distinct symbols in the data, along with any associated data, like the relative frequencies of the symbols (4). Coding involves applying the model to each symbol in the data to produce a compressed representation of the data, preferably by assigning short codes to frequently occurring symbols and long codes to infrequently occurring symbols (4). A variety of dictionary methods, such as the Ziv-Lampel algorithms (5,6), can be employed to achieve this (7). Likewise, the Huffman algorithm (8) or some form of arithmetic coding could also be applied to yield a compaction in data (7). However, methods that rely on evolving models may not perform adequately for sequences of genomic proportions. Such limitations will certainly be exacerbated by the recent surge in large-scale metagenomic data sets.

In the case of DNA sequences, the finite set of nucleotide symbols {A, C, G, T} can be efficiently modeled as a corresponding set of binary values {00, 01, 10, 11} (9). This model constitutes an effective binary representation where each nucleotide base is directly coded by two bits. This assumes that sequence data are indeed composed solely from the four symbols of the nucleotide set. However, this assumption is not guaranteed to be met and a nucleotide sequence may include additional wildcard symbols, like N or S (4). Therefore, to reconcile the potential occurrence of symbols other than the expected four nucleotide bases, any unexpected symbol is randomly converted into one of the valid symbols that it represents (4). Eliminated wildcards are subsequently restored during sequence decompression (4).

The study of the compression of sequence data began with the work of Grumbach and Tahi (10,11), and separately with the work of Milosavijevic (12) and the work of Rivals et al. (13). Since then several major compression tools have been developed. While a variety of different underlying approaches have been employed, all of these efforts draw on the large body of existing work on general data compression, particularly text compression algorithms. In this work, I present the Differential Direct Coding algorithm, a general-purpose nucleotide compression protocol that can differentiate between sequence data and auxiliary data by supporting the inclusion of supplementary symbols that are not members of the set of expected nucleotide bases, thereby offering reconciliation between sequence-specific and general-purpose compression strategies.

Nucleotide sequence compression strategies

Evolving models

Most previous approaches to nucleotide sequence compression consider a sequence as a finite length string of symbols where each nucleotide base corresponds to an individual symbol. On this basis, information content can be assessed and repeating patterns can be exploited using dictionary methods that progressively evolve models for data by encoding selected strings of symbols as tokens (7). In general, dictionary based compression protocols, such as the Ziv-Lampel algorithms (5,6), are entropy encoders and will compress a string of n symbols to nE bits, where E is the entropy of the string (7).

While some sequence compression tools, like DNASequitur (14) and RNACompress (15), use grammar-based compression algorithms, most use some form of evolving model driven by a dictionary based algorithm, typically derived from the Ziv-Lampel algorithms (5,6). Both BioCompress (10) and BioCompress-2 (11), along with GenCompress (16), DNACompress (17), DNAPack (9) and CASToRe (18–20) all involve the detection of approximate repeats to evolve a model for the encoding of a given sequence. While dictionary based algorithms are often applied to string-like data to achieve general purpose compression, their effective use is contingent on having a sufficiently large input file (7). However, as input size increases, the running time of some algorithms becomes unmanageable, especially those that use greedy approaches for the selection of repeat segments (9). Moreover, nucleotide sequences often need to be subdivided into discretely accessible records and this reduces the effectiveness of compression strategies that rely on evolving data models (4). Arithmetic coding can be used to overcome this limitation but does not typically offer the speed required for modern database applications (4).

Direct coding

Williams and Zobel (4) developed a direct coding strategy for nucleotide sequence compression, including wildcard symbols. The first stage involves replacing each wildcard symbol with a random nucleotide from the set of nucleotides represented by the given wildcard (4). Eliminated wildcards are maintained in a separate structure, rather than deleting them which would alter the semantics of the sequence (4). After wildcard elimination, the resulting sequence is composed of only four different symbols corresponding to the four expected nucleotide bases and each base can be coded using two bits (4). Instead of a space-inefficient fixed-length integer representation, a variable-byte representation is used where seven bits are used to code an integer and the least significant bit indicates whether or not the current byte is followed by another byte (4). Decompression requires two steps: the first of which involves mapping the two bit codes back to their nucleotide bases (4). This is followed by decoding the wildcard tuples and overwriting nucleotide bases at the appropriate locations with the proper wildcard symbol (4).

Direct coding offers a rapid and uniform method of compression that is not affected by the size of the input file. However, wildcard elimination and restoration require at least a two-phase process for either compression or decompression operations. Furthermore, eliminated data require storage in a secondary structure and that structure must include additional information about the location of its data for use at restoration time. Finally, sequences that have been compressed by direct coding are not readily re-compressible by alternative compression strategies that might increase the overall factor of compression.

Differential direct coding (2D)

Objectives

With the current surge in metagenomic data sets compression strategies must be developed to accommodate large data sets that are comprised of multiple sequences and a greater proportion of auxiliary data, such as sequence headers. Compression protocols developed specifically for sequence data offer good compression ratios but may perform poorly on large data sets or data sets that contain a significant amount of auxiliary data. In comparison, general-purpose compression utilities can easily compress large heterogeneous data files but cannot take advantage of the predominantly limited range of symbols that occur in sequence data. Therefore, the 2D algorithm is designed to provide a general-purpose nucleotide compression protocol that can differentiate between sequence data and auxiliary data, thereby offering reconciliation between the specific and general extremes of data compression. The following list enumerates the specific objectives of 2D:

1. Linear execution time to support large data sets: both compression and decompression operations must support implementations with a complexity of O(n) for execution time.

2. Support for the inclusion of supplementary symbols that are not members of the set of expected nucleotide bases: auxiliary symbols can be used to represent wildcards, annotation data or special subsequences, such as functional domains or special repeats.

3. Single phase direct coding: the compression phase must require only a single pass with no wildcard elimination phase and no storage of data in secondary structures or temporary intermediate files. Likewise, the absence of secondary data storage must permit a single pass restoration process for the decompression phase.

4. Lossless compression: the original sequence must be obtained following decompression. This can be implemented either with respect to sheer sequence only, that is regardless of line breaks and formatting, or optionally with respect to the verbatim line-by-line layout of the original sequence data.

5. Sequence type indifference: it must not be necessary to specify whether a given sequence is DNA or mRNA prior to compression or decompression.

6. Polypeptide decompression: it must be possible to optionally restore a compressed nucleotide sequence directly to a polypeptide chain of amino acids based on an indicated reading frame.

7. Amenable to further compression: A 2D-encoded sequence must be readily compressible by other compression utilities to optionally provide potential further compression of the original sequence.

Model

To provide linear execution time, 2D uses a static model to encode sequence data along with any other content that may be contained within the input. For DNA 2D expects {A, C, G, T} and for mRNA 2D expects {A, C, G, U}. By taking the union of these sets, the set of expected symbols for the 2D model becomes {A, C, G, T, U}. This removes the burden of explicit declaration of sequence type. In the event of non-nucleotide symbols, 2D supports the set of traditional ASCII values, from 0 to 127, inclusive. The motivation for such a rich lexicon of symbols is not merely to accommodate the handful of wildcards. In addition to wildcards, the other ASCII symbols could be used to support the direct inclusion of annotation data or to denote special subsequences, such as functional domains or special repeats. The representation of domains and repeats through additional symbols can be optionally applied to add a degree of structure-based coding within the 2D protocol, thereby increasing the overall efficacy of the compression method. The values for the non-printing ASCII characters are particularly good candidates for reassignment since supporting them does not offer utility for wildcards or annotation data. Finally, 2D needs to support a single general-purpose value for occurrences of symbols that are not categorized by the two previously defined sets.

To achieve compression, it is necessary to represent multiple bases with a single byte, as in the two-bits-per-base schema. 2D uses direct coding on a triplet (three consecutive nucleotide bases) basis for the following reasons. First, this allows for three nucleotide bases to be consolidated into a single byte, rather than multiple bytes. Second, by compressing on a triplet basis, rather than a two-bit basis, unexpected symbols can be coded directly. This removes the need for a wildcard elimination phase and for storage of wildcard data in a secondary structure. This is beneficial both at compression time and decompression time. Last, representation in terms of triplets makes 2D highly amenable to decompression as a polypeptide sequence of amino acids by interpreting the triplets as codons.

The 2D model accommodates a total of 125 different triplets according to any of the nucleotide bases at any of the three triplet positions, such that the set of codons is {AAA, AAC, … , UUT, UUU}. Although some combinations should never occur because they violate the nucleotide base subsets for DNA and mRNA, such as ‘UUT’, these instances are accommodated in order to provide simplified arithmetic translation. Also, 128 different ASCII symbols are supported as extra symbols and a single unknown flag is included to denote a symbol that belongs to neither set. Table 1 shows the 2D model for representing symbols as either aggregate groups (triplets), wildcards or special data (single characters), or as unknown.

Table 1.

The 2D data model^a

Type	Description	Range	Compressible
Auxiliary	ASCII	0 to 127	No
Sequence	Triplet	−1 to −125	Yes
Unknown	?	−128	No

^aFor sequence data, auxiliary data and unknown values, the range of byte values is listed as well as whether the data will be compressed or uncompressed.

Coding

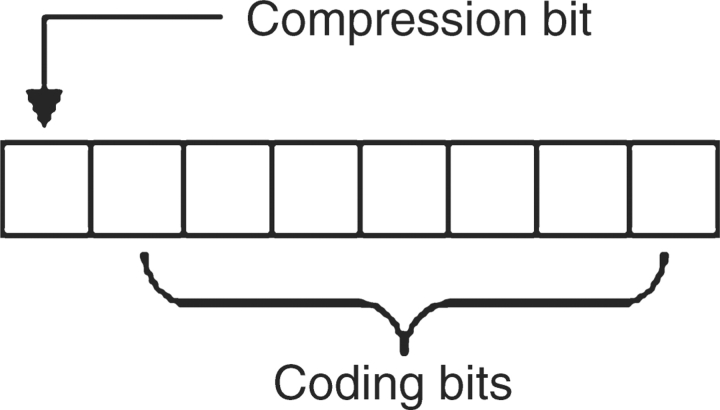
At the lowest level, 2D uses a signed byte that can range in value from −128 to 127 inclusive. Conceptually, the low seven bits of each byte are used for coding and the most significant bit is used as a compression flag. This schema is shown in Figure 1.

Figure 1.

The 2D byte coding schema. The seven least significant bits are used to encode data. The most significant bit is used as a flag to indicate the context of the byte as either compressed data or uncompressed data.

Symbols are sequentially parsed into triplets if each member is a valid nucleotide base. A valid triplet is assigned a single value ranging from 1 to 125 inclusive and the compression flag is set, equating to assigning a value between −1 and −125 inclusive. 2D will attempt to differentiate between sequence data and other symbols and if an unexpected value occurs that is interpretable as an ASCII value ranging from 0 to 127 inclusive, then this value is stored verbatim and the compression flag is not set, equating to assigning a value from 0 to 127 inclusive. In the event of an unexpected value, the other members of the current triplet must also be encoded individually and uncompressed, whether nucleotide bases or not, in order to maintain the current reading frame to support interpretation as an accurate polypeptide. By default, implementations can assume that the desired reading frame begins with the start of the sequence. However, multiple reading frames are easily supported by encoding the first symbol or the first two symbols as uncompressed data and then commencing the 2D process. Finally, in the event of an unknown symbol 2D denotes this by storing it uncompressed as the minimum possible signed byte value, −128. The values −126 and −127 are currently unused. Table 2 illustrates the 2D encoding steps to produce a compressed nucleotide sequence from an input string of symbols that includes an auxiliary symbol.

Table 2.

The 2D encoding process^a

Step	Input sequence	Triplet	Uncompress count	Encoded sequence
0	ACTCNTGAGA	Empty	0	Empty
1	CTCNTGAGA	A	0	Empty
2	TCNTGAGA	AC	0	Empty
3a	CNTGAGA	ACT	0	Empty
3b	CNTGAGA	Empty	0	∼
4	NTGAGA	C	0	∼
5a	TGAGA	Empty	0	∼C
5b	TGAGA	Empty	0	∼CN
6	GAGA	Empty	1	∼CNT
7	AGA	G	0	∼CNT
8	GA	GA	0	∼CNT
9a	A	GAG	0	∼CNT
9b	A	Empty	0	∼CNTÀ
10	Empty	A	0	∼CNTÀA

^aAn example of encoding process is given for the sequence ACTCNTGAGA that contains the auxiliary symbol N. The remaining input symbols, any symbols cached in the triplet structure, the value of the uncompress count (a variable to offset compression after the occurrence of an auxiliary symbol), and the encoded sequence are shown for each step in the process.

Algorithm

The following psuedocode describes the core 2D compression algorithm that takes an input string and returns a 2D encoding of the input sequence as a byte array. A more complete demonstration tool has been implemented using Java to support the Windows-1252 character set for Windows platforms and the MacRoman character set for Apple Macintosh platforms. This tool is available as an accompanying JAR file that will compress and decompress sequence data on the basis of entire files rather than individual strings. It should be noted that this particular implementation defines lossless in terms of file sequence rather than specific line formatting. Decompressed data are restored into lines with lengths of mod 3. For example, if the source file's sequence was parsed into lines of 70 symbols each, then the restored file's sequence will have line lengths of 69, 69, 72, 69, 69, 72, etc. This was done in an effort to increase overall compression while maintaining readability. However, if required, a completely faithful line-by-line version can be easily implemented at the cost of a minor reduction in overall compression. Future efforts could include a purely byte-based implementation, rather than character-based, to maximize the degree of compression, particularly if file layout and formatting are not requisites. The use of blocked I/O should also be considered.

begin

byte list = new List

 char triplet = new Array

 int baseCount = 0

 int nonCompressCount = 0

 foreach character c in input string

  if nonCompressCount = 0 then

   if c is a nucleotide base then

    triplet at position baseCount = c

    baseCount = baseCount + 1

    if baseCount = 3 then

     convert triplet to byte b and add b to list

     reset triplet

     baseCount = 0

   else

    foreach character t in triplet

     convert t to byte b and add b to list

    endfor

    convert c to byte b and add b to list

    reset triplet

    nonCompressCount = 2 - baseCount

    baseCount = 0

  else

   convert c to byte b and add b to list

   nonCompressCount = nonCompressCount - 1

 endfor

return list as byte Array

end

Compression ratio

Because 2D uses a direct coding schema, its compression ratio, as defined by original size divided by encoded size, can be approximated by a general formula. Assuming a requirement of one byte to represent an uncompressed symbol as a character, the following considerations can be used to derive a predictive formula. If the sequence is assumed to be composed only of nucleotide bases and has a length of L symbols and therefore a size of L bytes, then its encoded size will be (L/3 + L mod 3) bytes which is the sum of all triplets plus any remaining symbols. However, it is likely that auxiliary symbols will occur at some approximate frequency. Since the occurrence of one or more of such symbols within a given triplet will cause all of the triplet members to be encoded at a cost of one byte each, there is an added cost of two bytes to each triplet (this triplet now requires three bytes instead of one) that contains one or more auxiliary symbols. Therefore, two bytes must be added to the encoded size for each occurrence of an auxiliary symbol and there will be 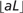such symbols, where a is the frequency of auxiliary symbols and the auxiliary symbols are randomly distributed, rather than packed together. Thus, the size of a 2D encoded sequence can be approximated by the following general formula:

This formula can be substituted into the original definition for compression ratio to provide a general formula for the 2D compression ratio:

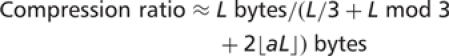Benchmarking

In order to test 2D, it was used to compress several bacterial genomes and its performance was compared against several other compression utilities. The Bacillus subtilis and Escherichia coli K12 MG1655 genomes were selected because they are commonly used model genomes and the Mycoplasma genitalium genome was selected because of its small size and the expectation that some of the compression utilities may perform poorly with sequence data of genomic proportions. All genomes were downloaded from the NCBI FTP server and the files were not modified in any way, thereby conserving the header data as well as the actual genomic sequence. Except for GenCompress, all compression utilities were run on an iMac5,1 with 3 GB of memory. The MS-DOS executable for GenCompress was run on a Gateway laptop with comparable hardware and 1 GB of memory. It should be noted that the benchmarking process itself incurs a certain amount of computational overhead and therefore may introduce an artifact of inflated execution times. However, this effect can be minimized by using sufficiently long sequences.

The results show that gzip provided the best compression ratios while 2D had the fastest execution times. If 2D was applied and followed immediately with gzip, this provided the best compression ratios and at execution times that were still faster than gzip alone. The MS-DOS executable for GenCompress failed before completion after a considerable execution time, even for the smallest genome. Despite the similarity in compression ratios for the 2D-compressed genomes the frequencies of the auxiliary symbols were 2.1E–05 (89 out of 4 214 719) for B. subtilis, 1.9E–05 (88 out of 4 639 763) for E. coli K12 MG1655, and 1.3E–04 (73 out of 580 149) for M. genitalium. However, in all cases the auxiliary symbols were contained only in the sequence header, a single line FASTA identifier at the beginning of each file. Therefore, the actual sequences were compressed uniformly and the overall compression ratios were similarly impacted by the condensed occurrence of a similar number of auxiliary symbols at the start of each file. Table 3 summarizes the compression results.

Table 3.

Genomic compression benchmarking^a

Compression method	Source genome
	Bacillus subtilis			Escherichia coli K12 MG1655			Mycoplasma genitalium
	Size (bytes)	Ratio	Time (ms)	Size (bytes)	Ratio	Time (ms)	Size (bytes)	Ratio	Time (ms)
None	4 274 929	1.000	N/A	4 706 046	1.000	N/A	588 437	1.000	N/A
GenCompress	0	Ø	58 363 756	0	Ø	27 887 599	0	Ø	8 127 438
2D	1 465 177	2.918	717.5	1 612 930	2.918	788.9	201 721	2.917	100.5
gzip	1 300 308	3.288	1671.3	1 431 844	3.287	1819.4	174 398	3.374	254.5
2D + gzip	1 093 657	3.909	824.9	1 214 444	3.875	891.3	145 727	4.038	182.8

^aCompression data for GenCompress, 2D, gzip and 2D + gzip was obtained using three bacterial genomes. File size, compression ratio and execution time are given for each algorithm with respect to each genome. Execution time is the average result from 100 trials with the exception of GenCompress which is the shortest execution time obtained after three consecutive failures.

Decompression for 2D was also tested by restoring the 2D-compressed genomes. A consistent file size increase of one byte was observed in all cases along with an increase in file length of one line. Unless a sequence has a last line length that is divisible by three when combined with any symbols that may already be cached in the compression buffer, then there will be either one or two remainder symbols. The current implementation will treat any remainder symbols as uncompressible symbols and deposit them on their own line at the end of the compressed sequence. In the case of the test genomes, the compressed files became one line longer than their source files because they each had remainder symbols that were uncompressible. This resulted in the creation of one new line for each compressed file and this increase was propagated during decompression. To verify this, the last line of symbols from each decompressed file was merged with the previous line and both the original line count and original file size were restored. Table 4 shows the decompression results.

Table 4.

Genomic decompression benchmarking^a

Source genome	File size (bytes)			File inflation		Decomp. time (ms)
	Normal	2D Comp.	2D Decomp.	Bytes	Lines
Bacillus subtilis	4 274 929	1 465 177	4 274 930	1	1	923.9
Escherichia coli K12 MG1655	4 706 046	1 612 930	4 706 047	1	1	1042.3
Mycoplasma genitalium	588 437	201 721	588 438	1	1	116.2

^aDecompression data was obtained using the 2D compressed genomes. File sizes are given for the original source file, the compressed file and the decompressed file, with respect to each genome. The differences between the original sizes and the restored sizes are also given along with the respective execution times. Execution time is the average result from 100 trials.

To test its robustness for use with very large data sets, 2D was used to compress the Sargasso Sea metagenome, a 918.1 MB FASTA format file available from the Sorcerer II Expedition website (21). This file is interesting because it contains a very large ratio of auxiliary data to sequence data since the metagenome is broken into a vast number of individual FASTA records rather than having a single header at the beginning. 2D performance was measured against gzip, bzip2 and against 2D in combination with gzip. As with the genomes, 2D had a faster execution time than gzip, while gzip had a better compression ratio. Moreover, bzip2 yielded an even better compression ratio in slightly less time than gzip but was considerably slower than 2D. However, the combination of both 2D and gzip produced the best compression ratio in less time than gzip alone or bzip2. Table 5 summarizes the results for compression of the metagenome.

Table 5.

Metagenomic compression benchmarking^a

Compression method	Sargasso sea metagenome
	Size (bytes)	Ratio	Time (ms)
None	962 651 334	1.000	N/A
2D	419 368 931	2.295	145 115.0
gzip	261 995 558	3.674	315 564.6
bzip2	238 973 241	4.028	301 924.0
2D + gzip	220 487 270	4.366	153 175.8

^aCompression data for 2D, gzip, bzip2, and 2D + gzip was obtained using the Sargasso Sea metagenome. File size, compression ratio and execution time are given for each algorithm. Execution time is the average result from five trials.

It was observed that 2D read 11 418 321 lines from the source file but wrote 11 959 572 lines to the compressed file resulting in a gain of 541 251 lines and a definite decrease in the compression ratio that was obtained for the metagenome. The Sargasso Sea metagenome is composed of 811 372 sequence fragments. Since each sequence begins with a header of auxiliary symbols, any remaining symbols from a previous sequence are written to their own line before processing the upcoming header. The current implementation does this in an effort to maintain human readability between sequences. Future implementations should abandon this behavior to improve the overall compression ratio.

Conclusion

2D provides a general-purpose nucleotide compression protocol that can differentiate between sequence data and auxiliary data thereby offering reconciliation between sequence-specific and general-purpose compression strategies. This makes 2D suitable for any type of sequence data, including very large data sets, such as metagenomes. Because it supports the inclusion of auxiliary symbols that are not members of the set of expected nucleotide bases, the source sequence can contain a rich lexicon of added symbols that can represent wildcard symbols, annotation data or special subsequences, such as functional domains or special repeats. The representation of domains and repeats through additional symbols can be applied to add a degree of structure-based coding within the 2D protocol, thereby providing a means to increase the overall degree of compression. Also, the encapsulation of unexpected symbols within the primary representation removes the need for a wildcard elimination phase and storage of wildcard data in a secondary structure. This is also a benefit at decompression time when unexpected symbols must be restored. 2D employs compression by triplets making the compressed representation immediately amenable to interpretation as a polypeptide. 2D-encoded sequences may be subsequently compressed by other compression protocols to further the overall degree of compression as demonstrated by its combination with gzip. 2D has the potential to have a beneficial impact on disk traffic for database queries and other disk intensive operations.

Supplementary data

Supplementary data are available at DATABASE Online.

Funding

Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant to Gabriel Moreno-Hagelsieb.

Conflict of interest statement. None declared.