Abstract
Extracranial patterns of scalp potentials and magnetic fields, as measured with electro‐ and magnetoencephalography (EEG, MEG), are spatially widespread even when the underlying source in the brain is focal. Therefore, loss in signal magnitude due to cancellation is expected when multiple brain regions are simultaneously active. We characterized these cancellation effects in EEG and MEG using a forward model with sources constrained on an anatomically accurate reconstruction of the cortical surface. Prominent cancellation was found for both EEG and MEG in the case of multiple randomly distributed source dipoles, even when the number of simultaneous dipoles was small. Substantial cancellation occurred also for locally extended patches of simulated activity, when the patches extended to opposite walls of sulci and gyri. For large patches, a difference between EEG and MEG cancellation was seen, presumably due to selective cancellation of tangentially vs. radially oriented sources. Cancellation effects can be of importance when electrophysiological data are related to hemodynamic measures. Furthermore, the selective cancellation may be used to explain some observed differences between EEG and MEG in terms of focal vs. widespread cortical activity. Hum Brain Mapp, 2010. © 2009 Wiley‐Liss, Inc.
Keywords: magnetoencephalography, electroencephalography, forward model, inverse problem, cerebral cortex, cortical patch analysis
INTRODUCTION
Electro‐ and magnetoencephalography (EEG, MEG) are methods to study electrical brain activity by recording scalp potentials and extra‐cranial magnetic fields [Cohen and Halgren, 2009; Gevins et al., 1995; Hämäläinen et al., 1993]. EEG and MEG provide millisecond time resolution for noninvasive detection of human brain activity, and estimates of the locations of the underlying sources can be constructed on the basis of the spatial distribution of the EEG and MEG over the head [Baillet et al., 2001]. In part, the spatial resolution in EEG and MEG source estimates is limited by the spatial spread of the signal patterns generated even by focal sources. The spread depends on the distance between the sources and the sensors; the minimum distance is limited by the thickness of the skull and scalp, and, in the case of MEG, the thickness of the Dewar vessel containing the superconducting SQUID sensors. When multiple sources are simultaneously active, their signal patterns are superimposed, and cancellation of signals of opposite polarity may occur. Cancellation reduces the overall signal‐to‐noise ratio, thereby contributing to the difficulty of source estimation. In general, when interpreting EEG and MEG data, it is important to take into consideration the overall pattern of simultaneous activation across the brain. This is different from such techniques as functional magnetic resonance imaging (fMRI) in which the signals from individual voxels can be observed largely independently. Here, we attempt to characterize cancellation effects in EEG and MEG signal patterns.
The sources of EEG and MEG signals are described in terms of primary currents [Plonsey, 1969; Tripp, 1983]. The active primary currents give rise to the electric potential distribution, which can be measured on the scalp using EEG. In addition, there will be associated passive volume currents at locations where the gradient of the electric potential differs from zero. However, the primary currents, together with the conductivity geometry of the head, determine the electric potentials and the volume currents; therefore, it is convenient to express the signals conceptually as functions of the primary currents. The main contribution to the primary currents detectable with EEG and MEG comes from ionic currents in the apical dendrites of cortical pyramidal cells, which are mostly aligned perpendicular to the local cortical surface [Hämäläinen et al., 1993; Lopes da Silva, 1991; Okada et al., 1999]. These currents result from both postsynaptic and active transmembrane currents. For symmetry reasons, the signals from other types of active currents at the cellular level are expected to cancel out macroscopically or generate electric potentials and magnetic fields which fall off rapidly with distance. These invisible currents include transmembrane currents themselves, postsynaptic currents in stellate cells or in the basal dendrites of pyramidal cells, as well as the quadrupole‐like current patterns associated with action potentials [Humphrey, 1968a, b; Lorente de No, 1947]. Therefore, it is reasonable to assume that the primary currents underlying the extracranial EEG and MEG signals are located in the cortical gray matter, oriented perpendicular to the cortical surface.
In EEG and MEG source analysis, the basic element for the primary current distribution is a current dipole, which summarizes the net effect of the microscopic currents within a volume of a few cubic millimeters, or a few square mm of cortical surface. At the intermediate spatial scale of about 1 cm and above, the folding of the cerebral cortex adds a macroscopic geometric factor, which can be examined using the detailed anatomical information provided by structural MRI. For example, the spatial frequency spectrum of cortical gyrification has been related to the pattern of spatial coherence in scalp EEG [Freeman et al., 2003]. Cancellation of the EEG and MEG signals occurs when the cortical activity extends over a region where the surface normal, and therefore, also the orientation of the source elements, changes. In particular, cancellation occurs when the activation involves opposing walls of a sulcus or a gyrus. Figure 1A depicts simulated EEG and MEG signals from two current dipoles of opposite direction in the primary visual cortex in the calcarine region, which mostly cancel out when the dipoles are active simultaneously. Even at the spatial scale of several centimeters, corresponding to activity distributed over multiple regions across the whole cortex, large amount of cancellation of spatially overlapping EEG or MEG signal patterns can occur. Partial cancellation is illustrated in Figure 1B with sources in the inferior occipitotemporal region of the left and right hemispheres.
Figure 1.
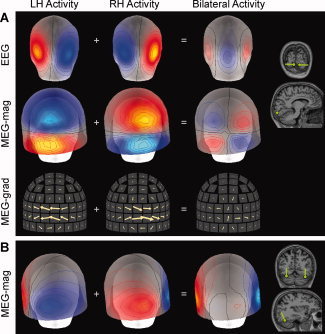
Examples of cancellation of EEG and MEG signals. A: Simulated data generated by two current dipoles in the primary visual cortex of the left and right hemispheres. The maps depict spatial patterns of signals over the occipital region when each dipole is active alone (LH: left hemisphere, RH: right hemisphere), and when the two dipoles are active simultaneously. Top: EEG isocontour maps; red and blue indicate positive and negative scalp potentials, respectively. Middle: MEG magnetometer isocontour maps; red and blue indicate positive and negative radial component of the magnetic field. Bottom: MEG gradiometer signals; each arrow depicts the signal in a pair of planar gradiometers. The arrows have been rotated by 90 degrees from orientation of the actual gradient vectors, to match the orientation of the arrows with the direction of underlying source currents. The locations (green dots) and orientations (green lines) of the dipoles are indicated in coronal and sagittal MRI slices. This example illustrates how cancellation can occur in all three types of sensor arrays, when sources of opposite orientation are close to each other. B: Maps of MEG magnetometer signals for bilateral inferior temporal sources. For this particular source configuration, the cancellation is specific to mid‐occipital MEG magnetometer sensors. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
We refer to local patches of activity as extended sources, whereas distributed source patterns may consist of multiple local foci or patches of activity in separate regions of the cortex. This terminology is useful also in the context of source estimation: on one hand, a single equivalent dipole is usually an adequate model, not only for very small foci, but also for moderately extended source patches, such as those corresponding to various types of sensory evoked responses. On the other hand, distributed source models are particularly useful for widely spread activation that consists of multiple simultaneously active functional areas, as is often the case, e.g., with language‐related activity. In the present study, we explore the cancellation effects in EEG and MEG signals using a realistic reconstruction of the cortical surface [Dale et al., 1999; Dale and Sereno, 1993; Fischl et al., 1999]. For quantitative analysis, we calculated a measure of cancellation for multiple randomly distributed source dipoles across the cortex as well as for locally extended patches of activity.
MATERIALS AND METHODS
Forward Model
The forward model is used to calculate the signals in a set of sensors, due to dipolar source elements of unit magnitude. The relationship between the EEG and MEG signals (signal vector v, with the dimension equaling the number of sensors) and the source amplitudes (source vector q, with the dimension equaling the number of dipole elements) is linear: v = A q, where A is the forward matrix, often also called the lead‐field matrix. The column vectors a j of A correspond to the signal patterns generated by a single source element of unit amplitude whereas each row of A contains samples of the lead‐field or sensitivity pattern of a given sensor. To calculate A, one needs to specify the location and orientation of each source element, the electromagnetic properties of the tissues within the head (in particular, the conductivity geometry), and the location, orientation, and configuration of the sensors. Here, we restricted the sources to be located on a realistic reconstruction of the cortical surface, oriented perpendicular to the surface, used the boundary element model (BEM) for the conductivity geometry of the head, and chose commonly used whole‐head EEG and MEG sensor array configurations.
The forward model was based on data from a 42‐year‐old male volunteer subject. The procedures were approved by the Massachusetts General Hospital Institutional Review Board. High‐resolution structural T1‐weighted magnetic resonance images (MRIs) were acquired on a 1.5 T Siemens scanner (TR = 2530 ms, TE = 3.25 ms, flip angle = 7, 128 sagittal slices, slice thickness = 1.3 mm, voxel size = 1.3 × 1.0 × 1.3 mm3). A surface representation for the cerebral cortex was constructed from the MRI using the FreeSurfer software [Dale et al., 1999; Fischl et al., 1999]. A mesh of about 300,000 vertices was created, with an average distance of about 1 mm between neighboring source points. Each vertex on the surface corresponding to the gray‐white matter border was selected to represent the location of an MEG and EEG source element (current dipole). Selecting the inner surface of the cerebral cortex, rather than, e.g., the middle of the gray matter, helped to avoid numerical instabilities that can occur if the dipoles are very close to the brain‐skull interface, where the conductivity change is large. In our forward model, sources were included also in the noncortical medial regions corresponding to corpus callosum and thalamus that complete the closed surface representation of each hemisphere. The orientation of each source element was assumed to match the local surface normal.
The conductivity geometry of the head was modeled using a boundary element model with three compartments: the brain, the skull, and the scalp. The boundaries were determined from the MRI by identifying the inner and outer surfaces of the skull and the outer surface of the skin [Hamalainen and Sarvas, 1989; Oostendorp and van Oosterom, 1989]. Each surface consisted of 5,120 vertices; the linear collocation method was used in the BEM calculations [Mosher et al., 1999]. This provides a reasonable accuracy for most cortical source locations [Yvert et al., 1996]. The accuracy of the forward model for the most superficial sources close to the inner surface of the skull may suffer from the sparseness of the BEM vertices [Fuchs et al., 2001]. However, these inaccuracies are expected to have only small effect on the cancellation explored in the present study, except if very large values for the elements of the forward matrix are obtained because of numerical instabilities in the BEM calculations. To exclude this possibility, we checked that there were no outliers (very large values) among the elements of the forward matrix. The conductivity ratios of 1:0.0125:1 were assumed for brain:skull:scalp [Geddes and Baker, 1967].
We used existing MEG and EEG sensor configurations based on actual experimental setup, with a 306‐channel MEG system (VectorView, Elekta Neuromag) and an EEG cap with 60 scalp electrodes. Of the MEG sensors, 102 were magnetometers, measuring the magnetic field component approximately radial to the surface of the head, and 204 were planar first‐order gradiometers, measuring the tangential derivative of the radial component of the magnetic field. The location and orientation of the MEG sensor array with respect to the head were determined with the help of small marker coils approximating magnetic dipoles attached to the head. The position of the marker coils and the EEG electrodes with respect to anatomical landmarks (nasion, preauricular points, and several additional points on the scalp and face) were determined with a 3D digitizer (Polhemus).
Cancellation Index
To quantify cancellation effects, we compared the length of the signal vector generated by n simultaneous sources
| (1) |
with the sum of the signal vector lengths for the same sources when active individually
| (2) |
Here a ij are the elements of the forward matrix, M is the number of sensors. For cortical patch analysis, the forward solution a j for each source element in Eqs. (1) and (2) was scaled by the area δj associated with the source, i.e., a j was replaced by δj a j.
The cancellation index I C was defined as:
| (3) |
which ranges from 0 to 1. If the net signal pattern for simultaneous sources is zero, then α = 0 and I C = 1, corresponding to full (100%) cancellation. If there is no overlap between the signal patterns of the individual sources, then α = β and I C = 0, indicating absence of cancellation.
Simulated Source Patterns
We calculated the cancellation index for two types of source configurations: (1) individual source elements (current dipoles) distributed randomly across the cortical surface and (2) patches of uniform activity within the cortex.
For the distributed dipole configuration, the number n of simultaneous source elements ranged from a single dipole up to the total number of vertices in the reconstructed cortex representation. The amplitudes for the source elements were derived from a random zero‐mean Gaussian distribution. The cancellation index I C(n) was estimated by averaging the values obtained for 1,000 random selections of n dipoles.
The cortical patches consisted of neighboring source elements within a given distance (“radius”) from the center of the patch. The distances were computed along the cortical surface using the Dijkstra algorithm [Lin et al., 2006]. The radius of a patch was varied from 1 to 50 mm (the largest patches corresponding to n = 15,000 dipole elements). Two hundred locations for the patches were chosen randomly on the cortical surface.
To relate the cancellation index for patches with the local curvature properties of the cortex, we computed an orientation nonuniformity index I O, defined as:
| (4) |
where
| (5) |
is the averaged dipole moment vector within a patch, and
| (6) |
is the area of the patch; δj is the area associated with a single vertex and n j is the corresponding surface normal vector. If all dipole elements within a patch have the same orientation, then I O = 0. If the dipole moment vectors are oriented such that their sum is zero, then I O = 1. This is analogous to a “closed source” configuration, in which the net dipole moment cancels out, resulting in minimal measurable signal when distance between the sensors and the patch is large compared with the size of the patch.
RESULTS
Randomly Distributed Dipoles
As shown in Figure 2, the mean cancellation index I C for randomly distributed dipoles on the cortical surface increased monotonically as a function of the number of source elements. Notable cancellation occurred even with a small number of sources: I C reached the value of about 0.5 with only five simultaneous dipoles. A small difference between EEG and MEG was seen for n < 100, with I C being larger for EEG than for MEG. For large values of n, I C approached unity; e.g., with 10,000 dipoles I C was ∼0.99, suggesting that substantial cancellation of EEG and MEG signals takes place when many sources are simultaneously active.
Figure 2.
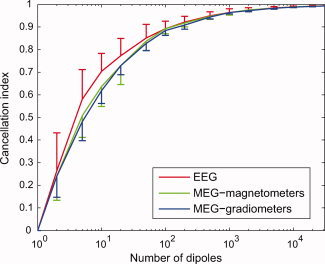
Cancellation index I C for randomly distributed sources. The index was computed for an array of 60 EEG electrodes, 102 MEG magnetometers, and 204 MEG gradiometers. The mean and standard deviation over 1,000 random selections of n dipoles are shown. For clarity, the standard deviation bars are plotted one‐sided only. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Extended Patches of Activity
An example of EEG and MEG signal patterns generated by uniformly activated cortical patches of two different sizes is shown in Figure 3. The signal pattern due to a small patch is likely to be similar to that of a single dipole (Fig. 3A), whereas substantial cancellation is expected to occur when the patch is large enough to extend to opposite walls of a sulcus or a gyrus (Fig. 3B,C). To emphasize the cancellation effect per source element, the maps in Figure 3 were scaled by the patch area. Note, however, that the absolute peak signal magnitudes in this example were larger for the large patch than for the small patch, though only by a factor of about seven for EEG and two for MEG, i.e., much less than 25, which was the ratio of the areas.
Figure 3.
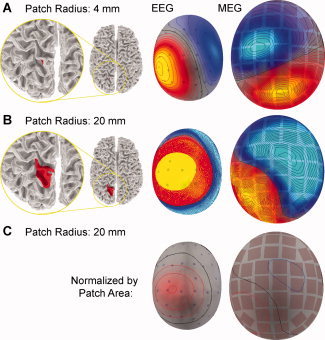
Examples of EEG and MEG signals for extended patches of uniform cortical activity. A patch with a 4‐mm (A) and 20‐mm (B) radius in the left parietal cortex is shown in red on a cortical surface representation reconstructed from anatomical MRI. The dots and squares indicate the locations of the EEG scalp electrodes and the MEG triple‐sensor units (one magnetometer and two gradiometers), respectively. Cancellation is illustrated by the signal per unit source element, obtained by plotting the maps for the 20‐mm patch normalized by the ratio of the areas of the two patches (C). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The mean value of the cancellation index I C for patches of different sizes is depicted in Figure 4. For very small patches, I C was close to zero, consistent with neighboring dipole elements having a similar orientation and consequently the signal patterns summating with little cancellation in either EEG or MEG. For intermediate patches (radii between 2 and 10 mm), I C increased rapidly as a function of the patch size, reaching I C = 0.5 for a radius of 10 mm; this suggests that the local curvature affected the orientation of the dipole elements within a patch, resulting in partial cancellation of the signals patterns. For large patches, the cancellation index depended only weakly on the size of the patch, reaching I C = 0.9 for MEG and ∼0.8 for EEG for patches with a radius of 50 mm. Thus, in contrast to the case of randomly distributed dipoles (cf. Fig. 2), there appeared to be a prominent difference between EEG and MEG in the cancellation of signals from large patches of uniform cortical activity. Note that it is essential here that all the dipole elements within a patch have the same polarity, corresponding to currents flowing either outward or inward with respect to the cortical surface.
Figure 4.
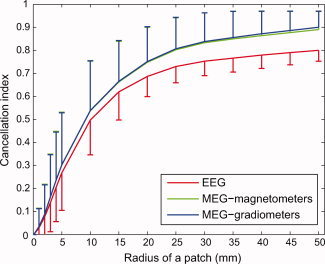
Cancellation index I C for cortical patches. The mean and standard deviation over 200 randomly located simulated patches of uniform activity for each of the different radii shown. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The relationship between the cancellation index I C for cortical patches and the corresponding orientation nonuniformity index I O is shown in Figure 5. I C is a measurement of the actual cancellation of the EEG and MEG signals, whereas I O only takes into account the mean dipole moment vector across the source elements within a patch, ignoring the location of each element. Figure 5 indicates that I C and I O were highly correlated. In the case of EEG, the two indices were close to being equal for most of the patches, suggesting that the cancellation effects in EEG can be well approximated by the orientation nonuniformity, i.e., the cancellation was proportional to the net dipole moment obtained by summing the individual dipole moment vectors. For MEG, however, there were many patches for which I C > I O, i.e., points that were above the diagonal in Figure 5. For smaller patches, for which I C = 0.2–0.6, the occasional large values of I C for MEG can be understood in terms of the orientation of the net dipole moment being radial, resulting in very little MEG signal, i.e., α = 0 in Eq. (1). For large values of the indices, the points for MEG clustered around I C = 0.9 and I O = 0.8 instead of the diagonal, suggesting that there was more cancellation than would be predicted simply by the net dipole moment vector. Inspection of the distribution as a function of the patch size indicated that these points correspond to the largest patches. These off‐diagonal points found for MEG but not for EEG are presumably related to selective cancellation of tangential as compared with radial source components.
Figure 5.
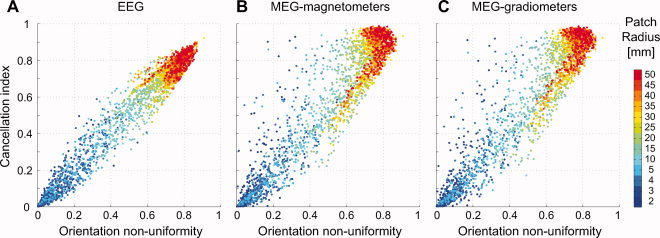
Comparison of the cancellation index I C and the orientation non‐uniformity measure I O for cortical patches. Data from simulated patches with different radii up to 50 mm are shown for EEG (A), MEG magnetometers (B), and MEG gradiometers (C). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
DISCUSSION
We quantified cancellation effects in EEG and MEG signal patterns due to cortical sources using an anatomically accurate model of the cortex. Substantial cancellation was found both for randomly distributed sources and for extended patches of activity. Later, we discuss implications of signal cancellation that depends on the distribution and extent of cortical activation to the interpretation of EEG and MEG data, particularly in terms of the integration of multimodal brain imaging data and different characteristics of EEG and MEG.
Relevance of Signal Cancellation in EEG and MEG Studies
Several sources of data suggest that both spontaneous and event‐related cortical activity is likely to be spatially extended [Halgren, 2004]. The cortex is highly interconnected, with each neuron receiving and sending ∼10,000–100,000 synapses with other neurons. A variety of data, including direct intracranial EEG recordings obtained in subjects undergoing diagnostic procedures prior to surgical therapy for epilepsy [Halgren et al., 1998], indicates that cortical activity can spread widely in less than 30 ms. This suggests that with the possible exception of early sensory evoked responses, patterns of activation are often sufficiently widespread that the effects of cancellation are relevant to interpretation of EEG and MEG data.
Prominent cancellation is expected when the two walls of a sulcus are simultaneously active. Functional areas often cover both sides of a given sulcus. A well‐known example is the primary visual cortex, which is organized so that visual stimuli extending across the horizontal meridian will produce sources that cancel across the calcarine fissure. Cancellation may also occur where the opposite sides of the sulcus belong to distinct neurocognitive systems. For example, in the Sylvian fissure, primary and association auditory cortices in the ventral bank are contrasted with somatosensory and other cortices dorsally [Hari et al., 1993]. Also, bilateral activation of regions facing the interhemispheric fissure may produce cancellation (cf. Fig. 1A); such regions include the visual medial occipital, cingulate, and supplementary motor areas [Lang et al., 1991].
An important goal of many MEG and EEG studies is to determine the spatiotemporal patterns of source activity underlying the measured signals. Characterization of cancellation effects, combined with sensitivity analyses [de Jongh et al., 2005; Goldenholz et al., 2009; Hillebrand and Barnes, 2002], can provide valuable insights into what can and cannot be detected with EEG and MEG. The present study was based on the properties of the forward matrix only; thus, the results are not specific to any particular source estimation method. In the calculation of the electric potentials and magnetic fields, we assumed a piecewise homogeneous conductor of arbitrary shape and implemented the computations with a boundary‐element method, commonly used for EEG and MEG source estimation. More detailed head models that take into account local variations in conductivity and its anisotropy are not expected to change the major patterns of the forward solutions [Haueisen et al., 2002], and thus not to change much the cancellation measures.
The cancellation index for distributed sources is expected to depend somewhat on the design of the sensor array. For example, the overlap of signals, and therefore also the cancellation index I C, for sources located far apart is likely to be smaller for differential sensors, such as planar MEG gradiometers compared with magnetometers, or bipolar or Laplacian EEG derivation compared with a referential derivation. In general, meaningful comparisons between different sensor array designs require that the signal‐to‐noise ratio of the measurements is taken into account [Ahonen et al., 1993], which was beyond the scope of the present study. The similarity of the graphs for MEG magnetometers and gradiometers in Figure 2, however, suggest that the cancellation index is not overly sensitive to the specific sensor configuration.
Also, the exact number of sensors in the array does not have a major effect on the cancellation analysis. For example, the cancellation index in Figures 2 and 4 were almost identical for MEG gradiometers and MEG magnetometers, even though the number of gradiometers was twice the number of magnetometers. It appears that the arrays used here adequately captured those spatial frequencies that dominate the signal patterns and, therefore, also the cancellation effects. Increasing the sensor density would result in signals that are similar in neighboring sensors; this is expected to affect the cancellation index minimally, as its definition was such that, e.g., doubling the number of sensors by including each channel twice does not alter the value of the index. It is unlikely that the differences seen between EEG and MEG were due to the differences in the number of sensors. As will be discussed below, the main differences in the cancellation effects found between EEG and MEG are consistent with selective cancellation of radial vs. tangential source components, which is independent of the specific sensor arrays used.
Implications for Multimodal Spatiotemporal Brain Imaging
Cancellation effects are of concern when electrophysiological EEG and MEG data are compared with hemodynamic measures (fMRI, positron emission tomography, optical imaging) [Dale and Halgren, 2001] or with invasive intracranial recordings [Halgren et al., 1998; Lu and Williamson, 1991]. At the spatial scale of up to a few square millimeters of cortical surface, the net signal from a complex pattern of microscopic neural currents was represented by a single current dipole element in our forward model. This is adequate in practice, as only the dipolar term of the multipole expansion for a complex pattern of microscopic source currents contributes significantly to the recorded potentials and fields when the distance from the source to the sensors is much larger than the extent of the source [Nunez, 1995]. Details of the local current patterns and microscopic cancellation effects are beyond the spatial resolution of presently available non‐invasive imaging techniques. Thus, detailed quantitative comparisons with electrophysiological and hemodynamic measures have to rely on information provided by invasive intracranial recordings [Schroeder et al., 1998; Ulbert et al., 2001; Vaughan, 1982] and biophysical modeling [Jones et al., 2007; Murakami and Okada, 2006].
At the intermediate spatial scale of a few square centimeters of cortex, represented here by patches of extended activity, anatomical information about the local folding of the cortical surface can be used to estimate cancellation effects. In addition, information provided by fMRI about the spatial extent of local regions of activity could be incorporated in the cancellation analysis. Assumptions about activity within cortical patches can also be incorporated in inverse modeling [Fuchs et al., 1999; Han et al., 2007; Kincses et al., 1999; Lapalme et al., 2006; Lin et al., 2006].
At the whole‐cortex scale, cancellation of EEG and MEG can be large even for randomly distributed simultaneous sources. The reduction in the signal‐to‐noise ratio per source element due to cancellation may result in some active areas being detected with fMRI but not with EEG or MEG. This does not appear to be a serious problem, however, for approaches in which fMRI is used to suggest likely locations for the EEG and MEG sources: simulation studies have indicated that the inclusion of such noncontributing regions as fMRI priors have only little effect on the EEG and MEG source estimates [Ahlfors and Simpson, 2004; Im et al., 2005; Liu et al., 1998].
Differences Between EEG and MEG in Cancellation of Signals From Extended Sources
The cancellation analysis with extended patches of activity indicated a systematic difference between EEG and MEG that may have interesting implications to the interpretation of combined recordings of EEG and MEG. If a patch of uniform activity extends over multiple sulci and gyri, selective cancellation of signals from sources of particular orientation can occur. The dipole moments of source elements in the two walls of a sulcus point to opposite directions, resulting in strong cancellation of extracranial signals, whereas the sources on the crown of a gyrus and the bottom of a sulcus have the same direction and, thus, produce similar signal patterns that summate with minimal cancellation. In the lateral, dorsal, frontal, and posterior regions of the cerebral cortex, the canceling sources in sulcal walls are mainly tangentially oriented, whereas the noncanceling ones are radial. Since MEG is insensitive to radially oriented sources [Grynszpan and Geselowitz, 1973], strong cancellation is expected for MEG, whereas the radial sources will still generate prominent EEG signals [Eulitz et al., 1997; Freeman et al., 2009].
The roles of tangential and radial sources are interchanged in the ventral and medial parts of the cortex. For these regions, the main orientation of the nonopposing gyral source elements is tangential, whereas the canceling sources in the sulcal walls have a predominantly radial orientation. Therefore, signals from extended sources in these regions should be present in both EEG and MEG. However, as mentioned above, bilateral activity of functional areas in the medial wall of the cerebral hemispheres is likely to result in strong cancellation [Lang et al., 1991].
Selective cancellation of radial vs. tangential sources could underlie some of the differences seen between EEG and MEG in cognitive event‐related responses [Eulitz et al., 1997]. For example, the amplitude of the P300 component is typically large in central scalp EEG electrodes, whereas in MEG the P300 is often small and scattered across sensors [Siedenberg et al., 1996]. This is consistent with signal patterns generated by large patches of activity, for which the EEG is expected to mostly reflect the superficial radial sources on the top of the gyri, but the corresponding MEG only reflects the residual signals remaining from incomplete cancellation of tangential sources. A widely distributed pattern of cortical activity related to the P300 has also been observed in intracortical recordings [Halgren et al., 1998] and in fMRI [Kiehl and Liddle, 2003]. The difference in the selective cancellation of EEG and MEG signals could also be helpful in identifying the presence of extended regions of synchronized oscillatory activity [Freeman et al., 2009].
Selective cancellation of spontaneous background activity is also likely to contribute to differences in the SNR of event‐related activity in EEG and MEG. For example, inter‐ictal epileptogenic discharges are sometimes detected either in EEG or in MEG but not necessarily in both [Iwasaki et al., 2005; Knake et al., 2006; Lin et al., 2003]; explanation for this may lie in the combination of differential sensitivity of EEG vs. MEG to the source of interest [de Jongh et al., 2005; Goldenholz et al., 2009; Hillebrand and Barnes, 2002] as well as in the selective cancellation of widespread background brain activity [de Munck et al., 1992]. These considerations support the view that EEG and MEG provide complementary information of human brain activity [Cohen and Cuffin, 1983; Hari and Ilmoniemi, 1986; Wood et al., 1985] and that these two closely related measures should be combined for optimal results. Both experimental [Sharon et al., 2007] and theoretical [Molins et al., 2008] results have suggested that the accuracy of source estimates can improve beyond the capabilities of EEG or MEG alone by combining data acquired with the two methods.
CONCLUSIONS
Substantial amount of cancellation can occur in extracranial EEG and MEG signals generated by simultaneously active sources. For extended patches of activity, selective cancellation of signals due to sulcal vs. gyral sources can result in a systematic difference between EEG and MEG. These effects are independent of the source estimation method employed and can be important in explaining differences in experimental data obtained with EEG and MEG.
Acknowledgements
The authors thank David Cohen, Anders Dale, Ksenija Marinkovic, Maria Mody, and Suresh Narayanan for useful discussions and comments.
REFERENCES
- Ahlfors SP, Simpson GV ( 2004): Geometrical interpretation of fMRI‐guided MEG/EEG inverse estimates. Neuroimage 22: 323–332. [DOI] [PubMed] [Google Scholar]
- Ahonen AI, Hamalainen MS, Ilmoniemi RJ, Kajola MJ, Knuutila JE, Simola JT, Vilkman VA ( 1993): Sampling theory for neuromagnetic detector arrays. IEEE Trans Biomed Eng 40: 859–869. [DOI] [PubMed] [Google Scholar]
- Baillet S, Mosher JC, Leahy RM ( 2001): Electromagnetic brain mapping. IEEE Signal Proc Mag 18: 14–30. [Google Scholar]
- Cohen D, Cuffin BN ( 1983): Demonstration of useful differences between magnetoencephalogram and electroencephalogram. Electroencephalogr Clin Neurophysiol 56: 38–51. [DOI] [PubMed] [Google Scholar]
- Cohen D, Halgren E ( 2009): Magnetoencephalography In: Squire LR, editor. Encyclopedia of Neuroscience, Vol. 5, pp. 615–622. Oxford: Academic Press. [Google Scholar]
- Dale AM, Halgren E ( 2001): Spatiotemporal mapping of brain activity by integration of multiple imaging modalities. Curr Opin Neurobiol 11: 202–208. [DOI] [PubMed] [Google Scholar]
- Dale AM, Sereno MI ( 1993): Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: A linear approach. J Cogn Neurosci 5: 162–176. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI ( 1999): Cortical surface‐based analysis. I. Segmentation and surface reconstruction. NeuroImage 9: 179–194. [DOI] [PubMed] [Google Scholar]
- de Jongh A, de Munck JC, Goncalves SI, Ossenblok P ( 2005): Differences in MEG/EEG epileptic spike yields explained by regional differences in signal‐to‐noise ratios. J Clin Neurophysiol 22: 153–158. [DOI] [PubMed] [Google Scholar]
- de Munck JC, Vijn PC, Lopes da Silva FH ( 1992): A random dipole model for spontaneous brain activity. IEEE Trans Biomed Eng 39: 791–804. [DOI] [PubMed] [Google Scholar]
- Eulitz C, Eulitz H, Elbert T ( 1997): Differential outcomes from magneto‐ and electroencephalography for the analysis of human cognition. Neurosci Lett 227: 185–188. [DOI] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Dale AM ( 1999): Cortical surface‐based analysis. II: Inflation, flattening, and a surface‐based coordinate system. NeuroImage 9: 195–207. [DOI] [PubMed] [Google Scholar]
- Freeman WJ, Ahlfors SP, Menon V ( 2009): Combining fMRI with EEG and MEG in order to relate patterns of brain activity to cognition. Int J Psychophysiol 73: 43–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman WJ, Holmes MD, Burke BC, Vanhatalo S ( 2003): Spatial spectra of scalp EEG and EMG from awake humans. Clin Neurophysiol 114: 1053–1068. [DOI] [PubMed] [Google Scholar]
- Fuchs M, Wagner M, Kastner J ( 2001): Boundary element method volume conductor models for EEG source reconstruction. Clin Neurophysiol 112: 1400–1407. [DOI] [PubMed] [Google Scholar]
- Fuchs M, Wagner M, Kohler T, Wischmann HA ( 1999): Linear and nonlinear current density reconstructions. J Clin Neurophysiol 16: 267–295. [DOI] [PubMed] [Google Scholar]
- Geddes LA, Baker LE ( 1967): The specific resistance of biological materials—A compendium of data for the biomedical engineer and physiologists. Med Biol Eng 5: 271–293. [DOI] [PubMed] [Google Scholar]
- Gevins A, Leong H, Smith ME, Le J, Du R ( 1995): Mapping cognitive brain function with modern high‐resolution electroencephalography. Trends Neurosci 18: 429–436. [DOI] [PubMed] [Google Scholar]
- Goldenholz DM, Ahlfors SP, Hamalainen MS, Sharon D, Ishitobi M, Vaina LM, Stufflebeam SM ( 2009): Mapping the signal‐to‐noise‐ratios of cortical sources in magnetoencephalography and electroencephalography. Hum Brain Mapp 30: 1077–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grynszpan F, Geselowitz DB ( 1973): Model studies of the magnetocardiogram. Biophys J 13: 911–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halgren E ( 2004): How can intracranial recordings assist MEG source localization? Neurol Clin Neurophysiol 2004: 86. [PubMed] [Google Scholar]
- Halgren E, Marinkovic K, Chauvel P ( 1998): Generators of the late cognitive potentials in auditory and visual oddball tasks. Electroencephalogr Clin Neurophysiol 106: 156–164. [DOI] [PubMed] [Google Scholar]
- Hämäläinen MS, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV ( 1993): Magnetoencephalography—Theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Modern Phys 65: 413–497. [Google Scholar]
- Hamalainen MS, Sarvas J ( 1989): Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE Trans Biomed Eng 36: 165–171. [DOI] [PubMed] [Google Scholar]
- Han J, Kim JS, Chung CK, Park KS ( 2007): Evaluation of smoothing in an iterative lp‐norm minimization algorithm for surface‐based source localization of MEG. Phys Med Biol 52: 4791–4803. [DOI] [PubMed] [Google Scholar]
- Hari R, Ilmoniemi RJ ( 1986): Cerebral magnetic fields. Crit Rev Biomed Eng 14, 93–126. [PubMed] [Google Scholar]
- Hari R, Karhu J, Hamalainen M, Knuutila J, Salonen O, Sams M, Vilkman V ( 1993): Functional organization of the human first and second somatosensory cortices: A neuromagnetic study. Eur J Neurosci 5: 724–734. [DOI] [PubMed] [Google Scholar]
- Haueisen J, Tuch DS, Ramon C, Schimpf PH, Wedeen VJ, George JS, Belliveau JW ( 2002): The influence of brain tissue anisotropy on human EEG and MEG. NeuroImage 15: 159–166. [DOI] [PubMed] [Google Scholar]
- Hillebrand A, Barnes GR ( 2002): A quantitative assessment of the sensitivity of whole‐head MEG to activity in the adult human cortex. NeuroImage 16: 638–650. [DOI] [PubMed] [Google Scholar]
- Humphrey DR ( 1968a) Re‐analysis of the antidromic cortical response. I. Potentials evoked by stimulation of the isolated pyramidal tract. Electroencephalogr Clin Neurophysiol 24: 116–129. [DOI] [PubMed] [Google Scholar]
- Humphrey DR ( 1968b) Re‐analysis of the antidromic cortical response. II. On the contribution of cell discharge and PSPs to the evoked potentials. Electroencephalogr Clin Neurophysiol 25: 421–442. [DOI] [PubMed] [Google Scholar]
- Im CH, Jung HK, Fujimaki N ( 2005): fMRI‐constrained MEG source imaging and consideration of fMRI invisible sources. Hum Brain Mapp 26: 110–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwasaki M, Pestana E, Burgess RC, Luders HO, Shamoto H, Nakasato N ( 2005): Detection of epileptiform activity by human interpreters: Blinded comparison between electroencephalography and magnetoencephalography. Epilepsia 46: 59–68. [DOI] [PubMed] [Google Scholar]
- Jones SR, Pritchett DL, Stufflebeam SM, Hamalainen M, Moore CI ( 2007): Neural correlates of tactile detection: A combined magnetoencephalography and biophysically based computational modeling study. J Neurosci 27: 10751–10764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiehl KA, Liddle PF ( 2003): Reproducibility of the hemodynamic response to auditory oddball stimuli: A six‐week test‐retest study. Hum Brain Mapp 18: 42–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kincses WE, Braun C, Kaiser S, Elbert T ( 1999): Modeling extended sources of event‐related potentials using anatomical and physiological constraints. Hum Brain Mapp 8: 182–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knake S, Halgren E, Shiraishi H, Hara K, Hamer HM, Grant PE, Carr VA, Foxe D, Camposano S, Busa E, Witzel T, Hamalainen MS, Ahlfors SP, Bromfield EB, Black PM, Bourgeois BF, Cole AJ, Cosgrove GR, Dworetzky BA, Madsen JR, Larsson PG, Schomer DL, Thiele EA, Dale AM, Rosen BR, Stufflebeam SM ( 2006): The value of multichannel MEG and EEG in the presurgical evaluation of 70 epilepsy patients. Epilepsy Res 69: 80–86. [DOI] [PubMed] [Google Scholar]
- Lang W, Cheyne D, Kristeva R, Beisteiner R, Lindinger G, Deecke L ( 1991): Three‐dimensional localization of SMA activity preceding voluntary movement. A study of electric and magnetic fields in a patient with infarction of the right supplementary motor area. Exp Brain Res 87: 688–695. [DOI] [PubMed] [Google Scholar]
- Lapalme E, Lina JM, Mattout J ( 2006): Data‐driven parceling and entropic inference in MEG. NeuroImage 30: 160–171. [DOI] [PubMed] [Google Scholar]
- Lin FH, Belliveau JW, Dale AM, Hamalainen MS ( 2006): Distributed current estimates using cortical orientation constraints. Hum Brain Mapp 27: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin YY, Shih YH, Hsieh JC, Yu HY, Yiu CH, Wong TT, Yeh TC, Kwan SY, Ho LT, Yen DJ, Wu ZA, Chang MS ( 2003): Magnetoencephalographic yield of interictal spikes in temporal lobe epilepsy. Comparison with scalp EEG recordings. NeuroImage 19: 1115–1126. [DOI] [PubMed] [Google Scholar]
- Liu AK, Belliveau JW, Dale AM ( 1998): Spatiotemporal imaging of human brain activity using fMRI constrained MEG data: Monte Carlo simulations. Proc Natl Acad Sci USA 95: 8945–8950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes da Silva F ( 1991): Neural mechanisms underlying brain waves: From neural membranes to networks. Electroencephalogr Clin Neurophysiol 79: 81–93. [DOI] [PubMed] [Google Scholar]
- Lorente de No R ( 1947): A study of nerve physiology In: Studies From the Rockefeller Institute for Medical Research New York: Rockefeller Institute for Medical Research, 1947, Vol. 132, chapter 16. [PubMed] [Google Scholar]
- Lu ZL, Williamson SJ ( 1991): Spatial extent of coherent sensory‐evoked cortical activity. Exp Brain Res 84: 411–416. [DOI] [PubMed] [Google Scholar]
- Molins A, Stufflebeam SM, Brown EN, Hamalainen MS ( 2008): Quantification of the benefit from integrating MEG and EEG data in minimum l2‐norm estimation. NeuroImage 42: 1069–1077. [DOI] [PubMed] [Google Scholar]
- Mosher JC, Leahy RM, Lewis PS ( 1999): EEG and MEG: Forward solutions for inverse methods. IEEE Trans Biomed Eng 46: 245–259. [DOI] [PubMed] [Google Scholar]
- Murakami S, Okada Y ( 2006): Contributions of principal neocortical neurons to magnetoencephalography and electroencephalography signals. J Physiol 575: 925–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunez P ( 1995): Neocortical Dynamics and Human EEG Rhythms. New York: Oxford University Press. [Google Scholar]
- Okada Y, Lahteenmaki A, Xu C ( 1999): Comparison of MEG and EEG on the basis of somatic evoked responses elicited by stimulation of the snout in the juvenile swine. Clin Neurophysiol 110, 214–229. [DOI] [PubMed] [Google Scholar]
- Oostendorp TF, van Oosterom A ( 1989): Source parameter estimation in inhomogeneous volume conductors of arbitrary shape. IEEE Trans Biomed Eng 36: 382–391. [DOI] [PubMed] [Google Scholar]
- Plonsey R ( 1969): Bioelectric Phenomena. New York: McGraw‐Hill. [Google Scholar]
- Schroeder CE, Mehta AD, Givre SJ ( 1998): A spatiotemporal profile of visual system activation revealed by current source density analysis in the awake macaque. Cereb Cortex 8: 575–592. [DOI] [PubMed] [Google Scholar]
- Sharon D, Hamalainen MS, Tootell RB, Halgren E, Belliveau JW ( 2007): The advantage of combining MEG and EEG: Comparison to fMRI in focally stimulated visual cortex. NeuroImage 36: 1225–1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siedenberg R, Goodin DS, Aminoff MJ, Rowley HA, Roberts TP ( 1996): Comparison of late components in simultaneously recorded event‐related electrical potentials and event‐related magnetic fields. Electroencephalogr Clin Neurophysiol 99: 191–197. [DOI] [PubMed] [Google Scholar]
- Tripp JH ( 1983): Physical concepts and mathematical models In: Williamson SJ, Romani G‐L, Kaufman L, Modena I, editors. Biomagnetism: An Interdisciplinary Approach. New York: Plenum Press; pp 101–139. [Google Scholar]
- Ulbert I, Karmos G, Heit G, Halgren E ( 2001): Early discrimination of coherent versus incoherent motion by multiunit and synaptic activity in human putative MT+. Hum Brain Mapp 13: 226–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan HG Jr ( 1982): The neural origins of human event‐related potentials. Ann N Y Acad Sci 388: 125–138. [DOI] [PubMed] [Google Scholar]
- Wood CC, Cohen D, Cuffin BN, Yarita M, Allison T ( 1985): Electrical sources in human somatosensory cortex: Identification by combined magnetic and potential recordings. Science 227: 1051–1053. [DOI] [PubMed] [Google Scholar]
- Yvert B, Bertrand O, Echallier JF, Pernier J ( 1996): Improved dipole localization using local mesh refinement of realistic head geometries: An EEG simulation study. Electroencephalogr Clin Neurophysiol 99: 79–89. [DOI] [PubMed] [Google Scholar]


