Abstract
Pre-steady-state stopped-flow analysis of E. coli D-3-phosphoglycerate dehydrogenase (PGDH) reveals that the physiological inhibitor, L-serine, exerts its effect on at least two steps in the kinetic mechanism, but to very different degrees. First, there is a small, but significant effect on the dissociation constant of NADH, the first substrate to bind in the ordered mechanism. The effect of serine is mainly on the binding off-rate, increasing the Kd to 5 μM and 23 μM from 0.6 μM and 9 μM respectively, for the two sets of sites in the enzyme. A more profound effect is seen after the second substrate is added. Serine reduces the amplitude of the signal without a significant effect on the observed rate constants for binding. The serine concentration that reduces the amplitude by 50% is equal to the K0.5 for serine inhibition. The data are consistent with the conclusion that serine binding eliminates a conformational change subsequent to substrate binding by formation of a dead-end quaternary complex consisting of enzyme, coenzyme, substrate, and effector. Thus, the mechanistic basis for V-type regulation in this enzyme is due to a reduction in the population of active species rather than to a differential decrease in the velocity of active species. Pre-steady-state analysis of serine binding to a mutant PGDH (W139F-E360W), demonstrates that each serine binding interface produces an integrated fluorescent signal. The observed rate data is complex but conforms to a model where serine can bind to two forms of the enzyme with different affinities. The integrated signal from each interface allows the amplitude data to clearly define the order of binding to each site and modeling the amplitude data with species distribution equations clearly demonstrates an alternate interface binding mechanism and the direction of the binding cooperativity.
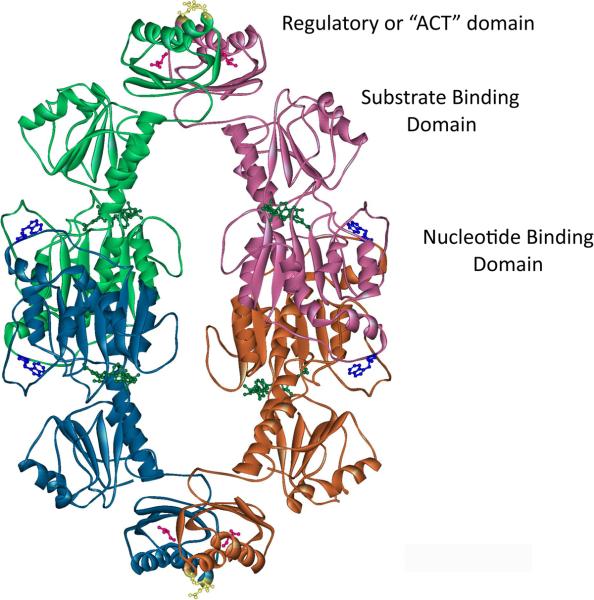
D-3-Phosphoglycerate dehydrogenase (PGDH1, E.C. 1.1.1.95) catalyzes an early step in the biosynthesis of L-serine by converting D-3-phosphoglyceric acid to hydroxypyruvic acid phosphate (HPAP), utilizing NAD+ as a coenzyme (1). In vitro, the equilibrium of the reaction lies far in the opposite direction so that the enzyme is most commonly assayed by monitoring the conversion of HPAP and NADH to phosphoglycerate and NAD+ by following the decrease in absorbance at 340 nm (2–4). In either direction, the reaction is inhibited by L-serine, the physiologic end-product of the synthetic pathway (3). E. coli PGDH is a tetramer made up of four identical subunits (Figure 1), each of which contains three distinct domains, the nucleotide binding domain, the substrate binding domain, and the regulatory domain (5). The regulatory domain binds the inhibitor, L-serine, and is recognized as the archetypical ACT domain. ACT domains are found in many proteins, primarily from bacteria, and function in binding small molecules (6, 7). These proteins function mainly in amino acid metabolism and as transcription factors. The ACT domain derives its name from three of the proteins, Aspartate kinase, Chorismate mutase, and TyrA, originally discovered to possess this motif from a PSI-Blast search of the NCBI non-redundant protein sequence database (6). The subunit interfaces in the PGDH tetramer are formed between two sets of nucleotide binding domains and two sets of ACT domains. L-serine binds at the interface between ACT domains, forming hydrogen bond contacts with both domains across the interface. Each pair of ACT domains displays 180° symmetry, with two serine binding sites at each interface for a total four serine binding sites.
Figure 1. The Structure of E. coli PGDH.
The structure of E. coli PGDH (pdb 1psd) is shown in ribbon diagram. Each of the subunits are colored to distinguish them in the figure. The positions of the domains are labeled. L-Serine (Pink) is shown in ball and stick form bound to two sites at each ACT domain interface (Green-Pink and Blue-Orange subunits). The position of E360 is shown in yellow ball and stick form in the ACT domains (top and bottom of figure). NADH (Green) and W139 (Blue) are shown in ball and stick form at each active site cleft.
Early work on E. coli PGDH demonstrated that it underwent V-type allosteric regulation where the binding of the inhibitor, L-serine, functioned primarily in reducing the rate of catalysis rather than the binding of substrate and coenzyme (3, 8). Early transient kinetic studies of serine binding utilized the observation that the fluorescence at 420 nm, due to a resonance energy transfer to bound NADH when excited through the protein tyrosine and tryptophan residues, decreased with increasing serine concentrations (9). The authors concluded that serine inhibits PGDH allosterically and that the rapid binding of serine to the enzyme is followed by a slower reversible isomerization. This resulted in the proposal of an “R” to “T” state conformational change model where serine binds preferentially to a “T” state at low concentrations and increasingly to an “R” state at high serine concentrations. This model was based primarily on the observation that the IC50 for steady state inhibition of activity was approximately 5 μM, while the half-maximal increase in the observed rate constant for the conformational transition based on this fluorescence change was approximately 55 μM. More recently, our studies, using hybrid tetramers of PGDH (10), demonstrated that almost complete inhibition of activity was produced after only 2 of the 4 serine binding sites were occupied. Equilibrium dialysis studies of serine binding demonstrated that the remaining 2 serine binding sites could be occupied but did not contribute significantly to the inhibition of activity (11, 12).
All of the early transient kinetic studies (8, 9) were done in the presence of NADH because the enzyme preparations available at that time had between 1–3 NADH molecules bound per tetramer. Recent transient kinetic analysis of E. coli PGDH (13) demonstrated that the NADH could be removed by first converting it to NAD+, so that analyses could also be conducted with coenzyme-free enzyme. This showed that substrate binding is ordered, with NADH binding first, and that the very tight binding of NADH was the result of a slow conformational change that occurred after the initial binding of the coenzyme. The rate constants determined for this conformational change showed that it occurred only in the absence of substrate and did not occur during continuous turnover of the enzyme. These studies demonstrated that the enzyme appeared to possess two sets of active sites, with one set predominating during continuous turnover. Both sets of sites bind NADH, but with different affinities, and the turnover of substrate to product is 4–5 fold faster at one set of sites than the other. The rate-limiting step in the direction of NADH oxidation was shown to be a conformational change that occurs between the binding of substrate and the conversion to products and that was kinetically distinguishable from another conformational change that also occurred after substrate binding and that could be observed optically.
The present study investigates the effect of the physiological inhibitor, L-serine, on the individual steps in the kinetic mechanism and demonstrates that while the inhibitor has an effect on NADH binding, its major effect involves the prevention of a conformational change that occurs after substrate binding and before catalytic turnover. This is accomplished by the formation of a dead-end complex of enzyme, serine, NADH, and substrate. This complex effectively reduces the amount of active enzyme and manifests itself as a modulation of the velocity of the reaction. The formation of this complex is the mechanistic basis for the V-type regulation of activity in this enzyme. Transient kinetic analysis of serine binding revealed that binding of serine to the last two sites, while not contributing substantially to inhibition of activity, produces a conformational change that contributes to the fluorescent signal. This is the basis for the discrepancy between the serine concentration that produces inhibition and that which produces the fluorescent signal. Furthermore, by engineering a fluorescent reporter at the serine binding interface, the exact order of serine binding to each of the four sites could be directly determined.
Materials and Methods
E. coli PGDH was expressed and isolated as previously described (13). Steady-state activity was monitored by following the change in absorbance at 340 nm from the conversion of NADH to NAD+. α-Ketoglutarate, a stable analog of the physiological substrate, hydroxypyruvic acid phosphate (HPAP) was used as the substrate (14). The concentration of native enzyme was determined using an E 1% of 6.7 at 280 nm (15).
Stopped-flow Fluorescence Spectroscopy
Pre-steady state kinetic analyses were performed with an Applied Photophysics Model SX-20 stopped-flow spectrometer. The reactions and all reagents were thermostated at 25° C with a circulating water bath. NADH binding was monitored by fluorescence resonance energy transfer (FRET) between protein tryptophan residues and bound NADH. The single tryptophan residue was excited at 295 nm and fluorescence was measured at 420 nm with a 420 nm band pass filter (13). The binding of α-ketoglutarate was measured in the presence of NADH by monitoring the increase in fluorescence at 340 nm as previously described (13). Serine binding was monitored by following the change in fluorescence of an engineered tryptophan residue at the serine binding interfaces. In this case, the protein was excited at 295 nm and the fluorescence change was measured with a 320 nm cutoff filter. All reactions were performed in 20 mM potassium phosphate buffer, pH 7.5.
A total of 1,000 points were collected for each trace and at least 10 individual traces were averaged at each set of conditions. The binding transients were analyzed either with the Pro-Data Viewer fitting software provided with the instrument or with the data fitting function of KinTek Global Kinetic Explorer (16, 17) and fit to a single or a sum of exponential functions defined as
| (Eq. 1) |
where Y is the fluorescence intensity at time t, kobs,i is the observed rate of the ith process with an amplitude of Ai and C is an offset value (18, 19). For NADH binding, linear plots of the observed rate (kobs) versus ligand concentration were fit to,
| (Eq. 2) |
where k1is the constant for the on rate and k−1 is the constant for the off rate for binding. For hyperbolic plots of the observed rates (kobs) versus ligand concentration were fit to,
| (Eq. 3) |
where Kd is the dissociation constant for binding and k2 and k−2 are the forward and reverse rate constants of a subsequent conformational change, respectively. Plots that display a decreasing kobs with increasing ligand concentration indicated a rate limiting conformational change prior to binding (20, 21) and were fit to,
| (Eq. 4) |
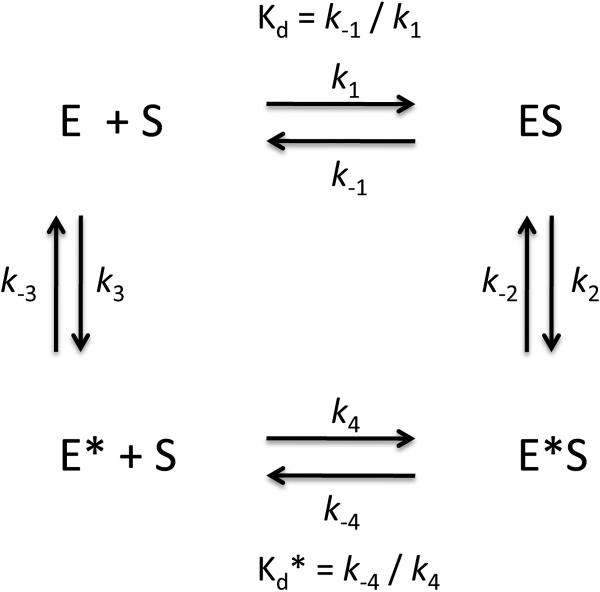
where k3 and k−3 are the forward and reverse rate constants of the conformational change and Kd* is the dissociation constant for ligand binding. Equations 3 and 4 can be combined into Scheme 2 (20) where ligand can bind either before or after the conformational change. The rate constants can be obtained by fitting to,
| (Eq. 5) |
where the rate and dissociation constants correspond to those in equations 3 and 4. With reference to Scheme 2, Kd = k−1/k1 and Kd* = k−4/k4.
Scheme 2.
The amplitudes of the stopped-flow data for serine binding to W139F-E369W were modeled with the equations for distribution of bound species derived from the Adair equation for 4 binding sites (22, 23),
| (Eq. 6) |
where ELi / ELtot are the fraction of each ligand bound enzyme species i, L is the ligand concentration, Ki are the Adair constants, and ELi are the numerators for each species with i bound ligands, where
| (Eq. 7) |
| (Eq. 8) |
| (Eq. 9) |
| (Eq. 10) |
Steady State Serine Binding
Steady-state serine binding to the W139F-E360W mutant was determined by titration with L-serine and monitoring the fluorescence quenching of the single tryptophan residue adjacent to the serine binding site at 360 nm after excitation at 295 nm. The fluorescence signal and ligand concentrations were corrected for dilution. The data was fit to a form of the Hill equation,
| (Eq. 11) |
Where F is the fluorescence, F0 is the fluorescence in the absence of ligand, ΔF is the total fluorescence change, L is the serine concentration, n is the Hill coefficient, and K 0.5 is the serine concentration at half the maximum fluorescence change. The net Kd for the binding is equal to K0.5n (24).
Results
Pre-Steady State Kinetic Analysis of NADH Binding in the Presence of L-Serine
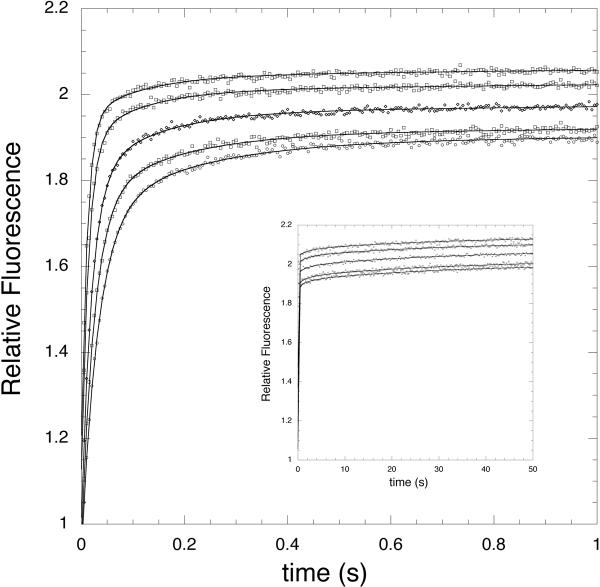
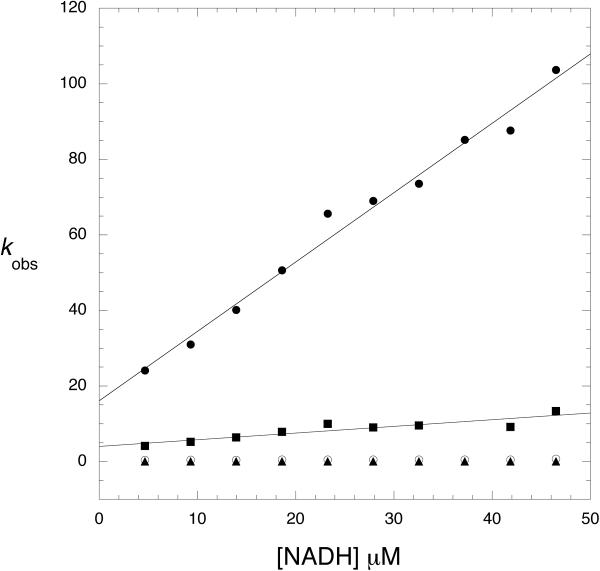
Previous work has shown that substrate binding to E. coli PGDH is ordered, with NADH binding first (13). In order to look at the effect of serine on coenzyme binding, PGDH that is free of bound NADH combined with saturating concentrations of L-serine was rapidly mixed with increasing concentrations of NADH in the stopped flow instrument. The resulting transients fit best to 4 exponentials (two sets of two exponentials) that showed a fast initial rise in signal followed by a slower, low-amplitude rise (Figure 2). When the observed rates (kobs) were plotted versus NADH (Figure 3), the kobs of two of the exponentials increased with increasing NADH concentration and two remained constant. This was qualitatively the same as was observed for NADH binding to PGDH in the absence of serine (13). In that case, the data indicated the presence of two sets of sites for NADH where the concentration dependent binding of NADH was followed by a relatively slow conformational change. Fitting the concentration dependent curves for binding in the presence of serine to equation 2 shows that the main effect of serine on NADH binding is to increase the off rate. Compared to the case where serine is absent, this results in a 15-fold increase in the Kd for NADH binding from 0.6 μM to 9 μM for one set of sites and a 5-fold increase from 5 μM to 23 μM for the other set of sites. As was the case for NADH binding in the absence of serine, the binding step exhibiting the fastest rates and yielding a Kd of 9 μM predominated, accounted for approximately 70% of the amplitude.
Figure 2. Time course of NADH Binding to E. coli PGDH in the presence of Saturating Levels of L-Serine.
The transients for NADH binding are shown for two time ranges, 0–1 s and 0–50 s (inset). The FRET signals are monitored at 420 nm after excitation at 295 nm. The enzyme concentration is 2.5 μM subunit. The transients are shown for 10, 15, 20, 35, and 45 μM NADH from lower to higher relative fluorescence. All data points are plotted for the 0–1 s range and every 50th data point are plotted for the 0–50 s range. The lines are fits of the data to equation 1 for 4 four exponentials.
Figure 3. Observed Rates for NADH Binding to Native PGDH in the Presence of Satutrating Levels of L-Serine.
The observed rates (kobs) derived from the pre-steady state transients are plotted versus NADH concentration. kobs 1(●), kobs 2 (■), kobs 3 (○), kobs 4 (▲). The solid lines are fits of the data to equation 2. The protein concentration was 2.5 μM subunit.
Pre-Steady State Kinetic Analysis of α-Ketoglutarate Binding in the Presence of L-Serine
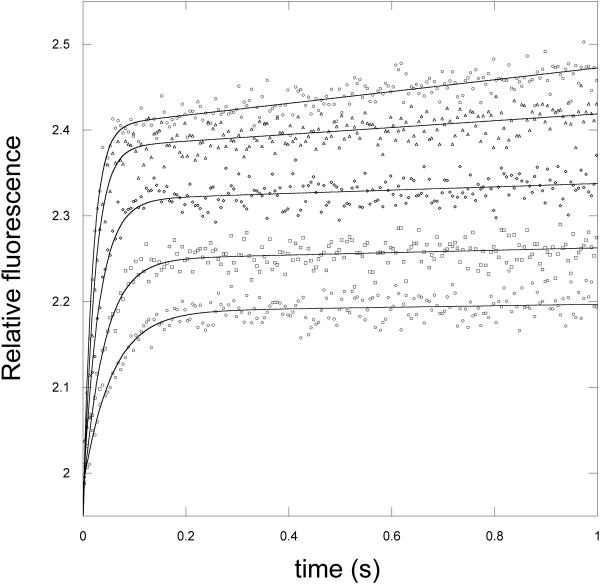
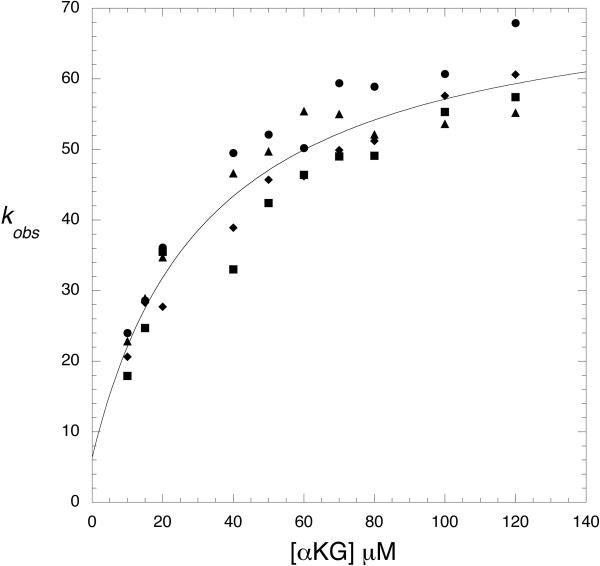
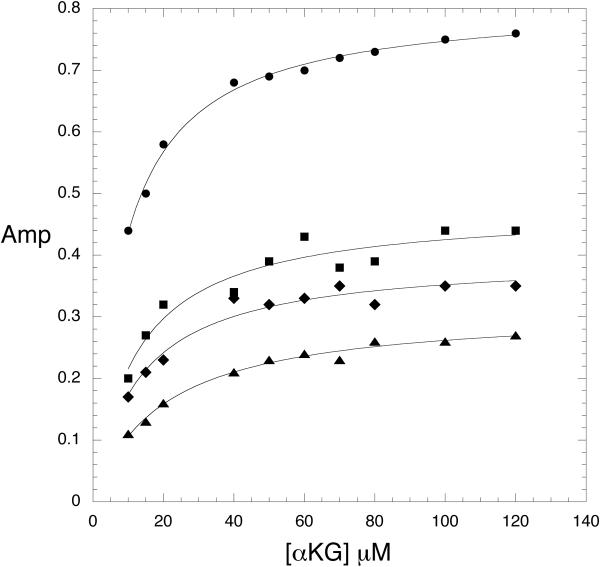
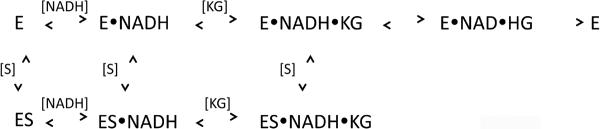
When α-ketoglutarate binding is measured in the absence of serine, a fluorescence signal cannot be detected unless NADH is already bound to the enzyme. In this case, a time dependent decrease in the 420 nm signal is observed as well as a complementary increase in fluorescence at 340 nm due to the enhancement of tryptophan fluorescence. When the signal is monitored as a function of α-ketoglutarate concentration, the transients fit best to 2 exponentials representing the 2 sets of sites consistent with that observed for NADH binding. The plots of kobs versus α-ketoglutarate concentration in the absence of serine were hyperbolic and yielded a Kd for binding as well as forward and reverse rate constants for a subsequent rate limiting conformational change (13). When PGDH, combined with saturating concentrations of NADH and serine, was rapidly mixed with α-ketoglutarate, no signal was detected. Closer examination at serine concentrations in the range of the K0.5 for serine inhibition (1–4 μM) produced a measurable signal (Figure 4) and revealed that the major effect of serine was to lower the amplitude of the fluorescence signal rather than substantially affect the observed rates. In fact, as the serine concentration is increased, data for one of the 2 sets of sites is lost since its amplitude was already at a low level. Figure 5 and 6 show the data for the major site and demonstrate that the observed rates as a function of α-ketoglutarate concentration are similar at all serine concentrations shown to that in the absence of serine (Figure 5). As the serine concentration is increased, the amplitude of the signal decreases (Figure 6), and at higher serine concentrations, the amplitude decreases to zero. This indicates that serine binding reduces the population of enzyme species capable of converting substrates to products. This results in the dead-end species composed of enzyme, serine, coenzyme, and substrate depicted in scheme 1 (ES·NADH·KG) and explains the basis for the V-type inhibition.
Figure 4. Time course of a-Ketoglutarate Binding to E. coli PGDH in the presence of 2 mM L-Serine.
The increase in signal at 340 nm is monitored with excitation at 295 nm in the presence of saturating levels of NADH (250 μM). Protein concentration is 2 μM subunit. The transients are shown for 10, 15, 40, 60, and 100 μM α-ketoglutarate from lower to higher relative fluorescence. The lines are fits of the data to equation 1 for a single exponential.
Figure 5. Observed Rates for a-Ketoglutarate binding to Native PGDH in the presence of Low Levels of L-Serine.
The observed rates (kobs) derived from the pre-steady state transients are plotted versus α-ketoglutarate concentration. The kobs are determined in the presence of 0 (●), 2 (■), 3 (◆), and 4 μM (▲) L-serine. The solid line is a fit of the average of the values to equation 3. The protein concentration was 2 μM subunit and the NADH was 250 μM.
Figure 6. Amplitudes for a-Ketoglutarate binding to Native PGDH in the presence of Low Levels of L-Serine.
The amplitudes of the fits to equation 1 from the pre-steady-state transients that yielded the observed rates in Figure 3 are plotted versus α-ketoglutarate concentration. The amplitudes are determined in the presence of 0 (●), 2 (■), 3 (◆), and 4 μM (▲) L-serine. The lines are fits of the data to the equation for a rectangular hyperbola.
Scheme 1.
Transient Kinetics of L-Serine Binding to W139F-E360W PGDH
Attempts to follow serine binding by monitoring the change in fluorescence of the native protein as originally described (9) were not successful because signal intensity was very low and the data were not reproducible. Instead, serine binding was monitored using a mutant PGDH, W139F-E360W. It was previously shown that E360W PGDH is optically quenched upon serine binding (25). In order to study serine binding with the stopped flow instrument, a new mutant was constructed by removing the native tryptophan residue at position 139 so that the only fluorescence signal would be due to the single tryptophan at position 360. The location of E360 relative to the serine binding site is shown in Figure 1. The resulting double mutation, W139F-E360W, exhibited catalytic activity comparable to that of the native enzyme and was effectively inhibited by L-serine. The K0.5 for enzymatic activity of W139F-E360W was determined to be 15.4 ± 0.4 μM and the Hill coefficient was 2.2 ± 0.1. This compares favorably to the native enzyme with a K 0.5 of 2.3 ± 0.4 μM and a Hill coefficient of 1.9 ± 0.1.
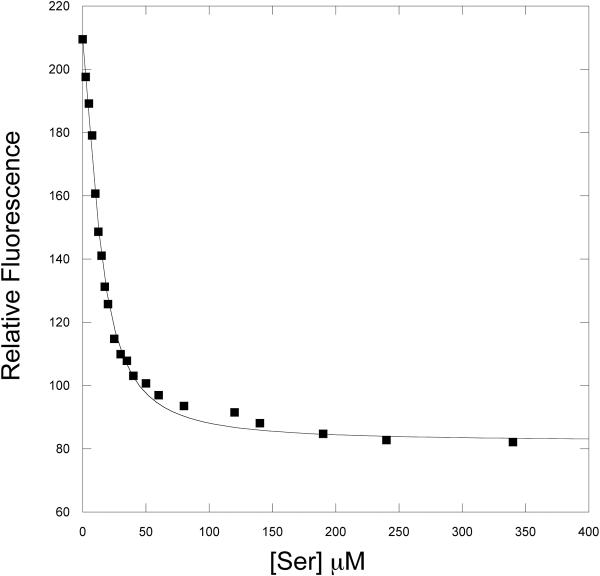
Figure 7 shows the steady state quenching of W139F-E360W as a function of serine concentration. Fitting the curve to equation 11 yields a K0.5 for fluorescence quenching of 13.6 ± 0.5. This compares favorably to a K0.5 for serine inhibition of approximately 15 μM. Thus, considerable quenching occurs at low serine concentrations in the range where serine inhibition of enzyme activity occurs.
Figure 7. Steady-State Titration of PGDH mutants with NADH.
The quenching of tryptophan fluorescence as a function of L-Serine concentration is plotted. L-Serine was added in successive aliquots to 2.5 μM enzyme (subunits) solutions of W139F-E360W PGDH (■). The solid line is a fit of the data to equation 11.
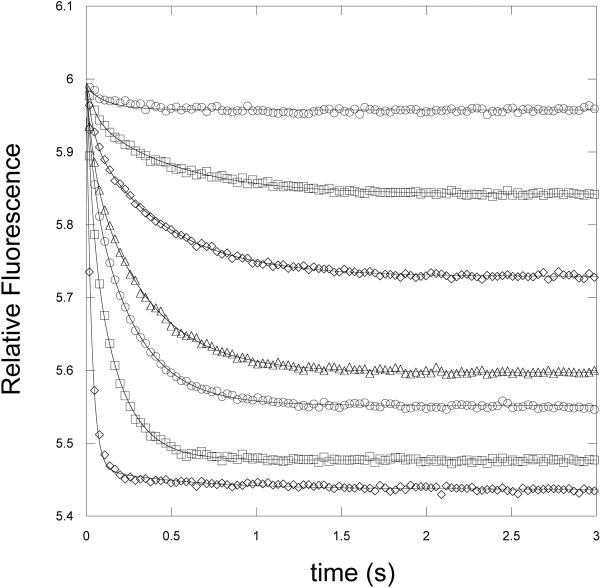
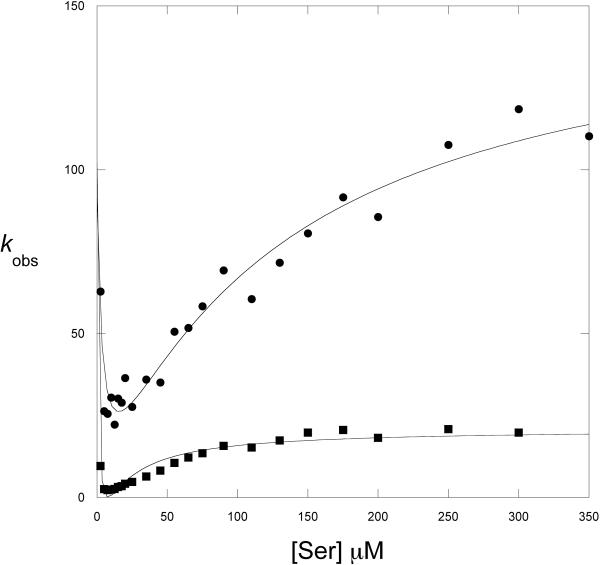
Serine binding to W139F-E360W was monitored by stopped-flow analysis by measuring the fluorescence of the single tryptophan residue of the enzyme at <320 nm when it is excited at 295nm. Rapid mixing of W139F-E360W with L-serine in the presence of 250 μM NADH produced a time dependent decrease in fluorescence that fit best to 2 exponentials (Figure 8). Since serine binds to 4 separate sites on the tetrameric enzyme, and it has been shown that serine binds cooperatively (26), a sequential binding mechanism would be expected to produce four binding transients if each binding event produced its own signal. However, attempts to fit the data to 4 exponential functions resulted in relatively poor fits with large error values. Additional very fast steps that occur during the mixing but prior to detection of the fluorescent signal are ruled out because no significant change in the fluorescence signal occurred during the dead-time of the instrument. A plot of kobs versus serine concentration derived from the data is complex (Figure 9). The kobs appear to decrease with increasing serine concentration before once again increasing as serine concentration increases. Both curves appear to be non-linear with the lower curve clearly demonstrating a rate-limiting step. Inspection of the fractional amplitudes from these two exponential functions (Figure 10) demonstrates that they change as a function of serine concentration. At low concentrations, one amplitude increases while the other decreases. Then, after reaching maximum and minimum values, the trend is reversed. This observation is consistent with a sequential binding model where an increase in one species results in a decrease of the preceding species. The amplitudes of the transients that produce the plot with the higher kobs values (kobs2) increase at high serine concentrations approaching unity while the other amplitude decreases approaching zero. Therefore, the binding function defined by this plot (aobs2) is the terminal event and that defined by the more rate-limited plot (aobs1) precedes it. A similar relationship is also noted at very low serine concentrations where another change in amplitude direction appears to take place. The enzyme is present at a concentration of 0.5 μM subunit and the serine concentrations are from 2.5 μM to 350 μM. At this enzyme concentration, lower serine concentrations do not produce a sufficiently strong signal for analysis.
Figure 8. Time course of binding of L-Serine to W139F-E360W PGDH.
The decrease in signal at <340 nm is monitored with excitation at 295 nm in the presence of NADH (250 μM). Protein concentration is 0.5 μM subunit. The transients are shown for 3.5, 7.5, 10, 15, 20, 45, and 130 μM L̃serine from higher to lower relative fluorescence. The lines are fits of the data to equation 1 for 2 exponentials.
Figure 9. L-serine Binding to W139F-E360W PGDH.
The observed rates (kobs) derived from the pre-steady state transients are plotted versus L-Serine concentration. kobs 1(■), kobs 2 (●). The protein concentration was 0.5 μM subunit. The lines are fits of the data to equation 5.
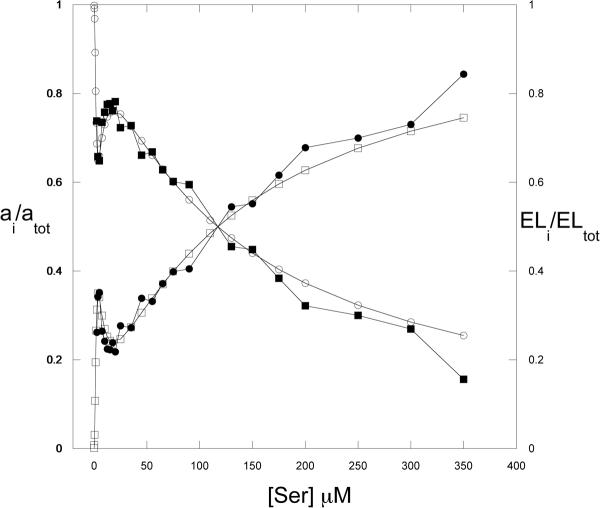
Figure 10. Amplitude Data from L-serine Binding to W139F-E360W PGDH.
The amplitudes derived from fitting the pre-steady state transients of L-Serine binding to W139F-E360W PGDH are plotted; aobs 1(■), aobs 2 (●). The data were modeled to the theoretical distribution of bound species for a 4 Step sequential binding mechanism based on Adair constants of 15, 0.5, 3, and 120. The theoretical distribution of species shown represents E + EL1 + EL3 (□) and EL2 + EL4 (○). In this case, L in the general equations refers to serine. The solid lines do not represent a fit to an equation, but simply connect the data points.
The observation of only two transients, rather than four, might be explained if the fluorescence quenching signals emanate from each of the two serine binding interfaces (see Figure 1). To explore this further, the amplitude changes were compared to a theoretical distribution of species based on equations derived from the Adair equation for four sites. Figure 10 demonstrates that the amplitudes can be closely modeled if the fractional distribution for the zero, first, and third (E+EL1+EL3) and the second and fourth (EL2+EL4) ligand occupancy are summed, respectively. Without employing the summation approach, the minima and maxima observed in the amplitudes cannot be modeled successfully. The Adair constants used for this modeling were arrived at empirically and were initially chosen in consideration of the K0.5 for inhibition of activity and the binding behavior observed previously with equilibrium dialysis of the E360W mutant enzyme. The earlier studies (11) showed that binding of the first two serines are positively cooperative while binding of subsequent serines are negatively cooperative. The Adair constant for the first binding event was set in the vicinity of the K0.5 for inhibition of activity. Since binding of the first two serines is positively cooperative, the second Adair constant is set lower than the first. Note that with positive cooperativity for the second ligand to bind, the EL1 species will approach zero at concentrations of ligand above the dissociation constant for the second ligand so that it is never present in appreciable quantities (Figure S1). Neither of these two values is particularly critical for the modeling as long as they are sufficiently small and indicate positive cooperativity. The last two Adair constants are the more critical for the range of concentrations in that they define the drop in the EL2 species with the subsequent increase in the EL4 species and decrease in the EL3 species. The amplitude data modeled best when the third and fourth Adair constant were set at 3 and 120 μM, respectively. The latter value corresponds to the concentration of serine at which the two amplitudes are equimolar (ai / atot = 0.5).
The modeling of the amplitudes further suggested that the two kobs plots (Figure 9) also represented integrated signals from each of the two serine binding interfaces and the nature of the data suggested that serine could bind to two forms of the enzyme with different affinities for serine (Scheme 2) as described for the binding of glucose to Gluckokinase (20) and the binding of bromide to Haloalkane Dehaologenase (21). Equation 5 (20) combines equations 3 and 4 to describe kinetics where there are two affinities for the ligand and characterized first by a decreasing kobs followed by an increasing kobs that may reach a plateau if there is a subsequent rate limiting step. As can be seen in Figure 9, fitting to equation 5 produced reasonably good fits to the data and show that the data conform to the model. However the errors associated with the fitting were large. This lack of constraint was also observed with equation 5 in the Dehalogenase paper cited above (21). In order to reduce the complexity of the fitting, the values for Kd and Kd* were estimated from the curves and incorporated into equation 5. This produced values for k2 and k−3 with reasonable errors. However, the values for k3 and k−2, still produced large errors. These values are determined primarily at the minima of the kobs plots where serine concentration is low. Because of the difficulty in measuring the response at these low levels of serine, the variability in the data is greater and the data are less reliable. However, equation 3 indicates that k−2 is determined at the y-intercept of that curve. Equation 4 indicates that k3 is determined by the minima at low ligand concentration. These characteristics allow one to estimate probable values and conclude that k−2 is much smaller than k2 and k3 is much smaller than k−3.
Discussion
The stopped-flow analysis of the effect of L-serine on the kinetic mechanism of E. coli PGDH indicates that at least two steps are affected but to very different extents. First, the main effect of L-serine on NADH binding is an increase in the off-rate for the ligand that increases the dissociation constants for binding by 15 and 5 fold for the two sets of sites, respectively. However, even with this increase, the dissociation constants remain relatively low at approximately 9 and 23 μM. Similar to that seen with binding in the absence of serine (13), the amplitude of the tighter binding site predominates. The very slow conformational change following NADH binding in the absence of substrate that was observed in the absence of L-serine (13) is also still observed (Figure 2).
On the other hand, the signal observed as a result of substrate binding (α-ketoglutarate) in the presence of serine is more complex. Consistent with early reports (3, 8), although there is a measurable effect on the affinity of coenzyme, the major effect for substrate appears to be on the rate of the reaction since the data show no effect by serine on substrate binding, consistent with a V-type enzyme. However, rather than somehow slowing the rate of turnover of an individual molecule, the velocity modulation appears to occur by way of the formation of a dead-end complex of enzyme, serine, coenzyme, and substrate. Thus, the velocity modulation is the result of decreasing the population of active enzyme rather than a differential decrease in velocity of the active enzyme. The serine concentration where the amplitude is approximately 50% lower than in its absence corresponds closely to the serine concentration producing 50% inhibition of activity, both being in the 2–3 μM range.
Monitoring serine binding with W139F-E360W PGDH gave very good signal levels but produced complex plots of kobs vs serine. The amplitude data were revealing in that they provided evidence that each transient was produced by more than one binding event that alternated in the step-wise binding mechanism. The two exponentials correspond to two serine molecules binding at the same interface to produce an integrated signal. This allows the exact order of binding to be determined from modeling of the bound species distribution. The results of this analysis clearly indicate that the first and third ligand bind at one interface and the second and fourth bind at the opposite interface (Figure 1). As the first serine binds, the amount of the unbound enzyme decreases with a corresponding increase in EL1. Because of the positive cooperativity, the second serine binds simultaneously with the first so that EL2 predominates, and EL1 is not present in appreciable quantities. As EL3 forms, EL2 decreases and similarly, as EL4 increases, EL3 decreases. The binding of serine 3 and serine 4 to alternate interfaces requires that serine 1 and serine 2 also bind to alternate interfaces. This conclusion is entirely consistent with the earlier hybrid tetramer studies (10) that concluded that the enzyme appeared to exhibit half-of-the-sites behavior, that the activity of the active sites was primarily inhibited by serine binding to the same subunit as the active site, that only the binding of the first two serines were responsible for maximum inhibition, and that the functional active sites were on both sides of the nucleotide binding domain interface.
The complexity of the kobs plots is due to the fact that they are composed of multiple binding events. The amplitude modeling suggests that at the serine concentrations used (which are dependent on the enzyme concentration needed to produce a good signal) the signal is dominated by the last two binding events. The kobs data can be fit reasonably well to a model that indicates serine can bind to two forms of the enzyme with different affinities. Before isomerization, the binding of serine is weak and this pathway does not compete effectively with the isomerization until higher ligand concentrations are achieved which causes a switch in the dominant pathway. This interpretation is consistent with the relative estimated values of Kd and Kd*, where Kd is significantly larger than Kd* in both. In addition, k3 must be greater than zero in order for the two forms of the enzyme to be present. Also, if k−2 is close to or equal to zero, dissociation of serine from E*S would proceed through E* rather than ES.
The serine binding sites are far from the active site and initial serine binding is thought to produce a conformational change in the enzyme. The two forms of the enzyme in scheme 2 may result from the initial serine binding event that occurs at low serine concentration rather than a pre-existing equilibrium in the absence of serine. Although the data do not formally allow a preexisting equilibrium to be excluded, simulation of Scheme 2 with KinTek Global Explorer (16) demonstrates the feasibility of the hypothesis that the initial conformational change (formation of E* in scheme 2) may result from the initial binding of serine. The simulation was performed with the estimated rate constants from Table 1 and the dissociation constants of 15 and 0.3 μM for initial binding to each interface that were used for the amplitude simulation (note that in this scenario, E in Scheme 2 already has 1 serine bound for each interface for a total of 2). The simulation indicates that at the lowest serine concentration used, 2.5 μM, over 50 % of the enzyme species would already have 2 or more serine molecules bound and be within the pathways shown in Scheme 2. At 10 μM serine it is over 80 %. This provides additional support for the notion that the data are dominated by the final two binding events and that the two forms of the enzyme to which the last two serines bind (Scheme 2) could be induced by the binding of the first two serines.
Table 1.
Estimates of Kinetic Constants
| kobs1 | kobs2 | |
|---|---|---|
| Kd | ~12 μMa | ~120 μMa |
| k2 | 61± 4 s−1 | 161 ± 18 s−1 |
| k−2 | (0–10 s−1)b | (0–5 s−1)b |
| Kd* | ~1 μMa | ~1 μMa |
| k3 | (>0–20 s−1)b | (>0–2 s−1) b |
| k−3 | 88± 7 s−1 | 166 ± 22 s−1 |
Constrained during fitting
Estimated from Figure 9
The work with hybrid tetramers of E. coli PGDH (10) clearly demonstrated that inhibition of activity was essentially completely dependent on the binding of the first two serine molecules. The last two serine molecules could also bind to the enzyme at higher ligand concentrations but did not significantly contribute to the inhibition. In light of this conclusion, a substantial portion of the conformational change that can be observed optically from intrinsic fluorescence signals is not consequential to the mechanism of inhibition by serine. Thus, the conformational change that is observed coincident with complete occupancy of the serine binding sites is somewhat enigmatic in that it has no known consequence or purpose and warrants further study.
This investigation, along with the previous determination (13) of the step-wise rate constants in the kinetic mechanism of E. coli PGDH, has defined the essential kinetic step affected by serine binding to the regulatory site within the ACT domain of the enzyme. During continuous turnover of the enzyme in the direction of NADH oxidation, there are at least two separate conformational transitions. Both follow the binding of the substrate, which is the second ligand to bind at the active site in the ordered mechanism, and both occur prior to coenzyme and substrate turnover. One is observable as an optical signal in the stopped-flow instrument and is not rate limiting in the absence of effector, while the other, which is rate limiting, is not observed optically. It is not possible to tell from the available data the order in which they occur or whether one or both of them is prevented by effector binding.
A large number of mutant forms of E. coli PGDH have been produced (10, 27, 28–32). However, their evaluation has been limited to a steady-state analysis that only permits assessment of effects on Km and kcat. This study, as well as the initial transient kinetic analysis (13), will allow a much more detailed investigation of the consequences of these mutations on the individual rate constants of the individual steps of the reaction pathway. This will provide a much more detailed view of the allosteric process of enzyme regulation and further our understanding of control mechanisms in general and that of the ACT domain in particular.
Supplementary Material
Acknowledgments
Supported by grant # GM 56676 (G. A. G.) from the National Institutes of Health
Footnotes
Abbreviations used are: PGDH, D-3-phosphoglycerate dehydrogenase; HPAP, hydroxypyruvic acid phosphate (also called phosphohydroxy pyruvate); FRET, fluorescence resonance energy transfer.
Supporting Information Available: A plot of the theoretical distribution of species from the modeling of the amplitude data for L-serine binding to W139F-E360W E. coli PGDH. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Walsh DA, Sallach HJ. Comparative studies on the pathways for serine biosynthesis in animal tissues. J. Biol. Chem. 1966;241:4068–4076. [PubMed] [Google Scholar]
- 2.Pizer LI, Sugimoto E. 3-Phosphoglycerate dehydrogenase (Escherichia coli) Meth,. Enzymol. 1971;17(part 2):325–331. [Google Scholar]
- 3.Sugimoto E, Pizer LI. The mechanism of end product inhibition of serine biosynthesis. I. Purification and kinetics of phosphoglycerate dehydrogenase. J. Biol. Chem. 1968;243:2081–2089. [PubMed] [Google Scholar]
- 4.Merrill DK, McAlexander JC, Guynn RW. Equilibrium constants under physiological conditions for the reactions of D-3-phosphoglycerate dehydrogenase and L-phosphoserine aminotransferase. Arch. Biochem. Biophys. 1981;212:717–729. doi: 10.1016/0003-9861(81)90416-1. [DOI] [PubMed] [Google Scholar]
- 5.Schuller DJ, Grant GA, Banaszak LJ. The allosteric ligand site in the Vmax-type cooperative enzyme phosphoglycerate dehydrogenase. Nat. Struct. Biol. 1995;2:69–76. doi: 10.1038/nsb0195-69. [DOI] [PubMed] [Google Scholar]
- 6.Aravind L, Koonin EV. Gleaning non-trivial structural, functional and evolutionary information about proteins by iterative database searches. J. Mol. Biol. 1999;287:1023–1040. doi: 10.1006/jmbi.1999.2653. [DOI] [PubMed] [Google Scholar]
- 7.Grant GA. The ACT domain: A small molecule binding domain and its role as a common regulatory element. J. Biol. Chem. 2006;281:33825–33829. doi: 10.1074/jbc.R600024200. [DOI] [PubMed] [Google Scholar]
- 8.Dubrow R, Pizer LI. Transient kinetic and deuterium isotope effect studies on the catalytic mechanism of phosphoglycerate dehydrogenase. J. Biol. Chem. 1977;252:1539–1551. [PubMed] [Google Scholar]
- 9.Dubrow R, Pizer LI. Transient kinetic studies on the allosteric transition of phosphoglycerate dehydrogenase. J. Biol. Chem. 1977;252:1527–1538. [PubMed] [Google Scholar]
- 10.Grant GA, Xu XL, Hu Z. Quantitative relationships of site to site interaction in Escherichia coli D-3-phosphoglycerate dehydrogenase revealed by asymmetric hybrid tetramers. J. Biol. Chem. 2004;279:13452–13460. doi: 10.1074/jbc.M313593200. [DOI] [PubMed] [Google Scholar]
- 11.Grant GA, Xu XL, Hu Z. The relationship between effector binding and inhibition of activity in D-3-phosphoglycerate dehydrogenase. Prot. Sci. 1999;8:2501–2505. doi: 10.1110/ps.8.11.2501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Grant GA, Hu Z, Xu XL. Hybrid tetramers reveal elements of cooperativity in Escherichia coli D-3-phosphoglycerate dehydrogenase. J. Biol. Chem. 2003;278:18170–18176. doi: 10.1074/jbc.M213050200. [DOI] [PubMed] [Google Scholar]
- 13.Burton RL, Hanes JW, Grant GA. A stopped flow kinetic analysis of substrate binding and catalysis on Escherichia coli D-3-phosphoglycerate dehydrogenase. J. Biol. Chem. 2008;283:29706–29714. doi: 10.1074/jbc.M805180200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhao G, Winkler ME. A novel alpha-ketoglutarate reductase activity of the serA-encoded 3-phosphoglycerate dehydrogenase of Escherichia coli K-12 and its possible implications for human 2-hydroxyglutaric aciduria. J. Bacteriol. 1996;178:232–239. doi: 10.1128/jb.178.1.232-239.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Al-Rabiee R, Zhang Y, Grant GA. The mechanism of velocity modulated allosteric regulation in D-3-phosphoglycerate dehydrogenase. Cross-linking adjacent regulatory domains with engineered disulfides mimics effector binding. J. Biol. Chem. 1996;271:13013–13017. doi: 10.1074/jbc.271.22.13013. [DOI] [PubMed] [Google Scholar]
- 16.Johnson KA, Simpson ZB, Blom T. Global Kinetic Explorer: A new computer program for dynamic simulation and fitting of kinetic data. Anal. Biochem. 2009;387:20–29. doi: 10.1016/j.ab.2008.12.024. [DOI] [PubMed] [Google Scholar]
- 17.Johnson KA, Simpson ZB, Blom T. FitSpace Explorer: An algorithm to evaluate multidimensional parameter space in fitting kinetic data. Anal. Biochem. 2009;387:30–41. doi: 10.1016/j.ab.2008.12.025. [DOI] [PubMed] [Google Scholar]
- 18.Johnson KA. In: Kinetic analysis of Macromolecules. Johnson KA, editor. Oxford University Press; New York: 2003. pp. 1–18. [Google Scholar]
- 19.Johnson KA. Transient-state kinetic analysis of enzyme reaction pathways. The Enzymes. 1992;XX:1–61. [Google Scholar]
- 20.A. Kim YB, Kalinowski SS, Marcinkeviciene J. A pre-steady state analysis of ligand binding to human glucokinase: Evidence for a preexisting equilibrium. Biochemistry. 2007;46:1423–1431. doi: 10.1021/bi0617308. [DOI] [PubMed] [Google Scholar]
- 21.B. Schanstra JP, Janssen DB. Kinetics of halide release of haloalkane dehalogenase: Evidence for a slow conformational change. Biochemistry. 1996;35:5624–5632. doi: 10.1021/bi952904g. [DOI] [PubMed] [Google Scholar]
- 22.Adair GS. The Osmotic Pressure of Haemoglobin in the Absence of Salts. Proc. R. Soc. Lond. A. 1925;109:292–300. [Google Scholar]
- 23.Grant GA. Methods for analyzing cooperativity in phosphoglycerate dehydrogenase. Meth. Enzymol. 2004;380:106–131. doi: 10.1016/S0076-6879(04)80005-3. [DOI] [PubMed] [Google Scholar]
- 24.Weiss JN. The Hill equation revisited: uses and misuses. FASEB J. 1997;11:835–841. [PubMed] [Google Scholar]
- 25.Grant GA, Xu XL. Probing the regulatory domain interface of D-3-phosphoglycerate dehydrogenase with engineered tryptophan residues. J. Biol. Chem. 1998;273:22389–22394. doi: 10.1074/jbc.273.35.22389. [DOI] [PubMed] [Google Scholar]
- 26.Grant GA, Hu Z, Xu XL. Cofactor binding to Escherichia coli D-3-phosphoglycerate dehydrogenase induces multiple conformations which alter effector binding. J. Biol. Chem. 2002;277:39548–39553. doi: 10.1074/jbc.M208019200. [DOI] [PubMed] [Google Scholar]
- 27.Al-Rabiee R, Zhang Y, Grant GA. The mechanism of velocity modulated allosteric regulation in D-3-phosphoglycerate dehydrogenase. Site-directed mutagenesis of effector binding site residues. J. Biol. Chem. 1996;271:23235–23238. doi: 10.1074/jbc.271.38.23235. [DOI] [PubMed] [Google Scholar]
- 28.Grant GA, Kim SJ, Xu XL, Hu Z. The contribution of adjacent subunits to the active sites of D-3-phosphoglycerate dehydrogenase. J. Biol. Chem. 1999;274:5357–5361. doi: 10.1074/jbc.274.9.5357. [DOI] [PubMed] [Google Scholar]
- 29.Grant GA, Xu XL, Hu Z. Role of an interdomain Gly-Gly sequence at the regulatory-substrate domain interface in the regulation of Escherichia coli D-3-phosphoglycerate dehydrogenase. Biochemistry. 2000;39:7316–7319. doi: 10.1021/bi000218y. [DOI] [PubMed] [Google Scholar]
- 30.Grant GA, Hu Z, Xu XL. Specific interactions at the regulatory domain-substrate binding domain interface influence the cooperativity of inhibition and effector binding in Escherichia coli D-3-phosphoglycerate dehydrogenase. J. Biol. Chem. 2001;276:1078–1083. doi: 10.1074/jbc.M007512200. [DOI] [PubMed] [Google Scholar]
- 31.Grant GA, Hu Z, Xu Xiao Lan. Amino acid residues mutations Uncouple cooperative effects in Escherichia coli D-3-phosphoglycerate Dehydrogenase. J. Biol. Chem. 2001;276:17844–17850. doi: 10.1074/jbc.M009957200. [DOI] [PubMed] [Google Scholar]
- 32.Grant GA, Hu Z, Xu XL. Identification of amino acid residues contributing to the mechanism of cooperativity in Escherichia coli D-3-phosphoglycerate dehydrogenase. Biochemistry. 2005;44:16844–16852. doi: 10.1021/bi051681j. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.