Optimized EPI for fMRI studies of the orbitofrontal cortex: compensation of susceptibility-induced gradients in the readout direction

Abstract

Object Most functional magnetic resonance imaging (fMRI) studies record the blood oxygen leveldependent (BOLD) signal using gradient-echo echo-planar imaging (GE EPI). EPI can suffer from substantial BOLD sensitivity loss caused by magnetic field inhomogeneities. Here, BOLD sensitivity losses due to susceptibility- induced gradients in the readout (RO) direction are characterized and a compensation approach is developed.

Materials and Methods Based on a theory describing the dropout mechanism, an EPI sequence was optimized for maximal BOLD sensitivity in the orbitofrontal cortex (OFC) using a specific combination of an increased spatial resolution in the RO direction and a reduced echo time. Using measured BOLD sensitivity maps and a breath hold experiment, the model and compensation approach were tested.

Results Using typical fMRI EPI parameters, susceptibility-induced gradients in the RO direction caused dropouts in the OFC and the inferior temporal lobe. Optimizing the echo time and spatial resolution effectively reduced the dropout as predicted by the theory.

Conclusion The model-based compensation approach effectively reduces BOLD sensitivity losses due to susceptibility-induced gradients in the RO direction. It retains the high temporal resolution of single-shot EPI and can be readily combined with methods for the compensation of susceptibility-induced field gradients in the phase-encoding and through-plane direction.

Introduction

Gradient-echo echo-planar imaging (GE EPI) is widely used for functional magnetic resonance imaging (fMRI) of the brain. GEEPI is sensitive tomicroscopicmagnetic field alterations caused by blood oxygen level-dependent (BOLD) susceptibility effects in areas of neuronal activity [1]. However, it is also sensitive to macroscopic field inhomogeneities caused by the differences of magnetic susceptibility of air and tissue which may result in local image distortions and signal losses. Geometric image distortion may be corrected to a great extent by various on-line and off-line methods [2–6]. However, signal dropouts remain a problem. The missing signal has often compromised fMRI studies of the inferior frontal, the medial temporal and the inferior temporal lobes [7,8].

Several methods have been developed for reducing susceptibility related signal losses (e.g., [9–16]). Most of these approaches focus on dropouts caused by field gradients in the slice selection direction [10–12,16]. The majority of early fMRI studies used relatively thick slices in comparison to the in-plane voxel dimension (e.g., a ratio of 2:1 was typical), so in-plane gradients caused much smaller intravoxel frequency offsets and phase dispersion than through-plane gradients. Z-shimming is a widely used dropout compensation technique based on this rationale [11,12,16]. It forms a composite image from a series of measured images, each acquired with a different compensation gradient pulse in the slice selection direction [17]. Thus, it enables a range of susceptibility-induced gradients in the slice direction to be counterbalanced.

In more recent studies using thinner slices it has been shown that in-plane gradients in the phase-encoding (PE) direction may also cause severe dropouts in EPI, because they lead to spatially localized echo time shifts reducing the BOLD sensitivity and may even shift the gradient echo outside the acquisition window—resulting in a total signal loss [13–15]. Different techniques have been developed to reduce this type of dropout, such as applying gradient prepulses in the PE direction [14] and changing the slice orientation so that the PE component of the susceptibility-induced gradient is reduced [13]. Also reduction of the EPI acquisition time and inverting the PE gradient polarity [15] help to decrease these artifacts. A fast and efficient method optimizes the slice tilt, PE gradient polarity, and z-shim gradient prepulse [15, 18]. However, it has been shown that even when optimizing those parameters residual dropouts in the orbitofrontal cortex (OFC) and inferior temporal lobes remain [18].

Here, we show that these previously reported residual dropouts [18] may be explained by susceptibilityinduced gradients in the readout (RO) direction. To our knowledge, we show for the first time that the echo time shifting due to susceptibility-induced gradients in the PE direction modulates the dropout due to susceptibility-induced gradients in the RO direction. We discuss the possibilities for reducing the dropout due to susceptibility-induced gradients in the RO direction and propose a method for signal recovery in certain regions of the OFC. The method is based on an optimal choice of echo time and spatial resolution in the RO direction, informed by the theory describing the dropout mechanism. Optimized scan parameters are given for the two most frequently used field strengths of 1.5T and 3 T. The technique can be combined with methods for the compensation of other types of signal losses, e.g., z-shimming [11, 13].

Theory

BOLD sensitivity

In fMRI experiments based on the BOLDeffect as measured by GE EPI, the local BOLD sensitivity (BS) can be theoretically estimated from

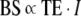where I is the local intensity in the T*₂-weighted image [14]. TE is the effective echo time including echo time shifts due to gradients in the PE direction [14]. Note that this simple relationship is only strictly correct for a monoexponential decay of the MR signal. From Eq. (1) it is obvious that losses in the BOLD sensitivity due to susceptibility-induced gradients can be caused by a reduction of the image intensity or shortening of the effective echo time.

Signal dropouts caused by susceptibility-induced gradients in the RO direction

Since it has been previously described how susceptibility-induced gradients in the through-plane [11,13] and PE direction [14] cause signal loss, we focus here on signal loss caused by susceptibility-induced gradients (G^susc_x) in the RO direction. We consider the case of EPI with cartesian sampling (Fig. 1a, cyan solid line) and assume that the field of view L_x,L_y in the RO and PE directions, respectively, is scanned with a resolution of Δx and Δy. The gradient G^susc_x causes a shift of the echo in the k_x/RO direction in k-space. The shift increases linearly with the duration between the RF pulse and each echo in the EPI echo train, resulting in a shifted and sheared k-space trajectory (Fig. 1a, red dotted line). If an additional compensation gradient G^comp_x in the RO direction is switched on for the duration τ before the data acquisition, the total k-space shift ΔK_susc at the local echo time TE is

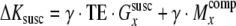with the compensation gradientmoment M^comp_xx =G^comp_x· τ, and γ being the gyromagnetic ratio. In the presence of a susceptibility-induced gradient in the PE direction (G^susc_y ) the effective echo time is given by 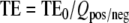with 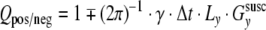for a positive or negative PE prewinder moment [14, 15], where TE₀ is the nominal echo time as entered on the scanner interface and Δt is the echo spacing

Fig. 1.

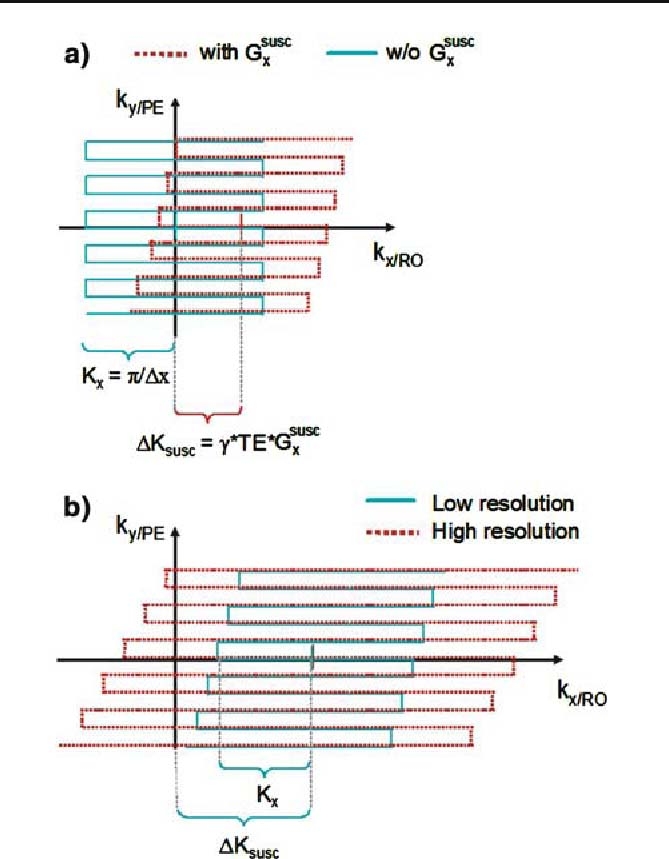
Distortion of EPI k-space trajectories caused by susceptibility-induced gradients in the readout (RO) and phase-encoding (PE) direction. a In the absence of susceptibility-induced gradients, the k-space trajectory is determined by the imaging gradients (cyan solid line). A susceptibility-induced gradient in the RO direction (G^susc_x) distorts and shifts the k-space trajectory (red dotted line), leading to a shift of the center of the trajectory by ΔK_susc. b If the trajectory is distorted so much that it does not traverse the k-space center, i.e.,ΔK_susc exceeds the k-space coverage (cyan solid line), the main gradient echo is not acquired, yielding severe dropouts. By increasing the spatial resolution and thus k-space coverage in the RO direction the lost signal may be recovered (red dotted line)

Severe signal loss occurs if the echo is shifted outside the acquisition window (Fig. 1b, cyan solid line), i.e., if the k-space shift ΔKsusc at TE exceeds the sampled k-space window in the RO direction

.

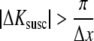As can be seen from Eqs. (2) and (3), the maximal susceptibility-induced gradient which can be tolerated before dropouts occur depends on the RO resolution Δx and the effective local echo time TE. The echo time may be modified locally by susceptibility-induced gradients in the PE direction, resulting in an interaction of the in-plane gradients in the RO and PE direction on signal dropouts. In contrast to the susceptibility-induced gradients in the PE direction, the gradients in the RO direction do not shift the echo time significantly (maximally by Δt/2), so the local TE and thus the BOLD sensitivity are minimally affected. However, the signal is abruptly lost when the central echo falls outside the acquisition window (when the shift exceeds Δt/2). Even before the echo is completely shifted outside the acquisition window, the point-spread-function (PSF) may be altered, leading to intensity fluctuations and a reduction in spatial resolution (for simulations of susceptibility-induced distortions of spiral trajectories and PSF, see [19]).

We can use Eqs. (2) and (3) to calculate the spatial resolution and TE required to avoid dropouts due to susceptibility-induced gradients in the RO direction. At 3T, susceptibility gradients are limited to approximately 300 µT/m in most brain areas (e.g., for the most severely affected OFC see [20]). The minimal TE providing adequate BOLD sensitivity is in the range of 25 ms-30 ms [2, 21]. Thus, using a TE = 25 ms at 3T and assuming a maximal |G^susc_x| ≈ 300 µ T/m the lowest RO resolution not causing dropouts is Δx = 1.5 mm. At 1.5T with a maximal |G^susc_x| ≈ 150 µ T/m (estimated from the values at 3 T) and aminimal TE of about 35–40 ms [21], the respective resolution is approximately Δx = 2mm at TE= 37ms. Note that we have neglected any local echo time shifts for this simplified calculation. However, if significant echo time shifts occur and can be predicted, the maximal local TE should be used instead of the nominal TE₀ in Eq. (2).

Methods

The study consisted of four different experiments. The first experiment was designed to delineate brain regions where compensation techniques [13,15,18] for susceptibility-induced gradients in the through-plane and PE direction do not recover the signal loss. The second and third experiment were designed to demonstrate the predicted dependence of the dropout on the susceptibility-induced gradient, the compensation gradient prepulse moment (M^comp_x), and the local TE. The fourth experiment investigated whether an increased RO resolution would recover the BOLD sensitivity in the orbitofrontal cortex (OFC) in an fMRI breath hold experiment as theoretically predicted.

General methods: data acquisition and analysis

For all experiments, unless otherwise noted in the individual experimental sections, the following procedures, techniques, and parameters were used. For each experiment one volunteer was scanned in a 1.5 T whole-body scanner (Magnetom Sonata, Siemens Medical,Erlangen, Germany) or a 3T head scanner (Magnetom Allegra, Siemens Medical). The whole-body scanner was operated with a body transmit and a head receive coil, the head scanner with a head transmit-receive coil. The volunteers (2 females, 1 male, age 32–37 year) gave written informed consent according to the guidelines of the local ethics committee.

The manufacturer’s standard automatic 3D-shim procedure was performed at the beginning of each experiment, correcting for first and second order distortions in the static magnetic field within the imaged volume. We implemented single-shot EPI sequences which allowed us to freely choose the moment M^comp_x of the compensation gradient prepulse in the RO direction, the moment of the z-shimming gradient prepulse, and the PE gradient polarity. The details of the imaging parameters for each experiment are given separately. EPI magnitude images, echo time (TE) maps, and BOLD sensitivity (BS) maps were reconstructed from the complex measurement data using a generalized reconstruction method based on the measured EPI k-space trajectory to minimize ghosting [22]. The TE maps and BS maps were estimated according to the procedures in Deichmann et al. [14], i.e., the local TE was determined from the local phase evolution during the acquisition and the BS was then determined by Eq. (1).

A field map was recorded for distortion correction, anatomical reference, and simulating EPI dropouts. The parameterswere at 1.5 T/3T: double echo FLASH, 64/48 oblique transverse slices, slice thickness = 2 mm, gap between slices = 1 mm, repetition time TR = 1,170/761 ms, flip angle α = 90°, short TE = 10 ms, long TE = 14.76/12.46 ms, BW = 260 Hz/pixel, PE direction anterior-posterior, field of view FOV = 192 × 192 mm², matrix size 64 × 64, flow compensation. Using the FieldMap toolbox [4, 23], fieldmaps were estimated from the phase difference between the images acquired at the short and long TE and unwrapped [24]. After spatial smoothing (Gaussian kernel, FWHM = 6mm) of each field map and applying a brain mask created by the Brain Extraction Tool [25], voxel displacements for the EPI images were determined from the field map and imaging parameters. Distortion correction was performed by applying the inverse displacement to the EPI magnitude images (displacement maps were resliced in the EPI space by trilinear interpolation), TE maps, and BS maps without a correction for the intensity distortions.

The gradients of the field inhomogeneities were estimated by numerical differentiation from the field maps. We used 8th order sinc interpolation and smoothed the field maps with FWHM = 3mm (trading signal-to-noise ratio (SNR) for higher resolution; [4]). The field maps, gradient maps, and all images derived from EPI (magnitude, TE, BS) were coregistered and resliced [26]. The field inhomogeneity gradient maps were used to calculate maps of predicted signal dropout in the measured EPI images on the basis of our theory given the chosen imaging parameters, i.e., TE, spatial resolution, echo spacing Δt, slice tilt, and compensation gradient prepulse moment M^comp_x. We simulated the effects of both in-plane and through-plane field gradients. Since the effects of through-plane gradients had been described previously [14, 15], results were only reported for the dropouts due to the in-plane gradients. All data analyses and simulations were performed using SPM2 ([26]; WellcomeTrust Centre forNeuroimaging,London,UK) and custom-made scripts in Matlab7 (The MathWorks, Natick, MA).

Experiment 1: determination of regional signal dropouts that cannot be recovered by compensation of susceptibility-induced gradients in the through-plane and PE direction

In this 1.5T experiment we investigated those brain areas where signal losses cannot be recovered using the established compensation technique for susceptibility-induced gradients in the through-plane and PE direction [13, 15]. The technique relies on an optimal slice tilt, z-shimming gradient prepulse, and PE gradient polarity to minimize signal losses [18]. To determine the parameter set optimizing the BS for each brain region, EPI were acquired with different z-shim gradient moments from M^comp_z = −4mT/m×ms to +4 mT/m×ms (in steps of 1mT/m×ms), different slice tilts from −45° to +45° from the transverse plane (in steps of 15°), and different PE gradient polarities. For each parameter set, five EPI volumes were recorded. The first four volumes were discarded to allow for T1-equilibration. The following were the basic EPI imaging parameters: 48 slices, slice thickness = 2 mm, gap between slices = 1 mm, TR = 4.4 s, α = 90°, TE₀ = 50 ms, BW = 2,298 Hz/pixel, bandwidth in PE direction BWPE = 31.2Hz/pixel, PE direction anterior-posterior, FOV = 192 × 192mm², matrix size 64 × 64. A maximal BS map was calculated from all BS maps acquired with different parameters. The maximal BS map displayed the highest BS in each voxel achievable using optimally adjusted parameters. A subset of these data was used previously to construct a BS atlas [18] where further details on the data analysis and BS maps can be found. The maximal BS map was qualitatively assessed for residual signal losses by comparison with the anatomical FLASH image. It was further assessed whether the residual BS losses coincided with high amplitudes in the susceptibility-induced gradients.

Experiment 2: signal dropouts due to susceptibility-induced gradients in the RO direction and the effect of a compensation gradient prepulse in the RO direction

In this 1.5T experiment, we assessed how the signal dropouts vary when compensation gradient prepulses are applied in the RO direction before the k-space acquisition. The moment was varied from M^comp_x = −3m T/m×ms to +3 mT/m×ms in steps of 1mT/m×ms. For each moment, five EPI volumes were recorded. The first four volumes were discarded to allow for T1-equilibration. The EPI imaging parameters were the same as in Experiment 1. Since the OFC was a main target region of this study, dropouts due to field gradients in the PE direction in this area were minimized by tilting the oblique transverse slices by 30° towards the coronal plane (with the anterior edge being more superior than the posterior edge) while using a positive PE gradient polarity according to Deichmann et al. [13]. The measured EPI images were assessed qualitatively to identify signal losses dependent on the compensation gradient prepulse moment M^comp_x. We then compared the dropouts in the image recorded with zero prepulse to our theoretical prediction.

Experiment 3: dependence of signal dropouts on the effective local echo time TE

In this experiment, we investigated the dependence of the signal loss on the effective TE at 1.5 T. The effective local echo time TE depends not only on the nominal echo time TE₀ but also on the field gradients in the PE direction and the polarity of the PE imaging gradient. When the PE imaging gradient polarity is inverted, the shift in TE is reversed. To assess how the signal dropouts in EPI vary due to the local echo time shifting, EPI images with different gradient prepulse moments in the RO direction and different PE gradient polarities were recorded. For each of the two PE polarities, the prepulse moment was varied from M^comp_x = t=4mT/m×ms to +4 mT/m×ms in steps of 1mT/m×ms. For each prepulse moment and PE polarity, ten EPI volumes were recorded (same EPI parameters as in Experiment 1, except for TE₀ = 70ms, TR= 5.4s, z-shim gradient prepulse moment = −1.5mT/m×ms). The first four volumes were discarded to allow for T1-equilibration and the remaining six volumes were averaged to increase the SNR. The calculated TE maps were assessed for echo time shifts due to susceptibility-induced gradients in the PE direction. Based on this information, the theoretically predicted dropouts, and the measured EPI images were assessed qualitatively for local TE dependent signal losses.

Experiment 4: recovering BOLD sensitivity losses

In this experiment at 3T, we determined whether an increase of resolution can recover the BOLD contrast-to-noise ratio (CNR) in the OFC areas affected by susceptibility-induced gradients in the RO direction. Although the BOLD sensitivity (BS) may be estimated from a single EPI image [14], we additionally conducted an fMRI breath hold experiment [27] to exclude the possibility that an increase in the estimated BS is masked by an increased temporal noise. Breath holding as a hypercapnic challenge reliably increases the cerebral blood flow and the BOLD signal, and is comparable to CO₂ inhalation, as shown in previous studies [27].

The fMRI experiment comprised three sessions. Each session consisted of four blocks of breath holding (30 s duration) alternating with blocks of free breathing (45 s duration), beginning and ending with free breathing. The subject was cued at the beginning of each block via head phones. Relatively long breath holding/free breathing periods were chosen to maximize the BOLD signal changes and to allow a steady breathing state to be reached.

To reduce the residual dropouts in the OFC, EPI images were acquired with the optimal parameters as given in the Theory section: resolution of 1.5mm in the RO direction and 3mm in the PE direction, and TE₀ = 25 ms. The other EPI parameters were: 46 oblique transverse slices tilted by 30°, slice thickness = 2 mm, gap between slices = 1 mm, TR = 2.99 s, α = 90°, TE₀ = 25 ms, BW = 1,953 Hz/pixel, BWPE = 27.9Hz/pixel, PE direction anterior-posterior, FOV = 192 × 192mm², matrix size 128 × 64 (ROx PE), z-shim gradient prepulse moment = −1mT/m×ms. For anatomical reference, a high-resolution T₁-weighted 3D image was used that was previously acquired at 1.5 T (3D MDEFT [28]; FOV = 256×224, matrix size 256×224, 176 partitions, slab thickness 176 mm, τ₁ = 222.6ms, τ₂ = 307.4ms, TR = 12.24 ms, TE = 3.56 ms, α = 23°, BW = 106 Hz/pixel).

In order to determine the impact of spatial resolution on signal dropouts, images were reconstructed from the k-space data at the full resolution of 1.5mm (high resolution) and the reduced resolutions of 3mm (intermediate resolution) and 4mm (low resolution) in the RO direction. The lower resolution images were calculated by limiting the image reconstruction to the central portion of data in regridded k-space, taking into account ramp sampling. By using the identical k-space raw data and resampling, any bias in the comparison of the different resolutions due to different physiological noise, head motion, or scanner instabilities is avoided.

The low, intermediate and high resolution EPI time series were identically preprocessed and statistically analyzed using SPM2. The EPI images were corrected for motion, distortions, and for interactions of motion and distortions using the FieldMap toolbox [5,23] and the variance weighted smoothed field map. All images were coregistered, resliced, and smoothed with a Gaussian kernel of FWHM = 5 mm. The time series of each voxel was high-pass filtered with a cut-off period of 150 s.

A general linear model (GLM) was applied to the time series of each voxel [29]. Breath holding blocks were modeled as a boxcar reference function which was convolved with a Gaussian function (σ =7.48 s) to account for the delayed and dispersed blood flow response. In order to reduce artifacts caused by head motion, covariates derived from the head motion parameters (six per scanned volume) were included in the GLM [30] as effects of no interest. Temporal autocorrelations were modeled by a first order autoregressive model. Activated voxels were determined by testing for significant positive correlation of the measured signal with the modeled response, i.e., significant signal increase due to the breath holding. T statistics were estimated for each voxel and activations passing a fixed voxel-wise threshold of t > 3.12 were considered significant (corresponds to P < 0.001).

For a direct comparison of the BOLD CNR of the lower and high resolution images, the image intensity of each time point and voxel of the preprocessed lower resolution time series was subtracted from the image intensity of the corresponding time point and voxel of the high resolution time series. This differential time series reflected the signal difference between the two resolutions and therefore also the BOLD signal difference. The differential time series was statistically analyzed the same way as the individual time series, however, the motion parameters of both individual time series were included as regressors in the GLM. All voxels that showed a higher activation for the higher spatial resolution were determined by testing for significant positive correlation of the differential signal with the modeled breath holding BOLD response. Activations passing a fixed voxel-wise threshold of t > 3.12 and a cluster size of 0.12 ml were considered significant. The statistical maps were masked with a brain mask generated from the T₁-weighted anatomical MDEFT image [25].

Results

Experiment 1: determination of regional signal dropouts that cannot be recovered by compensation of susceptibility-induced gradients in the through-plane and PE direction

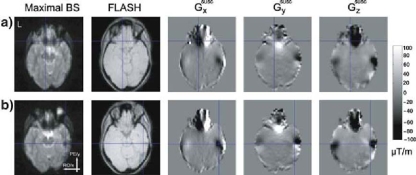
Figure 2 (left) shows maps of the highest achievable BS when for each voxel the best combination of slice tilt, PE gradient polarity, and z-shim gradient moment is chosen. Even under these ideal conditions, comparison with the FLASH reference image (second from left) revealed areas of severe signal loss in parts of the posterior gyrus rectus, and the orbital parts of the inferior and superior frontal gyri (Fig. 2a). In addition to these orbitofrontal areas, prominent BS losses occurred in parts of the inferior temporal gyri and fusiform gyri (Fig. 2b). These dropouts coincided with large susceptibility-induced gradients in the RO direction (Fig. 2, center images), but not with large susceptibility-induced gradients in the PE and slice select direction (Fig. 2, two right most images).

Fig. 2.

Residual signal dropouts despite compensation of susceptibility-induced gradients in the through-plane and phase-encoding (PE) direction (at 1.5 T) located in the a orbitofrontal cortex, b inferior temporal lobes and fusiform gyri. Map of the maximal BOLD sensitivity that can be achieved by optimized compensation (left), anatomical FLASH image (second from left), map of susceptibility-induced gradients (three right most images)

Experiment 2: signal dropouts due to susceptibility-induced gradients in the RO direction and the effect of a compensation gradient prepulse in the RO direction

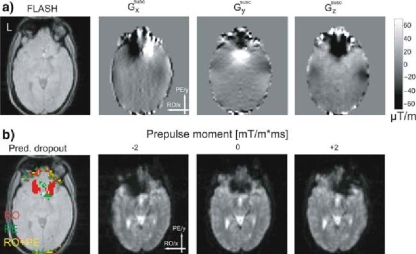
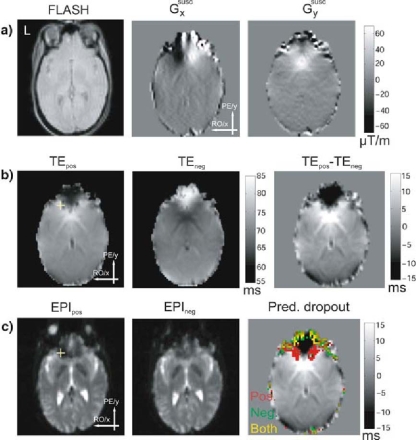
In this experiment at 1.5T, we assessed how the signal dropouts in EPI vary when compensation gradient prepulses with different moments are applied in the RO direction. Figure 3a shows maps of the susceptibility-induced gradients G^susc_x, G^susc_y, G^susc_z as estimated from the individual field map. The maximal magnitudes of the susceptibility-induced field gradients in the OFC exceeded 100 µT/m in all directions. However, in most dropout regions |G^susc_x| was less than ∼160 µT/m. The first image of Fig. 3b highlights areas that according to the theory should suffer from signal dropouts due to in-plane susceptibility gradients as determined from the field maps. As theoretically predicted from the measured gradients G^susc_xG^susc_y, dropouts due to gradients in the RO direction occurred in the left and the right OFC (similar to the residual dropouts in Experiment 1). Dropouts due to gradients in the PE direction occurred in the posterior medial part of the OFC. The EPI images also showed an overall reduction of signal intensity in the OFC which can be attributed to the through-plane gradient. As expected from the measured susceptibility-induced gradient in the RO direction, a positive gradient prepulse in the RO direction recovered signal from the left OFC, but increased the signal loss in the right OFC. Conversely, a negative prepulse recovered signal in the right OFC, but decreased the signal in the left OFC (Fig. 3b, three right most images).

Fig. 3.

Signal dropouts in the orbitofrontal cortex (OFC) caused by field inhomogeneities (at 1.5 T). a Anatomical FLASH image and maps of susceptibility-induced gradients for the same slice and the three principal directions. b Areas of predicted signal dropout (given a zero prepulse moment) due to the different susceptibility-induced in-plane gradients (left) and EPI images acquired with different gradient prepulse moments in the readout (RO) direction (three right most images)

Experiment 3: dependence of signal dropouts on the effective local echo time TE

In this experiment, we investigated the dependence of the signal loss on the effective local echo time TE. Figure 4 shows the field gradient maps (a), TE maps (b), and EPI images (c) for the same slice for both PE gradient polarities. Depending on the polarity of the PE gradient, a given value of G^susc_y caused an increase or decrease of the effective local TE. A U-shaped area in the OFC showed an increased effective TE with positive PE polarity and a decreased effective TE with negative PE polarity (Fig. 4b). In areas where an increased effective TE coincided with large gradients in the RO direction, dropouts were exacerbated. For example, the voxel marked by the yellow crosshair in Fig. 4c suffered from more pronounced dropouts in the case of the positive PE polarity because, in this case, TE was increased, reducing the cut-off value of G^susc_x.

Fig. 4.

Dependence of signal dropouts on the local effective echo time TE (at 1.5 T). a Anatomical FLASH image and maps of susceptibility-induced in-plane gradients for the same slice. b The left two images show TE maps for both phase-encoding (PE) polarities, and the third image shows the difference of the two TE maps. c The left two images show EPI images for both PE polarities. The third image shows predicted dropouts due to susceptibility-induced gradients in the readout (RO) direction for both PE polarities

Experiment 4: recovering BOLD sensitivity losses

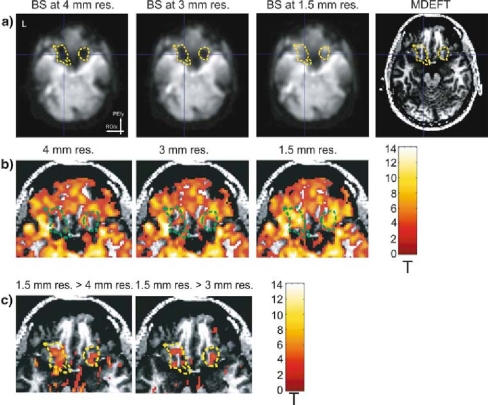
In an fMRI breath hold experiment conducted at 3T, we assessed whether an increased spatial resolution in the RO direction can recover the BOLD sensitivity (BS) in OFC dropout areas. As shown in Fig. 5a, the low (4mm) and intermediate (3mm) resolution images exhibited a reduction in the estimated BS in the left and right OFC (left and center left) in comparison to the high resolution images (1.5 mm, center right). For optical guidance, the yellow contours encircle areas where the estimated BS was at least 40% higher for the high resolution image than the low resolution image. Figure 5b shows that significant BOLD signal changes were absent in the low resolution images (left) during the breath holding in areas suffering from susceptibility-induced gradients in the RO direction (green contours). Clearly, most of these areas were activated in the high resolution images (Fig. 5b, right). The intermediate resolution recovered only parts of this BOLD sensitivity loss with fewer areas being activated than for the high resolution image (Fig. 5b, center). A direct comparison of the observed BOLD signal changes further confirmed the increased BOLD CNR of the high resolution images in these dropout areas (Fig. 5c). Note that the recovered BOLD signal change is largest in gray matter, as physiologically plausible (Fig. 5c).

Fig. 5.

Recovering BOLD sensitivity (BS) dropouts using an optimized spatial resolution (at 3 T) a Spatially smoothed BS maps estimated from the complex EPI data and T1-weighted MDEFT image. Significant dropouts (at the lower resolution) due to susceptibility-induced gradients in the readout direction are encircled by the yellow contours. b Statistical maps of significant signal changes due to breath holding (t > 3.12). c Statistical maps display areas where the high resolution image showed significantly higher activation than the low resolution image and the intermediate resolution image, respectively, (t > 3.12, minimal cluster size >0.12ml). The maps are superimposed over the zoomed T₁-weighted MDEFT image

Discussion

We have presented a theory describing EPI signal losses caused by susceptibility-induced magnetic field gradients in the readout (RO) direction and validated it experimentally. Based on the theory we have devised a dropout compensation technique and have shown its efficiency in an fMRI breath hold experiment. The theory predicts that the field gradients in the RO direction distort the k-space trajectory and may shift the main gradient echo outside the acquisition window—yielding severe signal loss (Fig. 1). This type of signal loss is determined by the amplitude of the susceptibility-induced gradient, the effective local echo time (TE) and the spatial resolution in the RO direction. To our knowledge, we have shown for the first time how the local echo time shifting caused by susceptibility-induced gradients in the phase-encoding (PE) direction affects the dropout caused by susceptibility-induced gradients in the RO direction (Fig. 4). The theory was validated by different experiments studying the dependence on the underlying susceptibility-induced field gradients, the spatial resolution, the echo time, and a gradient compensation prepulse applied in the RO direction.

Although it has been realized in principle that strong gradients in the RO direction can cause signal losses in EPI [31,32], most compensation techniques have focused on susceptibility-induced gradients in the through-plane direction [11,17,33] and more recently on the PE direction [13–15]. The compensation methods addressing gradients in the RO direction either do not separate the qualitatively and quantitatively different effects of susceptibility-induced gradients in the PE direction from those of gradients in the RO direction [7,34] or do not consider gradients in the PE direction at all [32]. Here, we have accounted for the susceptibility-induced gradients in both the RO and PE direction and provided a simple analytical model to predict BOLD sensitivity (BS) losses.

Our theory has various implications for EPI of regions affected by susceptibility-induced gradients in the RO direction. These dropouts occur with EPI parameters commonly used for fMRI: for example, when selecting a nominal echo time of TE₀ = 50 ms and a spatial resolution of 3mm at 1.5T, signal is lost for even moderate susceptibility-induced gradients in the RO direction exceeding ±78 µT/m. Values of this magnitude are commonly observed in the OFC and inferior temporal lobe at this field strength and result in severe signal loss. From the theory it is clear that the commonly employed compensation techniques for dephasing in the through-plane [11,33] or PE direction [13,15] cannot recover signal lost due to gradients in the RO direction (see also Fig. 2).

Very often BS losses are reduced by simply increasing the in-plane spatial resolution and/or decreasing the nominal echo time. However, special care must be taken when modifying these parameters. Simply increasing the overall in-plane spatial resolution both in the RO and PE direction potentially compromises the EPI quality, because an increased resolution in the PE direction requires the acquisition of more PE lines and thus a significantly longer overall slice acquisition time. This reduces the temporal resolution and leads to a longer minimal echo time, possibly exacerbating signal loss [13]. Increasing the spatial resolution also reduces the baseline signal-to-noise ratio. Shorter nominal echo times recover signal lost due to susceptibility-induced gradients in the RO direction. However, the BS in fMRI might not be improved by this strategy, because exceedingly short echo times reduce the BS [14].

For the effective compensation of dropouts due to susceptibility-induced gradients in the RO direction, we have implemented and tested an EPI sequence using high spatial resolution in the RO direction only. In contrast to an increased PE resolution, an increased RO resolution has less impact on the total acquisition time, avoiding the aforementioned problems of a longer acquisition. For example, for a fixed maximal gradient amplitude of 40 mT/m×ms and slew rate of 200 mT/m×ms doubling the resolution in the RO direction from Δx = 3mm to Δx = 1.5mm increases the echo spacing by approximately 50%. In fact, the total acquisition time per slice is increased by less than 25%, because the center of the acquisition window is fixed at the nominal TE value and fat saturation and RF excitation add to the acquisition time. Doubling the PE resolution, however, would double the encoding time and thus increase the total acquisition time per slice by ca. 50%.

As derived in the Theory section, we recommend a RO resolution Δx = 1.5mm and a nominal echo time TE₀ = 25 ms at 3T, and a RO resolution Δ x=2mm and a nominal echo time TE₀ = 37 ms at 1.5 T. On one hand, it can be expected that the increased spatial resolution leads to a reduced signal-to-noise ratio (SNR) in well-shimmed areas and a prolonged TR which would further reduce the SNR per time. On the other hand, it has been shown that at 3T the loss in SNR due to the higher resolution does not lead to a similar reduction in the BOLD sensitivity, because the physiological noise level is similar to the thermal noise level at this high SNR [35,36]. For example, fMRI experiments were performed with a similarEPI sequence but with even higher resolution (1.5mm isotropic) and successfully detected activations located in the lateral geniculate nucleus [37].

This dropout compensation method can and should be combined with other dropout compensation methods such as z-shimming [11,13] to compensate for susceptibility-induced gradients in the through-plane direction. The combination with an optimized slice tilt [13] and PE gradient polarity [15] can be particularly synergistic. They do not only directly help to reduce dropouts due to susceptibility-induced gradients in the PE direction, but prevent a prolongation of the local echo time, thus reducing dropouts due to susceptibility-induced gradients in the RO direction. This can be a particularly efficient compensation technique, because it only requires a simple tilting of the slice. An adapted slice tilt can also be used to reduce the component of the susceptibility-induced gradient in the RO direction. For a more detailed discussion on how to optimize the slice tilt, the PE gradient polarity, and the z-shim gradient moment please refer to [18].

As an alternative to rectilinear GE EPI, non-rectilinear k-space readout schemes may be used to reduce dropouts due to in-plane gradients. In particular, spiralin or spiral-in/-out EPI acquisitions were successfully used to recover signal losses [38]. The spiral-in readout reduces signal losses, because the outer k-space is acquired at short echo times which allows for refocusing of strong susceptibility-induced gradients. Therefore, in general any acquisition scheme sampling k-space from the outside to the center is expected to reduce dropouts as compared to the opposite k-space acquisition scheme. Atheory similar to that presented here describing dropouts due to in-plane susceptibility gradients has been derived for spiral acquisitions [19].

Conclusions

We have presented a theory and experimental evidence showing that susceptibility-induced gradients in the EPI readout (RO) direction cause severe signal loss. We have developed a simple model allowing for an efficient simulation of EPI dropouts and an informed choice of EPI parameters depending on the given field inhomogeneities in a region of interest. We provide guidelines for avoiding this type of signal loss by using a specific combination of an increased spatial resolution in the RO direction and a reduced echo time. In particular, optimized parameters are reported for fMRI of the OFC at 1.5 T and 3 T. The presented approach can and should be combined with existing techniques for reduction of BOLD sensitivity losses due to susceptibility-induced gradients in the phase-encoding direction and through-plane direction [13–15,18].