Learning to reach by reinforcement learning using a receptive field based function approximation approach with continuous actions

Abstract

Reinforcement learning methods can be used in robotics applications especially for specific target-oriented problems, for example the reward-based recalibration of goal directed actions. To this end still relatively large and continuous state-action spaces need to be efficiently handled. The goal of this paper is, thus, to develop a novel, rather simple method which uses reinforcement learning with function approximation in conjunction with different reward-strategies for solving such problems. For the testing of our method, we use a four degree-of-freedom reaching problem in 3D-space simulated by a two-joint robot arm system with two DOF each. Function approximation is based on 4D, overlapping kernels (receptive fields) and the state-action space contains about 10,000 of these. Different types of reward structures are being compared, for example, reward-on- touching-only against reward-on-approach. Furthermore, forbidden joint configurations are punished. A continuous action space is used. In spite of a rather large number of states and the continuous action space these reward/punishment strategies allow the system to find a good solution usually within about 20 trials. The efficiency of our method demonstrated in this test scenario suggests that it might be possible to use it on a real robot for problems where mixed rewards can be defined in situations where other types of learning might be difficult.

1 Introduction

In robotics as well as other applications it is required to match the employed learning method to the task. A somewhat extreme example makes this very clear: it is useless to employ methods for the learning of induction logic to the learning of motor skills, like the tying of a shoe lace, whereas such methods are useful for the learning of all kinds of declarative knowledge.

Even within one domain, for example the field of motor learning, one has still many choices of learning methods depending on the different target applications and the choice of the method can much influence success and efficiency of learning. Many times supervised learning methods are chosen, because they are well controlled and fast. For example learning from demonstration can be used to teach a robot certain skills like simple manipulations of objects (Breazeal and Scassellati 2008; Schaal et al. 2003; Dillmann 2004). Supervised learning requires an explicit error function between outcome and the taught examples for controlling the learning progress. Reinforcement learning (RL) is more general, because such an error function is not anymore required and the system learns from receiving general feedback about the goodness of its actions. Commonly, the less specific feedback of RL will, however, lead to slower convergence times especially in systems with many degrees of freedom, which have large state-action spaces. To improve on this an appropriate representation of the state-action space has to be found. An appropriate match between problem and method can lead to major learning successes like in the works of Schaal and colleagues, who concentrate on the task of predefined trajectory following, and use RL approaches tuned to this task (Peters and Schaal 2006a, 2007, 2008).

In the present study, we will also focus on a reinforcement learning system in a relatively large space asking, how to bring together a useful, generalizable representation of the state-action space with a combination of reward and punishment strategies. Such a problem commonly exists when robots have to learn to calibrate their own actions relative to a desired outcome (which defines the reward). For example, Learning to fill a glass could be learned from demonstration by a human and “copied” by the robot, but it is known (A. Ude, personal communication) that the results of such a plain learning attempt are not satisfactory (spill-over, low filling level). With an RL method we can, however, recalibrate the learned parameter set as it will suffice to correct the robot’s action close to the glass, leading to a small state-action space. Here we have a natural situation where a combination of rewards and punishments can be used: the filling level (recorded from the human’s action) would be the primary reward, spill over would be a punishment, and the distance to the target would be a secondary reward.

To generalize beyond this example problem we focus here on the learning of visual servoing, where the approach to an object is guided by the visual difference measure between the end-effector of the robot arm and the target object. This more complex learning problem (as compared to the recalibration mentioned above) is chosen to demonstrate how far we can go with the newly introduced method. For an excellent introduction to visual servoing the reader is referred to (Hutchinson et al. 1996; Chaumette and Hutchinson 2007a,b). A visual servoing control schema uses the Jacobian matrix to gradually reduce the difference between the end-effector and the target object. However, the estimation of the Jacobian matrix becomes quickly hard as the number of joints and consequently the redundancy of the robot system increases. The high number of degrees of freedom, especially in humanoid robot arms and anthropomorphic hands, together with the necessity to handle constraints in joint space (singular configurations, self- collision and mechanical joint limits avoidance) as well as in object space (obstacles) makes visual servoing in highly redundant robot systems a difficult problem.

Several methods exist for solving the visual servoing problem, some are control-based (Espiau et al. 1992; Hosoda and Asada 1994; Hutchinson et al. 1996; Horaud et al. 1998), while others focus on learning (Shibata and Ito 1999; Martinez-Marin and Duckett 2004; Perez and Cook 2004; Leonard and Jagersand 2004).

Methods range from conventional neural networks, where some classical work had been performed early by the group of Schulten (Martinetz et al. 1990) and Torras [mainly in the domain of inverse kinematics learning, Ruis de Angulo and Torras (2005a); Ruis de Angulo and Torras (2005b)], to the now dominating methods of reinforcement learning (RL). Indeed a very large number of articles has appeared in the last years on RL for learning arm control as well as learning grasping. A large diversity of methods has been suggested exemplary represented by the papers cited here, Arm: Tham and Prager (1993); Kobayashi et al. (2005); Li et al. (2006);Wang et al. (2006); Peters and Schaal (2006b); Grasp: Moussa and Kamel (1998); Moussa (2004); Rezzoug et al. (2006). This diversity arises due to the fact that conventional RL methods (Sutton 1988;Watkins 1989;Watkins and Dayan 1992), for which rigorous convergence proofs exist, cannot be directly used as the state-action spaces in robot control are too large and convergence will take far too long, especially when using continuous actions, like here. As a consequence, the state-action value function of the used RL-method needs to be approximated by so-called function approximation methods. This is where the diversity arises as there is a terrifically high number of possible such methods existing (e.g. Tesauro 1995; Horiuchi et al. 1997; Fukao et al. 1998; Gross et al. 1998; Enokida et al. 1999; Qiang et al. 2000; Takahashi et al. 1999; Takeda et al. 2001; Kabudian et al. 2004; Wiering 2004; van Hasselt and Wiering 2007; Sugiyama et al. 2007 for a textbook discussion see Sutton and Barto 1998) and it lies at the discretion of the researcher to invent more. Convergence to the optimal solution can in general not be rigorously assured anymore. However, this aspect is of minor importance for a robot application as any trial will have to be interrupted if it is too long. Thus, as soon as these systems reach a “good solution” within “reasonable” time, the used method appears acceptable from an applied perspective. Especially when considering the task of learning to calibrate an action using a desired outcome as a reward one is interested to perform this calibration quickly and will be satisfied with any action which is good enough to obtain this outcome.

To achieve this we will adopt a strategy inspired by the place field system of rats, which is used for navigation learning as suggested by several models (Foster et al. 2000; Arleo and Gerstner 2000; Strösslin et al. 2005), and use overlapping place fields to structure our state-action space (Tamosiunaite et al. 2008). Rats run on the ground and are, thus, faced with a 2D target problem with a 2DoF motion needing about 500 place fields in a 1×1 m arena for good convergence (Tamosiunaite et al. 2008). On the other hand, the simulated arm, we use, operates in a 3D target domain with a 4DoF angle space for which we require 10,000 4D place fields. As a consequence, efficient strategies for structuring the reward space are required, too, without which convergence to a good solution would take too long. Thus, this paper will compare different types of visual (distance dependent) and non-visual (touch, angle configuration) rewards showing that, with this combination of methods, it is generically possible to find a good solution within about 20 trials.

2 Methods

2.1 General setup

Figure 1 shows the setup of our system in 3D as well as two planar projections. The arm has two joints with two angles each (azimuth α _1,2 and elevation ϕ _1,2) covering a 3D reaching space of 4.0³ units³ (each arm segment is 1.0 unit long). The target for reaching is a sphere with diameter 0.84 units. Joint angles are constraint between 0 and 360°. Hence, when at a constraint the arm needs to go back. This simulates similar constraints in human (e.g. elbow constraint) or robot arms.

Fig. 1.

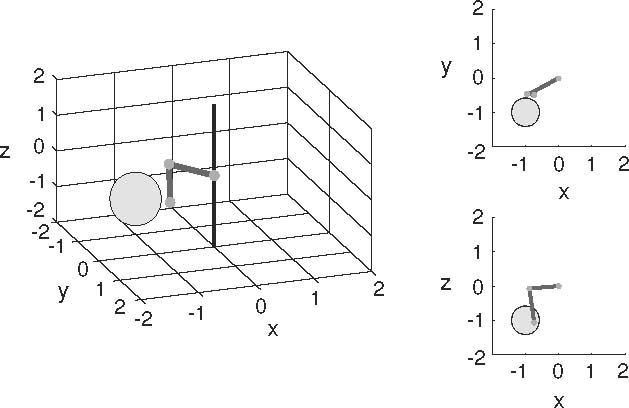
Two-joint arm and an object for reaching in 3D space as well as two projections (x, y) and (x, z) of the arm and the target object for reaching

The control and learning circuit used for arm acting and learning is provided in Fig. 2. The four joint angles are considered to form a 4D-state space. In the state space spherical, binary 4D-kernels ϕ ^k with a diameter between 1, 382 and 3, 358 (uniform distribution) are formed in a 4D-space of 10, 000⁴ units⁴. Those kernels, of which we use 10, 000 in total, have eight trainable connections to themotor units (total of 80, 000 connections). Kernels centers are distributed with a uniform distribution and a coverage of about 10–12 kernels overlapping for any given 4D-location is obtained. A kernel is active, with an output value of 1, as soon as the 4D-joint angle vector falls into the topographical region covered by the kernel, otherwise kernel output is zero. As kernels are overlapping, total activity is then given by the average over active kernels (see definition of Q-values below).

Fig. 2.

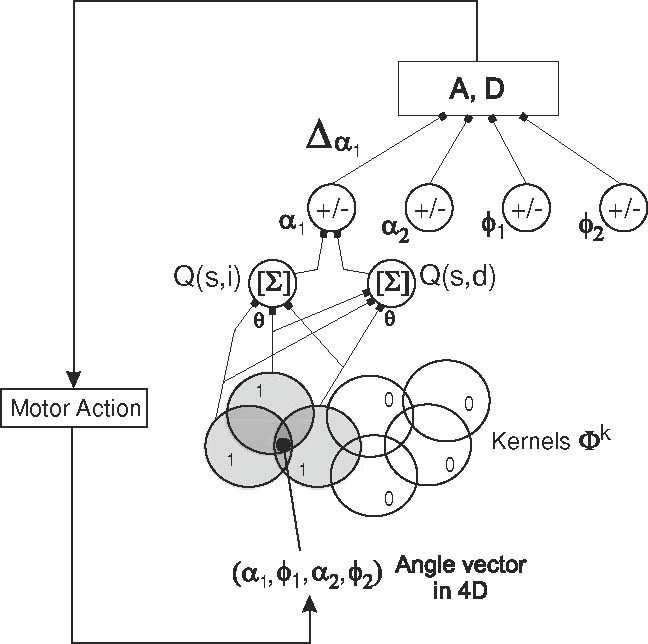
Schematic diagram of learning and action generation in our system. The angle vector (bottom) represents a location in 4D space and, thus, stimulates the gray kernels which fire while the white kernels are not stimulated and do not fire. The layers of units above calculate the finally required values A and D (top box see Eqs. 3, 4) which control the motors and move the joints to a new position

According to the trajectory forming strategy (see below) the actual movement is then generated from the motor unit activity. The trajectory forming strategy includes, for example, the exploration-exploitation trade-off and trajectory smoothing (if applicable).

The employed learning scheme uses a certain type of Q learning with state-action value function approximation, where function approximation is introduced through the fact, that we are not using discrete states, but state information is, instead, provided by the activity of the kernels (commonly called ‘feature vectors’ in the reinforcement learning literature) as described above.

Let us use the proximal joint (subscript “1”), and its azimuth component α ₁ to explain our methods. Explanation is the same for other angular components. We will be operating with Q values, and for the component α ₁ two Q-values will be defined: Q _α1 (s, i ) and Q _α1 (s, d), where a = i or a = d denotes the possible actions (increase, decrease of angle) and s a state. Q values are obtained through function approximation:

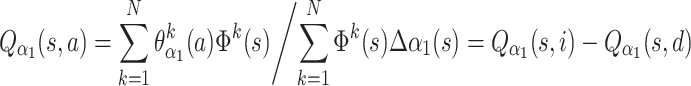where Φ ^k (s) is the activation function of the kth kernel (either 0 or 1 in our case) in state s, ϑ ^k_α1 (a) are the weights from the k-th kernel to the motor units for the two possible actions, and N is the overall number or kernels in the system. Weights θ are adapted through learning as described in the subsection on Q learning below.

Next we calculate the difference Δ _α1 (s) used for continuous action formation:

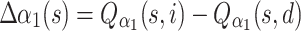Movement direction D is given by the sign function

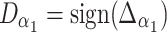and movement amplitude A by the absolute value normalized against the other components, which are calculated in the same way (now omitting s for simplicity):

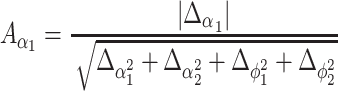Normalization leads to a situation where the movement vector is formed proportional to the increase/decrease values, but the total length of the vector is kept fixed. This is done to preserve the topology of the space in which learning takes place.

To cover a full sphere, normally the polar representation for azimuth is defined over 360° and for elevation over 180°. With the methods used here both, azimuth and elevation, are defined over 360° leading to duplicate angular space and, hence, an over-representation. Yet it is unnecessary to introduce any compensatory space transformation as the learning overcomes the over-representation anyways. For the same reason, the action space is duplicate, too, but this has the nice aspect of allowing us to treat actions at the angular constraints in a continuous way avoiding having to deal with wrap-around problems. Noise of around 7% of the movement amplitude was added to each step. This imitates imperfections in the control of the angle in a real robot and introduces the required exploration component into our model. This way exploration stays “near the path” which leads to faster convergence than random exploration, which we had also tried but abandoned for this reason.

Movement strategies with smoothing were employed. All new steps in angle space were made as a combination of the currently calculated steps combined with the previous steps:

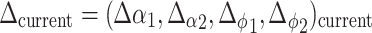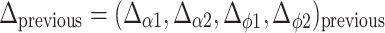using:

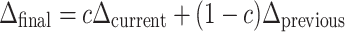where c = 0.6 was used. Smoothing helps to avoid jerky movements in the beginning of learning and also influences the process of learning, as in Q learning with function approximation, which we are using here, the convergence pattern is dependent on the paths performed during learning.

Finally, if a newly calculated angle falls outwith the constraint boundaries, then random steps with uniform distribution in angle space are tried out until a point satisfying the constraints is obtained.

2.2 Learning method

From eight possible actions only four learn during a single step. These are the directions along which the actual movement has been taken. For example, if a particular angle has been increased, the unit, which has driven the increase, learns while the antagonistic ‘decrease unit’ will not be changed. Furthermore, learning will affect connections of all currently active kernels. Again we will demonstrate the learning rule for components representing angle α ₁.

Weight update follows an algorithm similar to conventional Q-learning (Watkins 1989; Watkins and Dayan 1992). For each angle, two actions a _i,d are possible: increase or decrease. Let us say the current state is described by angles s = (α ₁, ϕ ₁, α ₂, ϕ ₂)_current and some action a (increase or decrease) is chosen that leads to a state s′ = (α ₁, ϕ ₁, α ₂, ϕ ₂)_next. In our learning framework, the change in the value θ _α1 (a) of that state-action pair follows the mean across all activated kernels of s′:

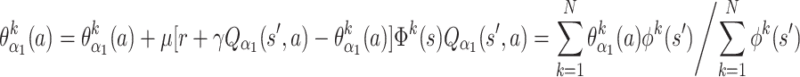where k is the number of the kernel to which the weight is associated, r the reward, μ < 1 the learning rate, γ < 1 the discount factor, Φ ^k (s) the activity function for kernel k in state s, Q _α1 (s′, a) the Q value of the system in the next state, for action a defined as:

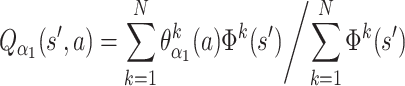Equivalent expressions are used for updating Q values for the angles ϕ ₁, α ₂ and ϕ ₂. Throughout this study we use μ = 0.7 and γ = 0.7. This rule is called averaging function approximation rule and is considered to perform more stably (Reynolds 2002) in function approximation schemes as compared to standard methods (e.g. see Sutton and Barto 1998).

Note, the algorithm is not so easy to attribute to standard Q- or to SARSA-learning. It is neither SARSA, because it does not take into account where the system has gone in the next step; nor is it Q-learning, as it does not consider which action is best in the next step. The algorithm rather considers if continuing along the current direction is valuable according to the Q-values of the next state Q _α1 (s′, a) and attempts to straighten the path.

Also Q-learning and SARSA-learning can be implemented onto the same function approximation scheme, for which we will give the equations in the following. For Q-learning we use:

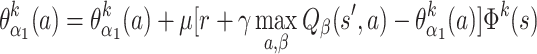where maximum operation runs over all actions a and all angles (α ₁, α ₂, ϕ ₁, ϕ ₂) here subsumed under the index β, finding the biggest value from all possible action descriptors associated with the state s. For SARSA learning we use

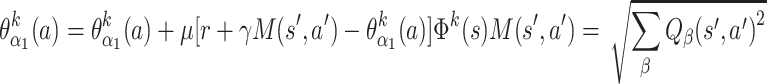where M(s′, a′) is defined by the magnitudes of the action components of the next performed action:

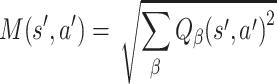where β runs over all four angles.

Finally, to reduce computing time, we have introduced a variable path-length limit. If the arm has not reached the target within this limit, it is reset to the start and all changes in Q-values learned during this trial are undone. For a new experiment, path length limit starts with l(1) = 1,000, and further develops according to the following recurrent equation:

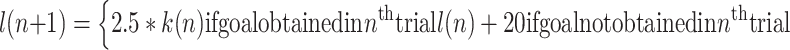. where k(n) is the number of steps to goal in trial n. That is, the limit comparable to the previous path to the goal is imposed once the goal has been obtained, but if the goal is not obtained in some trial, then the limit is relaxed by 20 units.

2.2.1 Reward structure

Different rewards have been used, alone and in combination, in this study (Fig. 3) normalized to a maximal reward of 1. Highest reward is (usually) obtained on touching the target (Fig. 3a), but we also define a vision-based reward structure (Fig. 3b). For this, we assume that the distance between tip of the arm and target can be evaluated. Distance dependent reward is then defined linearly along this distance. Different combinations of distant dependent and touch rewards are shown in panels c1 and c2 of Fig. 3. Panel d shows an approach distance (differential) dependent reward structure were reward is only given if the arm has approached the target, while reward is generally zero if the arm has moved away. These reward structures are using absolute distance x to define the reward. By contrast, we have also used a differential, relative reward structure (Fig. 3e). For this we first normalize the distance to target at the start of an experiment to one. Then reward is given according to the relative approach d. Hence a larger step towards target was rewarded more than a smaller one, where absolute distance does not play any role. In the following, we will always refer to the different rewards used in individual experiments using the panel labels from Fig. 3.

Fig. 3.

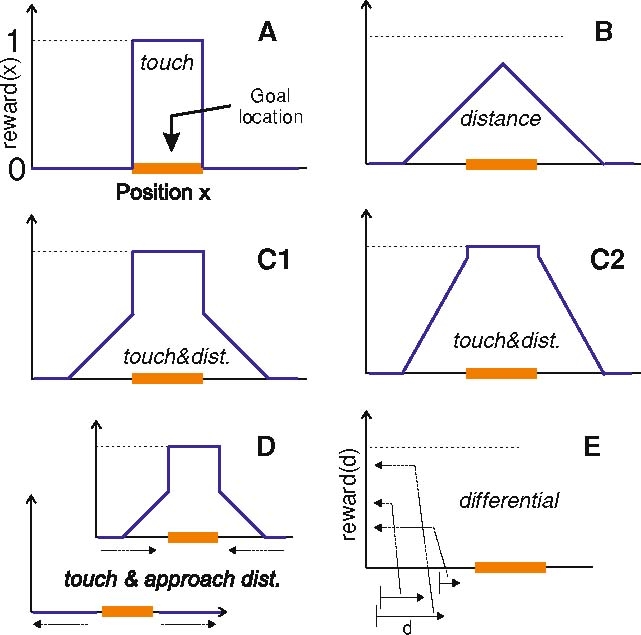
Schematic representation of different types of rewards used in this study. The bar in the middle of the x-axis represents the target location. Reward can be given only there a or on approach b or combining approach with touch (c1, c2). d depicts a situation where reward is given on approach (top) but not on leaving (bottom, see direction of the arrows). e Shows a purely differential reward calculated by how far the arm has moved forward to the target

Furthermore, we also introduced punishments (negative rewards) for approaching the constraint boundaries. For this, we were increasing punishment linearly, starting with zero at a distance of 1/20th of the field width to the border up to a certain maximal value reached when touching the border. Maximal values were changed in different experiments and details will be given below.

3 Results

3.1 Individual convergence patterns

The main aim of the paper is to demonstrate condensed statistical results that help comparing convergence of learning processes using various reward structures and other learning parameters. However, before presenting those statistics, we will show examples of individual training sessions to provide a better intuition about the behavior of this system. In Fig. 4 five qualitatively different cases of system development are shown: (a) quick convergence, (b) delayed convergence, (c) intermittent episode of divergence, (d) bad convergence; and (e) the persistently falling back onto a wrong trajectory, when the optimal trajectory has already been learned. The bars shown in black demonstrate successful runs; the bars shown in gray are for unsuccessful runs, where the limit for the path length was exhausted before the goal was reached. For these experiments, a D type reward (Fig. 3) has been used. It is of interest to make a practical remark here: cases shown in Fig. 4 panels c and e are largely irrelevant from a practical point of view as any robot learning system of this kind would either have to be controlled by an operator or—at least—would require a stopping criterion, which tells the machine to stop as soon as it has found a reasonably good solution. In both cases the longer trajectories, which occur later in (c) or in an interspersed way in (e), would just be ignored (or not even be recorded). Note, Fig. 4 showed five archetypical examples.Many times transitions between them exist, which cannot easily be distinguished. As a consequence, from now on we will not separate these cases anymore and perform statistical analyses always across whole data sets. In the following for every experiment we train the system for 20 trials and then for another 100 trials we will determine the average trajectory length and the percentage how often the system has reached the goal. As this is indicative of the average convergence property of a certain setup, it will allow us to compare strategies. In general we repeat every experiment 50 times.

Fig. 4.

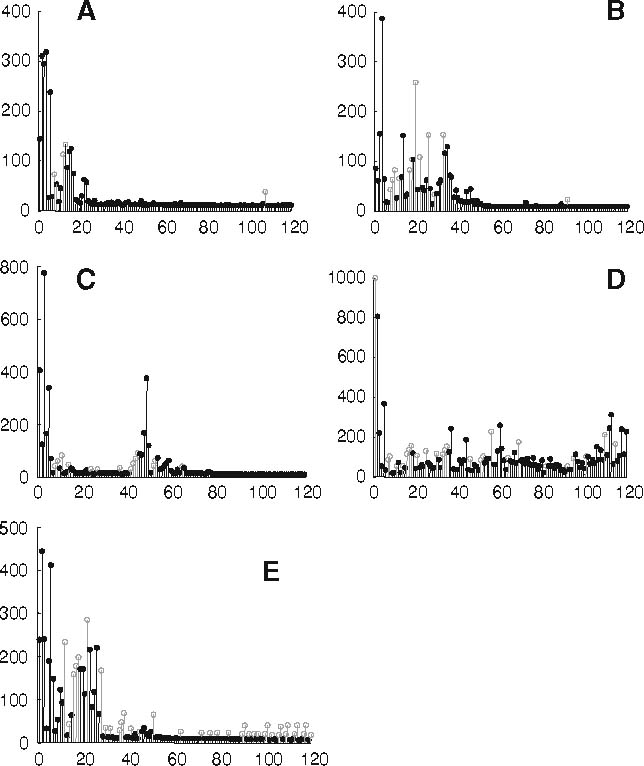
Different example runs. a Quick convergence to a good trajectory within about 22 trials. b Delayed convergence (≈50 trials). c Quick convergence in less than 20 trials and thereafter some divergence and re-convergence to a different trajectory. Note from a practical perspective the robot would just stop learning after about trial 20 and the second phase is not of relevance. d Badly convergent case. e Good convergence but with interspersed other, longer trajectories (light shading). Also here the robot would normally stop learning after having found the better trajectory and ignore the others

Observations show that for best learning regimes divergent cases never occur, but various intermittent phenomena, or delayed convergence were present. For bad regimes about three to five divergence cases happen during 50 experiments, and quick and clearly convergent cases are relatively rare (e.g. 15 out of 50), the biggest proportion being taken by delayed convergence or by cases with intermittent behaviors.

3.2 Comparison of learning modes

In the simplest case reinforcement is only given when the target is actually hit (reward type A). Note, this would correspond to a task of finding an unknown object in the dark. As touching is a singular, rare event, this leads to a pronounced temporal credit assignment problem for large state-action spaces such as here. Thus, this case will only be considered for comparison reasons and not analyzed any further.

Of much more relevance for robotic applications is the case where visual information is used to position the arm (visual servoing) and this can be encoded by a distance dependent reward structure (reward type B).On touching additional reward may be given (reward type C). Furthermore, it makes sense to avoid giving a distance dependent reward when the arm has actuallymoved away from the target (reward type D). First, experiments to compare influence of these three different basic reward structures were performed. In Fig. 5a the average number of steps to target is shown and in (b) the percentage of cases reaching the goal is presented. The bars show the standard deviation of the distributions. We observe that in the case where vision is excluded the trajectories of the arm are around ten times longer as compared to cases with vision. Standard deviation is 218 steps, and is clipped to preserve the scale of the figure. Similarly, the percentage of attaining the goal without vision is only around 50%. This happens because in 3D space the target only takes a small part of the total space and it is not easy to hit it by chance. Furthermore, due to the singular reward structure, kernels with non-zero Q-values after around 100 runs are still too sparse to give clear indications about preferred trajectories in the 4D angle space. Runs for distance rewards (middle column) are substantially longer and the percentage of successful trials is smaller, as compared to the case that includes the approach distant dependent component (right column). Thus, in the following, we will focus our attention on cases with a approach distant dependent reward component, as these have noticeable better convergence properties compared to the others.

Fig. 5.

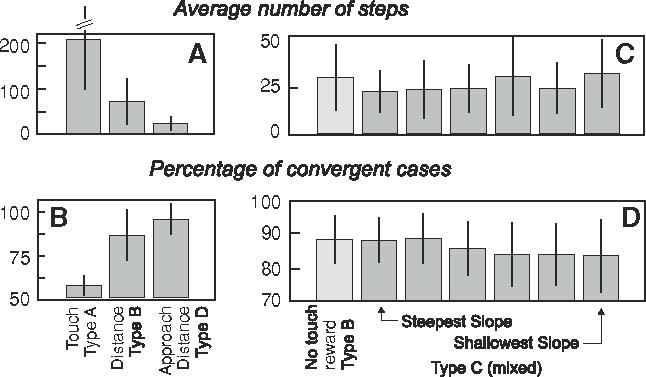
Statistics for different reward types. a, b Two distance dependent reward types (right) compared to touch-only reward (left). Annotations at the bottom refer to the annotations introduced in Fig. 3. c, d Comparison of different slopes for distance dependent rewards. For c, d slope values from left to right are: 1/3 (no touch reward case), 1/3, 1/4, 1/5, 1/10, 1/20, 1/50, reaching values at the goal boundary correspondingly: 0.86, 0.65, 0.52, 0.26, 0.13, 0.05. Touch reward is 1

Next we analyze the steepness of the distance dependent reward curve in Fig. 5c, d. Reward for reaching the target was kept at one and the slope of the distant dependent reward was varied from 0.86 (almost reaching one, the value of the touch reward) at the border of the target for the steepest slope to down to 0.05 for the shallowest slope. One can observe that for steep slopes (c, d left) values are quite similar and better than for shallow slopes. The first column shows the limiting case when no special reward for touching was applied. Here the entire process of approaching the target was regulated using exclusively distance-dependent rewards. This case in terms of convergence appears among the best cases, but step length was longer than for some of the mixed cases. Thus, for further experiments we were choosing slope steepness 0.25, which seems a good compromise. Using this steepness parameter, more reward structures were explored in Fig. 6a, b. In the columns from left to right, we compare (1) differential reward (type E), (2) approach distance (type D), (3) a variant of type D, where we always give the same amount of reward r = 0.3, and (4) type D but applying punishment of the same size as reward on approach would be, if the action leads away from the goal by more than a certain distance. In general results are very similar where the rightmost column is slightly better than the others.

Fig. 6.

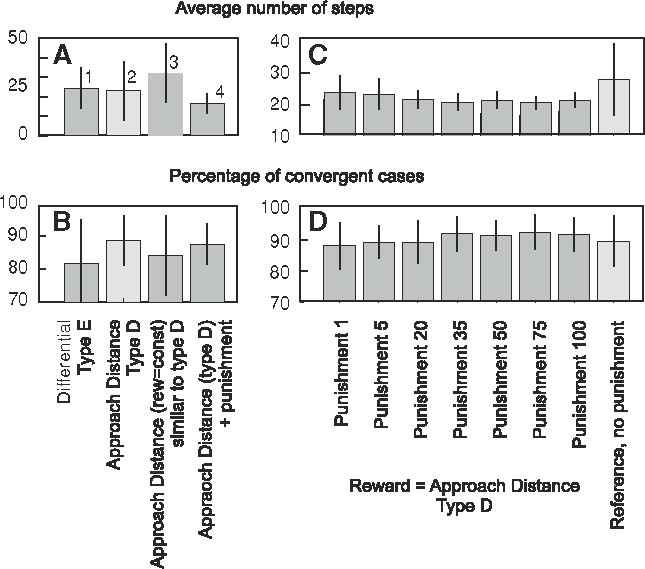
Statistics for other types of rewards. a, b As per annotation at the bottom (see Fig. 3). c, d Reward Type D is combined with punishment on approaching the maximally allowed joint angles. Note light gray shaded cases are identical across panels

When applying distant dependent rewards, the problem arises that the joint might be drawn to go towards some direction, though this movement is not allowed due to physical limitations of the joint construction. For example here the joints were not allowed to cross the border of 0–360°. The position and size of the reward was chosen such that again and again learning tried to violate these constraints. This problem can be mitigated best by applying punishment also at the constraints as described in the methods section. This additional mechanism leads to a noticeable improvement of convergence times (Fig. 6c) and a much higher percentage of convergent cases (Fig. 6d).

In the columns from left to right in Fig. 6c, d maximal punishment is 1, 5, 20, 35, 50, 75 and 100. The rightmost column shows a control experiment without punishment. Reward structure was the same as in panels A,B column 2. Hence gray shaded columns in panels a, b are the same as those in c, d.

One can observe that punishment at constraints in general improves rate and speed of convergence. Performance of learning first increases with increasing punishment values and approaches an optimum around a punishment of 35–75 and then slightly drops again. Of importance, however, is that punishment at constraint works rather reliably over a large parameter range and that the variances have been drastically reduced. Hence quick convergence became rather reliable with this mechanism.

Combining constraint-based punishment, specifically employing the case with the maximal punishment value 35, with punishment for going away from the reward, as described before (column 4 in panels A,B), did not provide better results, remaining in the range of an average of 13–14 steps to the goal with around 90% of successful trials.

The system was also tested with changing the position of the goal, and reverting positions of start and goal, to exclude possibilities of some special circumstances which were only providing good performance for one specific task. Trials with changed position were providing similar average trajectory length, and success percentage results.

3.3 Comparison of methods

3.3.1 Comparing different update methods using the same function approximation

In the following section, we will use always the same function approximation method and compare different update algorithms like Q-learning and SARSA-learning with our path straightening PS as well as with a fully discounted version of the algorithms (Fig. 7). In general, all methods produce similar results where the path straightening method is only non-significantly better than the others. Hence, while reward structure and function approximation methods are clearly influencing the performance in a critical way, the choice of Q-value update method does less so. “Fully-discounted” refers to a simulation where γ = 0 has been used. This case also produces similar results arguing that it would be possible for this problem to reduce the learning problem and even operate with fully-discounted rewards. Note, all update equations (Q, SARSA, PS) become the same when using γ = 0.Care, however, has to be taken in this case that there are no states with zero or indistinguishable reward, where a fully discounted method would fail. As this can in general not be assured, a fully discounted procedure should not be adopted. In general, the conclusion of this subsection is that the actual choice of the update method is not critical as long as an appropriate function approximation as well as reward structure is being used.

Fig. 7.

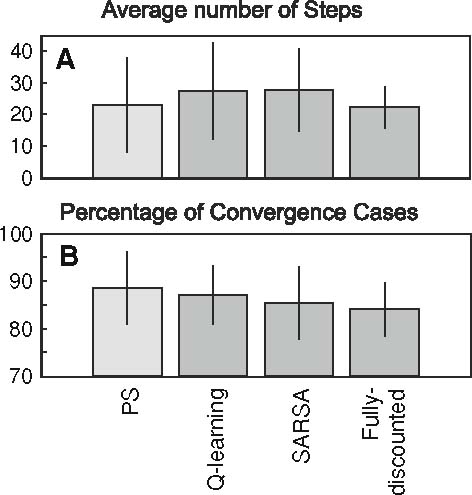
Statistics for other types of learning methods. PS = path straightening (our method). We used reward type D, no punishment, discount factor γ = 0.7 for all cases except case “fully discounted”, where we have γ = 0

3.3.2 Comparing to natural actor critic reinforcement learning

Peters and Schaal (2006b, 2007, 2008) use policy gradient methods for robotic applications. These form a different class of RL methods as compared to the one analyzed in this study, as the policy is updated not in every step, but only after several trajectories have been produced. Also no representation of state is being considered, but actions are described directly. As currently natural actor-critic RL is often considered to be the method of choice in robotics we made a comparison of our method to the version of the episodic natural-actor critic with time-variant baseline for learning the same reaching task, following Peters and Schaal (2008). We have made a simplifying assumption that the best path to goal is straight. We were describing the trajectory by a difference equation:

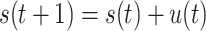where state vector s(t)=[α ₁(t), ϕ ₁(t), α ₂(t), ϕ ₂(t)}]^T includes the analyzed angles, and u(t) is a 4D control signal. We used the following normal distribution N(·) for the control signal: u(t) ∼ N(θ, σ}² I), where θ is a 4D vector of control averages and I is the 4 × 4 unit matrix. The value of σ determines the variability (“exploration”) in the different trajectories.

Reward was provided under reward structure C (Fig. 3), where in each step the distance to the target was evaluated and a bigger reward was given on touching the target. We did not use the (D)-reward structure (Fig. 3) preferred in our on-line method, as the preliminary assumption for the implemented natural actor-critic was a straight trajectory and the (D)-structure is only meaningful when curved trajectories are allowed. We used a discount factor of γ = 0.95, to emphasize rewards that are obtained earlier. If the trajectory was leaving the allowed angle range (0, 360γ), negative rewards of the size of −1 were given. Each trajectory was composed of 15 steps of the same average length as for our on-line learning method. We always used the same total trajectory length (that is, we did not stop the trajectory after a touching event had happened) and were giving maximum reward several times, if the trajectory stayed in the volume of the object for several steps.

We used the natural actor-critic algorithm with timevariant baseline to optimize θ and σ. An experiment was made using the same initial position of the arm, as well as the same position of the ball as in our on-line learning experiments. We were using hand-tuned parameters, as proposed by Peters and Schaal (2008). Learning for this type of algorithm is divided into “epochs”. Every epoch consists of 20 trajectories after which the gradient needed for the RL-update could be calculated. One learning “trial” consists of n epochs, where we usually chose n = 50 leading to 1,000 executed trajectories. Step size for the gradient calculation was tuned to obtain quick convergence and at the same time relatively stable optimization performance. Using less than 20 trajectories in a single epoch to evaluate the gradient made the learning process unstable. Initial values for θ were chosen randomly from the interval [−1, 1] with uniform distribution.

At first we observed that usually one learning trial (50×20 traj.) was enough for the algorithm to lead to a good final trajectory. In Fig. 8a an example of a well convergent trial is shown, while in Fig. 8b we show an example with delayed convergence. This shows that (similar to our algorithm) convergence varies and, thus, we performed 100 learning trials for a statistical analysis (100 × 50 × 20 traj.) were we used 100 different initial values for the θ-vector. From this statistics, in Fig. 8c the average number of successful reaches obtained at a certain epoch is shown. The marked crossing point (x = 16.48, y = 15) is of interest as this represents 15 successful reaches after on average 16.48 epochs of here amounting to about 329.54 performed trajectories. By contrast, in our algorithm we get 15 successful reaches after about 20 trajectories (as we do not have to use epochs, hence, for us every “epoch” is just one single trajectory). However, the intermediate trajectories may be longer (curved) in our case.

Fig. 8.

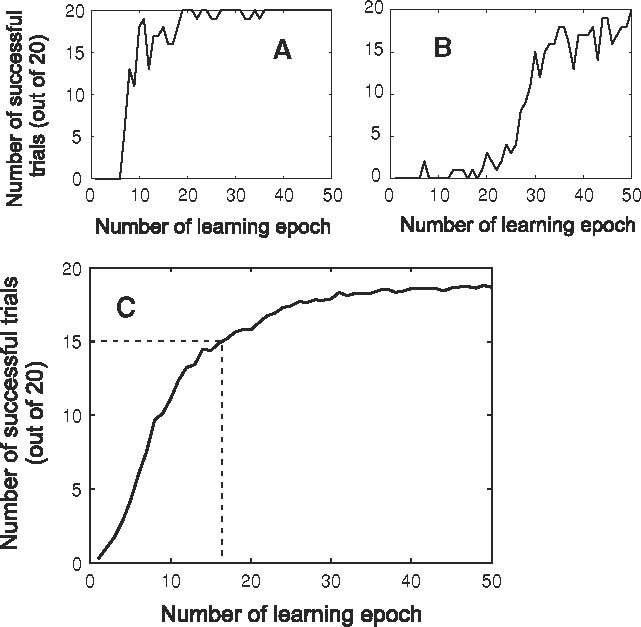
Learning curves for natural actor-critic: a good convergence example, b delayed convergence example. c average number of successful trials to reach an object

4 Discussion

In this paper, we have developed a novel action approximation scheme for reinforcement learning, and implemented three methods: path straightening, Q-learning and SARSA -learning based on this scheme. This kernel based approach for value function approximation was inspired by the place-field system in the hippocampus of rodents (Tamosiunaite et al. 2008). Our focus lay on a comparison of different reward structures and we could show that a combination of distance dependent rewards with constraint punishment and extra reward on touching will lead to a fast convergence to “a good” trajectory.

A central problem for the use of RL in large state-action spaces is that convergence of conventional methods will take far too long. Thus, value function approximation is required for which a wide variety of methods exists. Alas, only few of them have proven convergence properties (Sutton and Barto 1998; Gordon 2001; Reynolds 2002; Szepesvari and Smart 2004) and those are in praxis many times not the fastest ones. Hence, the field of applied robotics is largely uninterested in the mathematical rigor of a given method as long as the trade of is reasonable between goodness of solution and time to find it. From a practical perspective, on any humanoid robot learning will be stopped by force as soon as a predefined variable, which handles this trade-off, approaches a desired threshold.

The control of a multi-joint arm poses a terrific problem for RL methods as the state-action spaces are in general very high, needing to cover a space-time continuous system within which redundant solutions exist. While a very large number of papers exist on space-time continuous low-dimensional problems (e.g. Qiang et al. 2000; Gross et al. 1998; Gaskett et al. 2000), only few articles try, to tackle this problem with a reasonable degree of complexity in a high dimensional system (Perez and Cook 2004; Peters and Schaal 2007, 2008). Also many times action spaces of the problems solved are discrete or quite limited (Enokida et al. 1999; van Hasselt and Wiering 2007; Martinez-Marin and Duckett 2004) and, even if continuous state representations are used, actions are kept discrete in continuous task approximations (Enokida et al. 1999; Li et al. 2006). This is possible when action spaces are small, but with bigger action spaces (4D in our case) the usage of discrete actions becomes impractical. If continuous actions are to be used, often methods for the interpolation of discrete samples are employed relying on weighted sums or wire fitting (Gaskett et al. 2000; Takeda et al. 2001; van Hasselt and Wiering 2007). Instead, here we are offering a generic approach to continuous action formation, where reinforcement learning is implemented on the features defining continuous actions.

A recent and quite successful contribution to RL in robotics concerns the so-called natural-actor critic method (Peters and Schaal 2006b, 2007, 2008). This algorithm belongs to the class of policy gradient methods (Williams 1992; Baxter and Bartlett 2000; Sutton et al. 2000), which are structurally quite different from the one analyzed here (see Sect. 3.3.2 above for details). Policy gradient methods work directly with action representations, and thus need much less parameters than on-line RL methods. Also one can choose appropriate representation of the initial trajectory. The advantageous feature of the implemented natural actor critic method, to our observation, is that the convergence performance does not decrease too dramatically with rising dimensionality of the problem, what is very important in robotic applications. Yet the natural actor-critic in our implementation was quite sensitive to parameter choices, and the number of trajectories required to obtain a good policy was one order of magnitude larger than for our on-line method. The inventors of the natural actor critic method originally implemented it in a different context. They start with a very close to target trajectory and attempt to improve it, while here the method was applied for learning from scratch, without any “close to target” initial trajectory. Although formulation of robot learning tasks as in (Peters and Schaal 2006a, 2008), with a very close to optimal initial trajectory obtained from demonstration is very appealing, tasks exist (especially for when there is a large mismatch in embodiment between human and robot) where there is no possibility to obtain a (human-) demonstration, and our current experiments indicate that on-line learning methods, like the method proposed here, may be more efficient in such “learning from scratch” tasks.

Another theoretical development of the current study is the analysis of different reward structures for RL in visual servoing tasks. Robotic applications tend to be multidimensional, and if a reward is provided only at the goal, then additional means to guide a robot to the target are required, like ‘learning from easy missions’ (hence, bootstrapping the system with simple tasks) or using simpler controllers (like teachers, Martinez-Marin and Duckett 2004), otherwise learning times would be impractically long. In image based visual servoing (IBVS) systems, richer reward structures were many times used, attempting to achieve convergence in bigger state spaces (Leonard and Jagersand 2004; Perez and Cook 2004). We analyzed and compared about half a dozen of vision-based reward structures and studies addressing applications of visual servoing could gain from that comparison using the structures that performed best according to our modeling. Although we are investigating these structures in the framework of position based visual servoing (PBVS), similar ones could be applied to IBVS, using visual error instead of distance. Possibly some adaptations of the method we used here would be required, as mapping from distance to visual features is rather complex.

Of specific interest is that our formalism is very simple and can still handle large state-action spaces in a moderately high-dimensional problem. Currently, this method is being implemented on ARMAR III, a humanoid robot built by the University of Karlsruhe (Asfour et al. 2006). Each arm has seven degrees of freedom: three DOF in the shoulder, two DOF in the elbow and two DOF in the wrist. For this purpose, a control schema of the arm is realized which makes use of hypothesis and results from neurophysiology on human movement control (Soechting and Flanders 1989a,b). Soechting and Flanders have shown that arm movements are planned in shoulder-centered spherical coordinates and suggest a sensorimotor transformation model that maps the wrist position on a natural arm posture using a set of four parameters, which are the elevation and azimuth (yaw) of both the upperarm and forearm similar to the problem addressed in the current paper. Once these parameters are obtained for a given position of the wrist, they are mapped on the joint angles of the shoulder and elbow of the robot arm, which completely define the wrist position. For more details the reader is referred to (Asfour and Dillmann 2003). In the Introduction we had mentioned the task of recalibrating an agents movement, which is the task to be performed by ARMAR III. The agent holds a container full of liquid and needs to learn filling another glass standing in front. Figure 9 shows a simulation of this task and the agent’s performance. A full description of this simulation and its modeled physics goes beyond the scope of this paper. This figure, however, is meant to show the efficiency of our new method in a task which is difficult to achieve by methods other than reinforcement learning and we note that already after three trials (a) the agent has learned the task to more than 50%. In panel (b) one sees that the agent moves around over the glass and keeps on pouring liquid until its container is empty. Panel (c) shows the vector field of Q-values, which point towards the center of the glass. This experiment carries a natural reward structure (liquid filled) and is, thus, well-adapted to the assumptions of RL and the methods developed here allow solving this task with very few trials only. In the central part of this paper we deal, however, with position based visual servoing (Chaumette and Hutchinson 2007a), assuming that the inverse kinematics is not known and that the arm has to learn to target an object without this knowledge. This task had been chosen as it is much harder than the glass-filling problem and we wanted to show that our methods still reach quite a high performance in order to raise confidence in this approach.

Fig. 9.

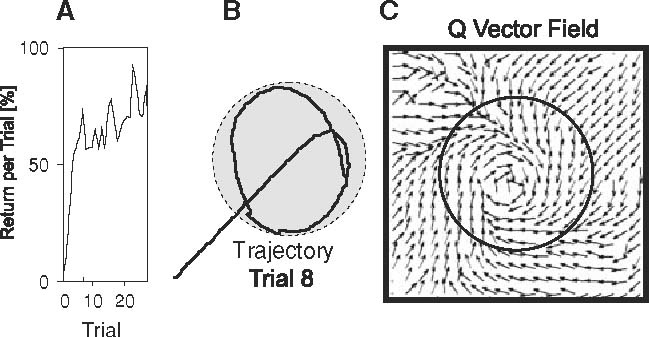
Example of a glass-filling RL task as mentioned in the Introduction, where the agent learns to recalibrate a prior learned target position. The simulated agent is supposed to learn approaching a glass (circles) to optimally pour liquid into it. The reward is defined as the amount of liquid filled into the glass. The agent starts exploring from a location close to the glass, reached for example by plain visual servoing or by learning from demonstration. a Return versus number of trials. b Example trajectory. c Q-vector field after 20 trials

In summary, our method is meant to provide a solution with some practical relevance for robotics, but, given the kernel structure, it is also possible to combine it with a newly developed biophysical framework for implementing Q- or SARSA learning by an LTP/LDT based differential Hebbian framework (Wörgötter and Porr 2005;Kolodziejski et al. 2008). Hence, from a biophysical point of view receptive field based (i.e., kernel based) function approximation could indeed operate in a Hebbian network emulating not just correlation based unsupervised, but also reward based reinforcement learning.