ADAPTIVE DATA ANALYSIS OF COMPLEX FLUCTUATIONS IN PHYSIOLOGIC TIME SERIES

Abstract

We introduce a generic framework of dynamical complexity to understand and quantify fluctuations of physiologic time series. In particular, we discuss the importance of applying adaptive data analysis techniques, such as the empirical mode decomposition algorithm, to address the challenges of nonlinearity and nonstationarity that are typically exhibited in biological fluctuations.

1. Introduction

One of the great challenges of contemporary biomedical science is to understand more fully the dynamics of living systems in health and disease. The importance of this challenge is highlighted by headlines announcing unexpected, life-threatening side effects of once-promising drugs, as well as the serendipitous discoveries deriving from “outside the box” approaches to major public health problems, for example, in heart disease and cancer biology. The basis of such unexpected findings, both negative and positive, is the extraordinary complexity of physiologic systems, which exceeds that of the most challenging systems in the physical world. These systems defy understanding based on traditional mechanistic models and conventional biostatistical analyses.

The overall aim of this paper is to develop a deeper understanding of the dynamics underlying healthy biological systems and what occurs when these systems lose their robustness due to aging or disease. We will address these fundamental questions from data analysis perspective. Specifically, why novel adaptive data analysis techniques essential to understand these important issues are. However, because of the nonlinear complexity of these biological systems, it is unrealistic to achieve this goal purely by a traditional engineering (reductionist) approach in which one disassembles the system into its constituent pieces, studies each component in detail, and finally puts them back together, recreating the original entity. Even in rare cases where this type of reductionist program can be accomplished, the integrative system’s behavior typically surprises expectations based solely on the information gathered through analyzing each component in isolation. In everyday parlance, this well-known effect is referred to as the whole being different than the sum of the parts. In the language of complex systems, it is known by the term “emergent properties.” In nonlinear systems, the composite or group behavior (of molecules, cells, organs, individuals, and even societies) cannot be fully understood by simply “adding up” the components. Instead, one needs rigorous, new approaches to model, measure and analyze a system’s integrative behavior.

2. Complex System Approaches

Central to this enterprise are computational tools and models that usefully represent the behavior of the intact system. These system-level measurements and models also need to capture certain generic and robust properties of complex biological systems, such that they have a wide range of applications across many disciplines. To this end, we have focused on studying the output signals generated by complex biological systems. The dynamical fluctuations of these signals in health and disease provide a unique window into the free-running behavior of the integrative systems.

To identify system-level behaviors that are critical to our understanding of healthy dynamics and of pathological disturbances, we pursued investigations under the framework of three complementary hypotheses:

1. The complexity of a biological system reflects its ability to adapt and function in an ever-changing environment.

2. Biological systems need to operate across multiple scales of space and time, and hence their complexity is also multiscale and hierarchical.

3. A wide class of disease states, as well as aging, appear to degrade this biological complexity and reduce the adaptive capacity of the system. Thus, loss of complexity may be a generic, defining feature of pathologic dynamics, and the basis of new diagnostic, prognostic, and therapeutic approaches.

To investigate the above hypotheses by studying the dynamical fluctuations of output signals generated by complex biological systems. We developed some innovative approaches in recent years. These system approaches and their associated computational tools promise to provide insights into a wide range of biomedical problems. Examples include forecasting catastrophic events such as epileptic seizures and sudden cardiac arrest, studying gene evolution, searching and categorizing large biomedical and other types of databases, and screening for drug toxicity and effcacy, to name but a few. These diverse applications are strong indications of the potential of these new approaches to advance the science of complex systems.

3. The Origin of Physiologic Variability

Dynamical fluctuations in the output of complex biological systems with multiple interacting components often exhibit remarkably complicated patterns. Such fluctuations have long been ignored by conventional analyses. Indeed, the presence of these fluctuations is often assumed to simply reflect the fact that biological systems are being constantly perturbed by external and intrinsic noise. However, recent findings by our group and others clearly indicate that these complex fluctuations exhibit interesting structures that were not previously anticipated.^1–6 More importantly, these fluctuations may also contain useful information about the emerging complexity of the systems.^7–13 Here we develop a dynamical system perspective to understand the origin of these fluctuations.

3.1. State space representation

In dynamical systems research, it is common to describe a system by a set of variables. If defined properly, these so-called state variables can uniquely determine the state of the system and the time course of its revolution (see Fig. 1).

Fig. 1.

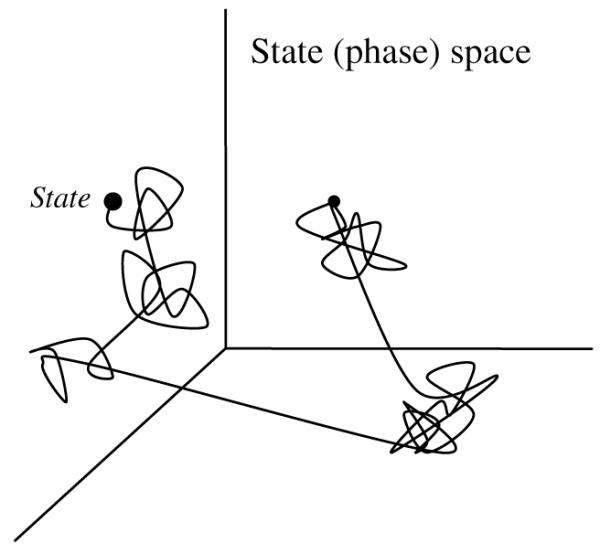
A schematic illustration of 3-D state space. In this example, a system is fully described by 3 state variables. At any given moment, the system is represented as a point (state) in this space. The trajectory of the system traces out the time evolution of changes of the system’s state.

Assuming that how a system changes in time is purely deterministic, then the goal of the state space approach is to find equations of motion for the underlying dynamics in order to understand, predict, and control the system.

However, for biological systems, this approach is not feasible due to two intrinsic difficulties. First, the state space is of very high dimensionality, and not all variables can be measured. For example, to fully describe the state of human physiology, one might need to monitor hundreds of variables (including heart rate, blood pressure, body position, muscle tone, oxygen and multiple hormones level in the blood, etc). Although macroscopic variables can be used as state variables to reduce the dimensionality of the state space, it is unclear what the proper macroscopic variables are in this case. Furthermore, biological systems are not purely deterministic, many stochastic factors constantly influence them. Although these two considerations significantly limit the application of tools developed in dynamical system analysis to biological systems, the state space representation is still a useful picture conceptually.

3.2. System complexity as a measure of adaptability

As we discussed previously, a meaningful quantification of the complexity of a biological system should be related to the system’s capacity to adapt and function in an ever changing environment. The system that can adapt to the most external challenges (stresses) will have the best advantage for survival. Therefore, we propose that biological systems have been evolving to increase their dynamical capacity (complexity). As a result, biological systems we observed today are highly complex since they are the products of a very long evolutionary process. We also hypothesized that aging and disease will degrade a systems complexity, since they represent a less adapted system.

Using the state space concept, an external perturbation (challenge or stress) to a biological system requires the system to move from one location to a different area of the state space in order to adapt to the perturbation. A healthy system should be able to easily move from one area to another, while a diseased system has a very limited ability to adapt, and thus cannot move to other regions of the state space.

Complexity is a measure of a system’s capacity to adapt, therefore, it should be related to the total available volume of the state space. Theoretically, we can measure the size of the available state space by either observing the system’s trajectory for a very long time (asymptotically, the underlying dynamical system will visit all available state space), or by perturbing the system with all possible stresses and calculate the volume of the state space being covered. However, both implementations are not realistically feasible. Therefore, we proposed an alternative way to derive the desirable information as will be discussed in the following sections.

3.3. Analogy of Brownian motion

In 1905, Einstein published several important papers that took physics into a completely new world. In addition to his famous papers on special relativity and photoelectric effect, his paper on Brownian motion also had a great impact. In that paper, he concluded that the same random forces which cause the erratic Brownian motion of a particle suspended in fluid would also cause drag (viscosity) if the particles were pulled through the fluid. In other words, by measuring the spontaneous fluctuation of the particle at rest, one can know how much dissipative frictional force one must do work against, if one tries to perturb the system in a particular direction.

This derivation between spontaneous fluctuations without external perturbation and the system’s response to perturbation is of fundamental importance. It is later generalized as the fluctuation dissipation theorem.¹⁴ It motivated the investigation of fluctuating phenomena in statistical physics of the 20th century.

We hypothesized that the same principle can be applied to the state space representation. If our assumption is true, then we can simply measure the spontaneous fluctuations of a system in the state space when it is under free-running condition, and use that information to predict the ability that a system can adapt when encounters a challenge. Similar to Einstein’s finding for Brownian particle, the greater the spontaneous fluctuation, the easier for it to move (lower viscosity) in that space when external perturbation is applied.

This assumption dramatically simplifies our task of defining a system’s complexity. Next, we will discuss how to construct a surrogate state space when there is only limited information on state variables.

3.4. Surrogate state space

In the past several years, we have successfully developed an innovative algorithm to probe the state space indirectly. The goal was to overcome the barrier that in real-world condition, one can only monitor a very limited set of physiologic signals (as state variables). Effectively, we are observing a low-dimensional projection of a trajectory embedded in the much higher dimension of state space. Therefore, it is critical to extract as much information as possible from any single physiologic variable to gain some insight into the high dimensional state space.

For deterministic dynamical systems, there are rigorous approaches, such as the Poincaré map, to study a high dimensional trajectory in a low dimensional subspace. Similarly, in chaos theory, recurrence plots¹⁵ and phase-space portraits¹⁶ are frequently used techniques for this purpose. However, physiologic systems do not meet the criterion (e.g., deterministic and periodic) for applying these analyses. Off-the-shelf usage of those tools to biological time series may lead to misleading conclusions.

Our approach was to take advantage of the fact that an integrative physiologic system will have complex coupling between different components of the system. In biological systems, these couplings often exhibit different spatial and temporal scales. Therefore, by investigating any given signal at various time scales, we can probe the other dimensions of the abstract state space.

By combining these concepts discussed in this section, we have implemented some useful computational algorithms to quantify features related to complexity of biological systems from fluctuating time series of physiologic variables. Our definition of a system’s complexity also ensures that our index closely reflect the general health status of the system. In the next section, we will briefly discuss the algorithms we have developed.

4. Quantifying a System’s Complexity

For practical purposes, it is useful to quantify the degree of complexity of a biological system by examining its dynamical fluctuations. Such metrics have potentially important applications both with respect to evaluating dynamical models of biological systems and to clinical monitoring. Substantial attention, therefore, has been focused on defining a quantitative measurement of complexity.^{9–13,17–21} However, no consensus has been reached on this issue. We have used an alternative view, as discussed in previous sections, to look at these biological variabilities to derive some useful measurements of how complex a system is.

Over the past several years, our group have developed quantitative algorithms to probe some of the generic features of complex systems and applied these computational tools to the understanding of the underlying system dynamics. For example, we have introduced fractal scaling,^22,23 multiscale entropy (MSE)^24,25 and time irreversibility²⁶ analysis techniques and applied them to the study of the cardiac dynamics of healthy subjects and patients with different types of pathologies. The former technique quantifies the information content of a signal across multiple time scales and the latter quantifies the degree of temporal irreversibility over multiple time scales. Time irreversibility is a property related to the unidirectionality of the energy flow across the boundaries of a living system, which utilizes free energy to evolve to more hierarchically ordered structural configurations and less entropic states in comparison with the surrounding environment.

Based initially on the analysis of the cardiac rhythm^24,25 (under neuroautonomic control) and gait dynamics,²⁷ we have shown that healthy systems, those with the highest capacity to adjust to continuous (and often unpredictable) changes of internal and external variables, generate the most physiologically complex and the most time irreversible signals. We have shown further that both multiscale variability and time irreversibility properties degrade with aging and disease. These results challenge traditional mechanisms of physiologic control based on classical homeostasis (single steady state dynamics) and are of interest from a number of other perspectives, including basic modeling of regulatory systems and practical bedside applications.

5. Technical Challenges and Adaptive Signal Analysis

In this section, we will briefly discuss the importance of applying adaptive signal analysis techniques, in conjunction with the complexity related methods described above, to obtain more accurate quantitative measurements of complex biological systems.

5.1. Problem of nonstationarity

The quantitative tools we have developed, such as the multiscale entropy (MSE) analysis, for the analysis of complex physiologic time series are based on generic concepts that are fundamental to biological systems. As a result, these tools are readily applicable to many different biomedical problems. However, since physiologic time series are typically nonstationary, there are important technical issues that need to be addressed in order to obtain reliable results.

For example, the MSE analysis was derived from stationary processes. In practice, time series need not to be strictly stationary according to the mathematical definition to yield meaningful results. However, nonstationarities appearing on scales larger than those considered for MSE analysis may substantially affect our measurements. Such nonstationarities need to be taken care of prior to performing the MSE analysis. Our study of postural sway time series²⁸ indicates that by properly detrending the time series on scales greater than those being measured by the MSE, the analysis provides robust and consistent results. The empirical mode decomposition (EMD) technique²⁹ is a very adequate candidate for pre-processing the data, since it provides a systematic way to detrend the data without a priori assumptions of what type of trend the data may possess.³⁰

5.2. Nonlinear dynamical coupling among components of system

A fundamental question about complex biological systems is how does the observed complex dynamics, as quantified by our complexity related measurements, emerge from integrated system functions. Understanding possible mechanisms of healthy complexity is important both on the basic scientific level and on the practical level, where clinical interventions can be proposed to maintain or restore this dynamical complexity. By observing the degradation of dynamical complexity in disease and aging, one realizes that life-threatening pathologic conditions are typically accompanied by either complete de-coupling between sub-components of the whole system, or a strong “mode-locking” among them. In contrast, a healthy biological system usually displays intermittent coupling between its sub-systems. Each component of the system may engage and then dis-engage with other components of the system. This type of on-and-off “cross-talk” between different parts of a complex system (reminiscent of how different instruments are integrated together in a symphony orchestra) seems to be a prominent characteristic of healthy biological function. As a result, quantifying the coupling among different sub-system components is critical to our understanding of the complex system as a whole. From a data analysis point of view, one should be able to characterize the coupling between the two components of a system by simultaneously collecting the signals that represent those components. However, technically, quantifying the coupling is not an easy task. The main difficulties are due to the fact that both signals are often nonstationary, and the coupling between them is usually nonlinear and intermittent. To quantify the intermittency, the analysis method has to separate any local variation and collate the different scales of the intermittent processes separately and cleanly in both temporal and scale variables. Here the recently developed Ensemble EMD³¹ has the potential to offer great help.

Therefore, it is essential to apply adaptive data analysis techniques to address the nonlinear and nonstationary challenges as demonstrated by recent works of our group and others.^32–34 For example, we have applied the EMD algorithm to study the role of coupling between blood pressure and cerebral flood flow in cerebral autoregulation. Cerebral autoregulation is a mechanism that involves dilatation and constriction of arterioles to maintain relatively stable cerebral blood flow in response to changes of systemic blood pressure. Traditional assessments of cerebral autoregulation use Fourier-based techniques, such as transfer function analysis, that fail to yield robust and consistent results in typical clinical settings. The EMD method substantially improves our ability to accurately quantify the dynamical interactions between blood pressure and cerebral blood flow.^32–34 Furthermore, since the EMD can provide phase and frequency information on instantaneous basis, analysis of its dynamical feature (i.e., how do these interaction change over time) becomes feasible. Future work along this direction may have clinical importance and also provide mechanistic understanding toward the theory of dynamical complexity we proposed.

6. Discussion

We have developed a generic framework for extracting “hidden information” in time series generated by complex biological systems. Specifically, we discussed the underlying assumptions that make it possible to probe the behavior on the system level via examining the dynamical fluctuations of a single variable. We also proposed meaningful measurements of complexity for biological systems that are based on the framework we developed. We have used those complexity measures to study the outputs of cardiac heartbeat regulatory system,²⁵ gait dynamics,²⁷ and postural control.²⁸ Briefly, we found that, under free-running conditions, the dynamics of healthy systems are the most complex, as measured by the multiscale entropy and time irreversibility methods, and that complexity breaks down with aging and disease. We also studied the effects of a noise-based therapeutic intervention designed to improve postural balance²⁸ on the overall complexity of the postural sway dynamics. We found that there is an increase in multiscale complexity during the application of this intervention. This finding supports the notion of using dynamical biomarkers for assessing noise-based and other types of therapeutic interventions. However, one needs to be aware of potential technical issues when applying these new measures to physiologic time series. In this paper, we discussed how to utilize the EMD technique to overcome the problems when data are not “well-behaved.” Thus the EMD approach constitutes an essential step of complex physiologic signal analysis.