Analysis of coupled model uncertainties in source-to-dose modeling of human exposures to ambient air pollution: A PM_2.5 case study

Abstract

Quantitative assessment of human exposures and health effects due to air pollution involve detailed characterization of impacts of air quality on exposure and dose. A key challenge is to integrate these three components on a consistent spatial and temporal basis taking into account linkages and feedbacks. The current state-of-practice for such assessments is to exercise emission, meteorology, air quality, exposure, and dose models separately, and to link them together by using the output of one model as input to the subsequent downstream model. Quantification of variability and uncertainty has been an important topic in the exposure assessment community for a number of years. Variability refers to differences in the value of a quantity (e.g., exposure) over time, space, or among individuals. Uncertainty refers to lack of knowledge regarding the true value of a quantity. An emerging challenge is how to quantify variability and uncertainty in integrated assessments over the source-to-dose continuum by considering contributions from individual as well as linked components. For a case study of fine particulate matter (PM_2.5) in North Carolina during July 2002, we characterize variability and uncertainty associated with each of the individual concentration, exposure and dose models that are linked, and use a conceptual framework to quantify and evaluate the implications of coupled model uncertainties. We find that the resulting overall uncertainties due to combined effects of both variability and uncertainty are smaller (usually by a factor of 3–4) than the crudely multiplied model-specific overall uncertainty ratios. Future research will need to examine the impact of potential dependencies among the model components by conducting a truly coupled modeling analysis.

1. Introduction

Human exposures to atmospheric pollutants can be quite complex due to the spatial and temporal nature of emissions, meteorology and human activities. Variations in both the ambient pollution concentrations and behavioral factors influence individuals contact with pollutants found indoors and outdoors. Traditionally, different types of models have been used to provide the critical linkages between pollutant emissions from natural and anthropogenic sources, concentrations in various media, human exposures to indoor and outdoor pollutants and the delivered dose to the body resulting from contact with these pollutants. In order to support its actions to protect human health and the environment, the U.S. Environmental Protection Agency (EPA) uses a wide range of models in linking air pollution emissions to ambient concentrations to human exposures and to delivered pollutant dose to human respiratory system. However, each modeling component within the source—concentration—exposure—dose continuum contributes imprecision to predictions depending on the complexity of the underlying environmental, personal exposure or biological condition represented by each model. Uncertainty is also introduced because of processes or information only available at a higher spatial or temporal scale and lack of compatibility of the scales of each model. Probabilistic human exposure models developed by EPA for air pollution, such as the SHEDS-PM, Stochastic Human Exposure and Dose Simulation model for Particulate Matter (PM), incorporate the inherent variability and uncertainty information in the model inputs, parameters and results (Burke et al., 2001). In contrast, air emissions and concentrations models by EPA, such as the Sparse Matrix Operator Kernel Emissions (SMOKE), National Mobile Inventory Model (NMIM), and Community Multiscale Air Quality (CMAQ) (Byun and Schere, 2006) models are mechanistic models that simulate environmental processes in a deterministic fashion. Previous studies as summarized by Hanna et al. (2005) have focused on the uncertainties in concentrations estimated by air quality models. However, these studies do not propagate the uncertainties to exposure and dose models. One of the key challenges in conducting an integrated source-to-dose modeling is the difficulty of quantifying coupled model uncertainties. Here we examine the topic seldom addressed, namely the impact of cascading modeling errors, when outputs from models are used as inputs into other models, in a sequential manner. We make some simplifying assumptions by ignoring small but possible interdependencies or feedbacks between the different models that are being coupled. Since each of the individual models used to predict emissions—concentrations, concentrations—exposures and exposures—dose relationships have unique characteristics, our proposed methodology explicitly characterizes the relative importance of variability vs. uncertainty for each of these models in performing an integrated source—dose modeling analysis. We demonstrate the application of our approach for conducting coupled model uncertainty analysis through a case study on source-to-dose modeling of population exposures to ambient PM_2.5 (Particulate Matter <2.5 microns in aerodynamic diameter) in North Carolina during July 2002.

2. Methodologies for estimating modeling uncertainties

2.1. Sources of variability and uncertainty

Models are hypotheses regarding how a system behaves in response to changes in its inputs. Model development involves choices regarding what to include and at what level of detail. Sources of uncertainty include measurement error, statistical sampling error, non-representativeness of data, and structural uncertainties in scenarios and models. Scenarios are assumptions regarding the factors that define the scope of the assessment, such as the averaging time, geographic and temporal scale, exposed population of interest, and others. If the modeling approach omits any of the elements of the scenario of interest, then the estimates could be biased. Model uncertainty is influenced by the extent of verification and validation, whether the model is extrapolated beyond the range of its evaluation, and whether there are alternative theories upon which alternative modeling approaches could be developed (e.g., Cullen and Frey, 1999).

Variability arises from true heterogeneity across people, places, or time. Variability is an inherent property of the system being modeled. Some types of variability cannot be reduced (e.g., characteristics of individuals vary with respect to age and gender). In these cases, variability can be stratified into more homogeneous subgroups and an analysis can focus on the strata of most interest. In other cases, it may be possible to control or alter the range of variability (e.g., lowering peak values of ambient pollutant concentration by controlling emissions). Some variation arises because of stochastic processes, such as turbulent eddy diffusion. Knowledge of variability is critical to decision making regarding risk management, such as regarding how to reduce variations in exposures or reduce the frequency and magnitude of high exposures.

In some cases, variability and uncertainty might be difficult to separate (e.g., stochastic variability that also leads to lack of knowledge regarding the true average concentration for a short time period at a specific location) or it may not be necessary to separate them (e.g., if one were to estimate exposure for a randomly selected individual). Here, our goal is to explicitly consider factors that lead to spatial and temporal variations in ambient concentration, exposure, and dose as variability, and factors that lead to lack of knowledge regarding the true value of concentration, exposure, and dose at a given time and location as uncertainty.

Uncertainty arises because of lack of knowledge regarding factors affecting exposure or risk. Typically, there is a trade-off between the value of additional information (i.e., in terms of ability to make a decision with less potential for error) versus the potential downside risks of decision making under the current state of knowledge.

2.2. Variability and uncertainty in individual model predictions

In modeling ambient PM_2.5 concentrations, air quality models incorporate emissions and meteorological data in characterizing complex atmospheric physical and chemical processes by mathematical parameterization. Ambient PM_2.5 levels are influenced by direct emissions of particulate matter, as well as, emissions of precursors such as NO_x, VOCs, SO_x, and ammonia. For anthropogenic emission sources, inter-source variability in emissions arises because of differences in design, feedstocks, ambient conditions, and maintenance practices. The uncertainty in an inventory depends on the geographic area, averaging period, time of year, types of emission sources, and other factors (NARSTO, 2005). In addition to emissions, there are also uncertainties in the structure of air quality models, including the formulation of the advection, dispersion, gas-phase chemistry, aerosol thermodynamics, mass-transfer and deposition processes.

Uncertainties in the exposure and dose model predictions, such as those based on the SHEDS-PM model, are also influenced by parameter and structural model uncertainties. Common input or parameter uncertainties with the SHEDS-PM model, include imprecision in: (a) the parameters used to estimate concentrations in the various locations individuals spend time (outdoors, indoors and in vehicles), such as indoor infiltration, deposition, and emission rates for PM and information on the type and use of mechanical ventilation; (b) the mobility and time-activity information for the different population cohorts, and (c) the parameters for estimating pulmonary deposition of size-specific PM by age, gender, activity level and susceptibility status. Even though current probabilistic human exposure or dose models incorporate the important behavioral and physical processes influencing exposures to PM of outdoor origin (Burke et al., 2001; Georgopoulos et al., 2005), due to lack of appropriate data, structural uncertainties with these models have not been adequately evaluated. However, model intercomparisons would be valuable for providing estimates of structural model uncertainties for these types of models (Driver and Zartarian, 2008).

2.3. Estimating coupled model uncertainties

Fig. 1 demonstrates the informational connections between the main components of an integrated source-to-dose assessment. For example, the assessment of emissions needs to be based on influential factors (e.g., human activity) as well as support downstream analysis of air quality impacts. Emissions need to be estimated at spatial and temporal resolutions, and for appropriate speciation of chemicals and agents of health concern, that support downstream analysis of air quality impacts. However, there is also coupling between key inputs to both the emissions and air quality assessment, such as meteorological or climatologic factors that affect both emissions and pollutant transport and transformation (e.g., temperature, humidity, barometric pressure, rain, snow, storms, etc.).

Fig. 1.

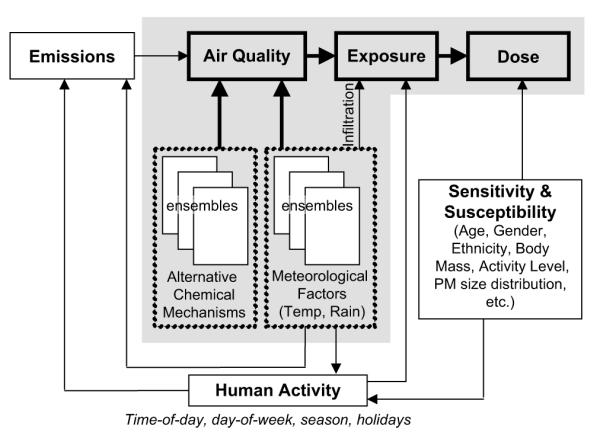
Factors relevant to linking source-to-dose models (shaded area indicates focus of this paper).

Furthermore, air quality can also affect human activity. For example, modification of human behavior in response to air quality advisories would lead to changes in activity, which could affect emissions, air quality, and exposure, and which in turn could affect dose and risk characterization. Likewise, there is a critical need to properly integrate the air quality and exposure components. Human activities, as well as building ventilation practices may change as a function of season, outdoor temperature and meteorology. Although many of these linkages between temperature, meteorology, human activity and exposures may be modest, nevertheless there is some possibility of significant interdependencies among them. However, this issue has not yet been addressed fully. Finally, in terms of producing appropriate modeling results for sub-acute or chronic health effects applications, averaging time(s) other than the 24-h averages considered here may be needed.

Ideally, uncertainties resulting from coupling multiple models should be studied by performing a joint sensitivity and uncertainty analysis of the different models included within the integrated modeling framework. At this time, however, the state-of-the-art models for each of the emissions, air quality, exposure and dose components have not yet been directly coupled, even for providing deterministic point estimates. Therefore, the approach taken here is to assess the typical ranges and distributions of variability and uncertainty for the air quality, exposure, and dose components individually within a linked source-to-dose modeling analysis, over the shaded area shown in Fig. 1. To simplify our analysis, an assumption is made that there are no structural uncertainties in the scenario, and that model uncertainties can be quantified probabilistically in terms of precision and accuracy of the model output.

The air quality model estimates hourly average ambient PM_2.5 concentrations that were aggregated to daily-average values for specific grid cells based on input data for emissions, meteorology, chemistry, and initial and boundary conditions. The air quality model produces an estimate of concentration at a given location and time. The exposure model produces an estimate of inter-individual and intra-individual variability in exposure that is dependent, in part, on ambient concentrations and the averaging time used. The dose model produces an estimate of dose that is dependent on the estimated exposure for each individual. The estimated dose is based on coupling of the air quality (C), exposure (E), and dose (D) models, which is represented conceptually, as:

$$\text{Dose}=\mathrm{C}\left(\frac{\mathrm{E}}{\mathrm{C}}\right)\left(\frac{\mathrm{D}}{\mathrm{E}}\right)$$ (1)

where,

• C = daily-average ambient concentration from the output of an air quality model (μg/m³);

• E/C = the ratio of daily-average exposure to daily-average ambient concentration, based on an exposure model;

• D/E = the ratio of average daily dose to daily-average exposure, based on a dose model.

In the simplified situation in which each of these three models components contributes both variability and uncertainty, the overall variability and uncertainty in dose is a multiplicative combination of the three components (denoted by the Variable X_i in Eqs. (2)-(4) below). For independent X_i, the variance in the dose, Var(Y), can be linearly approximated based on Taylor series expansion, as:

$$\mathrm{Var}\left(Y\right)\approx \sum _{i=1}^n\left\{{\left(\frac{\partial Y}{\partial X_i}\right)}^2\mathrm{Var}\left(X_i\right)\right\}$$ (2)

where,

• Y = Output of coupled model framework (i.e. Dose)

• X_i = Outputs of individual models in a coupled framework (e.g., C, E/C, D/E)

Thus, the basic conceptual framework for estimating the overall variability and uncertainty used in this analysis can be expressed as:

$$\text{Dose}=Y=X_1\times X_2\times X_3,$$ (3)

or

$$Y=(X_1\times {\epsilon }_1)\times (X_2\times {\epsilon }_2)\times (X_3\times {\epsilon }_3)$$ (4)

where, X₁, X₂, X₃ are the normalized variables (i.e., each variable value divided by its arithmetic mean) corresponding to C, E/C and D/E, respectively; and ε₁, ε₂ and ε₃ are the associated prediction error terms.

In Eq. (4) the variances of the X_i terms represent variability and the variances of the ε3_i terms represent uncertainty. Multiplicative errors are assumed since prediction errors are often proportional to the magnitude of the quantity being measured.

Based upon typical ranges of variability and uncertainty associated with each of the three model components, a numerical simulation was conducted in which both variability and uncertainty were quantified for each component and propagated to the output using a two-stage Monte-Carlo methodology. Analytical probability distributions, mainly lognormal or normal distributions are fit to represent the variability or the uncertainty for each of the three coupled modeled variables. The best statistical fits for the variability distributions were found to be lognormal distributions. For uncertainty distributions we assumed multiplicative normal distributions with mean equal to 1, except for cases in which the coefficient of variation (CV) was greater than 0.3, where we chose a lognormal distribution. The CV is equivalent to the standard deviation (σ) divided by the arithmetic mean. To avoid estimating negative values for highly uncertain quantities, lognormal distributions were used in these cases. Since the variables are normalized first, all of the variability distributions have arithmetic means of 1 and are thus represented, as:

$$X_i~\mathrm{Ln}(x_g,{\sigma }_i)\text{or}{X}_i~N(1,{\sigma }_i)\text{and}{\epsilon }_i~N(1,{\sigma }_{{\epsilon }_i})$$ (5)

where,

• x_g denotes the geometric mean

• σ_i or σ_εi denote either the geometric or arithmetic standard deviations of the underlying variability and the uncertainty distributions.

In conducting our coupled uncertainty calculations we used Crystal Ball Version 7.0 software to simulate over 100,000 iterations of variability and uncertainty simulations using the fitted normal or lognormal distributions with arithmetic mean = 1, and the calculated CV (in this case equal to σ since the mean is equal to 1 for the normalized data).

3. Model descriptions and inputs

3.1. Air quality model

The Community Multiscale Air Quality (CMAQ) model was used to simulate the PM_2.5 concentrations using an Eulerian grid structure. The model inputs include chemical emissions and the results from a numerical weather simulation model. CMAQ simulates advection, dispersion, gas-phase chemistry, aerosol thermodynamics and mass-transfer, and deposition. We simulated the time period from June 24, 2002 to July 30, 2002. The first seven days were excluded from the analysis to eliminate sensitivity to initial conditions. The spatial domain included most of the Eastern United States at a 12 km horizontal resolution and 14 vertical layers up to 100 mbar. Meteorological inputs are from the PSU/NCAR mesoscale model, also known as MM5 (Grell et al., 1994). Emissions were generated using the SMOKE emissions processing system (http://www.smoke-model.org/version2.3.2/html/ch02s16.html). Emissions data for motor vehicles are from MOBILE 6 (http://www.epa.gov/otaq/m6.htm); power plant emissions were from Continuous Emission Monitors (http://www.epa.gov/camddataandmaps/). Biogenic volatile organic carbon and NO_x emissions were simulated using BEIS v.3.13 (Schwede et al., 2005) and are derived using the same meteorological fields as the air quality simulations. All other emission sources were from the 2001 National Emission Inventory (http://www.epa.gov/ttn/chief/net/critsummary.html).

A variety of different physical and chemical parameterizations were available for CMAQ and the models used to generate the inputs. An ensemble of these modeling options was used to approximate the uncertainty inherent in the structure of the model. We selected a subset of twelve different model configurations known to have the largest impact on air quality simulation (Hogrefe et al., 2001; Gilliam et al., 2006), including three configurations of the planetary boundary layer/land surface model, two convective mixing schemes, and two chemical mechanisms. The combinations of planetary boundary layer model (PBL) and land surface model (LSM) are the Asymmetric Convective Model (PBL) (Pleim and Chang, 1992) and Pleim—Xiu LSM (Xiu and Pleim, 2001), the Medium Range Forecast PBL (Hong and Pan, 1996) and Noah LSM (Ek et al., 2003), and the Mellor—Yamada—Janjic PBL (Janjic, 1994) and Noah LSM (Ek et al., 2003). The two convective mixing schemes are Kain—Fritsch (Kain, 2004) and the Grell Cumulus Convective Scheme (Grell, 1993). We selected the Carbon Bond IV (Gery et al., 1989) and Carbon Bond 2005 (Sarwar et al., 2008) chemical mechanisms.

3.2. Exposure and dose model

The Stochastic Human Exposure and Dose Simulation Model for Particulate Matter (SHEDS-PM) uses a probabilistic approach to simulate the time-series of inhalation exposure and dose for individuals that demographically represent a population of interest based on PM concentrations supplied as input to the model. The generation of the time-series involves stochastic processes utilizing numerical Monte-Carlo sampling techniques to characterize the variability within an individual over time and between individuals across a population. Uncertainty in the model output is estimated by incorporating the knowledge- or measurement-based uncertainty associated with the inputs through multiple iterations of the model. The overall structure of the SHEDS-PM model has been described in detail elsewhere (Burke et al., 2001; Georgopoulos et al., 2005). The SHEDS-PM model estimates the contribution of PM from ambient or outdoor air separately from the contribution of PM from other sources (e.g., smoking). This separation is maintained throughout the exposure and dose calculations, producing results for the daily-averaged exposure and total daily dose due to PM from outdoor sources (ambient PM exposure and dose) versus that due to indoor PM sources (non-ambient PM exposure and dose) for each simulated individual.

The daily-average PM_2.5 concentrations in North Carolina from CMAQ for a one month time period (July 1–30, 2002) described above were used as the input PM_2.5 concentration data for SHEDS-PM (version 3.5). The 12 × 12 km² gridded data from CMAQ was interpolated to the census tract centroids of all 1563 census tracts within North Carolina. A representative population for the simulation was generated using demographic proportions for each census tract from US Census 2000 data (gender, age, employment status, and worker commuting census tract). One percent of the total population of North Carolina (all gender—age combinations) was simulated for a total of 81,266 individuals across all of the census tracts in North Carolina. This translated to a total of 2,437,980 person-days over the 30-day simulation period, which was determined to be a large enough sample size to produce numerically stable results for variability.

Each simulated individual was randomly assigned a longitudinal time-series of location and activity information for the 30-day simulation using human activity diaries from EPA’s Consolidated Human Activity Database (CHAD) (http://www.epa.gov/chadnet1/). Diaries were randomly assigned to each simulated individual from those matching gender, age, and employment status from available CHAD diaries collected during the summer season (defined as June, July and August). A different CHAD diary was assigned for each individual for weekdays, Saturdays, and Sundays. The PM_2.5 concentration for each individual’s CHAD diary locations was calculated using the interpolated CMAQ concentration for their home census tract, and distributions of indoor/outdoor PM_2.5 concentration relationships for different diary locations (home, office, school, store, restaurant/bar, other indoor, and in vehicles). A mass balance equation was used to calculate indoor PM concentrations for the home location that included parameters for air exchange, penetration, and deposition, as well as emission strengths for indoor PM sources (e.g., cooking). PM concentrations for the other indoor locations were calculated using equations developed from regression analysis of available indoor and outdoor measurement data for offices, schools, stores, and restaurants/bars as described in Burke et al. (2001) that accounted for both the ambient and non-ambient contributions to PM levels in these indoor locations. For vehicles, both the elevated roadway concentrations and removal efficiency for PM were accounted for in the regressions. The impact of commuting was included for employed individuals, using a database of home-work census tract commuting proportions from the US Census 2000 to randomly assign the individual to a different census tract during diary activities corresponding to “work”. The PM concentration for the work census tract was used to calculate the location concentration during work activities only.

Daily-average PM_2.5 exposure for each individual was estimated using the calculated PM_2.5 concentration and time spent in different locations from the assigned CHAD diary locations. Total daily PM_2.5 deposited dose was also estimated for each simulated individual using the PM_2.5 exposure, activity level-specific inhalation rates based on the activities in the assigned diaries (McCurdy, 2000), and cumulative deposition to various regions of the respiratory tract based on empirical equations from the ICRP model (ICRP, 1994). A bimodal particle size distribution was simulated for PM_2.5 based on data for the eastern US (US EPA, 2004). A density of 1 g/cm³ was used to convert particle counts by size to mass.

4. Results

4.1. Variability and uncertainty in the concentration predictions

CMAQ PM_2.5 model results for July 2002 were examined in multiple ways. We calculated both spatial and temporal CDFs (cumulative distribution functions) and CVs (Coefficient of Variation or standard deviation divided by the arithmetic means) based on the baseline ensemble member or mean of the 12 ensembles across the nearly 1000 model grid cells in North Carolina. We did not observe any significant variation in the temporal CVs in NC. We also assessed whether spatial variability differs from one day to another (or by day of the week). In order to match the specifications of the SHEDS model these values were also interpolated at 1563 census tract centroids in North Carolina. The overall (i.e., across all 30 days and 1563 census tracts) normalized concentration values were fit well by a lognormal distribution with a CV of 0.52. A similar fit of 30-day averages of model results by each of the 100 counties resulted in a lower variability CV of 0.18.

For quantifying the CMAQ model uncertainties we performed inter-ensemble comparisons, as well as, comparing the model results with the 32 daily-average PM_2.5 concentrations observed at Air Quality System (AQS) monitoring stations (http://www.epa.gov/air/data/aqsdb.html) in North Carolina. We compared model CDFs to corresponding measurement data from the 32 monitoring stations operating in North Carolina during the study period. A typical comparison for Raleigh area is shown in Fig. 2. Approximately 10 days of daily-average PM_2.5 data were available from each station. We estimated the distribution of the percentage difference in modeled versus measured values. Based on the inter-ensemble analysis we found the CMAQ model uncertainties to be about CV = 0.15. However, as shown in Fig. 2, the observed value does not always fall within the ensemble range; there are sources of uncertainty beyond the differences in model representation. This ensemble does not comprise a probability sample, and thus may not represent the entire range of possible outcomes. To generate a more comprehensive estimate of uncertainty, we calculated the model error when compared to the observed values (Hanna and Davis, 2002). The CV of the model error is 0.30 and is calculated as:

$$\mathrm{CV}=\frac{{\sigma }_{\text{model}-\text{observations}}}{{\mu }_{\text{observations}}}$$ (6)

where, σ is the standard deviation of the model error and μ is the arithmetic mean of the observations.

Fig. 2.

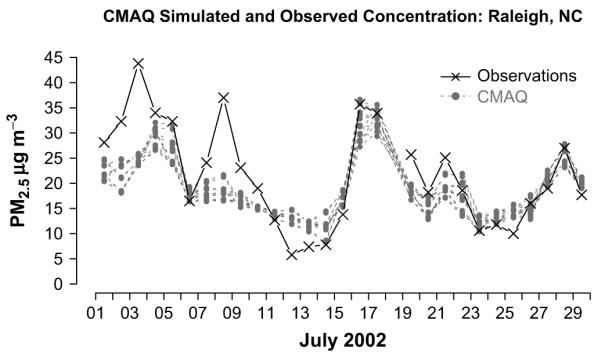
Ensemble CMAQ simulated and observed concentrations near Raleigh, NC. Large deviations on July 3–9 are due to wildfire events that are not captured by the emission inventory.

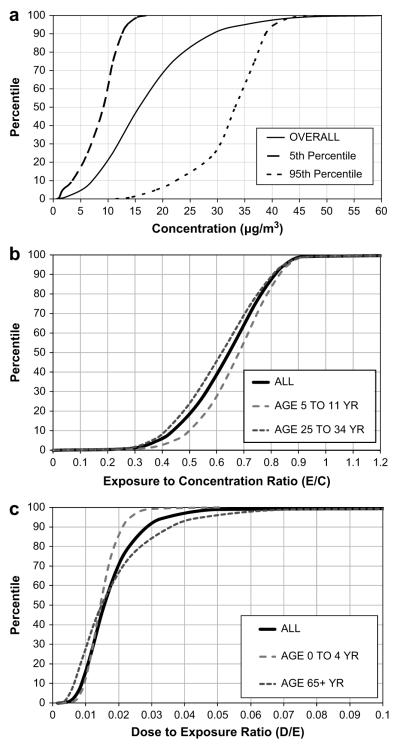
The resulting variability and uncertainty CVs were used as the base case during coupled model runs (Table 1). Since the model prediction uncertainties varied somewhat by time period or geographic location, we also chose a range of low, mixed and high uncertainty values shown in Table 1. Fig. 3a shows the overall variability in the predicted CMAQ PM_2.5 concentrations. The variability in PM_2.5 concentrations between dates is also shown in this figure. For example, the 95th percentile for PM_2.5 concentrations across North Carolina on each of the 30 days in July 2002 ranged from 11 to 48 μg/m³. As part of ongoing work, the use of data fusion and Bayesian model averaging techniques are being used to make combined inferences from both model predictions and monitored data.

Table 1.

Coefficients of variation for variability and uncertainty for alternative input assumptions used in coupled model uncertainty analysis.

Description	Case	C	E/C	D/E
Variability (Base)	Base (overall)	0.52	0.23	0.53
	Alternative-1 (county average)	0.18	0.01	0.03
	Alternative-2 (individual average)	0.17 (census tract)	0.12 (individual)	0.46 (individual)
Uncertainty	Base	0.3	0.3	0.4
	Low	0.25	0.2	0.3
	High	0.45	0.4	0.5
	Mixed-1	0.25	0.3	0.5
	Mixed-2	0.3	0.3	0.3

Numbers shown in bold are treated as lognormal distributions others are fit to normal distributions.

Fig. 3.

Variability in the modeled daily-average: concentrations (a), exposure/concentration ratios (b), and dose/exposure ratios (c).

4.2. Variability and uncertainty in the exposure and dose predictions

SHEDS-PM produced distributions of personal exposures to PM_2.5 as well as PM_2.5 dose for North Carolina during July 2002. Summary statistics for the daily PM_2.5 concentration, exposure, and dose across all simulated individuals over the 30-day simulation are shown in Table 2. The SHEDS-PM model results for ambient PM_2.5 exposure and dose were used to provide the exposure to concentration (E/C) and dose to exposure (D/E) ratios needed for the coupled model uncertainty analysis described above. These ratios were analyzed in a number of different ways to understand the variability in the results. Fig. 3b and c show variability distributions for the SHEDS-PM_2.5 E/C and D/E ratios, respectively, for all individuals combined as well as for selected age groups that illustrate the variability within and between age groups. Differences between age groups were greater for the D/E ratios than for the E/C ratios, indicating that physiological differences across ages impacts the variability in PM_2.5 dose. Statistical frequency distributions were then fit to the normalized E/C and D/E values by each of the three metrics of interest (i.e., overall, county and individual) as shown in Table 1. The base case overall variability distribution for E/C was best fit by a normal distribution with a CV of 0.23. The base case overall D/E variability distribution was best fit by a lognormal distribution with a CV of 0.53. When the SHEDS-PM results were averaged by county the variability in both the E/C and D/E ratios was quite low (CV of 0.01 and 0.03 respectively). When averaged by individual over 30 days, the variability in the E/C and D/E ratios was similar to that overall (CV of 0.12 and 0.46 respectively), indicating that inter-individual differences were a major contributor to the overall variability.

Table 2.

Summary statistics for daily PM_2.5 concentration, exposure and dose for North Carolina during July 1–30, 2002.

PM2.5 Variable	Mean	Std. dev.
Ambient concentration (μg/m3)	17.22	9.05
Exposure (μg/m3)
Total	14.40	8.21
Ambient	10.96	6.34
Dose (mg)
Total	0.286	0.257
Ambient	0.196	0.169

The uncertainty distributions were derived from both the results from the 2-D Monte-Carlo parameter uncertainty analysis runs and from the comparison of predicted SHEDS results with measured total personal PM exposures for a PM panel study conducted in Raleigh, NC (Burke et al., 2002). The parameter uncertainty values were found to be fairly small, around CV = 0.15 (Fig. 4). Furthermore, the measured vs. predicted for total PM_2.5 exposures were also small for the Raleigh PM panel data (around CV = 0.15). However, since we needed the uncertainty for the E/C ratios in this analysis we calculated the sum of the two variances for E and C in estimating a CV of 0.30 for E/C as a base case. We were not able to perform a parameter uncertainty analysis for the dose module of the SHEDS model at this time. We assumed for the base case overall uncertainty simulations can be represented by a normal distribution with a CV of 0.40. In order to examine the impact of likely ranges in our base case assumptions, we also added four more uncertainty specifications to address the likely ranges in the uncertainty specifications (i.e., low, two mixed and a high case) as shown in Table 1.

Fig. 4.

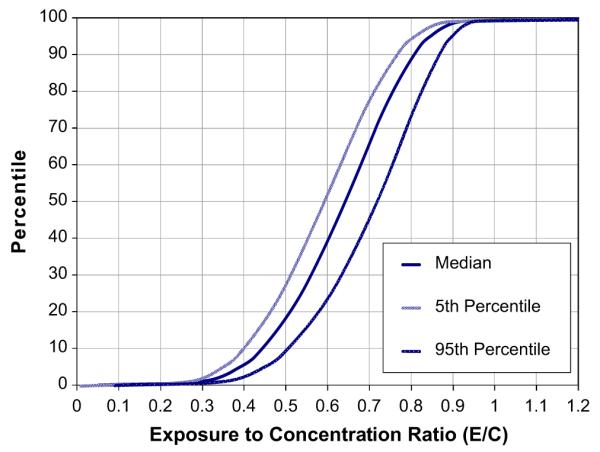
Distribution for parameter uncertainty in the SHEDS-PM daily-average exposure/concentration ratios.

4.3. Variability and uncertainty in coupled model predictions

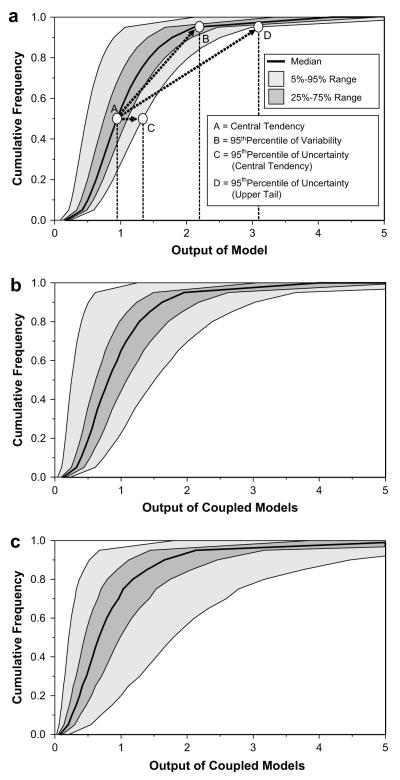
Table 3 provides the results from the coupled model uncertainty analysis for each of the base and alternative simulation cases described above. These case studies assume that either there is no bias (systematic error) or that such biases have been corrected in a prior step. For each analysis we provide three different measures of either variability or uncertainty combined. Specifically, three ratios are calculated using the various points (A, B, C, D) selected from the 50th or 95th percentiles of the simulated variability or uncertainty distributions shown in Fig. 5a, as follows:

$$\text{Variability Ratio}=\frac{\mathrm{B}}{\mathrm{A}}$$

$$\text{Uncertainty Ratio}=\frac{\mathrm{C}}{\mathrm{A}}$$

$$\text{Overall Uncertainty Ratio}=\frac{\mathrm{D}}{\mathrm{A}}$$

Table 3.

Predicted variability and uncertainty for coupled models under alternative input assumptions.

Variability	Uncertainty	No. of coupled models	Variability ratioa	Uncertainty ratiob	Overall uncertainty ratioc	“Crude” uncertainty ratiod
Base	Base	1	2.2	1.4	3.2
		2	2.4	1.9	4.5	6.8
		3	3.2	2.7	8.7	29.3
	Low	1	2.2	1.5	3.4
		2	2.4	1.6	3.8	6.7
		3	3.2	2.0	6.6	22.7
	High	1	2.2	2.3	5.2
		2	2.4	2.6	6.2	14.5
		3	3.2	5.7	18.4	80.7
	Mixed-1	1	2.2	1.4	3.2
		2	2.4	1.7	4.2	7.4
		3	3.2	2.8	9.1	36.5
	Mixed-2	1	2.2	1.5	3.3
		2	2.4	1.9	4.7	7.1
		3	3.2	2.5	8.2	24.7
Alternative-1	Base	1	1.4	1.4	1.9
		2	1.4	1.7	2.4	2.8
		3	1.4	3.1	4.2	5.9
Alternative-2	Base	1	1.3	1.4	1.8
		2	1.4	1.7	2.4	3.3
		3	2.2	2.1	4.8	12.5

^aRatio of 95th percentile of variability to central tendency (i.e., 50th percentile of uncertainty for the 50th percentile of variability) (see Fig. 5a).

^bRatio of 95th percentile of uncertainty for the central tendency to central tendency (see Fig. 5a).

^cRatio of 95th percentile of uncertainty for the 95th percentile of variability to central tendency (see Fig. 5a).

^dCrude ratio is based on the product of the “overall ratio” for each of the models included in the coupled model analysis.

Fig. 5.

Two-dimensional probabilistic representation of variability and uncertainty in outputs of: air quality concentration model (a), coupled concentration and exposure models (b) and coupled concentration, exposure and dose models (c) for base case variability and base case uncertainty assumptions.

The variability ratio represents the ratio of 95th percentile of variability to central tendency (i.e., 50th percentile of uncertainty for the 50th percentile of variability). The uncertainty ratio represents the ratio of 95th percentile of uncertainty for the central tendency to central tendency. The overall uncertainty ratio is a measure of the combined effect of both variability and uncertainty, and represents the ratio of 95th percentile of uncertainty for the 95th percentile of variability to central tendency. Table 3 provides for each of the case studies evaluated how this and other variability or uncertainty ratios change as models are sequentially combined. Note that these results are expressed in a nondimensional form relative to a mean value for each selected output. Namely, C alone (only one individual model), then C and E/C coupled (two models coupled) and then C and E/C and D/E combined (three models coupled). Fig. 5a—c shows how the base case variability and uncertainty distributions expand as three models are sequentially coupled together. For the base case simulations the overall uncertainty ratio increases from 3.2 to 4.5 and then to 8.7 when all three models are coupled. The latter value is still about 3 fold less than the “crude uncertainty ratio” of 29.3, if one were to crudely estimate this overall ratio simply by multiplying each model’s overall ratios together. Table 3 also shows that coupled model uncertainties can be greater than the base case if the assumed uncertainties in each of the models are higher than the base case simulations. The high uncertainty case study yields an overall uncertainty ratio of 18.4 compared to a corresponding “crude uncertainty ratio” of 80.7. In general, however, the coupled model uncertainties, across all simulation case studies, are usually about 3–4 times less than the corresponding crude ratios. For the three models combined, we found a nearly perfect linear fit (R² = 0.98) to these data, represented by the regression model:

$$\begin{array}{cc}\hfill \text{Overall Uncertainty Ratio}=& 2.7+\left(0.19\right)\hfill \\ \hfill & \times \left(\text{Crude Uncertainty Ratio}\right)+\epsilon \hfill \end{array}$$ (7)

5. Summary and conclusions

Understanding the influence of variability and uncertainty in model inputs and structure is important for characterization of the accuracy and precision of model results. Most of the environmental, exposure and dose models used in the analysis of source-to-dose relationships for environmental pollutants are quite complex. These models rely upon many types of physical, chemical, behavioral or biological information with varying degrees of inherent variability or uncertainty. In addition to understanding the nature and impact of these various sources of variability or error within each model, it is also essential to understand how these errors propagate, as multiple models are linked together in an integrative assessment. We studied this problem by focusing on human exposures to ambient PM, which is relevant not only to the investigations of health effects of PM but to many other chemical-specific exposure or risk assessments. Our case study of PM in North Carolina combined three distinct types of models: concentration, exposure and dose models. We used a 2-Dimensional Monte-Carlo simulation methodology to numerically calculate the propagation of errors, when one, two or three models are combined. We found that as more models are coupled together both the variability and uncertainty in the resulting model predictions increases. However, for the models that we selected, the increase in either the variability or in the uncertainty ratios separately, were found to be small (factor of 2 or less). On the other hand, the increase in the joint variability and uncertainty or the overall uncertainty ratio was somewhat higher (about factor of 2–3). In comparison, crude uncertainty ratios, where individual overall model uncertainties are directly multiplied, were much greater (about a factor of 3–4) than our predicted overall uncertainty ratios. These findings are generally consistent with statistical expectations when either basic normal or lognormal distributions are linearly multiplied or added.

These results have important implications for integrative assessments that need to estimate the overall accuracy and precision in the predictions when multiple models are combined. We recommend that a special effort be made to estimate the variability, uncertainty and overall uncertainty ratios for each of the models used in the chain of calculations. In particular, the overall ratio is a good measure of a conservative range of errors associated with each of the models. Short of repeating the simulations performed here, we suggest using an estimate based on Eq. (6) or an approximate factor of 2–3 (as opposed to the crude uncertainty ratio of about a factor of 5) to estimate the likely range of overall coupled model uncertainties, when three models are linked together.

We recognize also some of the limitations of our analysis. In particular, potential relationships or feedbacks between the various models or model elements may result in collinearities among the different variables. However, the numerical simulation approach adopted here can be used to explore the impact of such correlations by using correlated draws. A more complicated future analysis may attempt to differentiate the sources of uncertainties in modeled ambient concentrations, such as due to emissions, meteorology, transport, transformation and deposition. In this paper we studied modeling uncertainties dealing with exposures to ambient PM only. The study of exposures to both indoor and outdoor PM would pose similar additional complexities due to the fact that the total exposures/ambient concentration variable will be correlated with ambient concentrations. The simulations for exposures to total PM would necessarily have to incorporate such dependencies or correlations explicitly. In general, chemicals with indoor or multiple sources will require a more complex analysis of factors influencing the underlying variability and uncertainty distributions and the resulting modeling errors. However, most of these are tractable problems which can be addressed with currently available numerical analysis tools. Finally, we recommend performing a set of truly coupled modeling analyses, in order to evaluate our results by jointly characterizing the variability and uncertainties in the overall model predictions.

6. Disclaimer

The United States Environmental Protection Agency through its Office of Research and Development funded and managed the research described here under an Interagency Personnel Agreement with Dr. Chris Frey at North Carolina State University. This manuscript has been subjected to Agency review and approved for publication.