Abstract
Missing genotype data can increase false-positive evidence for linkage when either parametric or nonparametric analysis is carried out ignoring intermarker linkage disequilibrium (LD). Previously it was demonstrated by Huang et al. [1] that no bias occurs in this situation for affected sib-pairs with unrelated parents when either both parents are genotyped or genotype data is available for two additional unaffected siblings when parental genotypes are missing. However, this is not the case for autosomal recessive consanguineous pedigrees, where missing genotype data for any pedigree member within a consanguinity loop can increase false-positive evidence of linkage. False-positive evidence for linkage is further increased when cryptic consanguinity is present. The amount of false-positive evidence for linkage, and which family members aid in its reduction, is highly dependent on which family members are genotyped. When parental genotype data is available, the false-positive evidence for linkage is usually not as strong as when parental genotype data is unavailable. For a pedigree with an affected proband whose first-cousin parents have been genotyped, further reduction in the false-positive evidence of linkage can be obtained by including genotype data from additional affected siblings of the proband or genotype data from the proband's sibling-grandparents. For the situation, when parental genotypes are unavailable, false-positive evidence for linkage can be reduced by including genotype data from either unaffected siblings of the proband or the proband's married-in-grandparents in the analysis.
Key Words: Consanguinity, False positives, Linkage analysis, Linkage disequilibrium (LD)
Introduction
Until the 21st century, genome scans for pedigree data relied on the use of microsatellite markers to localize disease/trait susceptibility genes [2]. Currently, for linkage studies, single nucleotide polymorphisms (SNPs) are rapidly replacing microsatellite markers for whole genome scans and fine mapping due to the development of automated large-scale genotyping technologies which facilitate inexpensive and rapid genotyping of SNP marker loci. Additional advantages of SNP marker loci are their low mutation rates and high density across the genome. However, since SNPs are diallelic, their informativeness is usually lower than that of microsatellite markers, with the highest heterozygosity (H) = 0.5 and Polymorphism Information Content (PIC) = 0.375. Due to the lower heterozygosity, denser maps of SNP loci are necessary for genome scans. At present two commercially produced panels of SNP markers are commonly used for linkage genome scans: the Illumina panel with 6,056 SNP marker loci [3] and the Affymetrix panel with 10,204 SNP marker loci [4]. The information content of both of these panels surpasses the information content of the commonly used panel of 400 microsatellite markers spaced approximately every 10 cM [5]. Owing to the decreasing cost of SNP genotyping, a new trend is to genotype panels developed for whole-genome scan association studies for linkage studies; these panels can contain >500,000 SNP marker loci. Due to the density of the SNP markers used for genome scans, there can be considerable linkage disequilibrium (LD) between neighboring marker loci. In contrast, the amount of intermarker LD is negligible for genome scan microsatellite panels. Due to their low heterozygosity, for the analysis of SNP marker loci, multipoint analysis is almost always carried out in order to increase informativeness of the marker loci and thereby enhance the power of a given data set.
When carrying out linkage analysis there is no one program which can overcome all the obstacles of analyzing numerous marker loci with intermaker LD in medium to large pedigree structures. Almost all currently available linkage analysis programs assume linkage equilibrium between marker loci with the exception of LINKAGE/FASTLINK [6] and MERLIN [7, 8]. However, these two linkage programs do have their drawbacks. LINKAGE/FASTLINK can only perform parametric linkage analysis on a very limited number of marker loci. MERLIN is limited in the size of the pedigree structure that can be analyzed; there can be no recombination between marker loci that are in LD, and analyses allowing for LD can be time consuming. For both programs, estimates of the haplotype frequencies can be inaccurate if the analyzed pedigrees only have a limited number of founders or if accurate population specific haplotype frequencies are not available from other sources such as the HapMap project [9]. Due to these limitations, linkage analysis is often carried out using programs such as ALLEGRO [10, 11] and SIMWALK2 [12, 13], which do not incorporate intermarker LD in the analysis.
It has been well documented that misspecification of single maker allele frequency can lead to false-positive evidence of linkage [14, 15] when pedigree genotype data is missing. Analogously, the unrealistic assumption of linkage equilibrium can lead to erroneous haplotype inference and increased type I error [1,16,17,18]. Huang et al. [1] demonstrated that for nuclear pedigrees with unrelated parents, when parental genotype data is missing, ignoring intermarker LD (D′ > 0.4) introduces false-positive evidence of linkage for both parametric and nonparametric linkage analysis. The bias is eliminated when genotype data is available from either both parents or two additional unaffected siblings [1].
The effect of missing genotype data for consanguineous pedigrees has not been previously evaluated. Although consanguineous pedigrees can be used to study both complex and Mendelian traits, they are most commonly used for the study of autosomal recessive Mendelian traits due to the additional linkage information provided by these pedigrees compared to kindreds with unrelated parents. Consanguineous pedigrees have been highly beneficial in mapping genes for autosomal recessive diseases, in particular for traits with locus heterogeneity. For example, over 70 autosomal recessive nonsydromic hearing impairment genes have been localized [19] using consanguineous pedigrees. In this article it is demonstrated that, in contrast to pedigrees where the parents are unrelated, for consanguineous pedigrees segregating an autosomal recessive trait false-positive evidence of linkage is increased even when genotype data is available for both parents or the affected proband's two unaffected siblings. The problem persists if parental genotypes are missing, even when all founders are genotyped within the pedigree. For a first-cousin mating, only when great-grand parents, grand-parents and parents are genotyped is the problem of false-positive evidence for linkage completely eradicated. It is unusual to be able to obtain DNA from all family members in gene mapping studies using consanguineous pedigrees, since members in the upper generations are usually deceased. Although false-positive linkages are not totally eliminated, their occurrence is greatly reduced by the availability of both parental and two affected siblings’ genotype data or grand-parental genotype data. An additional factor that can increase the false-positive evidence for linkage in consanguineous pedigrees is cryptic consanguinity. For pedigrees ascertained from communities where consanguineous marriages have occurred for generations, true familial relations of all pedigree members are rarely known. Missing relationship data can further increase false-positive evidence for linkage when intermarker LD is not incorporated in the analysis.
Methods
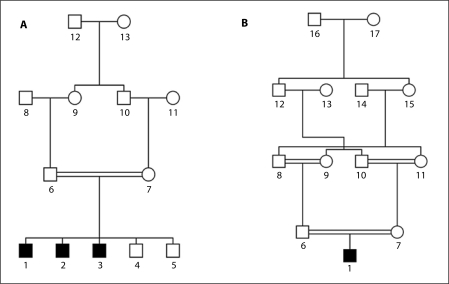
In order to investigate the effect of missing genotype data, haplotype data was generated using the SimPed program [20] for a variety of pedigree structures. Haplotype data was generated for first-cousin consanguineous pedigrees with affection status consistent with an autosomal recessive mode of inheritance; the phenotype status for all family members within the consanguinity loops is unaffected, and offspring of the consanguineous first-cousin mating is comprised of an affected proband with two affected and two unaffected siblings (Pedigree A, fig. 1). In order to evaluate whether there is an increase in the false-positive evidence for linkage for consanguineous pedigrees segregating traits with an autosomal dominant or X-linked recessive mode of inheritance, the affection status of family members in pedigree A (fig. 1) was modified. For the autosomal dominant inheritance model the affection status of the father (individual 6), paternal grandmother (individual 9) and great grandfather (individual 12) were all made affected and for the X-linked recessive inheritance model the great-grandfather (individual 12) phenotype status was modified to be affected.
Fig. 1.
Pedigree A and B were used for the simulation studies. Pedigree A displays the structure of the first-cousin consanguineous mating and pedigree B contains multiple consanguinity loops. Males and females are represented as squares and circles, respectively. The filled symbols represent affected individuals while unaffected individuals are represented by clear symbols. The affected proband is individual 1 in both pedigree drawings and has an inbreeding coefficient of 0.0625 in pedigree A and 0.15625 in pedigree B.
To evaluate the effect of missing genotype data when consanguineous mating occurs between more distantly related individuals, haplotype data was also generated for a pedigree structure with a second-cousin consanguineous mating with an affected proband and two affected and two unaffected siblings. For the second-cousin consanguineous mating all pedigree members within the consanguinity loop phenotype were made unaffected.
To examine the effects of cryptic inbreeding, haplotype data was generated for a pedigree with an affected proband whose maternal grandparents are both full siblings of the paternal grandparents and also a first-cousin of the paternal grandparent for whom they are not a sibling (Pedigree B, fig. 1).
Haplotype data for two marker loci with equal [Marker 1 and 2 both with minor allele frequency (MAF) = 0.5 (model 1) or MAF = 0.2 (model 2)] and unequal allele frequencies [Marker 1 MAF = 0.5 and Marker 2 MAF = 0.3 (model 3)] were generated for all family members under the null hypothesis of no linkage between the disease and the marker data. For models 1 and 2, D′ and r2 between the two completely linked marker loci were varied between 0 and 1. For model 3 the allele frequencies at the two marker loci are not equal, when D′ = 1, r2 = 0.43. Unless otherwise stated, the results reported within the text are for model 1 for D′ = r2 = 1.
For the analysis of families with a single affected proband, all additional siblings were removed. Likewise, to study the effect of available genotype data for additional affected or unaffected siblings, irrelevant siblings were removed from the pedigree. To examine the effect of cryptic consanguinity, for pedigree B all family members with the exception of the affected proband (individual 1), his parents (individual 6 and 7), grandparents (individuals 8, 9, 10 and 11) and grandmother's parents (individuals 12 and 13) were removed so that pedigree B resembled pedigree A (fig. 1). The proband in pedigree A has an inbreeding coefficient of 0.0625 while the inbreeding coefficient for the proband in pedigree B is 0.15625. To evaluate the effect of missing genotype data for parents, grandparents and great-grandparents, genotype data was stripped from selected family members.
For each of the pedigree structures, haplotype data was generated for 500 pedigrees. For those pedigrees where the affection status was consistent with autosomal recessive inheritance, parametric multipoint analysis was carried out under a fully penetrant autosomal recessive model. For the first-cousin consanguineous pedigrees with affection statuses consistent with an autosomal dominant mode of inheritance, parametric multipoint analysis under a fully penetrant autosomal dominant model was utilized. For the first-cousin consanguineous pedigrees with affection statuses consistent with an X-linked autosomal recessive mode of inheritance, haplotype data were generated following inheritance patterns for the X chromosome [20] and parametric multipoint analysis was carried out utilizing a fully penetrant X-linked recessive model. Unless otherwise stated, the results given are for parametric multipoint analysis under an autosomal recessive mode of inheritance. The disease allele frequency was set equal to 0.001 for all analyses, and the marker data was analyzed under linkage equilibrium using the generating allele frequencies. Multipoint parametric analysis allowing for linkage admixture [21] was carried out using the ALLEGRO program. For each D′/r2 value evaluated a total of 200 replicates were generated and analyzed. The average was taken for the maximum heterogeneity LOD (HLOD) and α, the proportion of linked families with the disease locus completely linked to the map of marker loci. The HLOD was evaluated at seven levels of D′/r2 for each of the three allele frequency models; the generating haplotype frequencies for model 1 and 2 can be viewed in table 2 of Huang et al. [1]. To evaluate whether false-positive evidence of linkage was removed when intermarker LD was incorporated in the analysis, MERLIN was used to estimate haplotype frequencies and reanalyze the generated pedigree data.
Results
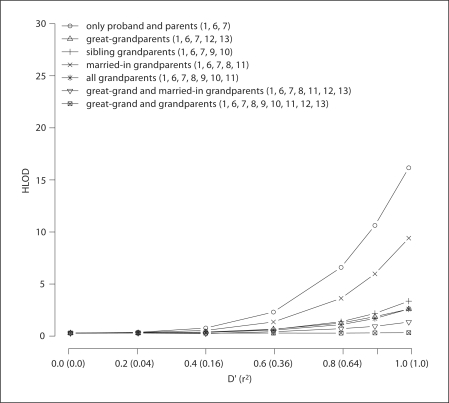
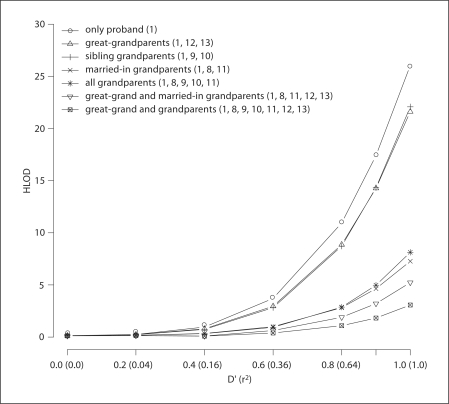
Figures 2 and 3 display the resulting HLODs for analysis carried out under an autosomal recessive mode of inheritance for a first-cousin consanguineous mating with a single affected offspring. For the pedigree structure A (fig. 1), haplotype data was generated for two markers with equal allele frequency (Model 1). For figure 2 the first-cousin parental genotype data is available and HLOD and α were evaluated for various configurations of available genotype data, while figure 3 displays the results when parental genotype data is missing. Table 1 displays HLOD and α when parental genotype data is either available or missing for Model 1 when D′ = r2 = 1. The false-positive evidence for linkage is high when only genotype data is available for the parents and the proband (HLOD = 16.22) and increases when genotype data is only available for the proband (HLOD = 26.05). Genotyping grandparents and great-grand parents is beneficial in reducing false-positive evidence for linkage: however, the false-positive evidence for linkage only disappears when the parents, grandparents and great-grandparents are all genotyped (HLOD = 0.17) (fig. 2). In the case where parental genotype data is missing, even if the grandparents and great-grandparents are genotyped, the false-positive evidence for linkage remains (fig. 3 and table 1). Although it is unusual to have genotype data available for great-grandparents, grandparents can often be ascertained. This additional genotype data greatly aids in the reduction of false-positive evidence for linkage in some situations: if the parental genotypes are not available, then genotyping the married-in-grandparents (individuals 8 and 11) is most effective (HLOD = 7.27; α = 0.20) in reducing the false-positive evidence for linkage compared to genotyping the sibling-grandparents (individuals 9 and 10) (HLOD = 20.08). However, when all grandparents are genotyped the HLOD is slightly higher than when only married-in-grandparents’ genotype data is available, and the proportion of linked families is reduced (HLOD = 8.13; α = 0.15). When parental genotypes are available, genotyping both sets of grandparents (HLOD = 2.47) only offers a slight improvement in reducing the false-positive evidence of linkage compared to only genotyping the sibling grandparents (HLOD = 3.24), while only genotyping the married-in grandparents is not as effective in reducing the false-positive evidence of linkage (HLOD = 9.37).
Fig. 2.
Displays on the Y axis the average maximum HLOD scores for 500 firstcousin consanguineous pedigrees analyzed under an autosomal recessive mode of inheritance when parental genotype data is available. Two markers with equal allele frequencies were simulated unconditional on the disease phenotype. The strength of intermarker LD is displayed on X axis, denoted by D′ values followed by r2 in parentheses. Each plotted line is the HLOD versus D′ (r2) for different available pedigree genotype data, with the number(s) in parentheses indicating for whom within Pedigree A (fig. 1) is genotype data available.
Fig. 3.
Displays on the Y axis the average maximum HLOD scores for 500 firstcousin consanguineous pedigrees analyzed under an autosomal recessive mode of inheritance when parental genotype data is missing. Two markers with equal allele frequencies were simulated unconditional on the disease phenotype. The strength of intermarker LD is displayed on X axis, denoted by D′ followed by r2 values in parentheses. Each plotted line is the HLOD versus D′ (r2) for different available pedigree genotype data, with the number(s) in parentheses indicating for whom within Pedigree A (fig. 1) is genotype data available.
Table 1.
The average maximum HLOD and α values for model 1 where both marker loci have equal allele frequencies and D′ = r2 = 1.0 when various family members are genotyped in pedigrees with a first-cousin consanguineous mating segregating an autosomal recessive trait
| Member genotyped | ID number(s) in pedigree A | No parental genotypes |
With parental genotypes |
||
|---|---|---|---|---|---|
| HLOD | α | HLOD | α | ||
| Proband | 1 | 26.05 | 0.33 | 16.22 | 0.28 |
| 1 additional affected sibling | 1, 2 | 26.77 | 0.19 | 5.50 | 0.09 |
| 1 additional unaffected sibling | 1, 4 | 10.24 | 0.22 | 13.61 | 0.24 |
| 2 additional affected, siblings | 1, 2, 3 | 29.24 | 0.13 | 2.09 | 0.02 |
| 2 additional unaffected siblings | 1, 4, 5 | 5.80 | 0.15 | 11.35 | 0.20 |
| 1 additional affected and unaffected siblings | 1, 2, 4 | 7.97 | 0.12 | 4.45 | 0.09 |
| 2 additional affected and unaffected siblings | 1, 2, 3, 4, 5 | 2.87 | 0.02 | 1.78 | 0.02 |
| Great-grand parents | 1, 12, 13 | 21.62 | 0.31 | 2.46 | 0.12 |
| Sibling grandparents | 1, 9, 10 | 22.08 | 0.24 | 3.24 | 0.09 |
| Married-in grandparents | 1, 8, 11 | 7.27 | 0.20 | 9.37 | 0.20 |
| All grandparents | 1, 8, 9, 10, 11 | 8.13 | 0.15 | 2.47 | 0.08 |
| Great-grand parents and married-in grandparents | 1, 8, 11, 12, 13 | 5.23 | 0.18 | 1.21 | 0.09 |
| Great-grand parents and all grandparents | 1, 8, 9, 10, 11, 12, 13 | 3.07 | 0.08 | 0.17 | 0.01 |
The results are shown for when parental genotypes are available and unavailable. The first column states for which additional family members are genotype data available in addition to the proband and the second column displays the ID number(s) for these individuals as shown in pedigree A (fig. 1).
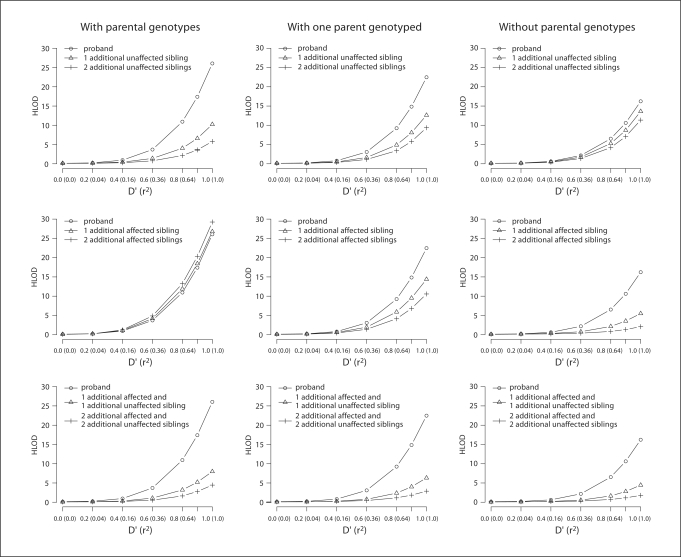
Unlike the case for unrelated parents [1], for first-cousin consanguineous matings, genotyping two unaffected siblings of the affected proband did not eradicate false-positive evidence for linkage (HLOD = 5.80) when parental genotypes are missing (fig. 4 and table 1); however, genotyping two unaffected siblings of the affected proband was of greater benefit in reducing false-positive evidence of linkage than genotyping two additional affected siblings (HLOD = 29.24). When parental genotypes are available for a first-cousin mating, which siblings’ genotype data is most beneficial in reducing the false-positive evidence of linkage is reversed. In this case, genotyping two affected siblings of the proband is more effective in decreasing the false-positive evidence for linkage (HLOD = 2.09) compared to genotyping two unaffected siblings (HLOD = 11.35). In the case where genotype data is only available for one parent (HLOD = 22.47; α = 0.31), genotyping two additional affected siblings of the proband has a greater influence in reducing the proportion of linked families than the HLOD (HLOD = 10.58; α = 0.07) compared to genotyping two additional unaffected siblings (HLOD = 9.36; α = 0.19).
Fig. 4.
Displays for a first-cousin consanguineous mating for an autosomal recessive trait the effect of genotyping additional unaffected and affected siblings of the proband when no parental genotypes are missing (first column), parental genotypes are missing for one parent (second column) and both parents are genotyped (third column). For each panel on the Y axis is displayed the average maximum HLOD. The strength of intermarker LD is displayed on X axis, denoted by D′ followed by r2 in parenthesis. The results are displayed when genotype data for additional unaffected siblings (row 1), additional affected siblings (row 2) and additional affected and unaffected siblings (row 3) are included in the analysis.
The effect of missing genotype data was also evaluated for second-cousin consanguineous matings. When parental genotype data is unavailable and two additional affected siblings of the proband are genotyped, there is only a decrease in the proportion of linked families (α = 0.20) but no decrease in the HLOD = 26.58, compared to when only the proband is genotyped (HLOD = 25.94; α = 0.34). However, when there is missing parental genotype data, available genotype data for two unaffected siblings of the proband greatly reduces the false-positive evidence for linkage (HLOD = 2.50; α = 0.08). In the case where the consanguineous second-cousin parents are genotyped and there is one affected proband, there is still false-positive evidence for linkage (HLOD = 3.65; α = 0.13). This false-positive evidence for linkage is reduced when two additional unaffected siblings are genotyped (HLOD = 2.37; α = 0.08), but the reduction in false-positive evidence for linkage is not as dramatic as when an additional affected sibling is genotyped (HLOD = 0.97, α = 0.03).
For pedigrees with first-cousin consanguineous mating with data analyzed under an autosomal dominant model of inheritance or X-linked recessive mode of inheritance there was an increase in the HLOD and alpha when parental genotype data is missing. For a first-cousin consanguineous pedigrees with an autosomal dominant mode of inheritance, when genotype data is only available for the affected proband and one affected sibling the HLOD = 2.21 and α = 0.28; this modest increase in the false-positive evidence for linkage disappears when parental genotype data are available. For first-cousin consanguineous pedigrees with X-linked autosomal recessive mode of inheritance when genotype data is only available for an affected male proband and his affected male sibling, the false positive evidence of linkage is increased (HLOD = 7.43 and α = 0.32); the false-positive evidence for linkage completely disappears when maternal genotype data is available.
When consanguineous pedigree B (fig. 1) is analyzed removing consanguinity loops so only the proband's parents are first-cousins (fig. 1, pedigree A), the false-positive evidence for linkage is further inflated. When only the affected proband is genotyped in the pedigree with cryptic consanguinity the HLOD = 36.45 and α = 0.4. When both parents are genotyped the HLOD and α (22.21 and 0.34, respectively) are reduced, but for both situations the presence of cryptic consanguinity increases the false-positive evidence of linkage compared to when it is not present (see table 1). The false-positive evidence of linkage is eradicated (HLOD = 0.11) when all pedigree members are genotyped within the pedigree with cryptic consanguinity. In order to evaluate whether or not cryptic consanguinity has an effect when no consanguineous relationships are specified in the analysis, data was generated for pedigree B (fig. 1) but with two affected offspring. There is a slight increase in the false-positive evidence for linkage when neither parent is genotyped (HLOD = 19.15 α = 0.36) compared to when data is generated for pedigrees where the parents are unrelated to each other (HLOD = 14.20 α = 0.31). However, for this situation, the presence of cryptic consanguinity did not lead to an increase in false-positive evidence of linkage when both parents are genotyped (HLOD = 0.09).
The generated data was reanalyzed using the MERLIN program, estimating and incorporating intermarker LD in the analysis, and the false-positive evidence for linkage was eradicated for consanguineous pedigrees with missing genotype data. For example, analysis with MERLIN of pedigrees with a first-cousin consanguineous mating with only a single genotyped affected proband reduced the HLOD to 0.09. When cryptic consanguinity was present, MERLIN greatly reduced the false-positive evidence of linkage but it was not completely removed; the highest HLOD of 1.1 (α = 0.10) was obtained for first-cousin consanguineous pedigrees with cryptic inbreeding when genotype data was only available for the affected proband. When MERLIN was used to carry out the analysis, incorporating the generating haplotype frequencies in the analysis the HLOD = 1.1 (α = 0.10) was still inflated for the first-cousin consanguineous pedigrees with cryptic inbreeding when genotype data was only available for the proband.
It has previously been shown for sib-pairs where the parents are unrelated that r2 is a better predictor of the increase in the false-positive evidence for linkage than D′ [18]. This observation holds true for consanguineous pedigrees. When haplotype data is generated under model 3 when D′ = 1, r2 = 0.43, the HLOD is lower than for data generated under model 1 where r2 = D′ = 1. For example, the HLOD = 2.74 for model 3 and 16.22 for model 1 for a first-cousin consanguineous pedigree with available parental genotype data and a single affected proband. Another factor which affects the false-positive evidence for linkage is the Multilocus PIC (MPIC) [22]. The HLOD will increase with increasing MPIC for a fixed r2 value, pedigree structure and available genotype data. For example, for a first-cousin mating with one affected proband where parental genotype data is available for two markers each with equal allele frequency (Model 1), r2 = 1 and MPIC = 0.375 the HLOD = 16.22 and α = 0.28 for the same pedigree configuration and two segregating markers with an r2 = 1, MAF = 0.2 (Model 2) and MPIC = 0.2688 the HLOD decreases to 6.53 and α to 0.22. It should also be noted that as r2 decreases for set allele frequencies the MPIC increases. For example, for two markers with equal allele frequency (Model 1) when r2 = 0.64 and r2 = 0.36 the MPIC = 0.5039 and MPIC = 0.5958, respectively. Although MPIC increases, decreasing r2 always has a greater effect in reducing the false-positive evidence for linkage than MPIC (see 2, 3, 4).
Discussion
For two-point linkage analysis and multipoint analysis when there is no intermarker LD and genotype data is available for founders but not all pedigree members (e.g. parental genotypes), no bias of the LOD score will occur since reconstruction of genotypes is not based upon estimates of allele frequencies but only on the genotype data of family members [14, 15]. For consanguineous pedigrees where the trait is inherited in an autosomal recessive mode of inheritance, even if all founders are genotyped but parental genotypes are missing, if intermarker LD is ignored in the analysis there can be false-positive evidence of linkage, because haplotype frequencies can be incorrect and contribute to the inflation of the LOD score. For single markers there is no bias in this situation, since although the genotypes cannot always be reconstructed the probabilities for each compatible genotype is correct and is not influenced by incorrectly specified allele frequencies.
Although consanguineous pedigrees can be used to study traits with an autosomal dominant, X-linked or complex mode of inheritance, these pedigrees, unlike pedigrees with autosomal recessive mode of inheritance, do not offer any additional linkage information compared to pedigrees of comparative size without consanguinity. For example, for a fully penetrant autosomal dominant trait a pedigree with a first-cousin consanguineous mating (fig. 1, pedigree A with individuals 6, 9 and 12 phenotype status changed to affected) provides the same amount of linkage information as the same pedigree structure with the proband's mother (individual 7) unrelated to the other pedigree members. For the autosomal dominant mode of inheritance, whether consanguinity is present or not the meioses inherited from individual 7 by her affected and unaffected offspring provides no linkage information and likewise the meioses which she inherits from her mother and father (individuals 10 and 11) does not provide linkage information.
For pedigrees where the trait follows an X-linked recessive mode of inheritance for first cousin consanguineous matings and also for unrelated parents, when genotype data is available for the female carrier (individual 7) it is known with complete accuracy which haplotypes are transmitted to her affected and unaffected male children. Therefore only when the carrier female is missing her genotype data will haplotype probabilities be incorrect when intermaker LD is not incorporated in the analysis.
When analyzing consanguineous pedigrees for which there is missing genotype data, it is necessary to proceed with caution when analysis is being carried out ignoring LD. The amount of false-positive evidence for linkage can be evaluated by generating haplotype data for any pedigree structure(s) unconditional on the disease status using, for example, the SimPed program. If there is an inflation of false-positive evidence for linkage, simulation can be used to estimate empirical p values using haplotype frequencies estimated from the pedigree data if the sample size is sufficiently large or from publicly available databases. However, even if a simulation study indicates only a modest or no increase in false-positive evidence for linkage, the results may be incorrect due to cryptic consanguinity. Usually knowledge of family relationships is incomplete due to information only being available for no more than 4–5 generations and, additionally, spouses may not know their exact consanguineous relationship. Therefore, the amount of consanguinity within a pedigree is often underestimated. Although true familial relationships cannot be reconstructed, it is possible to evaluate whether cryptic consanguinity is present within pedigrees using the methods described by [23]. The increase in false-positive evidence for linkage in the pedigrees with cryptic consanguinity is not only because of the use of incorrect haplotype frequencies but also due to the misspecification of the pedigree structure. It has previously been shown that not completely specifying familial relationships can also bias the false-positive rate when intermarker LD is not present for affected-sibpair methods [24, 25] as well as parametric linkage analysis and homozygosity mapping [26, 27].
In order to increase the speed of linkage analysis, consanguineous pedigrees can initially be analyzed ignoring LD, and those regions for which there is either suggestive or significant evidence of linkage can be reanalyzed incorporating intermarker LD. This analysis can be done using the MERLIN program if the pedigrees are not large. Larger pedigrees can be analyzed using LINKAGE/FASTLINK, but only a very limited number of marker loci can be analyzed simultaneously, thus reducing the informativeness of the marker data. When analysis is carried out with either program, biases in the estimate of haplotype frequencies can occur if there are only a limited number of founders available. Another analysis option is to use haplotype frequencies from published data such as HapMap (www.hapmap.org); however, data is only available for a limited number of ethnic backgrounds at this time. If the pedigrees under analysis do not come from the same population as those individuals being used to estimate haplotype frequencies, the haplotypes may not be representative and give rise to false-positive evidence of linkage. For the examples given in this article, there was a sufficiently large sample to estimate haplotype frequencies and the pedigrees were small enough to analyze using MERLIN. For the examples shown, false-positive evidence for linkage was almost completely removed by carrying out linkage analysis incorporating intermarker LD in the analysis, except when cryptic inbreeding was present. Given an adequate number of small to medium sized pedigrees, MERLIN is a viable analysis tool to distinguish true from false-positive linkage signals. However, for many studies of consanguineous pedigrees with autosomal recessive inheritance, analysis with MERLIN will not be a feasible solution to eradicate false-positive evidence of linkage due to intermarker LD because of large pedigree structures and/or insufficient number of observed genotypes to estimate haplotype frequencies.
Acknowledgements
This work was supported by the National Institutes of Health Grant R01-DC03594.
References
- 1.Huang Q, Shete S, Amos CI. Ignoring linkage disequilibrium among tightly linked markers induces false-positive evidence of linkage for affected sib pair analysis. Am J Hum Genet. 2004;75:1106–1112. doi: 10.1086/426000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Weber JL, Broman KW. Genotyping for human whole-genome scans: Past, present, and future. Adv Genet. 2001;42:77–96. doi: 10.1016/s0065-2660(01)42016-5. [DOI] [PubMed] [Google Scholar]
- 3.Murray SS, Oliphant A, Shen R, McBride C, Steeke RJ, Shannon SG, Rubano T, Kermani BG, Fan JB, Chee MS, Hansen MS. A highly informative snp linkage panel for human genetic studies. Nat Methods. 2004;1:113–117. doi: 10.1038/nmeth712. [DOI] [PubMed] [Google Scholar]
- 4.Kennedy GC, Matsuzaki H, Dong S, Liu WM, Huang J, Liu G, Su X, Cao M, Chen W, Zhang J, Liu W, Yang G, Di X, Ryder T, He Z, Surti U, Phillips MS, Boyce-Jacino MT, Fodor SP, Jones KW. Large-scale genotyping of complex DNA. Nat Biotechnol. 2003;21:1233–1237. doi: 10.1038/nbt869. [DOI] [PubMed] [Google Scholar]
- 5.Wilcox MA, Pugh EW, Zhang H, Zhong X, Levinson DF, Kennedy GC, Wijsman EM. Comparison of single-nucleotide polymorphisms and microsatellite markers for linkage analysis in the coga and simulated data sets for genetic analysis workshop 14:Presentation groups 1, 2, and 3. Genet Epidemiol. 2005;29(suppl 1):S7–S28. doi: 10.1002/gepi.20106. [DOI] [PubMed] [Google Scholar]
- 6.Cottingham RW, Jr, Idury RM, Schaffer AA. Faster sequential genetic linkage computations. Am J Hum Genet. 1993;53:252–263. [PMC free article] [PubMed] [Google Scholar]
- 7.Abecasis GR, Cherny SS, Cookson WO, Cardon LR. Merlin – rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet. 2002;30:97–101. doi: 10.1038/ng786. [DOI] [PubMed] [Google Scholar]
- 8.Abecasis GR, Wigginton JE. Handling marker-marker linkage disequilibrium: Pedigree analysis with clustered markers. Am J Hum Genet. 2005;77:754–767. doi: 10.1086/497345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Altshuler D, Brooks LD, Chakravarti A, Collins FS, Daly MJPD, Consortium IH. A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gudbjartsson DF, Thorvaldsson T, Kong A, Gunnarsson G, Ingolfsdottir A. Allegro version 2. Nat Genet. 2005;37:1015–1016. doi: 10.1038/ng1005-1015. [DOI] [PubMed] [Google Scholar]
- 11.Gudbjartsson DF, Jonasson K, Frigge ML, Kong A. Allegro, a new computer program for multipoint linkage analysis. Nat Genet. 2000;25:12–13. doi: 10.1038/75514. [DOI] [PubMed] [Google Scholar]
- 12.Sobel E, Lange K. Descent graphs in pedigree analysis: Applications to haplotyping, location scores, and marker-sharing statistics. Am J Hum Genet. 1996;58:1323–1337. [PMC free article] [PubMed] [Google Scholar]
- 13.Weeks DE, Sobel E, O'Connell JR, Lange K. Computer programs for multilocus haplotyping of general pedigrees. Am J Hum Genet. 1995;56:1506–1507. [PMC free article] [PubMed] [Google Scholar]
- 14.Freimer NB, Sandkuijl LA, Blower SM. Incorrect specification of marker allele frequencies: Effects on linkage analysis. Am J Hum Genet. 1993;52:1102–1110. [PMC free article] [PubMed] [Google Scholar]
- 15.Knapp M, Seuchter SA, Baur MP. The effect of misspecifying allele frequencies in incompletely typed families. Genet Epidemiol. 1993;10:413–418. doi: 10.1002/gepi.1370100614. [DOI] [PubMed] [Google Scholar]
- 16.Huang Q, Shete S, Swartz M, Amos CI. Examining the effect of linkage disequilibrium on multipoint linkage analysis. BMC Genet. 2005;6(Suppl 1):S83. doi: 10.1186/1471-2156-6-S1-S83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schaid DJ, McDonnell SK, Wang L, Cunningham JM, Thibodeau SN. Caution on pedigree haplotype inference with software that assumes linkage equilibrium. Am J Hum Genet. 2002;71:992–995. doi: 10.1086/342666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Boyles AL, Scott WK, Martin ER, Schmidt S, Li YJ, Ashley-Koch A, Bass MP, Schmidt M, Pericak-Vance MA, Speer MC, Hauser ER. Linkage disequilibrium inflates type i error rates in multipoint linkage analysis when parental genotypes are missing. Hum Hered. 2005;59:220–227. doi: 10.1159/000087122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Van Camp G, Smith RJH: Hereditary hearing loss homepage: Http://webhost.Ua.Ac.Be/hhh/ 2007.
- 20.Leal SM, Yan K, Muller-Myhsok B. Simped: A simulation program to generate haplotype and genotype data for pedigree structures. Hum Hered. 2005;60:119–122. doi: 10.1159/000088914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ott J. Linkage analysis and family classification under heterogeneity. Ann Hum Genet. 1983;47:311–320. doi: 10.1111/j.1469-1809.1983.tb01001.x. [DOI] [PubMed] [Google Scholar]
- 22.Goddard KA, Wijsman EM. Characteristics of genetic markers and maps for cost-effective genome screens using diallelic markers. Genet Epidemiol. 2002;22:205–220. doi: 10.1002/gepi.0177. [DOI] [PubMed] [Google Scholar]
- 23.Leutenegger AL, Prum B, Genin E, Verny C, Lemainque A, Clerget-Darpoux F, Thompson EA. Estimation of the inbreeding coefficient through use of genomic data. Am J Hum Genet. 2003;73:516–523. doi: 10.1086/378207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Genin E, Clerget-Darpoux F. Consanguinity and the sib-pair method: An approach using identity by descent between and within individuals. Am J Hum Genet. 1996;59:1149–1162. [PMC free article] [PubMed] [Google Scholar]
- 25.Leutenegger AL, Genin E, Thompson EA, Clerget-Darpoux F. Impact of parental relationships in maximum lod score affected sib-pair method. Genet Epidemiol. 2002;23:413–425. doi: 10.1002/gepi.10190. [DOI] [PubMed] [Google Scholar]
- 26.Liu F, Elefante S, van Duijn CM, Aulchenko YS. Ignoring distant genealogic loops leads to false-positives in homozygosity mapping. Ann Hum Genet. 2006;70:965–970. doi: 10.1111/j.1469-1809.2006.00279.x. [DOI] [PubMed] [Google Scholar]
- 27.Miano MG, Jacobson SG, Carothers A, Hanson I, Teague P, Lovell J, Cideciyan AV, Haider N, Stone EM, Sheffield VC, Wright AF. Pitfalls in homozygosity mapping. Am J Hum Genet. 2000;67:1348–1351. doi: 10.1016/s0002-9297(07)62966-8. [DOI] [PMC free article] [PubMed] [Google Scholar]