Abstract
Objective
To derive a difference equation based on mass conservation and on alveolar tidal volumes for the calculation of Functional Residual Capacity. Derive an equation for the FRC from the difference equation. Furthermore, to derive and validate a step response equation as a solution of the difference equation within the framework of digital signal processing where the FRC is known a priori.
Methods
A difference equation for the calculation of Functional Residual Capacity is derived and solved as step response of a first order system. The step response equation calculates endtidal fractions of nitrogen during multiple breath nitrogen clearance. The step response equation contains the eigenvalue defined as the ratio of FRC to the sum of FRC and alveolar tidal ventilation. Agreement of calculated nitrogen fractions with measured fractions is demonstrated with data from a metabolic lung model, measurements from patients in positive pressure ventilation and volunteers breathing spontaneously. Examples of eigenvalue are given and compared between diseased and healthy lungs and between ventilatory settings.
Results
Comparison of calculated and measured fractions of endtidal nitrogen demonstrates a high degree of agreement in terms of regression and bias and limits of agreement (precision) in Bland & Altman analysis. Examples illustrate the use of the eigenvalue as a possible discriminator between disease states.
Conclusion
The first order step response equation reliably calculates endtidal fractions of nitrogen during washout based on a Functional Residual Capacity. The eigenvalue may be a clinically valuable index alone or in conjunction with other indices in the analysis of respiratory states and may aid in the setting of the ventilator.
Keywords: physiologic monitoring, respiration disorder, functional residual capacity, nitrogen washout, digital signal processing, mechanical ventilators
Introduction
Functional Residual Capacity, FRC, is the lung volume at the end of a relaxed expiration to atmospheric pressure. The FRC is affected by lung diseases and thus is a central measure for diagnosis, treatment and monitoring in anesthesia and intensive care. The calculation of FRC from measurement of multiple breath nitrogen washout (MBNW) when abruptly changing the fraction of inspired oxygen (FIO2) was introduced by Darling [1]. The method entailed the measurement of the mixed expiratory fraction of nitrogen before and after a step increase in oxygen and can be explained with the following simple example. Start with a person spontaneously breathing room air. The inspired fraction of oxygen, FIO2, is 0.21 and the balance is N2, i.e. FIN2 = 0.79. Assume dry alveolar fractions of O2 = 0.16, FAO2, of N2 = 0.79, FAN2, and of CO2 = 0.05, FACO2. If the equilibrium between FIN2 and FAN2 is disrupted by having the person inhale at FIO2 of 1 while exhaling into a bag, eventually all alveolar nitrogen will be transferred to the bag. FRC equals VN2 divided by the change in fraction of nitrogen that was in the lung:
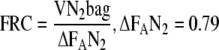 |
. VN2bag can be found by multiplying the bag nitrogen fraction with the total volume accumulated in the bag. With the advent of the nitrogen analyzer [2], the mass spectrometer [3] and the use of high precision spirometers the washout could be followed on a breath-by-breath basis [4]. This refinement eliminated the need for the bag and replaced the numerator in Equation (1) with the expired volumes of nitrogen summed over the number of breaths. The modification is heavily reliant on the exact synchronization of analysis of FN2 and expired volume for the calculation of breath-by-breath volume of nitrogen. Modern modifications of MBNW have utilized flow measurement synchronized with measurement of nitrogen fractions [5]. The next refinement allows for any step change in nitrogen. The example above utilized FIO2 to step FAN2 from 0.79 to 0. Instead, any step change in FIO2 could be used to create a corresponding step change in nitrogen.
Later, Darling et al. [6] established the ratio of functional residual air, R, divided by the sum of functional residual air and effective tidal volume, T′, as ‘dilution rate’, r, describing the nitrogen clearance curve:
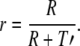 |
. This factor multiplied by initial alveolar fraction of nitrogen and raised to the power of breath number allowed for the calculation of fraction of nitrogen in the expired volume of air. Fowler [7] expanded the concept of the alveolar dilution factor to encompass three lung phases and introduced the term ‘pulmonary nitrogen clearance delay’, adding another characterization of the nitrogen clearance curve. The list has since been extended by investigators in pulmonary physiology, see [8, 9].
Recently, a modification of the MBNW method has been introduced [10], implicitly utilizing a first order difference equation for the calculation of FRC based on mass conservation and a change in FIO2 of 0.1. In the present study, the difference equation is solved for the step response using basic digital signal processing (DSP) techniques [11] where the step is interpreted as the nitrogen fraction change initiating the measurement. The resulting step response equation by comparing calculated clearance data to experimental and clinical washout data. Finally, we discuss technical and clinical limitations in addition to characteristics of the measurement.
Methods and Materials
The modified MBNW and difference equation
The first order difference equation based on mass conservation of nitrogen over one breath after a step change in inhaled N2 fraction is described in Equation (3).
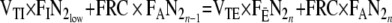 |
The step change in nitrogen occurs at breath index n = 0. The step is from 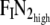 to
to 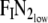 which will lead to N2 washing out.
which will lead to N2 washing out. 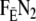 is an average breath fraction of expired gas which includes gas from anatomical (series) dead space.
is an average breath fraction of expired gas which includes gas from anatomical (series) dead space. 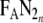 depends on the fraction of the immediately preceding breath
depends on the fraction of the immediately preceding breath 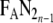 . VTI and VTE designate inspiratory and expiratory tidal volumes. In all equations the notation ‘FRC’ designates relaxed end-expiratory volume regardless of PEEP. A refinement is to measure the lung volume to the exclusion of tidal anatomical dead space, VDTanat. Thus, the VTE and VTI of Equation (3) must be replaced by the alveolar tidal volumes, VATE and VATI. Also, using endtidal CO2 fraction, FETCO2, as approximating alveolar fraction, FACO2, the following equations can be used to calculate the alveolar tidal volumes:
. VTI and VTE designate inspiratory and expiratory tidal volumes. In all equations the notation ‘FRC’ designates relaxed end-expiratory volume regardless of PEEP. A refinement is to measure the lung volume to the exclusion of tidal anatomical dead space, VDTanat. Thus, the VTE and VTI of Equation (3) must be replaced by the alveolar tidal volumes, VATE and VATI. Also, using endtidal CO2 fraction, FETCO2, as approximating alveolar fraction, FACO2, the following equations can be used to calculate the alveolar tidal volumes:
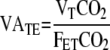 |
, where VTCO2 is the tidal excretion of CO2.
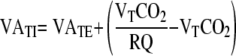 |
RQ is the respiratory quotient defined as 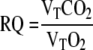 . The value of RQ depends on the composition of substrate being metabolized. For example, RQ = 1 when carbohydrates are being metabolized and RQ = 0.7 when fat is being metabolized. The range of RQ is typically from 0.7 to 1.0 with reservation for gluconeo- and lipogenesis [12]. A fixed value of RQ of 0.8 is used in Equation (5).
. The value of RQ depends on the composition of substrate being metabolized. For example, RQ = 1 when carbohydrates are being metabolized and RQ = 0.7 when fat is being metabolized. The range of RQ is typically from 0.7 to 1.0 with reservation for gluconeo- and lipogenesis [12]. A fixed value of RQ of 0.8 is used in Equation (5).
For the purpose of accumulating the in- and expired volumes of nitrogen, the fractions of nitrogen are calculated as residue. This obviates the need of a nitrogen analyzer.
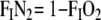 |
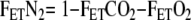 |
Substituting for alveolar volumes and endtidal fractions, Equation (3) becomes:
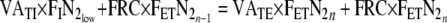 |
This is a first order difference equation. This difference equation represents sampling of a continuous process. The FIN2 and FETN2 are based on samples from the continuous FCO2 and FO2 signals according to Equations 6 and 7, see Figure 1. VATI and VATE are calculated according to Equations (4) and (5).
Fig. 1.
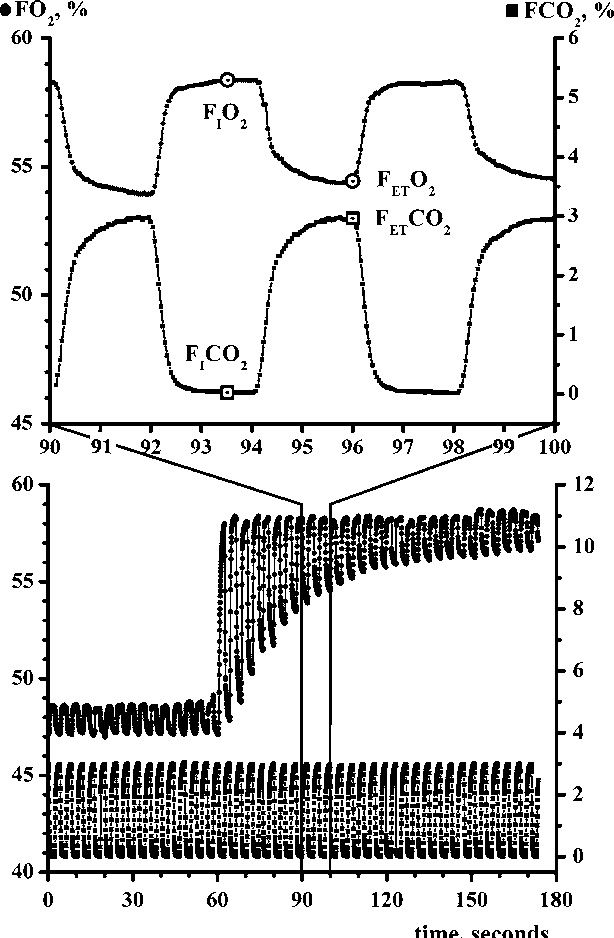
Sampling at two frequencies, the waveform sampling rate and two samples per breath sampling rate. Lower frame: the continuous sampling of FO2 (left y-axis) and FCO2 (right y-axis) during a N2 washout procedure. From these tracings (enlarged in upper frame) two samples of FO2 and FCO2 are sampled once during inspiration and as endtidal values for entering into Equations 6 and 7.
In the presence of alveolar (parallel) dead space, FETCO2 < FACO2 and, as a result, the equations include alveolar dead space.
Two solutions to Equation (8) will be given. First, the FRC is found by summing both sides of Equation 8 over the total number of breaths,
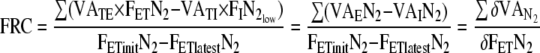 |
. FETinitN2 denotes the initial condition at time n equals −1 which is the time sample before the step (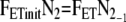 ). FETlatestN2 represents
). FETlatestN2 represents 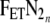 when n equals the most recent breath. In general, VATE, VATI and
when n equals the most recent breath. In general, VATE, VATI and 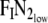 can vary with n and may be replaced by
can vary with n and may be replaced by 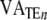 ,
, 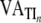 and
and 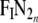 respectively. Second, Equation 8 is solved for the step response using the FRC calculated by Equation (9)
respectively. Second, Equation 8 is solved for the step response using the FRC calculated by Equation (9)
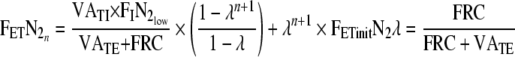 |
In this solution, the values, VATI, VATE and 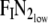 are assumed to remain constant during the washout. For a full derivation, see Appendix A. This is an equation that gives the FETN2 for a particular breath without iteration and can be used to determine the applicability of a first order model. Some implications of Equation 10 are immediately apparent:
are assumed to remain constant during the washout. For a full derivation, see Appendix A. This is an equation that gives the FETN2 for a particular breath without iteration and can be used to determine the applicability of a first order model. Some implications of Equation 10 are immediately apparent:
λ is related to the time constant of the N2 clearance.
As the VATE increases,
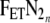 decays faster consistent with a faster lung washout at larger tidal breaths.
decays faster consistent with a faster lung washout at larger tidal breaths.If the FRC becomes large compared to the VATE, then λ approaches 1 and there is very slow decay consistent with a small tidal breath requiring more breaths to change the concentration of a large lung volume (FRC).
As n → ∞,
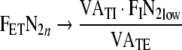 . The
. The 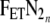 will not reach
will not reach 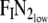 when RQ ≠ 1 since VATI ≠ VATE. One would expect a good match between the measured FETN2 sequence compared to the calculated values if the system being measured is indeed first order.
when RQ ≠ 1 since VATI ≠ VATE. One would expect a good match between the measured FETN2 sequence compared to the calculated values if the system being measured is indeed first order.
Experimental and clinical validation
The modified MBNW has been extensively validated in a metabolic lung model [10]. In this paper, the prediction of FETN2 by the FRC step response equation was validated by comparing calculated to measured values of FETN2 from washout procedures in one experimental and two clinical settings. The clinical measurements were made as part of two other studies for which the Ethical Committee of the Medical Faculty at Göteborg University approved the studies and informed consent was obtained from the patients, next of kin or volunteers, respectively. Thus, they represent examples and are not the result of a selection powered to demonstrate differences between the normal and disease categories.
Model. An experimental setup using an O2-consuming/CO2-producing metabolic lung model previously described [10, 13]. The model was ventilated in volume controlled ventilation with a GE Engström Carestation ventilator (Madison, WI, USA). Settings comprised two FRCs (1.8, 2.9 L), two tidal volumes (500, 750 mL) and two steps of FIO2 (0.1, 0.3) at  200 mL/min and RQ 1. FRC measurements were computed with the commercial software algorithm based on Equation 9 detailed above. Simultaneously, data were collected and entered into Equation 10.
200 mL/min and RQ 1. FRC measurements were computed with the commercial software algorithm based on Equation 9 detailed above. Simultaneously, data were collected and entered into Equation 10.
Patients. Patient recordings were performed either in the operating theater using GE ADU/5 ventilator or in the intensive care unit (ICU) using a Servo 900C or Servo 300 ventilator (Siemens Elema, Solna, Sweden). Subjects with assumed normal lungs were measured peroperatively and patients with diseased lungs in the intensive care unit, where positive pressure ventilation was instituted due to respiratory failure. The eigenvalues, λ, were calculated for one patient with Acute Respiratory Distress Syndrome (ARDS), one with heart failure (HF), two patients with chronic obstructive pulmonary disease (COPD), and one obese patient with normal lungs (perioperative registration). Mono- vs biexponential fits were examined in one of the ICU patients (COPD) and in the bariatric patient.
Volunteers. Recordings in healthy volunteers (two female and one male) spontaneously breathing while attached to a high flow CPAP system via a snorkeling mouthpiece and equipped with a nose clip in supine, sitting and standing position.
In patients and volunteers, respiratory monitoring and gas sampling were performed with Datex-Ohmeda spirometry module in an AS/3 intensive care monitor. Data were collected using Datex-Ohmeda S/5 Collect version 4 software (Datex-Ohmeda, Helsinki, Finland) and analyzed using Lung Monitor (plug-in to Datex-Ohmeda S/5 Collect) or proprietary software programmed in Test- Point (Measurement Computing Corporation, Norton, MA, USA). The Test-Point program previously formed part of the validation study [10].
Statistics
Agreement between calculated and measured values of FETN2 was assessed by Bland & Altman analysis [14] in terms of bias and limits of agreement.1 An error percentage, calculated according to [15] below 30 was accepted as sign of good agreement. Calculated and measured values were analyzed by means of regression and R2. Patient and volunteer characteristics and results are reported in Table 1.
Table 1.
Patients and volunteers entered in evaluation of step response derivation
| Patients ID, sex and age | Description | PEEP (cm H20) | VAT (mL) | Eigenvalues | BL F102; ΔFN2 | FRC (mL) | # | Bias | Upper & lower limit of agreement | slope; | constant |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 030930, M, 76 | ICU, sepsis, COPD | 5 | 375 | 0.79 | 0.4 | 1480 | 7 | −0.82 | 2.13 & −3.76 | 1.15; | −6.49 |
| 10 | 0.84 | 0.1 | 2090 | ||||||||
| 15 | 0.88 | 0.2 | 2346 | ||||||||
| 20 | 0.91 | 3045 | |||||||||
| 031110, M, 65 | ICU, sepsis, COPD | 12 | 235 | 0.89 | 0.4 | 1850 | 6 | −0.21 | 2.32 & −2.7 | 1.13; | −5.35 |
| 18 | 0.90 | 0.1 | 2200 | ||||||||
| 0.2 | |||||||||||
| 0.3 | |||||||||||
| 031120, M, 48 | ICU, HF | 10 | 216 | 0.85 | 0.4 | 1228 | 6 | −0.04 | 2.1 & 2.2 | 1.09; | −4.46 |
| 15 | 0.86 | 0.1 | 1336 | ||||||||
| 0.2 | |||||||||||
| 0.3 | |||||||||||
| 040216, F, 42 | ICU, ARDS, SLE | 10 | 280 | 0.72 | 0.5 | 600–800 | 8 | 0.04 | 0.7 & −0.63 | 0.93; | 2.7 |
| 15 | 0.77 | 0.1 | 1040 | ||||||||
| 040415, F, 35 | Laparoscopic, bariatric surgery | 0 | 435 | 0.64 | 0.4 | 798 | 6 | 0.08 | 1.42 & −1.26 | 0.93; | 3.34 |
| 10 | 0.67 | 0.5 | 950 | ||||||||
| 20 | 0.74 | 0.1 | 1200 | ||||||||
| ALL patients | 35 | −0.297 | 1.989 & −2.58 | 1.07; | −3.05 | ||||||
| Volunteers ID, sex and age | |||||||||||
| CO, F, 40 | Sitting, standing | 0 | Variable | 0.83 | 0.2 | 2500 | 6 | −0.01 | 1.12 & −1.2 | 0.99; | −1.19 |
| 10 | 0.88 | 0.2–0.3 | 2900 | ||||||||
| COH, M, 29 | Sitting | 0 | Variable | 0.74 | 0.2 | 1400 | 4 | 1.46 | 7.6 & −4.7 | 0.98; | 0.45 |
| 5 | 0.83 | 0.2 | 2400 | ||||||||
| 10 | 0.85 | 0.45 | 2668 | ||||||||
| AB, M, 38 | Supine | 0 | Variable | 0.77 | 0.2–0.3 | 1750 | 6 | −0.35 | 1.7 & −2.4 | 1.03; | 1.18 |
| 5 | 0.79 | 0.2 | 2184 | ||||||||
| 10 | 0.77 | 0.35 | 2125 | ||||||||
| ALL volunteers | 16 | 0.16 | 3.5 & −3.2 | 1.02; | −0.97 |
Age, sex, location of measurement, PEEP and FN2 changes, baseline F1O2 and FRC. Results of Bland & Altman analysis of agreement and regression analysis.
Results
Model. There was an excellent correspondence between 178 pairs of measured and calculated values of FETN2 in six washout procedures using the step response equation, see Figure 2. Bland & Altman analysis showed bias of 0, upper and lower limits of agreement of 0.49 and −0.5 and error 1.3%, see Figure 3. The regression equation showed a slope of 1.0, intercept −0.12 and R2 0.98 with a p < 0.001.
Fig. 2.
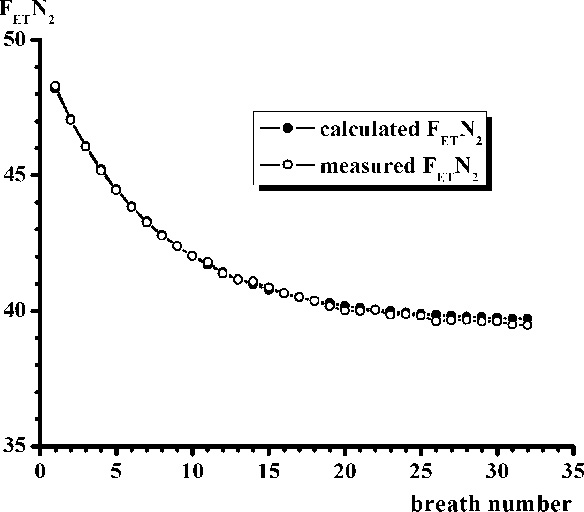
Calculated and measured FETN2 during N2 washout in metabolic lung model. ΔFN2 0.3, FRC 1800 mL, VAT 270 mL, eigenvalue 0.86,  187 mL/min. The regression equation has a slope of 1.02 and a R2 of 0.999.
187 mL/min. The regression equation has a slope of 1.02 and a R2 of 0.999.
Fig. 3.

Bland & Altman plot of agreement between pairs of measured and calculated FETN2 according to step response derivation in metabolic lung model. The FRC of the lung model was 1800 mL. Bias 0, upper and lower limits of agreement of 0.25 and −0.5.
Patients. We analyzed 35 washout procedures from five patients. PEEP levels varied from 0 to 20 cm H2O, FRC ranged from 600 to 3000 mL, δFETN2 from 0.1 to 0.3 and baseline FIO2 from 0.2 to 0.5. Individual tidal volumes were unchanged during manipulation of PEEP. There was good agreement between 1222 pairs of measured and the calculated values of FETN2. Bland & Altman analysis showed bias of 0.3, upper and lower limits of agreement of 2 and −2.6, error 4.9%, see Figure 4. The regression equation showed a slope of 1.07, intercept −3.0, R2 0.98 with a p < 0.001. At comparable PEEP levels λ in ARDS (λARDS) patient was 0.734, in patient with heart failure (λHF) 0.846, in COPD patients 0.842 and 0.889 (λCOPD) and in perioperative normal adult lung (bariatric patient) 0.654 (λperiop). Standard deviations omitted due to paucity of measurements at PEEP level. Eigenvalues showed as expected clear relationship to PEEP levels, see Figure 5.
Fig. 4.
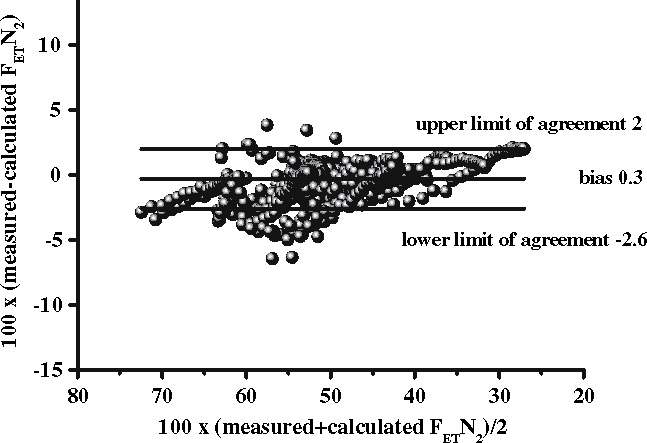
Bland & Altman plot of agreement between pairs of measured and calculated FETN2 according to step response derivation in 35 N2 washout procedures in five patients. Bias of 0.3, upper and lower limits of agreement of 2 and −2.6. The regression equation showed a slope of 1.07, intercept −3 and R2 0.98 with a p < 0.001.
Fig. 5.
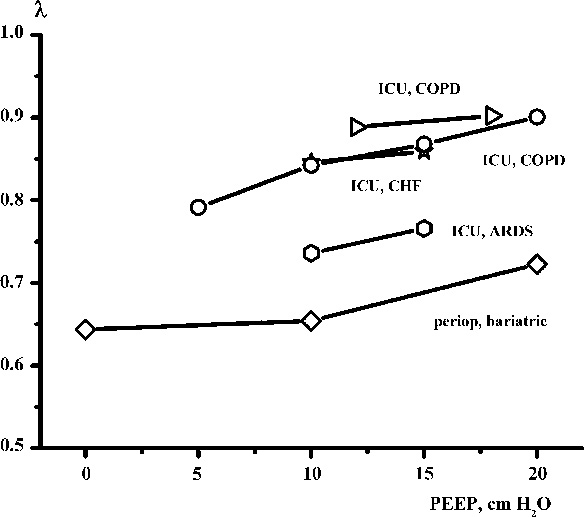
λ as a function of PEEP in five patients.
In the analysis of mono- vs. bicompartmental analysis we found a difference between mono- and biexponential fit to measured FETN2 in the ICU (COPD) patient whereas there was no notable difference in the bariatric patient. The number of patients and measurements preclude consideration statistical significance.
Volunteers. A total of 16 washout procedures were analyzed. PEEP levels varied from 0, 5 to 10 cm H2O, FRC ranged from 1400 to 2900 mL, δFETN2 0.2 to 0.45 and baseline FIO2 from 0.21 to 0.3. There was good agreement between 524 pairs of measured and the calculated values of FETN2 using the step response equation. Bland & Altman analysis showed bias of −0.16, upper and lower limits of agreement at 3.2 and −3.5 and an error 6.4%. The regression equation showed a slope of 0.97, intercept 1.9 and R2 0.98 with a p < 0.001 (Figure 6).
Fig. 6.
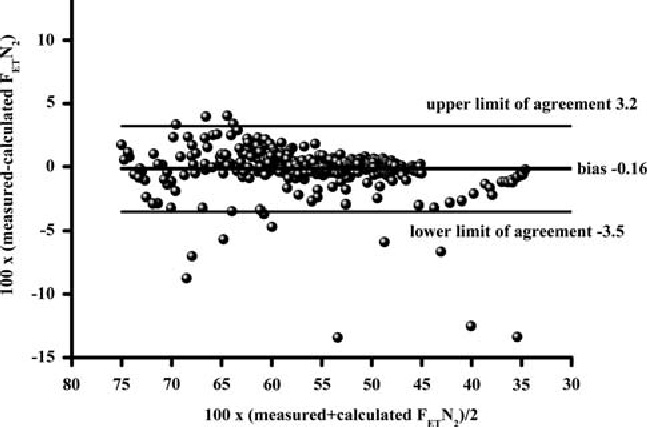
Bland & Altman plot of agreement between pairs of measured and calculated FETN2 according to step response derivation in 16 N2 washout procedures in three healthy volunteers. Bland & Altman analysis showed bias of −0.16, lower and upper limits of agreement at 3.2 and −3.5. The regression equation showed a slope of 0.97, intercept at 1.9 and R2 0.98 with a p < 0.001.
Discussion
We take as a starting point the mathematical derivation of a modified version of the multiple breath nitrogen washout method for calculation of FRC. Using the result of the FRC calculation, a step response equation was derived based on techniques from DSP and used to calculate the course of FETN2 during washout. These calculated values were then compared to measured data from an experimental setup, patients and volunteers. We found excellent alignment between measured and calculated nitrogen clearance using a single compartment, first order metabolic lung model. The first order model also fitted measurements in patients with various respiratory conditions and in healthy, spontaneously breathing volunteers. The eigenvalue of the step response was shown to be dependent on PEEP level and to be different among healthy and diseased states of the lung. The sample size, however, does not allow for any statistically significant inferences, but the results may indicate a diagnostic and prognostic method to be verified in further studies. Technical and clinical characteristics and limitations of the modified MBNW method and first order step response equation are addressed in the following.
Nitrogen clearance in the framework of Digital Signal Processing
The present study is — to our knowledge — the first attempt at deriving the equivalent of the alveolar dilution ratio first introduced by Darling [6] by solving the underlying first order difference equation based on mass conservation of alveolar contents of N2. The eigenvalue, λ, is equal to Darling’s r in Equation (2). This ratio was revived by Wagner [8] as a term in Linear Programming of ventilation/volume ratios and by Rossing [16]. Wagner and Rossing published their research before Oppenheim and Schaffer published their work [11] on DSP, which forms the basis of this study. Using techniques made popular by the field of DSP, enables one to frame the problem in the form of a difference equation and solve for the step response. DSP has entered the mainstream subsequent to many of the early works on MBNW. Reformulating the subject in a DSP framework should allow algorithms from that field to improve or extend MBNW algorithms. The present study details nitrogen clearance as a first order process characterized by an eigenvalue, λ and compares actual values of FETN2 to values predicted by the step response equation. The degree of agreement confirms that the nitrogen washout is dominated by a first order process and the tools of DSP are applicable in this setting.
Clinical impact and uses for λ. The term λ = FRC/(FRC+VATE) is the eigenvalue for the first order system. This paper provides an alternative derivation for λ in the more general framework of DSP. Results in the present study showed higher λ in healthy adult lungs and in patients with COPD and lower values in patients with ARDS. λ by definition reflects FRC and this capacity in turn is influenced by PEEP. In addition, λ is reminiscent of the strain relationship (VT/FRC) which according to the ‘baby lung’2 concept [17] should not exceed 0.8 to +1. In terms of λ this corresponds to a value of 0.55–0.5 at PEEP of 0 cm H2O. For the bariatric patient (see Figure 5) the strain is perilously close to this limit. It may not be clinically justifiable to measure λ by setting PEEP at zero (ZEEP), but as the value is linearly related to PEEP by virtue of the lung compliance, a series measurement at PEEP levels above zero can be used to extrapolate to a value of λ corresponding to ZEEP. The λ or the strain relationship could be considered a discriminator for classifying lung states but may not be sufficient in isolation. Since λ has a dependency on the ventilator settings through FRC (and as a corollary PEEP) and VATE, calculation of λ at several tidal volumes would likely be a better discriminate. Further, these ratios in conjunction with other features such as hemodynamics would be an excellent start for a feature vector that could be used for pattern classification. The pattern classifier would be used to distinguish between different lung states and act as a guide for optimal ventilation therapy. There seems to be a vast field for further studies in this respect.
Sensitivity of FRC to varying or fixed RQ. The washout procedure posits that the O2-consumption and CO2-excretion, the end-expiratory lung volume as well as hemodynamics are stable at baseline before washout and that no interventions are undertaken during the washout period which will alter this, e.g. changes in inotropic support with inherent thermogenic effects or changes in ventilatory settings. In our formulation, RQ is fixed at 0.8, although in reality RQ can be between 0.7 and 1.0 depending on the metabolic state of the patient. In this context it can be shown that for a FIO2 of 0.5, a ΔFETN2 of 0.1, a ΔRQ of 0.1 and 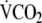 200 mL/min the error in FRC amounts to approximately 180 mL bias.
200 mL/min the error in FRC amounts to approximately 180 mL bias.
Tissue contribution to nitrogen clearance. Equality in Equation 3 assumes that N2 is neither taken up nor excreted from blood and tissues. Estimates of tissue nitrogen uptake and excretion do, however, exist [18, 19]. The modified MBNW utilizes a ΔFN2 of 0.1 and accordingly the volume excreted will be diminished to approximately 10 mL. However, repeating the ΔFN2 with an identical change in opposite direction and averaging the results for FRC compensates for this error [10].
Approximation of gas fractions. The FIN2 and FETN2 are calculated as residue after subtraction of appropriate fractions of O2 and CO2 and entered into the calculation of VN2 by multiplication with VA. This assumes that the dead spaces of O2, CO2 and N2 are identical within the clinical range of expired volume, which is supported by the findings in [20, 21]. Likewise, it is assumed that the ΔFIO2 equals the calculated ΔFETN2 and ΔFAN2. Furthermore, FETO2 and FETCO2 measurements are used to approximate FAO2 and FACO2 although there is evidence to the contrary in the case of FETCO2 [22, 23]. Typically, the FETCO2 will be lower than FACO2 and FETO2 will be higher than FAO2 due to imperfect mixing and alveolar dead space. These differences partially compensate each other in calculation of FETN2.
Fixed VTIand VTEin Equation10vs. variable VTIand VTEin Equation9. The modified MBNW method incorporates breath-by-breath measurement and calculation of VATI, and VATE allowing for variation of tidal volumes during the washout. In the step response derivation these volumes are assumed to be constant. The discrepancy becomes obvious when examining FRC measurements performed during spontaneous ventilation where breath-to-breath variation of inspiratory and expiratory tidal volumes in quiet breathing typically amounted to 50–100 mL during the washout procedure. The potential of using λ from the step response solution of the difference equation to classify lung pathologies applies more to mechanical ventilation where the volumes are constant.
Mono- vs. multiexponential washout. Washout was clearly not monoexponential in the case of emphysematous (COPD) lung with compartments of differing mechanical properties. A better curve fit was accomplished by a biexponential equation, which in the framework of DSP translates into a second order difference equation. The modified MBNW method based on a first order difference equation, however, will still be able to calculate the FRC given the measurement period is extended to allow for slow compartments to empty in the case of COPD lungs. The first order difference equation solution to a step input assumes that washout is monoexponential and deviations from this will cause increased lack of agreement between measured and calculated values. This was demonstrated in the fitting of washout data to a mono- vs. a biexponential equation in the case of the COPD/ICU and the perioperative bariatric patient.
Conclusion
We have presented a modified MBNW method in terms of a first order difference equation which was solved for the step response of FETN2 to a step change in FIO2. The step response prediction of FETN2 was validated under experimental and clinical conditions. We found excellent agreement between measured and calculated values of FETN2. A central concept of the step response equation, the eigenvalue, showed different values in healthy and diseased lungs. The MBNW difference equation has some interesting implications for the roles of serial and parallel dead spaces. The step response equation opens up research avenues within digital signal processing and the characterization of ventilatory states.
Acknowledgements
The authors are indebted to Robert Q. Tham, MS, PhD, GE Healthcare, Madison, Wisconsin for constructive comments to early drafts of the manuscript, to Professor Paul Myles, Department of Anaesthesia and Perioperative Medicine, Alfred Hospital Melbourne for advice on Bland & Altman analysis and to Cecilia Olegård, MD, Department of Anaesthesia and Intensive Care, Sahlgrenska University Hospital, Gothenburg for providing examples of patient and volunteer FRC recordings.
Appendix A
The derivation of the step response solution is as follows. In Equation (8), define the step response as 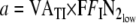 for n ≥ 0, e VATE + FRC, b = FRC,
for n ≥ 0, e VATE + FRC, b = FRC, 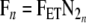 and the initial condition as FETinitN2: Utilizing a substitution technique:
and the initial condition as FETinitN2: Utilizing a substitution technique:
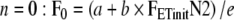 |
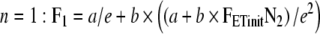 |
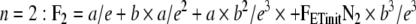 |
In general,
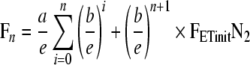 |
Let λ = b/e and Equation 13 simplifies into:
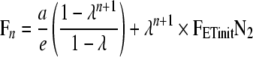 |
Substitute back to the original variables:
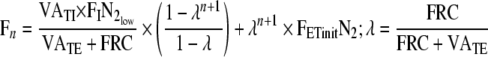 |
Footnotes
Bland & Altman analysis is utilized in spite of the methods, measured and calculated values of FETN2, are not independent but mathematically linked.
The ‘baby lung’ concept requires the strain to be calculated at FRC without PEEP (ZEEP).
Conflict of interest: Gary Choncholas and Erkki Heinonen are employees in the company implementing the FRC algorithm in a critical care ventilator. Soren Sondergaard has lectured for and received economic support from the same company.
Choncholas G, Sondergaard S, Heinonen E. Validation and clinical application of a first order step response equation for nitrogen clearance during FRC measurement.
References
- 1.Darling RC, Cournand A, Richards DW. Studies on the intrapulmonary mixture of gases. III. An open circuit method for measuring residual air. J Clin Invest. 1940;19:609–618. doi: 10.1172/JCI101163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lilly JC. Mixing of gases within respiratory system with a new type nitrogen meter. Am J Physiol. 1950;161:342–351. doi: 10.1152/ajplegacy.1950.161.2.342. [DOI] [PubMed] [Google Scholar]
- 3.Robertson JS, Siri WE, Jones HB. Lung ventilation patterns determined by analysis of nitrogen elimination rates; use of mass spectrometer as a continuous gas analyzer. J Clin Invest. 1950;29:577–590. doi: 10.1172/JCI102295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wolfe WA, Carlson LD. Studies of pulmonary capacity and mixing with the nitrogen meter. J Clin Invest. 1950;29:1568–1575. doi: 10.1172/JCI102398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wrigge H, Sydow M, Zinserling J, Neumann P, Hinz J, Burchardi H. Determination of functional residual capacity (FRC) by multibreath nitrogen washout in a lung model and in mechanically ventilated patients. Accuracy depends on continuous dynamic compensation for changes of gas sampling delay time. Intensive Care Med. 1998;24:487–493. doi: 10.1007/s001340050601. [DOI] [PubMed] [Google Scholar]
- 6.Darling RC, Cournand A, Richards DW, Domanski B. Studies on intrapulmonary mixture of gases. V. Forms of inadequate ventilation in normal and emphysematous lungs, analyzed by means of breathing pure oxygen. J Clin Invest. 1944;23:55–67. doi: 10.1172/JCI101473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Fowler WS, Cornish ER, Jr., Kety SS. Lung function studies. VIII. Analysis of alveolar ventilation by pulmonary N2 clearance curves. J Clin Invest. 1952;31:40–50. doi: 10.1172/JCI102575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wagner PD. Information content of the multibreath nitrogen washout. J Appl Physiol. 1979;46:579–587. doi: 10.1152/jappl.1979.46.3.579. [DOI] [PubMed] [Google Scholar]
- 9.Wauer HJ, Lorenz BA, Kox WJ. FRC measurement in intensive care patients. A definition of standards. Anaesthesist. 1998;47:844–855. doi: 10.1007/s001010050634. [DOI] [PubMed] [Google Scholar]
- 10.Olegard C, Sondergaard S, Houltz E, Lundin S, Stenqvist O. Estimation of functional residual capacity at the bedside using standard monitoring equipment: a modified nitrogen washout/washin technique requiring a small change of the inspired oxygen fraction. Anesth Analg. 2005;101:206–212. doi: 10.1213/01.ANE.0000165823.90368.55. [DOI] [PubMed] [Google Scholar]
- 11.Oppenheim AV, Schafer RW. Discrete-time signal processing. Englewood Cliffs, N.J.: Prentice Hall, 1989: p. xv, 879 p.
- 12.Frayn KN. Calculation of substrate oxidation rates in vivo from gaseous exchange. J Appl Physiol. 1983;55:628–634. doi: 10.1152/jappl.1983.55.2.628. [DOI] [PubMed] [Google Scholar]
- 13.Stenqvist O, Sonander H, Lofstrom B, Nilsson K. An oxygen-consuming model lung for evaluation of anaesthetic circuits. Acta Anaesthesiol Scand. 1982;26:322–326. doi: 10.1111/j.1399-6576.1982.tb01774.x. [DOI] [PubMed] [Google Scholar]
- 14.Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res. 1999;8:135–160. doi: 10.1191/096228099673819272. [DOI] [PubMed] [Google Scholar]
- 15.Bendjelid K, Schutz N, Suter PM, Romand JA. Continuous cardiac output monitoring after cardiopulmonary bypass: a comparison with bolus thermodilution measurement. Intensive Care Med. 2006;32:919–922. doi: 10.1007/s00134-006-0161-2. [DOI] [PubMed] [Google Scholar]
- 16.Rossing RG, Danford MB. A comparison of continuous distributions of parameters of exponential decay curves. Biometrics. 1968;24:117–134. doi: 10.2307/2528464. [DOI] [PubMed] [Google Scholar]
- 17.Gattinoni L, Pesenti A. The concept of “baby lung”. Intensive Care Med. 2005;31:776–784. doi: 10.1007/s00134-005-2627-z. [DOI] [PubMed] [Google Scholar]
- 18.Anderson D, Nagasawa G, Norfleet W, Olszowka A, Lundgren C. O2 pressures between 0.12 and 2.5 atm abs, circulatory function, and N2 elimination. Undersea Biomed Res. 1991;18:279–292. [PubMed] [Google Scholar]
- 19.Ruppel G. Manual of pulmonary function testing. St. Louis: Mosby, 1998: p. xii, 365 p.
- 20.Bartels J, Severinghaus JW, Forster RE, Briscoe WA, Bates DV. The respiratory dead space measured by single breath analysis of oxygen, carbon dioxide, nitrogen or helium. J Clin Invest. 1954;33:41–48. doi: 10.1172/JCI102868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Saidel GM, Lin JS. Transport abnormalities from single-breath dynamics of Ar, CO2 and O2. Respir Physiol. 1986;64:253–266. doi: 10.1016/0034-5687(86)90119-2. [DOI] [PubMed] [Google Scholar]
- 22.Giannella-Neto A, Paoletti P, Fornai E, Giuntini C. Estimates of mean alveolar gas in patients with chronic airways obstruction. Eur Respir J. 1989;2:451–460. [PubMed] [Google Scholar]
- 23.Koulouris NG, Latsi P, Dimitroulis J, Jordanoglou B, Gaga M, Jordanoglou J. Noninvasive measurement of mean alveolar carbon dioxide tension and Bohr’s dead space during tidal breathing. Eur Respir J. 2001;17:1167–1174. doi: 10.1183/09031936.01.00063301. [DOI] [PubMed] [Google Scholar]


