Intra-household work time synchronization

Abstract

If partners derive utility from joint leisure time, it is expected that they will coordinate their work schedules in order to increase the amount of joint leisure. In order to control for differences in constraints and selection effects, this paper uses a new matching procedure, providing answers to the following questions: (1) Do partners coordinate their work schedules and does this result in work time synchronization?; (2) which partners synchronize more work hours?; and (3) is there a preference for togetherness? We find that coordination results in more synchronized work hours. The presence of children in the household is the main cause why some partners synchronize their work times less than other partners. Finally, partners coordinate their work schedules in order to have more joint leisure time, which is evidence for togetherness preferences.

1 Introduction

The benefits of marriage that are usually stressed by economic theory are the possibility of joint consumption of household goods and the gains of division of labor. It is, however, likely that individuals do not only derive utility from marriage because of these material benefits alone. They might also derive utility from spending leisure time together. If this is the case, it can be hypothesized that it pays off for married or co-habiting individuals to synchronize their work hours, assuming that individuals within a household can coordinate their work schedules. This paper contributes to the existing models of time allocation by considering synchronization of work times instead of the work time quantities and by examining couples preferences for togetherness.

In traditional time allocation models individuals maximize their utility by choosing an optimal time allocation scheme given a budget and a time constraint.1 These models focuss on choosing the optimal quantities of market work, household work and leisure time. If couples derive utility from spending leisure time together then it is important not only to consider the time quantities, but also the timing of certain activities. In other words, the amount of market work and timing of market work are interdependent. This makes the utility maximization problem more difficult and also influences labor supply decisions.

There is empirical evidence that parents prefer to spend joint leisure time with there children (see Hallberg & Klevmarken, 2003). When parents synchronize their work times better, they are able to spend more joint leisure time with their children as a family. On the other hand, having young children influences the degree of work time synchronization negatively (see Hallberg 2003; Hamermesh, 2000; Van Velzen, 2001). Since paid child care is expensive it pays off for parents to de-synchronize their work times, because by caring themselves the cost of child care are reduced. Suppose that each parent first chooses a fixed amount of work hours and then chooses a work time schedule. Making paid child care more available at a lower price might result in less de-synchronized work times, resulting in more joint leisure time while labor supply remains constant.

Although many papers examine what influences the amount of work hours that individuals work on the market, relatively few papers consider the timing of market work hours. Furthermore, there are relatively few papers that simulate a control group in order to control for differences in constraints between households and selection effects such that solely the coordination effect on work timing is examined. Hamermesh (1996, 2000) was among the first who paid attention to the extent to which couples synchronize their work times. In Hamermesh (2000) each non-single male is replaced with a randomly selected non-single male and each non-single female with a randomly selected non-single female thereby generating random couples. Comparing the work time overlap2 between the real couples and the generated random couples he finds that the real couples synchronize their work hours to allow for joint leisure more than the generated random couples.

Jenkins and Osberg (2005) and Hallberg (2003) test if partners coordinate their work schedules and as a result synchronize their work times. Jenkins and Osberg replace each non-single male with a single male with similar characteristics and each non-single female with a single female with similar characteristics.3 Comparing the work time overlap of the matched singles with the real couples they find that real couples have about 5 percent more work time overlap. Hallberg (2003) matches a single male and a single female into a pseudo couple and then matches this pseudo couple to a real couple conditioned on certain personal characteristics following a matching algorithm of Rubin (1979) which uses mahalanobis distances. A matched single can be regarded as the nearest neighbor of the non-single given the singles sample. Comparing the work timing of the pseudocouples with the real-couples, Hallberg (2003) finds evidence of coordination on synchronous work times and finds that market work and leisure timing are intrahousehold dependent.

It can be questioned however, if constraints imposed by society are indeed the same for singles and couples. If singles face different constraints imposed by society then it might be that the observed difference of work time overlap is due to differences in constraints. For example, living expenses are relatively higher for singles. Furthermore, singles do not have the possibility to gain from division of labor or have other benefits from living together. Another point that can be made is that singles with (young) children are a rather specific group. Their time allocation choices are likely to be different compared non-single individuals.

It can be argued that there is a selection problem. Individuals who have more synchronized work times (and therefore more synchronized leisure time) have a higher probability of meeting each other. In this case, finding a significant higher work time overlap might be the consequence of a selection effect. It is also possible that singles synchronize work time with other singles. If they are in search for a partner they synchronize their time with other singles in the same social group. Nonsingles already have a partner and therefore might not synchronize their work times to the same extent. Finding a significant lower work time overlap might then also be the consequence of a selection effect.

The outline of this paper is as follows. First, we test if there is work time synchronization by using a matching strategy where couples are first matched to other couples and then switch partners. The couples that remain after the partner-switch are referred to as pseudo couples. Comparing the work time overlap between the real couples and the pseudo couples reveals whether partners coordinate their work schedules and whether coordination results in more synchronized work hours. Furthermore, we examine why some couples are better in coordinating their work times compared to other couples.

Second, we examine if there is a preference for togetherness. Partners who coordinate their work schedules have more potential joint leisure time. Better coordination of work schedules and preference for togetherness should then result in more joint leisure time.

The paper is organized as follows. Section 2 presents a theoretical time allocation model. Section 3 describes the data that are used. Section 4 proposes a matching strategy where couples are matched to other couples. Section 5 examines, first, if there is a synchronization effect, which can be attributed to active coordination of couples. This section also examines why some couples synchronize their work times more than other couples do. Section 6 studies if there is a preference for togetherness. Finally Sect. 7 concludes.

2 Time allocation model

Consider a two-person household where individuals within the household allocate their time to market work or to leisure time.4 A time period T is defined, which can be a day or a week, and it is assumed that this time period is divided in equal time units t. For simplicity T can be defined as one day, and one time unit can be defined as one hour.

If both individuals within the household allocate their tth hour to leisure then this tth hour is considered as joint leisure time. All other allocation choices of both individuals will not result in joint leisure time. The possible leisure timing allocation schemes for all units t is then represented as:

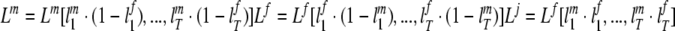where l^s_t indicates one if individual s consumes leisure at the tth hour and zero otherwise, for s = m(ales), f(emales). Note that L^s is leisure time that is spent alone. The maximization problem of the household can now be described as:

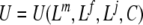subject to the following constraint:

Where C is consumption and w_st is the wage rate of individual s of hour t. Wage rates are assumed to be exogenous and may vary over time. Partners maximize the household utility function subject to Eq. 3.

Individuals will choose paid work at hour t if the market wage is higher than the reservation wage for that particular hour. However, the reservation wage is not only determined by preferences to consume market goods but also by preferences to spend leisure time together. The first component has to do with the quantity of leisure time, while the second component has to do with the timing of market work. Furthermore, the model shows that the optimal amount of joint leisure time is influenced by the timing strategy of both partners and also by the time and budget constraints.

3 General data information

In November 2001, a Dutch survey was held named the ‘The Condition of the Country’. This survey was the initiative of the Research Institute SCHOLAR of the University of Amsterdam (Schooling, Labor Market and Economic Development) and conducted by the Netherlands Press Association, a coordinating institute for regional newspapers. The total number of subscriptions is about 1.7 million, equally spread over the Netherlands. The questionnaire contains information on market work, household work, and child care for both partners simultaneously. Moreover, there is information about the financial situation, health, education, training, career and social environment. Finally, there is a wide spectrum of attitude questions with respect to work, political and life events and measures of individual well being. We have data on 3,074 couples.

The following work timing question was posed to respondents and their partner if they had one:

“At what time do you normally start (end) working?”

Respondents could answer this question accurately to the minute. Using this work timing question it is possible to generate an ‘overlap’ variable for individuals who are married or co-habiting:

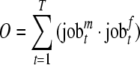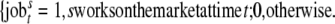Where O represents the work time overlap variable and job^s_t represents if, respectively, the male or female works on the market at time t. For reasons of simplicity we converted this variable into one that is measured in hours with a precision of 2 decimals.

4 Matching procedure and descriptive statistics

In this section we propose a matching strategy where each (real) couple is first matched to another couple from the sample based on certain characteristics. The matched couples are referred to as simulated real couples (SRC). Then couples switch partners and the couples that remain after the partner switch are referred to as pseudo couples. Comparing the work time overlap between the real couples and the pseudo couples gives information on whether partners coordinate their work schedules and whether coordination result in more synchronized work hours.

This matching method has advantages over the matching methods used in Jenkins and Osberg (2005) and Hallberg (2003). First the selection effect is less of a problem, since the partners of the real couples and matched couples are married or living together and have the same amount of work time overlap. Furthermore, the constraints imposed by society are similar for couples and matched couples when the individuals of the couple and matched couple have about the same personal characteristics.

Consider a couple where the individuals of the couple are denoted by M_i and F_i. Conditioned on personal characteristics couple {M_i;F_i} is matched to another couple {M_j;F_j}, which we will refer to as simulated real couple (SRC).5 Then both couples switch partners so that we have two new couples, {M_j;F_i} and {M_i;F_j}, which we will refer to as pseudo couples (PC1 and PC2)

All four couples face the same constraints imposed by society but there is coordination between the individuals of the real couple and the simulated real couple while there is no coordination between the individuals of the pseudo couples. In order to test the work time synchronization hypotheses we do the following:

1. Compare the timing of market work {M_i;F_i} and {M_j;F_j} and find no significant difference in the timing of market work.

2. Compare the timing of market work of, respectively, {M_i;F_i} and {M_j;F_j} with the possible pseudo couples, i.e. {M_i;F_j} and {M_j;F_i} and find a significant difference in the timing of market work.

Comparing the timing of market work between {M_i;F_i} And {M_j;F_j} gives more information regarding the quality of the match. Finding a significant difference in the timing of market work between, respectively, {M_i;F_i} and {M_j;F_j} with both pseudo couples is then empirical support for work time overlap between the individuals of a household due to coordination (a more elaborate explanation is given in Appendix).

When households are matched to other households this happens on the basis of an identification number. First each household receives an identification number based on characteristics of the household members. The following personal characteristics are used as matching variables:

1. Education level in three categories (low, middle and high).

2. Age in three categories (18–35; 35–50 and 50–65).

3. Having children who are living at homes (dummy)

4. The number of individuals living in the respondents community measured on a five point scale (<5,000; 5,000–20,000; 20,000–50,000; 50,000–100,000; >100,000).

5. Work hours in 22 categories, so that each couple should work approximately the same amount of hours on the market (we defined >21 h as one category).

Exact matching of couples based on these personal characteristics gives 449 unique groups containing information of 1,772 couples. It is possible that some groups contain more than two couples since there is more than one exact match for a certain couple. In this case a couple is randomly drawn from that group with equal probability given that the couple that is drawn is not the real couple itself.

The descriptive statistics of the real couples and the simulated real couples are shown in Table 1. The simulated real couples have about similar descriptive statistics compared to the real couples. The differences in means in Table 1 between the simulated real couples and the real couples are not significant. Although a child-dummy variable was used to match couples, Table 1 shows that the number of children between certain age levels are very similar. The individuals of the real couples and the simulated real couples have about the same personal characteristics and hence the constraints imposed by society is considered to be the same for these couples.

Table 1.

Descriptive Statistics of the one-to-one matched couples

	Real couples			SRC
	N	Mean	SD	N	Mean	SD
Age of male	1,758	43.412	9.607	1,758	43.462	9.601
Education level male	1,758	6.047	1.810	1,758	6.065	1.805
No. of children between 0 and 4	1,758	.157	.798	1,758	.144	.750
No. of children between 4 and 12	1,758	.378	1.310	1,758	.374	1.250
No. of children between 12 and 18	1,758	.376	1.925	1,758	.351	1.795
Work hours male	1,758	8.929	.646	1,758	8.923	.647
Living area male	1,758	2.078	.814	1,758	2.078	.814
Age of female	1,758	42.258	9.629	1,758	42.230	9.592
Education level female	1,758	5.660	1.885	1,758	5.642	1.880
No. of children between 0 and 4	1,758	.157	.798	1,758	.144	.750
No. of children between 4 and 12	1,758	.378	1.310	1,758	.374	1.250
No. of children between 12 and 18	1,758	.376	1.925	1,758	.351	1.795
Work hours female	1,758	7.855	1,7587	1,758	7.850	1.756
Living area female	1,758	2.078	.814	1,758	2.078	.814

5 Empirical results

5.1 Do partners coordinate their work schedules?

Before comparing the work time overlap between the real couples and the pseudo couples we should compare the work time overlap of the real couples with that of the simulated real couples. A t-test which compares the work time overlap of both real couples can be regarded as a simulation quality test. If the descriptive statistics are very similar but the difference in work time overlap turns out to be significantly different from zero, this indicates that the simulated real couples are not ‘good quality’ look alikes. Table 2 indicates that real couples and simulated couples have on average the same amount of work time overlap, which indicates that the simulated real couples are good quality look alikes.

Table 2.

T-test overlap difference—matching real couples with simulated real couples

	Real couples	Simulated real couples	Difference
Mean	7.375	7.393	−.017
SE of mean	.047	.047	.036
SD of mean	1.997	1.970	1.529
number of observations	1,772	1,772	1,772

Note:^* Significant at 10% level, ^** Significant at 5% level, ^*** significant at 1% level

Tables 3 and 4 show the t-test results where the mean work time overlap of the real couples and simulated real couples is compared to that of the pseudo couples (PC1 and PC2). Both tables indicate that the pseudo couples have significantly less work time overlap compared to the real couples and simulated real couples. The difference in work time overlap averaged 0.092 h over all matches, which is about 5.5 min each day.6

Table 3.

Test if mean work time overlap between the real couples and psuedo couples is different

	Compare overlap variable with PC1			Compare overlap variable with PC2
	Real couples	PC1	Difference	Real couples PC2	PC2	Difference
Mean	7.375	7.286	.089	7.375	7.299	.076
SE of mean	.047	.047	.018***	.047	.046	.032**
SD of mean	1.997	1.967	.763	1.997	1.936	1.355
Number of observations	1,772	1,772	1,772	1,772	1,772	1,772

Note:^* Significant at 10% level, ^** Significant at 5% level, ^*** Significant at 1% level

Table 4.

Test if mean work time overlap between the simulated real couples and the pseudo cosples is different

	Compare overlap variable with PC1			Compare overlap variable with PC2
	Simulated real PC1 couples	PC1	Difference	Simulated real couples	PC 2	Difference
Mean	7.393	7.286	.107	7.393	7.299	.093
SE of mean	.047	.047	.033***	.047	.046	.018***
SD of mean	1.970	1.967	1.373	1.970	1.936	.768
Number of observations	1,772	1,772	1,772	1,772	1,772	1,772

Note:^*Significant at 10% level. ^** Significant at 5% level. ^*** Significant at 1% level

The significant higher work time overlap for the real couples and simulated real couples compared to the pseudo couples can be regarded as the result of work time synchronization due to coordination. Our findings are in line with the findings of Jenkins and Osberg (2005) and Hallberg (2003), although the synchronization effect is smaller.

5.2 Which partners synchronize more work hours?

Although we find that partners on average coordinate their work time it is possible that partners of certain ‘types’ of households will coordinate their work schedules differently compared to other ‘types’ of households. It is, for example, possible that partners coordinate their work schedules such that their work hours are de-synchronized. Consider a couple with a young child and suppose that this couple tries to maximize the amount of hours that their child spend with at least one of the parents. In this case coordinating work schedules can result in de-synchronization behavior of work times. So instead of performing a t-test for the whole sample, it is informative to perform a t-test for sub-groups.

Table 5 shows the t-test results for sub-groups which can be seen as dif-in-dif estimation results. The first column indicates the characteristic on which the t-test is based, like for example if there are children present in the household between 0 and 4. We refer to this group as treatment group for notational convenience. The non-treated are then those households where there are no children present between 0 and 4 and the treated are those households where there are children present between 0 and 4. For both the treated and the non-treated we can perform a t-test that compares how much the work time overlap differs compared to the control group. Note, that in this section we refer to a control group, treated households and non-treated households, which can be confusing. The control group for each household is defined as the average work time overlap of both Pseudo Couples. The treated households are those households that have a certain characteristic. Given a certain treatment, it holds that we can still refer to a control group for both the treated and non-treated.

Table 5.

T-tests using treatment groups

Treatment	Non-treated		treated
	No. of obs.	DNT	No. of obs.	DT
Children between 0 and 4	1,601	.084***	171	.066
Children between 4 and 121,42	1,423	.095***	349	.033
Children between 12 and 18	1,473	.093***	299	.030
Education male low	1,489	.078***	283	.111*
Education male med.	1,289	.085***	483	.075*
Education male high	766	.088**	1006	.078***
Education female low	1,395	.082***	377	.083**
Education female med.	1,189	.083***	583	.082**
Education female high	960	.082***	812	.083***
Age male 1,772 35	1,334	.069**	438	.125***
35 < Age male < 50	902	.098***	870	.066**
50 < Age male < 65	1,308	.086***	464	.072*
Age female < 35	1,293	.067**	479	.124***
35 < Age female < 50	883	.100***	889	.066**
50 < Age female < 65	1,368	.086***	404	.071*
Household income low	1,195	.101***	577	.044
Household income med.	1,194	.100***	578	.047
Household income high	1,155	.045*	617	.153***

Note:^* Significant at 10% level, ^** Significant at 5% level, ^*** Significant at 1% level

The information given in Table 5 is twofold. First, it shows if households that have the opportunity to coordinate their work schedules, synchronize their work hours better compared to households that do not have the opportunity to coordinate their work schedules. Second, it shows if certain households coordinate their work schedules better than others given certain characteristics.

Table 5 shows that couples without children coordinate their work schedules which results in more work time overlap compared to the control group. For couples with children this is not found. These findings are in line with research by Hamermesh (2000), Hallberg (2003) and Van Velzen (2001). However, although we do find that children negatively influences the degree of work time synchronization, we find no empirical evidence that couples with children coordinate their work schedules such that their work hours are de-synchronized.

Partners in all education levels coordinate their work schedules resulting in more work time overlap. The level of education does not seem to influence the extent to which this happens.

Partners in all age groups tend to synchronize their work hours, but the effect is strongest for households where one of the two partners is, or both partners are, younger than 35. This is surprising since these types of household are most likely to have young children present in the household. One can reason that young individuals at the beginning of their careers are looking for a job that best suits them and are therefore possible job hoppers. In this choice process they might also include the timing of work.

Household income matters, but only for those households who are in the highest income category. Partners with a high household income coordinate their work schedules and have three times as much work time overlap compared to partners who have a low or medium household income. High income households can afford more hours of (in)formal child care than low income households leading to more synchronized work schedules.

In general Table 5 indicates that the possibility of coordination will result in more work time overlap. The absence of children and being in the highest income category seems to be the main cause of why some partners synchronize their work times substantially more compared to others.

6 Is their a preference for togetherness?

Although the estimation results suggest that partners coordinate their work schedules, this does not imply that they have a preference for togetherness. It is still possible that the small amount of time that is synchronized is not spent with the partner, but is spent on activities without the partner. In order to see if there is a preference for togetherness we examine if coordination of work schedules influences the amount of time that partners are together.

First, we will estimate the following equation by mean of OLS:

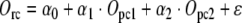where O stands for work time overlap of, respectively, the real couple and the two pseudo couples. The difference between the real couple and the pseudo couples is that the partners of the real couples can coordinate their work schedules. Therefore the variation in O_rc caused by coordination of work schedules is captured by ε. We then obtain ε and estimate the following equation using OLS:

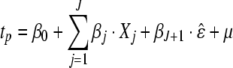The left hand side variable is the number of hours that partners spend with each other during an average day. This variable is regressed on certain personal or households characteristics and the ^ε term. The characteristics that are used are age, education level, having children between certain age levels, making use of child care and how satisfied the respondent is with the relationship.7 The satisfaction level with the relationship is a subjective measure where respondents are asked to report how satisfied they are with their relationship on a one to ten scale. The estimation results are shown in Table 6.

Table 6.

Togetherness estimates

Variable	gB	t-value
ln agemale	−.739	−.920
ln agefemale	.233	.300
ln edumale	−.518	−3.530
ln edufemale	.105	.710
No children present	.371	2.810
Child present between 0 and 4	−.014	−.170
Child present between 4 and 12	−.048	−.940
Child present between 12 and 18	−.013	−.500
Making use of child care	−.521	−2.720
Sat. with partner	.154	2.060
^ε	.198	2.280
Constant	4.334	3.910
R-squared	.0649
No. of obs.	982

Unfortunately, there is a drop in the number of observations. This is caused by the fact that many partners did not answer the question how many hours they spend with their partner on a normal day in the week.

The children effect and the effect of the education level of the female and the effect of satisfaction level with the partner are not surprising. The presence of children has a negative influence on the joint leisure time of parents which is also found by Hamermesh (2000), Hallberg (2003) and Van Velzen (2001). Higher educated females tend to work more job hours and this constrains the number of hours that both partners can spend together. Partners that are more satisfied with their relationship derive more utility from spending time together and hence these partners spend more time together than partners who are less satisfied.

The ^ε term is also significant and has a coefficient of .198. This means that if partners coordinate their work schedules and as a consequence synchronize their work times one hour more, this will result in 0.198 h more joint leisure time. This empirical result can be seen as evidence for the preference of togetherness.

7 Conclusion

If couples derive utility from spending leisure time together, it is expected that these couples will coordinate their work schedules in order to increase the amount of joint leisure time.

Hamermesh (2000), Jenkins and Osberg (2005) and Hallberg (2003) find empirical evidence that couples synchronize leisure by adjusting their working schedules, timing of household work and leisure. They adopt a simulation method where singles are matched to non-singles and assume that the constraints imposed by society are similar for singles and non-singles.

It is likely that singles face different constraints than non-singles do. As economic theory suggests, there are economies of scale to marriage or to living together. Furthermore, if singles are matched to non-singles then the significant higher work time overlap might be the consequence of a selection effect. Hence, it is not possible to identify if a significant higher work time overlap is due to the difference in constraint imposed by society, due to a selection effect or is the consequence of coordination of work schedules.

This paper answers three questions: First, do partners coordinate their work schedules leading to increased synchronization? Second, which partners synchronize more work hours? Finally, is there a preference for togetherness?

We propose a matching strategy where couples are first matched to other couples and then switch partners. Then we compare the work time overlap of the two couples before the partner switch with the work time overlap of the two couples after the partner switch. In this case the selection effect diminishes since both real couples are married or living together and have the same amount of work hours overlap. Furthermore, the constraints imposed by society are similar, since the individuals of the real couples and the simulated real couples have about the same personal characteristics, are all married or living together and have about the same work time overlap.

There is empirical support for market work synchronization in the Netherlands. Although the effect is small, we find that pseudo couples have significantly less work time overlap compared to real couples of about 5.5 min per working day. The small effect can be partly due to fact that in this paper it is assumed that partners coordinate their work schedules in order to synchronize their work hours each day. However, it might be the case that partners synchronize their work times in a week dimension. It is for example possible that partners choose to work 36 h per week, and divide these hours over 4 days instead of the usual 5. This would give them one extra non-labor day.

In general we find that the possibility of coordination will result in more work time overlap. It is likely that children have the effect of desynchronizing work schedules while synchronization of work schedules may be the rule in the absence of children.

Again notice that the assumption that partners synchronize their work times in a day dimension can be crucial. Consider again the two partners that decide to work four days per week instead of 5 and assume that they have a young child. What will they do with there extra non-labor day? Do they de-synchronize that day in order to take care of the children. Do they synchronize that work day in order to spend time together with their child?

The empirical results show that individuals tend to coordinate their work schedules in order to spend more time with each other, which is evidence for togetherness preferences. If partners coordinate their work schedules and as a consequence synchronize their work times one hour more, this will result in 0.198 h more joint leisure time. The preference for togetherness and having children have a opposing effect on work timing.

For further research it is interesting to relax the assumption that partners synchronize their work times each day. The synchronization effect is likely to be larger if we allow for the fact that partners might synchronize their work times each week or even each month. Furthermore, it is important to focus more on the trade-off between the preference for togetherness and how children affect work timing, since this influences labor supply decisions.

1,2,3,4,5,6,7

Appendix

This appendix shows that it is necessary to simulate one couple that is very similar to the real couple from the total sample of real couples. Simulating one couple rather similar to the real couple enables us to generate two pseudo couple outcomes and two real couple outcomes for each household.

Consider a couple in our sample where the individuals of the couple are denoted by M_i and F_i. Conditional on personal characteristics M_i is matched to another male drawn from the sample M_−i. F_i is matched to another female drawn from the sample F_−i. The simulated male and female are denoted by M_js and F_ks and together they are considered to be a pseudo couple.8

To give a simple example, suppose that we condition merely on the education level of males and females, which is measured on a 1 to 8 point scale. Suppose furthermore that there are three households with education levels [E_m, E_f]:

Household	Emale	Efemale
A	8	7
B	6	5
C	6	5

Household A will now receive identification number 87 while household B and C receive identification number 65. Therefore, based on education level household B and C can be matched. Note that this method requires that there is be an exact match between the two households.

The simulated situation can be graphically illustrated as follows:

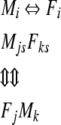The arrows indicate that there is interaction (communication or coordination) between two individuals. If we would like to test that synchronization of leisure time results from coordination between two individuals, at least to some extent, then comparing the possible joint leisure time between (M_i; F_i) and (M_js; F_ks) is not sufficient. This is shown by the following steps:9

1. There is coordination between M_i and F_i

2. There is no coordination between M_js and F_ks

3. M_js interacts with F_j and F_ks interacts with M_ks.

4. Assume for simplicity that M_k = M_i.

5. • Case 1: F_j has different personal characteristics than F_i
   • Case 2: F_j has similar personal characteristics than F_i
6. Suppose case 1 holds and a positive significant difference is observed in the timing of work between (M_i; F_i) and (M_js; F_ks). This positive significant difference can be caused by

   1. Coordination between M_i and F_i
   2. Coordination between M_js and F_j
   3. Difference personal characteristics of F_j and F_i. Due to this difference the two couples ((M_js;F_j) and (M_i;F_i)) are facing different constraints imposed by society.
7. Suppose case 2 holds and a positive significant difference is observed in the timing of work between (M_i;F_i) and (M_js;F_ks). This positive significant difference can be caused by

   1. Coordination between M_i and F_i
   2. Coordination between M_js and F_j
8. Empirical support for work time synchronization is then found if:

   1. Comparing timing of market work (M_i;F_i) and (M_js;F_j) and finding no significant difference in the timing of market work.
   2. Comparing timing of market work of, respectively, (M_i;F_i) and (M_js;F_j) with the possible pseudo couples, i.e. (M_i;F_j) and (M_js;F_i). Finding that real couples time their market work better compared to the pseudo couples, in the sense that there is significantly more overlap.