Efficient Constrained Local Model Fitting for Non-Rigid Face Alignment

Abstract

Active appearance models (AAMs) have demonstrated great utility when being employed for non-rigid face alignment/tracking. The “simultaneous” algorithm for fitting an AAM achieves good non-rigid face registration performance, but has poor real time performance (2-3 fps). The “project-out” algorithm for fitting an AAM achieves faster than real time performance (> 200 fps) but suffers from poor generic alignment performance. In this paper we introduce an extension to a discriminative method for non-rigid face registration/tracking referred to as a constrained local model (CLM). Our proposed method is able to achieve superior performance to the “simultaneous” AAM algorithm along with real time fitting speeds (35 fps). We improve upon the canonical CLM formulation, to gain this performance, in a number of ways by employing: (i) linear SVMs as patch-experts, (ii) a simplified optimization criteria, and (iii) a composite rather than additive warp update step. Most notably, our simplified optimization criteria for fitting the CLM divides the problem of finding a single complex registration/warp displacement into that of finding N simple warp displacements. From these N simple warp displacements, a single complex warp displacement is estimated using a weighted least-squares constraint. Another major advantage of this simplified optimization lends from its ability to be parallelized, a step which we also theoretically explore in this paper. We refer to our approach for fitting the CLM as the “exhaustive local search” (ELS) algorithm. Experiments were conducted on the CMU Multi-PIE database.

1 Introduction

The successful automatic registration and tracking of non-rigidly varying geometric landmarks on face is a key ingredient to the analysis of human spontaneous behaviour. Until recently, popular approaches for accurate non-rigid facial registration and tracking have centered upon inverting a synthesis model (or in machine learning terms a generative model) of how faces can vary in terms of shape and appearance. As a result, the ability of such approaches to register an unseen face image is intrinsically linked to how well the synthesis model can reconstruct the face image. Perhaps the most well known application of inverting a synthesis model for non-rigid face registration can be found in the active appearance model (AAM) work first proposed by Cootes and Edwards [10]. Other closely related methods can be found in the morphable models work of Blanz and Vetter [5]. AAMs have since gone on to become the defacto standard in non-rigid face alignment/tracking [7,11,14].

Unfortunately, from a registration/tracking perspective AAMs have inherent problems when attempting to fit generically to face images. This problem can be directly attributed to the balance both models need to find in terms of their representational power (i.e., the models ability to synthesize face images). If the representational power is too constrained the method can do a good job on a small population of faces, but cannot synthesize faces outside that population. On the other hand, if the representational power is too unconstrained, the model can easily synthesize all faces but can also synthesize other non-face objects. Finding a suitable balance between these two extremes in a computationally tractable manner has not been easily attained through an invertible synthesis paradigm. A good review on this problem can be found in [11].

Recently, a novel approach for non-rigid face registration/tracking was proposed by Cristinacce and Cootes [9] referred to as a constrained local model (CLM). CLMs are considered close cousins to Active Shape Models (ASMs) [8] another popular method for non-rigid face registration (see Section 1.1 for clarification on their differences). CLMs attempt to abandon the direct link made between non-rigid face synthesis and registration in methods like AAMs. A CLM is able to register a non-rigid object through the application of an ensemble of patch/region experts to local search regions within the source image being registered. Given an appropriate non-rigid shape prior for the object, the response surfaces from these local regions are then employed within a joint optimization process to estimate the global non-rigid shape of the object. A major advantage of CLMs over conventional methods for non-rigid registration such as AAMs lies in their ability to: (i) be discriminative and generalize well to unseen appearance variation; (ii) offer greater invariance to global illumination variation and occlusion; (iii) model the non-rigid object as an ensemble of low dimensional independent patch experts; and (iv) not employ complicated piece-wise affine texture warp operations that might introduce unwanted noise.

In this paper we propose a novel efficient approach for non-rigid face registration/tracking based on a number of extensions to the CLM framework by,

• Simplifying the optimization of the cost criteria in a CLM by dividing the problem of finding a single complex registration/warp displacement into that of finding N simple warp displacements. From these N simple warp displacements, a single complex warp displacement is estimated using a weighted least-squares constraint. Another major advantage of this simplified optimization lends from its ability to be parallelized, a step which we also theoretically explore in this paper. We refer to this efficient optimization strategy as exhaustive local search (ELS) algorithm. (Section 4.1)

• Replacing the original non-linear patch-experts suggested in [9] with a linear support vector machine (SVM). The advantage of linear over non-linear experts stems from computational efficiency of computing the output score of a patch-expert using a single, rather than multiple, intensity templates. Although making the patch-experts less complicated we illustrate that our proposed method is superior in alignment performance to computationally complex AAM fitting algorithms. (Section 4.2)

• Employing a composite warp update rather than an additive warp update within the CLM framework. The advantage of composite over additive warp updates are especially useful when there is substantial scale changes between frames in a video sequence. (Section 4.1)

An additional contribution we make in this paper is made by comparing our efficient CLM implementation against two canonical forms of AAM fitting, namely the “simultaneous” and “project-out” algorithms. The simultaneous algorithm [14,2] is able to fit an AAM robustly but is known to have poor real time performance (2-3 fps). The project-out algorithm [14,2] is able to achieve faster than real-time speed (> 200 fps), but suffers from poor generic alignment/tracking performance. In Section 5 we analyze the algorithmic complexity of these two algorithms in comparison to our proposed ELS algorithm. We also report results that our ELS algorithm can obtain real-time tracking speeds (35 fps) whilst outperforming the simultaneous algorithm in terms of registration performance.

1.1 CLMs vs. ASMs

Active shape models [8] (ASMs) are a popular approach for non-rigidly aligning faces and have found numerous expressions and extensions in computer vision literature [18,15,21]. For all intensive purposes, however, one can consider an ASM as a CLM that employs a 1D rather than 2D local search around each landmark in the in the current PDM warp estimate. The 1D search direction for each point in an ASM is estimated as the normal to the contour at each current point estimate. In contrast, however, a CLM employs a 2-D search around each point estimate. We believe an inherent benefit of CLMs over ASMs lies in their employment of a 2D versus 1D local search. As speculated by Milborrow [15], a 2D response captures more information around the landmark, and this information, if used wisely, should give better results.

In Cristinacce and Cootes’ original CLM formulation [9] the patch-experts adaptively change during the fitting process. This fitting process is quite similar to the “simultaneous” [1] fitting strategy employed in traditional AAMs where both the shape and appearance (for the CLM case patch-experts) models are optimized to minimize the reconstruction error of the source image. The “project-out” [1] fitting strategy for fitting AAMs employs a static appearance model (in a similar manner to the canonical ASM method [9]) to drastically speed up the computational efficiency of the fitting procedure. For similar reasons (i.e., computational efficiency) our proposed CLM framework employs static, rather than adaptive, patch-experts during fitting. Our CLM extension approach differs to canonical ASMs also by: (i) employing discriminative patch experts trained on “aligned” and “misaligned” training examples, (ii) employing confidence scores in the fitting procedure, and (iii) employing an inverse composition warp update.

2 Learning the Shape Prior

Before we can fit an AAM or CLM we have to define how the face can vary spatially. A point distribution model (PDM) [6] is used in both methods for a parametric representation of the non-rigid shape variation. The non-rigid warp function can be described as,

$$W(\mathbf{z};\mathbf{p})=\mathbf{z}+\mathbf{Vp}$$ (1)

where $\mathbf{z}={[{\mathbf{x}}_1^T,\dots ,{\mathbf{x}}_N^T]}^T$, p is a parametric vector describing the non-rigid warp, and V is the matrix of concatenated eigenvectors. N is the number of patch-experts. Procrustes analysis [6] is applied to all shape training observations in order remove all similarity. Principal component analysis (PCA) [4] is then employed to obtain shape eigenvectors V that preserved 95% of the similarity normalized shape variation in the train set. In this paper, the first 4 eigenvectors of V are forced to correspond to similarity (i.e., translation, scale and rotation) variation of the mean shape. Readers are encouraged to inspect [14] for more details on how a similarity transform can be expressed as a 4 dimensional linear basis. This new PDM is now able to move under 2D similarity transformations, as well as the original linear PDM variation. This is, however, not the same as moving under the linear shape variation followed by the 2D similarity transformation. This approximation has been reported [14] to have minimal effect of face alignment performance when being used in conjunction with AAMs and is employed throughout the experiments in this paper due to its computational efficiency.

3 Fitting Active Appearance Models

The central mechanism for fitting an AAM to an unseen source image is to employ a generative linear model to approximate how the holistic appearance of the object varies with alignment.

$$T({\mathbf{z}}^{\prime })\approx T(\mathbf{z})+\mathbf{K}\mathbf{\Delta }\mathbf{p}$$ (2)

The vector $\mathbf{z}={[{\mathbf{x}}_1^T,\dots ,{\mathbf{x}}_N^T]}^T$ is a concatenation of individual pixel 2D coordinates x within the template image T. The relationship between z and z′ is dictated by a warp function z′ = W(z; p) that maps the image positions z to a set of new positions z′ based on the warp parameters p. In early work on image alignment this warp was assumed to be rigid (e.g., optical flow), however, in modern AAM applications the warp function can be learnt from an ensemble of training landmarks describing the non-rigid shape of the object being modeled as described by the PDM in Equation 1.

The notation employed in this paper shall depart slightly from canonical methods in order to easily allow the inclusion of patches of intensity at each coordinate rather than just pixels. This notation change is employed so as to make the study of algorithm complexity between AAM and CLM fitting algorithms in Section 5 more elegant. When a template T is indexed by the coordinate vector x it not only refers to the pixel intensity at that position, but the P × P support region around that position. When we refer to T(x) it refers to an P² dimensional intensity vector. Similarly, when we refer to T(z) = [T(x₁)^T,…,T(x_N)^T]^T this refers to a NP² dimensional vector concatenation of patch intensity vectors corresponding to each coordinate x within the vector z. For additional robustness, the P × P¹ support region is extracted after the image has been suitably normalized for scale and rotation to a base template. This ensures that T(z′) and T(z) are equal when they are perfectly aligned in terms of their pixel coordinates z. Finally, we define the steepest descent matrix as

$$\mathbf{K}={\left[\frac{\partial W(\mathbf{z};\mathbf{0})}{\partial \mathbf{p}}\frac{\partial T(\mathbf{z})}{\partial \mathbf{z}}\right]}^T$$ (3)

where the matrix $\frac{\partial W(\mathbf{z};\mathbf{0})}{\partial \mathbf{p}}$ is the Jacobian matrix of the vector z = W(z; 0) with respect to the parametric warp p. The matrix $\frac{\partial T(\mathbf{z})}{\partial \mathbf{z}}$ is an extremely sparse Jacobian matrix of the form

$$\frac{\partial T(\mathbf{z})}{\partial \mathbf{z}}=\left[\begin{array}{ccc}{\mathbf{G}}_{{\mathbf{x}}_1}& \dots & \mathbf{0}\\ ⋮& \ddots & ⋮\\ \mathbf{0}& \dots & {\mathbf{G}}_{{\mathbf{x}}_N}\end{array}\right]$$ (4)

where G_x is the 2 × P² local gradient matrix for each set of P² intensities centered around x. One can see that the matrix K is factorized in terms of local gradients G_x and holistic warp constraints $\frac{\partial W(\mathbf{z};\mathbf{0})}{\partial \mathbf{p}}$.

Based on the generative model in Equation 2 we now have a framework inverting the linear synthesis model so as to align the template image T(z) to an unlabeled source image Y containing the object. We can estimate the warp update, using a least-squares criteria, as

$$\mathbf{\Delta }\mathbf{p}={\mathbf{K}}^{+}[Y({\mathbf{z}}^{\prime })-T(\mathbf{z})]$$ (5)

where K⁺ denotes the pseudo-inverse of K. Note that we are solving for the warp displacement between the source image Y(z′) and the base template T(z), not T(z′) as employed in our generative model in Equation 2. As a result, for Equation 5 to work effectively we must assume that the aligned source image be similar in appearance to the template (i.e., T(z) ≈ Y(z)). An extension to this approach will be briefly discussed in Section 3.1 for situations where the appearance of Y(z) varies substantially from T(z). The full gradient-descent algorithm can be seen in Algorithm 1. The inverse compositional update in Step 3 is required, as opposed to a simple additive update, because we are solving for the incremental warp update W(z; Δp) not the parameter update Δp. This allows us to pre-compute K, rather than re-estimate it at each iteration from W(z; p); leading to sizable computational savings. Readers are encouraged to inspect [3] for a full treatment on this subject. The type of optimization in Algorithm 1 is commonly referred to as Gauss-Newton optimization. Other least-squares variants have been evaluated in [3] such as the Newton and Levenberg-Marquardt optimization. We employ Gauss-Newton optimization in our work due to its robust performance and fast convergence properties.

Input:- template (T), source image (Y), steepest descent matrix (K) initial warp guess (p), index to the template (z), threshold (∈)

Output:- final warp (p)

1. Warp the source image Y with z′ = W(z; p)

2. Estimate the warp update Δp using Equation 5 and the error image [Y(z′) − T(z)].

3. Update the warp using the inverse compositional step [3],

   $${\mathbf{z}}^{\prime }=W(\mathbf{z};\mathbf{p})\leftarrow W(\mathbf{z};\mathbf{p})\circ W{(\mathbf{z};\mathbf{\Delta }\mathbf{p})}^{-1}$$

4. Repeat steps 1-3 until ∥Δp∥ < = ∈ or max iterations reached.

Algorithm 1. Algorithm for aligning the template T with source image Y using a generative model and inverse compositional warp update.

3.1 Simultaneous and Project Out Extensions

As originally defined in [6] an AAM varies not only in shape, but appearance. Therefore, the linear generative model in Equation 2 should be extended [2] to also incorporate appearance variation,

$$Y({\mathbf{z}}^{\prime })\approx T(\mathbf{z})+\mathbf{K}\mathbf{\Delta }\mathbf{p}+\mathbf{A}\mathbf{\Delta }\mathbf{\lambda }$$ (6)

where $\mathbf{A}={\left\{A_i(\mathbf{z})\right\}}_{i=1}^m$ is an ensemble of m appearance eigenvectors and Δλ is the appearance update. These appearance eigenvectors are estimated from the offline aligned training images of the object. As per Equation 2 the matrix K is the steepest descent matrix of the current template T(z) and Δp is the warp update. One can then solve for both warp Δp and appearance Δλ updates,

$${[\mathbf{\Delta }{\mathbf{p}}^T,\mathbf{\Delta }{\mathbf{\lambda }}^T]}^T={[\mathbf{K},\mathbf{A}]}^{+}[Y({\mathbf{z}}^{\prime })-T(\mathbf{z})]$$ (7)

This update equation is substituted for Equation 5 in Step 2 of the gradient descent algorithm outlined in Algorithm 1. At the end of Steps 1-3 of each iteration we must also update the template by the appearance update Δλ,

$$T(\mathbf{z})\leftarrow T(\mathbf{z})+\sum _{i=1}^m\mathbf{\Delta }{\mathrm{\lambda }}_i{A}_i(\mathbf{z})$$ (8)

and the Jacobian matrix $\frac{\partial T(\mathbf{z})}{\partial \mathbf{z}}$,

$$\frac{\partial T(\mathbf{z})}{\partial \mathbf{z}}\leftarrow \frac{\partial T(\mathbf{z})}{\partial \mathbf{z}}+\sum _{i=1}^m\mathbf{\Delta }{\mathrm{\lambda }}_i\frac{\partial A_i(\mathbf{z})}{\partial \mathbf{z}}$$ (9)

The simultaneous extension (SIM) to the generative approach has a considerable computational cost as the template T(z), Jacobian matrix $\frac{\partial T(\mathbf{z})}{\partial \mathbf{z}}$ and steepest descent matrix K needs to be re-estimated at each iteration. In order to reduce the computational cost, one way to simplify the simultaneous algorithm is to “project out” the appearance variation in Equation 6, which is referred as the project out (PO) algorithm [2]:

$$\mathbf{\Delta }\mathbf{p}={[\mathbf{K}-{\mathbf{AA}}^T\mathbf{K}]}^{+}[Y({\mathbf{z}}^{\prime })-T(\mathbf{z})]$$ (10)

As a result, the matrix [K − AA^T K]⁺ in Equation 10 remains constant in each iteration and can be pre-computed.

4 Fitting Constrained Local Models

A constrained local model (CLM) can loosely be defined as an ensemble of patch-experts, learnt in a discriminative fashion on the patch intensities for each landmark position in the object, as well as a shape prior describing how object can non-rigidly vary. Unlike AAMs, CLMs are designed for registration only not synthesis. Given a source image Y, and borrowing the patch indexing notation used in Section 3, we can formally pose CLM fitting as the following optimization problem,

$$\arg \underset{\mathbf{p}}{\min }\sum _{k=1}^N{E}_k\left\{Y({\mathbf{x}}_k+{\mathbf{V}}_k\mathbf{p})\right\}$$ (11)

where E_k() is the inverted classifier score function obtained from applying the kth patch expert to the source image patch intensity Y(x_k + Δx_k). The displacement Δx_k is constrained to be consistent with the PDM defined in Equation 1, where the matrix V can be decomposed into submatrices V_k for each kth patch expert, i.e., $\mathbf{V}={[{\mathbf{V}}_1^T,\dots ,{\mathbf{V}}_T^N]}^T$.

In general, it is difficult to solve for p in Equation 11 as E_k() is a discrete function due to Δx only taking on integer values and there is no guarantee for E_k() being convex. Previous methods have either used general purpose optimizers (e.g., Nelder-Mead simplex [16]) or attempted to pose the problem as a form of graph optimization [9,13]. Unfortunately, general purpose optimization techniques, such as Nelder-Mead simplex [16], are often computationally expensive and require good initialization. In order to employ graph optimization techniques like loopy belief propagation it has been shown that the warp function W(z; p) needs to be spatially sparse as described in [13].

4.1 Exhaustive Local Search (ELS)

In this paper we advocate a novel approach for solving Equation 11 accurately and efficiently. We refer to our approach as the Exhaustive Local Search (ELS) method. In our approach we propose not to optimize for the holistic warp update Δp directly, but rather optimize for N local translation updates Δx and then constrain them all to lie within the subspace spanned by $\mathbf{J}=\frac{\partial w(\mathbf{z};\mathbf{0})}{\partial \mathbf{p}}$. The local translation updates are chosen by,

$$\mathbf{\Delta }{\mathbf{x}}_k=\arg \underset{\mathbf{\Delta }\mathbf{x}\in R}{\min }{E}_k\left\{Y({\mathbf{x}}_k+\mathbf{\Delta }\mathbf{x})\right\}$$ (12)

where R is the neighborhood 2D integer search window ² for each landmark, with each of these updates being concatenated into the vector $\mathbf{\Delta }\mathbf{z}={[\mathbf{\Delta }{\mathbf{x}}_1^T,\dots ,\mathbf{\Delta }{\mathbf{x}}_N^T]}^T$. The warp update is then estimated by a weighted least-squares optimization,

$$\mathbf{\Delta }\mathbf{p}={({\mathbf{JWJ}}^T)}^{-1}\mathbf{JW}\mathbf{\Delta }\mathbf{z}$$ (13)

where the weighting matrix W is defined as the diagonal matrix,

$$\mathbf{W}=\mathit{diag}\{w_{x1},w_{y1},\dots ,w_{xN},w_{yN}\}$$ (14)

Our proposed indirect approach can be seen in Algorithm 2. A major advantage of our proposed approach in Algorithm 2 comes about from how to solve for Δz. Since Δz consists of N independent translational warps it now becomes computationally feasible to solve Δz through an exhaustive search within a local region. As we shall demonstrate empirically in Section 7 this is extremely advantageous as we no longer need to rely on linear approximations to how the object varies as previously required by gradient-descent approaches. In Section 4.2 we will go on to discuss how the weighting matrix W is estimated on patch expert confidences. A number of alternate strategies could also be employed to further improve the robustness, mostly notably the employment of different robust error functions [17,1] to adaptively change W.

Input:- template (T), source image (Y), Jacobian matrix $\frac{\partial W(\mathbf{z};\mathbf{0})}{\partial \mathbf{p}}$ initial warp guess (p), index to the template (z), threshold (∈)

Output:- final warp (p)

1. Warp the source image Y with z′ = W(z; p)

2. Estimate the local coordinate updates $\mathbf{\Delta }\mathbf{z}={[\mathbf{\Delta }{\mathbf{x}}_1^T,\dots ,\mathbf{\Delta }{\mathbf{x}}_N^T]}^T$ and weight matrix W.

3. Estimate the warp update Δp using Equation 13, the coordinate update vector Δz and weight matrix W.

4. Update the warp using the inverse compositional step [3],

   $${\mathbf{z}}^{\prime }=W(\mathbf{z};\mathbf{p})\leftarrow W(\mathbf{z};\mathbf{p})\circ W{(\mathbf{z};\mathbf{\Delta }\mathbf{p})}^{-1}$$

5. Repeat steps 1-4 until ∥Δp∥ < = ∈ or max iterations reached.

Algorithm 2. Algorithm for aligning the template T with source image Y indirectly by solving for Δz at each iteration and then estimating Δp indirectly through the application of a constraining parametric warp.

4.2 Estimating Patch Experts

An integral component of our approach in Algorithm 2 is that we are able to obtain accurate local estimates of Δx = [Δx, Δy]^T for each patch coordinate update with confidence weight w_x and w_y for movement in the x- and y-directions. For our work we shall assume that w_x = w_y and refer to this weight as w_x. Leveraging the large amount of previous work [19] in rigid object registration we employed a discriminative classifier for each patch coordinate x. Positive examples were obtained for the patch at various scales [0.8, 1, 1.2] and rotations [−8°, −1°, 0, +4°, +8°]. Negative examples were obtained by shifting the patch centers so their is at least a 25% of the patch size (in both patch width and height) from the true positions. Scale and rotation variations were also added to the negative examples.

We chose to employ a linear support vector machine (SVM) for each of our N patch experts. The choice of classifier for our work is largely arbitrary with our framework allowing the employment of other discriminant classifiers such as boosting schemes [4] (e.g., AdaBoost, GentleBoost, etc.) or relevance vector machine (RVMs) [4]. A linear support vector machine was chosen, over other kernel varieties, due to its computational advantages in that,

$$E\left\{Y(\mathbf{x}+\mathbf{\Delta }\mathbf{x})\right\}=-\sum _{i=1}^{\mathit{NS}}{\alpha }_i{T}_i{(\mathbf{x})}^{T}Y(\mathbf{x}+\mathbf{\Delta }\mathbf{x})=-Y{(\mathbf{x}+\mathbf{\Delta }\mathbf{x})}^T\sum _{i=1}^{\mathit{NS}}{\alpha }_i{T}_i(\mathbf{x})$$ (15)

allowing for ${\sum }_{i=1}^{\mathit{NS}}{\alpha }_i{T}_i(\mathbf{x})$ to be pre-computed rather than evaluated at every Δx. We define E{Y(x + Δx)} as the decision value for aligning patch intensities Y(x + Δx) with the NS support vectors T_i(x) and support weights α_i. We should note that the intensity patches Y(x + Δx) and T_i(x) are forced to have zero mean and unit norm during learning and evaluation. This was done to ensure that each patch expert was trained on observations that are independent of intensity fluctuations elsewhere in the image and ensured improved generalization and robustness of the patch experts.

An approximate probabilistic output can be obtained by fitting a logistic regression function [4] to the output of the SVM and the labels y = {not aligned, aligned},

$$\widehat{P}\left(y=1|E\left\{Y(\mathbf{x}+\mathbf{\Delta }\mathbf{x})\right\}\right)=\frac{1}{1+e^{aE\left\{Y(\mathbf{x}+\mathbf{\Delta }\mathbf{x})\right\}+b}}$$ (16)

Since the values E{} and labels y have to be independent a five-fold cross validation procedure was employed in order to estimate the logistic parameters a and b. To obtain the weightings w_x for a patch coordinate x in Algorithm 2 we apply Equation 16 such that

$$w_{\mathbf{x}}=\widehat{P}\left(y=1|E\left\{Y(\mathbf{x}+\mathbf{\Delta }\mathbf{x})\right\}\right)$$ (17)

5 Algorithmic Complexity

An immediate reaction to solutions which utilize an exhaustive search is in general negative as “exhaustive” has a history of being associated with “in-efficient”. A valid criticism of our exhaustive local search (ELS) approach is its use of the exhaustive search, especially when the exhaustive search is conducted inside a loop which locates the local optimum. It is the goal of this section to demonstrate that for reasonable parameter values, the overall performance of the algorithm is comparable to gradient descent methods.

In order to compare performance, there are a number of parameters which impact the execution time of each algorithm. The three parameters N, T and P are shared by all algorithms and refer to the number of patches, the number of pixels used in each patch and the number of parameters required to model the shape variation. The project out (PO) and simultaneous (SIM) algorithms have an additional parameter B which refers to the number of parameters which model the appearance variation. Finally, the parameter S defines the number of search positions that the exhaustive search step of the exhaustive local search algorithm will conduct its search in for each patch. For simplicity, the patch and the search window were constrained to be square which was simplified further by relating S to T using the equation $\sqrt{S}=\alpha \sqrt{T}$.

Input:- template (T), source image (Y), Jacobian matrix $\frac{\partial W(\mathbf{z};\mathbf{0})}{\partial \mathbf{p}}$ initial warp guess (p), index to the template (z), threshold (∈)

Output:- final warp (p)

1. Warp the source image Y with z′ = W(z; p)

2. Estimate the warp update Δp:

   • Simultaneous -

     • Using Equation 5 and the error image [Y(z′) − T(z)].

       O (NT(P + B)²) + O ((P + B)³)

   • Project Out -

     • Using the pre-computed approximation calculated prior to iterating and the error image [Y(z′) − T(z)].

       O (NT (P + B)) + O ((P + B)²)

   • Exhaustive Local Search -

     • Estimate the local coordinate updates $\mathbf{\Delta }\mathbf{z}={[\mathbf{\Delta }{\mathbf{x}}_1^T,\dots ,\mathbf{\Delta }{\mathbf{x}}_N^T]}^T$ and weight matrix W.

       O (α²NT²)

     • Estimate the warp update Δp using Equation 13, the coordinate update vector Δz and weight matrix W.

       O (P²N+P³)

3. Update the warp using the inverse compositional step [3],

   $${\mathbf{z}}^{\prime }=W(\mathbf{z};\mathbf{p})\leftarrow W(\mathbf{z};\mathbf{p})\circ W{(\mathbf{z};\mathbf{\Delta }\mathbf{p})}^{-1}$$

4. Repeat steps 1-3 until ∥Δp∥ < = ∈ or max iterations reached.

Algorithm 3. Algorithmic Complexity.

For sake of clarity, in Algorithm 3 we outline the main steps of the SIM, PO and ELS algorithms and compare them side by side, and show the dominant components of the execution time functions within each iteration using the Big-Oh (O) notation. As we can see from the comparison, the ELS method is faster than the SIM method as α is typically much less than P + B. It can also be seen that the PO method is still faster than the proposed approach as usual parameter values consist of α²T > (P + B) and P² N ≫ (P + B)².

To visualize the complexity outlined in Algorithm 3 in an application, our experimentation using N = 68 patches to model the shape variation has determined reasonable parameter values for P and B (which become essentially constants for a fixed N) to be P = 20 and B = 70. This leaves the variable T which is in common with all the algorithms and the α parameter which is specific to the exhaustive local search method. Figure 1 diagrammatically shows the information in Algorithm 3 using the above parameter values for varying square patch sizes with side length $\sqrt{T}$. To see the effect that the search area S = α²T has on the execution time of the exhaustive local search algorithm, multiple curves corresponding to varying α values have been added. As expected the PO method has a much faster execution time with respect to the SIM and to the ELS algorithm for large patch areas. For smaller patch sizes, the PO method offers a moderate improvement in performance.

Fig. 1.

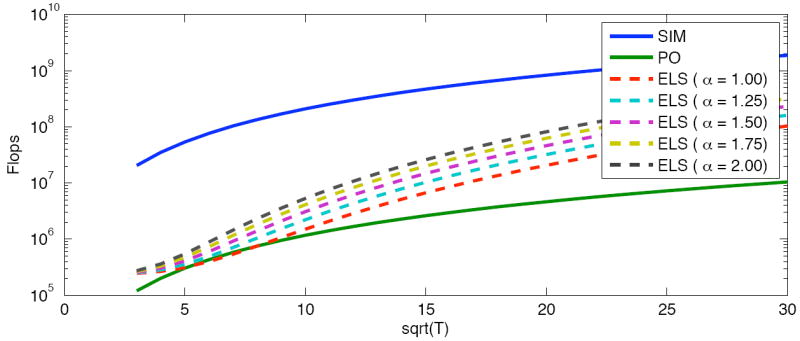
The exhaustive local search (ELS) algorithm’s complexity relative to the simultaneous (SIM) and project out (PO) on a single processor.

An advantage that the ELS method has over the SIM and PO methods is that the exhaustive search can be performed independently. A straightforward improvement in computational time can be achieved by utilizing more than one processing unit in order to conduct the exhaustive search for each patch in parallel. For the SIM and PO methods, however, because they are holistic gradient descent methods, there is no straightforward way to speed up the optimization process using multiple processors. With recent advances in low cost multi-core desktop computing and the emergence of general purpose graphics processing units, this type of modification is very attractive.

To incorporate the number of processing units into the exhaustive local search computation time equations, an additional parameter N_PU is added to the first step of the exhaustive local search method which changes ³ the algorithmic complexity to

$$\mathrm{O}\left(\frac{{\alpha }^{2}N}{N_{PU}}T\right).$$

The effect this has on the overall computation time per iteration is shown in Figure 2 for a patch area of T = 9 × 9 and a search area of S = α²T = 15 × 15. As can be seen, with at least four processing units, the computation time is reduced to below that of the PO algorithm.

Fig. 2.

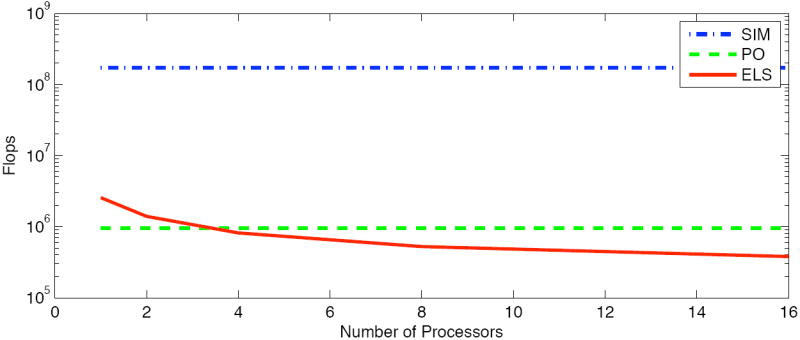
The exhaustive local search (ELS) algorithm’s complexity relative to the simultaneous (SIM) and project out (PO) on multiple processors.

At the time of writing we have patch-based versions of the SIM, PO and ELS algorithms written in C++. We conducted registration/tracking experiments on a variety of video sequences to ascertain the real-time tracking speed of each algorithm. Our experiments were conducted on a MacBook-Pro 2.33 GHz machine with 4GB of ram. Our code was written to explicitly take advantage of the OpenCV and Intel Integrated Performance Primitives (IPP) and Math Kernel Library (MKL) performance libraries. For all three algorithms we used 68 fiducial points and a PDM with 21 degrees of freedom. For the SIM and PO algorithms we used an appearance basis with 76 appearance degrees of freedom. For the ELS algorithm we used a search window of 15 × 15 pixels for each patch-expert. During our real-time evaluation we were able to obtain speeds of 2.4, 212.6, and 35.3 frames per second (fps) on average for the SIM, PO and ELS algorithms respectively. This result confirms our theoretical complexity analysis of the SIM, PO and ELS algorithms. We should note that our current ELS implementation takes advantage of only a single processor when evaluating patch-experts. We would also like to note that ELS is not the only method to fit a CLM that can take advantage of parallel architectures (e.g., robust convex quadratic fitting (RCQF) in [20]). However, we believe the analysis undertaken in this section gives a strong indication of the computational advantages of CLMs over AAMs during fitting.

6 Data and Evaluation

We conducted our registration experiments on a subset of the MultiPIE face database [12]. A subset of 250 images was chosen from this database with each image referring to a different subject ⁴. Within this set 125 were used for learning with the other 125 being used for fitting. All the images were hand annotated with 68 fiducial points (see Figure 6 for an example). In all our experiments the similarity normalized base shape template had an inter-ocular distance of 50 pixels. To test the ability of our algorithms to correctly register a previously unseen source image we synthetically generated random initial warps. We randomly generated warps W(z; p) in the following manner. We used the center of the left eye, the center of the right eye and the tip of the nose in the base template. We then perturbed these points with a vector generated from white Gaussian noise. The magnitude of this vector was controlled to give either 5, 7.5 or 10 pixels root mean squared point error (RMS-PE) from the ground-truth coordinates. We chose these 3 initial starting points based on our offline experiments with the OpenCV Viola & Jones face detector [19], which regularly gave us an initial starting point between 5 – 10 RMS-PE. A similarity transform was then estimated to describe the change between these perturbed points and the base template shape. The resultant similarity transform was then composed with the ground truth warp of the source image (in relation to the base template) to obtain the random initial warp for that image.

Fig. 6.

Examples of alignment performance on a single subject’s face. Rows 1, 2 and 3 illustrate the alignment for the initial warp perturbation, simultaneous, and our exhaustive local search respectively. Columns 1, 2, and 3 illustrate the alignment for initial warp perturbation of 10, 7.5 and 5 pixels RMS-PE respectively.

During alignment, we employed the following strategy for estimating alignment error. Given the ground-truth shape of the source image we apply a similarity transform that minimizes the alignment error with the average base template shape. We then apply this same similarity transform to the estimated shape of the source image and then compute the RMS-PE between the 68 points. In all our experiments 10 random warps were created for each source image in the evaluation set. These same sequence of random warps were used for each algorithm being evaluated so as to allow for a fair comparison. To compare all our algorithms we employed an alignment convergence curve (ACC) [9]. These curves have a threshold distance in RMS-PE on the x-axis and the percentage of trials that achieved convergence (i.e., final alignment RMS-PE below the threshold) on the y-axis. A perfect alignment algorithm would receive an ACC that has 100% convergence for all threshold values.

7 Experiments

The central focus of this paper is to compare non-rigid alignment algorithms in the presence of “unseen” appearance variation. We tested our proposed algorithm on the MultiPIE face database where 125 faces were picked randomly for learning, and the other 125, of different appearance and identity, being used for evaluation. We separated our experiments into two major sections. First, in Section 7.1 we investigated whether a patch-based warp is advantageous over a holistic warp within a gradient descent framework. Second, in Section 7.2 we illustrated that given a patch-based warp, an Exhaustive Local Search (ELS) strategy is superior to an AAM fitting strategy.

7.1 Holistic vs. Patch Warp Methods

In the canonical implementation of the AAM for face fitting a holistic piecewise affine warp function was normally used instead of the patch-warp function described in Section 3 of our AAM implementation. In our algorithm complexity analysis of the AAM algorithm in Section 5 we use the patch-warp function not the canonical piece-wise affine warp function. For completeness, we have conducted a comparison between the two warp functions for AAM alignment.

An example is shown in Figure 3 to illustrate the differences between the holistic piece-wise affine and patch-based warp functions. As we can see, the patch-based warp has an inherent advantage over the holistic warp in that it only performs a similarity transform on the source image from which patch regions are then extracted. Even when noise is present in the alignment the patch-based warped image still looks like a face. The holistic warp, however, employs a complicated piece-wise affine warp based on the pixels which can lead to strange looking images when noise is present in the alignment. The comparison experiments on the MultiPIE face database further support the arguments. Figure 4 shows AAM alignment results of the SIM algorithm for different initial RMS-PE: (a) 10 pixels, (b) 7.5 pixels and (c) 5 pixels. As we can see the patch warp algorithm outperforms the holistic piece-wise affine in all cases.

Fig. 3.

Graphical depiction of the holistic and patch-based warp representations under different alignment: The source images under different alignment are shown in column (a). The resulting representations from the holistic and patch-based warps are shown in column (b) and (c), respectively. The top row shows the ground truth alignment, where both the holistic and patch-based representations give faithful approximation to the original image. However, when the alignment is perturbed by noise, as shown in the bottom row, the holistic representation gives a largely distorted result (b), which is not close to the original image (e.g., eye texture is largely distorted). However, the patch-based representation, which performs only the global inverse similarity transform, generates a reasonable result (c) (e.g., eye texture is not distorted).

Fig. 4.

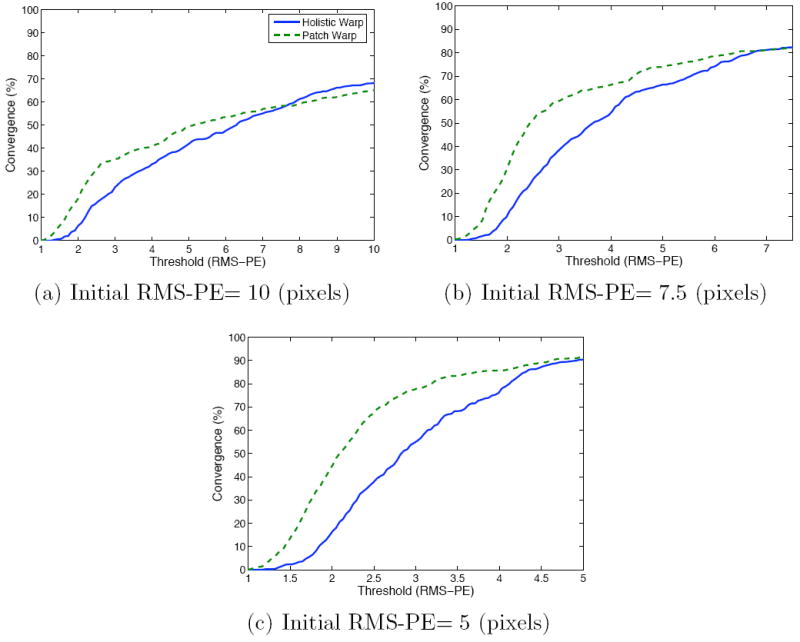
Results depict how the patch warp algorithm outperforms the holistic algorithms for different initial RMS-PE: (a) 10 pixels, (b) 7.5 pixels and (c) 5 pixels.

7.2 Comparison between SIM, PO and ELS

In this section, we compared our algorithm against the well known AAM simultaneous (SIM) and project out (PO) extensions [2] described in Section 3.1. These two algorithms were chosen as our benchmark due to their good performance and natural abilities to deal with appearance variation. Results for our comparison can be seen in Figure 5. In this figure we can see the ACCs for three different initial warp perturbations of 10, 7.5 and 5 pixels RMS-PE. Inspecting Figure 5 one can see that the SIM and PO algorithms receive extremely poor performance, in comparison to our approach, for initial RMS-PEs of 10 and 7.5 pixels. This result can be confirmed visually if we inspect the first and second columns of Figure 6. We can understand this result if we take into account the nature of the gradient-descent strategy employed as it is attempting to solve for warp and appearance change simultaneously through a linear generative model. Since the initial starting point is so far away from the ground-truth point and the number of free parameters it is attempting to solve is so large (21 warp parameters and 76 appearance parameters) it easily falls into local-minima. Our approach, however, circumvents these problems by performing N exhaustive searches of a local patch region and then indirectly estimating the non-rigid warp updated through a weighted least-squares optimization as described in Algorithm 2. We can see that for a large initial RMS-PE there is great benefit in employing our approach.

Fig. 5.

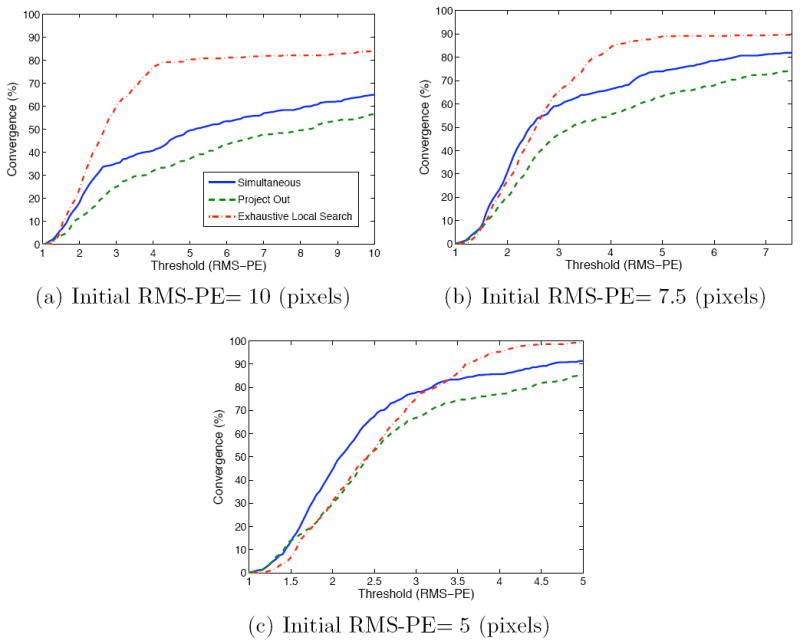
Results depict how our proposed algorithm outperforms the gradient-descent simultaneous and project out algorithms in nearly all cases. For large initial RM-S-PE of (a) 10 pixels and (b) 7.5 pixels our approach has clearly better convergence properties than the gradient-descent methods. For a smaller initial RMS-PE of (c) 5 pixels our method performs similarly to the simultaneous approach, with the simultaneous approach exhibiting slightly better convergence performance.

It is interesting to note, however, that the performance of the SIM algorithm is actually slightly superior (in that it keeps a higher convergence rate for longer) to our own for a smaller initial RMS-PE of 5 pixels. This result can be explained by the intrinsic difference between our algorithm and the gradient-descent SIM algorithm. Specifically, the simultaneous algorithm attempts to solve for the warp update Δp directly through a generative linear model. As the initial starting point gets closer to the ground-truth point the better that linear approximation becomes leading to improved convergence performance. Our algorithm, on the other hand, solves for the warp update Δp indirectly by exhaustively searching N local regions and then constraining that result. Although robust, it is not solving for the warp update Δp directly and is susceptible to some intrinsic error as a result of the indirect optimization. On balance, however, our proposed approach receives good performance even for smaller initial RMS-PE as can be seen by the alignment examples in the third column of Figure 6 and can be considered an improvement over the conventional gradient-descent simultaneous algorithm due to its robust behavior across a wide variety of initializations.

8 Discussion

In this paper we investigated the problem of computationally efficient non-rigid face registration/tracking in the presence of appearance variation. We proposed a novel extension to the CLM framework for non-rigid registration/tracking. We improved upon the canonical CLM formulation, to gain real-time speed, in a number of ways by employing: (i) linear SVMs as patch-experts, (ii) a simplified optimization criteria, and (iii) a composite rather than additive warp update step. Most notably, our simplified optimization criteria for fitting the CLM divides the problem of finding a single complex registration/warp displacement into that of finding N simple warp displacements. From these N simple warp displacements, a single complex warp displacement is estimated using a weighted least-squares constraint. Another major advantage of this simplified optimization lends from its ability to be parallelized, a step which we also theoretically explore in this paper. We refer to our approach for fitting the CLM as the “exhaustive local search” (ELS) algorithm.

As part of our analysis we compared our ELS algorithm against two well known AAM fitting approaches namely the “simultaneous” (SIM) and “project-out” algorithms. In our analysis we demonstrated that the ELS algorithm could obtain real-time fitting speeds of over 35 fps, compared to the SIM algorithm’s speed of 2-3 fps. Additionally, in our analysis we demonstrated that the ELS algorithm also achieved superior alignment performance to the SIM algorithm in nearly all circumstances. In future work we would like to explore the possibility of making the ELS algorithm more parallelized to further increase speed. In combination with this speedup we could also explore more sophisticated methods of solving the full CLM cost fitting function. We have made some inroads towards this goal with a new approach for CLM fitting we refer to as emphrobust convex quadratic fitting (RCQF) [20] which employs the entire response surface, rather than the maximum, during fitting.