Abstract
Background
To support malaria control strategies, prior knowledge of disease risk is necessary. Developing a model to explain the transmission of malaria, in endemic and epidemic regions, is of high priority in developing health system interventions. We develop, fit and validate a non-spatial dynamic model driven by meteorological conditions that can capture seasonal malaria transmission dynamics at the village level in a malaria holoendemic area of north-western Burkina Faso.
Methods
A total of 676 children aged 6–59 months took part in this study. Trained interviewers visited children at home weekly from December 2003 to November 2004 for Plasmodium falciparum malaria infection detection. Anopheles daily biting rate, mortality rate and growth rate were evaluated. Digital meteorological stations measured ambient temperature, humidity and rainfall in each site.
Results
The overall P. falciparum malaria infection incidence was 1.1 episodes per person year. There was strong seasonal variation in P. falciparum malaria infection incidence with a peak observed in August and September, corresponding to the rainy season and a high number of mosquitoes. The model estimates of monthly mosquito abundance and the incidence of malaria infection correlated well with observed values. The fit was sensitive to daily mosquito survival and daily human parasite clearance.
Conclusion
The model has demonstrated potential for local scale seasonal prediction of P. falciparum malaria infection. It could therefore be used to understand malaria transmission dynamics using meteorological parameters as the driving force and to help district health managers in identifying high-risk periods for more focused interventions.
Keywords: local scale, modelling, prediction, Plasmodium falciparum malaria, under five years, endemic region
Malaria continues to be a deadly disease and action towards its control remains challenging for researchers and policymakers. To support control strategies, prior knowledge of disease risk is necessary. Developing a model to explain the transmission of malaria, in endemic and epidemic regions, is of high priority in developing health system interventions. As malaria is a vector-borne disease, the life cycle of its vector, the female Anopheles mosquito, drives the transmission. The life cycles of both the vector and the parasite within the vector depend on the microclimate.
Since the early 20th century, there have been attempts to understand malaria transmission dynamics, through mathematical modelling, to support control efforts. Ross developed the first model to predict malaria transmission and spread of the disease, and later concluded that increasing vector mortality significantly could eradicate malaria (1, 2). In the 1950s, George MacDonald, building on Ross’ model, concluded that, at equilibrium, the weakest link in the cycle of malaria transmission is the adult female Anopheles (3). His conclusions formed the basis of the global malaria eradication campaign, with DDT targeted at adult female Anopheles. In the 1970s, Dietz and Molineaux, in the Garki project, developed a more sophisticated model, clearly considering human immunity interacting with transmission (4–6).
Further, Halloran and colleagues considered the population-level effects of potential stage-specific vaccines (7). Since then, malaria modelling has drawn significant attention. Populations are modelled as large numbers of interacting individual humans and individual mosquitoes, each with its own characteristics and dynamics (6). Further steps towards biological realism have included the effects of weather (8–16). With the shift back from malaria control to elimination and possible eradication (17–20), a number of current models are focusing on drug resistance (21, 22) and vaccine development (23).
The lack of data in many components of malaria transmission has restricted modelling efforts to a regional scale, since a significant pool of data is needed to test and fit the different sets of parameters. Even though available models are informative for developing global, regional or national malaria control strategies, they are limited in their applicability at local sites. However, local conditions are the main drivers of malaria transmission (24). Thus, better understanding of these conditions and transmission dynamics through modelling may be more informative and relevant for local control efforts.
This study elected to develop and validate a non-spatial dynamic model, driven by meteorological conditions, which can capture seasonal malaria transmission dynamics, at the scale of a single village. This was achieved by using comprehensive field data that included incident cases of human Plasmodium falciparum (Pf) malaria infection, as well as entomological and meteorological data. The focus for human infection was on children under five years, since they are the most vulnerable, and because most infections in this age group will be symptomatic and, therefore, more easily detected.
Methods
Study sites
This study was conducted in the town of Nouna and the villages of Cissé and Goni. These three sites are part of the Nouna Demographic Surveillance System (DSS) area (25). A detailed description of the study sites is given elsewhere (26).
Study population
A total of 676 children (Cissé: 171, Goni: 240 and Nouna: 265), aged 6–59 months, took part in this study. The children were selected in each site by systematic cluster sampling of households from the DSS database. A detailed description of the study population is given elsewhere (27).
Active case detection: Plasmodium falciparum infection
In each site, site-based interviewers visited the children weekly to assess their Pf malaria infection status and collect housing conditions data. The case detection methods are extensively described by Yé and colleagues (27).
The outcome measure was a Pf infection episode, defined as an axillary temperature of at least 37.5°C plus a positive malaria parasite test.
Entomological data
Mosquito population abundance was monitored by using a standard Center for Disease Control (CDC) Light Trap (LT) (28) from December 2003 through November 2004. Mosquitoes were captured on the first and second day of each month at each site in four randomly selected houses.
LTs fitted with incandescent bulbs were installed close to human volunteers sleeping under untreated mosquito nets in these houses for two consecutive nights from 18:00 to 06:00 hours. In addition, we used the Human Landing Collection (HLC) method, which involves one person sitting inside an uninhabited house and another outside, collecting mosquitoes that land on their exposed legs by using torchlight and test tubes. This was done in two shifts (18:00–24:00 hours and 24:00–06:00). HLC volunteers gave informed consent. They were given malaria prophylaxis and checked for fever for a fortnight after their participation in the study.
Field supervisors transported the mosquitoes caught to the laboratory in a cold-box. A technician in entomology counted and sorted the specimens by species. He classified mosquitoes caught by LT and HLC as ‘unfed’, ‘partly-fed’, ‘fully fed’, ‘semi-gravid’ or ‘gravid’ by external inspection (LT) or dissection (HLC). The technician checked for parity the ovaries of unfed HLC mosquitoes as described by Detinova (29) and Gilles and Warrell (30).
The age structure of the Anopheles gambiae population was assessed by calculating the parity (number of times eggs laid previously). A high fraction of nulliparous mosquitoes (mosquitoes that had never laid eggs) signifies a young population. This is used to estimate the proportion of infectious vectors to calculate the value of the infectious bite rate parameter.
Indoor human bite rates (3) were calculated for each month and site, as follows: Human bite rate: ma=Bs/P/n, where Bs is the number of A. gambiae caught indoors by HLT; P is the number of people involved in the capture and n is the total number of nights.
A. gambiae mortality (k-value) was calculated for each month and site. This expresses the number of vectors surviving from the egg stage to the adult stage. The monthly number of vectors was transformed into a natural logarithm. For a month with no vectors, the logarithm of one was calculated. Based on previous studies, we assumed the maximum number of eggs oviposited by individual mosquitoes was, e=100 eggs (31, 32) on average. To calculate k-value, the following formula (33) was used:
The resulting k-value was used to calculate the monthly mortality rate (m), an important parameter of our model, by using the formula: m=1−10−k-value.
Measurement of meteorological parameters
Three site-based meteorological units measured rainfall, temperature and relative humidity on the ground. Units were set for 10-second measurement cycles and 10-minute recording cycles. Details are given elsewhere (27).
Model development
Model description
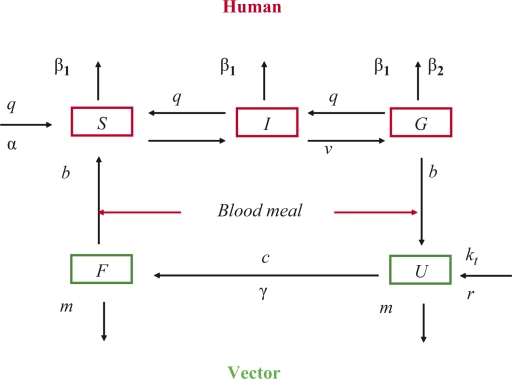
We used the so-called “compartmental model” developed by Ross (1) and adapted by MacDonald (3). These models were based on the assumption that the human population can be subdivided into three compartments: (1) susceptible (do not have malaria); (2) infected (have the parasite, but it has not yet developed to the gametocyte stage); and (3) infectious (are symptomatic and have the parasite at the gametocyte stage). Similarly, the vector population can be classified as: (1) susceptible (do not carry the parasite); (2) infected (fertilisation and sporogony); and (3) infectious (sporozoites in the salivary glands). The transmission process starts when an infected vector takes a blood meal from a human. The changes among the subpopulations in each compartment are determined by a set of parameters, like mosquito mortality, bite rate, growth rate, sporogony and gonotrophic cycle duration, and human malaria-induced mortality and parasite clearance rates. Most malaria models were constructed on these basic assumptions, as was the model by McKenzie and others (34) from which our model is derived. In our model, the mosquito population was divided into two subpopulations, non-infected and infected, since we assumed that every mosquito that feeds on an infected human would have 100% probability of becoming infectious if it survived long enough. The state and transition of the model (Fig. 1) shows the changes in each subpopulation given different parameters. These parameters are labelled with Greek characters and defined in Table 1. This model is an extension of a previous model, which was set to detect malaria in the dry season (35). That model was driven by entomological data and did not simulate the dynamics of the vector population. This current one has vector population dynamics, which is driven by temperature and rainfall. Since the dry season in the study region is characterised by total absence of rainfall, a model driven by rainfall would not have been appropriate to capture transmission. Appendix 1 provides the details of the mathematical expressions of the model and the specific assumptions.
Fig. 1.
State and transition of the dynamic model. Human: S, susceptible; I, infected; G, infectious. Vector: U, susceptible; F, infectious.
Table 1.
Definition of model parameters
| Parameters | Definition | Source |
|---|---|---|
| α | Daily natural per-capita human birth rate | DSS, recalculated in daily birth rate |
| β1 | Daily natural per-capita human death rate | DSS, recalculated in daily death rate |
| β2 | Daily malaria-induced per capita death rate in humans | Noun DSS, recalculated in daily death rate |
| q | Daily malaria clearance rate in humans | Fitted and compared with field data |
| v | Time delay for human host, from becoming infected to becoming infectious | Dietz et al. (4) |
| m | Daily mortality rate of vectors | Calculated and fitted |
| r | Daily mosquito per-capita intrinsic growth rate | Theoretical maximum of 10, precise value fitted from model |
| B | Daily bite rate of vectors | The lower bound if 1/gonotrophic cycle, precise value fitted from model |
| b | Daily rate at which vectors bite humans | b =B × HBI |
| γ | Daily probability of vector becoming infected after infectious bite | Fitted |
| c | Time delay for vector from infection to infectious stage | Sporogonic cycle, calculated using Detinova formula 111/(T°C –18) |
| Kt | Environmental carrying capacity | Kt=Pmm × akt |
Model implementation, prediction and testing
The model was driven by temperature, which defines the sporogonic and gonotrophic cycles, and by rainfall. Both meteorological values were used to calculate the carrying capacity (kt) described in Appendix 1. To train the model most of the parameters were estimated using field data collected in 2004. Because we did not have data for 2005, the outputs of the model, which consist of monthly mosquito numbers and cases of malaria infection, were compared with data from 2004. The model outputs were normalised to allow comparison with observed values. The normalisation was done by multiplying the monthly value of the model outputs with a constant obtained by dividing the highest value of the observed with the highest value of the model output.
The model was implemented in a Microsoft Excel spread sheet using a set of difference equations with one day step. Each of the variables representing the human and mosquito subpopulations was followed in a separate column. In addition, at each stage, the model calculated the daily changes of these variables. An offset function was used for processes with delay, such as mosquitoes becoming infectious at the end of the sporogonic cycle.
The model's goodness of fit Δ was determined by using the residual sum of squares (SS) of the difference between the predicted and the observed values of all months. The value of each parameter was determined successively by minimising SS (Table 2). This was continued for all parameters, until no further improvements in fit were possible, which was the common minimum for all parameters. Around the determined joint-optimal value for all parameters, each parameter was varied in turn to determine whether the fit was highly sensitive to the parameter values. A parameter was ‘sensitive’ if 10% variation in the parameter value caused 30% variation in Δ. This process was employed in lieu of sufficient data to allow calculation of confidence intervals. The Microsoft Excel ‘Solver Add-In’ function, which uses the Generalized Reduced Gradient (GRG2) method, was used for this process.
Table 2.
Model parameter values and bounds
| Parameters | Cissé [bounds] | Goni [bounds] | Nouna [bounds] |
|---|---|---|---|
| α | 0.000126 | 0.000126 | 0.000126 |
| β1 | 0.000096 | 0.000096 | 0.000096 |
| β2 | 0.000041 | 0.000041 | 0.000041 |
| q | 0.12 [0.10–0.17] | 0.12 [0.10–0.17] | 0.12 [0.10–0.17] |
| v | 10 days [9–15] | 10 days [9–15] | 10 days [9–15] |
| r | 2 | 2 | 2 |
| m | 0.15[0.06–0.20] | 0.15 [0.07–0.22] | 0.14[0.05–0.22] |
| b | 0.56[0.5–0.6] | 0.56[0.5–0.6] | 0.56[0.5–0.6] |
| γ | 0.79 | 0.79 | 0.79 |
| c | 10.6 days [9–14] | 13.3 days [9–14] | 9.9 days [9–14] |
The model predicted mosquito abundance and malaria incidence for each month and site for the year 2004. Output values were normalised versus the expected, by multiplying each predicted monthly value by a ratio which was obtained by dividing the observed highest value by the predicted value. The variances for the normalised prediction and observed values were calculated to assess the fit of the model for each site. Small variance suggests good representation of the field data by the model. The fit was also presented graphically, by plotting the monthly predicted and observed values.
Results
During follow up, out of the 676 children, 20 (3.0%) left the cohort, either because of death (11) or migration out of the study sites (9). Children were not always present at each visit; therefore, the overall person-years (PY) observed were 594.9.
Plasmodium falciparum malaria infection incidence
Out of 1,274 fever episodes, 635 were positive for Pf malaria infection, giving an infection incidence of 1.1 episodes per PY. The lowest incidence was observed in Nouna (0.8 per PY). In Cissé and Goni, the incidences were 1.2 and 1.3, respectively, but not significantly different. There was strong seasonal variation in the incidence, with higher rates in August and September (Table 3).
Table 3.
Plasmodium falciparum malaria infection incidence rates, per 1,000, per month and site
| Villages | ||||
|---|---|---|---|---|
| Months | Cissé | Goni | Nouna | All |
| Dec-03 | 159.2 | 122.0 | 88.9 | 136.6 |
| Jan-04 | 43.6 | 37.6 | 34.1 | 37.3 |
| Feb-04 | 137.9 | 38.1 | 57.5 | 69.1 |
| Mar-04 | 123.4 | 85.4 | 42.6 | 82.6 |
| Apr-04 | 14.6 | 59.2 | 125.3 | 72.0 |
| May-04 | 6.7 | 31.0 | 22.0 | 26.2 |
| Jun-04 | 6.3 | 29.1 | 12.4 | 20.9 |
| Jul-04 | 14.2 | 111.4 | 35.6 | 58.0 |
| Aug-04 | 268.6 | 220.7 | 83.2 | 220.2 |
| Sep-04 | 163.7 | 272.6 | 107.0 | 223.7 |
| Oct-04 | 129.6 | 200.1 | 126.5 | 152.5 |
| Dec-04 | 87.1 | 112.6 | 58.5 | 84.7 |
| Total | 1166.4 | 1278.7 | 692.1 | 1067.3 |
Entomological patterns
Using the LT and HLC method combined, with all species included across all sites, 16,657 mosquitoes were caught. The largest proportion of captured mosquitoes was Culex (72.19%), followed by A. gambiae (15.57%), Aedes (6.3%), Mansonia (4.6%), Anopheles funestus (1.5%) and Anopheles nili (0.1%). The highest number of A. gambiae was caught in Goni (n=1,431), followed by Cisse (n=598) and Nouna (n=565).
Meteorological conditions
All sites presented a similar pattern of meteorological conditions. The rainfall was concentrated in the months from May to October. The total amount of rainfall was higher in Nouna than in Cissé or Goni. The relative humidity pattern followed that of rainfall. The mean temperature was more or less similar in all sites. The average mean temperature for the whole period was lower in Goni, however, with high variation as compared to Cissé and Nouna. A detailed description of the meteorological conditions is given elsewhere (27).
Model simulation
Simulation of daily Anopheles gambiae abundance
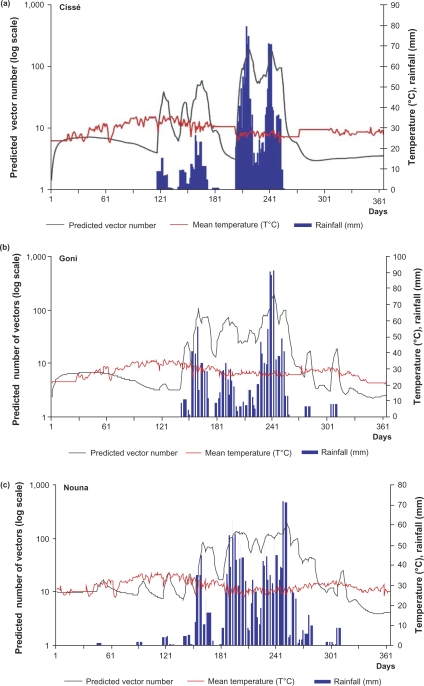
In all three sites, rainfall was followed by an increase in the mosquito population two weeks later (Fig. 2). In Cissé, mosquitoes were few (fewer than 10 per day) over the first 120 days of the year, corresponding to January through April. The first peak in mosquito numbers was observed on the 122nd day of the year, followed by a second peak, one month later. These peaks were all observed after a peak in rainfall. Two other peaks in mosquito abundance were observed after the second peak. These increases corresponded to July and August, months with high rainfall. From August on, the vector population decreased significantly and continued to do so towards the end of year, after the end of the rainy season.
Fig. 2.
Mean temperature and rainfall-based predictions of A. gambiae population abundance for each site: (a) Cissé, (b) Goni and (c) Nouna. Simulated A. gambiae population abundance (black curve) is plotted against the daily temperature (red curve) and the preceding two weeks’ cumulative rainfall (blue curve).
In Goni, the simulation produced several peaks in the vector population, following each peak in rainfall. As in Cissé, these peaks were clustered within a period from the 121st to 301st days of the year. This period corresponds with May through October. In contrast to Cissé, although there was some daily variation, the vector population remained high over this period, probably because of the higher amounts of rainfall. After the end of the rainy season, we observed a drop in the mosquito population.
The Nouna site had about the same pattern of mosquito abundance and distribution as Goni, even though rainfall was more abundant. The mosquito population increased shortly after the onset of the rainy season. It remained high (about 100/day), with some variation until the end of the rainy season, when levels decreased to less than 10 mosquitoes daily. As at the other two sites, the highest peak in the mosquito population was observed about two weeks after the highest peak of rainfall in August.
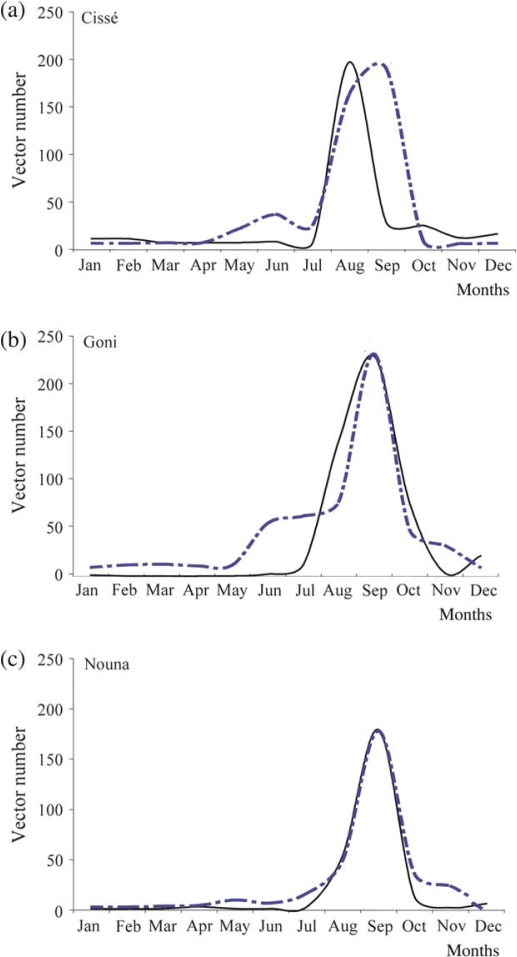
Monthly prediction of Anopheles gambiae abundance compared to observed vector numbers
The model predicted a peak in vector numbers for all sites in September, matching the observations for Goni and Nouna (Fig. 3). In Cissé, the peak in the number of caught mosquitoes was observed one month earlier, in August and this, therefore, did not match the prediction. Consistent across all sites, the model prediction matched with observed numbers from January through April, though the numbers were small. In June, in Cissé and Goni, there was a predicted increase in mosquito population which was not observed in the field. At all three sites, there was a significant decline (both predicted and observed) in the vector population in October, and both remained low in November and December.
Fig. 3.
Predicted monthly A. gambiae, compared to observed vector numbers in Cissé (a), Goni (b) and Nouna (c). The monthly prediction (broken line) of A. gambiae is compared with those caught in the field (full line).
Overall, the model predictions fit the observed data. The fit was better in Nouna, where we observed the least variance (Δ=∑(Oi×Pi)2=1696.5, SD=8.8); where O i is the observed number in the vector population in a month, and P i is the number predicted by the model. The variances for Goni and Cissé were 11,630.4 and 35,292.2, respectively.
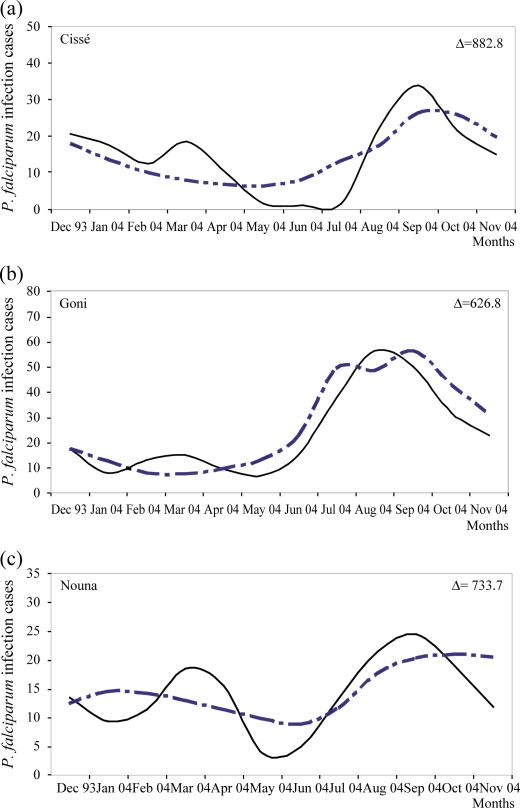
Monthly predicted Plasmodium falciparum malaria infection episodes compared to observed
Incident cases of Pf malaria infection among children were also simulated by the model, per site and per month (Fig. 4). For all sites, there was a seasonal pattern in Pf infection incidence. From December through June, the incidence decreased progressively, and then increased from July through September, after which another decrease was observed. Although the predicted and observed incidences were similar, there were some specific variations, expressed by the variation Δ. The model predictions matched the observed episodes better in Goni, where the smallest variance was observed (Δ=626.8, SE=6.6), versus Nouna (Δ=733.7, SE=4.8) and Cissé (Δ=882.8, SD=6.7).
Fig. 4.
Predicted monthly Plasmodium falciparum infection episodes versus observed episodes in Cissé (a), Goni (b) and Nouna (c). The monthly prediction (broken line) of episodes is compared with those observed in the field (full line).
Sensitivity of the model to different parameters
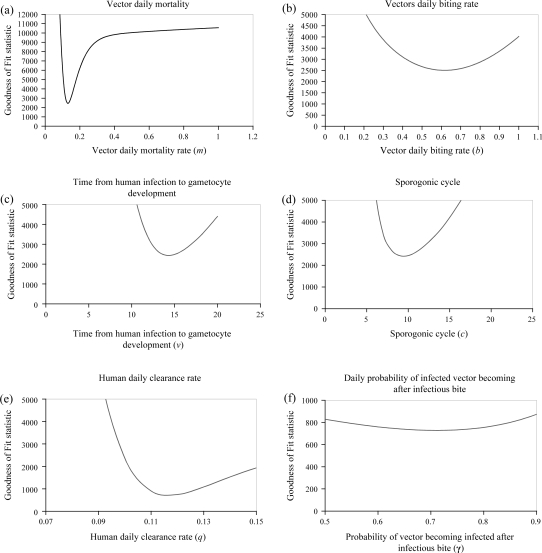
The dependence of the variance on the various parameters is presented in Fig. 5(a–f). Each parameter (X axis) is plotted against the variance (Y axis). The best value of the parameter is the one that causes the smallest variance. For instance in Fig. 5a: m shows that a value below 13% as well as values above cause high variance, but this stabilises after 40%; in Fig. 5b: the best value of b is 0.6 (one bite every two days); in Fig. 5c: the best value of v is 13 days; in Fig. 5d: the best value of c is nine days; in Fig. 5e: the best value of q is 11.6% and in Fig. 5f: the best value of γ is 71%.
Fig. 5.
Variation between the observed Plasmodium falciparum infection and the model output for single parameters.
Discussion
A dynamic model to predict malaria transmission among children under age five was developed. The model is composed of five difference equations that express changes in infectious status of the human and vector populations given temperature and rainfall conditions. The model simulated the vector population abundance and the human Pf malaria infection incidence for each of three ecological settings over one year. Most of the model parameters were calculated based on field data, and then fitted. The model was a good representation of Pf malaria infection in the region. The predicted mosquito populations and Pf malaria infection incidences were close to observed values.
Simulation of mosquito dynamics
Rainfall and temperature drive the vector population abundance. The dynamic model represented this adequately in all sites. Peak vector numbers observed about two weeks after a peak in rainfall are characteristic of the vector–rainfall relationship. Indeed, in ideal temperatures (28°C) and conditions, the development of A. gambiae from the egg to adult stage takes about 14 days (32, 36). The presence of water pools generated by rainwater allows the mosquitoes to lay their eggs, which then develop into adult mosquitoes if the water pools are sustained for at least 14 days. Some potential breeding sites could be expected in the area surrounding wells throughout the year. This is because of the constant spillage of water when people are fetching it. Sometimes, intentional pools are created for purposes of watering cattle. However, these pools are not common and only support a few mosquitoes. Because of the dry conditions in the area, the most important source of breeding sites remains rainfall water, and this explains the high abundance of mosquitoes during the rainy season. Rainfall was the main driver of vector abundance. As expected, in all sites the model detected few vectors (<10) during the dry season but vectors persisted, despite the total absence of rainfall during this season, probably because of breeding sites created around wells.
Monthly predictions of the number of vectors fit the numbers caught in the field, and, both predicted and observed numbers followed a similar pattern at all sites. This suggests that the model is a good representation of mosquito population dynamics. Some difference in the timing of peak abundance was observed in Cissé; where there was a deviation of one month between the predicted (September) and observed (August) peak. This may have been because of the soil texture in Cissé, which probably is not able to hold water on the surface long enough to allow vector development. However, this was not captured by the current model. Consistent across all sites, the model predicted vectors in May and June, though no vectors were observed in the field. This could be explained by the model being sensitive to any amount of rainfall; whereas, in the field, the quantity of rainfall in May and June was not enough to keep vector breeding sites.
Although the model produced a fair representation of the mosquito population, it could be improved by also simulating the immature stage (eggs, larvae and pupae) of the vector, which are strictly dependant on surface water availability. Mosquitoes need water to reproduce and the oviposition rate is assumed to be proportional to mosquito numbers and the daily rainfall filling local water pools (16). Further, direct correlation of rainfall amount with mosquito abundance could result in some estimation bias. This is because the availability and duration of surface water are also dependant upon the evaporation index, soil texture and moisture index. High evaporation will cause quick drying out of pools, whereas a lower consistency of soil texture and dry soil will lead to faster infiltration.
Simulation of Plasmodium falciparum malaria infection cases
Although some monthly differences were observed, probably due to the small number of cases, the general seasonal pattern was represented well by the model. However, the model is not sensitive to the sporogonic cycle. This implies that a small variation in ambient temperature would not result in major changes in incidence, and that time from human infection to gametocyte development is not a key in determining incidence rates.
The daily vector bite rate was found to be 0.56 per day. This would represent a gonotrophic cycle of 1.5 days, if every bite achieves a full blood meal. However, this is not always the case, as mosquitoes often return for second bites, if interrupted during their meal. Thus, the gonotrophic cycle may be longer than predicted by this model. The model is insensitive to precise values of b, (human bites per day) and this reduces the validity of the model as an estimator of gonotrophic cycle length. In addition, the model was developed assuming all vectors are anthropophillic, which is not necessarily the case. In fact, we expect this parameter to vary from one season to another (37).
The incidence of Pf malaria is dependent on two key parameters, which are the daily mortality rate of the vector and the parasite clearance rate in humans. These parameters can both be influenced by public health interventions. The daily mortality rate of the vector can be increased by vector control methods, such as indoor residual spraying, and vector numbers can be reduced by removing breeding sites. Effective treatment of patients will increase the malaria clearance rate in human (q), by protecting not only sick individuals, but also the surrounding population. The parasitological clearance rate (12%) was slightly slower than can be deduced from Müller and others (38), who witnessed 27% seven-day parasitological failure with chloroquine treatment. This would reflect 17% daily clearance. This discrepancy probably is a result of Müller and colleagues (38) having measured the asexual form clearance, while our focus was on the sexual form.
The model is driven by parasitological data for children under five, while the entire population contributes to the transmission. To account for this effect, we would need to survey the general population. This would require checking large numbers of asymptomatic individuals for subclinical infections. This raised technical and ethical issues. Nevertheless, it was assumed that parasite prevalence among children under five was not unlike that of the general population, even though clinical symptoms would not be present in many older individuals.
The model can be a useful tool for malaria control strategies especially in a low transmission context. It has the ability to quantify the context-specific risk of malaria, a precondition for cost-effective interventions. Although, the model was developed based on data collected in a specific context it can be used in a different setting. In that case the parameters would have to be measured locally and fitted without the need to change the model formulation. The fitting of the model was based on field data to make sure that mathematical formulae are plausible and describe the biological process of the transmission of the disease. For use in predicting malaria incidences in other settings, the critical inputs will be rainfall and temperature data, which nowadays can be obtained from satellite sources. Other parameters to be fitted may be obtained from the literature.
The strength of this model lies in its simplicity and its respect for the biological process of malaria transmission on the ground. However, to be cost-effective, the model's major drivers which are rainfall and temperature could be derived from remote sensing data as ground-based measurements are expensive to implement at local scale.
Although this is an academic work to reproduce the biological process of malaria transmission given different meteorological conditions, the ultimate aim is to produce a tool that can be used to refine malaria control strategies at health district level. The practical use of the model is in its prediction of the expected monthly number of malaria cases among under five children in different villages from given health districts based on rainfall and temperature data from either national meteorological stations or forecasting data from satellite. Such prior prediction of cases will help health planners at local level to better mobilise and allocate scarce resources to areas with most need. We plan to develop user-friendly software with the model in the background. The software will allow the input of basic data in order to produce the estimated monthly cases of malaria for different villages. However, we will first validate the model for different years within the frame of future studies that will generate relevant data for this purpose.
Conclusion
The model shows potential for local-scale seasonal prediction of Pf malaria infection rates and distribution. Thus, it could be used to understand malaria transmission dynamics, using meteorological parameters as a driving force, to help local district health bodies to identify the risk period for more focused interventions. However, we do not pretend to have captured 100% of the transmission dynamics. Further improvements to the model can be made.
Acknowledgements
The authors would like to express their gratitude to the Nouna Health Research Team and to participant's families.
Appendix 1. Model description
The dynamic concept in contrast to the static concept, tries to capture the transmission and biological processes of the disease. The model driven by temperature and rainfall was based on the assumption that the human population is divided into three categories: susceptible (S), malaria-infected (I) and infectious (G), and mosquito population is classified into two compartments: non-infections (U) and infectious, strongly affected by temperature and rainfall.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
Equations 1–3 describe the change in the human population while Equations 4 and 5 describe change in vector population. Each term is explained in detail below.
Change in uninfected human population:
| 1 |
Equation 1 describes the changes in the uninfected human population and includes four terms:
The first term is the natural growth rate which is expressed by α(S+I+G), assuming people are born healthy and irrespective of the health of the mother. As the model is simulated daily, this is expected to be negligible.
The second term is the malaria clearance expressed by q(I+G). We assume that people clear the infection at a fixed rate from all stages of the disease. We also assume that there is no immunity and no superinfection (additional infection starts after a new hepatic stage), contrary to Dietz et al. (4).
The third term is the human infection expressed by . It expresses the daily new infection within the human population. The expression is the probability of a single person not getting a bite from a specific mosquito; bF is the number of infectious mosquito biting in a day, given a daily biting rate per mosquito of b, is the probability of a specific person not getting bitten by any of the infectious mosquitoes. is the probability of a specific person getting bitten by one or more of infectious mosquitoes. Multiplying by S gives the number of uninfected peoples being bitten by at least one infectious mosquito in a day.
The fourth term β1 is the death rate in the population from all causes except malaria, assuming there is not link with malaria. Then β1 S is the number of death within the uninfected population.
In addition the following assumptions were made:
A mosquito bites only once in a gonotrophic cycle.
Mosquitoes bite randomly. No specific attraction to any subpopulation.
The stage of infection does not influence the mosquitoes biting habits.
An infectious bite necessarily causes Plasmodium falciparum infection.
Change in infected human population:
| 2 |
Equation 2 describes the changes in the infected (but not infectious) human population and includes three terms:
The first term is and as described above is the number of uninfected people being bitten by at least one infectious mosquito in a day.
The second term represents people that became infected v days ago. They have now mature gametocytes and are infectious. However, not all of those people are still available. They may have either died of malaria or other disease or they may have cleared their infection. For each day the probability of leaving the group early will be β1+β2+q. The probability of remaining in the group for a day is 1−(β1+β2+q). The probability of completing the whole process of v days is (1−(β1+β2+q))v.
The third term −(β1+β2+q)I represents the number of people that leave the infected stage by death or clearance.
In addition, the following assumptions were made:
β2 is constant and does not change according to the stage of the infection. We know the mortality could change per stage. We may leave it out of this equation for biological reasons.
q is not specific to the stage of the infection. We have two types of q clearance because of treatment and clearance because of immune system (natural clearance). We could also decide there is no natural clearance. We also know that drugs are stage specific (liver stage and blood stage).
Change in infectious human population:
| 3 |
Equation 3 describes the changes in the infectious human population and includes two terms:
The first term is described above.
The second term −(β1+β2+q)G represents the number of people that leave the infectious stage by death or clearance.
Change in the size of uninfected vector population:
| 4 |
Equation 4 describes the changes in the uninfected vector population and includes three terms:
The first term is the maturation of the larval stage. This term describes the number of larvae surviving to become mature mosquitoes. The numerator is the number of larvae expected to survive to maturity under ideal conditions. U+F is the total number of mosquitoes, assuming infectious status does not influence the fertility. r is the per mosquitoes fertility (number of eggs oviposited per day multiplied by the probability of each to develop into a mature mosquito under ideal condition). The denominator reflects the decrease in survival because of non-ideal conditions. The U+F expresses the density dependent limitation on larvae survival. The precise characteristic of this dependence is determined by the carrying capacity Kt. In principle, Kt varies with temperature, rainfall and humidity and should be measured from the field. Thus the number of larvae increases with the number of mosquitoes but is limited by carrying capacity. The number of the larvae surviving is dependent on the surface water available. As at this stage of research a full evapo-transpiration model is not available, K t is therefore assumed to be proportional to the previous weekly aggregated rainfall. K t =Pmm×akt. The value of akt is to be determined empirically.
The second term represents the new infections of mosquito at time t. bU is the number of uninfected mosquitoes biting in a day. The fraction is the probability of a single mosquito biting at random an infectious human out of the total human population. We multiply this by γ to reflect the probability of becoming infected.
The third term, mU, is the mortality of uninfected mosquitoes or the number of uninfected mosquitoes dying per day. m was calculated from the k-value (log generation mortality). In the study site setting, due to the constantly warm temperature, the gonotrophic cycle varies between two and three days. The survival of mosquitoes depends on the gonotrophic cycle and due to the stability of the cycle m was treated as constant. The precise value of m was empirically determined by fitting the model.
In addition the following assumptions were made:
Mosquitoes bite randomly and independent of their infectious status.
Survival is independent of the infectious status.
Change in the size of the infectious vector population:
| 5 |
Equation 5 describes the changes in the infected vector population and includes two terms:
The first term, is the number of mosquitoes infected c days ago, reduced by the survival. c is the sporogonic cycle given by Detinova (39) as 111/(T° −18).
The second term −mF is the number of infectious mosquitoes dying in a day.
In addition the following assumptions were made:
Infectious mosquitoes never clear their infectious status.
Mosquitoes are either infected or infectious.
Conflict of interest and funding
This project was co-funded by the German Research Council (DFG)- through the GK 793 program-University of Heidelberg and by the Union des Banques Suisses (UBS) Optimus Foundation.
References
- 1.Ross R. Studies on malaria. London: John Murray; 1928. [Google Scholar]
- 2.Utzinger J, Tozan Y, Singer BH. Efficacy and cost-effectiveness of environmental management for malaria control. Trop Med Int Health. 2001;6:677–87. doi: 10.1046/j.1365-3156.2001.00769.x. [DOI] [PubMed] [Google Scholar]
- 3.MacDonald G. Appendix I. Mathematical statement. In: MacDonald G, editor. The epidemiology and control of malaria. London: Oxford University Press; 1957. p. 201. [Google Scholar]
- 4.Dietz K, Molineaux L, Thomas A. Malaria model tested in the savannah. Bull World Health Organ. 1974;50:347–57. [PMC free article] [PubMed] [Google Scholar]
- 5.Molineaux L, Gramiccia G. The Garki project. Geneva: World Health Organization; 1980. pp. 1–311. [Google Scholar]
- 6.McKenzie FE, Samba EM. The role of mathematical modeling in evidence-based malaria control. Am J Trop Med Hyg. 2004;71:94–6. [PMC free article] [PubMed] [Google Scholar]
- 7.Halloran ME, Struchiner CJ, Spielman A. Modelling malaria vaccines. II: population effects of stage-specific malaria vaccines dependent on natural boosting. Math Biosci. 1989;94:115–49. doi: 10.1016/0025-5564(89)90074-6. [DOI] [PubMed] [Google Scholar]
- 8.RanDolph SE, Rogers DJ. Satellite data and disease transmission by vectors: the creation of maps for risk prediction. Bull Soc Pathol Exot. 2000;93:207. [PubMed] [Google Scholar]
- 9.Kleinschmidt I, Sharp BL, Clarke GP, Curtis B, Fraser C. Use of generalized linear mixed models in the spatial analysis of small-area malaria incidence rates in Kwazulu Natal, South Africa. Am J Epidemiol. 2001;153:1213–21. doi: 10.1093/aje/153.12.1213. [DOI] [PubMed] [Google Scholar]
- 10.Hay SI, Omumbo JA, Craig MH, Snow RW. Earth observation, geographic information systems and Plasmodium falciparum malaria in sub-Saharan Africa, remote sensing and geographical information system in epidemiology. Adv Parasitol. 2000;47:173–215. doi: 10.1016/s0065-308x(00)47009-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rogers DJ, Randolph SE, Snow RW, Hay SI. Satellite imagery in the study and forecast of malaria. Nature. 2002;415:710–5. doi: 10.1038/415710a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Craig MH, Snow RW, le Sueur D. A climate-based distribution model of malaria transmission in sub-Saharan Africa. Parasitol Today. 1999;15:105–11. doi: 10.1016/s0169-4758(99)01396-4. [DOI] [PubMed] [Google Scholar]
- 13.MARA/ARMA. Towards an atlas of malaria risk in Africa; First technical reports of the MARA/ARMA collaboration; Durban: 1998. [Google Scholar]
- 14.Martens WJ, Niessen LW, Rotmans J, Jetten TH, McMichael AJ. Potential impact of global climate change on malaria risk. Environ Health Perspect. 1995;103:458–64. doi: 10.1289/ehp.95103458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lindsay SW, Martens WJ. Malaria in the African highlands: past, present and future. Bull World Health Organ. 1998;76:33–45. [PMC free article] [PubMed] [Google Scholar]
- 16.Hoshen MB, Morse AP. A weather-driven model of malaria transmission. Malaria J. 2004;3:32. doi: 10.1186/1475-2875-3-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hommel M. Towards a research agenda for global malaria elimination. Malar J. 2008;7:S1. doi: 10.1186/1475-2875-7-S1-S1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Aguas R, White LJ, Snow RW, Gomes MG. Prospects for malaria eradication in sub-Saharan Africa. PLoS One. 2008;12:3. doi: 10.1371/journal.pone.0001767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Greenwood B. Can malaria be eliminated? Trans R Soc Trop Med Hyg. 2009;103:S2–5. doi: 10.1016/j.trstmh.2008.10.027. [DOI] [PubMed] [Google Scholar]
- 20.Maude RJ, Pontavornpinyo W, Saralamba S, Dondorp AM, Day NP, White NJ, et al. The role of mathematical modelling in malaria elimination and eradication (Comment on: Can malaria be eliminated?) Trans R Soc Trop Med Hyg. 2009;103:643–4. doi: 10.1016/j.trstmh.2009.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Koella JC, Antia R. Epidemiological models for the spread of anti-malarial resistance. Malar J. 2003;2:3. doi: 10.1186/1475-2875-2-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.White LJ, Maude RJ, Pongtavornpinyo W, Saralamba S, Aguas R, Effelterre TV, et al. The role of simple mathematical models in malaria elimination strategy design. Malar J. 2009;8:212. doi: 10.1186/1475-2875-8-212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fabrizio T, Nicolas M, Melissa P, Alain S, Thomas AS. Simulation of the cost-effectiveness of malaria vaccines. Malar J. 2009;8:127. doi: 10.1186/1475-2875-8-127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Garnham PCC. Malaria in Kisumu, Kenya colony. J Trop Med Hyg. 1929;32:207–16. [Google Scholar]
- 25.Yé Y, Sanou A, Gbangou A, Kouyaté B. Chapter 19 Nouna DSS. Canada: IDRC; 2002. INDEPTH. Demography and health in developing countries. Volume 1. Population, health and survival at INDEPTH sites. [Google Scholar]
- 26.Yé Y, Kyobutungi C, Louis RV, Sauerborn R. Micro-epidemiology of Plasmodium falciparum malaria: is there any difference in transmission risk between neighbouring villages? Malar J. 2007;6:46. doi: 10.1186/1475-2875-6-46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yé Y, Louis V, Simoboro S, Sauerborn R. Effect of meteorological factors on clinical malaria risk among children, using village-based meteorological stations and community-based parasitological survey. BMC Pub Health. 2007;7:101. doi: 10.1186/1471-2458-7-101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cano J, Berzosa PJ, Roche J, Rubio JM, Moyano E, Guerra-Neira A, et al. Malaria vectors in the Bioko Island (Equatorial Guinea): estimation of vector dynamics and transmission intensities. J Med Entomol. 2004;41:158–61. doi: 10.1603/0022-2585-41.2.158. [DOI] [PubMed] [Google Scholar]
- 29.Detinova TS. 1963. Méthodes à appliquer pour classer par groupes d’âge les diptères présentant une importance médicale. [Age-grouping methods in Diptera of medical importance] Geneva: Ser Monogr WHO No. 27. [Google Scholar]
- 30.Gilles HM, Warrell DA. Bruce-Chwatt's essential malariology. 3rd ed. London: Edward Arnold; 1993. [Google Scholar]
- 31.Takken W, Klowden MJ, Chambers GM. Effect of body size on host seeking and blood meal utilization in Anopheles gambiae sensu stricto (Diptera: Culicidae): the disadvantage of being small. J Med Entomol. 1998;35:639–45. doi: 10.1093/jmedent/35.5.639. [DOI] [PubMed] [Google Scholar]
- 32.Depinay JM, Mbogo CM, Killeen G, Knol B, Beier J, Carlson J, et al. A simulation model of African Anopheles ecology and population dynamics for the analysis of malaria transmission. Malar J. 2004;3:29. doi: 10.1186/1475-2875-3-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rogers DJ. Estimation of the mortalities of the immature stage. In: Youdeowei A, Service MW, editors. Pest and vector management in the tropics with particular reference to insects, ticks, mites and snails. London: Longman; 1983. pp. 139–59. [Google Scholar]
- 34.McKenzie FE, Wong RC, Bossert WH. Discrete-event simulation models of Plasmodium falciparum malaria. Simulation. 1998;71:250–61. doi: 10.1177/003754979807100405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yé Y, Sauerborn R, Simoboro S, Hoshen M. Using modelling to assess malaria infection risk during the dry season on a local scale in an endemic area of rural Burkina Faso. Ann Trop Med Parasitol. 2007;101:375–89. doi: 10.1179/136485907X176490. [DOI] [PubMed] [Google Scholar]
- 36.Jepson WF, Moutia A, Courtois C. The malaria problem in Mauritius: the binomics of Mauritian Anophelines. Bull Entomol Res. 1947;38:177–208. doi: 10.1017/s0007485300030273. [DOI] [PubMed] [Google Scholar]
- 37.Awolola TS, Okwa OO, Hunt RH, Ogunrinade AF, Coetzee M. Dynamics of the malaria vector populations in coastal Lagos, south-western Nigeria. Ann Trop Med Parasitol. 2002;96:75–82. doi: 10.1179/000349802125000538. [DOI] [PubMed] [Google Scholar]
- 38.Müller O, Traoré C, Becher H, Kouyate B. Malaria morbidity, treatment-seeking behaviour, and mortality in a cohort of young children in rural Burkina Faso. Trop Med Int Health. 2003;8:290–6. doi: 10.1046/j.1365-3156.2003.01030.x. [DOI] [PubMed] [Google Scholar]
- 39.Detinova TS. Age-grouping methods in Diptera of medical importance with special reference to some vectors of malaria. 1962. Geneva: Monogr Ser WHO No 47. [PubMed] [Google Scholar]