Abstract
The protein inference problem represents a major challenge in shotgun proteomics. In this article, we describe a novel Bayesian approach to address this challenge by incorporating the predicted peptide detectabilities as the prior probabilities of peptide identification. We propose a rigorious probabilistic model for protein inference and provide practical algoritmic solutions to this problem. We used a complex synthetic protein mixture to test our method and obtained promising results.
Key words: algorithms, alignment, combinatorial proteomics, computational molecular biology, databases, mass spectroscopy, proteins, sequence analysis
1. Introduction
In shotgun proteomics, a complex protein mixture derived from a biological sample is directly analyzed via a sequence of experimental and computational procedures (Aebersold and Mann, 2003; McDonald and Yates, 2003; Kislinger and Emili, 2005; Swanson and Washburn, 2005). After protease digestion, liquid chromatography (LC) coupled with tandem mass spectrometry (MS/MS) is typically used to separate and fragment peptides from the sample, resulting in a number of MS/MS spectra. These spectra are subsequently searched against a protein database to identify peptides present in the sample (Marcotte, 2007; Nesvizhskii, 2007). Many peptide search engines have been developed, among which Sequest (Yates et al., 1995), Mascot (Perkins et al., 1999), and X!Tandem (Craig and Beavis, 2004) are commonly used. However, after a reliable set of peptides is identified, it is often not straightforward to assemble a reliable list of proteins from these peptides. This occurs because some identified peptides, referred to as the degenerate peptides, are shared by two or more proteins in the database. As a result, the problem of determining which of the proteins are indeed present in the sample, known as the protein inference problem (Nesvizhskii and Aebersold, 2005), often has multiple solutions and can be computationally intractable. Nesvizhskii et al. (2003) first addressed this challenge using a probabilistic model, but different problem formulations and new solutions have recently been proposed as well (Nesvizhskii and Aebersold, 2005; Alves et al., 2007; Zhang et al., 2007).
Previously, we introduced a combinatorial approach to the protein inference problem that incorporates the concept of peptide detectability, i.e., the probability of a peptide to be detected (identified) in a standard proteomics experiment, with the goal of finding the set of proteins with the minimal number of missed peptides (Alves et al., 2007). As in the other combinatorial formulations (Zhang et al., 2007), the parsimony condition was chosen only for convenience reasons, without theoretical justification. Furthermore, parsimonious formulations often lead to the minimum cover set problem, which is NP-hard. Thus, heuristic algorithms following greedy (Alves et al., 2007) or graph-pruning strategies (Zhang et al., 2007) are used to solve the protein inference problem without performance guarantee.
In this article, we address protein inference by proposing a novel Bayesian approach that takes as input a set of identified peptides from any peptide search engine, and attempts to find a most probable set of proteins from which those identified peptides originated. We considered two Bayesian models in our approach. The basic model assumes that all identified peptides are correct, whereas the advanced model also accepts the probability of each peptide to be correctly identified in the sample by spectrum matching. Compared with the previous probabilistic models, such as ProteinProphet (Nesvizhskii et al., 2003), both of our models differ in two key aspects. First, our approach incorporates the prior probability of peptide identification (Tang et al., 2006), since it has been recently shown that even among the peptides that belong to the same protein, some peptides are commonly observed, while some others are not (Tang et al., 2006; Lu et al., 2007). This results in the fact that the peptides not identified by peptide search engines may have significant impact on the final solution. Second, we devise a rigorious model to incorporate dependences between the identification of peptides in the computation of the protein posterior probabilities and adopt a Gibbs sampling approach to estimate them. The results of this study provide evidence that our models achieve satisfactory accuracy and can be readily used in protein identification.
2. Methods
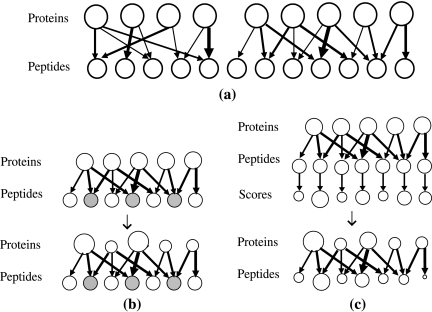
To illustrate the challenge of protein inference, we define the protein configuration graph (Fig. 1a), i.e., a bipartite graph in which two disjoint sets of vertices represent the proteins in the database and the peptides from these proteins, respectively, and where each edge indicates that the peptide belongs to the protein. We emphasize that the protein configuration graph is independent of the proteomics experiment, and thus can be built solely from a set (database) of protein sequences. Therefore, in constrast to the bipartite graph used previously (Zhang et al., 2007), where only the identified peptides and the proteins that contain those peptides were represented, our model also considers the non-identified peptides. A protein configuration graph is partitioned into connected components, each representing a group of proteins (e.g., homologous proteins) sharing one or more (degenerate) peptides. If there are no degenerate peptides in the database, each connected component will contain exactly one protein and its peptides. In practice, however, the protein configuration graph may contain large connected components, especially for protein databases of higher animals or those containing closely related species.
FIG. 1.
(a) A protein configuration graph consisting of two connected components. (b) Basic Bayesian model for protein inference, in which peptides are represented as a vector of indicator variables: 1 (gray) for identified peptides, and 0 (white) for non-identified peptides. (c) Advanced Bayesian model for protein inference, in which each peptide is associated to an identification score (0 for non-identified peptides). Sizes of circles reflect prior/posterior probabilities.
Given that the protein configuration graph can be interpreted as a Bayesian network with edges pointing from proteins into peptides, it is straightforward to show that protein inference can be addressed separately for each individual connected component. In this approach, the peptide identification results are first mapped to the protein configuration graph. We use a vector of indicator variables 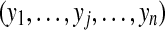 , referred to as the peptide configuration, to denote a set of identified peptides. Given the peptide configuration, the protein configuration graph can be simplified by removing proteins containing no identified peptides. We note, after the simplification, one connected component in the original protein configuration graph may be partitioned into several small components. A connected component is called trivial if it contains no identified peptides. Clearly, in this case protein inference is simple—none of the proteins should be present in the sample. Therefore, the protein inference problem can be reduced to finding the most likely protein configuration
, referred to as the peptide configuration, to denote a set of identified peptides. Given the peptide configuration, the protein configuration graph can be simplified by removing proteins containing no identified peptides. We note, after the simplification, one connected component in the original protein configuration graph may be partitioned into several small components. A connected component is called trivial if it contains no identified peptides. Clearly, in this case protein inference is simple—none of the proteins should be present in the sample. Therefore, the protein inference problem can be reduced to finding the most likely protein configuration 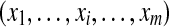 by analyzing non-trivial components only. In the basic model, all identified peptides are assigned equal probabilities (= 1) (Fig. 1b), whereas in the advanced model different probabilities are considered for different identified peptides depending on the associated identification scores
by analyzing non-trivial components only. In the basic model, all identified peptides are assigned equal probabilities (= 1) (Fig. 1b), whereas in the advanced model different probabilities are considered for different identified peptides depending on the associated identification scores 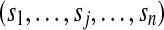 (Fig. 1c). Notation and definitions used in this study are summarized in Table 1.
(Fig. 1c). Notation and definitions used in this study are summarized in Table 1.
Table 1.
Notations and Definitions
| Notation | Definition |
|---|---|
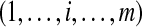 |
m proteins within a non-trivial connected component of the protein configuration graph |
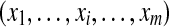 |
protein configuration: indicator variables of proteins' presences |
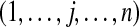 |
all n peptides from m proteins being considered |
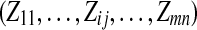 |
indicator variables of peptide j belonging to protein i if peptide j is a peptide from protein i, Zij = 1; otherwise Zij = 0 |
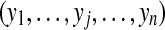 |
peptide configuration: indicator variables of peptides' presences if peptide j is present, yj = 1; otherwise yj = 0 |
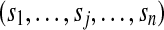 |
assigned scores of peptides if peptide j is not identified, sj = 0 |
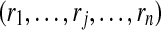 |
probabilities of peptides being correctly identified also the estimated probabilities of peptides' presences |
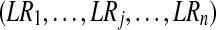 |
likelihood ratio between peptides's presences and absences |
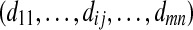 |
prior probabilities of peptides to be identified from proteins if Zij = 1, dij = the detectability of peptide j from protein i; otherwise, dij = 0 |
2.1. Basic Bayesian model
The basic model can be considered as a special case of the advanced model, in which the probabilities rj for different peptides j are limited to 0 (for non-idenfitied peptides) or 1 (for identified peptides). We first describe the basic model that formalizes the protein inference problem illustrated above, and will extend it to the advanced model in the next section. In practice, the basic model can be used if the probabilities rj are not provided, while the identified peptides are obtained at a stringent false discovery rate (FDR), e.g., 0.01, by either a heuristic target-decoy search strategy (Elias et al., 2005; Zhang et al., 2007; Elias and Gygi, 2007) or by probabilistic modeling of random peptide identification scores (Keller et al., 2002; Wu et al., 2006; Bern and Goldberg, 2007). In the next section, we extend this basic model to a more realistic model in which we incorporate different probabilities for different identified peptides that are estimated based on the peptide identification scores. When the probabilities of identified peptides are available, we expect the advanced model should perform better than the basic model.
Let us now consider m proteins and n peptides from these proteins within a non-trivial connected component of the protein configuration graph. Each protein i is either present in the sample or absent from it, which can be represented by an indicator variable xi. Therefore, any solution of the protein inference problem corresponds to a vector of indicator variables, 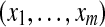 , referred to as a protein configuration. Given the set of identified peptides from peptide search engines (peptide configuration
, referred to as a protein configuration. Given the set of identified peptides from peptide search engines (peptide configuration 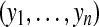 ), our goal is to find the maximum a posteriori (MAP) protein configuration, that is the configuration that maximizes the posterior probability
), our goal is to find the maximum a posteriori (MAP) protein configuration, that is the configuration that maximizes the posterior probability 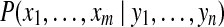 ,
,
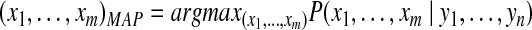 |
(1) |
Using Bayes' rule, the posterior probability can be expressed as
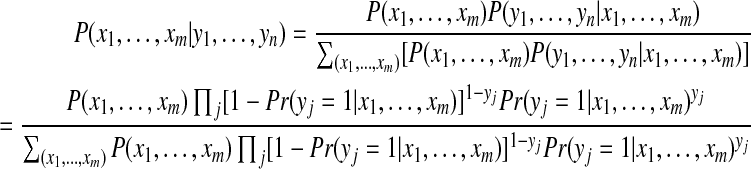 |
(2) |
where 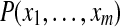 is the prior probability of the protein configuration. Assuming the presence of each protein i is independent of other proteins, this prior probability can be computed as
is the prior probability of the protein configuration. Assuming the presence of each protein i is independent of other proteins, this prior probability can be computed as
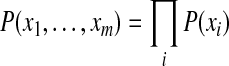 |
(3) |
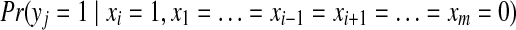 is the probability of peptide j to be identified by shotgun proteomics given the protein configuration
is the probability of peptide j to be identified by shotgun proteomics given the protein configuration 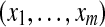 . Assuming that different proteins contribute independently to the identification of a peptide, we can compute it as
. Assuming that different proteins contribute independently to the identification of a peptide, we can compute it as
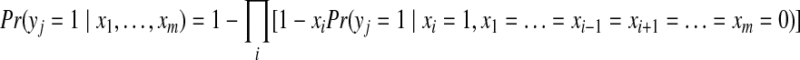 |
(4) |
where 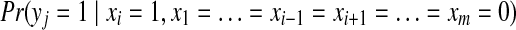 is the probability of peptide j to be identified if only protein i is present in the sample. As we previously showed, for a particular proteomics platform (e.g., LC-MS/MS considered here), this probability, referred to as the standard peptide detectability dij, is an intrinsic property of the peptide (within its parent protein), and can be predicted from the peptide and protein sequence prior to a proteomics experiment (Tang et al., 2006). Combining equations 2–4, we can compute the posterior probabilities for protein configurations as
is the probability of peptide j to be identified if only protein i is present in the sample. As we previously showed, for a particular proteomics platform (e.g., LC-MS/MS considered here), this probability, referred to as the standard peptide detectability dij, is an intrinsic property of the peptide (within its parent protein), and can be predicted from the peptide and protein sequence prior to a proteomics experiment (Tang et al., 2006). Combining equations 2–4, we can compute the posterior probabilities for protein configurations as
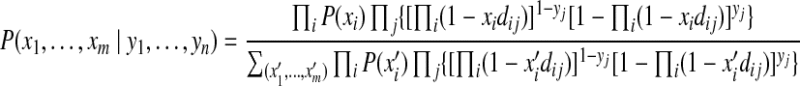 |
(5) |
Sometimes, we are also interested in the marginal posterior probability of a specific protein i to be present in the sample, which can be expressed as,
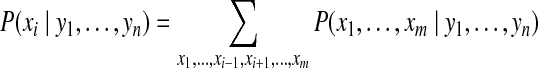 |
(6) |
2.2. Advanced Bayesian model
The basic model described above requires that all identified peptides have equal probability (= 1) of being correctly identified. Here we relax this assumption by introducing into the model a peptide identification score sj for each peptide j, which is the output of the peptide search engines. We assume the peptide identification score is highly correlated with the probability of a peptide being correctly identified and their relationship (denoted by 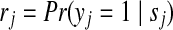 ) can be approximately modeled using probabilistic methods adopted by some search engines such as Mascot (Perkins et al. (1999)) or post-processing tools such as PeptideProphet (Keller et al. (2002)). Our goal is to compute
) can be approximately modeled using probabilistic methods adopted by some search engines such as Mascot (Perkins et al. (1999)) or post-processing tools such as PeptideProphet (Keller et al. (2002)). Our goal is to compute 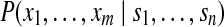 by enumerating all potential peptide configurations
by enumerating all potential peptide configurations
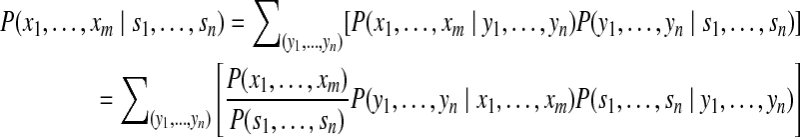 |
(7) |
Assuming that sj is independent of the presences of the other peptides (i.e. 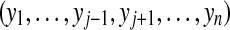 ) for each peptide j, we have
) for each peptide j, we have
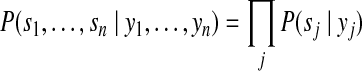 |
(8) |
and applying Bayes' rule, we have
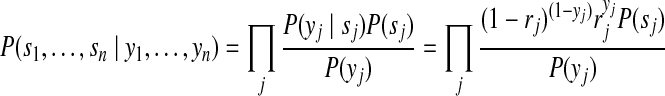 |
(9) |
where the marginal probability of a peptide j can be computed as
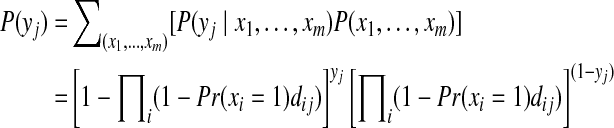 |
(10) |
Combining these equations, we can compute the posterior probability of protein configurations as
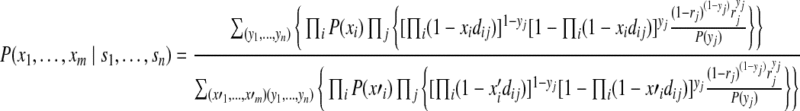 |
(11) |
If we do not assume any prior knowledge about the protein presence in the sample, we can set Pr(xi) = 0.5 in equations 5 and 11. In practice, prior knowledge, such as the species which the sample is from, the number of candidate proteins, and known protein relative quantities or protein families that are likely present in the sample, can be directly integrated into our Bayesian models. In the result section, we demonstrate this by applying 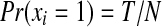 to all candidate proteins, where T is the estimated number of actual proteins in the sample, and N is the total number of candidate proteins in the database containing at least one identified peptide (Table 2).
to all candidate proteins, where T is the estimated number of actual proteins in the sample, and N is the total number of candidate proteins in the database containing at least one identified peptide (Table 2).
Table 2.
Number of MS/MS Spectra, Candidate Peptides, Candidate Proteins, and True Proteins in Each of the Three Sigma49 Datasets
| Experiment | No. of spectra | No. of candidate peptides | No. of candidate proteins | Estimated nos. of true proteins | No. of proteins for detectability training | Protein prior |
|---|---|---|---|---|---|---|
| 1 | 5297 | 739 | 514 | 55 | 25 | 55/514 |
| 2 | 5155 | 684 | 481 | 55 | 22 | 55/481 |
| 3 | 5034 | 626 | 393 | 50 | 19 | 50/393 |
The peptides with Peptide-Prophet probability >0.05 were considered as candidate peptides, and the proteins containing at least one candidate peptide were considered as candidate proteins. The number of true proteins is estimated by a preliminary run of the Bayesian inference algorithm. Protein prior represents the prior probabilities of proteins used in the Bayesian model.
Similarly, as in the basic model, we can also compute the posterior probability of a specific protein i present in the sample as
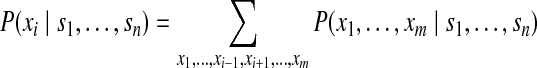 |
(12) |
and the marginal posterior probability of a peptide j as
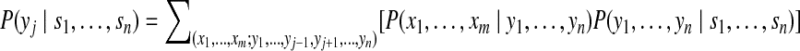 |
(13) |
2.3. Adjustment of peptide detectabilities
An adjustment of the predicted peptide detectabilities is necessary when applying them here, since the predicted standard peptide detectabilities (denoted as 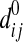 ) reflect the detectability of a peptide under a standard proteomics experimental setting, in particular, under fixed and equal abundances (i.e. q0) for all proteins (Tang et al., 2006). Assuming that the abundance of protein i in the sample mixture is qi instead of q0, the effective detectability of peptide j from this protein should be adjusted to
) reflect the detectability of a peptide under a standard proteomics experimental setting, in particular, under fixed and equal abundances (i.e. q0) for all proteins (Tang et al., 2006). Assuming that the abundance of protein i in the sample mixture is qi instead of q0, the effective detectability of peptide j from this protein should be adjusted to
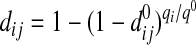 |
(14) |
Although we do not know qi explicitly, since the probability of a peptide j being correctly identified is given by rj (or yj for basic model), we can estimate qi by solving the equation  for a specific protein i. We note that this adjustment method may immediately lead to a new approach to absolute protein quantification (Lu et al., 2007). However, we will address the evaluation of its performance in our future work. Here, our goal is to utilize it to adjust the predicted standard peptide detectabilities based on the estimated protein abundances.
for a specific protein i. We note that this adjustment method may immediately lead to a new approach to absolute protein quantification (Lu et al., 2007). However, we will address the evaluation of its performance in our future work. Here, our goal is to utilize it to adjust the predicted standard peptide detectabilities based on the estimated protein abundances.
2.4. Gibbs sampling
Given a protein configuration graph, the peptide detectabilities (dij), and the probabilities of peptides being correctly identified (rj), the posterior distribution of protein configurations can be computed directly from equations 5 or 11, depending on which Bayesian model is used. This brute force method, which has computational complexity of O(2m) (for the basic model) or O(2m+n) (for the advanced model), is very expensive and only works for small connected components in the protein configuration graph.
Gibbs sampling is a commonly used strategy to approximate a high-dimensional joint distribution that is not explicitly known (Geman and Geman, 1984; Liu, 2002). We adopted this algorithm to achieve the optimal protein configuration with the MAP probability. The original Gibbs sampling algorithm considers one individual variable at a time in the multi-dimentional distribution. It, however, often converges slowly and is easily trapped by local maxima for long time. Several techniques have been proposed to improve the search efficiency of Gibbs sampling algorithm, such as random sweeping, blocking, and collapsing (Liu, 2002). Because in our case each variable xi to be sampled has small search space (i.e., {0,1}), we applied the block sampling technique in our Gibbs sampler algorithm (Algorithm 1). Without increasing the computational complexity, we adopt a novel memorizing strategy that keeps a record of all (as well as the maximum) posterior probabilities (and the corresponding protein configurations) among all configurations we evaluated during the sampling procedure, and report the maximum solution in the end. The memorized posterior probabilities are also used to calculate the marginal posterior protein probabilities in equations 6, 12, and 13. We sketched the block Gibbs sampling algorithms and the memorizing approach in Algorithm 1 for the advanced Bayesian model. A similar but simplified Gibbs sampling algorithm can be used for the basic Bayesian model.
Algorithm 1.
Gibbs sampler for protein inferencing using the advanced model
Input : Probabilities of correct peptide identification  and peptide detectabilities and peptide detectabilities  |
Output :MAP protein configuration  |
Initialize 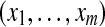 and and 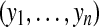 randomly; randomly; |
|
MaxPr ← 0; |
|
whilenot convergedo |
| c ← a random number between 0 and t; |
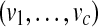 ← a random c-block from ← a random c-block from 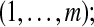 |
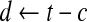 |
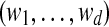 ← a random d-block from ← a random d-block from 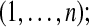 |
Compute normalizing factor 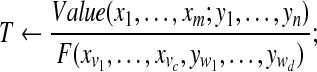 |
| #Note: for the 1st iteration, set T ← 1; |
forall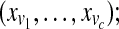 and and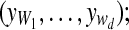 do do |
Compute 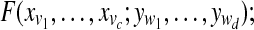 |
memorizing: 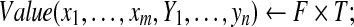 |
if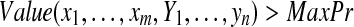 then then |
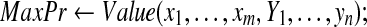 |
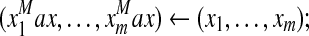 |
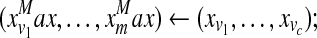 |
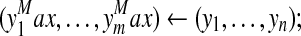 |
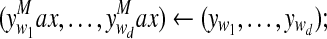 |
| end |
| end |
Sample 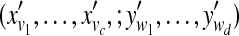 from normalized from normalized 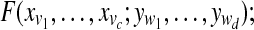 |
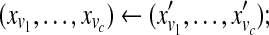 |
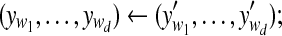 |
|
end |
Report MaxPr, 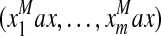 , and compute marginal probabilities; , and compute marginal probabilities; |
In these two algorithms discussed here, we have the following:
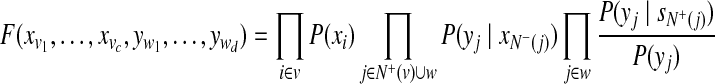 |
(15) |
where N+(.) represents the set of peptide nodes in the protein configuration graph that the current protein node (.) is linked, whereas N−(.) represent the set of protein nodes that the current peptide node (.) is linked; 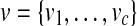 and
and 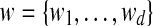 are the indeces of blocks for protein x and peptide y, repectively. For the basic model, the set of blocks w is empty (or d = 0). Hence,
are the indeces of blocks for protein x and peptide y, repectively. For the basic model, the set of blocks w is empty (or d = 0). Hence, 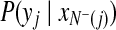 can be computed by equation 4, and
can be computed by equation 4, and 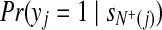 are set to rj.
are set to rj.
2.5. Datasets
We used three datasets from replicated LC/MS/MS analysis of a synthetic mixture of 49 standard proteins (called Sigma49), which was made available by Sigma Corporation for the assessment of protein analysis protocols. Tandem mass spectra of all three experiments were downloaded from the website at Vanderbilt University (Zhang et al., 2007).
3. Results
As in Zhang et al. (2007), prior to the protein inference, the MS/MS spectra acquired from Sigma49 sample in one LC/MS experiment were searched against the human proteome in Swiss-Prot database (version 54.2). PeptideProphet (Keller et al., 2002) was then used to assign a probability score for each identified peptide. To compute the peptide detectability, we trained separate predictors (neural networks) for each of three experiments. For each experiment, a protein is included in the training set only if (1) it contains at least two confidently identified peptides (i.e., PeptideProphet probability >0.95); and (2) it does not share any identified peptide (with PeptideProphet probability >0.05) with other proteins. The positive (detected) and negative (non-detected) training sets were composed of peptides from these proteins with PeptideProphet probability >0.90 and <0.10, respectively. The remaining peptides (with PeptideProphet probability between 0.1 and 0.9) were not used for training. To incorporate the changes of detectability due to the variation of protein abundances, we employed the quantity adjustment method described in previous section to obtain the standard peptide detectability, which is presumably equivalent to the detectability of a peptide at the standard abundance. After the predictors were trained, we used them to compute the standard detectabilities for all tryptic peptides from all proteins, which were subsequencely used in the Bayesian inference algorithms. Table 2 shows the details of the training datasets for each of the three experiments.
To set the probability rj for each peptide identification, we first converted the PeptideProphet probability into a likelihood ratio 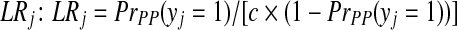 , where PrPP (yj = 1) is the PeptideProphet probability, and c is the ratio between the prior probabilities of the peptide's presence and absence; and then converted LRj to
, where PrPP (yj = 1) is the PeptideProphet probability, and c is the ratio between the prior probabilities of the peptide's presence and absence; and then converted LRj to 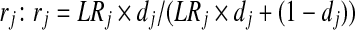 . For both models, we used block size 3 in the Gibbs sampler.
. For both models, we used block size 3 in the Gibbs sampler.
In the extended abstract of this work presented at RECOMB meeting (Li et al., 2008), we have compared the protein inference performances of the basic and advanced Bayesian models with that from ProteinProphet (Nesvizhskii et al., 2003) and the minimum missed peptide (MMP) approach we proposed previously (Alves et al., 2007) on the set of peptides identified using +2 precursor ions in Sigma49 sample. We concluded that the advanced Bayesian model gives better results than the basic model and previous published methods. We also showed the adjustment of peptide quantity and the incorporation of expected number of proteins into the protein prior estimation can improve the performance of protein inference. Here we extended our model in order to utilize all identified peptides regardless of their charge states. We note that all details of our model remain the same except that the detectability of a peptide is redefined as the probability of identifying this peptide as +1, +2 or +3 charged ions instead of +2 charged ions only in our previous model. We implemented the advanced Bayesian model accordingly with estimated protein priors (see the rightmost column in Table 2) and compared its results with ProteinProphet.
Sigma49 protein mixture sample were made by mixing 49 human proteins. However, repeated proteomics experiments confirmed the existence of many contaminant proteins in the mixture. In the three replicated LC/MS data sets, we analyzed here, 46 out of the 49 proteins were identified by at least one peptide with PeptideProphet probability >0.05 (see the leftmost column in Table 3). Table 3 shows the comparison between the results of ProteinProphet and that of the Bayesian inference model. It can be observed that Bayesian inference model outperforms ProteinProphet by reporting more true positive proteins, less false positive proteins and less false negative proteins in each of the three datasets.
Table 3.
Protein Inference Results on Three Sigma49 Dataset Using ProteinProphet (PP) and Bayesian Inference Model (BI)
| |
|
TP |
FP |
FN |
F-measure |
||||
|---|---|---|---|---|---|---|---|---|---|
| Experiment | No. of identified true proteins | PP | BI | PP | BI | PP | BI | PP | BI |
| 1 | 46/60 | 40.5/46.5 | 46/49 | 9.5/3.5 | 9/1 | 8.5/36.6 | 3/34 | 0.82/0.70 | 0.89/0.74 |
| 2 | 46/59 | 42.8/49.8 | 44/50 | 14.2/7.2 | 11/5 | 6.2/33.2 | 5/33 | 0.81/0.71 | 0.85/0.73 |
| 3 | 46/57 | 41.8/47.8 | 43/49 | 7.2/1.2 | 7/1 | 7.2/35.2 | 6/34 | 0.85/0.73 | 0.87/0.74 |
All results are evaluated based on the true positive (TP), false positive (FP) and false negative (FN) numbers of proteins, and and F-measure (F) in two categories of true proteins in the sample: model (49) proteins, and model proteins plus all contaminations (83 in total). The total number of identified true proteins (i.e., with at least one peptide hit of PeptideProphet probability >0.05) in these two categories are shown in the second column. MAP solutions were used as positive proteins for our probabilistic models; and 0.5 cutoff was used for ProteinProphet. ProteinProphet may report a group of undistinguishable proteins. Here we assigned an equal fraction value to each member in such group. As a result, some fractional values were assigned to TP/FP/FN protein numbers for ProteinProphet.
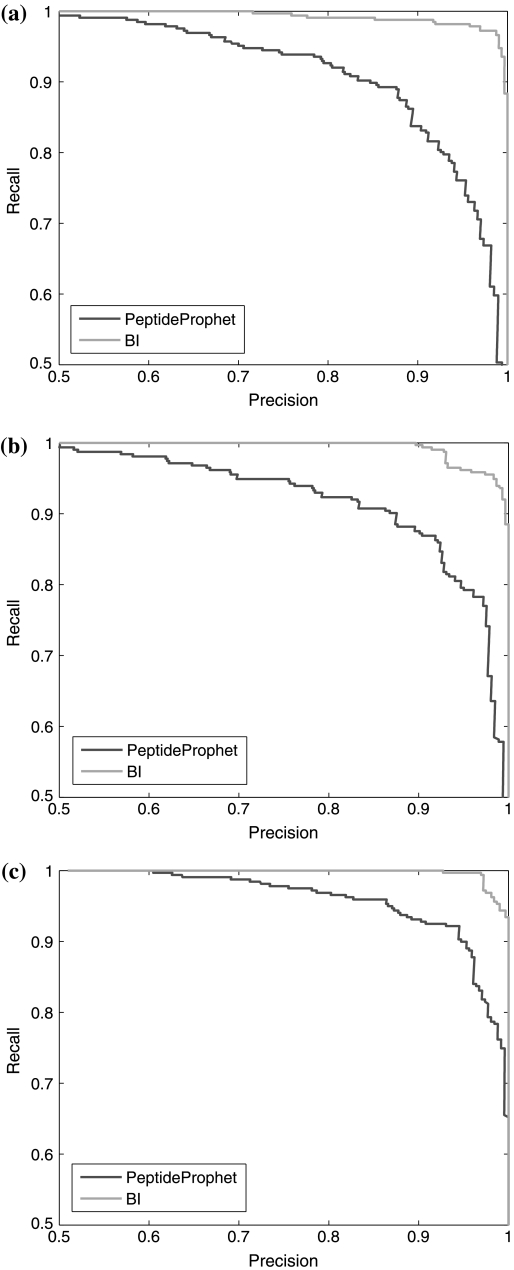
As mentioned in the methods section, the Bayesian inference model can also be used to calculate a posterior probability for each identified peptide (equation 13). This probability can be viewed as a re-evaluation of the possibility of each peptide identification being correct, taking into account not only the quality of the matching between the peptide and the MS/MS spectrum, but also the relationship among peptides (and their matching with the corresponding MS/MS spectra) from the same protein. Therefore, it should be a better way to assess the correctness of the peptide identification given a single LC/MS/MS experiment as a whole. Figure 2 shows the precision-recall curves for the peptide identification using posterior probabilities and the PeptideProphet probabilities that are used as input to Bayesian inference. On average, the posterior Bayesian inference can improve the accuracy of the peptide identification by approximately 6% for the Sigma49 datasets (Table 4).
FIG. 2.
Precision-recall curves of the peptide identification using posterior probabilities by Bayesian inference (light curves, denoted as BI in the figure legend) and the PeptideProphet probabilities (dark curves) for the Sigma49 datasets 1 (a), 2 (b), and 3 (c).
Table 4.
Posteror Peptide Inference Improves the Peptide Identification
| |
|
PP |
BI |
||||
|---|---|---|---|---|---|---|---|
| Experiment | No. of true proteins | AUC | acc | F-measure | AUC | acc | F-measure |
| 1 | 46 | 0.953 | 0.896 | 0.884 | 0.996 | 0.975 | 0.973 |
| 2 | 46 | 0.953 | 0.896 | 0.886 | 0.997 | 0.972 | 0.960 |
| 3 | 46 | 0.974 | 0.927 | 0.926 | 0.999 | 0.966 | 0.964 |
The Area Under the ROC Curve (AUC), the accuracy (acc) and the F-measure are used to compare the peptide identification results from PeptideProphet (PP) and after Bayesian inference (BI). The peptides identified from the model and contaminant proteins were considered as positive, whereas the rest identified peptides were considered negative.
4. Discussion
In this study, we proposed and evaluated a new methodology for protein inference in shotgun proteomics. The Bayesian approach proposed herein attempts to find the set of proteins that is most likely to be present in the sample. The new approach has several advantages over the existing methods: (1) it calculates or, if the global optimum is not reached, approximates a MAP solution for the set of proteins present in the sample and can also output the marginal posterior probability of each protein to be present in the sample; (2) it can output the marginal posterior probabilities of the identified peptides to be correct, given the entire experiment; (3) the Gibbs sampling approach used to approximate the posterior probabilities of protein configuration is a proven methodology, and its performance and convergence has been well-studied; and (4) our probabilistic models are based on clear assumptions, thus can be readily extended further.
It is common in proteomics for a sample to be analyzed multiple times in order to increase coverage of the proteome as well as to increase confidence in low sequence coverage proteins (Brunner et al., 2007). While not specifically addressed, the application of the Bayesian models described here adequately accommodates such data since peptide detectability, used as prior probabilities to estimate the probabilities of identified peptides, should assign lower values to those peptides not identified in all the replicate analyses. In addition, higher mammalian proteomes often contain multiple very similar homologous proteins due to recent gene duplications. Using existing protein inference algorithms, these proteins are frequently impossible to differentiate using shotgun proteomics, if some but not all of these proteins are present in the sample. We approached the problem by utilizing the different sets of tryptic peptides (and their detectabilities) among homologous proteins, including both the identified and non-identified peptides. Notably, although the MAP solution of the protein inference problem often reports the actual proteins (with relatively higher posterior probabilities then the other candidate proteins), they each may receive a low marginal posterior probability (e.g., <0.5). While we have not explicitly addressed this problem here, we note that the proposed models can easily treat a given set of proteins as a group and then compute the probability of their presence as a whole. We will test this functionality in future implementation of the models.
The peptide detectability is originally defined as a probability of a peptide to be identified in a standard shotgun proteomics experiment, in which all peptides are of equal abundances. To accommodate this definition, we originally trained the detectability predictor using a standard protein mixture (Tang et al., 2006). As a result, the predicted detectabilities may not be accurate for those peptides with very high or low abundances. Since the detectability of each peptide should be based on the abundance at which each peptide is present in the sample, we used estimated protein abundance values to adjust detectability both during the training and the protein inference. As a result, the inference results from our current Bayesian models not only report the presence of a protein, but also its abundance relative to the abundance of the standard proteomics experiment, even though in this article we only analyzed the first part of the results.
Acknowledgments
This project was supported by NIH grant R01 RR024236-01A1 and NCI grant U24 CA126480-01. H.T. and R.J.A. acknowledge support from NIH/NCRR grant 5P41RR018942. H.T. was partially supported by NSF award DBI-0642897. P.R. was partially supported by NSF award DBI-0644017.
Disclosure Statement
No competing financial interests exist.
References
- Aebersold R. Mann M. Mass spectrometry-based proteomics. Nature. 2003;422:198–207. doi: 10.1038/nature01511. [DOI] [PubMed] [Google Scholar]
- Alves P. Arnold R.J. Novotny M.V., et al. Advancement in protein inference from shotgun proteomics using peptide detectability. Pacif. Symp. Biocomput. 2007:409–420. [PubMed] [Google Scholar]
- Bern M. Goldberg D. Improved ranking functions for protein and modification-site identifications. Proc. RECOMB 2007. 2007:444–458. doi: 10.1089/cmb.2007.0119. [DOI] [PubMed] [Google Scholar]
- Brunner E. Ahrens C.H. Mohanty S., et al. A high-quality catalog of the Drosophila melanogaster proteome. Nat. Biotechnol. 2007;25:576–583. doi: 10.1038/nbt1300. [DOI] [PubMed] [Google Scholar]
- Craig R. Beavis R.C. TANDEM: matching proteins with tandem mass spectra. Bioinformatics. 2004;20:1466–1467. doi: 10.1093/bioinformatics/bth092. [DOI] [PubMed] [Google Scholar]
- Elias J.E. Gygi S.P. Target-decoy search strategy for increased confidence in large-scale protein identifications by mass spectrometry. Nat. Methods. 2007;4:207–214. doi: 10.1038/nmeth1019. [DOI] [PubMed] [Google Scholar]
- Elias J.E. Haas W. Faherty B.K., et al. Comparative evaluation of mass spectrometry platforms used in large-scale proteomics investigations. Nat. Methods. 2005;2:667–675. doi: 10.1038/nmeth785. [DOI] [PubMed] [Google Scholar]
- Geman S. Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Analysis Mach. Intell. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Keller A. Nesvizhskii A.I. Kolker E., et al. Empirical statistical model to estimate the accuracy of peptide identifications made by MS/MS and database search. Anal. Chem. 2002;74:5383–5392. doi: 10.1021/ac025747h. [DOI] [PubMed] [Google Scholar]
- Kislinger T. Emili A. Multidimensional protein identification technology: current status and future prospects. Expert Rev. Proteomics. 2005;2:27–39. doi: 10.1586/14789450.2.1.27. [DOI] [PubMed] [Google Scholar]
- Li Y.F. Arnold R.J. Li Y., et al. A Bayesian inference approach to protein inference problem in shotgun proteomics. Proc. 12th Annu. Int. Conf. Res. Comput. Mol. Biol. 2008:167–180. [Google Scholar]
- Liu J.S. Monte Carlo Strategies in Scientific Computing. Springer–Verlag; New York: 2002. [Google Scholar]
- Lu P. Vogel C. Wang R., et al. Absolute protein expression profiling estimates the relative contributions of transcriptional and translational regulation. Nat. Biotechnol. 2007;25:117–124. doi: 10.1038/nbt1270. [DOI] [PubMed] [Google Scholar]
- Marcotte E.M. How do shotgun proteomics algorithms identify proteins? Nat. Biotechnol. 2007;25:755–757. doi: 10.1038/nbt0707-755. [DOI] [PubMed] [Google Scholar]
- McDonald W.H. Yates J.R. Shotgun proteomics: integrating technologies to answer biological questions. Curr. Opin. Mol. Ther. 2003;5:302–309. [PubMed] [Google Scholar]
- Nesvizhskii A.I. Protein identification by tandem mass spectrometry and sequence database searching. Methods Mol. Biol. 2007;367:87–119. doi: 10.1385/1-59745-275-0:87. [DOI] [PubMed] [Google Scholar]
- Nesvizhskii A.I. Aebersold R. Interpretation of shotgun proteomic data: the protein inference problem. Mol. Cell Proteomics. 2005;4:1419–1440. doi: 10.1074/mcp.R500012-MCP200. [DOI] [PubMed] [Google Scholar]
- Nesvizhskii A.I. Keller A. Kolker E., et al. A statistical model for identifying proteins by tandem mass spectrometry. Anal. Chem. 2003;75:4646–4658. doi: 10.1021/ac0341261. [DOI] [PubMed] [Google Scholar]
- Perkins D.N. Pappin D.J. Creasy D.M., et al. Probability-based protein identification by searching sequence databases using mass spectrometry data. Electrophoresis. 1999;20:3551–3567. doi: 10.1002/(SICI)1522-2683(19991201)20:18<3551::AID-ELPS3551>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- Swanson S.K. Washburn M.P. The continuing evolution of shotgun proteomics. Drug Discov. Today. 2005;10:719–725. doi: 10.1016/S1359-6446(05)03450-1. [DOI] [PubMed] [Google Scholar]
- Tang H. Arnold R.J. Alves P., et al. A computational approach toward label-free protein quantification using predicted peptide detectability. Bioinformatics. 2006;22:481–488. doi: 10.1093/bioinformatics/btl237. [DOI] [PubMed] [Google Scholar]
- Wu F.-X. Gagne P. Droit A., et al. RT-PSM, a real-time program for peptide-spectrum matching with statistical significance. Rapid Commun. Mass Spectrom. 2006;20:1199–1208. doi: 10.1002/rcm.2435. [DOI] [PubMed] [Google Scholar]
- Yates J.R. Eng J.K. McCormack A.L., et al. Method to correlate tandem mass spectra of modified peptides to amino acid sequences in the protein database. Anal. Chem. 1995;67:1426–1436. doi: 10.1021/ac00104a020. [DOI] [PubMed] [Google Scholar]
- Zhang B. Chambers M.C. Tabb D.L. Proteomic parsimony through bipartite graph analysis improves accuracy and transparency. J. Proteome Res. 2007;6:3549–3557. doi: 10.1021/pr070230d. [DOI] [PMC free article] [PubMed] [Google Scholar]