Analysis of reflex modulation with a biologically realistic neural network

Abstract

In this study, a neuromusculoskeletal model was built to give insight into the mechanisms behind the modulation of reflexive feedback strength as experimentally identified in the human shoulder joint. The model is an integration of a biologically realistic neural network consisting of motoneurons and interneurons, modeling 12 populations of spinal neurons, and a one degree-of-freedom musculoskeletal model, including proprioceptors. The model could mimic the findings of human postural experiments, using presynaptic inhibition of the Ia afferents to modulate the feedback gains. In a pathological case, disabling one specific neural connection between the inhibitory interneurons and the motoneurons could mimic the experimental findings in complex regional pain syndrome patients. It is concluded that the model is a valuable tool to gain insight into the spinal contributions to human motor control. Applications lay in the fields of human motor control and neurological disorders, where hypotheses on motor dysfunction can be tested, like spasticity, clonus, and tremor.

1 Introduction

Human motor control is a continuous interaction between muscles, sensory organs and the central nervous system (CNS). Numerous modeling and experimental studies have tried to elucidate the role of the CNS in controlling movement and posture (e.g. Rack et al. 1984; Kearney et al. 1997; Prochazka et al. 1997). The lowest level of feedback is at the spinal cord, resulting in spinal reflexes. In van der Helm et al. (2002) a method was developed that allows a quantitative assessment of circuits that modulate the strength of spinal reflexes of the upper extremities during postural control in vivo. Force disturbances were applied at the hand while subjects had to minimize the deviations resulting from a force disturbance. Healthy subjects modulate the magnitude of their reflexes based on the frequency content of the force disturbance and these reflexes can provide up to half of the total joint stiffness. Literature suggests that presynaptic inhibition is the primary mechanism to modulate reflex strength (Stein and Capaday 1988). The reflex modulation can even result in negative feedback gains (i.e. positive feedback: negative feedback gains in a negative feedback loop) for disturbances containing only frequencies in a small bandwidth around a centre frequency (van der Helm et al. 2002). Theoretical studies showed that these adaptations to the disturbance properties, including the negative feedback gains, are optimal in the sense of performance (Schouten et al. 2001; De Vlugt et al. 2001). However, quantification of reflex gains in complex regional pain syndrome (CRPS) patients with tonic dystonia revealed their inability to achieve negative gains, although modulation of positive gains was still possible (Schouten et al. 2003).

System identification methods as used in van der Helm et al. (2002) and Schouten et al. (2003) estimate lumped feedback gain parameters for position, velocity and acceleration feedback in vivo, based on a linearization of the neuromuscular system. The reflexive feedback gains and the modulation thereof is the result of a network of motoneurons and interneurons at the spinal cord level. The present study will make a first attempt to model the neural network responsible for the reflexive feedback gain settings at the spinal cord. A neuromusculoskeletal model is presented, based on a biologically realistic neural network (BNN) describing the spinal segment which is connected with a musculoskeletal model. The BNN consists of 2,298 (inter) neurons, of which the strength and distribution of the synaptic connections were taken from Bashor’s model (Bashor 1998). The model can give insight into the neural mechanisms at the spinal cord, their functional effect on human motor control, and the setting of reflexive feedback gains. The model will be simulated using spike based signals and integrate-and-fire neurons, in order to stay close to biological reality. As the BNN model is rather complex, its robustness is assessed by analyzing the sensitivity of the individual BNN parameters onto the dynamics of the complete neuromusculoskeletal model (NMS).

Applications of the model lay in the field of motor control and movement disorders. In this study the model will be used to describe experimental findings of human posture control in healthy subjects (van der Helm et al. 2002), by simulating presynaptic inhibition to modulate the reflex strength. It will be investigated if negative lumped feedback gains can be obtained with presynaptic inhibition. Literature concerning the neural mechanisms to generate negative feedback gains is scarce. Negative feedback gains imply that the activation of a shortening muscle increases, and the activation of a lengthening muscle decreases, in mere contrast to the well-know mono-synaptic reflexes. Since shortening muscles do not provide Ia afferent feedback, the simultaneous lengthening of the antagonistic muscle might provide the necessary sensory input: reciprocal excitation, as suggested by Jankowska and Hammar (2002). Finally, in a pathological case the possible applications for movement disorders are demonstrated. The model is used to elucidate mechanisms involved in the setting of negative feedback gains. Dysfunction of such mechanisms could give insight into the pathophysiology of CRPS.

2 Method

First, a BNN was integrated with a musculoskeletal model of the human arm with proprioceptors, creating a complete NMS model. The musculoskeletal model represents the experimental set-up on the shoulder joint (van der Helm et al. 2002; Schouten et al. 2003). In these experiments the subject was seated in a chair while holding the handle of a linear actuator. The subject was positioned in such a way that the elbow made an angle of 90 degrees. Force perturbations applied through the handle resulted in ante-/retroflexion movements of the shoulder joint. Since the perturbations induced motion in one degree-of-freedom (DOF), the experimental setup was modeled as a single limb with a pair of antagonistic muscles. The BNN is based on the model of Bashor (1998), which includes a minimal set of spinal (inter)neurons necessary for reflex modeling. It is important to note that no further training of the synaptic connections was done. General data for the models for the muscle spindles and Golgi tendon organs were derived from literature (Prochazka and Gorassini 1998a,b; Crago et al. 1982).

Second, the NMS model was stimulated by force disturbances in computer simulations. The scheme of the model is given in Fig. 1. In the simulations, the force disturbance d(t) acted on the endpoint of the limb resulting in position deviations x(t). The BNN blended tonic supraspinal excitatory commands from the brain and reflexive feedback from proprioceptors (muscle spindles and Golgi tendon organs) into activation signals for both muscles. The lumped reflexive feedback gains were quantified by applying the procedure of van der Helm et al. (2002).

Fig. 1.

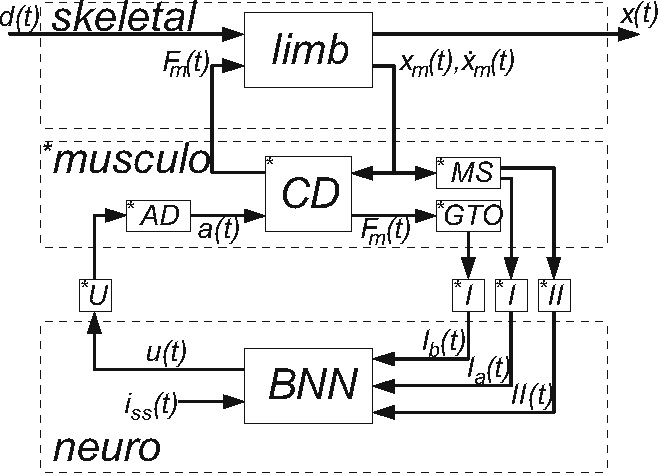
Scheme of the NMS model. d(t): external force disturbance which act to the limb; x(t): endpoint position; iss(t): supraspinal excitatory commands; F_m(t): muscle force from the contraction dynamics (CD); x_m(t): muscle stretch; 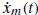: muscle stretch velocity; u(t): motoneuron activation. The muscle spindles (MS) and Golgi tendon organs (GTO) sense the muscle stretch, stretch velocity and force resulting in afferent signals on the I_a(t), I_b(t), and II(t) afferents respectively. These afferent signals have a conduction time τ_I or τ_II, depending on the afferent path, before reaching the BNN. After the conduction time τ_u(t), u(t) reaches the muscle and is converted into the muscle activation a(t) by the activation dynamics (AD). An asterisk (*) denotes the necessity to double the components for the flexor and the extensor muscles

Third, a sensitivity analysis was performed on the model, with two main goals. The first is to check whether the linear approximation method, used for obtaining lumped reflex gains, remains valid under large parameter changes in the highly non-linear BNN. The second goal is to quantify the amount of influence that each parameter has on the overall motor output, thus to determine the dominance of the BNN parameters.

Fourth and finally, the effect of presynaptic inhibition of the monosynaptic stretch reflex on modulating the lumped feedback parameters was investigated and neural mechanisms were analyzed for their ability to generate or prevent negative feedback gains. The results were compared to the experimental results for both healthy subjects and CRPS patients (van der Helm et al. 2002; Schouten et al. 2003).

2.1 Simulation model

2.1.1 Musculoskeletal model

Figure 2 shows the geometrical model representation of the human shoulder for postural control tasks. The model has one DOF and comprises a lumped massm_l of 2 kg on the endpoint of a 0.3 m long limb (l_l), on which two antagonistic muscles (normal length l_m = 0.3 m) act with a constant moment arm l_a of 0.04m (Stroeve 1999).

Fig. 2.

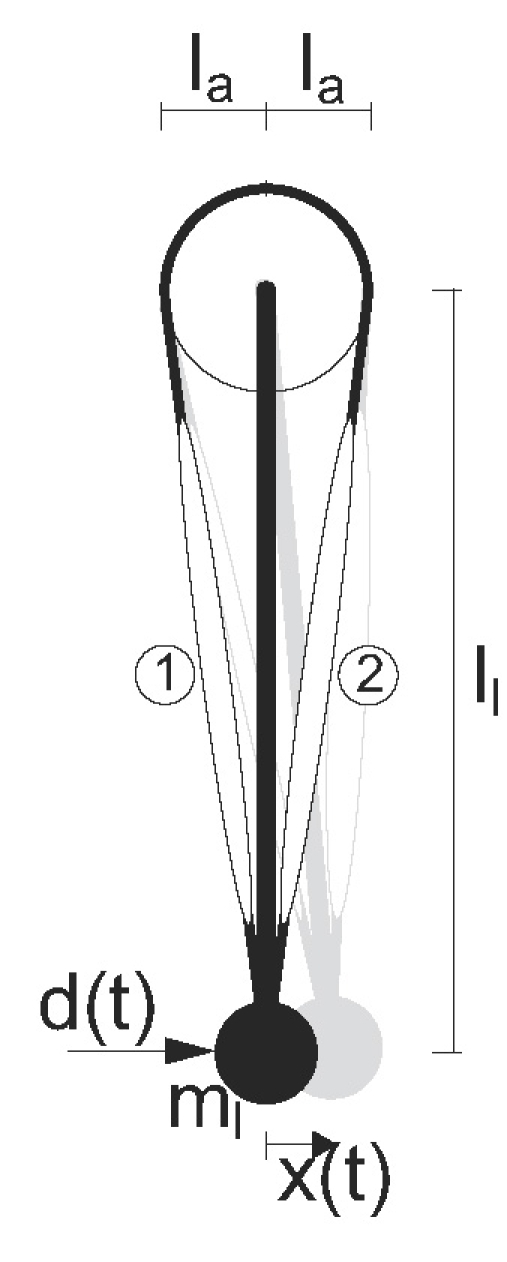
Geometrical representation of the one-DOF model of the human shoulder. The limb with concentrated mass m_l is actuated by two antagonistic muscles, (1) and (2), and disturbed by a force d(t) resulting in the position deviation x(t). The limb length is represented by l_l and the constant moment arm of the muscle force by l_a. The black figure is the limb in equilibrium or reference position; the grey figure is the limb after a small deviation

Using a non-linear model simulation of the experiment, Schouten et al. (2001) showed that a Hilltype muscle model underestimated the muscle stiffness and overestimated the muscle viscosity. Therefore, in the present study a simple linear muscle model representing experimental values was preferred above a non-linear model which can not predict the muscle visco-elasticity. The muscles were represented with a linearized model with activation a, muscle stretch x_m and stretch velocity 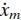as inputs. In the reference position, the stretch is defined as zero. The muscle force F_m(t) is given by: 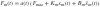with a maximum contraction force F_max of 800 N (Stroeve 1999), muscle stiffness K_m and damping B_m, and the activation dynamics: 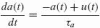where τ_a is the muscle activation time constant of 30 ms (Winters and Stark 1985), u(t) the motoneuron activation, and a(t) the muscle activation. Both u(t) and a(t) are normalized, ranging from 0 to 1.

In the study of van der Helm et al. (2002) an endpoint stiffness of 800 N/m and an endpoint damping of 40 Ns/m were found, representing the viscoelastic properties of the (co-contracted) muscles and surrounding tissues. Note that in the musculoskeletal model all the visco-elastic properties are accounted for in the muscles. The above mentioned endpoint values were converted to muscle stiffness K_m and damping B_m. It was shown that in the experiments muscle co-activation was approximately 40% of maximum Abbink (2002), resulting in a K_m of 56.3 kN/m and a B_m of 2.81 kNs/m.

2.1.2 Proprioceptors

Vital to any feedback control network is the quality of the sensory input. Prochazka and Gorassini (1998a,b) compared several mathematical models for their ability to predict the firing characteristics of muscle spindle primary afferents recorded chronically during normal stepping in cats. Jankowska and Hammar (2002) argued that the essential properties and organizations of spinal interneuronal systems in cat and man are comparable, and therefore relevant cat data and models are used in the NMS model of this study when human data and models are unavailable.

Muscle spindles provide muscle length and velocity information via two separate afferent spike train channels: the Ia afferent for both length and velocity information (conduction delay τ_I = 15 ms Winters and Stark 1985) and the slower II afferent for pure length information (τ_II = 30 ms Winters and Stark 1985). 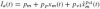Two equations are used to determine the spike rate (in sp/s) for both channels (Prochazka and Gorassini 1998a,b): 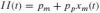where x_m(t) is the muscle stretch (in mm) and 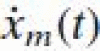the muscle stretch velocity (in mm/s). The constant p_m represents the mean firing rate and is arbitrarily set to 80 sp/s. The length change constant p_p and velocity constants p_ν1 and p_ν2 scale the length and velocity information. Although Prochazka and Gorassini (1998a, b) kept the p_p at 2 for the Ia afferent channel, in this study it is set to 13.5, equal to their choice for the II afferent channel. This increases the static component of the Ia afferent channel, as is expected for postural control tasks. Values for p_ν1 and p_ν2 (4.3 and 0.6) are claimed to be valid for both humans and cats and therefore used unaltered (Prochazka and Gorassini 1998a, b).

Golgi tendon organ models are far more scarce, but available literature suggest that the firing rate is linear with the force (Crago et al. 1982). The Ib afferent spike rate output is linear from zero to maximum isometric muscle force: 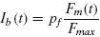where F_m is the muscle force (in N) and F_max the before mentioned maximum muscle force (800 N). With a mean muscle force of 40% of maximum, the Ib afferent output is arbitrarily set to the muscle spindles’ firing mean of 80 sp/s, hence giving the constant p_f a value of 200 sp/s.

2.1.3 Biological neural network

Bashor (1998) created a large-scale BNN model to study the dynamic interactions in neuron populations. He calibrated the model by examining its ability to reproduce known aspects of the reflexes, but without linking it to a musculoskeletal model. Here the BNN model is used to control a musculoskeletal model during postural control tasks. Early simulations showed that three adaptations to Bashor’s BNN model were required.

Firstly, the recurrent projections within neuron populations resulted in mass synchronized firing which disrupted the motoneuron to muscle signal. This mass-synchronization was considered an artifact which could have multiple origins, like the limited number of neurons in the network, the relatively large integration time step, the homogeneity of neuron properties and projection time delays and finally the absence of noise in the neural projections. Bashor (1998) already noted the synchronized firing and applied a moving average filter (100 ms) before plotting the signals. However, in this study these signals are the input to the muscles and applying a moving average filter would introduce additional artificial dynamics in the loop. Disabling the intra-populational projections made the neurons less responsive when the neurons were of the excitatory kind, and more when inhibitory. However, model-wide behavior was unaffected by these static gain changes and disabling largely reduced synchronized firing.

Secondly, the default connection strength to one specific group of interneurons, the inhibitory interneurons (IN, see Fig. 3), were too weak to generate any significant background firing on which (downwards) modulation was possible. Increasing all the synaptic connection strengths to the inhibitory interneurons provided a level of background activity comparable to the other interneurons, but did make them more responsive to input changes. These adaptations eliminated the lack of significant firing, without disrupting model-wide behavior.

Fig. 3.

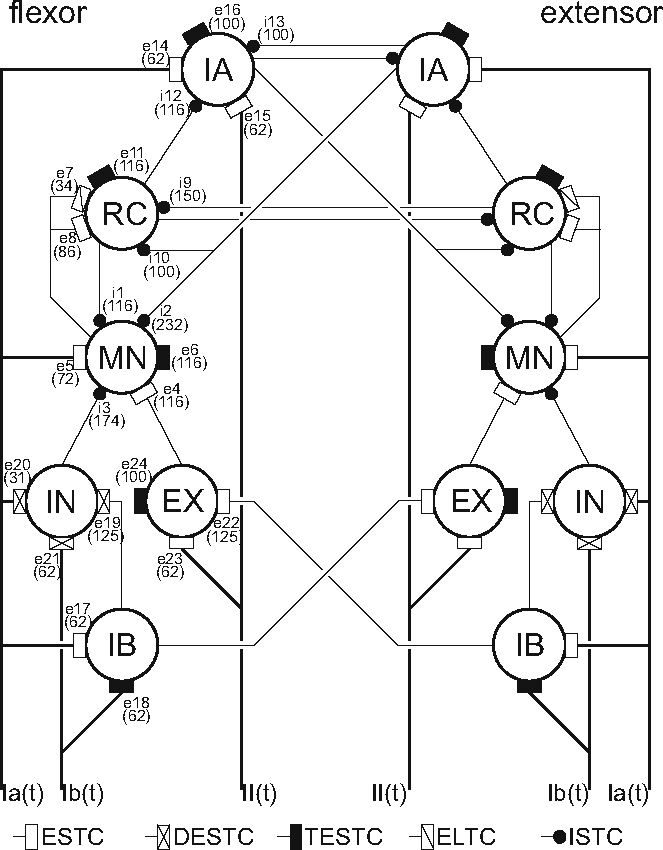
Neuron populations and their interconnections in the BNN of this study (based on Bashor 1998). Proprioceptive input comes through the Ia, Ib and II afferents and the firing rate output of the motoneurons drives the muscles in the musculoskeletal model. The supraspinal commands (i_ss, paths not displayed) excite the BNN via synapses e6, e11, e16 and e24. ESTC are the normal excitatory short time constant synapses, DESTC and TESTC the ESTC with double and triple connection strengths, ELTC the excitatory long time constant synapses and ISTC the inhibitory short time constant synapses. The neuron types are given inside the circles, where MN denotes the motoneurons, RC the Renshaw cells and IA, IB, IN and EX respectively the IA, IB, inhibitory and excitatory interneurons. The synapse identifying numbers are denoted by e.. (excitatory) or i.. (inhibitory) and the value between the brackets represents the number of terminals received from the indicated source by a representative cell

Thirdly, there were no II afferent pathways, important for the length information feedback from muscle spindles. II afferent paths are polysynaptic and possibly also reciprocally coupled to the motoneurons (Jankowska and Hammar 2002). A pair of II afferent paths was added including synaptic connections to the Ia and excitatory interneurons (EX). The synaptic connection strengths were made approximately equal to the Ia and Ib afferent connections.

The BNN generates the motoneuron activation u(t) by combining supraspinal excitations i_ss(t) and afferent signals from the muscle spindles and Golgi tendon organs. The network consists of motoneurons and several types of interneurons. The motoneurons directly drive the muscles; the interneurons are exciting or inhibiting intermediates (possibly recurrent or reciprocal) for passing the Ia, II, and Ib afferent information received from the proprioceptors on to the motoneurons.

The BNN model (Fig. 3) consists of a large population of 2,298 neurons (Bashor 1998). The neurons in the model are grouped in six antagonistic population pairs, representing motoneurons (MN, n = 169, for both the agonistic and the antagonistic population), Renshaw cells (RC, n = 196), and intermediating interneurons (Ia, Ib, inhibitory and excitatory interneurons, abbreviated by IA, IB, IN, EX respectively, n = 196 each). Pairs of Ia, II, and Ib afferent (n = 121 each) and supraspinal excitation fibers (n = 98) provide further input to the neurons.

Cell and network algorithms and the synaptic mechanism of the BNN are based on the SYSTM22 program using the PTNRN10 neuron model of MacGregor (1987), see also Bashor (1998). Input to the model are the spike trains S^k(t) to each neuron k, originating from supraspinal centers (tonic excitation) and from the Ia, II and Ib afferent nerves. 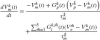The neuron model uses discrete equations with a time-step Δt of 1 ms, based on the following first order differential equations to calculate the potassium conductance G_p(t) (times resting conductance), the membrane potential V_m(t) (in mV) and the threshold potential V_t(t) (inmV) for every neuron k at time t (in ms): 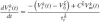where: 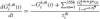and resulting in the spiking output for each neuron k: 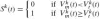where the superscript k denotes the neuron number (out of 2,298 network neurons), 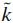the type of neuron (motoneuron, Renshaw cell or general interneuron), m the origin of the synaptic connection to neuron k (out of 3,558 neural, afferent or tonic descending sources), and 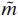the type of synaptic connection (ESTC, DESTC, TESTC, ELTC, or ISTC). All potentials are relative to the resting potential of a neuron (≈ −70 mV). See Table 1 for the parameter names and values of neurons and synapses and Fig. 3 for the synaptic connection strengths and numbers. Conductance changes G_i(t), produced by afferent and tonic descending excitation fiber input and cell to cell connections, increase or decrease the membrane potential V_m(t). The potential V_m(t) determines the threshold potential V_t(t)}. When the membrane potential V_m(t) is higher than the threshold potential V_t(t), the cell fires a spike on its output channel S(t) and the potassium conductance G_p(t) rises, creating a refractory period.

Table 1.

Properties of neuron and synpase types in the PTNRN10 neuron model and SYSTM22 program (MacGregor 1987) based on Bashor (1998, and personal communications)

Description		Neuron type
		MN	RC	IA,IB,IN,EX
B [-]	Sensitivity to potassium conductance	70	4	35
C [-]	Sensitivity to accommodation	0.6	0.7	0.6
V0 [mV]	Initial threshold	10	10	10
Vp [mV]	Equilibrium potential for potassium	−10	−10	−10
τm [ms]	Membrane time constant	5	5	5
τr [ms]	Refractory time constant	20	3	10
τt [ms]	Time constant for accommodation	25	25	25

		Synapse type
		ESTC	DESTC	TESTC	ELTC	ISTC
Gs [-]	Conductance change per transmission	0.01	0.02	0.03	0.01	0.01
Ve [mV]	Equilibrium potential for synaptic type	70	70	70	70	−10
τs} [ms]	Time constant for synaptic action	1	1	1	50	1

All potentials are relative to the resting potential of a neuron (≈ −70 mV).

The synaptic connections from neural, afferent or tonic descending sources to targeted neuron populations are randomly distributed in these populations in the MacGregor SYSTM22 program. Figure 3 shows the number of connections a single neurons receives from the projecting population and the type of synapse used to make that connection. The spike trains of the afferent fibers and supraspinal descending fibers were generated by Poisson processes with an instantaneous firing rate matching the spike rates of the fibers.

2.1.4 Normalized muscle activation

The motoneuron activation u(t) provides the input for the muscle activation dynamics, and is constructed by taking the average output over the motoneurons in the agonistic or antagonistic population and then applying a moving average filter (20 ms) to smooth the signals. The motoneuron output requires a conductance time τ_u of 10 ms before it reaches the muscle activation dynamics (Winters and Stark 1985).

With a tonic supraspinal excitatory input of 80 sp/s, the motoneurons have a mean firing rate of 25 sp/s, the Renshaw cells 100 sp/s and the interneurons from 15 to 40 sp/s. These firing rates are biologically realistic, while allowing for both up- and downwards variations. The average 25 sp/s output firing rate of the motoneurons is therefore set to equal the 40% of maximum activation into the muscle activation model (see Section 2.1.1).

2.1.5 Mono-, di- and tri-synaptic feedback paths

The flow of proprioceptive information from the muscle spindles and Golgi tendon organs may pass several interneurons before reaching the motoneurons. The exact path of the information flow has an influence on the net result of agonistic and antagonistic muscle activation. The net result for any path can be defined as positive or negative; a positive result for a feedback path starting at an agonistic proprioceptor is the increase in the activation of the agonistic muscles relative to the antagonistic muscles, either by increased activation of the agonistic or decreased activation of the antagonistic muscles. Crossing a reciprocal or inhibitory synapse will make the net result of the path negative; crossing another makes it positive again.

The net result of a path is thus dependent on the types and number of synaptic connections it crosses (see Fig. 3). The information from the proprioceptors may reach the motoneurons over many paths, yet for this network, the influence of a path decreases with the number of crossed synapses due to information dilution; any interneuron will output a mean result of all the, possibly conflicting, inputs. Therefore, paths crossing more than three synapses are ignored. All possible mono-, di- and trisynaptic paths in the spinal reflex model are given in Table 2. The total net result of the agonistic path on the agonistic motoneuron is also given.

Table 2.

Mono-, di- and tri-synaptic paths in the BNN (see Fig. 3)

Aff.	Syn.	Nrn.	Syn.	Nrn.	Syn.	Nrn.	result
Monosynaptic feedback path
Ia		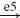MN					positive
Disynpatic feedback paths
Ia		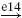IA		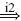MN			positive
Ia		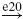IN		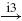MN			negative
Ib		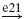IN		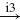MN			negative
II		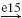IA		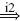MN			positive
II		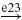EX		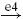MN			positive
Trisynpatic feedback paths
Ia		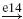IA		RC		MN	negative
Ia		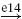IA		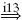IA		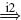MN	positive
Ia		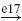IB		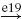IN		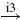MN	negative
Ia		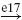IB		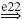EX		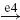MN	negative
Ib		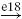IB		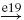IN		MN	negative
Ib		IB		EX		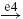MN	negative
II		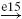IA		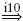RC		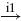MN	negative
II		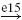IA		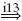IA		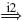MN	positive

Ia, Ib and II denote the type of afferent (first column: aff.), MN, RC, IA, IB, IN and EX the type of neuron (nrn.), and e.. and i.. the synaptic type of the connection (syn.), respectively excitatory and inhibitory, together with the synapse identifying number. A → corresponds to a connection within the agonistic or the antagonistic populations, whereas a ⟹ represents a connection from the agonistic to the antagonistic populations or vice versa. The last column (result) indicates whether the net result of the afferent to the muscles will be positive or negative; i.e. positive when an increase of the agonistic afferent activation also increases the agonistic muscle activation relative to the antagonistic muscle activation.

2.2 Lumped reflex model

In this study the relation between lumped feedback gains at endpoint level and neural network properties was analyzed. For each specific setting, the NMS model is simulated with a force disturbance applied to the endpoint of the limb and the resulting position deviations are recorded. The reflexive feedback gains are estimated by fitting a linear model to allow comparisons with experimental results of van der Helm et al. (2002) and Schouten et al. (2003).

2.2.1 Disturbance signal

The force disturbances d(t) used in this study are continuous wide-bandwidth signals, with a length of 9 s, a uniform power distribution between 0.6 and 20 Hz and a random phase. The signals are designed in the frequency domain, inverse fast Fourier transformed to time domain and then stored for use in the simulations. To allow linear model approximations, the force disturbance signal is scaled such that the root-mean-square (RMS) of the endpoint position is around 5 mm.

2.2.2 Data recording and processing

The force disturbance d(t) and position deviation x(t) are sampled at 1 kHz. From the 9 s over which each realization is simulated, only the last 8,192 samples are used. This removes any transient response coming from the NMS model. The signals are transformed to the frequency domain by fast Fourier transform (FFT) and the frequency response function (FRF) for the joint admittance Ĥ_nms(f) of the NMS model (see Fig. 4) is estimated from the appropriate spectral densities. 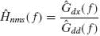where Ĝ denotes the auto (Ĝ_dd(f), Ĝ_xx(f)) and cross (Ĝ_dx(f)) spectral densities (hat denotes estimate). To improve the estimate and to reduce the variance of the estimators, each setting is simulated eight times with eight different disturbance realizations. The spectral densities resulting from these eight realizations are then averaged, where after another improvement of the estimate is achieved by averaging the spectral densities over four frequency bands (Jenkins and Watts 1968). After the averaging step, the spectral densities have a frequency resolution of 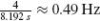Hz

Fig. 4.

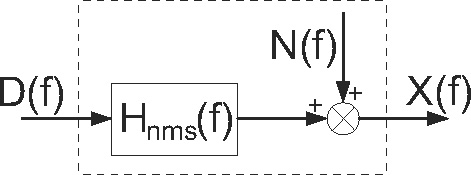
Block scheme of human postural control expressed in the frequency domain. H_nms(f): transfer function of the dynamics of the NMS model; D(f): external force disturbance; X(f): skeletal bone endpoint position; N(f): model remnant. The NMS dynamics (dashed box) are described by the linear transfer function H_nms(f), together with the remnant N(f), which is uncorrelated with D(f)

As a measure for the reliability of the estimated FRF the coherence is estimated: 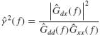By definition the coherence ranges between 0 and 1. A coherence of 1 at a specific frequency means that a linear relationship exists between the signals and the measurements contains no noise or nonlinearities at that frequency. Possible causes of low coherence must be found in nonlinearities in the BNN, since there is no noise in the simulation.

2.2.3 Fitting the linear model

Fitting a linear arm model on the estimated FRF of the joint admittance Ĥ_nms(s) quantifies the feedback gains in the linear model. These gains can then be compared with the results of van der Helm et al. (2002) and Schouten et al. (2003).

In the study of van der Helm et al. (2002) a linear model is developed to describe the joint admittance (see Fig. 5). The muscle visco-elasticity (including cocontraction) and the limb mass are described by a massspring-damper system, H_int(s): 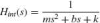with mass m, intrinsic damping b, and intrinsic stiffness k. The Laplace operator s equals λ + j2π f where λ = 0 because the initial transient response in the first second of simulation is removed from the recordings. The reflexive feedback is described by feedback gains for position k_p, velocity k_υ, and acceleration k_a in series with a single neural time delay τ_d, equal to the roundtrip delay of the Ia afferent.

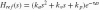
Fig. 5.

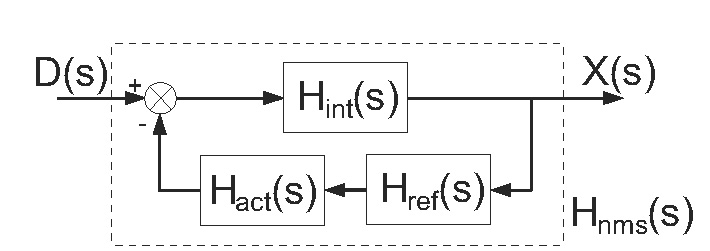
Block scheme of the linear arm model of which the transfer function H_nms(s) is derived. D(s): external force disturbance; X(s): skeletal bone endpoint position; H_int(s): intrinsic (muscle) dynamics; H_ref (s): reflexive dynamics; H_act(s): muscle activation dynamics

The muscle activation dynamics are modelled as a first order process H_act(s) with activation time constant τ_a. 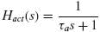Combining above equations gives the complete linear arm model, H_nms(s): 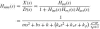In this study the values for the intrinsic properties, neural time delay and activation dynamics are taken from the simulationmodel, and are thus a priori known. The reflex gains (k_a, k_v, k_p) are estimated by fitting the linear arm model H_nms [Eq. (16)] on the FRF of the joint admittance Ĥ_nms(s [Eq. (11)], while keeping the intrinsic parameters, neural time delay and time constants fixed (m = 2 kg, b = 40 Ns/m, k = 800 N/m, τ_d = 25 ms, τ_a = 30 ms). To fit the linear model on the measured data, the following criterion function is minimized: 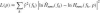where k indexes the frequency vector f_k, and p is the parameter vector (k_p, k_v, k_a). The criterion function is evaluated over the bandwidth of the disturbance signal (0.6–20 Hz). Because the FRFs have a large range of gain the logarithmic difference is better suited for the criterion function (Pintelon et al. 1994).

2.2.4 Linear model validation

The variance accounted for (VAF) is calculated to give an indication of the goodness of themodel fit, where the maximum VAF score of 1 indicates that the observed behavior is completely described by the linear model. 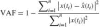where i indexes the sampled time vector. x(t_i) is the simulated output of the NMS model. 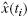is the forward simulated skeletal endpoint position using the original disturbance signals, the linear arm model and the estimated feedback parameters.

2.3 Model sensitivity

As described previously, the behavior of the BNN, determined by neuronal, synaptic and sensory parameters, is captured in the parameters of the lumped feedback model. It needs to be checked if this severely reduced model remains valid for changing BNN parameters. Furthermore, the sensitivity analysis should give insight in the effect of each BNN parameter on the arm dynamics.

The 55 parameters included in the analysis were: synaptic strengths (24), afferent and efferent delays (3), muscle activation time constant (1), sensory organ constants (7), tonic descending excitation rate (1), and single neuron model parameters (19). Since the intrinsic properties of the musculoskeletal model are linear in their parameters [Eq. (1)], they were not included in the sensitivity analysis. Each of the 55 parameters was varied by subsequently multiplying its default value with each of the seven factors 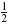, , 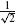, 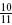1, 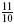, , 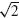2. For each of these settings, the BNN was run and the lumped parameter model was fitted on the results. To determine the validity of the lumped model, the variance accounted for (VAF) was determined for each fit, giving a measure of the goodness-of-fit of the output behavior of the lumpedmodel with respect to the BNN. Finally, a sensitivity measure S was determined for each parameter, which represents the amount of change that the variation has caused in the dynamics of the model. 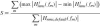where H^j_nms, j = 1 … 7 are the estimated transfer functions for the seven parameter variations, m indexes the frequency vector and H_nms,default is the estimated transfer function when all parameters have their nominal value. The sensitivity is evaluated over the frequencies with disturbance power. So sensitivity measure S is the normalized area, spanned by the gains of the seven transfer functions H^j_nms and represents the amount of spread that the variation has caused in the dynamics of the model. In a future study, these effects be studied in more detail by determining sensitivity measures between the BNN parameters and each separate reflex gain k_p, k_υ and k_a.

2.4 Case studies

In this study the application of the model is demonstrated in two cases, where the model is compared with experimental findings for healthy subjects and CRPS patients. First, the developed BNN model was used to elucidate mechanisms involved in the setting of negative feedback gains, as experimentally found in van der Helm et al. (2002). And second, dysfunction of such mechanisms could give insight into the pathophysiology of CRPS (Schouten et al. 2003).

2.4.1 Reflex modulation

Depending on the conditions healthy subjects modulate the magnitude of their reflexes (van der Helm et al. 2002). For specific conditions even negative feedback gains were found. Negative feedback gains (i.e. positive feedback: negative feedback gains in a negative feedback loop) can only be achieved by either an inhibitory effect of agonistic afferents on the agonistic muscle or an excitatory effect of the antagonist muscle. Stein and Capaday (1988), amongst others, suggested that presynaptic inhibition is the main neural mechanism to modulate the strength of the stretch reflex. In this study the model will be used to describe experimental finding of human posture control (van der Helm et al. 2002) by simulating presynaptic inhibition to modulate the reflex strength. It will be investigated if negative lumped feedback gains can be obtained with presynaptic inhibition. In the BNN of the present study, the effect of presynaptic inhibition is simulated by directly modulating the strength of the synapse of the monosynaptic stretch reflex (see Fig. 3, synapse e5). Increased presynaptic inhibition is modeled by lowering the synaptic strength of synapse e5 and vice versa. In the simulations, this synaptic strength is varied within a range of 0 to 3 times its default value.

2.4.2 Pathological case

Complex regional pain syndrome (CRPS), also known as reflex sympathetic dystrophy, is a painful condition typically following a minor injury to a limb. The symptoms may include movement disorders (Van Hilten et al. 2001), of which the most common form in patients with CRPS is tonic dystonia (Bhatia et al. 1993; Schwartzman and Kerrigan 1990). Dystonia is characterized by involuntary muscle contractions forcing the affected limbs into abnormal postures. The mechanisms responsible for tonic dystonia are still unknown, but involvement of inhibitory synapses in the spinal cord was suggested (Van Hilten et al. 2000).

Quantification of reflex gains in CRPS patients with tonic dystonia revealed their inability to achieve negative gains, although modulation of positive gains was still possible (Schouten et al. 2003). Presynaptic inhibition on its own can not cause negative feedback gains, but it can prevent the monosynaptic stretch reflex from being dominant over other paths within the BNN. To investigate whether neurotransmitter deficiencies can prevent the setting of negative feedback gains (Van Hilten et al. 2000; Jankowska and Hammar 2002), all present mono-, di- and trisynaptic paths were identified (see Table 2), and classified as either having a positive or negative result.Acandidate synapse was selected for its ability to disable some, but not all, di- or trisynaptic feedback paths. It was clear that the main paths with a negative result all pass the inhibitory interneurons (IN), and thereby the synapse between these interneurons and the motoneurons (synapse i3 in Fig. 3). Although other synapses convey negatively stimulating feedback, none are both disynaptic and coming from the Ia afferent channel. These last two conditions are important because: (a) in this network model every synaptic connection a path has to cross dilutes the information with information coming from other paths, and (b) the Ia afferent information has a stronger amplitude compared to the two other afferent channels (see Fig. 7). The synapse connecting the inhibitory interneurons to the motoneurons fitted the profile, as this synapse mediates all di-synaptic pathways and two out of six tri-synaptic pathways with a negative result (Table 2) which is essential for the generation of the negative feedback gains. While synapse i3 is disabled the monosynaptic stretch reflex synapse e5 (i.e. reducing the presynaptic inhibition) is increased again from 0 to 3 times the default strength in steps of 0.25 to mimic reflex strength modulation.

Fig. 7.

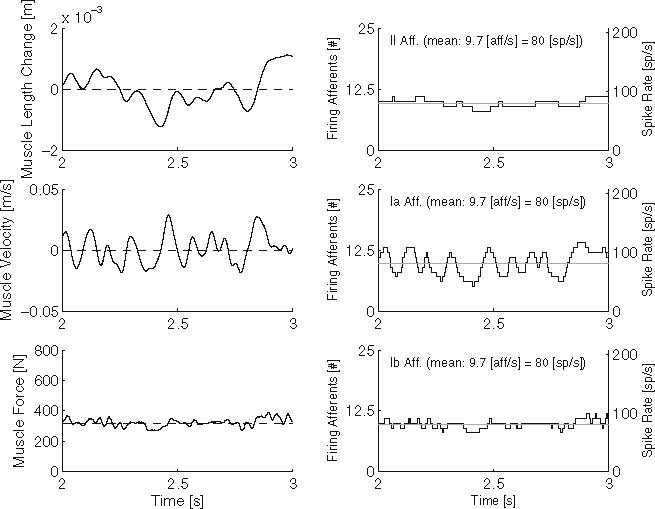
Typical muscle stretch, stretch velocity and muscle force signals (left plots) and the resulting II, Ia and Ib afferent activity (right plots). Dashed line indicates the average signal. The signals were recorded on the flexor side of the BNN during a single simulation with the default BNN setting. To improve readability, only a single second of the simulation is plotted

2.5 Tools and languages

The NMS model was developed using Matlab (© The MathWorks). All Fortran code in the SYSTM22 program (MacGregor 1987) was translated to Matlab code, as were the proprioceptor models. Simulating a single run of the NMS model took roughly 3.5 times the simulation length on a 1.8 GHz Windows (© Microsoft) machine with 1 GB of internal memory, so a 9 s simulation run took 31 s in real time. Note that each neural network set-up was simulated eight times, therefore taking 4 min to complete.

3 Results

Typical neuron activity during the default BNN setting is given in Fig. 6. The number of firing neurons is representative for the signal strength in the neuron pool. Similarly, typical muscle stretch, stretch velocity and muscle force signals together with the resulting II, Ia and Ib afferent activity are given in Fig. 7. In Fig. 7 it can be seen that the number of firing II afferents correlates to the muscle length, Ia afferents to the combination of muscle length and contracting velocity, and Ib afferents to the muscle force.

Fig. 6.

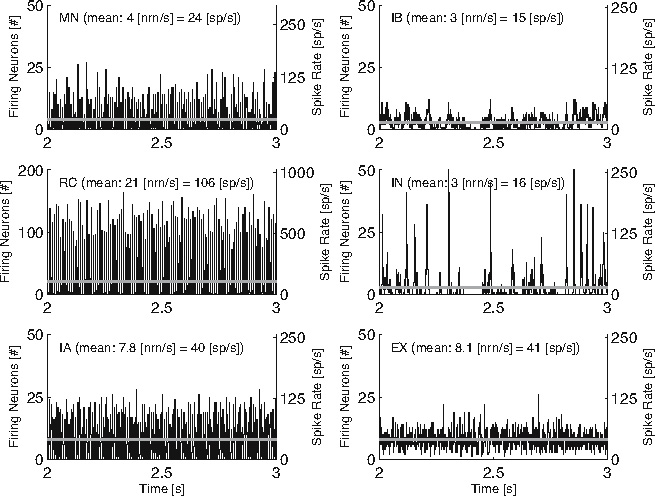
Typical neuron activity for the six agonistic neuron populations. Left y-axis: number of neurons firing a spike; right y-axis: related spiking frequency, averaged over the population. The grey horizontal lines indicate the number of neurons firing a spike and the spiking frequency, averaged over the entire simulation run. The signals were recorded on the flexor side of the BNN during a single simulation with the default BNN setting. To improve readability, only a single second of the simulation is plotted

3.1 Model sensitivity

Figure 8 shows the 15 most sensitive synaptic and sensory parameters. Generally, VAF is high (mean above 0.9), indicating that the linear lumped reflex model fits the simulated BNN data well and this linear approximation method is valid. There are three distinct outliers in the three most sensitive parameters. The first two directly affect the level of muscle co-contraction and the low VAFs are due to large arm deviations caused by reduced co-contraction, the third is due to the strong non-linear effect of the exponential p_v2 in the velocity term of the muscle spindle model [Eq. (3)]. The sensitivity measure S shows some distinct grouping in its outcome. The two most dominant signals (left plots) and the resulting II, Ia and Ib afferent activity (right plots). Dashed line indicates the average signal. The signals were recorded on the flexor side of the BNN during a single simulation with the default BNN setting. To improve readability, only a single second of the simulation is plotted parameters represent co-contraction through tonic descending excitation. The following three parameters are the velocity dependent Ia-afferent parameters (p_v1 and p_v2), together with the synaptic strength of the monosynaptic stretch reflex. Next, after the muscle activation time constant and afferent conduction delay, come two parameters related to force feedback through the Ib afferent. Finally, after the efferent time delay, there is a group of Ia-related parameters related to background spindle activity and position-dependent information (p_m and p_p). These results suggest that arm admittance (H_nms), as commonly acknowledged, is dominated by co-contraction and Ia-afferent feedback, while force feedback play a lesser, though not negligible role. Furthermore, time delays and the activation time constant have a strong effect on the arm dynamics. The group II-afferent plays a remarkably small role in the model. The most dominant II-afferent related parameter (at rank 26) has a sensitivity that is only one third of that of the least sensitive Ia-afferent related parameter.

Fig. 8.

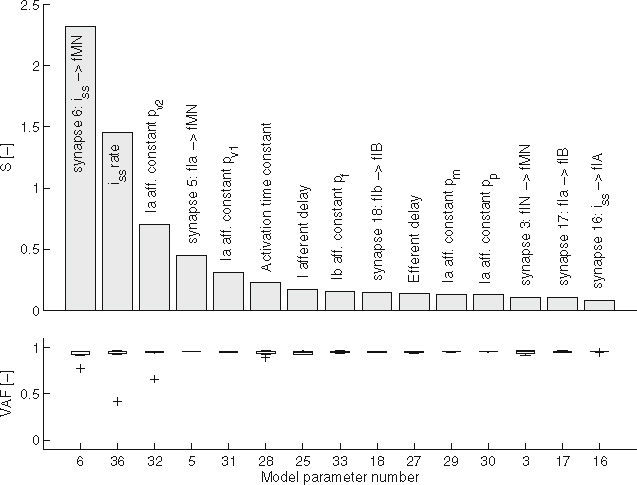
The 15 most sensitive synaptic and sensory parameters. Top: sensitivity measure S together with the parameter description; bottom: VAF of the lumped parameter model (mean ± SD over the seven variations factors)

Figure 9 shows the 15 most sensitive neuronal parameters. The three most sensitive neuronal parameters (the equilibrium potential of a short time constant excitatory synapse, the amount of threshold accommodation in the motoneurons and the resting threshold of all neurons) have strong effect on VAF. The low values here could all be explained by the motoneuron pools completely falling silent in one or more parameter settings. Three out of the six most sensitive parameters are motoneuron related. This makes sense, since all neuronal activity has to pass through the motoneurons before having any effect on the dynamics. The results further show that sensitivity of the neuronal parameters is generally higher than those of the synaptic and sensory parameters, while they are hard to get an accurate (experimental) value for.

Fig. 9.

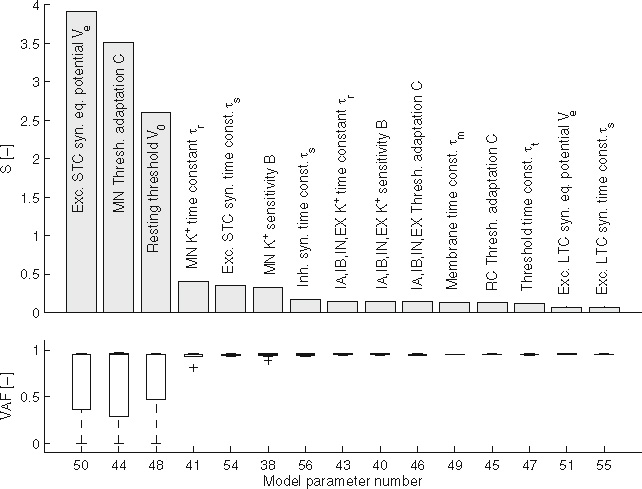
The 15most sensitive neuronal parameters (top) andVAF of the lumped parameter model (bottom)

3.2 Reflex modulation

By increasing the connection strength of the monosynaptic stretch reflex synapse (synapse e5), a decrease of presynaptic inhibition on this synapse was simulated. This is the main modulation mechanism for the velocity and position feedback information. Figure 10 gives the input force disturbance and output endpoint position deviation of three presynaptic inhibition settings (0, 1.5, and 3 times default strength). With increasing synaptic strength (decreasing synaptic inhibition) the position deviations decrease as a result of increased position and velocity feedback.

Fig. 10.

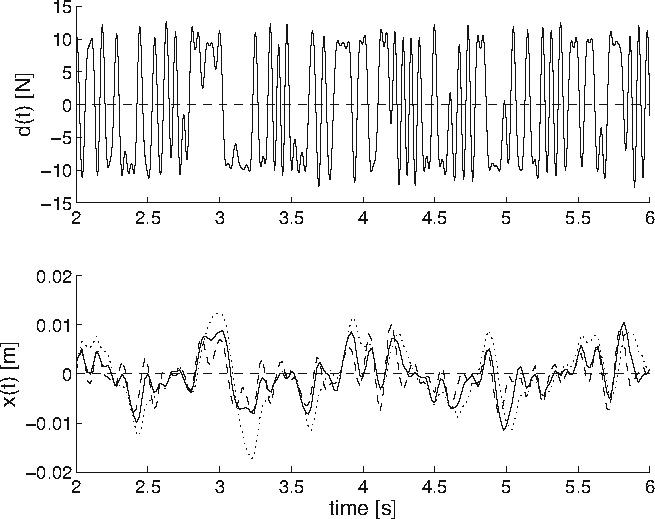
Force disturbance (above) and endpoint position displacement (below) of three different simulation runs. Monosynaptic stretch reflex synaptic strengths of 0 (dotted), 1.5 (solid) and 3 (dashed) times the default synaptic strength, simulating decreasing presynaptic inhibition on this synapse. To improve readability, only 4 s of a simulation are plotted

Figure 11 gives the FRF for the joint admittance (effect of force perturbation on position deviation) and the coherence for the same three settings. Increasing synaptic strength decreases the admittance at low frequencies (increased position feedback resembles stiffness, if the neural time-delays are neglected), while a peak in the gain at the eigenfrequency appears (oscillations).

Fig. 11.

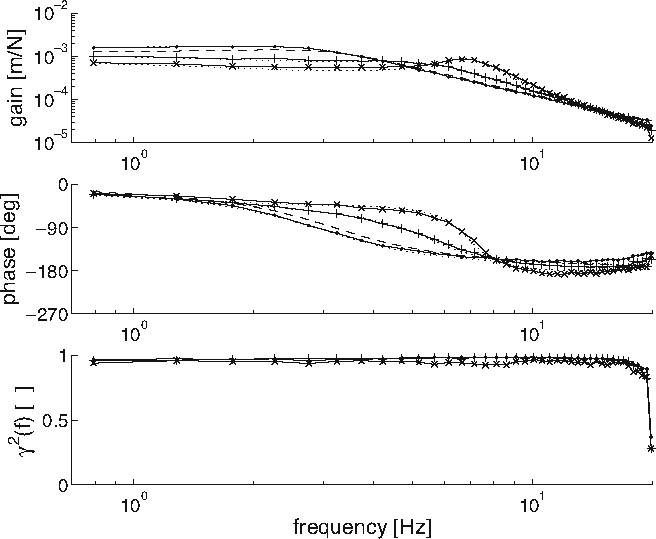
Gain (above), phase (middle) of the joint admittance, and the coherence 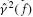(below). Monosynaptic stretch reflex synaptic strengths of 0 (dots), 1.5 (pluses) and 3 (‘x’-marks) times the default synaptic strength, simulating decreasing presynaptic inhibition on this synapse. Solid line: simulation; dotted line: linear model fit; and dashed line: simulation without afferent feedback

Plotting the results for the thirteen presynaptic inhibition settings displays a clear rising trend for all three feedback gains (Fig. 12, black lines), with negative gains for low synaptic strengths (high presynaptic inhibition). This plot shows thatmodulation of the reflexive feedback gains is possible by the presynaptic inhibition mechanism, and even negative gains are achievable. Furthermore, all three feedback gains increase simultaneously with the strength of the monosynaptic stretch reflex.

Fig. 12.

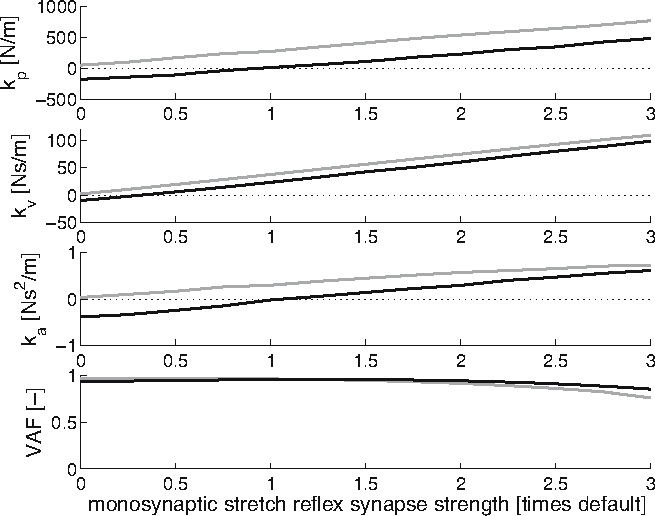
Feedback gain values for the position (k_p), velocity (k_v) and acceleration (k_a), together with the VAF scores, plotted against the monosynaptic stretch reflex synapse strength (relative to default strength). By increasing the monosynaptic stretch reflex synapse strength, a decreasing presynaptic inhibition is simulated; for maximum presynaptic inhibition, the monosynaptic stretch reflex synapse strength is 0. Black lines: normal situation; grey lines: pathological situation, synapse i3 was disabled

3.3 Pathological case

To verify the importance of feedback paths of the BNN for achieving negative feedback gains as absent with CRPS, the procedure of simulating presynaptic inhibition on the monosynaptic stretch reflex synapse was repeated. The main supplier of negative stimulation, the synapse between the inhibitory interneuron and the motoneuron (synapse i3), was disabled. Plotting for the presynaptic inhibition settings again displays a clear rising trend for all three feedback gain types (Fig. 12, grey lines). However, the negative feedback gains have disappeared, even at high presynaptic inhibition, while feedback modulation by the presynaptic inhibition mechanism is still possible.

4 Discussion

The NMS model of this study is the first attempt to explain the modulation of lumped reflexive feedback parameters with a physiologically based model of the spinal neural network. The model is an integration of a BNN based on Bashor (1998) with a one-DOF musculoskeletal model derived from human shoulder studies (Stroeve 1999; van der Helm et al. 2002; Schouten et al. 2003). Muscle proprioceptors obtained from the comparative studies of Prochazka and Gorassini (1998a, b) and Crago et al. (1982) provide the neural network with muscle length, velocity and force feedback from the musculoskeletal model. As a result, the parameters in the model (synapse strength, spike rates, etc) are physically interpretable, and might in the future be compared with measurements in order to validate the model.

The parameters in the BNN, such as distribution, number and strength of synaptic connections, have been adopted from Bashor (1998). Without any further adaptation of these parameters, i.e. without training the BNN, the neural network results of experiments with human subjects could be reproduced. Onemight assume that the neural network model structure and parameters are already optimized, since they are derived from direct neuro-anatomical observations. Bashor (1998) derived these parameters mainly from cat studies, assuming similarities between humans and cat. This study is based on the same assumption.

The main additions to the work of Bashor (1998) of this study are the connection of the BNN to a one-DOF musculoskeletal model with proprioceptive feedback, and the use of experimental results to compare the model behavior. Applications of the model lay in the field of motor control and movement disorders. In this study the model gives insight into the mechanisms behind the negative position and velocity feedback gains as identified in human posture control (van der Helm et al. 2002; Schouten et al. 2003).

4.1 Limitations

There are still many limitations to the present model, as it is a first attempt. The BNN uses only a small subset of neurons and connections present in the human spinal cord, the muscle model is a simple describing model based on human identification instead of a more biologically realisticmodel, andmodels and parameters of the proprioceptors are mainly based on cat data and further assumptions.

The BNN does include the major and well-known spinal connections and interneurons, representing a minimal set necessary for reflex modeling. However, the model used here did not explicitly include group II interneurons (Jankowska and Hammar 2002) and Ib excitory pathways (Prochazka et al. 1997), the number of neurons is barely sufficient to use distribution functions for neuron pools and interneuronal connections and does not reflect the vast amount of interneurons in the spinal cord. The model neglects the connections to other parts of the central nervous system, as well as the recurrent intra-populational connections to prevent artificial mass-synchronization. Finally, the neuron model is relatively simple and is merely descriptive about the processes involved in spike generation.

The linear visco-elastic muscle model used here instead of a Hill-type muscle models due to their poor representation of the muscle visco-elasticity (van der Helm et al. 2002),might in future be replaced by a more realistic, but more complicated, cross-bridge model. To improve simplicity and reduce the numerical burden the elasticity of the tendon is not incorporated in both the NMS model and the reflex gain model (Fellows and Rack 1987).

The sensor models of the muscle spindle and GTO have been based on animal experiments published in literature (Prochazka and Gorassini 1998a, b). These sensor models do not account for modulation through γ-motor neuron activity, and one might discuss if the experimental results for animals are representative for human experiments, in which the task instruction and perception have a dominant role for the feedback modulation (van der Helm et al. 2002). Secondly, other receptors like in the skin or joint are not included due to lack of available data.

However, taking all this into account, the integration of these separate components into the NMSmodel does result in a increased understanding of their interactions and the overall system performance. Nevertheless, it is currently investigated how to best increase the biological realism of the model.

4.2 Model verifications

Validating the NMS was restricted by the unavailability of (human) biological data for the components. The approach used here was to keep all parameters within biological supposed correct boundaries while verifying the components in black-box simulations where possible and analysis of the sensitivity of the model behavior on the neuronal, synaptic and sensory parameters.

Bashor (1998) summarized that his large-scale spinal segmental model, mainly based on cat data, produced predictable reflex responses when compared with stretch and Golgi tendon organ reflexes studies, and behaviors such as agonist excitation and reciprocal inhibition were both predicted and observed. The proprioceptors derived from the comparative analysis in Prochazka and Gorassini (1998a, b) were reported to give a good prediction of the firing characteristics of muscle spindle primary afferents recorded chronically during normal stepping in cats, with the key variable in achieving good predictions being muscle velocity. The problem of whether the above studies are valid for a human model was addressed by Jankowska and Hammar (2002). Their general impression arising from results of studies on human and cat reflex interneuronal systems was that these systems have more features in common than differing. They hypothesized that not only the properties investigated so far, but also other basic properties of human spinal interneurons, such as their membrane properties and their sensitivity to various chemical compounds, are comparable to those found in the cat.

The available black-box verifications for this NMS model and the sensitivity analysis do not suggest any abnormalities. Figures 6 and 7 show that neuron firing rates stay within biological plausible boundaries, and changing parameters in the BNN mechanisms produces many wanted or unwanted states, but with counterparts as observed in human subjects. The presumption that feedback gains can be controlled by presynaptic inhibition on the monosynaptic stretch reflex synapse (Stein and Capaday 1988) was corroborated with the results for the normal situation in Fig. 12. So, although the model is not validated, and possible differences between cat and human cannot be excluded, it is considered reliable for a mechanistic study as presented in this article. Nevertheless, the current model should be used for suggesting or hypothesizing rather than claiming cause-and-effect relations between neural mechanisms and motor behavior.

In the sensitivity analysis, focus was on the effect of the BNN model parameters to the overall system dynamics. Although the analysis has shown that uncertainties in parameter values (especially those of the individual neurons) can have a strong effect on motor output, the linear lumped reflex gain model can be fitted with a high VAF under large parametric variation. This means that, although exact biologically realistic values are hard to obtain for each separate model element, trends in model behavior can be reliably expressed in terms of reflex gain changes. Using the exact same methods, the effect on the individual lumped parameters will be determined in a future study. That means that changes in lumped parameters can be linked to the BNN parameters, which have actual physiological meaning.

4.3 Applications

In this study the BNN-basedNMS model was compared with two experimental cases: reflex strength modulation and a pathological case (CRPS).

During normal human postural control, humans modulate the strength of the reflex path depending on the conditions, where the reflex strength can even become negative (van der Helm et al. 2002). Figure 12 shows that to achieve negative feedback gains for position and velocity information, a high presynaptic inhibition of themonosynaptic stretch reflex synapse (synapse e5 in Fig. 3) is required, disabling the transfer from the Ia afferents to the motoneurons. The weaker this connection, the lower the feedback gains and vice versa. In effect, the high presynaptic inhibition disables the dominant monosynaptic stretch reflex path and allows negatively stimulating paths in the BNN to achieve the negative feedback gains.

Schouten et al. (2003) observed the inability of CRPS patients with dystonia to set negative feedback gains even though optimal posture control dictates these gains as desirable (Schouten et al. 2001; De Vlugt et al. 2001). However, the patients were still able to modulate the positive feedback gains. Suggestions that the inability to set negative gains is due to neurotransmitter deficiencies of inhibitory interneurons in the spinal neural network (Van Hilten et al. 2000; Jankowska and Hammar 2002) were investigated in this study. Analysis of all possible feedback paths in the BNN suggested the synaptic connections of the inhibitory interneurons to the motoneurons are essential to achieve negative feedback gains. Figure 12 shows that when the synaptic connections of the inhibitory interneurons to the motoneurons are disabled, even maximum presynaptic inhibition on the Ia afferent connection to the motoneuron cannot cause the identified position and velocity feedback gains to become negative. Modulation of the positive feedback gains is still possible by the regular control of this presynaptic inhibition on the monosynaptic stretch reflex synapse. Therefore, it is concluded that dysfunctional inhibitory synapses in important negative feedback paths, likely the result of a neurotransmitter deficiency, can prevent the setting of negative feedback gains and might shed light on “the problem of the relative importance of the deficient inhibition of α-motoneurons as one of the main causes of the hyperexcitability of these [motoneurons]“ (Jankowska and Hammar 2002).

4.4 Conclusion

In the NMS model of this study, a BNN of the spinal neural network was integrated with a musculoskeletal model, including proprioceptive feedback. In other studies modeling the complete human NMS system, the spinal network is simply neglected or extremely simplified, although a few models exist on animal NMS systems (e.g. Ekeberg and Grillner 1999; Ivashko et al. 2003). On the other hand, studies on biological realistic neural network behavior tend to focus on the network and lack closed loop interaction with a realistic system, like the musculoskeletal system. Applications of the current NMS model lay in the fields of motor control and neurological disorders, where hypotheses on motor dysfunction can be tested, like spasticity, clonus, and tremor.

To demonstrate the potential use of the model two applications were investigated. It was shown that (a) in the present model the combined actions of the monosynaptic stretch reflex synapse and the synapse between the inhibitory interneuron and the motoneuron play an important role in obtaining negative feedback gains, as experimentally found during human postural control (van der Helm et al. 2002) and (b) disabling the synapse between the inhibitory interneurons and the motoneurons could account for the previously unexplained nonnegative feedback gains in CRPS patients (Schouten et al. 2003).