A neuroeconomic theory of the decision process

Abstract

We develop a neuronal theory of the choice process (NTCP), which takes a subject from the moment in which two options are presented to the selection of one of the two. The theory is based on an optimal signal detection, which generalizes the signal detection theory by adding the choice of effort as optimal choice for a given informational value of the signal for every effort level and a cost of effort. NTCP predicts the choice made as a stochastic choice: That is, as a probability distribution over two options in a set, the level of effort provided, the error rate, and the time to respond. The theory provides a unified account of behavioral evidence (choices made, error rate, time to respond) as well as neural evidence (represented by the effort rate measured for example by the level of brain activation). The theory also provides a unified explanation of several facts discovered and interpreted in the last decades of experimental economic analysis of choices, which we review.

To date, the economic model of choice has not been informed by the way the brain functions, although the literature contains numerous papers on neuroeconomics. By economic model, we mean one that disciplines the analysis of observations by an assumption of optimization that presumes that the economic agent has a mechanism for processing information (such as Bayes' rule) to arrive at choice based on a utility function. Observations include not only the choice between options, per se, but also additional data, including the length of time it takes to make choices, the number of errors in choices, and psychophysical measurements such as functional magnetic resonance imaging (fMRI). Including more than just the observed choices allows the data to have an additional disciplining effect on the theory. We extend this assumption of optimal behavior to the analysis of the brain process producing a choice. To do this, we assume that there is an unobservable choice that an agent makes, the consequences of which are reflected in all the observable data that can be measured in the choice process. That choice is the strength of effort devoted to processing information in reaching a decision between the options. As a conclusion, we propose a model that joins predictions of traditional psychological observations (time to decide and error rate) and predictions of relative brain activation (as measured by fMRI) dependent on exogenous characteristics of the decision environment.

Decision Processes and Economic Choice.

The economic theory of choice considers three different types of options: deterministic, risky, and ambiguous [Gilboa and Schmeidler's (1) theory describes how ambiguous choices are made].

In formal constructions of choice, the decision maker behaves as if making numerical calculations. Our model and subsequent tests of human economic choice are informed by recent findings on the processing of numerical magnitudes (2). Consider, for instance, a simple number comparison task: A human subject is shown a number on a screen and is asked to press a left button to indicate that the number is less than 55 and a right button to indicate that the number is greater than 55. An interpretation of the process is as follows: The human brain forms a spatial representation of numerical magnitudes. When a comparison stimulus is presented on a screen, stimuli are transferred stochastically to secondary areas of the occipital cortex and finally to areas distinctly responsible for making comparisons of spatial representations: the bilateral horizontal segment of the intraparietal sulcus, the left angular gyrus, and the bilateral posterior superior parietal lobe. Prior to announcing whether the number is considered greater than or less than 55, the subject in the experiment is accumulating noisy information generated by the experimental stimulus.

Several of the main modeling results in economic choice in this study are paralleled by results with numerical magnitudes. In studies of numerosity, there are reaction time and inconsistency effects with respect to distance from the comparison stimulus. The closer the number is to the comparison, the slower the reaction time and the more inconsistency. The distance effect with numbers has been replicated many times with humans and nonhuman primates. The underlying explanation of such phenomena is that number symbols, such as Arabic or Roman numerals or collections of dots (in the case of monkeys), are transformed to associative cortex, and a semantic representation is made downstream (see refs. 2 and 3). Such representations are noisy. For example, monkeys trained to match a sample will most frequently match three dots with three previously shown dots; they will match two and four dots less frequently and one and five dots rarely, if ever. The explanation for human judgment is that humans also work with a noisy representation, even of certain amounts, and that they map directly from the noisy representation to motor actions so that such actions are noisy in response to experimental stimuli (see ref. 2).

Noise in economic choice has a rich history. Early findings in studies of choice involve paired comparisons between deterministic outcomes. Thurstone (4) outlined a methodology in which a person was asked to choose between 2-tuples at a time, for example, (2 hats, 4 pairs of shoes) versus (4 hats, x pairs of shoes), where x was varied. Using this approach creates an estimated cutoff point z, such that for an x < z, 2 hats, 4 pairs of shoes will likely be preferred to 4 hats, x pairs of shoes, and for an x > z, 4 hats, x pairs of shoes will likely be preferred to 2 hats, 4 pairs of shoes. Thurstone's data revealed that subjects tend to reveal more noise in choices relative to a cutoff when x is close to the cutoff point (4, 5).

Mosteller and Nogee (6) measured reaction time in choosing between risky gambles during choices and were able to determine that the closer to indifference a subject was, the higher the reaction time tended to be. The net result in these early studies is that when distance comes into play between utilities, two things are affected: consistency and reaction time. Some examples of modeling noise in choice, such as Luce (7) and Tversky (8), give no explicit modeling of what produces the noise. In these efforts, scales can be found that represent the choices stochastically, but no process has been specified that produces the error. In related work, Loomes and Sugden (9) tested three competing models of stochastic choice, none of which gave an explicit representation of the stochastic choice process. What differs in our examination of noise from these earlier processes is that we treat the level of noise as an endogenous choice by the subject. Harrison (10) suggested that error in choices is itself a choice. Errors arise when an alternative is close to the maximum so that the implicit cost of making an error is low and the error is acceptable. The problem with this line of reasoning is that the decision maker needs to know the maximum value to assess if the judgment is close enough to the optimal judgment.

Decision field theory (DFT) is a related literature on the psychology of choice (11–13). In the paired-choice task, DFT presumes that the decision maker's choices are governed by a statistic that assesses the relative utility of the two options: In the dynamic setting, this statistic is aggregated over a number of comparisons. The statistic itself can lead to a match versus a nonmatch. Information on matches is accumulated until a boundary (which represents the required amount of information) is reached. DFT is a stochastic theory of choice that also models reaction time, like the neuronal theory of choice process (NTCP). The two theories differ in that in DFT the decision maker has no explicit control of the information generated in the choice process.

Several different areas of the brain have been isolated establishing a connection with NTCP. Arriving at internal representations of elements of NTCP, such as priors and revised probabilities, has been found to engage the limbic system and orbital frontal cortex (14, 15). For example, Preuschoff et al. (14) discover that revised assessments of both expected value and risk occur in the ventral striatum, although at different moments. These assessments can be viewed as inputs to NTCP. Response to reward in monkeys implicates elements of the orbital frontal as well as the ventral tegmental area (15, 16). These areas reflect a relationship with the probability of rewards and may serve as inputs to either the formation of priors or the updating process in NTCP.

Some studies have examined the relationship between brain activation and types of stimuli such as certainty, ambiguity, and risk. Hsu et al. (17) found evidence of ambiguous stimuli having an impact on the striatum, although Hsu et. al. use three different types of ambiguous stimuli, only one of which is like those discussed here. Huettel et. al. (18) found the reaction time difference for ambiguous and risky stimuli, such as those posited here, but did not find the same locus of activation for ambiguous stimuli. The difference can potentially be explained because the same type of representation of the ambiguous stimulus was not use in the Huettel et al. study.

The unification of these theories suggests the possible unification of what might be construed to be disparate findings of brain behavior. By casting the framework of choice in an effort-based selection and its related dependency on priors and updating suggests the various findings engaging the limbic system and more numerical systems are potentially interrelated.

Optimal Signal Detection.

In this study, we construct a unified theory of choice in that it recognizes that (i) subjects must make a decision of effort regarding how they will process stimuli to arrive at a decision and (ii) the various measurements, such as reaction time, fMRI, choice, and error, are interrelated from the standpoint of the theory. The theory disciplines the examination of behavioral data comprising more than just choice, which leads to a theory that is more extensive than traditional theories of choice. The model accommodates error by considering the internal milieu of the brain and moves beyond a static, stochastic theory of choice and signal detection theory. The model builds on the theory of static stochastic choice, interpreted as deriving from a single preference order, different from the random utility model of refs. 19 and 20. The choice set is a only a pair, as in refs. 21 and 22. Also, the static choice is derived from a fully specified dynamic theory of the decision process. The model develops the theory of random walk of the decision process, but extends it from perceptual choice to economic choice. The fundamental difference between the two is that in our theory, the quantity perceived is subjective, whereas in perception studies, it is an objective value—for example, the number of particles that move to the right, instead of to the left, or the probability of an event.

Model

Our model combines the main ideas from the theory of signal detection and the random walk models of decision, as, for example, in Ratcliff's (23) model, and extends them to the realm of economic decision. We introduce two major modifications to these models. First, because we want to extend our analysis to study the level of brain activity associated with a specified task, we introduce a variable, the level of effort, that affects the quality of the signal that the subject is observing; the signal can be of higher quality, but a higher level of effort must be provided. Second, the discipline imposed on the level of effort is that it must be the optimal level for the given task. This assumption of the model requires that the subject be familiar with the task and the environment and that he or she has selected the appropriate level of effort. Because we introduce this optimality requirement not only in the processing of the signal (see ref. 24), but in the observation, we call this an optimal signal detection model.

Our simple, one-period model has three parameters describing, respectively, the effectiveness of the effort (π), the marginal cost of information (γ), and the belief of the subjects (μ), which are going to be discussed in detail in this rest of this section. The theory will provide a link between these three parameters and observed data.

The subject has to choose one action out of a set A. The subject's payoff depends on the action and a state of nature that is unknown, θ ∈ Θ ⊂ R². Before his or her choice of action, the subject can observe a signal y ∈ Y, according to an experiment (i.e., a map from Θ to probabilities on Y) that depends on the level of effort, e ∈ E, the subject chooses, and the effectiveness parameter π (see Signal Structure for a discussion of this parameter). The probability of the signal y, given the true state θ and the effort e, is denoted by P_θ(y|e,π).

In a task of choosing between two options, the subject has to decide which option in the feasible set is optimal, so the set of options is the subject's set of actions. For example, the subject may be choosing between two lotteries, the lottery on the left and the lottery on the right, in which case we can describe the action set as {x₁,x₂}. The subject is trying to evaluate which of the two has a larger utility. He does not know the utility of the two options, so the unknown state is the value of the two utilities, θ = (u(x₁),u(x₂)) ≡ (θ¹,θ²). If the value θ was known, then the optimal choice would be clear: Choose the lottery with the largest value. He does not know the value, however, so his choice has to rely on a noisy signal on the comparative value of the two options.

Interpretation.

To help in the interpretation of the problem, we describe what the problem is in the standard word of a perfectly rational agent. A decision maker has an expected utility function u defined on the set of choices, a utility that he knows perfectly well. He is told that he can choose one out of a set of two options, D ≡{xⁱ: i = 1,2}. He is not told what the options are, only that they are drawn according to a probability measure known to him. Each option is labeled by a number. He has to select one of the options by communicating its number. Before he decides, he can observe informative signals on the utility to him of the options. He can affect the accuracy of the signal with a choice of effort e. These signals are realizations on a space Y of a probability P_θ(·|e) ∈ Δ(Y). Effort is costly.

The remaining exposition of the theory focuses on how effort (when it is assumed to be neuronal activity) interrelates with observed choice, reaction time, and error in choice. The tasks include stimuli that are certain, risky, and ambiguous. The choices are binary and the subject virtually chooses the object to the left or to the right.

We consider this comparative value to be represented by a function denoted by θ → A(θ₁, θ₂). This function is assumed to have two properties: It is strictly increasing in the first component and strictly decreasing in the second, and for every θ₁ and θ₂: A(θ₂, θ₁) = −A(θ₁, θ₂)). Examples of comparative value functions are: A(θ₁, θ₂) ≡ θ₁ − θ₂; A(θ₁, θ₂ ≡ log$\left(\frac{{\theta }_1}{{\theta }_2}\right)$. In the following, we focus on the first case.

Signal Structure.

We assume that this probability on the signal is only dependent on the comparative value A. The signal set is Y = {−1,1}. A signal equal to 1 denotes a match, and equal to −1 denotes a mismatch in Ratcliff's (23) terminology. A match means that the event “A greater than 0” is more likely than the complement; a mismatch means the opposite. This model is equivalent, but more convenient, to the one in which two independent signals are drawn, one for each of the the options, and which of the two is larger is revealed.

We finally assume that the signal provided by the experiment P is a location signal. Specifically, the probability of a match is given by

The effectiveness of the effort is affected by a real valued parameter π ≥ 0: The higher its value, the more precise the signal. The value of this parameter may depend on several features of the decision problem. For example, the value may be a function of the number of choices made by the subject (a measure of his or her experience with the task). Also, it may depend on the information quality of the signal: For example, if the choice is ambiguous, then the quality of information available to the decision maker is lower, and this may be modeled by a lower value of π.

The subjects has an initial belief on the states of nature, denoted μ ∈ Δ (Θ), where Δ(Θ) is the set of probability measures on Θ. We also denote

and by μ(dθ|y) the posterior probability of the subject on Θ given the signal y. A belief concentrated around the diagonal represents an environment where the decision maker expects little difference in value between the two options.

The Density Function f.

We make the following assumptions on the function f. First, there is no differential treatment of options on the right and on the left, that is, f(x) = f(−x). Second, the probability decreases as we move away from 0: If x > y > 0 then f(y) > f(x). For convenience, when we analyze the comparative statics effects of the changes in the values of the parameter we assume that f is differentiable. The properties of the comparison function A and the density function f imply on the experiment P that P_(θ1,θ2)(1;e) = 1 − P_(θ2,θ1)(1;e); P_(θ1,θ2)(1;e) = P_(θ2,θ1)(−1;e). Also, if θ₁ >θ₂, then P_(θ1,θ2)(1;e) > P_(θ2,θ1)(1;e).

As the effort tends to infinity, the probability of a match tends to 1 when A(θ) > 0 —that is, θ₁, the utility of option x₁, is larger than θ₂, the utility of option x₂. For example, if A(θ₁,θ₂) ≡ θ₁ − θ₂, then a mismatch occurs for sure in the limit if and only if θ₁ < θ₂. A natural assumption is that the prior belief μ is symmetric: If we denote S(θ₁,θ₂) = (θ₂,θ₁), then for any set O ⊆ Θ,

This assumption only reflects the fact that the subject does not expect higher utilities to be placed on the right rather than the left.

Cost of Effort.

The provision of effort in the observation and processing of the signal is costly. The cost depends directly on the effort but may also be influenced by other factors like the experience in the task or the quality of information that he has available. All these factors are summarized by a real parameter γ. Putting these elements together, the cost is

We assume that the function c is convex. A convenient example that we use in the Results section below is c(e) = $\frac{e^2}{2}$.

Results

The subject is choosing the optimal level of effort and, conditional on the signal observed, the best action:

where V is defined naturally by V ((θ₁, θ₂),a_i) = θ_i. It is easy to see that the optimal action is to choose x₁ if y = 1, and otherwise to choose x₂.

Given parameters (π, γ, μ) —describing, respectively, the effectiveness of the effort, the cost of the effort, and the belief—an optimal effort is determined, ê(π γ,μ). We assume that the optimal effort can be characterized by first-order conditions, but this may not be the case, as in the example discussed below where the density function f is the uniform distribution. In this case, a different method is necessary, such as an explicit computation.

The solution of the first order condition obtained by differentiating with respect to the effort is

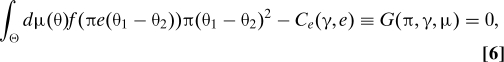or equivalently,

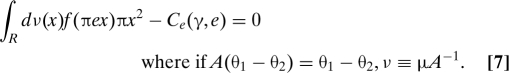Note that ν is symmetric around 0 because of the symmetry property of μ (Eq. 3). The second term, C_e(γ, e), is the marginal cost of effort. The first term is the marginal return of effort; that is, the expected marginal gain in the probability of making the right choice. Under our assumptions, the first order condition is sufficient.

A few properties of the optimal effort are clear. First, if the cost function is described by Eq. 4, effort is decreasing in the cost parameter γ: If γ₂ >γ₁, then for every π and μ, ê(π, γ₂, μ) ≤ ê(π, γ₁, μ). Clearly, ê(0, γ, μ) = 0, because the probability of making the right choice is independent of the effort, and effort is costly. Also, lim_γ→0 ê(π, γ, μ) = + ∞. Effort is strictly increasing in π for small values of π: ${{\displaystyle \text{lim}}}_{\pi \to 0}\frac{\partial \widehat{e}(\cdot ,\gamma ,\mu )}{d\pi }>0$.

Effective Effort.

To characterize how the optimal effort depends on π, consider (for every γ and μ) the effective effort η:

Clearly, for every γ and μ, η(0, γ,μ) = 0. The effective effort is increasing in π for every γ and μ: If π² > π¹, then η(π², γ,μ) > η(π¹, γ,μ). Also, effective effort increases without bounds: lim_π→+∞ η(π γμ) = + ∞. Just as with effort, effective effort is decreasing in the cost parameter γ.

Comparative Statics on Effort and Error Rate.

The comparative statics study of the effect in the increase in the effectiveness parameter and in the dispersion of beliefs follows easily from the implicit function theorem once one notes that the derivative of the first-order condition, with respect to effort, is always negative because

The effect on optimal effort of the effectiveness parameter π is nonmonotonic. The sign of $\frac{\partial \widehat{e}}{\partial \pi }$ is equal to the sign of

(see Eq. 6), where

Note that Df(0) = f(0) and Df is symmetric around 0, that is, Df(u) = Df(−u). To understand how effort changes with the effectiveness parameter π, note two key properties of Df for most common densities f. For example, a normal density, 0 mean, and unitary variance σ² has Df(u) = f(u)$\left(\frac{{\sigma }^2-{\mu }^2}{{\sigma }^2}\right)$. For the Laplace density, $f(u)=\frac{\alpha }{2}{e}^{-\alpha \left|u\right|}$, Df(u) = f(u)(1 − α|u|). First, Df changes sign only once on the positive real line; that is

Second, lim_u→∞ Df(u) = 0.

The effect of the effectiveness parameter π on optimal effort is the net result of two contrasting forces. An increase in π makes the return of effort higher, and this induces a higher effort. On the other hand, higher π gives a larger effective effort for the same effort, and cost can be saved (substitution effect). When the optimal effort is already large, the substitution effect dominates, and effort is reduced in response to an increase in π the opposite occurs when the optimal effort is small.

When the belief has only two points in the support, and the condition in Eq. 11 is satisfied, then the effect of the effectiveness parameter is, for the densities mentioned above, to increase the effort when the value of π is small and to decrease it when the value is large. This result follows from the two properties we pointed out in the text following Eq. 10.

We model the change in the dispersion formally by introducing a parameter D, where for every set O ⊂ Θ,

For example, an individual at the moment of making a choice may have an idea of the level of utility that is at stake and of the likely difference in the value of the two options. As D increases, both the expected value and the variance of the difference between the value of the two options increase. This increase is clear if we consider how the induced probability ν (introduced in Eq. 7) on the difference between θ¹ and θ² changes; that is, for every interval I, ν_D(I) = ν (D⁻¹I). From our assumptions on μ, the measure ν is symmetric around zero. The effect of the increase in the dispersion of the belief is similar to that of the increase in the effectiveness parameter. The sign of $\frac{\partial \widehat{e}}{\partial D}$ is the same as the sign of the

Probability of Error.

The mean probability of error is equal to 2∫_{{θ1 > θ2}} dμ(θ)P(−1|θ); that is

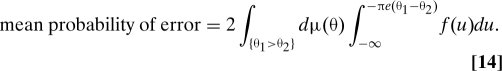Because the effective effort is decreasing in γ and increasing in π, the mean error is increasing in γ and decreasing in π.

When D increases, the error rate is determined by the behavior of the product of effort and D itself. In fact, the mean error rate as a function of D is

As D tends to infinity, and the density f is such that f(u) > 0 for every u, then the product eD tends to infinity, and therefore the mean error rate tends to 0. The example in A Simple Example (for a uniform density) shows that the condition that f is positive is necessary: The mean error rate is first decreasing in D, and then, for large values of D it is constant.

A Simple Example.

Let us consider a simple illustration. The density function f is the uniform distribution on the interval $[-\frac{1}{2},\frac{1}{2}]$. This density function is not differentiable, but we will verify that our comparative statics results hold by direct verification. The cost function is quadratic C(e) = $\gamma \frac{e^2}{2}$. Finally, the belief of the subject is a simple measure with two points in the support, both with equal probability: (B(1 + r),B(1 − r)) and (B(1 − r),B(1 + r)). The parameter B can be interpreted as a measure of the value at stake in the choice, and r can be interpreted as a measure of the spread of the belief. The induced measure ν has equal probability of D and −D, with D = 2Br.

In this case, the optimal level of effort is

This example illustrates well the main properties of the optimal effort function. First, the optimal effort is decreasing on the cost parameter γ. Second, the optimal effort is first increasing and then decreasing in the effectiveness parameter π. Finally, the measure of value B and of spread r effort have the same effect: The optimal effort is first increasing and then decreasing in their product. The intuitive reason for this latter result is the same we have seen for the effectiveness parameter π: When Br is large and effort is large, the substitution effect dominates.

The effective effort

is increasing in π, decreasing in γ, and first increasing and then decreasing in the product Br. The mean probability of error at the optimal effort behaves like the effective effort in all the parameters.

Predictions of the Theory.

The theory provides predictions linking the three parameters [effectiveness of the effort (π), the marginal cost of information (γ), and the belief of the subjects (μ)] to effort choice of the subject, as well as the effective effort (that is, the product of effort and effectiveness), and the error rate.* So the theory provides a link between the behavioral evidence (choice, error rate, response time) and neural evidence (the effort rate, as measured by the brain activation). We list below the predictions that are independent of the specific form of the density function. For specific cases, more precise results can be obtained, as indicated in the text.

1. A decrease in the marginal cost induces an increase of effort and effective effort provided and therefore a reduction of the error rate.

2. An increase in the effectiveness of the effort induces an increase in the effective effort; hence, a reduction of the error rate. This increase initially produces an increase in the level of optimal effort and then, for higher values of π, a decrease.

3. An increase in the spread and value of the belief initially produces an increase and then a decrease in the level of optimal effort, and therefore of the level of effective effort. It induces a decrease in the error rate in the limit.

Random Walk Model.

The general case in which the subject can make several observations allows predictions on the time to respond. Note that this is the prediction made for fixed beliefs and effort cost; we are comparing the effect of different realizations of the true utility with the subject. These predictions can be obtained by the analysis of the random walk model induced by the optimal solution. The subject can observe not one but several signals. We denote p = P_θ(1|e), and q = 1 − p. As in Ratcliff, the decision is taken when the sum of the values of the signals reaches a preassigned boundary. As in the simple model, p > 1/2 is the probability of a correct match.

This model can offer predictions on both the error rate (just like the simple model presented in the previous section) and the response time. The expected value of these two variables is well known from the analysis of the gambler's ruin problem (25). The random walk is defined on a subset of the nonnegative integers, and it transits from z to z + 1 with probability p, and to z − 1 with probability 1 − p. The walk ends when either the upper barrier a > 0 or the lower barrier (ruin) is equal to 0. We consider the symmetric case in which a is even and the process starts in the midpoint z = a/2. The two relevant formulas are the one for the probability of a mismatch (corresponding in the Gambler's ruin problem to the ruin of the gambler) and the expected duration of the game. The first is $q_z=\frac{{(q/p)}^{2z}-{(q/p)}^z}{{(q/p)}^{2z-1}}$, and the second is $D_z=\frac{z}{q-p}-\frac{2z}{q-p}\frac{1-{(q/p)}^z}{1-{(q/p)}^{2z}}$. These formulas can be used to simulate the error rate and response time for experimental data. A complete discussion of the multiperiod case is in Rustichini (26), where the boundaries are set endogenously in the optimization problem, rather than fixed (a considerable complication to the model). Rustichini shows that the response time is nonmonotonic in the effectiveness of the effort.

Discussion

In this study, we constructed a unified theory of choice that recognizes that (i) subjects must make a decision of effort regarding how they will process stimuli to arrive at a decision and (ii) the various measurements, such as reaction time, fMRI, choice, and error, are interrelated from the standpoint of the theory. Several important features of the theory, as evidenced previously, are as follows: (i) the basic elements of the theory are still choices between alternatives, whether certain, risky, or ambiguous; (ii) the evaluation of these choices proceeds as an approximate mathematical process; (iii) there is an understanding that choices are made with error (or alternatively, that there is noise in choice); (iv) the level of noise is endogenous (i.e., to some extent under the control of the subject); and finally, (v) choice can be reexamined as rational behavior.

A Stand on Rationality.

This paper has a rich history. Herbert Simon (27) remarked that “there is a complete lack of evidence that, in actual human choice situations of any complexity, … [rational] computations can be, or are in fact, performed … but we cannot, of course, rule out the possibility that the unconscious is a better decision maker than the conscious” (p. 104). We model the decision process under uncertainty as a problem in maximization governed by mental processes, the traces of which have observable neural correlates in brain imaging. The current model breathes meaning into unconscious computational processes associated with decision under uncertainty, its inherent error properties, and its observational content. Moreover, it offers a substantial extension to the interpretation that “if subjects implicitly take account of the effort cost of decision, then of course the subject's unconscious decisions are indeed better-superrational-than the conscious rational decision analysis predictions of the theorist/experimentalist” (28).

In further development of his thoughts on human decision, Simon (29) noted that

the necessity for careful distinctions between subjective rationality (… given the perceptual and evaluation premises of the subject), and objective rationality (… as viewed by the experimenter) … in the explanation of observed behavior … to predict how economic man will behave we need to know not only that he is rational, but how he perceives the world—what alternatives he sees, and what consequences he attaches to them. … We should not jump to the conclusion, however, that we can therefore get along without the concept of rationality.

Our model does not jump to any such conclusion and explicitly builds on both subjective and objective elements in decisions, and derives the observational implications of varying the parameters of those elements. Models of subjective effort-costly decisions imply the nonexistence of any coherent concept of objective rationality for individual decisions, alike for all. But “there is no denial of human rationality; the issue is in what senses are individuals rational and how far can we go with abstract objective principles of how ‘rational’ people ‘should’ act” (30).

Siegel (31, 32) acknowledged the key influence of Simon's (27) paper in leading him to model a hypothesized tradeoff between the subjective cost of executing a decision task (“boredom”) and monetary rewards in the particular context of predicting Bernoulli trials.

When theory fails experimental tests, a common reaction is to suppose that the rewards for decisions must not have been large enough to matter. This view has intuitive appeal, but it is devoid of empirical (predictive) content, in the absence of building on the intuition to reformulate standard theory. Also, it implies that economics is only about decisions in which rewards are large enough to matter and therefore does not address most of the day-to-day economic decisions of life.

Experimentalists have argued that this phenomenon may be a natural consequence of other motivations, besides monetary reward, that are arguments in individual utility functions. Thus Smith (33) suggested that the use of monetary rewards to induce pre-specified a value on decisions may be compromised by several considerations, one being the presence of transactions effort, generalizing Siegel (31, 32), who systematically varied reward levels to measure the effect on subjective decision cost in his model of binary choice prediction. The “failure to optimize” (i.e., objectively) can be related to what von Winderfelt and Edwards (34) called the problem of flat maxima, that is, a consequence of the low opportunity cost for deviations from the “optimal” outcome, as emphasized by Harrison (10, 35). This intuition led to the interpretation that because standard theory predicts that decision makers will make optimal decisions, despite how gently rounded the payoff function is, the theory is misspecified and needs modification. When the theory is properly specified, there should be nothing left to say about opportunity cost or flat maxima (i.e., when the benefit margin is weighed against decision cost, there should be nothing left to forgo).

What keeps this statement from being tautological is that it leads to predictions that are testable. Although one can look backward to the preceding (not exhaustive) literature review on decision cost, there are significant gaps in the previous work, which fails to provide a comprehensive formal treatment that predicts choices, response times, error rates, and brain activation in a decision maker. For example, Smith and Walker (30) showed that increasing the reward to choice (or decreasing decision cost) (i) increases effort, where effort is a postulated, unobserved intermediate variable, and (ii) increases the variance of decision error, which is their only observational prediction. By further postulating that increased experience lowers decision cost, they are able to conclude that increased experience will lower the variance of decision error, but there is no formal parametric treatment of experience. For example, Smith and Walker (36) reported first-price auctions in which reward levels and experience were systematically varied and found that the error variance declined both with increased reward and with increased experience.

This paper has provided a simple and testable setup for a theory of the decision process. It suggests a new direction of research in the investigation of the behavioral and neural foundation of the difference between the effects that operate through an improvement in the signal and those operating through a reduction of the cost of information processing. The interest of this distinction is clear from our results: A decrease in the marginal cost increases optimal effort, whereas the increase in the effectiveness of the effort has a nonmonotonic effect, through the combined effect of the complement and substitution effect.