Nucleosome positioning by genomic excluding-energy barriers

Abstract

Recent genome-wide nucleosome mappings along with bioinformatics studies have confirmed that the DNA sequence plays a more important role in the collective organization of nucleosomes in vivo than previously thought. Yet in living cells, this organization also results from the action of various external factors like DNA-binding proteins and chromatin remodelers. To decipher the code for intrinsic chromatin organization, there is thus a need for in vitro experiments to bridge the gap between computational models of nucleosome sequence preferences and in vivo nucleosome occupancy data. Here we combine atomic force microscopy in liquid and theoretical modeling to demonstrate that a major sequence signaling in vivo are high-energy barriers that locally inhibit nucleosome formation rather than favorable positioning motifs. We show that these genomic excluding-energy barriers condition the collective assembly of neighboring nucleosomes consistently with equilibrium statistical ordering principles. The analysis of two gene promoter regions in Saccharomyces cerevisiae and the human genome indicates that these genomic barriers direct the intrinsic nucleosome occupancy of regulatory sites, thereby contributing to gene expression regulation.

The recent flowering of tiled micro-arrays (1, 2) and chip-sequencing (3) approaches has provided an unprecedented opportunity to elucidate the extent to which the DNA sequence participates in the positioning of nucleosomes observed in vivo along eukaryotic chromosomes (4, 5). Among the results indicating that nucleosome formation is facilitated by the DNA sequence, it is known that some genomic sequences presenting a ≈10 bp periodicity of some di- or trinucleotides (e.g., AA/TT) show higher affinity for nucleosomes (6–9). The periodic positioning of these motifs over a few helical pitches would contribute to a global spontaneous curvature of DNA that would favor its wrapping on the histone surface (10, 11). However, the statistical significance of this 10-bp periodicity nucleosomal positioning signal remains a subject of great debate (4, 5, 12, 13). According to previous reports (12, 13), in Saccharomyces cerevisiae (1, 2), no more than 20% of the in vivo nucleosome positioning, above what is expected by chance, is determined by intrinsic signals in the genomic DNA. An alternative antipositioning signaling picture has recently emerged from bioinformatic studies (13–16) that bring to light the fact that the sequence is actually highly predictive of the nucleosome-free regions (NFRs) observed in vivo at gene promoters and terminations (1, 2). Excluding-energy barriers coded in the sequence would locally impair nucleosome formation and nonlocally influence the overall nucleosomal chromatin organization according to equilibrium statistical ordering principles (14, 17). Furthermore, by conditioning an activatory or inhibitory nucleosomal chromatin environment, these genomic energy barriers would contribute to gene regulation (18). In vivo genome-wide nucleosome positioning data encompass the influence of DNA-binding proteins and chromatin remodelers (19, 20), so that it is difficult to isolate the contribution of direct histone-DNA interaction in these data. To overcome this limitation, we performed an experimental study based on atomic force microscopy (AFM) imaging in liquid of nucleosome assembly on genomic sequences, at different loading levels, that provides direct single-molecule visualization and precise quantification of intrinsic nucleosome positioning. To investigate the role of the DNA sequence on nucleosome positioning and nucleosome organization, we assisted our AFM experimentation by some physical modeling of the nucleosome formation energy based on sequence-dependent DNA bending properties (14, 15) that remarkably reproduces recent in vitro genome-wide nucleosome occupancy data (21).

Results and Discussion

Combining AFM Imaging and Physical Modeling.

So far, except for a few studies of telomeric (22) and centromeric (23) nucleosomes, AFM was used to image, mainly in air, nucleosome assembly on specific positioning sequences (e.g., Xenopus 5S rDNA and 601 DNA sequences) and arrays of concatenated repetitions of these sequences (22–25). We carried out AFM experiments in aqueous solution (26) and imaged mononucleosomes reconstituted on genomic yeast and human DNA templates by using standard salt dialysis procedure (27). Selection of properly folded nucleosomes, determination of dyad position, and resulting positioning map are detailed in Data and Methods. As a theoretical guide, we developed a physical modeling of nucleosome assembly that relies on the computation of the free-energy cost of bending a DNA fragment of a given sequence from its natural curvature to the final superhelical structure around the histone core (see Data and Methods). Consistent with our previous works (14, 28, 29), we used the “Pnuc” structural bending trinucleotide coding table, experimentally established from nucleosome positioning data (30) to derive the effective potential. Then we extended this theoretical modeling to a grand canonical description of the equilibrium density of nucleosomes in this effective potential (see Data and Methods). When imposing that ≈30% of the sequence was covered by nucleosomes, we obtained nucleosome density profiles quite comparable with the nucleosome occupancy profiles observed in vitro (21): The mean Pearson correlation computed along the 12 million bps of the yeast genome is r = 0.70; a comparable high value r = 0.77 is obtained when using recent models based on statistical learning (16, 21) [actually, r = 0.81 between our model and the Field et al. model (16)]. Note that when adjusting the chemical potential to get 75% nucleosome coverage of the sequence, we got significantly lower correlations with in vivo data, namely r = 0.50 with Kaplan et al. data (21) and r = 0.30 with Lee et al. data (2). The weakest correlations observed for our model as for the Field et al. model (16) (r = 0.43 with in vivo Kaplan et al. data, and r = 0.33 with Lee et al. data), likely result from NFRs that are induced by external factors (transcription factors, remodelers, etc.) and are not taken into account by models that are mainly aimed to describe the effect of the DNA sequence on nucleosome positioning.

Thus the main advantage of the present study that combines in vitro AFM imaging and physical modeling is that for a same-DNA template, very instructive and complementary informations are made available: (i) by comparing the statistical positioning distribution of a single mononucleosome (which is not accessible in vivo) with the theoretical nucleosome energy profile, we are able to characterize the ability of the sequence to locally favor nucleosome formation, and (ii) by comparing the experimental nucleosome density profile obtained by increasing the nucleosome loading with the theoretical grand canonical nucleosome equilibrium density, we are in position to understand and quantify the extent to which the DNA sequence contributes to the collective organization of nucleosomes observed in vivo.

Genomic Energy Barriers Locally Inhibit Nucleosome Formation.

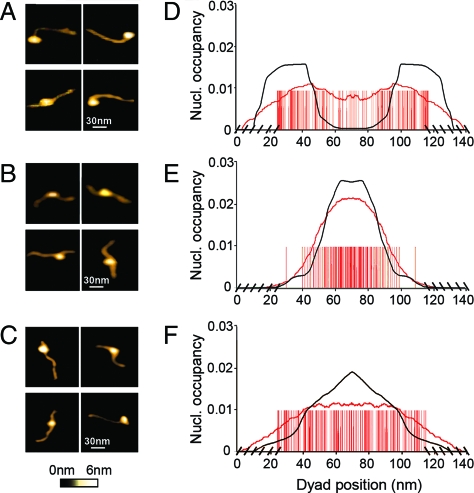
In a first experiment, we reconstituted a single nucleosome on three short (394, 386, and 387 bp) DNA templates (see Data and Methods). These three DNA fragments were selected in the yeast chromosome 3 according to the nucleosome formation energy profiles predicted by our physical modeling (Fig. 1). Two of these profiles display rather high-energy barriers corresponding to NFRs observed in vivo (2); for the first fragment (A), there is a barrier positioned at the center (Fig. 1A) whereas two energy barriers are bordering the second fragment (B) (Fig. 1B). As a reference, the third fragment (C) presents a flat energy profile without any barrier susceptible to impair nucleosome formation (Fig. 1C). As illustrated on a few characteristic single-molecule AFM images (Fig. 2A), the nucleosome is mostly observed at the edges of DNA fragment A. The statistical analysis of the (symmetrized) dyad-positioning distribution obtained from N = 107 molecules (Fig. 2D) confirms an enrichment at both extremities, whereas a lack of positioning events is noticeable at the center where the sequence- induced energy barrier is located (Fig. 1A). This experimental distribution is in good agreement (up to free-end effects) with the theoretical mononucleosome occupancy probability profile predicted by our physical modeling, which is a strong indication of the underlying control of the DNA sequence on nucleosome formation. This observation is corroborated by the mononucleosome positioning observed (N = 102) on DNA fragment B (Fig. 2B), where no nucleosome bound to the fragment ends because of the presence of inhibitory energy barriers (Fig. 1B). Indeed, the nucleosome density is mainly concentrated in the central region as predicted by our physical modeling, which explains the remarkable agreement observed between the experimental and theoretical symmetrized nucleosome occupancy probability profiles (Fig. 2E). Consistent with its featureless theoretical energy landscape (Fig. 1C), the experimental nucleosome occupancy profile (N = 105) obtained for DNA fragment C (Fig. 2F) turns out to be rather flat as the signature of a statistical homogeneous dyad-positioning distribution (Fig. 2C). This result confirms that the observed nucleosome positioning at the edges of fragment A (Figs. 2A and D) is not due to some possible entropic advantage (31) but more likely results from the exclusion from the energetically unfavorable central region (13–16). Similarly, the remarkable positioning of the nucleosome in the central region of DNA fragment B results from the excluding role of the bordering energy barriers and not from some positioning signal, as observed in a test AFM experiment with a 255-bp DNA fragment containing the 601 DNA sequence (Fig. S1 of the SI Appendix), which was recently shown to prevent the nucleosome from sliding (32). This first series of experiments demonstrates the excluding role of high-energy barriers that are encoded in the sequence and that preclude nucleosome formation.

Fig. 1.

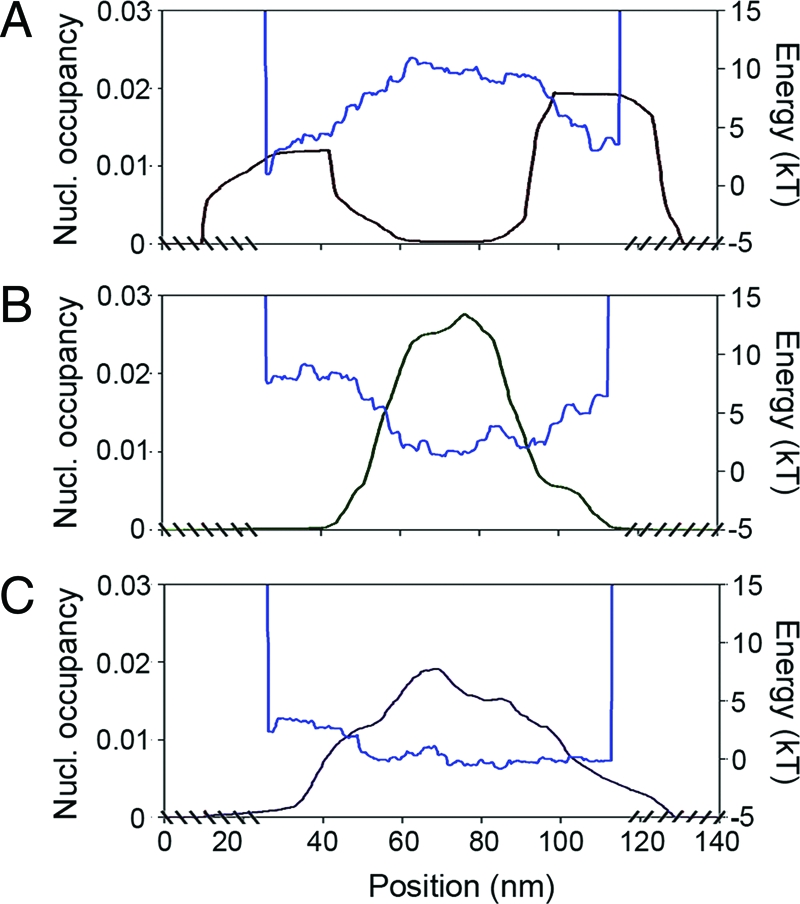
Theoretical nucleosome formation energy landscapes (blue) and nucleosome occupancy probability profiles (black) predicted by our physical modeling, for the three small yeast DNA fragments (see Data and Methods). (A) 394-bp fragment A. (B) 386-bp fragment B. (C) 387-bp fragment C. For each fragment, the chemical potential μ was adjusted so that the average number of nucleosomes is 1.

Fig. 2.

AFM imaging in liquid of mononucleosome positioning along the three small yeast (chr. 3) genomic DNA fragments. (A and D) Yeast DNA fragment A with L = 394 bp, N = 107 molecules. (B and E) Yeast DNA fragment B with L = 386 bp, N = 102. (C and F) Yeast DNA fragment C with L = 387 bp, N = 105. Frames A–C give examples of four single-molecule AFM images for each of these DNA templates respectively. D–F show the corresponding symmetrized dyad positioning distributions (see Data and Methods). A red bar was positioned at each experimentally detected dyad location and at its symmetrical position with respect to the center of the fragment; the cross-hatching at the edges corresponds to unphysical dyad positioning. The experimental nucleosome occupancy probability profile (red curve), obtained as a moving average of the symmetrized dyad density over a window of length 43.2 nm, is compared with the theoretical nucleosome occupancy probability profile (Fig. 1) after symmetrization (black curve). In the physical modeling, the boundary conditions were such that no nucleosome could settle on the sequence if not adsorbed on its total length (147 bp); the chemical potential μ was adjusted so that the average number of nucleosomes is 1 (See Data and Methods).

Genomic Excluding-Energy Barriers Condition the Collective Assembly of Neighboring Nucleosomes Consistently with Equilibrium Statistical Ordering Principles.

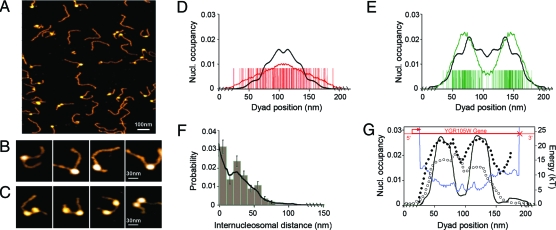
In a second series of experiments (Fig. 3), we reconstituted nucleosomes on a slightly longer (L = 595 bp) DNA fragment in yeast chromosome 7 that contains the gene YRG105W coding for a vacuolar membrane protein (see Data and Methods). This fragment is representative of the in vivo, highly organized nucleosomal chromatin observed in a majority of yeast genes that are constitutively expressed (2, 18, 33, 34). Two rather well-positioned nucleosomes (Fig. 3G) are bordered by two NFRs, one just upstream the transcription start site (TSS) facilitating the permanent access of activator/repressor (1, 2, 18, 33, 34) and another at the gene 3′ end possibly involved in transcription termination, antisense initiation, and recycling of RNA polymerase to the promoter by DNA looping (34). Our physical modeling of the nucleosome formation energy profile along yeast chromosomes confirms that a large number of these in vivo NFRs are actually coded in the DNA sequence via genomic energy barriers that impair nucleosome formation (or at least favor nucleosome eviction) (14, 15). Hence, these energy barriers participate in the regulation of the accessibility of promoter to transcription factor and of antisense preinitiation complexes at the 3′ end of genes. The presence of AATAAA and related elements in the 3′ NFR indicates that this excluding region is likely to play an important role in transcription termination by promoting cleavage and polyadenylation of the nascent mRNA transcript (34).

Fig. 3.

AFM imaging in liquid of mono- and dinucleosomes along the yeast (chr. 7) DNA fragment (L = 595 bp) containing the gene YRG105W. (A and B) Mononucleosomes. (A and C) Dinucleosomes. (D) Statistical analysis of mononucleosome positioning (N = 113 molecules); red bars correspond to experimentally detected dyad locations and to their symmetrical position with respect to the center of the fragment. The experimental nucleosome occupancy profile (red curve) is compared to the theoretical predictions of our physical modeling after symmetrization (black curve). (E) Statistical analysis of dinucleosome positioning (N = 62); for each image, green bars were drawn at both the two dyad positions and their symmetric locations with respect to the center of the fragment. The experimental nucleosome occupancy probability profile (green curve) is compared with the symmetrized theoretical profile (black curve). (F) Histogram of internucleosomal distances between dinucleosomes; the continous black line corresponds to the distribution predicted by the pair function (Eq. 5). (G) Oriented nucleosome occupancy probability distribution observed in vivo (2) (black dots) and predicted by the physical modeling (black curve); in red is shown the location of the YRG105W gene with the transcription start site (arrow) and the transcription termination site (cross). Theoretical nucleosome formation energy landscape (blue curve) and oriented nucleosome occupancy probability profile observed in vitro (21) (circles). Theoretical mononucleosome (D) and dinucleosome (E–G) nucleosome occupancy profiles were computed by adjusting the chemical potential μ in our physical modeling so that the average number of loaded nucleosome is 1 and 2, respectively (see Data and Methods).

AFM imaging of mononucleosomes reconstituted on this 595-bp DNA fragment (Figs. 3 A and B) shows a lack of positioning at the two extremities, consistent with the presence of two inhibitory energy barriers. Indeed, the statistical (symmetrized) dyad-positioning distribution obtained for N = 113 molecules (Fig. 3 D) is similar to the one previously observed for the short yeast DNA fragment B (Figs. 2 B and E). The mononucleosome density is mainly concentrated in the central genic region, whereas the 5′ promoter and 3′ downstream regions appear to be significantly depleted in nucleosome. The experimental nucleosome occupancy probability profile (Fig. 3 D) is rather flat in the gene, as predicted by our physical modeling. This profile attests to a homogeneous statistical dyad positioning inside the gene without any preferential location induced by the presence of an underlying sequence strongly favorable to nucleosome formation (Fig. 3 G). This conclusion is corroborated by the nucleosome occupancy distribution observed in vitro at low nucleosome density in a genome-wide experiment (21) (Fig. 3 G).

The statistical analysis of N = 62 dinucleosomes reconstituted on the same L = 595-bp yeast DNA fragment (Figs. 3 A and C), clearly reveals a bimodal (symmetrized) nucleosome occupancy probability profile with two privileged intragenic dyad locations, as expected from the physical modeling when fixing the chemical potential so that the average number of loaded nucleosomes is two (Fig. 3E). Because the physical modeling reproduces the oriented in vivo nucleosome occupancy profile (Fig. 3 G), our AFM imaging of in vitro nucleosome positioning is remarkably consistent with the one observed in vivo. Importantly, the two priviledged locations of maximal nucleosome occupancy observed in vivo (Fig. 3 G) did not emerge in the in vitro AFM mononucleosome occupancy distribution (Fig. 3 D) as well as in the genome-wide in vitro data (Fig. 3 G). This observation strongly suggests that the in vivo nucleosome positioning was not driven by the presence of some highly positioning DNA sequences but more likely corresponds to a global equilibrium ordering of two nonoverlapping objects confined between fixed excluding-energy barriers at both gene extremities (17). This nucleosome confinement scenario is confirmed by the internucleosomal distance distribution obtained from AFM imaging of dinucleosome positioning (Fig. 3 F). Following the theoretical equilibrium distribution predicted by the grand canonical physical modeling (Eq. 5), this distribution presents a main peak at small linker length (≲10 nm), corresponding to one or two helical pitches (extreme left and extreme right configurations in Fig. 3 C), and a lower secondary peak at larger linker length (≈25 nm) corresponding to less-probable configurations. The organizational role of inhibitory energy barriers is a second important result coming from our in vitro AFM imaging of nucleosome assembly on genomic DNA templates. Statistical nucleosome ordering is nucleated from these stable “genomic boundaries”, likely imprinted in the DNA sequence during evolution.

Genomic Energy Barriers Direct the Intrinsic Nucleosome Occupancy of Regulatory Sites.

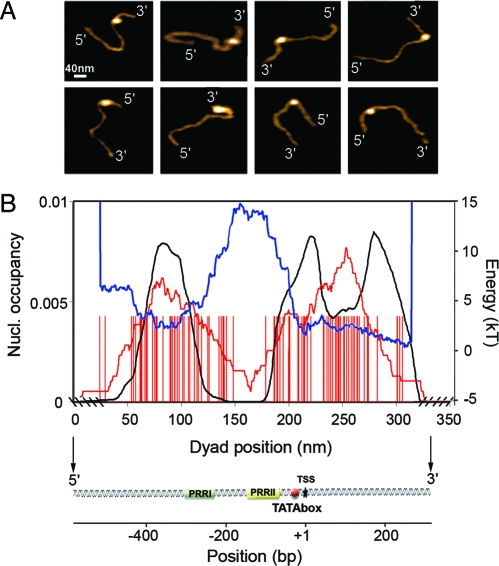
Finally, we investigated nucleosome assembly on a DNA fragment long enough to allow orientation by using a DNA topography profile without the need for end labelling susceptible to affect DNA structure and nucleosome positioning (see Data and Methods and Fig. S2 of the SI Appendix). We selected a L = 898-bp DNA fragment in the human genome that contains the promoter of the gene IL2RA, which plays a major role in the control of the immune system response. This fragment includes different functional elements: (i) the TSS, (ii) the core promoter with the TATA box, (iii) two positive regulatory regions (PRR), PRRI and PRRII lying at positions −289/−216 and −137/−64 upstream of the major TSS, respectively (Fig. 4 B). These regulatory elements are important for regulating inducible transcription of the IL2RA gene (35). Previous in vivo study in unstimulated T-cells (36) revealed that prior to transcription, an inhibitory nucleosome was positioned on the TATA box and TSS regions, therefore preventing both preinitiation complex (PIC) formation on the TATA box. In addition, this critically positioned nucleosome may also take part in the prevention of uncontrolled DNA melting in the TSS region (37). These properties make this promoter a suitable model to investigate the actual role of the DNA sequence in this peculiar repressive chromatin environment.

Fig. 4.

AFM imaging in liquid of mononucleosome positioning along the human ILR2A promoter DNA fragment (L = 898 bp). (A) Examples of molecules that were oriented using the DNA topography profile methodology (see Data and Methods and Fig. S2 of the SI Appendix). (B) Statistical analysis (N = 100 molecules) of dyad positioning (red bars) relative to the locations of the two regulatory regions PRRI and PRRII, the TATA box, and the TSS. The experimental nucleosome occupancy probability profile (red curve) is compared with the theoretical prediction of our physical modeling (black curve) when adjusting the chemical potential μ so that the average number of loaded nucleosomes is 1 (see Data and Methods). The blue curve corresponds to the theoretical nucleosome formation energy landscape.

From the analysis of N = 100 oriented DNA molecules loaded by a mononucleosome (Fig. 4 A), we confirmed the repressive nucleosome positioning on the TATA box and TSS as observed in vivo (36); we also revealed a favorable positioning region ≈350 bp upstream of the TSS that covers the regulatory sequence PRRI (Fig. 4 B). More importantly, the observed in vitro nucleosome occupancy probability profile is in remarkable agreement with the theoretical profile obtained from our physical modeling. There exists an energy barrier ≈150 bp upstream of the TSS that is coded in the sequence and that extends over the PRRII regulatory region, thus explaining the lack of nucleosome positioning recorded from −200 bp to −100 bp (Fig. 4 B). This stable genomic excluding-energy barrier further conditions, by classical parking phenomenon close to a wall (17), the observed repressive nucleosome positionings (i) at its right foot on the TATA box and TSS and (ii) at its left foot encompassing the PRRI region (Fig. 4 B). These results demonstrate the fundamental role of the DNA sequence in conditioning a peculiar local nucleosome chromatin structure that constitutively contributes to gene repression. Furthermore, by inhibiting nucleosome formation in the PRRII region, the sequence may favor DNA accessibility to HMGA proteins that are known to induce a negative torsional stress and, by accumulation, a negative supercoil that may help nucleosome remodeling and/or eventually nucleosome ejection (37, 38). Altogether, these experimental observations enlighten the importance of this sequence-induced local nucleosomal organisation for regulating inducible transcription of the IL2RA gene.

In conclusion, by combining physical modeling and AFM imaging in liquid, we demonstrated that sequences coding for high-energy barriers impair nucleosome formation and condition the collective assembly of neighboring nucleosomes consistently with equilibrium statistical ordering principles. By directing the positioning of these energy barriers relative to the TSS, the sequence contributes to the specification of the activatory or inhibitory role of the local chromatin environment. These studies are a step forward in imaging nucleosome assembly in various functional regions (promoters, replication origins, etc.). In particular, comparing in vivo nucleosome positioning data to intrinsic sequence-induced positioning will provide direct measurement of the action of external factors (DNA-binding proteins, remodelers, etc.) on chromatin architecture. The strategy developed here can also be generalized to real-time dynamical studies of nucleosome repositioning on genomic sequences.

Data and Methods

Preparation of DNA Fragments.

The DNA fragments were selected according to the energy landscape and nucleosome occupancy profile obtained from the physical modeling of nucleosome positioning (see Physical Modeling). The short (A, 394 bp; B, 386 bp; C, 387 bp) DNA fragments were obtained by PCR amplification with Taq polymerase (Promega) from yeast S. cerevisiae genomic DNA. Templates were amplified from sequences of yeast chromosome 3: A, 249050-249443; B, 61210-61595; C, 214107-214493 (SGD assembly database). The 595-bp-long sequence containing the gene YGR105W (698500-698950) located on yeast chromosome 7: 698436-699030, was amplified by PCR from genomic DNA. The human IL2RA promoter sequence (898 bp) on chromosome 10: 4433-5331 (NCBI, locus n° NG007403), was amplified by PCR with Taq polymerase (Sigma) from human genomic DNA.

Protein Purification and Nucleosome Reconstitution.

Recombinant full-length histone proteins of Xenopus laevis were overexpressed in bacteria and purified as previously described (39). Nucleosome reconstitution was performed by the salt dialysis procedure (27). The reaction was stopped in TE buffer (10 mM Tris-HCl, pH 7.4, 1 mM EDTA) and 10 mM NaCl. For all considered DNA templates, nucleosomes were reconstituted with histone/DNA ratio 1/0.8. The saturating loading of yeast chromosome 7 DNA fragment was obtained with a histone/DNA ratio of 1.1/0.8.

AFM.

AFM was performed in solution by using a Nanoscope IIIa microscope (Digital Instruments) equipped with a type-E scanner and in tapping mode, essentially as described in previous work (26). Ten microliters of a 1-nM reconstitution solution in imaging buffer (10 mM Tris-HCl, 1mM NiCl₂, pH 7.9) were deposited onto freshly cleaved mica and incubated for two minutes. A 100-μl drop of imaging buffer was added in the liquid cell prior to imaging. For scanning directly in the adsorption buffer, commercial silicon nitride probes (type NP-S, Veeco Instruments) were used at a drive frequency of 8–9.5 kHz and a set point of 0.3–0.4 V at constant temperature. AFM images were recorded from 1 × 1 μm or 2 × 2 μm frames, at a scan rate of 2.18 Hz and a resolution of 512 × 512 pixels.

Image Analysis.

AFM image treatment and analysis were done by using the “Scanning Adventure” software (40). Briefly, line-by-line second-order flattening was first applied, followed by thresholding and filtering. Zooms on individual mono- or dinucleosomes were performed, and the molecule path was skeletonized; then, topographical analysis and length measurements were carried out (Figs. S2 A–C of the SI Appendix). The results enabled a measurement of nucleosomal height and a mapping of the nucleosome position along DNA fragments. The position x of each nucleosome was considered to be the length corresponding to the midpoint of the DNA wrapping length named “dyad” (Fig. S2B of the SI Appendix).

The distributions of mononucleosome height obtained for the three short yeast DNA templates A, B and C, all display two discrete peaks centered at 1 and 2.9 nm (Fig. S3A of the SI Appendix). The largest peak value is slightly smaller than the expected height of 5.0 nm for the nucleosome core particle (NCP), as previously estimated by AFM in liquid when using a (3-aminopropyl) triethyoxysilane (APTES) surface treatment (23). The smallest peak value ≈1 nm corresponds to the height of subnucleosomal particles that do not contain the full histone octamer but more likely the histone tetramer. In all our AFM nucleosome positioning studies, nucleosomes were identified as peaks in the topographical profiles of height h ≥ 2 nm. The nucleosome diameter measured by AFM is usually larger than the real diameter because of tip convolution, which means that the actual entry/exit sites of DNA in the nucleosome cannot be unambiguously localized. For the sake of comparison with previous AFM studies (22, 23), the entry/exit sites were empirically determined by positioning the NCP at the position M corresponding to the local height maximum and fixing its diameter to the crystallographic value (41) d = 11 nm (Fig. S2 C of the SI Appendix). In this way, the length of free DNA outside the nucleosome, namely L₊ − L_S − (ℓ_M + d/2) for the longer arm and L₋ = ℓ_M − d/2 for the shortest one, could be measured as well as the corresponding length L_c of DNA that was complexed into nucleosome

where L is the total length of the considered DNA fragment. The distributions of complexed DNA length obtained for the sets of nucleosomes reconstituted on the three small yeast DNA fragments looked quite similar (Fig. S3B of the SI Appendix). The mean complexed length L_c was found ≈150 bp in agreement with the expected core particle length of 147 bp. Let us point out that some peak at L_c = 135 bp was observed for DNA fragment A where, as induced by the underlying sequence, a majority of nucleosomes were found to be located at the edges of the fragment (see Figs. 2A and D). We checked that those nucleosomes were the ones that were effectively partially wrapped by DNA. Note that, consistent with previous AFM studies in liquid (40), the DNA length was converted in bp by considering 0.36 nm as the average distance between the nearest neighbor bps in B-DNA (Fig. S3C of the SI Appendix).

From the measurement of L ₊, L ₋, and L _c (Fig. S2C of the SI Appendix), we positioned the dyad along the DNA fragment by adding L _c/2 to either L ₊ or L ₋. But to compare the so-obtained experimental dyad-positioning distribution to the nucleosome probability density predicted by our physical modeling, we needed to orient DNA. We succeeded doing it for the 898-bp-long IL2RA promoter fragment by making use of the AFM topography profile (Figs. S2 D and E of the SI Appendix). For all the other DNA fragments, for each AFM image, we counted twice the fragment by positioning the dyad according to the two possible orientations, namely the 5′-end is on the longest arm side or vice versa (Figs. 2 D–F, Figs. 3 D and E, and Fig. S1 B of the SI Appendix).

Physical Modeling.

Nucleosome density profile.

When focusing on the dynamical assembly of histone octamers along the DNA chain, chromatin can be reasonably modeled (14) by a fluid of 1D rods of finite extension l (the DNA wrapping length around the octamer), binding and moving in an external potential E(s,l) (the effective nucleosome formation potential at position s), and interacting through a hard core potential of size l. Within the grand canonical formalism, considering that the fluid is in contact with a thermal bath (at reciprocal temperature β) and a histone octamer reservoir (at chemical potential μ), the equilibrium density ρ(s) of hard rods in an external field E(s,l) obeys the nonlinear integral equation (42):

Nucleosome formation energy.

To compute the energy landscape E(s,l), we assumed that (i) DNA is an unshearable elastic rod whose conformations are described by the set of three local angles Ω₁(s) (tilt), Ω₂(s) (roll), Ω₃(s) (twist), and (ii) the DNA chain along the nucleosome at position s is constrained to form an ideal superhelix (41) of radius R = 4.19 nm and pitch P = 2.59 nm over a total length l which fixed the distribution of angular deformations (Ω_i ^nuc(u))_i=1,2,3, u = s,…,s + l. Within linear elasticity approximation, the energy cost for nucleosome formation is given by

where A ₁, A ₂ and A ₃ are the stiffnesses associated to the tilt, roll, and twist deformations around their intrinsic values Ω₁ ^o, Ω₂ ^o, and Ω₃ ^o, respectively. Consistent with our previous works (14, 28, 29), we used the “Pnuc” structural bending table (30), which was experimentally derived from the propensity of trinucleotides in nucleosomal sequences to be in phase with the helical pitch. This table is mainly a trinucleotide roll coding table (Ω₂ ^o), with zero tilt (Ω₁ ^o = 0) and constant twist (Ω₃ ^o = 2π/10.5). As the values of this bending table were arbitrarily assigned between 0 and π/18 rad, we performed the following affine rescaling Ω₂ ^o* = γΩ₂ ^o−η with γ = 0.4, η = 0.06, in order to get a comparable range of energy landscape fluctuations as was obtained in the experiments (14).

Nucleosome occupancy profile.

Eq. 2 has an explicit solution (43) that required numerical integration. We fixed the variance σ²(E) [σ(E) = 1.95 kT] and l = 146 bp, to match in vivo nucleosome positioning data by Lee et al. (2). The nucleosome occupancy probability profile P(s) was obtained by convolving the nucleosome density ρ(s) with the rectangular function Π of width l = 146 bp:

P(s) is the probability for a bp located at s to be occupied by a nucleosome of length 146 bp.

The theoretical probability of linker size x _l was computed by using the pair function associated with the underlying energy E(s,l) :

where Γ is a normalizing constant.