Frontoparietal white matter diffusion properties predict mental arithmetic skills in children

Abstract

Functional MRI studies of mental arithmetic consistently report blood oxygen level–dependent signals in the parietal and frontal regions. We tested whether white matter pathways connecting these regions are related to mental arithmetic ability by using diffusion tensor imaging (DTI) to measure these pathways in 28 children (age 10–15 years, 14 girls) and assessing their mental arithmetic skills. For each child, we identified anatomically the anterior portion of the superior longitudinal fasciculus (aSLF), a pathway connecting parietal and frontal cortex. We measured fractional anisotropy in a core region centered along the length of the aSLF. Fractional anisotropy in the left aSLF positively correlates with arithmetic approximation skill, as measured by a mental addition task with approximate answer choices. The correlation is stable in adjacent core aSLF regions but lower toward the pathway endpoints. The correlation is not explained by shared variance with other cognitive abilities and did not pass significance in the right aSLF. These measurements used DTI, a structural method, to test a specific functional model of mental arithmetic.

Mental arithmetic, the ability to manipulate numeric quantities in the mind, is important for everyday tasks, from paying a bill to estimating the time before a bus arrives. Functional magnetic resonance imaging (fMRI) studies have revealed a network of coactive areas in subjects performing mental arithmetic. Many studies have identified the intraparietal sulcus (IPS) and inferior parietal lobe as elements of this network, as well as parts of the inferior frontal lobe (e.g., refs. 1–8).

Successful performance in mental arithmetic tasks relies on efficient information transfer in this network. One way to characterize network dynamics is through diffusion tensor imaging (DTI), which provides a method for studying anatomical network properties that correlate with behavioral traits. This approach has proven powerful in the analysis of reading (see ref. 9 for a review). However, little is known about the relationship between white matter properties and performance on mental calculation tasks, with only two relevant DTI studies published to date. Barnea-Goraly et al. (10) used voxel-by-voxel group analysis and found correlations between mental arithmetic scores and fractional anisotropy (FA) in white matter adjacent to the left inferior parietal lobe and IPS in children with velocardiofacial syndrome, a condition associated with low arithmetic abilities. Van Eimeren et al. (11) found correlations between FA and children's written calculation scores in the left superior corona radiata and the left inferior longitudinal fasciculus.

Our approach is model driven: we capitalized on an identified network of cortical regions involved in mental calculation (12) to derive a prediction about specific fiber tracts. The triple-code model of number processing (1, 13, 14) implies that specific pathways in the left hemisphere communicate signals between regions that are active during mental arithmetic tasks. These pathways connect the inferior parietal lobe/IPS with precentral and inferior frontal regions. We used diffusion-weighted data to estimate this white matter tract (Fig. 1). After Catani (15), we call this tract the anterior superior longitudinal fasciculus (aSLF).

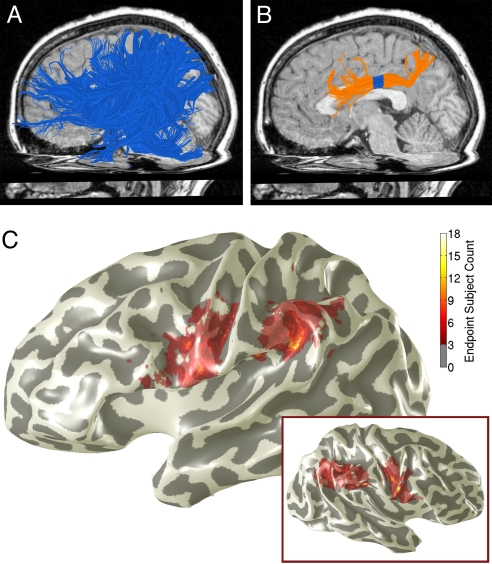
Fig. 1.

Identifying the aSLF. The aSLF was identified in individual subjects. (A) We estimated all of the long-range fibers in a hemisphere and selected fibers (blue) that intersect a large parietal ROI, extend anterior to the central sulcus, and do not cross the midsaggital plane. Fibers are from a 10-year-old boy. (B) The aSLF (orange) was defined from the fibers in A according to anatomical landmarks, as described in Methods. Diffusion properties were calculated from a 7-mm-long band toward the middle of the tract (blue). (C) The color overlay shows the vertices where tracts from ≥3 subjects intersected with the gray matter mask. Endpoints are shown from all subjects registered onto the cortical surface of an individual child (13-year-old girl). Endpoints are distributed over the inferior parietal lobe and precentral/inferior frontal gyrus. Inset: Same analysis for the right hemisphere.

We correlated diffusion properties from a central chunk of the left aSLF (Fig. 1B, Fig. S1) with accuracy scores from three types of mental arithmetic tasks: simple math facts, approximate addition, and exact addition. We investigated the specificity of the finding by identifying and measuring other specific tracts: the right aSLF and the arcuate fasciculus. By testing for brain–behavior correlations between measures of these white matter tracts and mental arithmetic, we put the functional model (1, 13, 14) to a direct test using independent methodology and data.

Results

FA in Left aSLF Correlates with Approximation Performance.

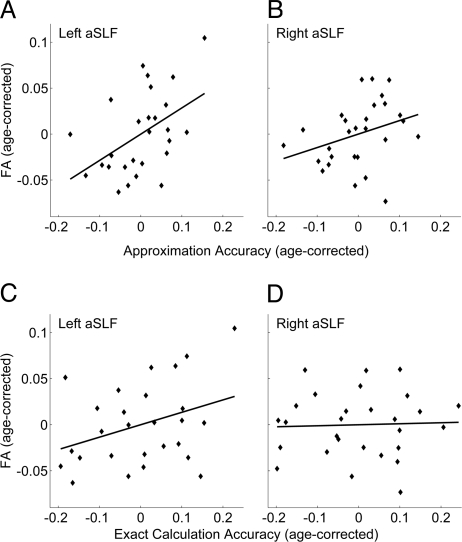
There is a significant correlation between the mental arithmetic approximation scores and FA in the left aSLF (Fig. 2A, Table 1). After partialling out the variance explained by subjects' age, this correlation is r (25) = 0.48 (P < 0.05, Bonferroni corrected for three math measures). The 95% confidence interval on this correlation coefficient, bootstrapped from 1,000 samples, is 0.13–0.74. In contrast, FA in the right aSLF shows only a nonsignificant (n.s.) correlation trend with approximate arithmetic skill [Fig. 2B; r (26) = 0.32, P = 0.11, uncorrected].

Fig. 2.

Mental approximation skill correlates with FA in left aSLF. Scatterplots show the relationship between age-corrected mental arithmetic scores and age-corrected FA. The horizontal axes measure the residuals of math scores regressed on age. The vertical axes measure the residuals of FA regressed on age. (A) There is a significant correlation between approximation accuracy and FA in the left aSLF [n = 27, r (25) = 0.48, P = 0.01]. (B and C) Correlations between approximation accuracy and FA in the right aSLF [n = 28, r (26) = 0.32, P = 0.11]; and exact arithmetic accuracy and FA in the left aSLF [n = 27, r (25) = 0.35, P = 0.08] trended toward significance. (D) Exact arithmetic did not correlate with FA in the right aSLF [n = 28, r (26) = 0.04, n.s.].

Table 1.

Correlations between mean FA in aSLF ROIs and scores on mental arithmetic tests, before and after controlling for age

Mental arithmetic tests	FA				Age
	Left aSLF (n = 27)		Right aSLF (n = 28)
	r	P	r	P	r	P
Before controlling for age
Simple facts	0.21	0.288	−0.05	0.820	0.16	0.404
Exact addition	0.40*	0.038	0.20	0.305	0.53†	0.003
Approximate addition	0.51†	0.006	0.41*	0.030	0.44*	0.020
Age	0.21	0.283	0.32	0.099	1.00	1.000
After controlling for age
Simple facts	0.17	0.389	−0.10	0.598
Exact addition	0.35	0.074	0.04	0.845
Approximate addition	0.48*	0.012	0.32	0.098

*, P < 0.05;

^†, P < 0.01.

The scatterplots for exact arithmetic measures show a trend (n.s.) toward a correlation between left aSLF FA and exact arithmetic [Fig. 2C; r (25) = 0.35, P = 0.08, uncorrected] but no relationship for right aSLF (Fig. 2D). See SI Text for further lateralization analyses. There is no significant correlation with simple math facts (left aSLF, P = 0.39; right aSLF, P = 0.60). The last finding could be explained by a ceiling effect, because most subjects scored close to 100% on the simple facts task (Fig. S2).

Left aSLF FA–Approximation Correlation Is Not Explained by Related Cognitive Achievement.

We tested the possibility that the correlation is explained by shared variance between the approximate arithmetic test and other cognitive abilities. For example, general cognitive abilities or number identification abilities rather than specific estimation abilities may account for the observed correlation. Likewise, the relationship could be due to differences in basic reading abilities: the aSLF was originally identified by Catani et al. (15) as connecting regions of the perisylvian language system, so the relationship we observed could be due to the language components of the math tasks. See Table S1 for correlations between behavioral control tasks and FA.

We correlated approximation scores with left aSLF FA after removing variance due to age, intelligence quotient (IQ) (Wechsler Intelligence Scale for Children-4, Full-Scale IQ) (16), Rapid Digit Naming (Comprehensive Test of Phonological Processing) (17), written calculation (Wide Range Achievement Test-4, Math Computation) (18), and Basic Reading (Woodcock-Johnson-III Tests of Achievement, Basic Reading Composite) (19) from both factors. One subject was excluded for failing to complete the control measures. With the five variables partialled out, the correlation between approximate calculation scores and FA in the left aSLF is r (24) = 0.49 (P = 0.024). We conclude that the correlation between FA and approximation ability in the left aSLF is not driven by these other cognitive factors.

Notably, written calculation does not account for a significant portion of the relationship between FA and mental approximation. Written calculation does correlate mildly with approximation scores at r (24) = 0.32 (P = 0.10) but does not correlate with FA in the left aSLF [r (24) = 0.002, P = 0.99]. The shared variance between approximation scores and written calculation, then, is separate from the shared variance between approximation scores and FA.

FA–Approximation Correlation Is Not Present in Adjacent Tracts.

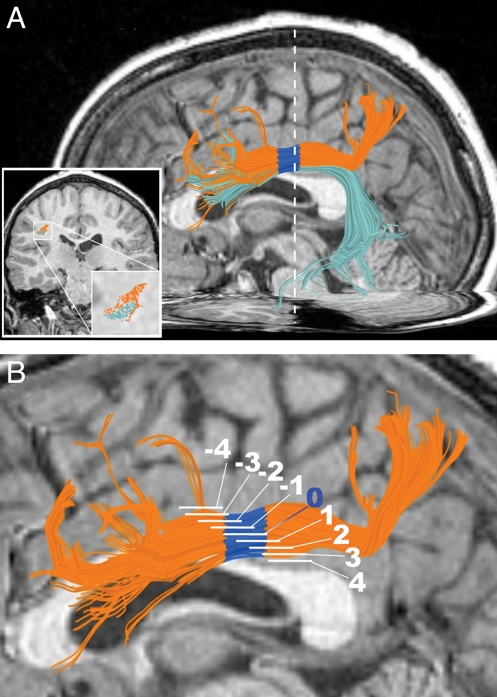
To test whether the observed relationship between FA and math scores is localized to the left aSLF, we identified in each subject a tract that runs adjacent to the aSLF and has roughly the same frontal termination region but a different posterior termination area in the temporal lobe (left arcuate fasciculus; Fig. 3A). We found no significant correlation between FA in the central portion of the arcuate fasciculus and any of the three math scores (Table 2).

Fig. 3.

Anatomical specificity. (A) Example of aSLF (orange) and arcuate fasciculus (frontotemporal SLF) (cyan) in a 10-year-old boy. FA in the arcuate fasciculus ROI does not correlate with approximate arithmetic scores, despite its location adjacent to the aSLF and shared voxels. White dotted line marks the position of the Insets, which show the relative positions of the tracts in a coronal plane (AC-PC coordinate y = −24). (B) To examine the sensitivity of results to the ROI selection procedure, the approximation–FA correlation was also tested in eight other overlapping ROIs per hemisphere. These were defined by sliding the ROI along the aSLF. White segments mark the position of the ROIs. The blue band (segment 0) represents the original ROI.

Table 2.

Correlations between mean FA in the left arcuate fasciculus and scores on mental arithmetic tests, before and after controlling for age (n = 23)

Mental arithmetic tests	FA, left arcuate
	r	P
Before controlling for age
Simple facts	0.16	0.43
Exact addition	0.25	0.22
Approximate addition	0.18	0.38
Age	0.10	0.63
After controlling for age
Simple facts	0.14	0.49
Exact addition	0.24	0.25
Approximate addition	0.15	0.47

When considering only the nonoverlapping portions of these adjacent tracts, the aSLF maintains its correlation with approximation scores [r (21) = 0.46, P = 0.03], whereas the arcuate fasciculus still fails to correlate with approximation scores [r (21) = 0.16, P = 0.47].

The findings demonstrate the anatomical specificity of the mental math correlation found in the aSLF; the correlation does not generalize to adjacent white matter paths. Hence, it seems that the aSLF in particular, rather than the white matter in the general location of the SLF, carries signals important for mental arithmetic.

Left aSLF Correlation Is Robust to Small Changes in Region of Interest Position.

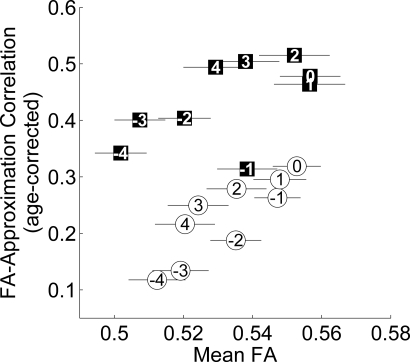
Region of interest (ROI) analyses necessarily involve voxel selection criteria, but it is desirable that the results are robust to the specific selection criteria applied (see Methods). To test whether the correlation is robust to variations in the chosen segment, we measured correlations from a series of overlapping segments along the aSLF (Fig. 3B). Mean FA increases in the segments closer to the center of the tract and decreases toward either end of the tract (Fig. 4). The segment used in the present analysis shows high mean FA compared with the other segments tested, because it was anatomically chosen for its proximity to the tightly bundled central portion of the tract.

Fig. 4.

FA–approximation correlation in multiple aSLF ROIs. ROIs near the middle of the aSLF, in the core of the white matter, have higher mean FA and higher age-corrected FA–approximation correlations. Circles (squares) denote ROIs along the right (left) aSLF. Numbers in the points correspond to segment numbers in Fig. 3B, with 0 denoting the original ROI. Error bars are ± 1 SEM.

The correlation between approximate arithmetic ability and FA in the tract is generally larger in segments with higher mean FA. Importantly, the strong math correlation found in the original left aSLF ROI is just as strong in four other ROIs within the core of the tract. The correlation degrades in more lateral portions of the tract, where tract estimates are less reliable and reflect the intersection of members of many tracts rather than just the bundle of interest. Note that in the right aSLF, sliding the ROI did not enhance the low correlation between FA and approximation ability.

Discussion

Analysis of the fMRI literature and current models of mental math led to the hypothesis that structural properties of left frontoparietal pathways may be correlated with certain mental math abilities. We found such a correlation between the aSLF microstructural properties and the ability to estimate approximate sums. The measurements show a high degree of specificity: the relationship does not generalize to other cognitive abilities or to adjacent white matter pathways. The results extend previous research findings that showed left hemisphere white matter relationships to math ability (10, 11). Importantly, the findings are consistent with a leading theory of number processing (1, 13, 14), which implicates the left inferior parietal lobe and IPS as posterior centers of the verbal and quantity aspects of arithmetic processing, and the left inferior frontal gyrus as a working memory and language center contributing to mental math calculations. The findings presented here establish an important role for the structural connections between cortical regions that were previously identified in fMRI studies of mental math abilities.

Functional Theories.

There are several hypotheses about the specific functions of the cortical regions connected by the aSLF. The bilateral IPS is perhaps the most commonly reported area of blood oxygen level–dependent (BOLD) activity in mental arithmetic tasks. The triple-code model posits that it is the brain's center of quantity representation (e.g., ref. 14). According to the same theory, the inferior parietal lobe, particularly the left angular gyrus, supports verbal number manipulation (14). The function of inferior frontal cortex in mental arithmetic is less agreed upon, but it may support working memory and linguistic task demands (4, 12). More recently, Cohen Kadosh and Walsh (8) suggested that these regions are the substrate of knowledge of arithmetic operators. The precentral gyrus commonly escapes interpretation in mental arithmetic theories, but Butterworth (20, 21) and Zago et al. (22) propose that precentral activity reflects traces of finger counting and subvocalization used in arithmetic in early childhood.

Separability of the Neural Substrates for Approximate and Exact Calculation.

The neuropsychological literature on math abilities is divided on whether approximate and exact calculations depend on different neural systems. Lesion data show that there is a double dissociation in performance on these two tasks (e.g., ref. 23). This suggests that at least a part of the computations takes place in distinct neural systems. Some fMRI studies indicate that the BOLD responses are not entirely overlapping during approximate and exact calculations (e.g., refs. 2, 5, and 24); other groups have failed to find such a difference (e.g., refs. 25 and 26).

FA in left aSLF correlates with approximation but not exact calculation scores. This supports the idea that different types of arithmetic rely on different neural substrates. However, there is a weak trend toward a correlation between FA in the left aSLF and exact arithmetic, and there is no statistically significant difference between the correlation values for approximate and exact arithmetic [left aSLF t (24) = 0.73, P > 0.4; right aSLF t (25) = 1.61, P > 0.10]. The entire pattern of data suggests that these two neural systems share certain common pathways but that they are not the same.

Related Neuroimaging Measurements.

Studies investigating individual differences in BOLD activation during mental arithmetic tasks have found effects primarily in inferior parietal regions and the IPS (27–29), with some mention of the inferior frontal gyrus (29). The present findings are consistent with these functional results.

Findings from a prior study (10) of the relationship between diffusion properties and math abilities may align with ours. The investigators reported that in a population of children with velocardiofacial syndrome—a condition associated with low arithmetic ability—FA in a left-hemisphere white matter region adjacent to the inferior parietal gyri and IPS correlated with mental arithmetic scores, and to a lesser degree so did left hemisphere white matter lying between the frontal and parietal lobes. The tract we studied travels between inferior parietal and frontal lobes; thus the previous findings may partially reflect differences in the tract studied here. However, our methods and findings differ in several ways. Most importantly, the prior study did not find left-hemisphere correlations with mental arithmetic in a nonimpaired control group. This may be due to smoothing and imperfect alignment of the tensor data to a common atlas space. The increased sensitivity of individual ROI analysis compared with whole-brain voxel-by-voxel group analysis is discussed in refs. 9 and 30.

Van Eimeren et al. (11) tested the relationship between written math scores and FA in many white matter regions, including the SLF, of which our tract of interest is a subset. They defined ROIs for each tract of interest by manually choosing a representative point on maps of FA and principal diffusion direction, then selecting voxels with similar eigenvalue/vector patterns nearby. This method does not separate the aSLF from the arcuate fasciculus, thus constraining a direct comparison between the findings. Using the entire SLF, the investigators did not find a significant correlation between written math scores and FA. Our data similarly show no significant correlation in aSLF with written math, only an association with mental arithmetic. This distinction supports the hypothesis in the education literature that mental and written arithmetic are significantly different skills (e.g., refs. 31–33).

FA is influenced by a range of physiological factors, including fiber density, axon diameter and myelination, cell membrane density (e.g., glia), and fiber coherence (34–36). The area of interest here is far from the ventricles, so it is unlikely that the correlation observed between FA and mental arithmetic scores is due to partial voluming with ventricles. The correlation is likely due to a combination of the remaining factors: axon diameter, fiber density, and fiber coherence.

Conclusions

The aSLF white matter pathways connecting inferior parietal and inferior frontal cortex seem to carry signals that are important for mental arithmetic approximation performance. Differences in the FA in this white matter tract, but not in adjacent tracts, correlate with individual subjects' ability to perform accurate and rapid approximate mental arithmetic. This correlation is independent of age, IQ, and reading ability. Neural signals essential for mental arithmetic approximation, but not written calculation abilities tested in schools, seem to depend on the aSLF. The measured diffusion parameter, FA, is influenced by several different physiological properties. In this case, fiber density, axon diameter, and fiber coherence are likely contributors. It is possible, for example, that children with higher approximation ability would also have higher fiber density, larger axon diameter, and/or stronger fiber coherence in the aSLF. Whether these differences have a genetic or experience–dependent origin cannot be determined from our data. Future studies may explore whether interventions and training on mental arithmetic may influence the properties of the aSLF or the BOLD signal in the cortical regions that project via the aSLF.

Methods

Subjects.

Thirty-four children [18 female, age 10–15 years; mean (SD), 12.6 (1.5) years] participated in behavioral testing. Of these, 28 also participated in MRI measurements [14 female, mean age (SD) 12.6 (1.6) years]. Data from three additional subjects were excluded because of imaging artifacts, behavioral data collection failure, and inability to follow task instructions, respectively. Imaging data were collected as part of the 4th year of a longitudinal reading study (37). All subjects were physically healthy and had no history of neurologic disease, head injury, attention deficit/hyperactivity disorder, language disability, or psychiatric disorder. All subjects were native English speakers and had normal or corrected-to-normal vision and normal hearing. The Stanford Panel on Human Subjects in Medical and Non-Medical Research approved all procedures. Written informed consent/assent was obtained from all parents and children.

Behavioral Assessment.

Each child participated in a 2-h behavioral testing session that included measures of reading and math ability. The math assessment lasted ≈30 min. Children were tested individually in a quiet room with the experimenter present. Stimuli were presented on a computer screen or using printed material.

Mental Arithmetic.

Subjects completed three computerized mental arithmetic tasks based on Dehaene et al. (2): (i) simple math facts, (ii) exact two-digit addition, and (iii) approximate two-digit addition. Each task included 48–50 problems. Subjects sat ≈24 inches from a computer monitor. Stimuli were Arial font size 24, presented in black on gray background. For each item, an arithmetic problem appeared on the screen with two answer options below. Subjects selected an answer by pressing the designated keyboard button corresponding to the side of the screen of their answer choice. Subjects had up to 6 s to respond. Within each task, the smaller operand was equally likely to be on the left or right side of the screen, as was the correct answer.

Simple math facts.

Multiplication tables with integers 2–9 and addition of addends 1–5. Response alternatives: (i) correct answer and correct answer ± 2 for multiplication (to avoid parity strategies), or (ii) correct answer and correct answer ± 1 for addition. The first two multiplication and addition problems were excluded from the analysis to eliminate possible noise due to task switching or task starting.

Exact and approximate addition.

Addends ranged from 10 to 40. Thirty of the items involved “carrying.” The first two items were excluded from the analysis. Problems in the exact and approximate tasks were the same, except the operands appeared in the reverse order in each task. For the exact addition task, answer options were the correct answer and either ±1 or ±10. For the approximate addition task, answer options were the correct answer rounded to the nearest decade and that decade ±20 or ±30.

Cognitive Skills.

Four behavioral measures served as cognitive controls. (i) Full-Scale IQ (Wechsler Intelligence Scale for Children-4) (16). IQ was assessed 3 years before study as part of the longitudinal study. Studies in populations and age ranges similar to ours found a negligible change in the age-standardized score over time (38). (ii) Written arithmetic score from the Wide Range Achievement Test-4 (18). In this age-standardized test, subjects answer as many written math problems as possible in 15 min. The test focuses on whole numbers, fractions, decimals, and all four basic operations. The fastest subjects also attempt advanced topics like variables. (iii) Basic Reading composite score from the Woodcock-Johnson-III Tests of Achievement (19). This age-standardized score measures children's ability to name out loud letters, words, and pseudowords. (iv) Rapid Digit Naming. This subtest of the Comprehensive Test of Phonological Processes (17) is a timed, age-standardized test in which children name digits in a matrix out loud as quickly as possible.

Neuroimaging.

MRI data were acquired on a 1.5-T Signa LX scanner (Signa CVi; GE Medical Systems) using a self-shielded, high-performance gradient system. A standard quadrature head coil, provided by the vendor, was used for excitation and signal reception. Head motion was minimized by placing cushions around the head and securing a strap across the forehead.

Data Acquisition.

The DTI protocol used eight repetitions of a 90-s whole-brain scan. The scans were averaged to improve signal quality. The pulse sequence was a diffusion-weighted single-shot spin-echo, echo planar imaging sequence (time to echo, 63 ms; time to repetition, 6 s; field of view 260 mm; 128 × 128 matrix size; ±110 kHz bandwidth; partial k-space acquisition). We acquired 60 axial, 2-mm-thick slices (no skip) for two b-values, b = 0 and b = 800 s/mm². The high b-value data were obtained by applying gradients along 12 diffusion directions (6 noncollinear directions). Two gradient axes were energized simultaneously to minimize time to echo, and the polarity of the effective diffusion-weighting gradients was reversed for odd repetitions to reduce cross-terms between diffusion gradients and imaging and background gradients. Although Jones (39) suggests that measuring more diffusion directions might be more efficient at reliably estimating diffusion tensors of arbitrary orientation, our signal-to-noise ratio is sufficiently high from our eight repeats to produce very reliable tensor estimates. We have confirmed this in a subset of subjects by comparing bootstrapped tensor uncertainty estimates from 40-direction data with the 12-direction data reported here. With our high SNR, tensor uncertainty is limited by physiological noise rather than measurement noise.

We also collected high-resolution T1-weighted anatomical images for each subject using an 8-min sagittal 3D spoiled gradient sequence (1 × 1 × 1 mm voxel size). The following anatomical landmarks were manually defined in the T1 images: the anterior commissure (AC), the posterior commissure (PC), and the midsagittal plane. With these landmarks, we used a rigid-body transform to convert the T1-weighted images to the conventional AC-PC aligned space.

Data Preprocessing.

Eddy current distortions and subject motion in the diffusion-weighted images were removed by a 14-parameter constrained nonlinear coregistration based on the expected pattern of eddy–current distortions given the phase-encode direction of the acquired data (40).

Each diffusion-weighted image was registered to the mean of the (motion-corrected) non–diffusion-weighted (b = 0) images using a two-stage coarse-to-fine approach that maximized the normalized mutual information. The mean of the non–diffusion-weighted images was automatically aligned to the T1 image using a rigid-body mutual information algorithm. All raw images from the diffusion sequence were resampled to 2-mm isotropic voxels by combining the motion correction, eddy–current correction, and anatomical alignment transforms into one omnibus transform and resampling the data using a 7th-order b-spline algorithm based on code from SPM5 (41).

An eddy current intensity correction (40) was applied to the diffusion-weighted images at the resampling stage.

The rotation component of the omnibus coordinate transform was applied to the diffusion-weighting gradient directions to preserve their orientation with respect to the resampled diffusion images. The tensors were then fit using a least-squares algorithm. We confirmed that the DTI and T1 images were aligned to within a few millimeters in the ROIs for this study. This confirmation was done by manual inspection by one of the authors (R.F.D.). In regions prone to susceptibility artifacts, such as orbitofrontal and inferior temporal regions, the misalignment was somewhat larger owing to uncorrected EPI distortions.

All of the custom image processing software is available as part of our open-source mrDiffusion package (http://white.stanford.edu/vistawiki/index.php/Software).

Fiber Tract Identification.

DTI fiber tractography and data analysis were performed using mrDiffusion and CINCH (42). For each subject we identified, bilaterally, fibers that extend from the IPS and the inferior parietal lobe to the ventral precentral gyrus and the inferior frontal lobe. The procedure was initiated by seeding the white matter of each hemisphere and tracking fibers from those seed points using a deterministic streamlines tracking algorithm (43–45) with a 4th-order Runge-Kutta path integration method (46) and 1-mm fixed-step size. A continuous tensor field was estimated using trilinear interpolation of the tensor elements. Starting from the initial seed point, fibers were traced in both directions along the principal diffusion axis. Fibers were estimated separately for each hemisphere. Path tracing proceeded until the FA fell to <0.15 or until the angle between the current and previous path segments exceeded 30°. Finally, only fibers with endpoints in the inferior parietal and inferior frontal cortices were selected.

Frontoparietal fibers were selected in each hemisphere using the following procedure. First, fibers longer than 250 mm and/or that crossed the midsagittal plane were removed. Fibers that did not cross AC-PC coordinate y = −42 (location of the central sulcus in the subject whose central sulcus was the most posterior) were removed, because we were interested in fibers that extend from posterior to anterior brain regions. Second, fibers were limited to those that passed through a manually defined box-shaped region covering a large portion of the parietal lobe (Fig. 1A). The box-shaped region extended from the lateral edge of the brain to the most lateral point of the parietooccipital sulcus, from the central sulcus to the most superior point of the parietooccipital sulcus, and from beneath the superior longitudinal fasciculus to the top of the brain. Third and finally, the aSLF was identified (Fig. 1B, orange) as those fibers that meet the following criteria: (i) fibers cross the central sulcus, (ii) fibers' posterior endpoints are on or lateral to the IPS and above the ventral border of the corpus callosum, and (iii) fibers do not extend below the axial plane that runs through the junction of the parietooccipital and calcarine sulci. For each hemisphere this resulted in a tract whose endpoints were in the inferior parietal lobule and the inferior frontal/precentral gyri (Fig. 1C). The researcher also performed minimal manual cleaning to eliminate looping fibers or fibers that were obviously not part of the tract of interest.

Post hoc exploration showed that the aSLF included a few fibers terminating in superior parietal lobe. These were excluded.

We limited the aSLF analysis to a 7-mm-long segment in the tightly bundled portion of the tract in the core of the white matter (Fig. 1B, blue). Because bundles of axons separate as they approach cortex, diffusion measurements toward the ends of the tracts are less reliable and reflect the intersection of members of many tracts rather than just the bundle of interest; they are also more susceptible to partial-voluming with gray matter. Clipping the ends off the tract of interest eliminates these hard-to-measure portions. We clipped at two coronal planes: anteriorly at each subject's central sulcus, as identified in an axial slice at the most dorsal part of the cingulate sulcus; and posteriorly at the coronal plane located 7 mm posterior to the anterior plane. The central sulcus creates an anatomical bottleneck for fibers in the aSLF as they travel to posterior cortex; it defines a location where frontal fibers converge into a tight bundle. Thus, clipping fibers within these borders limited the statistical analysis to those voxels that are fully within the tract of interest. Only the voxels in the clipped segment of the tract were used in the statistical analysis. See Fig. S2 for examples of the clipped ROIs from typical individuals, shown in axial plane images.

We successfully identified the right hemisphere aSLF in 28 of 28 subjects and the left aSLF in 27 of 28 subjects.

We identified the left arcuate fasciculus using the following procedure. The first step was the same as step 1 for frontoparietal fibers. Second, fibers terminating in the left inferior frontal lobe were selected. Third, the subset of the selected fibers that followed an arc around the Sylvian fissure was labeled as the arcuate fasciculus. Finally, fibers that turned ventrally toward the external/extreme capsule were excluded.

FA measurements were limited to a 7-mm segment defined by the coronal planes used in the aSLF analysis. This ROI was adjacent to and slightly overlapping the aSLF ROI. We successfully identified the left arcuate fasciculus in 23 of 28 subjects.

For each fiber node in each ROI, FA was calculated by the three eigenvalues that define each tensor (47, 48). Mean FA across nodes was computed for each ROI in each subject. The FA is the normalized SD of the three eigenvalues and indicates the degree to which diffusion is anisotropic.