The shape of a long leaf

Abstract

Long leaves in terrestrial plants and their submarine counterparts, algal blades, have a typical, saddle-like midsurface and rippled edges. To understand the origin of these morphologies, we dissect leaves and differentially stretch foam ribbons to show that these shapes arise from a simple cause, the elastic relaxation via bending that follows either differential growth (in leaves) or differential stretching past the yield point (in ribbons). We quantify these different modalities in terms of a mathematical model for the shape of an initially flat elastic sheet with lateral gradients in longitudinal growth. By using a combination of scaling concepts, stability analysis, and numerical simulations, we map out the shape space for these growing ribbons and find that as the relative growth strain is increased, a long flat lamina deforms to a saddle shape and/or develops undulations that may lead to strongly localized ripples as the growth strain is localized to the edge of the leaf. Our theory delineates the geometric and growth control parameters that determine the shape space of finite laminae and thus allows for a comparative study of elongated leaf morphology.

Laminae, or leaf-like structures, are thin, i.e., they have one dimension much smaller than the other two. They arise in biology in a variety of situations, ranging from the gracefully undulating submarine avascular algal blades (1) to the saddle-shaped, coiled or edge-rippled leaves of many terrestrial plants (2). The variety of their planforms and three-dimensional shapes reflects both their growth history and their mechanical properties and poses many physico–chemical questions that may be broadly classified into two kinds: (i) How does inhomogeneous growth at the molecular and cellular level lead to the observed complex shapes at the mesoscopic/macroscopic level? and (ii) how does the resulting mesoscopic shape influence the underlying molecular growth processes? At the molecular level, mutants responsible for differential cell proliferation (3) lead to a range of leaf shapes. At the macroscopic level, stresses induced by external loads lead to phenotypic plasticity in algal blades that switch between long, narrow, blade-like shapes in rapid flow to broader undulating shapes in slow flow (1). Understanding the origin of these morphological variants requires a mathematical theory that accounts for the process by which shape is generated by inhomogeneous growth in a tissue. Recent work has focused on some of these questions by highlighting the self-similar structures that form near the edge because of variations in a prescribed intrinsic metric of a surface (4, 5), and also on the case of a circular disk with edge-localized growth (6–8), but does not consider the subtle role of the boundary conditions at the free edge, the effect of the finite width of a leaf, or the phase space of different shapes that quantify the diversity in leaf morphology.

Motivated by our experimental observations of long leaves and artificial mimics thereof, here we address the question of the morphology of a long leaf or lamina of finite dimensions (length 2L, width 2W, thickness H, with H ≪ W < L). In particular, we pose mathematically a nonlinear boundary-value problem that accounts for the coupling of growth to the shape of a lamina. We analyze the resulting equations by using a combination of scaling concepts, asymptotics, and stability analysis to deduce the various morphologies that arise and show that the finite width of a long leaf leads to a qualitatively new class of shapes, such as saddles and rippled surfaces. We corroborate these by using numerical simulations to construct a simple phase diagram for the classification of the long leaf morphology.

Observations and Experiments

Shape of a Plantain Lily Leaf.

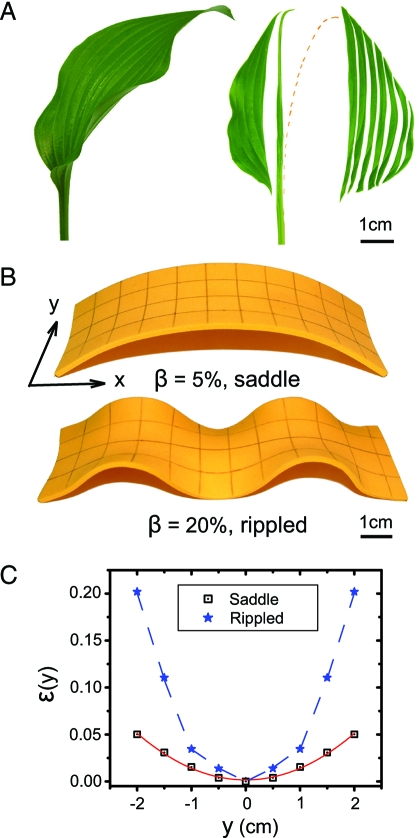
In Fig. 1 A, we show a typical long leaf of the plantain lily Hosta lancifolia. We see that the midvein curvature is largest near the distal end and monotonically decreases towards the base, whereas the lamina attached to the midvein is bent transversely so that the leaf is shaped roughly like a saddle, with negative Gaussian curvature. However, the edges of the leaf show a localized undulatory rippling pattern superposed on the global saddle-shape that is most prominent where the lamina is the widest. This morphology is relatively common in leaves and petals of vascular and avascular plants that grow in air and water, i.e., it is relatively independent of the effects of gravity. To focus on the relative role of inhomogeneous growth and the intrinsic elastic nature of the thin leaf, we cut the lamina into thin strips parallel to the midvein. We see that the relatively stiff midvein unbends from its naturally curved state (when the lamina is attached to it) to a straight state, except near its tip, whereas the relaxed length of the strips after they have straightened is different from that when they are part of the whole leaf. The strips further from the midvein extend more, i.e., the nonuniform distribution of growth-induced strain is such that it generates compressive stresses along the leaf edges, which can lead to buckling instabilities. These observations are consistent with prior measurements in vascular and avascular blades (1, 2), which show similar trends.

Fig. 1.

Experiments and observations of long leaf and ribbon morphology. (A) Shape of a plantain lily Hosta lancifolia leaf showing the saddle-like shape of the midsurface and the rippled edges. Dissection along the midrib leads to a relief of the incompatible strain induced by differential longitudinal growth and causes the midrib to straighten, except near the tip, consistent with the notion that the shape is a result of elastic interactions of a growing plate. The dashed red line is the original position of the midrib. (B) A foam ribbon that is stretched beyond the elastic limit relaxes into a saddle shape when the edge strain is β ∼ 5%, but relaxes into a rippled shape when the edge strain is β ∼ 20%. (C) The observed lateral strain ɛ(y) is approximately parabolic for the saddle-shaped ribbon but is localized more strongly to the edge for the rippled ribbon.

Shape of a Stretched Ribbon.

To mimic growth differentially in a thin lamina, we stretch a naturally flat thin foam ribbon (2 mm × 4 cm × 11 cm) inhomogeneously past its elastic limit and then unload it. The inhomogeneous residual plastic strains that remain cause the sheet to relax to a bent state. Moderate stretching strains (∼5%) lead to a saddle-like shape, and large stretching strains (∼20 %) lead to ripples along its edge, shown in Fig. 1 B, along with the lateral strain distributions shown in Fig. 1 C. This gradient in plastic strain is introduced easily by pulling the edges of the foam with fingers and it leads to a plastic strain that peaks along the edge and decreases toward the midline. We see that the effect of the inhomogeneous residual strain is equivalent to that of inhomogeneous, growth-induced strain*.

Analogous phenomena arise elsewhere and perhaps afford easier ways to understand the basic mechanism of shaping a lamina. For example, when knitting or crocheting a scarf, if the number of stitches or knots per unit length is increased as one moves away from the center line, the scarf first forms a saddle shape because such a shape easily accommodates the small excess length of the edges relative to the middle. Eventually, the edge length becomes so large that the edge itself starts to ripple. A similar phenomenon is seen in potato chips made by frying circular disks of soft, wet potatoes; the edges lose water and dry out first, after which their perimeter remains roughly constant. Additional drying of the interior causes the disk to shrink radially and thus leads to the potato chip to form a saddle shape with crinkled edges. In all these varied phenomena, it is the in-plane differential strain that results in the observed complex undulatory morphologies.

Theory of a Growing Blade

Generalized Föppl–von Kármán Equations.

To understand the observations and experiments described in the previous section, we consider a naturally flat, stress-free, thin, isotropic, elastic plate of thickness H, width 2W, and length 2L (H ≪ W < L) lying in the xy plane (x along the length and the normal z in the thickness direction). When such a plate grows inhomogeneously, different parts of it are strained relative to one another. To quantify this differential strain, we consider the deformation map that takes a point on the center–surface of the flat plate with coordinates (x,y,0) to its deformed state (x + u _x(x,y),y + u _y(x,y),ζ(x,y)). Here, (u _x(x,y),u _y(x,y)) is the in-plane displacement field and ζ(x,y) is the out-of-plane displacement. Then any point in the plate (x,y,z) will then be approximately mapped to (x + u _x(x,y) + zζ_,x,y + u _y(x,y) + zζ_,y,z + ζ(x,y))†. Here and elsewhere A _,x = ∂A/∂x. Then the in-plane strain tensor associated with this deformation field is given by ${\epsilon }_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})+\frac{1}{2}{\zeta }_{,i}{\zeta }_{,j}$, where i,j = x,y, and we have kept only the leading order terms in the gradients of the in-plane and out-of-plane displacement fields‡. The out-of-plane deformations are characterized by the curvature tensor, which in its linearized form, reads as κ_ij = ζ_,ij. The scale separation induced by the small thickness of the plate allows for a linear decomposition of the strain and curvature tensors to the sum of an elastic and a growth component. Then ɛ_ij = ɛ_ij ^e + ɛ_ij ^g − zκ_ij ^g, where ɛ_ij ^e(x,y) is the elastic strain tensor and ɛ_ij ^g(x,y) is the in-plane growth strain tensor, and similarly, κ_ij = ζ_,ij = ζ_,ij ^e + κ_ij ^g with κ_ij ^g the growth curvature tensor.

Assuming that the thin plate may be described as a linearly elastic material with Young's modulus E, Poisson's ratio ν, it has a 2D Young's modulus S = EH and bending stiffness B = EH ³/12(1 − ν²). Then the balance of forces in the plane and out of the plane for the thin plate lead to a generalized form of the Föppl–von Kármán plate theory (9) given by

where the operators ∇⁴ A = A _,xxxx + A _,yyyy + 2A _,xxyy and [A,B] = A _,xx B _,yy + A _,yy B _,xx − 2A _,xy B _,xy. Φ is the Airy function that defines the in-plane force per length according to N _x = Φ_,yy, N _y = Φ_,xx and N _xy = −Φ_,xy. Here Eq. 1 is the strain (in)compatibility relation, whose right side that has two components: (i) metric incompatibility due to the growth induced by Gaussian curvature ${\kappa }_G=\frac{1}{2}[\zeta ,\zeta ]={\zeta }_{,xx}{\zeta }_{,yy}-{\zeta }_{,xy}^2$, and (ii) metric incompatibility due to in-plane growth

Eq. 2 describes the balance of forces perpendicular to the sheet. The left side is the pressure induced by plate bending, whereas the first term on the right [ζ,Φ] = N _xκ_xx + N _yκ_yy + 2N _xyκ_xy is just a generalized Laplace law due to the in-plane forces and the curvature, and the second term on the right is the pressure induced by variations in the growth curvature tensor,

In general, the resulting strains (and stresses) feed back on the growth processes eventually shutting them down, although we do not consider this process here.

To complete the formulation of the problem, we need to specify the form of the growth strain tensor ɛ_ij ^g and the growth curvature tensor κ_ij ^g and some boundary conditions. Although a variety of forms of the growth tensors may be biologically plausible, here we restrict ourselves to a consideration of a single nonzero component of the growth tensor so that ɛ_xx ^g = ɛ_g(y), consistent with our own observations and experiments as well as earlier experiments (1, 3) on long, leafy blades with W < L. This leads to excess longitudinal growth along the ribbon that varies in magnitude transversely. We choose the power law form ${\varepsilon }_g(y)=\beta {(\frac{y}{W})}^n$ for all calculations mainly for convenience§, with β characterizing the maximum growth strain and n the gradient (or exponent) of differential growth.

For the case of a growing blade with straight edges parametrized by Γ ≡ (x = ±L,y = ±W), the condition that the boundaries are free of torques and forces implies that (9)

where (a,b) are the unit normal and tangent to the edge of the blade. We note that the boundary value problem in Eqs. 1–5 can be derived from a variational principle (SI Appendix), and also describes the thermoelastic deformations of a thin plate (9), with thermal strains being replaced by growth strains.

Dimensionless Equations for the Growth of a Long Lamina.

Motivated by our experiments and observations of laminae with transversely varying growth in the longitudinal direction, we consider the simplified setting for the generalized Eqs. 1 and 2 with λ_g = ɛ_xx,yy ^g ≡ ɛ_g,yy and Ω_g = 0 for an infinitely long lamina, i.e., L →∞. Further defining the dimensionless variables x̄=x/H; ȳ=y/H,ζ̄=ζ/H, $\overline{\Phi }=\Phi /E{H}^3,\overline{w}=W/H$, Eqs. 1 and 2 can be rewritten, on dropping the bars, as

where C = 12(1 − ν²), with the Poisson ratio ν = 0.3, subject to the boundary conditions of vanishing force and torque at the free edges, i.e.,

Analysis

Our experiments on foam ribbons show two characteristic buckling modes. For low values of the edge-strain, we find a global deformation associated with a long-wavelength saddle shape, whereas for larger values of the edge-strain, we find a short-wavelength edge rippled mode while the ribbon itself is flat on average. To explore the conditions when these different modes arise, we use a combination of scaling theory and stability and asymptotic analysis of various boundary value problems.

Scaling.

When the ribbon is doubly bent into a saddle shape with positive transverse curvature κ_y and negative longitudinal curvature −κ_x (Fig. 2 A), the contour length of the edge is longer than that of the center line, leading to a partial relaxation of the excess marginal growth strain by out-of-plane deformation. Assuming that the edge deflection δ ≪ w, the edge growth strain β ∼δκ_x whereas the lateral curvature κ_y ∼δ/w ². Interestingly, this implies that the Gaussian curvature κ_xκ_y ∼β/w ² is independent of δ in the neighborhood of the onset of buckling, suggestive of the presence of a soft mode of deformation. The dimensionless bending energy per length u _b = U _b/EWH ∼ β²/δ² + δ²/w ⁴, whereas the dimensionless stretching energy per length due to in-plane growth u _s ^g = U _s ^g/EWH ∼ β². At the onset of buckling, the dimensionless deflection δ ≃ 1, and u _s ^g ∼ u _b so that the critical strain for buckling, into a saddle shape β*∼1/w ², and is dependent on the dimensionless width of the ribbon due to growth strain gradients in that direction. A similar saddle shape is observed in a disc that grows anisotropically (7).

Fig. 2.

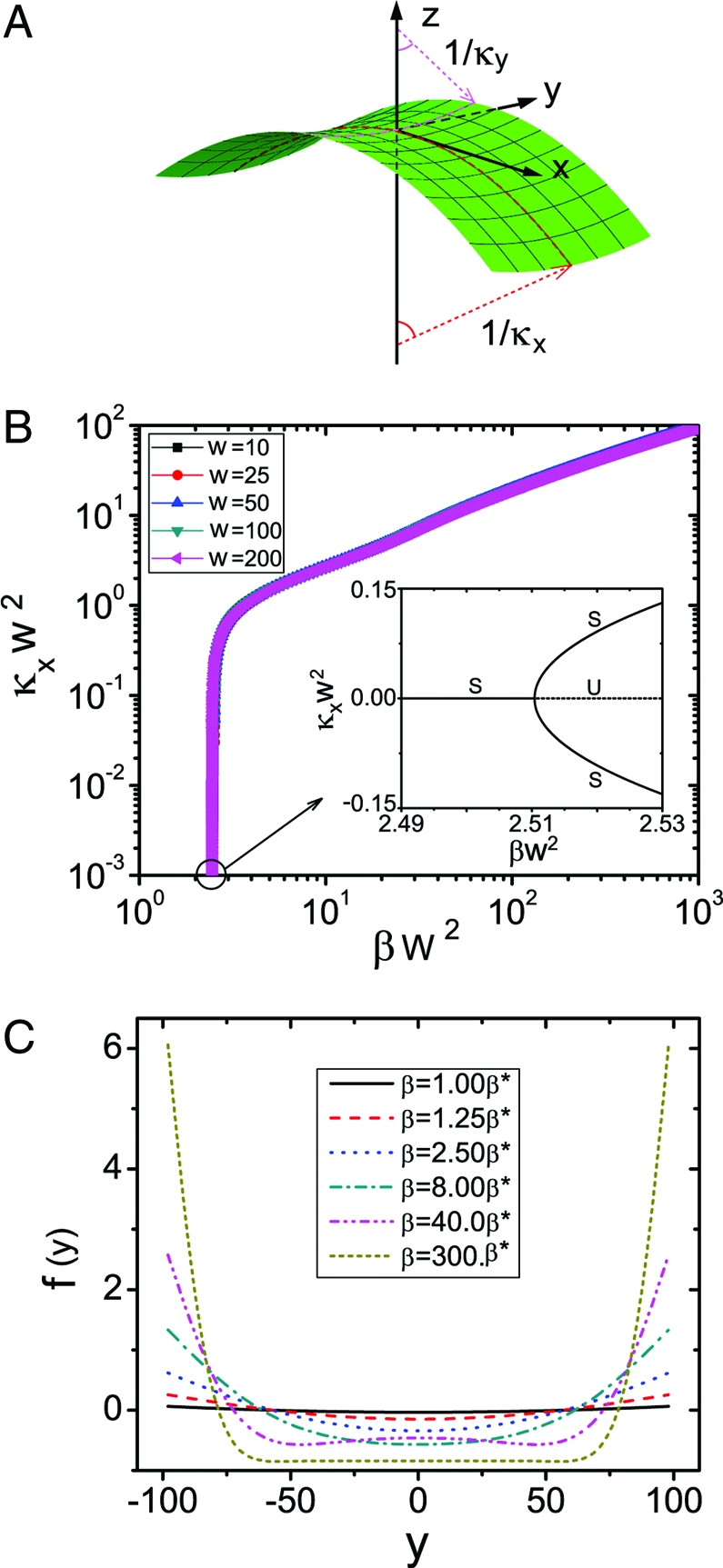
Characterization of saddle-shaped laminae. (A) A saddle shaped lamina corresponding to a scaled width w = 10, growth exponent n = 10, scaled maximum growth strain βw ² = 6.5 and κ_x w ² = 1.9. (B) The postbuckling behavior shows the scaled curvature κ_x w ² vs. βw ² on a log-log plot; the results for different w collapse onto a single curve. The Inset shows that the onset of buckling occurs via a supercritical pitchfork bifurcation, with κ_x w ∼(β − β*)^1/2, with β*w ² ≃ 2.51 for all values of the growth exponent n; only the positive branch is meaningful here. (Notation: S-stable, U-unstable.) (C) Cross-sectional profile f(y) for different values of the maximum growth strain β, when the critical growth strain β*w ² = 2.51 and w = 100.

Alternately, the sheet can buckle into a set of periodic ripples of wavelength Λ, and dimensionless wavenumber k = 2πH/Λ. Because these ripples are generated by differential strains that are largest along the lateral edges of the sheet, it is useful to consider the persistence of a pinch of amplitude δ and wavelength 1/k given by l _p ∼δ^1/2/k, (10, 11). Approximate inextensibility implies that β ∼ k ²δ², so that l _p ∼ β^1/4/k ^3/2. Since the wavenumber k is itself a function of β, this relation serves as a self-consistency check as we will see later. Depending on the ratio of l _p/w, we expect three types of buckling modes shown in Fig. 3 A.

Fig. 3.

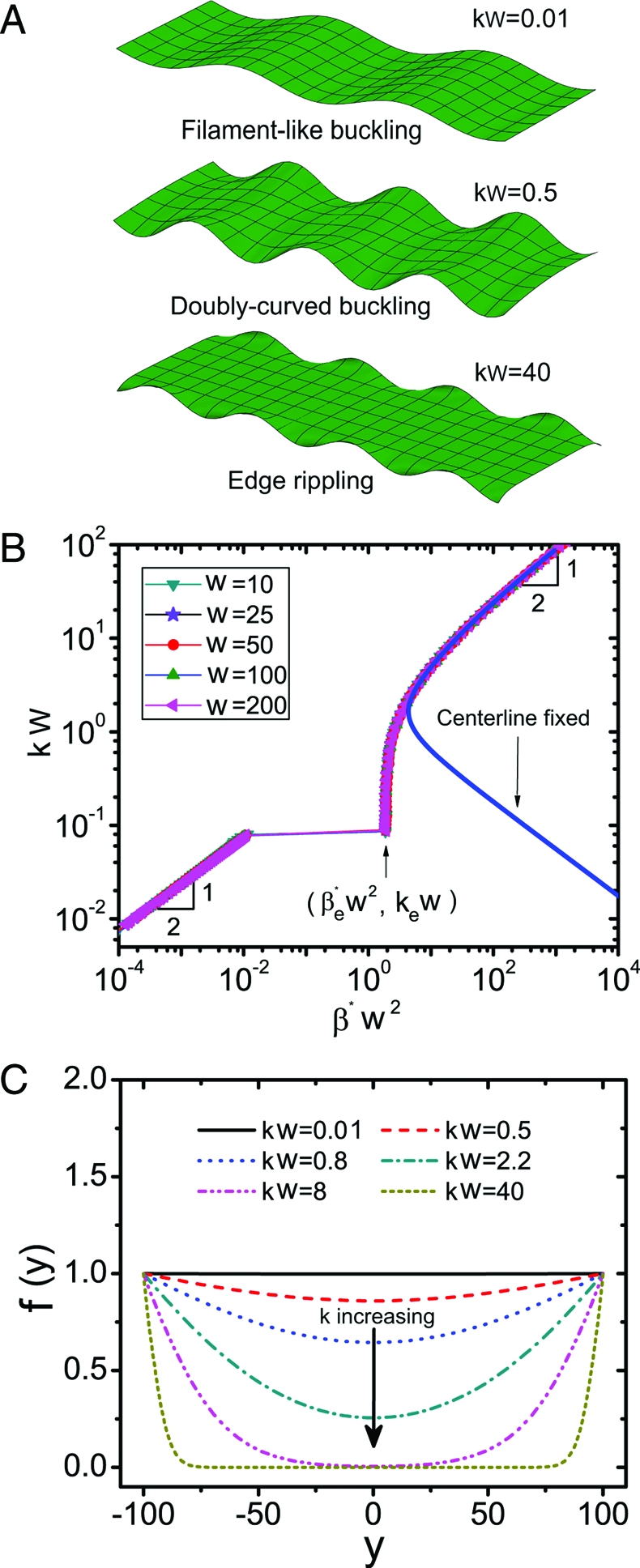
Characterization of rippled laminae. (A) Three types of periodic buckling modes arise depending on the persistence of an edge pinch, or equivalently the ratio of the wavelength of the mode 1/k to the width w. Filament-like buckling for kw ≪ 1, doubly-curved buckling for kw ∼1, and edge rippling for kw ≫ 1. (B) Rescaled critical strain wavenumber kw vs. β*w ², showing three distinct regimes associated with the above. The solid line corresponds to the case when the center-line of the ribbon is clamped. (C) The cross-sectional profile f(y) for different scaled wavenumbers, when w = 100, with the growth law ∈_g = β(y/w)¹⁰ shows how the periodic ripples localize to the edge as kw increases.

1. Filament-like buckling.

l _p ≫ w: The scaled longitudinal bending energy u _b ∼ k ⁴ is comparable with the stretching energy induced by growth u _s ^g ∼ β² and yields a critical strain β* ∼ k ². Then the pinch persistence length l _p ∼ β*^1/4/k ^3/2 ∼ 1/k ≫ w, i.e., there is essentially no variation laterally. The fact that β* is independent of the width and vanishes as k → 0 indicates that an infinitesimal edge-growth strain yields a corresponding critical wavelength that diverges. Though counterintuitive, this result is consistent with that for classical Euler-buckling of a strut where the dimensional buckling load F ∼B/L ² vanishes as column length L → ∞.

2. Doubly-curved buckling.

l _p ∼ w: The bending energy is the same of the saddle-like configuration, i.e., u _b ∼ (β² + 1/w ⁴). Comparing this with the stretching energy induced by growth, u _s ^g ∼ β² yields a critical strain β* ∼ 1/w ², now dependent on the width of the ribbon. The ribbon is now doubly curved with negative Gaussian curvature, and l _p ∼ w, i.e., the ripples on either edge interact.

3. Edge rippling.

l _p ≪ w: Comparing the dimensionless bending energy u _b ∼ l _p k ⁴ with the dimensionless stretching energy u _s ^g ∼ l _pβ² yields β* ∼ k ². Again, β* is not dependent on the width, whereas l _p ∼ 1/k ≪ w, i.e., the ripples are localized to the edge.

Stability of a Strained Ribbon.

To go beyond the scaling analysis above, we now solve the dimensionless Eqs. 6–8.

Saddle buckling.

When the characteristic in-plane growth strain reaches a critical value β*, the flat ribbon undergoes a transition to a saddle-shaped catenoid (Fig. 2). To approximate the shape, here we use a shallow-shell ansatz (Fig. 2 A), valid when |κ_x f(y)| ≪ 1, which reads

where ${\int }_{-w}^{w}f(y)dy=0$, and the longitudinal curvature κ_x > 0 is assumed to be constant.

Global in-plane force equilibrium in the longitudinal (x) direction requires that ${\int }_{-w}^w{N}_x={\int }_{-w}^w{\Phi }_{,yy}dy=0$, so that substituting the ansatz Eq. 9 into Eq. 6 and integrating twice yields Φ_,yy = −βγ_g + κ_x f, where ${\gamma }_g=\frac{{\varepsilon }_g-{\overline{\varepsilon }}_g}{\beta }$, and the average growth strain ${\overline{\varepsilon }}_g=\frac{1}{2w}{\int }_{-w}^w{\varepsilon }_g(y)dy=\frac{\beta }{n+1}$ for the power law form ${\varepsilon }_g=\beta {(\frac{y}{w})}^n$. Substituting the result into Eqs. 7 and 8 yields the governing boundary value problem for normal force balance at a cross-section

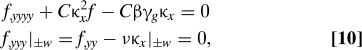which is analogous to the equation for a beam on an elastic foundation of stiffness Cκ_x ² subject to a distributed load Cβγ_gκ_x.

The condition of global torque balance in the longitudinal (x) direction requires that

where the first term in brackets is the dimensionless torque due to ribbon curvature, and the second term CfΦ_,yy is the dimensionless torque due to in-plane forces. To solve the boundary value problem given by Eqs. 10–11, we use the asymptotic expansion f(y;κ_x) = κ_x f ₁(y) + κ_x ³ f ₃(y) + …. to determine the critical growth strain β* at the onset of buckling, which yields (SI Appendix)

a result consistent with our scaling analysis. The instability arises via a supercritical pitchfork bifurcation, with κ_x ∼ (β − β*)^1/2 (Fig. 2 B Inset; see also SI Appendix). To further probe the shape beyond the onset of buckling, we look for a solution to Eq. 10 of the form f(y) = f _p(y) + f _h(y), where f _h(y) and f _p(y) are the homogeneous and particular solution of Eq. 10, combined with Eq. 11 to determine the relation between β and κ_x in the postbuckling regime (SI Appendix). In Fig. 2 B, we show the scaled longitudinal curvature κ_x w ² as a function of the scaled maximum growth strain βw ² for different scaled widths w and ${\varepsilon }_g(y)=\beta {(\frac{y}{w})}^{10}$. The collapse of all curves for various w onto a single master curve is consistent with the scaling law β* ≃ 2.51/w ², that follows from the asymptotic result Eq. 12. In Fig. 2 B, we also see the existence of a rapid increase in κ_x w ² ∈ [0.0,0.1] for βw ² ∈ [2.51,2.52], i.e., a small increase in the maximum growth strain β leads to a large change in the longitudinal curvature κ_x. This strongly nonlinear response is associated with a soft mode of deformation for the ribbon of nearly constant Gaussian curvature, i.e., κ_xκ_y ∼ β/w ², wherein the growth-induced stretching strain is accommodated by changing the mean curvature κ_x + κ_y ≃ β/δ + δ/w ².

In Fig. 2 C we show the cross-sectional profile of the ribbon f(y) for various values of the maximum growth strain β (we drop the dependence on w because there is no dependence on this parameter). At the onset of buckling, f(y) is approximately parabolic, as in our foam ribbon experiments (Fig. 1 B), so that it follows from Eq. 10 that Cκ_x ² f − Cβγ_gκ_x ≃ 0, i.e., f(w) ≃ β/κ_x. Then the transverse curvature κ_y ≃ β/κ_x w ², and finally κ_xκ_y ≃ β/w ², consistent with our scaling analysis. As the growth strain β is increased further, the cross-sectional of the ribbon flattens in the center. We examine the case of n = 2 for simplicity (see SI Appendix). As κ_x increases, the particular solution f _p of Eq. 10 becomes negligible compared with the homogeneous solution, with the result that f(y) ∼ e ^−ηz(cosηz − sinηz), where z = w − |y|, and the boundary layer width ξ_BL = 1/η = 0.78/κ_x ^1/2 independent of the growth gradient exponent n, i.e., the lateral deflection near the edges decays rapidly away from it. Indeed, as ξ_BL ≃ w or κ_x w ² ≃ 0.6, the ribbon shows the appearance of a boundary layer and when βw ² ≃ 80 (β = 40β* in Fig. 2 C), the lateral shape of the ribbon f(y) develops a pair of secondary minima. Later, when βw ² ≃ 750 (β = 300β* in Fig. 2 C), the ribbon is nearly cylindrical in the interior with a pair of strongly localized boundary layers along its lateral edges.

Periodic Rippling.

We now turn to the case of periodic rippling, assuming that the vertical deflection is of the form

Here k is the dimensionless wavenumber, f(y) is the cross-sectional profile of the surface, and we note that the sheet is on average flat, unlike for the saddle-shape. Assuming that the in-plane compatibility of Eq. 6 is satisfied, on substituting in Eq. 13 into Eq. 7 and using the boundary conditions in Eq. 5, we get the eigenvalue problem

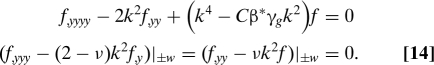We solve the boundary value problem given by Eq. 14 numerically by using the boundary value problem solver bvp4c in Matlab, with the scaled width w ∈ [10,200] to determine the relation between the critical maximum growth strain β* and the wavenumber of the instability k. In Fig. 3 B, we show that the scaled wavenumber kw as a function of the scaled critical growth strain β*w ² falls onto a single master curve, with three prominent features, a power-law scaling regime for kw ≪ 1, a plateau in the neighborhood of k _e w ≃ 0.09, followed by a jump in the neighborhood of β_e * w ² ≃ 1.9 and finally another power-law scaling regime when kw ≫ 1. These transitions are intimately related to the profile of the ribbon in cross-section. Indeed when k ≤ k _e ≪ 1/w, we see that the cross-sectional profile is almost flat (Top frame in Fig. 3 A corresponds to kw = 0.01), i.e., the ribbon exhibits periodic filament-like buckling of a 1D filament. Indeed, this follows directly from Eq. 14; when kw ≪ 1, f _,yyyy,f _,yy ≪ 1 so that β* ∼ k ² which vanishes when k → 0, consistent with our scaling in the limit when the persistence length of an edge-pinch l _p ≫ w (see SI Appendix for an asymptotic analysis of this mode). In the neighborhood of k _e w ≃ 0.09, there is a rapid change in β*w ² ∈ (0.01, 1.9), indicative of a sharp transition between two different buckling modes because of the large elastic energy required to trigger the doubly curved periodic ripples seen when k ≥ k _e. Then the ribbon is doubly curved (Middle frame in Fig. 3a corresponds to kw = 0.5), and there is little variation in the maximum growth strain with β*w ² ∈ (1.9,2.1), whereas the wavenumber varies enormously with kw ∈ (0.09,0.6), suggesting the ease of transformation of the shape of the periodic ripples in this regime, when l _p ∼w. Finally, when kw ≫ 1, the ribbon is strongly deformed in the neighborhood of the lateral edges (Bottom frame in Fig. 3 A corresponds to kw = 40). In this scaling regime, β* ∼ k ² asymptotically and the persistence length of the edge-pinch l _p ≪ w, so that the edges are essentially independent of each other.

To probe the role of the boundary conditions in Eq. 14 in characterizing these different periodic modes that couple the deformations along the ribbon to those perpendicular to it, we consider the alternative conditions f|₀ = f _,y|₀ = 0 along the axis of symmetry of the ribbon. Then the only possible mode is that of edge-rippling, shown as the solid blue curve in Fig. 3 B, which coincides with our master curve when kw > 3.0, i.e., the ripples are localized to the lateral edges. Earlier researchers (4, 5) have studied the self-similar edge ripples on the boundary of a semi infinite plate but missed the qualitatively different global saddle-like, filament-like buckling and doubly curved modes associated with the introduction of a finite width for the ribbon. Indeed, when we clamp the center line of the sheet, we find that when kw < 3.0 or l _p > w there is a rapid increase in the scaled critical growth strain β*, consistent with the elimination of the soft saddle-shaped modes.

Numerical Simulations

To corroborate and extend our scaling and stability analysis, we implement the inhomogeneous growth of a lamina in a discrete numerical model of a finite ribbon of width 2W, length L = 6W and thickness H ≪ W. This is derived by tiling the ribbon using equilateral-triangular elements (12) (dimensionless width w = W/H, length l = L/H and wavenumber $k=\frac{2\pi }{\Lambda }H$). Then the elastic energy is the sum of the stretching energy $F_s=\frac{\sqrt{3}S}{4}{\Sigma }_{ij}{(r_{ij}-a_0)}^2$, where r _ij is the current spring length and a ₀ is the rest spring length and the bending energy $F_b=\frac{B}{\sqrt{3}}{\Sigma }_{\alpha \beta }{({\overrightarrow{n}}_{\alpha }-{\overrightarrow{n}}_{\beta })}^2$, where ${\overrightarrow{n}}_{\alpha }$ and ${\overrightarrow{n}}_{\beta }$ are the unit normal vectors of the two facets (see SI Appendix). The growth strain ɛ_g is modeled by changing the rest length of the spring a ₀ to a ₀(1 + ɛ_g(y)), where ɛ_g(y) = β(y/W)ⁿ with n = 10 and a damped molecular dynamics method (13) is used to minimize the system energy.

In Fig. 4 we show the resulting stability diagram indicating the regimes of existence of the flat, saddle, and rippled phases as a function of the characteristic growth strain β and the scaled width w. The stability boundary between the flat and saddle phase as well as that between the saddle and rippled phase both show a power-law scaling β*∼1/w ², consistent with our scaling and analytical results. To understand why the saddle-shaped morphology appears first as the growth strain β is increased, we note that the characteristic critical strain for the filament-buckling mode β*∼k ² is smaller than that for the saddle-buckling mode β*∼1/w ² only when the wave number k is sufficiently small. Here, the finite length of our numerical ribbon leads to a finite-size effect or equivalently a cutoff as seen in our numerical simulations. At the onset of doubly curved buckling shown in Fig. 3 B when k _e w ≃ 0.09, so that the minimum ribbon length to width ration required $l/w\ge \frac{2\pi }{0.09}\simeq 70$ to accommodate one wavelength. Saddle buckling shown in Fig. 2 B will arise when the growth strain β*w ² = 2.51, which corresponds to a wavelength kw ≃ 0.9 in Fig. 3 B requiring a minimum $l/w=\frac{2\pi }{0.9}\simeq 7$ to accommodate one wavelength. In our simulations, l/w = 6, so that saddle buckling occurs first as shown in Fig. 4, consistent with our analysis above. As w increases, we expect the two lines to become indistinguishable, although there is a subtle mathematical issue of the order of limits as both w/l → 0, w → ∞. For large values of both the growth strain and the width of the blade, we see the appearance of a new shape that globally has positive Gaussian curvature and rippled edges. This is because the large localized extension of the edges puts the central region of the blade in tension that is then relieved by a spherical mode of deformation. This coupling between the localized edge modes and the global elliptical/hyperbolic modes might be similar to that seen in a variety of pattern-forming systems, including buckled elastic sheets (14), a topic to be explored elsewhere.

Fig. 4.

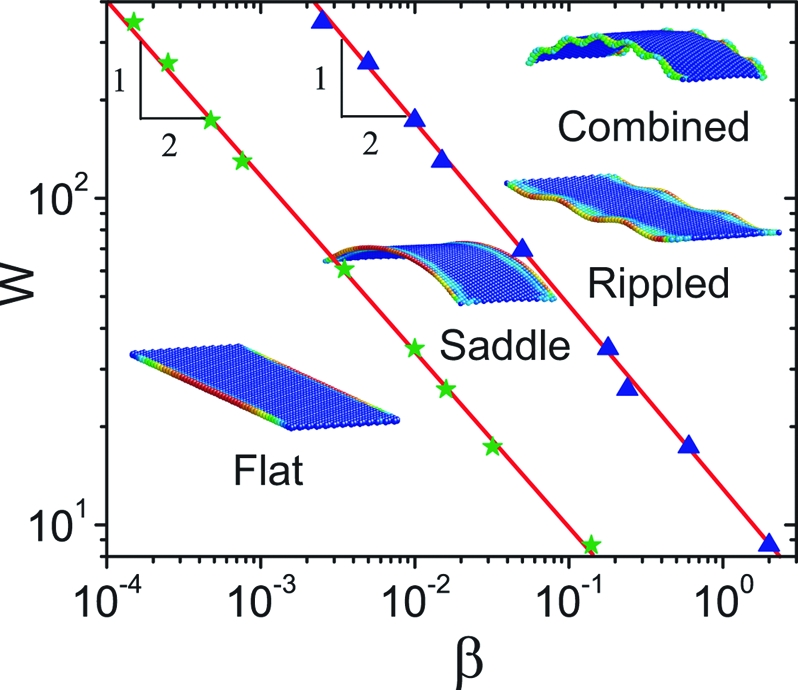
Numerical simulations yield a phase diagram for the different undulatory shapes of a long, growing ribbon as a function of the maximum edge growth strain β and the scaled width W. The boundaries that demarcate the different phases follow the scaling β* ∼ 1/w ², consistent with our scaling and analytic estimates (see Eq. 12 and SI Appendix). We use the power law ∈_g = β (y/w)¹⁰.

Discussion

In our study, we have addressed the origin of complex undulatory morphologies in artificial and natural laminae in terms of the gradients in the in-plane elastic strain. Our general mathematical theory for a growing lamina predicts a critical strain for the onset of buckling and is applicable to a variety of systems including inhomogeneous biological growth, thermal expansion, hydraulic swelling (6), plasticity (2) etc. In particular, for a leaf of finite width and length, we find a saddle-shaped lamina arises via a pitchfork bifurcation, whereas larger strains lead to localized ripples along the edges that can coexist with the saddle-shaped lamina. Our scaling, stability, and asymptotic analysis quantify the conditions under which these different morphologies exist, and our numerical simulations allow us to determine a shape-space diagram in terms of the dimensionless width of the lamina and the maximum lateral growth strain. In addition to laying out a minimal framework for the comparative morphology of long, undulating leaves, our study also maps out a strategy for the control of the shape of artificial laminae by using edge actuation rather than surface actuation.